Abstract
We present iCluster, a fast and efficient algorithm that clusters a set of images while co-registering them using a parameterized, nonlinear transformation model. The output is a small number of template images that represent different modes in a population. This is in contrast with traditional approaches that assume a single template to construct atlases. We validate and explore the algorithm in two experiments. First, we employ iCluster to partition a data set of 416 whole brain MR volumes of subjects aged 18-96 years into three sub-groups, which mainly correspond to age groups. The templates reveal significant structural differences across these age groups that confirm previous findings in aging research. In the second experiment, we run iCluster on a group of 30 patients with dementia and 30 age-matched healthy controls. The algorithm produced three modes that mainly corresponded to a sub-population of healthy controls, a sub-population of patients with dementia and a mixture group that contained both types. These results suggest that the algorithm can be used to discover sub-populations that correspond to interesting structural or functional “modes.”
1 Introduction
Historically, computational anatomy studies have mainly been hypothesis-driven, aiming to identify and characterize structural or functional differences between, for instance a group of patients with a disease of interest and control subjects. With the increasing availability of medical images, unsupervised algorithms offer the ability to probe the population and potentially discover sub-groups that may differ in unexpected ways. This paper proposes an efficient probabilistic clustering algorithm, called iCluster, for computing one or more templates that summarize a given population of images. The algorithm simultaneously co-registers all images using a nonlinear transformation model parameterized via B-splines [16]. Additionally, it computes a small number of template images that represent the modes of the population and assigns each image to a template. The templates are guaranteed to live in an affine-normalized space, i.e., they are spatially aligned with respect to an affine transformation model.
Using two experiments, we demonstrate that the modes of the population discovered by iCluster capture known structural differences and similarities. On a population of 416 brain MRI of subjects aged 18-96 years, the algorithm computed 3 unique templates that mainly comprised of young brains (mean age 31), older middle aged brains (mean age 69) and elderly brains (mean age 79). In another setting, we demonstrate that the modes discovered by the algorithm reflect the two groups of subjects (with mild dementia and healthy) in the population. These results suggest that iCluster can be used to probe a population of images to discover important structural or functional “modes.”
2 Background and Prior Work
In medical imaging, the term atlas usually refers to a (probabilistic) model of a population of images, with the parameters learned from a training data set [5,20]. In its simplest form, an atlas is a mean intensity image, which we call a template [2,4,15,21]. Yet, richer statistics, such as intensity variance or segmentation label counts, can also be included in the atlas model [8]. Atlases are used for various purposes including normalization of new subjects for structure and function localization, segmentation or parcellation of certain structures of interest and group analysis to identify pathology related changes or developmental trends.
Atlas construction requires a dense correspondence across subjects. Earlier techniques used a single image - either a standard template [4], or an arbitrary subject from the training data set [9] - to initially align the training subjects using a pairwise registration algorithm. Other techniques focused on determining the least biased template from the training set [12,14]. A single template approach faces substantial methodological challenges when presented with a heterogeneous population, such as patients and matched normal control subjects in clinical studies. To circumvent this, more recent approaches aim to co-register the group of images simultaneously without computing a group template [18,22]. These algorithms, however, do not compute the multiple modes of the population. A recent work [3] presented a method that automatically identified the modes of a population using the mean-shift algorithm. This approach solved pairwise registrations to compute each inter-image distance, which slowed down the algorithm substantially. Moreover, the multi-modality of the population was not modeled explicitly, making it difficult to extract a representation of the heterogeneous population. An alternative strategy is to use all training images as the atlas [10]. A new subject is registered with each training image and segmentation is based on a fusion of the manual labels in the training data. This approach is not suitable for anatomical variability studies, where a universal coordinate frame is necessary to identify and characterize group differences.
In this paper, we develop a probabilistic framework for joint registration of a set of images into a common coordinate frame, while clustering them into a small number of groups, each represented by a template image. Similar to [1], we employ a simple mixture of Gaussians model and a maximum likelihood framework which we solve using Generalized Expectation Maximization (GEM). Our algorithm can also be viewed as an extension of the approach of [19], which solves the registration problem as an initial, separate step. We implement iCluster using a 3D nonlinear transformation model parameterized via B-splines [16]. Our framework yields an efficient, fast, scalable and flexible algorithm that offers at least two advantages over traditional population analysis methods which are typically hypothesis driven and work with single templates. First, it removes the sensitivity of the co-registration and atlas coordinate frame to the selected target. Second, it provides a novel, unsupervised way to probe the population for different modes. Analyzing the discovered sub-populations and their representative templates promises to advance our understanding of dominant structural or functional changes due to pathology or development.
3 The Model and Algorithm
We assume that the input images are generated from a small number of templates . Thus, for each n ∈ {1, . . . , N}, there exists k ∈ {1, . . . , K} such that:
| (1) |
where is an admissible spatial warp, such as a parameterized nonlinear transformation, εn(x) is spatially independent, non-stationary Gaussian noise with zero mean and standard deviation σ(x). The unknown assignment between individual images and templates is of interest and defines a clustering of the images. To model the possibly unbalanced nature of cluster sizes, we define an unknown prior on the template frequencies, and denote this by {πk}.
We use θ = {{Tk}, {πk}, σ, {Φn}} to denote the pooled set of model parameters. Marginalizing over all possible template indices, we obtain the probability of observing a particular image:
| (2) |
where is the Gaussian density with mean μ and standard deviation σ(x). We formulate the problem of atlas construction as a maximum likelihood estimation:
| (3) |
where L(θ) denotes the log-likelihood. We use a Generalized Expectation Maximization (GEM) algorithm to solve Eq. (3). For a fixed θ0 value, using Jensen’s inequality we form a lower bound for L(θ):
| (4) |
where qk(In; θ0) = πkpk(In; θ0)/(Σk’ πk’pk’(In; θ0)) is the posterior probability that In was generated from Tk and c is a constant that does not depend on θ. Note that L(θ0) = Q(θ0; θ0). The GEM algorithm iteratively improves this lower bound. Let θ(i) be the guess of θ at the (i)’th iteration. Computing Q(θ; θ(i)) - or, equivalently - is the E-step. The M-step updates θ to increase Q(θ; θ(i)). In our formulation, we use a coordinate ascent strategy in the M-step and divide it into two sub-steps: (1) the T-step (“T” stands for template) where we compute the closed form expressions for the template parameters {{Tk}, {πk}, σ} that maximize Q; and (2) the R-step (“R” stands for registration) where we numerically solve for the transformation parameters {Φn}. The algorithm can be summarized as follows:
E-step
Given the model parameters from the i’th iteration, the algorithm updates the posterior cluster probabilities as:
| (5) |
and . These probabilities can be seen as “soft memberships,” where would indicate a “hard membership” in cluster k.
T-step
Given the posterior probability estimates and transformation parameters , the algorithm updates its estimates of the templates {Tk}, template priors {πk} and variance image σ2 for which we derive closed-form expressions:
| (6) |
| (7) |
R-step
Given the new template parameters and memberships the spatial transformations are updated as:
| (8) |
where is the “effective template” (i.e., target image in registration) for image In at iteration (i + 1). This is a weighted average of the current templates and the weights are membership probabilities. A single transformation Φn is estimated for each image, since the model assumes that an image is generated from a single template Tk. Current membership probabilities determine which template the image should be aligning with. We solve the non-convex optimization problem (8) using a gradient-descent optimizer, a B-spline transformation model on an 8 × 8 × 8 control point grid and a multi-resolution strategy. The registration of each image is done in parallel, since the optimization does not depend on the other images. The local convergence nature of gradient-descent guarantees that the lower bound on the log-likelihood is improved, not maximized, at each step; hence the name Generalized EM.
The above algorithm does not guarantee that the computed template images are in alignment. To introduce a notion of common coordinate frame, we use an initial affine normalization step that co-registers all the images using a single dynamic mean image and an affine transformation model. This step is one of the popular co-registration algorithms used in practice [12].
In group-wise registration, one needs to anchor the registration parameters to avoid global transformation drifts across subjects [18,22]. We extend this strategy to the multi-template setting by constraining each point to lie at the average location of corresponding points across the images in each cluster. To impose this constraint, we use the soft memberships :
| (9) |
Marginalizing Eq. (9) over k yields , which is the anchoring constraint used by group-wise registration methods [18,22]. We apply the constraint of Eq. (9) at each iteration by projecting all the subjects’ gradients of the registration objective function onto an appropriate space determined by the memberships of all subjects. This is an extension of subtracting the average gradient from the individual gradients, as proposed by [18].
Each iteration of the algorithm has a computational complexity and memory requirement of , where N is the number of input images, K is the number of templates and M is the number of voxels. We use multi-threading in ITK [11] to implement a parallelized version of iCluster. Similar to [22], we employ a stochastic sub-sampling strategy to speed up the algorithm. At each iteration, a random sample of less than 1% of the voxels is used to compute the soft memberships, templates, template priors, standard deviation image and to update transformation parameters.
4 Experiments
We used the OASIS data set [13] which consists of 416 pre-processed (skull stripped and gain-field corrected) brain MR images of subjects aged 18-96 years including individuals with early-stage Alzheimer’s disease (AD).
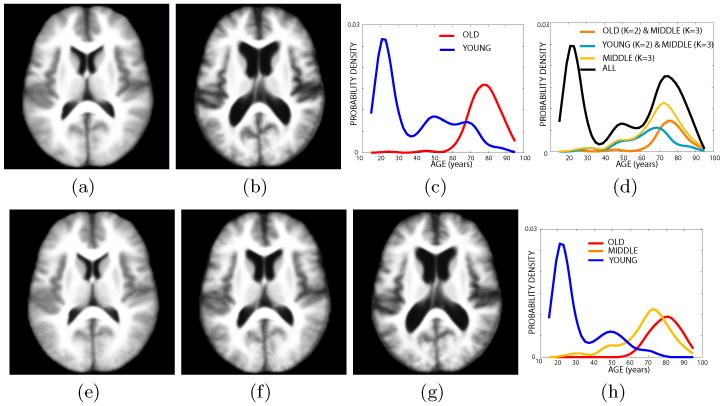
In the first experiment, we ran iCluster on the whole data set while varying the number of templates: K = 2-6. Each run took approximately 4-8 hours on a 16 processor PC with 128GB RAM. For K = 2, 3 the algorithm computed 2 and 3 unique, structurally different templates, respectively. These templates were robust: they were the same for random subsets of the data set of as little as 60 subjects. For larger values of K, however, the computed templates were not all unique, or corresponded to single outlier subjects, or were not robust to random sub-sampling of the data set. Fig. 1 shows the two and three robust templates computed with K = 2 and K = 3. The figure includes the age distributions estimated using Parzen windowing with a Gaussian kernel and a standard deviation of 4 years for each cluster identified by the algorithm (Fig. 1-c and 1-h).
Fig. 1.
Top row: Two templates in the OASIS data set: (a) young subjects, (b) older subjects; (c) the cluster-specific age distribution for K =2; (d) the age distribution that reveals the relationship between the ages of subjects in clusters identified for K=2 and for K=3. Bottom row: Three templates in the OASIS data set: (e) young subjects, (f) older middle-aged group and (g) elderly subjects; (h) the corresponding age distribution. See text for details.
Each template corresponds to a unique age group: for K = 2, we have a group of young subjects (mean age 39) and a group of elderly subjects (mean age 78); and for K = 3 we have young subjects (mean age 31), an older middle aged group (mean age 69) and elderly subjects (mean age 79). Fig. 1-d illustrates the intersection between the middle age distribution for K = 3 and the distributions for K = 2. This plot reveals that the middle aged group for K = 3 consists of two sub-populations: (1) a younger group of subjects that are in the young group for K = 2 and (2) an older age group in the elderly for K = 2. These results suggest that the dominant structural modes in this large population are mainly due to aging. However, analyzing the decomposition of the whole age distribution (shown in black in Fig. 1-d) indicates that iCluster does not simply find the three major age modes. Specifically, the small, middle peak around 50 years is robustly included with the younger population for both K = 2 and K = 3. Furthermore, with three modes, the algorithm identifies an older middle aged group that has a significant overlap with the elderly group. This could suggest that some brains “age faster than others.” Further analysis of the anatomical structures is needed to validate this.
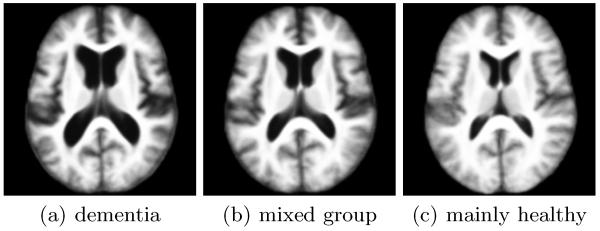
In a second experiment, we used a set of 60 subjects from the OASIS data set. Thirty of these were diagnosed with very mild to mild dementia and probable AD, while the other thirty individuals were age-matched controls with no sign of clinical dementia at the time of scanning. iCluster robustly identified three modes in this population. Template 1 (shown in Fig. 2-a) consists of 17 subjects, 14 of which have dementia. Template 3 (Fig. 2-c) consists of 17 subjects, 16 of which are healthy. Template 2 (Fig. 2-b), on the other hand, is a mixture group that contains 15 patients and 11 healthy subjects. For K = 2 (templates not shown), there was a significant overlap between the two groups: in the first group 21 out of 31 subjects had dementia, while in the second group 20 out of 29 subjects were healthy controls. The fact that most of the healthy subjects from the first, patient-dominant group and most of the patients from the second, healthy-dominant group were pooled to generate a third, mixed group in K = 3 may be indicative that dementia is not a simple, binary state. Rather, the mixture group may represent a population of individuals with borderline dementia or a type of pathology other than dementia that seems to be dominant in the first template population for K = 3.
Fig. 2.
Three templates for the “30 dementia+30 healthy data set.”
In both experiments, enlarged ventricles are obvious in the older and dementia templates when compared to the younger and healthy populations, respectively. This structural change due to aging and dementia has been reported in the literature [7,17]. Further analysis is required to understand the structural differences between the discovered modes. The intermediate groups (the older middle aged in the first experiment and the mixture group in the dementia experiment) can provide interesting insights into structural changes due to aging and dementia.
5 Discussion
We presented a fast and efficient image clustering algorithm for co-registering a group of images, computing multiple templates that represent different modes of the population and determining template assignments. We demonstrated our algorithm in two experiments, which revealed age and disease-related modes of the population. Our results confirm previous findings and lead to interesting insights that suggest future research directions in computational anatomy.
The proposed framework can be further explored in various ways. One can employ a richer transformation model, with a prior on the transformations. This will incorporate deformation costs into the membership computations, similar to deformation-based population analysis approaches [6]. Also, general image-to-image distances, such as Mutual Information, can be derived using more flexible models than an additive Gaussian. This promises better results in cases where inter-image intensity variations are significant. Furthermore, one can use a model selection strategy to automatically determine the optimal number of modes. The proposed algorithm can be straightforwardly used with other types of datasets, such as fMRI or DTI, to identify functional or connectivity based modes of a population.
Acknowledgements
The authors would like to thank Bruce Fischl, Koen Van Leemput and B.T. Thomas Yeo for helpful discussions. We would also like to extend our appreciation to Dr. Randy Buckner for making the OASIS dataset available. Support for this research is provided in part by the following sources: NIH NIBIB NAMIC U54-EB005149, NIN NCRR NAC P41-RR13218, NIH NCRR mBIRN U24-RR021382, NIH NINDS grant R01-NS051826, and the NSF CAREER 0642971 grant.
References
- 1.Allassonniere A, Amit Y, Trouve A. Towards a coherent statistical framework for dense deformable template estimation. J.R. Statist. Soc.B. 2007;69:3–29. [Google Scholar]
- 2.Ashburner J, Neelin P, Collins DL, Evans A, Friston K. Incorporating prior knowledge into image registration. Neuro Image. 1997;6(4):344–352. doi: 10.1006/nimg.1997.0299. [DOI] [PubMed] [Google Scholar]
- 3.Blezek D, Miller J. Atlas stratification. Medical Image Analysis. 2007;11(5):443–457. doi: 10.1016/j.media.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Collins DL, et al. Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. J. comput. assist. tomogr. 1994;18(2):192–205. [PubMed] [Google Scholar]
- 5.De Craene M, et al. LNCS . Multi-subject registration for unbiased statistical atlas construction. In: Barillot C, Haynor DR, Hellier P, editors. MICCAI 2004. Vol. 3216. Springer; Heidelberg: 2004. pp. 655–662. [Google Scholar]
- 6.Davatzikos C, et al. A computerized approach for morphological analysis of the corpus callosum. Journal of Computer Assisted Tomography. 1996;20(1):88–97. doi: 10.1097/00004728-199601000-00017. [DOI] [PubMed] [Google Scholar]
- 7.DeCarli C, et al. Longitudinal changes in lateral ventricular volume in datients with dementia of the alzheimer type. Neurology. 1992;42 doi: 10.1212/wnl.42.10.2029. [DOI] [PubMed] [Google Scholar]
- 8.Fischl B, et al. Automatically parcellating the human cerebral cortex. Cerebral Cortex. 2004;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- 9.Guimond A, Meunier F, Thirion JP. Average brain models: A convergence study. INRIA; 1999. Technical Report 3731. [Google Scholar]
- 10.Heckemann RA, et al. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- 11.Ibanez L, et al. The ITK Software Guide. 2005. [Google Scholar]
- 12.Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphism atlas construction for computational anatomy. Neuro Image. 2004;23:151–160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- 13.Marcus DS, et al. Open Access Series of Imaging Studies (OASIS): Cross-Sectional MRI Data in Young, Middle Aged, Nondemented, and Demented Older Adults. Journal of Cognitive Neuroscience. 2007;19:1498–1507. doi: 10.1162/jocn.2007.19.9.1498. [DOI] [PubMed] [Google Scholar]
- 14.Park H, et al. LNCS . Least biased target selection in probabilistic atlas construction. In: Duncan JS, Gerig G, editors. MICCAI 2005. Vol. 3750. Springer; Heidelberg: 2005. pp. 419–426. [DOI] [PubMed] [Google Scholar]
- 15.Woods RP, et al. Automated Image Registration: II. Intersubject Validation of Linear and Nonlinear Models. Comp. Assisted Tomography. 1998;22(1):153–165. doi: 10.1097/00004728-199801000-00028. [DOI] [PubMed] [Google Scholar]
- 16.Rueckert D, et al. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Transaction of Medical Imaging. 1999;18:712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- 17.Scahill RI, et al. A longitudinal study of brain volume changes in normal aging using serial registered magnetic resonance imaging. Arch. Neurol. 2003;60:989–994. doi: 10.1001/archneur.60.7.989. [DOI] [PubMed] [Google Scholar]
- 18.Studholme C, Cardenas V. A template free approach to volumetric spatial normalization of brain anatomy. Pattern Rec. Letters. 2004;25:1191–1202. [Google Scholar]
- 19.Tsai A, et al. An EM algorithm for shape classification based on level sets. Medical Image Analysis. 2005;9:491–502. doi: 10.1016/j.media.2005.05.001. [DOI] [PubMed] [Google Scholar]
- 20.Twining CJ, et al. LNCS . A unified information-theoretic approach to groupwise nonrigid registration and model building. In: Christensen GE, Sonka M, editors. IPMI 2005. Vol. 3565. Springer; Heidelberg: 2005. pp. 1–14. [DOI] [PubMed] [Google Scholar]
- 21.Woods RP, et al. Creation and use of a Talairach-compatible atlas for accurate, automated, nonlinear intersubject registration, and analysis of functional imaging data. Human Brain Mapping. 1999;8(2-3):73–79. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<73::AID-HBM1>3.0.CO;2-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zöllei L, et al. LNCS . Efficient population registration of 3d data. In: Liu Y, Jiang T, Zhang C, editors. CVBIA 2005. Vol. 3765. Springer; Heidelberg: 2005. pp. 291–301. [Google Scholar]