Abstract
We propose a new adaptive sampling approach to determine free energy profiles with molecular dynamics simulations, which is called as “repository based adaptive umbrella sampling” (RBAUS). Its main idea is that a sampling repository is continuously updated based on the latest simulation data, and the accumulated knowledge and sampling history are then employed to determine whether and how to update the biasing umbrella potential for subsequent simulations. In comparison with other adaptive methods, a unique and attractive feature of the RBAUS approach is that the frequency for updating the biasing potential depends on the sampling history and is adaptively determined on the fly, which makes it possible to smoothly bridge nonequilibrium and quasiequilibrium simulations. The RBAUS method is first tested by simulations on two simple systems: a double well model system with a variety of barriers and the dissociation of a NaCl molecule in water. Its efficiency and applicability are further illustrated in ab initio quantum mechanics∕molecular mechanics molecular dynamics simulations of a methyl-transfer reaction in aqueous solution.
INTRODUCTION
In computer simulations of many processes in complex systems, which include conformational changes, molecular recognition, and chemical reactions, a common and important task is to determine the free energy profile along the chosen reaction coordinates.1 As a statistical property, the free energy profile can be taken as a measure of the probability of finding a system in a series of given states.2, 3 To compute the correct probability distribution, a prerequisite is to have good statistics. However, due to the existence of high free energy barriers, the transitions between distinct thermodynamic states of interest constitute rare events, which, in general, make it infeasible to achieve sufficient sampling with a straightforward application of molecular dynamics or Monte Carlo simulations.
Over the years, many methods4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 have been developed to enhance the sampling of rare events. For the determination of free energy profiles, one commonly employed strategy is to add an artificial biasing potential into the Hamiltonian of the system, which is exemplified by the umbrella sampling (US) method.5, 28 In typical US simulations, the potential energy of the system is biased with a series of umbrella potentials, which are usually in the form of a harmonic function, centered on successive values of the reaction coordinate. For each umbrella window, equilibrium simulations are carried out and the biased probability distribution (e.g., histogram) is obtained. Given that the overlaps in the phase space between adjacent windows are sufficient, the free energy profile along the reaction coordinate can be obtained with the weighted histogram analysis method (WHAM).29 This approach has been widely employed and proved to be powerful in many applications; however, its efficiency is quite dependent on the choice of the windows and biasing potentials. The ideal choice of the biasing potential would be the negative of the free energy profile, so that the uniform sampling along the chosen reaction coordinate can be achieved. Unfortunately, such information is exactly what we try to obtain from simulations and is not known in the first place. One promising method to circumvent this inherent challenge is the adaptive US,6, 25, 30, 31, 32 in which a series of staged, quasiequilibrium simulations are performed with an evolving biasing potential. For each subsequent simulation, its adaptive biasing potential is the inverse of the currently estimated free energy profile, which is often determined by using WHAM (Ref. 29) to combine the results from all previous simulations.
With the very similar spirit of adaptivity, several nonequilibrium approaches have been proposed to achieve the uniform sampling, such as Wang–Landau approach,33, 20 the adaptive biasing force,21, 18, 34 nonequilibrium metadynamics,8, 13, 35 adaptive dynamics,11, 36 and self-healing US.12 Among them, the metadynamics method has attracted the most attention and has been widely applied in several fields with quite some success.35 In metadynamics,8, 13, 35 which is also often called as the hill method, a sum of history-dependent Gaussian potentials (centered at the visited spots) is added to the Hamiltonian of the system to fill up the free energy wells, so that the system is forced to explore previously unvisited configuration spaces. Such a procedure recursively flattens the free energy barriers that separate distinct thermodynamic states of interest, and the underlying free energy profile can be recovered from the updated history under some conditions. The height and width of the added Gaussian potential are important factors to determine the accuracy and efficiency of the metadynamics simulation, and several strategies have been developed, which include a Wang–Landau recursive scheme to adaptively update its height.37 Meanwhile, one straightforward way to further improve the accuracy of the resulted metadynamics free energy profile is to perform some additional equilibrium US simulations.35, 38
Very recently, a self-healing US approach12 has been proposed, in which a time-dependent bias potential is continuously self-adapted during a single simulation based on a recursive relation for the probability density. In comparison with the adaptive US, a key attractive feature for the self-healing approach is that the history-dependent bias potential is continuously updated on the fly with a set of simple formula instead of using WHAM to combine all previous simulation data. By achieving the uniform sampling along the reaction coordinate, the free energy profile can be obtained as the negative of the resulted biasing potential.
Inspired by the self-healing US approach,12 we propose here a repository based adaptive US (RBAUS) method, in which a sampling repository is continuously updated based on the latest simulation data, and the accumulated knowledge and sampling history are then employed to determine whether and how to update the biasing umbrella potential for subsequent simulations. A unique and attractive feature of the RBAUS method is that it bridges nonequilibrium and equilibrium simulations. In the following, we will first present the theoretical method and computational details. Then, several tests will be presented to demonstrate the efficiency and applicability of the RBAUS approach, which includes simple model systems as well as ab initio quantum mechanics∕molecular mechanics (QM∕MM) molecular dynamics simulations of chemical reactions in solution. From these tests, some unique features of the RBAUS method will also be illustrated.
THEORY AND METHOD
Umbrella sampling
The free energy profile A(η) along a predefined reaction coordinate η(R) is related to the probability distribution ρ(η),
| (1) |
with
| (2) |
where kB is the Boltzmann constant, T is the absolute temperature, R represents all spatial coordinates of the system, H0 refers the system Hamiltonian, and c can be any constant. Given a canonical ensemble of structures generated with Hamiltonian H0, the ensemble average can be simply computed as
| (3) |
where N0(η) refers to the count of configurations with a given value of η in the canonical ensemble generated with Hamiltonian H0.
In US5, 12 with a biased Hamiltonian Hb,
| (4) |
the probability distribution ρ(η) for the unmodified system can be obtained by the following relation:
| (5) |
Thus, with Nb(η) as the number of configurations with a given value of η in the canonical ensemble generated with the biased Hamiltonian Hb, ρ(η) can be computed as
| (6) |
We can see that with Vb(η)=0 in Eq. 6, it becomes Eq. 3. Thus, for a given biased ensemble, Nb(η) can be considered as the raw sampling number of the given value of η along the reaction coordinate, and we can define K(η)=Nb(η)eVb(η)∕kBT as the corresponding unbiased knowledge about the given value of η from this biased simulation.
It should be noted that if the chosen reaction coordinate η is nonlinear in the Cartesian coordinates, a Jacobian matrix determinant term needs to be included to obtain the potential of mean force (PMF) along η,
| (7) |
The ∣J∣ stands for the Jacobian factor.39 For example, if the distance of two particles r is chosen as the reaction coordinate, the corresponding PMF (r) would be
| (8) |
Repository based adaptive umbrella sampling
The main idea of the RBAUS approach is that a sampling repository is continuously updated based on the latest simulation data, and the sampling history and accumulated knowledge are employed to determine whether and how to update the biasing umbrella potential to achieve more uniform sampling for subsequent simulations.
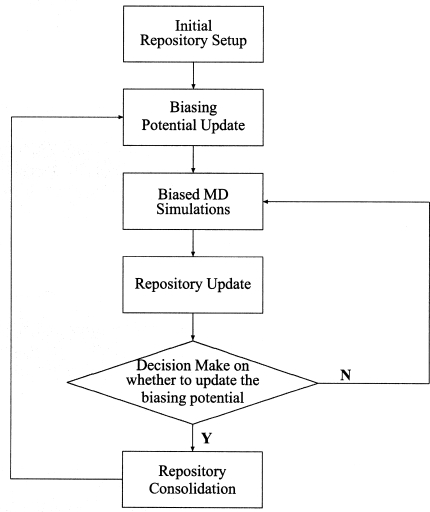
Consider the determination of the free energy profile along a predefined reaction coordinate η(R), the sampling repository mainly stores and updates two kinds of information: the accumulated raw sampling number NS(η) and the accumulated unbiased knowledge K(η). With the profile of NS(η), the ratio of its largest value of NS(η) to its lowest value can be easily calculated. Here, we call it as the “histmax-histmin ratio” (HHR). If the subsequent simulation still explores the previously oversampled region more often than the previously undervisited one, the HHR will increase. On the other hand, the decrease in HHR indicates that the subsequent biased simulation is achieving more uniform sampling along the reaction coordinate. Thus, we can see that the change in HHR in simulations can be employed to determine whether the currently employed biasing umbrella potential needs to be updated to encourage more uniform sampling. Meanwhile, the accumulated unbiased knowledge K(η) can be employed to calculate the free energy profile on the fly, which can be employed to update the biasing potential Vb(η) if needed. Therefore, we can see that in comparison with other adaptive sampling approaches, a unique feature of the RBAUS approach is that the frequency for updating the biasing potential depends on the sampling history and is adaptively determined on the fly. In the following, we present a practical RBAUS simulation scheme:
Step 0: Initial repository setup. In numerical simulations, it is a common practice to divide the reaction coordinate η into Z bins. For each bin i, we set an initial value of NS[i]=0, and K[i]. K[i] refers to the accumulated knowledge about the [i] bin. Without any prior information about the system, one might simply set K[i] to be uniform with a small number of 0.001.
- Step 1: Biasing potential update. With the accumulated unbiased knowledge K[i], the free energy profile A[i] can be calculated with the following equation:
The biased potential Vb is then obtained based on the negative of the calculated free energy profile. It should be noted that with Eq. 9, A[i] would be zero when K[i] is equal to the average of the accumulated knowledge among all bins, which is a desired property for constructing the biased potential. Meanwhile, from the accumulated raw sampling number NS[i], the reference HHR can be easily obtained by(9)
when min(NS)>0. If min(NS)=0, the HHR can be set to a large value, such as 1000.(10) Step 2: Biased simulations. Perform molecular dynamics simulations with the biased Hamiltonian H0+Vb. For a certain period of time, such as 1 ps, we will collect the raw histogram h[i], which is the number of sampled configurations in each bin.
- Step 4: Decision made on whether to update the biasing potential. With the calculated HHRC and the reference HHR, we have devised the following heuristic criteria to decide how to proceed next:
- Case I: If HHRC is larger than 10 or HHRC is larger than 1.1HHR, update is needed. Thus, go to Step 5.
- Case II: If HHRC is less than 10 and HHRC is less than 1.1HHR, update is NOT needed. Thus, go to Step 2 with the same Vb, and set HHR to be min(HHRC,HHR).
Step 5: Repository consolidation. Here, the accumulated unbiased knowledge in the sampling repository is consolidated by setting K[i]=kconstK[i]. kconst equals to 1 when HHRC is less than 10, and is set to a value of 0.618 when HHRC is larger than 10. Go to Step 1.
The above scheme is summarized into a flow chart shown in Fig. 1. When the sampling along the reaction coordinate is close to the uniform, case II in Step 4 would be always fulfilled. Thus, the biasing potential would not be updated anymore, and the simulation turns into being a quasiequilibrium one. In Steps 4 and 5, one criterion that we have employed is whether the value of HHRC is larger than 10. This is often the case at the initial stage of the simulation, and it indicates that a certain region along the reaction coordinate is rarely sampled and the employed biasing potential is quite far away from the optimal. Thus, the biasing potential should be updated as often as possible. Meanwhile, since the unbiased knowledge accumulated at this initial simulation stage is likely not reliable, a scaling factor kconst (less than 1.0) is employed in Step 5. In our experiments, we found that values between 0.2 and 0.8 yield reasonable performance. Smaller values of kconst tend to throw away too much information from previous simulations, while a value of 1.0 throughout the simulation makes the result quite dependent on the initial simulation setup. It would be better to make this kconst to be adaptive. In our current implementation, we have set kconst to be 0.618 when HHR is larger than 10, and the value is switched to 1.0 when HHR is less than 10. It should be noted that the current scheme is not optimal, but it is found to be quite robust and efficient in several very different test cases, as presented in Sec. 4. In principle, a Bayesian updating scheme can be employed here, and the work along this direction is currently in progress and will be presented in future publications.
Figure 1.
The flow chart for the repository based adaptive US approach.
We would like to point out that the embarrassingly parallel simulations can be very easily implemented in the RBAUS. Basically, in Step 2, a number of replicas with different initial structures along the reaction coordinate can be simulated in parallel with the same bias potential, and the raw histogram will be collected from all replica simulations instead of one single simulation. Meanwhile, the collection time in Step 2 can be correspondingly reduced in multireplica simulations to collect the same amount of sampling data as in the single-replica simulation. This means that if one single-replica simulation needs 1 ps to collect data, eight-replica simulations would only need 0.125 ps for each replica. It would be noted that such parallel simulations are very natural for adaptive simulations,36 which include adaptive umbrella sampling32 and metadynamics.40
IMPLEMENTATION AND COMPUTATIONAL DETAIL
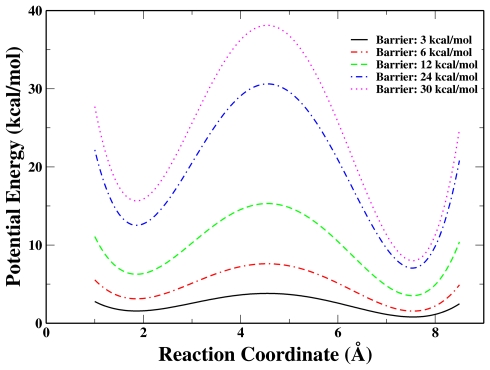
We have implemented the above presented RBAUS simulation scheme in the TINKER4.2 suite of molecular simulation program41 and an ab initioQM∕MM program, which is based on modified GAUSSIAN03 package42 and TINKER4.2.41 The biasing potential is represented by the shape-preserving smoothing spline, and the TSPSS module in Renka’s tension spline curve-fitting package (TSPACK) (Ref. 43) has been used. We have tested the implemented scheme in three very different systems. The first one is a very simple model system: two particles interacting with a double well potential. We have set a variety of barriers between two wells, ranging from 3 to 30 kcal∕mol, which represent typical barriers that need to be simulated in complicated processes such as conformational changes and chemical reactions. Then, we turn to a more realistic, complex, and well studied system:44, 45, 46 the Na+ and Cl− ion pair association in water, which has a quite low barrier of a few kcal∕mol. Finally, we have employed the RBAUS simulation scheme for a more challenging task: ab initio QM∕MM MD simulation of Cl−+CH3Cl→ClCH3+Cl− reaction in water, which has an experimental free energy barrier of 26.6 kcal∕mol.47
Double well model potential
In this simple model system, two particles interact with each other via a double well potential which has the following form:
| (12) |
We make the barriers between the two minima range from 3 to 30 kcal∕mol by setting the coefficients as the following below (in Fig. 2):
Figure 2.
Illustration of five double-well potentials with barriers of 3, 6, 12, 24, and 30 kcal∕mol, respectively.
We have employed 50 bins along the reaction coordinate from 1.0 to 8.5 Å. To discourage the system to visit the region with either the reaction coordinate of less than 1.0 Å or larger than 8.5 Å, a harmonic wall has been applied outside of the [Rcleft,RcRight], which is Ewall(Rc)=10.0(Rc−Rcleft)(Rc−RcRight). Such a wall potential has also been applied in the other two test cases. The RBAUS MD simulation is performed with the following simulation parameters: 1 fs time step, 1 amu for the mass of the particle, and 300 K temperature. It should also be noted that for this simple model system, its reference PMF is the same as the potential energy curve. To check the convergence of RBAUS MD simulations, we have calculated the root-mean-square deviation (RMSD) of the simulated PMF with respect to the reference one,
| (13) |
Sodium chloride ion pair in water
The system is made up of a sodium ion, a chloride ion, and 254 water molecules in a cubic box with periodic boundary conditions. The dimension of the box is 19.7429 Å, and a cutoff distance of 9 Å has been used for the van der Waals and electrostatic interactions. The simulation of the system is performed in the constant volume, constant temperature (300 K) by using the modified TINKER program.41 The TIP3P water model48 was utilized, the force field parameters for sodium and chloride ions were developed by Aqvist,49 and the van der Waals radii has been adapted for AMBER combining rule.50 The distance between Na+ and Cl− has been chosen as the reaction coordinate, and the bin width has been assigned to be 0.1 Å. The above simulation protocol has been employed in RBAUS simulations as well as in conventional umbrella simulations. To obtain the reference PMF, we have employed 21 umbrella windows along the reaction coordinate from 2.4 to 7.5 Å. For each window, 0.2 ns equilibration was performed and followed by 3 ns data collection. The histograms along the reaction coordinate were determined for all windows and were pieced together with WHAM.51, 29, 28
Cl−+CH3Cl→ClCH3+Cl− reaction in aqueous phase
For this methyl-transfer reaction, the reaction coordinate Rc is defined as Rc=rCCl′−rCCl, where Cl′ is the leaving atom. The solutes were described at the HF∕6-31G* level, which has been known to describe such methyl-transfer reactions well with a reasonable computational cost.52 The solutes were solvated with a 15 Å sphere with 796 water molecules described by the TIP3P (Ref. 48) water model. A spherical boundary condition has been employed, in which solvent molecules within 13 Å sphere of the sphere center were allowed to move during simulations. To calculate the reference free energy profile, we have employed conventional umbrella simulations. A total of 33 umbrella windows along the reaction coordinate have been employed. For each window, the configurations were collected for 80 ps for the data analysis after the equilibration period of 10 ps at 300 K. The histograms along the reaction coordinate were determined for each window and were pieced together with WHAM (Refs. 51, 29, 28) to calculate the free energy profile.
RESULTS AND DISCUSSION
Model system 1: Double well model potential
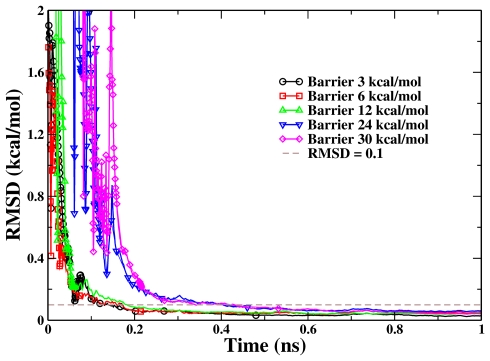
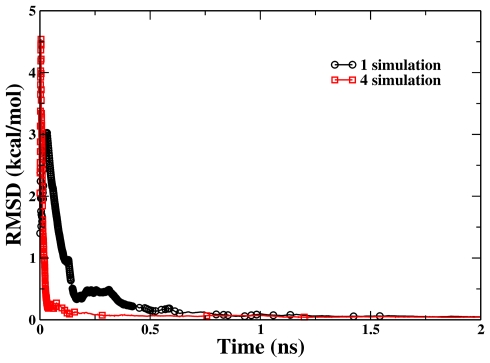
We have applied the presented RBAUS scheme with the same set of simulation parameters to all five different barrier potential models, with the barriers ranging from 3 to 30 kcal∕mol. As shown in Fig. 3, for these five very different barriers, the convergences of the simulations are all very efficient. Even for the system with very high barriers, such as 24 and 30 kcal∕mol, it only takes less than 0.5 ns to have the error in calculated PMF to be lower than 0.1 kcal∕mol. Figure 3 also indicates that the convergence for a system with a lower barrier is faster than for the higher barrier system, which is expected and desired. However, we would like to point out that to achieve such efficient convergence for these very different barriers, using the same simulation protocol is not a trivial task. For example, it would not be the case if the repository consolidation step (Step 5 in Fig. 1) was skipped. Meanwhile, in Fig. 3, the empty symbols represent the biasing-potential-updating points. We can see that for each curve, the updating becomes less often when the simulation goes on, and there is almost no updating after 0.5 ns. These illustrate a unique and attractive feature of the RBAUS approach: it smoothly bridges nonequilibrium and quasiequilibrium simulations.
Figure 3.
The RMSD of the calculated PMFs from single-replica RBAUS simulations with respect to the reference one for all five double-well model systems. The dashed line indicates the RMSD value of 0.1 kcal∕mol. The point symbols represent the biasing-potential-updating points.
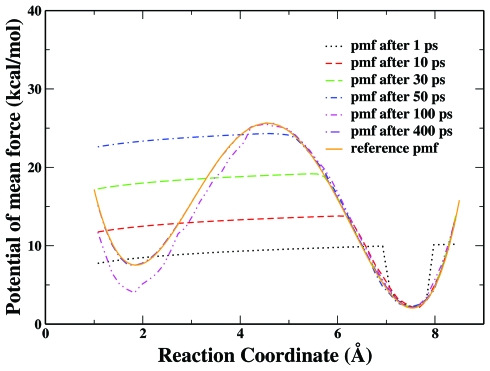
In Fig. 4, a series of calculated potentials of mean force at different simulation times (1 ps, 10 ps, 30ps, 50 ps, 0.1 ns, 0.4 ns) are presented for the model system with a barrier of 24 kcal∕mol. This illustrates how the RBAUS scheme works. For this particular simulation, it initially samples the minima near 8 Å, and it takes about 50–100 ps to flatten a barrier of about 24 kcal∕mol. After about 0.1 ns, it has sampled almost the entire area of the reaction coordinate, but there is still some noticeable error in the minima near 2 Å. At 400 ps, we can see that the calculated curve overlaps almost perfectly with the reference curve. It should be noted that the added biasing potential is based on the negative of the calculated free energy profile, which increasingly flattens the free energy surface and leads to more uniform sampling along the reaction coordinate.
Figure 4.
The calculated PMFs obtained from the RBAUS simulation with single replica at different simulation times for the double-well model system with a barrier of 24 kcal∕mol.
Meanwhile, as shown in Fig. 5, embarrassingly parallel simulations can be straightforwardly implemented and can significantly reduce the wall time to reach the convergence if sufficient parallel computational resources were available. With 0.1 kcal∕mol as the convergence criteria, the simulation with eight replicas converges after 26 ps, while that with four replicas converges after 64 ps. Meanwhile, the simulation with multiple replicas turns into the quasiequilibrium stage much earlier than the single-replica simulation. For multireplica simulations, we can see that the biasing potential update is not needed after about 30 ps for eight replicas and 130 ps for four replicas. It should be noted that although embarrassingly parallel simulations may not necessarily save much of the total CPU time, it is quite attractive for the new generation of supercomputers, which are likely to have many more CPUS with relatively small increase in the processor speed.
Figure 5.
The RMSD of the calculated PMFs from multireplica RBAUS simulations with respect to the reference one for the double-well model system with a barrier of 24 kcal∕mol. The dashed line indicates the RMSD value of 0.1 kcal∕mol. The point symbols represent the biasing-potential-updating points.
Model system 2: A sodium chloride ion-pair in water
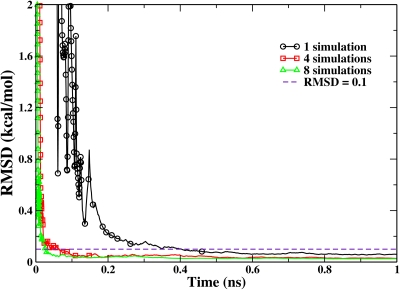
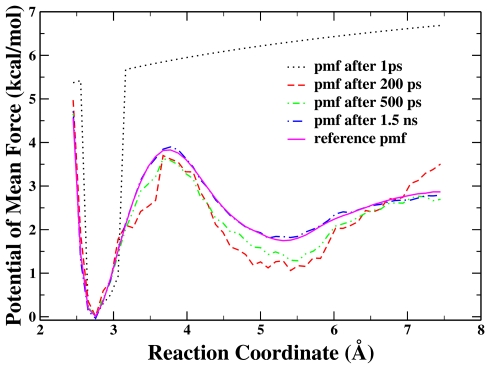
To test the RBAUS method in a more realistic system, the dissociation of a sodium chloride ion pair in aqueous solution has been studied. The distance between Na+ and Cl− was chosen as the reaction coordinate. The reference PMF for comparison was calculated for the same system with conventional US by using 21 umbrella windows and 3 ns sampling time for each window. Figure 6 illustrates the calculated PMFs at different simulation times with the RBAUS method by using only one replica. We can see that the calculated PMF at 1.5 ns from the single-replica RBAUS simulation is almost indistinguishable from the reference one. The calculated PMF differences between the contact and solvent-separated ion pairs and their transition barrier are 2.1 and 3.9 kcal∕mol, respectively, with the RBAUS simulation, which are in excellent agreement with the values of 2.1 and 3.8 kcal∕mol from the conventional US. Figure 7 presents the evolution of the RMSD of the calculated PMFs from both single-replica and four-replica RBAUS simulations with respect to the reference one. We can see that similar to the model system 1, the convergence of the four-replica RBAUS simulations is much faster than the one-replica simulation, and for each curve, the updating becomes less often when the simulation goes on.
Figure 6.
The calculated PMFs obtained from single-replica RBAUS simulation at different simulation times for the dissociation of a sodium chloride ion pair in aqueous solution. The reference PMF is obtained from US simulations with 21 windows and 3 ns simulation for each window.
Figure 7.
The RMSD of the calculated PMFs from single-replica and four-replica RBAUS simulations with respect to the reference one for the dissociation of a sodium chloride ion pair in aqueous solution. The point symbols represent the biasing-potential-updating points.
Model system 3: Cl−+CH3Cl→ClCH3+Cl− reaction in aqueous phase
To further demonstrate its feasibility and efficiency, the RBAUS scheme has been employed to determine the free energy profile of the Cl−+CH3Cl→ClCH3+Cl− reaction in water with Born–Oppenheimer ab initio QM∕MM molecular dynamics simulations. At each time step, the forces on atoms in both QM and MM regions together with the total energy are calculated with ab initio QM∕MM method on the fly, and the Newton equations of motion are integrated. Such simulations have been recently demonstrated to be feasible and successful in studying enzyme reactions.53, 54
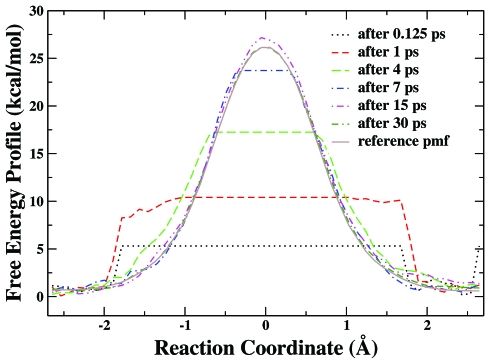
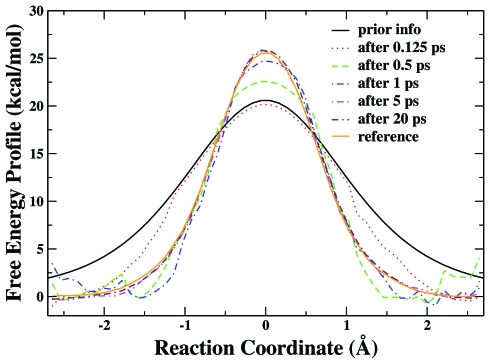
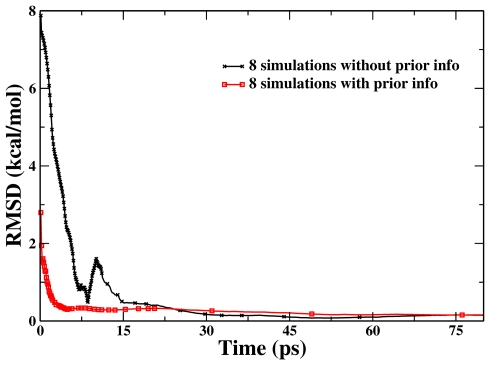
In this Cl− identity SN2 reaction, the formation of one C⋯Cl bond is accompanied by the breaking of the other C⋯Cl bond. By choosing the difference of these two bond lengths as the reaction coordinate, we have carried out an eight-replica RBAUS molecular dynamics simulation with HF∕6-31G* QM∕MM method to map out its potential of mean force. A series of calculated PMFs at different simulation times (after 0.125, 1.25, 4, 7, 15, and 30 ps) are shown in Fig. 8. We can see that it only takes about 10 ps RBAUS simulation to overcome a free energy barrier of about 26 kcal∕mol, and the free energy profile obtained from eight-replica RBAUS molecular dynamics simulations at 30 ps is in excellent agreement with the reference curve obtained from conventional US with 33 windows and 80 ps trajectory long for each window. The free energy barrier obtained at 30 ps from RBAUS is 25.6 kcal∕mol, which is very comparable with the US result of 25.5 kcal∕mol. Meanwhile, Fig. 9 illustrates how some prior information can be used to further enhance the sampling efficiency of RBAUS simulations, and Fig. 10 shows the RMSD of the calculated PMFs for both simulations with and without prior information. The free energy barrier obtained after 5 ps from RBAUS with this prior information is 26.0 kcal∕mol, which is also close to the US result.
Figure 8.
The free energy profiles of Cl−+CH3Cl→ClCH3+Cl− reaction in aqueous solution calculated by eight-replica RBAUS simulations without prior information at different simulation times. The reference free energy profile is obtained from the US with 33 windows and 80 ps simulation for each window.
Figure 9.
The free energy profiles of Cl−+CH3Cl→ClCH3+Cl− reaction in aqueous solution calculated by eight-replica RBAUS simulations with prior information at different simulation times. The reference PMF is obtained from the US with 33 windows and 80 ps simulation for each window.
Figure 10.
The RMSD of the calculated free energy profiles with respect to the reference one for Cl−+CH3Cl→ClCH3+Cl− reaction in aqueous solution by eight-replica RBAUS simulations with and without prior information. The point symbols represent the biasing-potential-updating points.
Here, the supposed prior information about this reaction is represented by an Eckart potential function,55, 56
| (14) |
where
| (15) |
| (16) |
The s→−∞ region is the reactant and the s→+∞ is the product. The V0 is the energy difference between reactant and transition state, ΔV is the difference between reactant and product, and α refers to the width of the curve. Here, we choose V0 to be 20 kcal∕mol, ΔV to be 0 kcal∕mol, and α to be 1.5. This supposed prior information is employed to set the initial value of K[i] in the initial repository setup (Step 0). Since the employment of such prior knowledge effectively reduces the height of the reaction barrier to overcome, it is not surprising that it leads to a faster convergence than the simulation without employing the prior information, as shown in Figs. 910.
CONCLUSION
In this work, we have proposed a RBAUS method to determine the free energy profile along chosen reaction coordinates. In comparison with other adaptive sampling methods, a unique and attractive feature of the RBAUS method is that the frequency for updating the biasing potential is not predetermined but depends on the sampling history and is adaptively determined on the fly. Thus, the RBAUS method smoothly bridges nonequilibrium and quasiequilibrium simulations. By using the “repository” paradigm, it is straightforward to employ parallel simulations and to use all of the other prior information to enhance the sampling efficiency. The tests on several very different systems with barriers ranging from 3 to 30 kcal∕mol demonstrated its efficiency and applicability, which are very encouraging. Meanwhile, it should be noted that the presented RBAUS method has much room to be further improved and extended, such as to integrate a Bayesian updating method into the RBAUS approach and to determine multidimensional free energy surfaces. The work along these directions are currently in progress in our laboratory and will be presented in later publications.
ACKNOWLEDGMENTS
This work has been supported by the National Science Foundation (No. CHE-CAREER-0448156) and National Institute of Health (No. R01-GM079223). We appreciate the computational resources and support provided by NYU-ITS.
References
- Chipot C. and Pohorille A., Free Energy Calculations: Theory and Applications in Chemistry and Biology (Springer, New York, 2007). [Google Scholar]
- Kirkwood J. G., J. Chem. Phys. 10.1063/1.1749657 3, 300 (1935). [DOI] [Google Scholar]
- Landau L. D. and Lifshiz E. M., Statistical Physics, 2nd ed. (Pergamon, New York, 1969), pp. 343–353. [Google Scholar]
- Zwanzig R. W., J. Chem. Phys. 10.1063/1.1740409 22, 1420 (1954). [DOI] [Google Scholar]
- Patey G. N. and Valleau J. P., J. Chem. Phys. 10.1063/1.431685 63, 2334 (1975). [DOI] [Google Scholar]
- Mezei M., J. Comput. Phys. 10.1016/0021-9991(87)90054-4 68, 237 (1987). [DOI] [Google Scholar]
- Jarzynski C., Phys. Rev. E 10.1103/PhysRevE.56.5018 56, 5018 (1997). [DOI] [Google Scholar]
- Laio A. and Parrinello M., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.202427399 99, 12562 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- E W. and Vanden-Eijnden E., Lect. Notes Comput. Sci. Eng. Springer-Verlag, Berlin, 39, 35 (2004). [Google Scholar]
- Maragliano L. and Vanden-Eijnden E., Chem. Phys. Lett. 446, 182 (2007). [Google Scholar]
- Lelievre T., Rousset M., and Stoltz G., J. Chem. Phys. 10.1063/1.2711185 126, 134111 (2007). [DOI] [PubMed] [Google Scholar]
- Marsili S., Barducci A., Chelli R., Procacci P., and Schettino V., J. Phys. Chem. B 10.1021/jp062755j 110, 14011 (2006). [DOI] [PubMed] [Google Scholar]
- Bussi G., Laio A., and Parrinello M., Phys. Rev. Lett. 10.1103/PhysRevLett.96.090601 96, 090601 (2006). [DOI] [PubMed] [Google Scholar]
- Kastner J. and Thiel W., J. Chem. Phys. 10.1063/1.2052648 123, 144104 (2005). [DOI] [PubMed] [Google Scholar]
- Gallicchio E., Andrec M., Felts A. K., and Levy R. M., J. Phys. Chem. B 10.1021/jp045294f 109, 6722 (2005). [DOI] [PubMed] [Google Scholar]
- Hamelberg D., Mongan J., and Mccammon J. A., J. Chem. Phys. 10.1063/1.1755656 120, 11919 (2004). [DOI] [PubMed] [Google Scholar]
- Rosso L., Minary P., Zhu Z. W., and Tuckerman M. E., J. Chem. Phys. 10.1063/1.1448491 116, 4389 (2002). [DOI] [Google Scholar]
- Darve E., Wilson M. A., and Pohorille A., Mol. Simul. 10.1080/08927020211975 28, 113 (2002). [DOI] [Google Scholar]
- Rahman J. A. and Tully J. C., J. Chem. Phys. 10.1063/1.1469605 116, 8750 (2002). [DOI] [Google Scholar]
- Wang F. G. and Landau D. P., Phys. Rev. E 10.1103/PhysRevE.64.056101 64, 056101 (2001). [DOI] [Google Scholar]
- Darve E. and Pohorille A., J. Chem. Phys. 10.1063/1.1410978 115, 9169 (2001). [DOI] [Google Scholar]
- Gullingsrud J. R., Braun R., and Schulten K., J. Comput. Phys. 10.1006/jcph.1999.6218 151, 190 (1999). [DOI] [Google Scholar]
- Sugita Y. and Okamoto Y., Chem. Phys. Lett. 10.1016/S0009-2614(99)01123-9 314, 141 (1999). [DOI] [Google Scholar]
- Sprik M. and Ciccotti G., J. Chem. Phys. 10.1063/1.477419 109, 7737 (1998). [DOI] [Google Scholar]
- Bartels C. and Karplus M., J. Comput. Chem. 18, 1450 (1997). [DOI] [Google Scholar]
- Voter A. F., Phys. Rev. Lett. 10.1103/PhysRevLett.78.3908 78, 3908 (1997). [DOI] [Google Scholar]
- Grubmuller H., Phys. Rev. E 10.1103/PhysRevE.52.2893 52, 2893 (1995). [DOI] [PubMed] [Google Scholar]
- Roux B., Comput. Phys. Commun. 10.1016/0010-4655(95)00053-I 91, 275 (1995). [DOI] [Google Scholar]
- Kumar S., Bouzida D., Swendsen R. H., Kollman P. A., and Rosenberg J. M., J. Comput. Chem. 10.1002/jcc.540130812 13, 1011 (1992). [DOI] [Google Scholar]
- Bartels C., Schaefer M., and Karplus M., J. Chem. Phys. 10.1063/1.480139 111, 8048 (1999). [DOI] [Google Scholar]
- Rajamani R., Naidoo K. J., and Gao J. L., J. Comput. Chem. 10.1002/jcc.10315 24, 1775 (2003). [DOI] [PubMed] [Google Scholar]
- Wang J., Gu Y., and Liu H. Y., J. Chem. Phys. 10.1063/1.2346681 125, 094907 (2006). [DOI] [PubMed] [Google Scholar]
- Calvo F., Mol. Phys. 10.1080/00268970210158632 100, 3421 (2002). [DOI] [Google Scholar]
- Henin J. and Chipot C., J. Chem. Phys. 10.1063/1.1773132 121, 2904 (2004). [DOI] [PubMed] [Google Scholar]
- Ensing B., De Vivo M., Liu Z. W., Moore P., and Klein M. L., Acc. Chem. Res. 10.1021/ar040198i 39, 73 (2006). [DOI] [PubMed] [Google Scholar]
- Lelievre T., Rousset M., and Stoltz G., J. Comput. Phys. 222, 624 (2007). [DOI] [PubMed] [Google Scholar]
- Li H., Min D., Liu Y., and Yang W., J. Chem. Phys. 10.1063/1.2769356 127, 094101 (2007). [DOI] [PubMed] [Google Scholar]
- Babin V., Roland C., Darden T. A., and Sagui C., J. Chem. Phys. 10.1063/1.2393236 125, 204909 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boresch S. and Karplus M., J. Chem. Phys. 10.1063/1.472358 105, 5145 (1996). [DOI] [Google Scholar]
- Raiteri P., Laio A., Gervasio F. L., Micheletti C., and Parrinello M., J. Phys. Chem. B 10.1021/jp054359r 110, 3533 (2006). [DOI] [PubMed] [Google Scholar]
- Ponder J. W., TINKER, Software Tools for Molecular Design, Version 4.2 (The most updated version for the TINKER program can be obtained from J. W. Ponder’s world wide web site at http://dasher.wustl.edu/tinker., 2004).
- Frisch M. J., Trucks G. W., Schlegel H. B.et al. , GAUSSIAN 03, Revision B.05 (Gaussian, Inc., Pittsburgh, PA, 2003).
- Renka R. J., ACM Trans. Math. Softw. 19, 81 (1993). [Google Scholar]
- Koneshan S. and Rasaiah J. C., J. Chem. Phys. 10.1063/1.1314341 113, 8125 (2000). [DOI] [Google Scholar]
- Friedman R. A. and Mezei M., J. Chem. Phys. 10.1063/1.469418 102, 419 (1995). [DOI] [Google Scholar]
- Berkowitz M., Karim O. A., Mccammon J. A., and Rossky P. J., Chem. Phys. Lett. 10.1016/0009-2614(84)85660-2 105, 577 (1984). [DOI] [Google Scholar]
- Mclennan D. J., Aust. J. Chem. 31, 1897 (1978). [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 10.1063/1.445869 79, 926 (1983). [DOI] [Google Scholar]
- Aqvist J., J. Phys. Chem. 10.1021/j100384a009 94, 8021 (1990). [DOI] [Google Scholar]
- Cornell W. D., Cieplak P., Bayly I., Gould I. R., Merz K. M., Ferguson D. M., Spellmeyer D. C., Fox T., Caldwell J. W., and Kollman P. A., J. Am. Chem. Soc. 10.1021/ja00124a002 117, 5179 (1995). [DOI] [Google Scholar]
- Ferrenberg A. M. and Swendsen R. H., Phys. Rev. Lett. 10.1103/PhysRevLett.61.2635 61, 2635 (1988). [DOI] [PubMed] [Google Scholar]
- Chandrasekhar J., Smith S. F., and Jorgensen W. L., J. Am. Chem. Soc. 10.1021/ja00322a059 106, 3049 (1984). [DOI] [Google Scholar]
- Wang S., Hu P., and Zhang Y., J. Phys. Chem. B 10.1021/jp067147i 111, 3758 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu P., Wang S., and Zhang Y., J. Am. Chem. Soc. 130, 3806 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckart C., Phys. Rev. 10.1103/PhysRev.35.1303 35, 1303 (1930). [DOI] [Google Scholar]
- Miller W. H., J. Am. Chem. Soc. 10.1021/ja00517a004 101, 6810 (1979). [DOI] [Google Scholar]