Abstract
The multiscale coarse-graining (MS-CG) method [S. Izvekov and G. A. Voth, J. Phys. Chem. B 109, 2469 (2005);J. Chem. Phys. 123, 134105 (2005)] employs a variational principle to determine an interaction potential for a CG model from simulations of an atomically detailed model of the same system. The companion paper proved that, if no restrictions regarding the form of the CG interaction potential are introduced and if the equilibrium distribution of the atomistic model has been adequately sampled, then the MS-CG variational principle determines the exact many-body potential of mean force (PMF) governing the equilibrium distribution of CG sites generated by the atomistic model. In practice, though, CG force fields are not completely flexible, but only include particular types of interactions between CG sites, e.g., nonbonded forces between pairs of sites. If the CG force field depends linearly on the force field parameters, then the vector valued functions that relate the CG forces to these parameters determine a set of basis vectors that span a vector subspace of CG force fields. The companion paper introduced a distance metric for the vector space of CG force fields and proved that the MS-CG variational principle determines the CG force force field that is within that vector subspace and that is closest to the force field determined by the many-body PMF. The present paper applies the MS-CG variational principle for parametrizing molecular CG force fields and derives a linear least squares problem for the parameter set determining the optimal approximation to this many-body PMF. Linear systems of equations for these CG force field parameters are derived and analyzed in terms of equilibrium structural correlation functions. Numerical calculations for a one-site CG model of methanol and a molecular CG model of the ionic liquid are provided to illustrate the method.
INTRODUCTION
Classical atomistic molecular dynamics (MD) simulations1, 2 have provided great insight into the equilibrium fluctuations of biomolecular systems, such as proteins3, 4 and lipid bilayers.5, 6 Unfortunately, though, the properties that make atomically detailed MD simulations such a powerful tool for investigating the equilibrium properties and local fluctuations of biomolecular systems also limit their application for studying slowly evolving complex processes involving large scale fluctuations that are critical in important biological processes such as self-assembly of the HIV-1 viral capsid7 or signal transduction in immune response.8, 9 These cellular processes evolve on timescales of microseconds or longer and cannot be thoroughly investigated with atomically detailed MD simulations that must be propagated with a timestep that is sufficiently small to accurately resolve the highest frequency vibrations between atoms in the condensed phase.
These limitations in atomistic MD have motivated tremendous interest in the development of coarse-grained (CG) models for investigating complex molecular processes.10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 CG models provide a reduced low-resolution description of a given system in which molecules are described by sites representing groups of atoms. Consequently, CG models are expected to be highly computationally efficient, both because many fewer degrees of freedom are involved in simulating a CG model and also because high frequency intramolecular vibrations have been subsumed into the CG sites and incorporated into averaged effective interactions between sites. Moreover, these low-resolution models are particularly attractive for studying slowly evolving biomolecular processes in which large scale structural changes and not atomic interactions are of principal interest. In such cases, explicit atomistic detail may actually obscure the interesting or important features of a given process. As indicated in the early work of Levitt and Warshel,17 the promise of CG models is that the essential physical forces driving protein folding may be well described by effective interactions between relatively few low-resolution CG sites. In this case, CG models provide not only an efficient computational tool but also a simplified representation and understanding of complex molecular phenomena.
Nevertheless, it is clear that the effective interactions between CG sites are implicitly determined by atomic interactions. It is therefore a key underlying assumption in the development and simulation of many CG models that the results of the CG model are consistent with the results that would be obtained using an atomically detailed model. Consequently, a great deal of research has focused on determining the effective interactions between CG sites.10, 11, 12, 13, 16, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45 Recently, Izvekov and Voth have introduced the multiscale coarse-graining (MS-CG) method37, 36 that employs a variational procedure for deducing effective CG interactions directly from force information obtained from atomically detailed simulations. Applications of the MS-CG method have included the development of accurate CG models for a number of complex systems, including pure and mixed lipid bilayers,36, 44 simple fluids37, 38, 39 and ionic liquids,40 mixed resolution models of transmembrane proteins,41 small peptides,42 monosaccharides,45 and even carbon nanoparticles.43
The companion paper,46 hereafter referred to as Paper I (see also Refs. 47, 48, 49), provided a formal statistical mechanical framework for the MS-CG method, formulating a precise definition and identifying sufficient conditions for consistency between a CG model and a particular atomically detailed model. In the context of this theory, a CG model is consistent in configuration space with a given atomistic model of the same system if both (1) every configuration of the atomically detailed model can be mapped onto a configuration of the CG model, and (2) the equilibrium coordinate distribution of the CG sites for the CG model is equal to the equilibrium coordinate distribution of the CG sites determined by the atomistic equilibrium coordinate distribution and the map from the atomistic configuration space onto the CG configuration space. The sufficient conditions for consistency impose some mild restrictions on the definition of the CG model and identify a formal prescription (i.e., the MS-CG variational principle) for calculating the “potential energy function” for a consistent CG model from the properties of the atomistic system. Paper I also showed that this potential energy function is, in fact, the many-body potential of mean force (PMF) governing the equilibrium distribution of sites in the atomistic model. This many-body PMF is the free energy surface upon which the probability distribution for the CG sites is defined.
The framework developed in Paper I considered a CG force field as a set of vector valued functions of the CG configuration with each element of this set specifying a force on a CG site. The space of all possible CG force fields defines a vector space of CG force fields. The CG force field determined by the many-body PMF and all possible approximations to this CG force field are vectors in this space. In principle, a complete set of basis vectors spanning the space of all possible CG force fields may be constructed. A particular set of coefficients for these basis vectors identifies a particular CG force field. These coefficients then play the role of parameters for the CG force field and each vector in the basis set specifies how the force on each CG site depends on the associated coefficient (parameter) as a function of the CG configuration.
Paper I also proved that if both (1) the MS-CG variational calculation is performed using this imagined complete set of force field basis vectors and (2) the sampled trajectory provides an accurate approximation to a canonical ensemble average, then the MS-CG variational calculation will determine the CG force field that is derived as gradients of the many-body PMF. Performing this variational calculation with a complete set of force field basis vectors is equivalent to parametrizing a completely flexible many-body CG force field.
In practice, though, this exact many-body CG interaction potential cannot be either calculated or used in simulations. Instead, CG force fields that are implemented in computer simulations often assume additive intramolecular and intermolecular interactions, each involving two, three, or four sites (see, e.g., Ref. 16 for a CG model with a more complex interaction potential). The forces resulting from these interactions may be represented by a finite set of basis vectors that span a vector subspace of trial CG force fields. As a consequence of the assumed form for the CG interaction potential, the force field derived from the exact PMF will, in general, not be an element of this subspace because the many-body PMF cannot always be adequately represented by sums of few-body terms. The companion paper defined a distance metric for the space of CG force fields and demonstrated that (in the limit of adequate sampling) the MS-CG variational calculation determines the CG force field within a given vector subspace of trial force fields that is closest to the force field derived from the exact many-body PMF. In this sense, the MS-CG variational principle determines an “optimal approximation” of a particular form that is specified by the interactions included in the CG force field to the exact many-body PMF.
The present manuscript further develops this theory by considering the application of the MS-CG variational principle for determining CG force fields of complex molecular systems. Section 2A represents the CG force field as a linear combination of force field basis vectors with coefficients that serve as force field parameters. Section 2B derives and analyzes the linear least squares problem for these parameters. Section 3 provides numerical illustrations of this methodology. Calculations for a one-site model of methanol highlight the robustness of the MS-CG variational method by considering various basis sets, approximations, and numerical solvers. Calculations for a multisite model of the ionic liquid demonstrate the power and flexibility of the method in determining both bonded and nonbonded interactions for a more complex molecular system. The methodology described in Sec. 2 and the numerical illustrations presented in Sec. 3 are discussed in Sec. 4. Concluding remarks and directions for future work are then provided in Sec. 5.
COMPUTATION OF THE CG POTENTIAL
Paper I presents the basic theory of a CG model that is consistent with an atomistic model. Paper I also shows how to construct a CG model that is consistent with a specific atomistic model and how to employ the MS-CG variational principle to determine the many-body PMF for the CG model. As in Paper I, we consider CG models in which there are no rigid intramolecular constraints. We also assume that the CG model under consideration is to be constructed in a way that satisfies the restrictions stated in Paper I. Paper I discussed a variety of choices that are possible in constructing the CG model. Here, we restrict attention to a specific subset of those choices that we believe may be particularly useful. In particular, we assume that no atom is involved in the definition of more than one CG site. The dIi coefficients (see Paper I for more details) are then chosen so that the atomistic force FI on site I is simply the unweighted sum of the atomistic forces acting on the atoms involved in the definition of that site. We note in passing that if the CG site masses are appropriately chosen, the equilibrium momenta distribution of the CG model will be equal to the distribution implied by the atomistic model and the relevant CG mapping. (See Paper I for more details about this and other considerations in constructing a consistent CG model.) As a final preliminary remark, we note that while in Paper I the symbols U and F were reserved for the exact many-body PMF and the force field derived from its gradients, in the present work these symbols are used to represent the MS-CG potential and the associated MS-CG force field, which are approximations to the exact PMF and CG force field that are obtained using the MS-CG variational principle.
Basis functions to represent the coarse-grained potential
To implement the variational calculation discussed in Paper I, it is necessary to construct basis functions for use in constructing approximations to the CG potential. The negative of gradients of those basis functions with regard to the CG site positions then are basis functions for the CG force field.
To construct these basis functions, we regard the CG potential as a sum of various types of contributions each of which is analogous to one of the types of contributions used to describe intramolecular and intermolecular interactions in an atomistic model. The CG potential is regarded as a sum of electrostatic interactions between pairs of charged sites, nonbonded and bonded interactions between pairs of sites, bond angle bending energies, and internal rotation energies. Then, for each type of contribution (with the exception of the electrostatic interactions), we construct flexible basis functions that can represent the functional form appropriate for that type of contribution. In effect, we use physical intuition to decide on what contributions to include and how to represent them, but the net result is a set of basis functions for the variational calculation. Using this procedure generates CG potentials that are of a form such that existing computer programs for atomistic models can straightforwardly be modified to perform simulations of the CG model. In this subsection, we discuss how this can be done for certain types of contributions to the CG potential.
The first step is to classify the CG sites on the various molecules according to their chemical nature and to determine which sites are to be regarded as directly bonded. Then a charge should be assigned to each site. Previous applications of the method have demonstrated that, for certain systems,36, 41, 42, 44 the effects of long-ranged electrostatic interactions between atoms may be reproduced with short-ranged nonbonded interactions between CG sites. In such cases, each site can be assumed to have a zero charge. An alternative is to assign each CG site a charge equal to the net charge of the atoms involved in the definition of the site. In any case, it is important, of course, that the total net charge assigned to the sum of all the sites is zero. The Coulomb contribution to the CG potential is
| (1) |
where RI denotes the position of CG site I and QI is the charge assigned to site I and the summation is over distinct pairs of sites.
The various types of non-Coulombic interactions that are easily included in the CG potential U(RN) are the following: (1) a bond vibration interaction for two bonded sites on the same molecule, (2) an angle bending interaction for two bonds formed by the same site to two other sites, (3) an internal rotation interaction for a dihedral angle defined by the positions of four sequentially bonded sites, and (4) a pairwise nonbonded interaction for two sites on different molecules as well as for sites on the same molecule that are separated by more than three bonds. For simplicity, we assume that a bond vibration interaction potential can be regarded a function of the scalar distance between the two bonded sites. We assume that an angle bending interaction potential can be regarded as a function of only the bond angle. We further assume that an internal rotation interaction can be regarded as a function of only the dihedral angle. We also assume that a nonbonded interaction potential can be regarded as a function of only the scalar distance between the two sites. In each case, the functional form of the interaction depends on the chemical nature of the sites. In all cases, the interaction is expressed as a function of a scalar variable (a distance or an angle), but the value of that variable is determined by the positions of two, three, or four sites, depending on the type of interaction.
With these assumptions, the CG potential can be written as
| (2) |
Here, ζ denotes one of the four types of non-Coulombic contribution listed above (e.g., a bond vibration energy), i denotes one of the functional forms for an interaction of type ζ (e.g., the function appropriate for vibration of a bond of a specific type on a specific type of molecule), γ denotes a specific set of sites that has an interaction of type ζ described by the functional form i (e.g., a specific pair of such bonded sites on a specific molecule), xζ denotes the scalar variable for that interaction (e.g., the distance between the two bonded sites), and {R}γ denotes the positions of the set of sites γ (e.g., the positions of the two specific sites associated with γ). The sum is over all types of contributions ζ, all functional forms i that describe the type of interaction, and over all sets of sites γ for which that functional form applies. The function Uζi(x) describes the dependence of the contribution on the relevant scalar variable (e.g., the bond stretching energy as a function of bond distance). The function xζ({R}γ) gives the scalar variable as a function of the relevant site positions.
The corresponding CG forces are
| (3) |
where
| (4) |
For each Uζi, we construct a set of basis functions uζid(x) that are functions of only the scalar variable appropriate for the interaction and represent the function as a linear combination of basis functions as follows:
| (5) |
We define
| (6) |
Then we have
| (7) |
| (8) |
where
| (9) |
Equation 8 explicitly demonstrates that the CG force field depends linearly on the coefficients ϕ that are to be variationally determined. To simplify the following discussion, it is convenient to replace the summation in Eq. 8 that runs over each interaction type ζ, each functional form i describing the interaction type ζ, and each coefficient d employed in representing the associated potential function Uζi, with a single summation over all ND coefficients in the CG force field. The force on CG site I in configuration RN may then be re-expressed as
| (10) |
where each value of the index D corresponds to one of the possible combinations of the three indices ζid in Eq. 8.
See Appendix A for a brief discussion of the basis functions, fζid, used in the present work. The particular set of basis functions employed for representing a given set of interactions may play an important role in the success of the method and is the subject of present research. See Appendix B for a discussion of the vector valued functions GI;D(RN). More complicated contributions, such as three-body nonbonded interactions and bonded interactions that include interactions between bond stretches and bond angle variations, can also be constructed but have not been used to date.
Linear equations for the MS-CG force field
For each D in Eq. 10, the set of N functions GD={G1;D(RN),…,GN;D(RN)} is a member of an abstract vector space of CG force fields defined in Paper I. Each of the N elements of a generic member of that space is a function that specifies a force on one of the N CG sites. The set of ND abstract vectors {G1,…,GND}, whose functions appear in Eq. 10, forms a basis for a subspace of the abstract vector space of CG force fields. A set of ND coefficients {ϕ1,…,ϕND} then specifies a non-Coulombic contribution, which is in this subspace, to the CG force field F that is defined by Eq. 10. This set of ND basis vectors does not span the complete space of all possible CG force fields. Consequently, given this set of basis vectors, the CG force field derived from the many-body PMF is, in general, not equal to the sum of Coulombic and non-Coulombic contributions expressed in Eq. 10.
As discussed in Paper I, the MS-CG variational principle can be used to determine the CG force field that is in the subspace just mentioned and that is the unique optimal approximation, within that subspace, for the force field derived from the exact many-body PMF. In the present work, the CG force field is defined by Eq. 10 and the MS-CG variational principle is employed to determine the optimal approximation of this form to the many-body PMF. The parameters {ϕD,D=1,…,ND} that minimize the function
| (11) |
| (12) |
where
| (13) |
determine this optimal approximate CG force field, which we shall refer to as the MS-CG force field. In Eq. 11, is the total force on the atoms involved in the definition of CG site I in configuration and the angular brackets denote an average over the configurations sampled by an atomically detailed MD simulation. As defined in Eq. 13, the quantity is the difference between the total force on the atoms involved in the definition of site I and the electrostatic forces on CG site I in the CG representation of the same configuration. (Note that one may also choose to include all interactions, including Coulombic, in the total forces, resulting in only the variationally determined CG interactions remaining in the final MS-CG potential.) Equation 12 replaces the time average in Eq. 11 with an explicit sum over the nt sampled configurations and also expresses the MS-CG force as an explicit function of the CG force field coefficients {ϕD} according to Eq. 10. According to Eq. 11, the MS-CG force field also provides the best fit, in a least squares sense, among all CG force fields of this form, to the chosen instantaneous atomistic forces on the CG sites when averaged over sites and sampled configurations.36, 37, 50, 51
Equation 12 demonstrates that the MS-CG force field is determined by a linear least squares problem52, 53, 54 for the force field parameters, {ϕD}. There exist many numerical methods for solving linear least squares problems of this type.52, 53, 54, 55, 56 In principle, all methods lead to the same solution. However, in practice, the numerical accuracy and computational expense of various numerical methods may differ. Further consideration of numerical methods for minimizing the MS-CG residual is facilitated by re-expressing Eq. 12 in explicit matrix notation. In the following, denotes a column vector of 3ntN elements, where each element is a Cartesian component of a vector describing a force on a particular CG site, I, in a particular sampled atomistic configuration, . The quantity then is a similar column vector of 3ntN elements, for I=1,…,N and t=1,…,nt, where each element is a Cartesian component of the force on a CG site, I, in a sampled configuration, , generated by a basis function, D. The matrix formed from ND columns, each of which is a vector for D=1,…,ND, is a matrix, , of 3ntN rows and ND columns. The set of ND parameters forms a vector, , the Dth element of which is simply ϕD. In this notation, the MS-CG residual may be expressed as
| (14) |
where T denotes the vector∕matrix transpose. is a quadratic function of the coefficients in that is bounded from below by zero. If the set of ND vectors is linearly independent, then the matrix is full rank and the minimum of this quadratic form is unique. The following analysis will assume that this is the case. However, it is demonstrated in Sec. 3 that the MS-CG variational principle may also be employed when is not full rank. Appendix C further discusses this possibility.
The quadratic function expressed in Eq. 14 may be minimized by various numerical methods that treat the matrix of 3ntN row and ND columns, .52, 53 In particular, the matrix may be numerically analyzed using techniques such as QR decomposition or singular value decomposition (SVD).52, 53 The resulting matrix decomposition may then be employed to determine the parameter set {ϕD} that provides the true minimum of Eq. 11. Alternatively, iterative techniques involving may be employed to minimize the residual.52, 53, 54, 55, 56 However, in previous applications of the MS-CG method, the matrix has been too large to efficiently treat with available computer memory and the CG force field parameters {ϕD} have been determined by minimizing using a block-averaging (BA) approximation.36, 37 To make such an approximation, the nt configurations are partitioned into disjoint sets (blocks). A residual of the form given in Eq. 12 is calculated and minimized separately for each block to determine the parameters {ϕD} associated with each block of data. For each D, the average of ϕD over all blocks is calculated, and the results give a set of {ϕD} coefficients that approximately minimize the total χ2 in Eq. 12. Further discussion of the BA approximation is provided in Appendix D.
The MS-CG residual may also be expressed in terms of the normal (i.e., symmetric) matrix of ND rows and ND columns as follows:
| (15) |
where and . The elements of and are given by
| (16) |
| (17) |
for D,D′=1,…,ND. There exist various numerical techniques for minimizing the MS-CG residual that address the normal matrix . The MS-CG force field parameters may be determined by numerically minimizing the positive definite quadratic function in Eq. 15 using standard iterative methods such as steepest descent or conjugate gradient methods that involve iterative multiplication with the normal matrix .53, 54, 55, 56 Alternatively, the MS-CG force field may be determined by directly solving the normal system of ND equations for ND unknowns48, 53 obtained from finding the stationary point satisfying , for D=1,…,ND
| (18) |
This system of equations may be directly solved using standard methods such as Gaussian elimination or LU decomposition.52 For sufficient sampling (i.e., sufficiently large nt), numerical methods that address the normal matrix, , of ND rows and ND columns require much less memory than methods that treat the matrix, , of 3ntN rows and ND columns in Eq. 14. However, the condition number for the normal matrix is the square of the condition number for the nonsquare matrix .52, 53 Consequently, numerical methods that address the normal matrix may be less accurate than those that involve the matrix . This issue may be partially alleviated by appropriate preconditioning of .54
RESULTS
The previous section demonstrated that the MS-CG method determines an optimal approximation to the many-body PMF by numerically solving a linear least squares problem for the CG force field parameters. The present section illustrates this method for two liquid systems: methanol and the 1-ethyl-3-methylimidazolium nitrate ionic liquid. By considering a one-site CG model for methanol, various basis sets for the nonbonded force field and different methods for solving the MS-CG equations may be directly compared. Calculations for the ionic liquid system demonstrate the application of the MS-CG method for determining a molecular CG force field. The reader is referred to Refs. 36, 37, 38, 39, 40, 41, 42, 43, 44, 45 for additional applications of earlier versions of the MS-CG methodology.
MS-CG methanol model
An all-atom model of 1000 methanol molecules was simulated for 1.0 ns with an integration timestep of 1.0 fs using the DḺPOLY software package.57 Interactions between atoms were modeled using parameters from the OPLS-AA force field58 and did not include rigid constraints. The simulation was performed in the constant NVT ensemble in a cubic box of V=(40.9 Å)3 under periodic boundary conditions1, 2 with the temperature T=300 K maintained by the Nose–Hoover thermostat.59, 60 Long-ranged electrostatic interactions were calculated using the Ewald method61 and both the real-space contribution to the Ewald sum and the short-ranged nonbonded interactions were truncated at 12.2 Å. The coordinates, velocities, and forces for each atom were recorded every 1.0 ps during the course of the trajectory to obtain nt=1000 configurations.
A single CG site was assigned for each methanol molecule and the {cIi} coefficients were defined so that the coordinates of each CG site correspond to the center of mass for the associated methanol molecule. The CG mapping operator defined in Eq. (9) of Paper I was applied to each configuration sampled from the atomistic trajectory to generate nt CG configurations. The radial distribution function (RDF) for the CG sites was calculated from the mapped configurations and is presented as the dashed curve in Fig. 1. The mass for each site was defined as the total mass of the methanol molecule and the momentum of each site was computed by mapping the atomistic momenta according to Eq. (10) in Paper I.46 The distribution of momenta for the sites was calculated and is presented as the dashed curve in Fig. 2. The present mapping is appropriate for developing a CG model that will be consistent in phase space with the given atomistic model according to the theory presented in Paper I.
Figure 1.
The RDFs computed from simulations of the atomistic (dashed curve) and MS-CG (solid curve) model of methanol are compared. The difference between the two curves results from the use of basis functions that describe the CG force field as a sum of pairwise additive terms. This small difference indicates that the many-body PMF for the one-site CG model of methanol is well represented by a sum of pair-additive interactions between sites.
Figure 2.
The distribution of the velocities of CG sites in the y direction computed from MD simulations of the atomistic (dashed curve) and MS-CG (solid curve) model of methanol.
For the one-site methanol model, the parameter QI=0 for each CG site I because each methanol molecule has zero net charge. The MS-CG interaction potential was therefore defined by a sum of short-ranged nonbonded central pair potentials, Uζi=US, between identical CG sites. The pair forces between CG sites were represented with either discrete delta, linear spline, or cubic spline basis functions that are defined in Appendix A. For each basis set, the pair force was represented using a uniform grid with grid points separated by 0.0529 Å and the pair force was assumed to vanish for intersite distances greater than 12.0 Å. The set of basis functions, {fSd(R)}, representing these pair forces, then determined the set of force field basis vectors, {GD}, for a vector subspace of trial CG force fields.
For each set of basis functions described in Appendix A, the MS-CG force field was determined by minimizing the residual using a biconjugate gradient algorithm55, 56 employing iterative vector-matrix multiplication with the matrix . Even for the present simple system of N=1000 molecules and using sparse matrix techniques, the 3ntN by ND matrix requires significant computational memory and iterative minimization with could not be efficiently performed using all nt=1000 sampled configurations. Consequently, the BA solution was obtained by partitioning the set of nt configurations into nB=100 disjoint sets (blocks) of configurations each, such that each block corresponded to ten configurations sampled consecutively during the trajectory. The biconjugate gradient algorithm55, 56 was employed with the matrix determined by the configurations in block B to iteratively minimize the MS-CG residual function for each block independently and the resulting 100 CG force functions were averaged. Further discussion of the BA approximation is provided in Appendix C, where it is demonstrated that the error in the BA approximation may be systematically reduced by shuffling configurations between blocks.
Additionally, the MS-CG residual was iteratively minimized using the same biconjugate gradient algorithm55, 56 with the normal matrix determined by each set of basis functions. (In this application, the biconjugate gradient algorithm is equivalent to a conjugate gradient algorithm.) For each calculation with the normal matrix, was right-preconditioned54, 56 so that the Euclidean norm of each column in the processed matrix was rescaled to unity. Table 1 presents estimates of the condition number for the normal matrix both before and after preprocessing. Preconditioning has a dramatic effect on the condition number (and thus the convergence and accuracy of the solution) for the normal equations. In each case, the condition number was estimated by explicitly determining all of the singular values or eigenvalues for the relevant matrix using the SVD algorithm implemented in the LAPACK library62 and calculating the appropriate ratio.
Table 1.
Parameters describing calculations using various methods for minimizing the MS-CG residual function to obtain the methanol CG pair force. The total number of parameters, ND, the magnitude of the MS-CG residual, , and the condition number (both before and after preconditioning) obtained from iteratively minimizing the residual using either the normal matrix (normal) or the nonsymmetric matrix with the block-averaging (BA) approximation are presented for each basis set. The BA result for the cubic spline has been presented for both 980 (b) and 1000 (c) configurations. Poor sampling of the core region in the 99th block introduced statistical error into the BA calculation for the cubic spline basis set resulting in an abnormally high magnitude residual. Every other variational calculation described in the table employed the same 1000 configurations sampled from atomistic MD simulations of the methanol as discussed in the text. In each calculation employing the BA approximation, these 1000 configurations were partitioned into 100 disjoint sets of 10 configurations each, the MS-CG variational calculation was performed with the configurations in the block, and the resulting 100 calculated force curves were averaged.
| System | Basis | Condition No. | ND | (kcal mol−1 Å−1)2 | |
|---|---|---|---|---|---|
| Original | Preconditioned | ||||
| BA | Delta | ⋯ | ⋯ | 210 | 21.1396 |
| BA | Linear | ⋯ | ⋯ | 210 | 21.1031 |
| BA | Cubic | ⋯ | ⋯ | 420 | 21.1238a∕24.9257b |
| Normal | Delta | 240 856 | 7.5521 | 210 | 21.1396 |
| Normal | Linear | 3.1487×106 | 12.344 | 210 | 21.0964 |
| Normal | Cubic | 9.9103×1012c | 27.913 | 420 | 21.2624 |
From 980 configurations.
From 1000 configurations.
Should be considered a lower bound.
Table 1 also presents the magnitude of the MS-CG residual function evaluated for the CG force fields calculated using either the or the matrix to iteratively minimize the residual function for each basis set. The CG force field calculated by iteratively minimizing the MS-CG residual function using the biconjugate gradient algorithm with the normal matrix determined by the linear spline representation yielded the smallest value for the residual function. The associated CG pair force is presented as the solid curve in the inset of Fig. 3. It is clear that, upon preconditioning, the normal matrix becomes sufficiently well conditioned to obtain an accurate solution. The differences between the three CG pair forces obtained by iteratively minimizing the MS-CG residual function with the normal matrix in each basis set are presented as the thin curves in the background of Fig. 3. The differences between the CG pair force calculated by treating the normal matrix in the linear spline basis and the CG pair forces calculated by treating in each basis are presented as the thick curves in the background of Fig. 3. All of the calculated pair forces are very similar for intersite separations greater than 3 Å.
Figure 3.
The inset presents the pair CG force calculated using the linear spline basis and a conjugate gradient algorithm involving the normal matrix to iteratively minimize the MS-CG residual. This force function provides the most accurate approximation to the many-body PMF obtained in the present calculations. See Table 1. The main figure presents the difference between this calculated force and force calculated in various other ways. “Normal” refers to the use of the normal matrix and a conjugate gradient algorithm, whereas “block-averaged” refers to the use of nonsymmetric matrix, a biconjugate gradient algorithm, and the BA approximation. “Delta” refers to the use of the delta function basis, “linear” refers to the use of the linear spline basis, and “cubic” refers to the use of the cubic spline basis representation. All the calculations used approximately the same large number of configurations and so all are subject to approximately the same statistical error. The small differences among the curves for R>3 Å demonstrate that in this case the systematic error in the BA approximation is negligible for the block size used and that the calculated CG force function is insensitive to the basis set used and the algorithm used to minimize the residual.
Two other independent calculations of the CG pair forces were performed. The CG pair force was calculated using LU decomposition to directly solve the normal system of equations in the discrete delta function basis. Additionally, the CG pair force was calculated by employing the BA approximation to minimize the MS-CG residual function via the biconjugate gradient method employing the matrix determined by the cubic spline basis, but with additional rows added to the matrix for each block B. These additional rows in the matrix are not required by the variational calculation. For each grid point, these equations (approximately) ensure the continuity of the first derivative of the pair force represented by the cubic spline basis.36, 37 Although not presented in Fig. 3, the CG pair forces obtained by these two independent calculations are very similar to the pair forces included in the figures and described above. These numerical results along with those presented in Fig. 3 for the one-site CG model of methanol indicate that the MS-CG variational calculation is quite stable. The MS-CG force field is relatively insensitive to the method used to minimize the residual function as well as to the basis functions employed in representing the CG interactions. Furthermore, these results indicate that the BA approximation does not introduce significant systematic error into the calculation of the pair force field for the one-site CG model of methanol.
As discussed in Appendix C, because each methanol molecule generates an excluded volume, there is a “core region” of distances between the centers of methanol molecules, R<Rcore, that is never sampled during the atomistic MD simulations. Consequently, the force field parameters describing the interaction between CG sites within this core region cannot be determined from the atomistic simulations. From Fig. 1, it can be seen that Rcore≈2.7 Å. Moreover, because of poor sampling near this core region, the pair potential cannot be accurately calculated for R=Rcore+ϵ, for some small positive ϵ that depends both on the force data and the basis set. Artifacts arising from the inadequate sampling of the core region are easily recognized as anomalous spikes or unphysical attractive wells in the pair force for small R. These artifacts have been discarded from the results in Fig. 3. The MS-CG force curves have been extended into the core region by simply defining the pair force for R<Rcore to be the maximum repulsive force for R≈Rcore that has been unaffected by sampling artifacts, as shown in the figures. In practice, this approach introduces little error into the MS-CG method because these small intersite distances are rarely sampled in either atomistic or CG simulations and because it is clear from Figs. 13 that ϵ⩽0.2 Å. Other interpolations of the force curves into the unsampled core region are clearly possible.
MD simulations of the CG one-site methanol model were then performed using the CG pair force that was determined by solving the normal system of equations in the linear spline basis set and that has been presented in the inset of Fig. 3. As shown in Fig. 3, the MS-CG force field parameters near the core region were determined so that the magnitude of the repulsive force in the core region was a constant with magnitude equal to the largest force determined outside of the core region, i.e., for R=Rcore+δR, as discussed above. After extending the CG pair force into the core region, the CG pair force was then tabulated as a function of distance on a finer grid of 0.005 29 Å using the linear spline basis functions. The associated pair potential energy function was also tabulated as a function of distance on this finer grid by integrating the linear basis functions. The resulting tables were provided as input into the DḺPOLY software package,57 which further interpolated the pair force and pair potential via a three-point interpolation scheme.
The CG one-site methanol model was then simulated for 2.0 ns in the constant NVT ensemble with an integration timestep of 2.0 fs using the DḺPOLY MD program.57 The same volume and temperature were used in the CG simulations as in the atomistic simulations and the Nose–Hoover thermostat59, 60 was used as before. Configurations and velocities were sampled every 2.0 ps and the CG site-site RDF and momenta distribution were computed from 1000 sampled phase space points. These CG distribution functions are presented as the solid curves in Figs. 12. It is clear that the MS-CG one-site methanol model determined from the linear least squares problem described in Sec. 2 quantitatively reproduces the pair structure of the liquid and reproduces the momentum distribution essentially exactly. The agreement of the two momentum distributions is, of course, a trivial consequence of the fact that both distributions are Maxwell–Boltzmann distributions for the same mass and temperature. Moreover, the agreement in Fig. 1 between the RDFs computed for the atomistic and CG methanol models demonstrates that the pair-additive potential employed in the CG model provides an adequate approximation to the many-body PMF for the one-site methanol model. Figures 12 together illustrate the concept of consistency in phase space introduced in Paper I.
MS-CG ionic liquid model
The molecular structure of the ionic liquid pair is presented in Fig. 4. Ionic liquids have demonstrated great potential for industrial and other applications.63, 64 However, because of their complex and glassy phase behavior, the physical properties of certain ionic liquids cannot be adequately investigated with atomically detailed models.40 Consequently, the ionic liquid provides a good system to illustrate the capability of the MS-CG method for developing consistent CG models of complex molecular systems.
Figure 4.
The molecular structure of the ion pair is represented with five CG sites. CG sites A, B, C, and E describe the cation, while site D describes the anion. The coordinates of each site are defined by the center of mass coordinates for the atoms involved in the site.
An atomically detailed nonpolarizable model of 64 ion pairs was simulated with the DḺPOLY software package57 for 60 ns after equilibration using an integration timestep of 1.0 fs. The atomistic force field did not include rigid constraints and has been previously described in Refs. 65, 66. The simulation was performed in the constant NVT ensemble in a cubic cell with V=(25.0 Å)3 under periodic boundary conditions.1, 2 The temperature T=400 K was enforced with the Nose–Hoover thermostat59, 60 and the Ewald method61 was employed to calculate long-ranged electrostatic interactions, with both short-ranged nonbonded interactions and the real-space contribution to the Ewald sum truncated at 12.0 Å. The atomic coordinates, velocities, and forces were sampled from this trajectory every 1.0 ps to obtain nt=6×104 configurations.
The CG mapping for the ionic liquid system represented each cation with four distinct CG sites and each nitrate ion with a single CG site as illustrated in Fig. 4 and described in Table 2. The two terminal methyl groups and also the methylene group of the cation were represented by single CG sites, B, E, and C, respectively. The planar cationic ring was represented with CG site A and the planar nitrate anion by CG site D. This level of coarse-graining can be considered fairly “aggressive.” The {cIi} CG mapping coefficients defined in Eq. (9) of Paper I were determined such that the coordinates of each site correspond to the center of mass for the atoms involved in the site. Every atom in the atomistic model is involved in the definition of one and only one CG site. The mapping was applied to the sampled configurations to obtain nt CG configurations. RDFs, as well as bond-stretch, bond-angle, and bond-dihedral distributions were then calculated for the sites from these mapped CG configurations. Selected distribution functions are presented as the dashed curves in Figs. 56. The mass of each site was defined as the total mass of the atoms involved in the site. This CG mapping is sufficient to ensure that the CG model will be consistent in configuration space with the atomistic model of the ionic liquid system if the CG potential energy function is equal to the many-body PMF for the atomically detailed model.46 Moreover, the definitions of the CG site masses and mapping coefficients are appropriate for developing a CG model that will be consistent in phase space with the given atomistic model according to the theory presented in Paper I.
Table 2.
Parameters describing the CG mapping for the ionic liquid system. The coordinates for each site were defined by the center of mass coordinates for the set of atoms involved in the definition of the site. The mass and charge for each CG site were determined by summing the total masses and charges for the atoms involved in each site.
| CG site name | Involved atoms | Mass (amu) | Charge (e) |
|---|---|---|---|
| A | 1 2 3 4 5 9 10 11 | 67.0740 | +0.470 516 |
| B | 6 12 13 14 | 15.0340 | +0.219 052 |
| C | 7 15 16 | 14.0260 | +0.234 142 |
| E | 8 17 18 19 | 15.0340 | +0.076 290 |
| D | Nitrate ion | 62.0100 | −1.000 000 |
Figure 5.
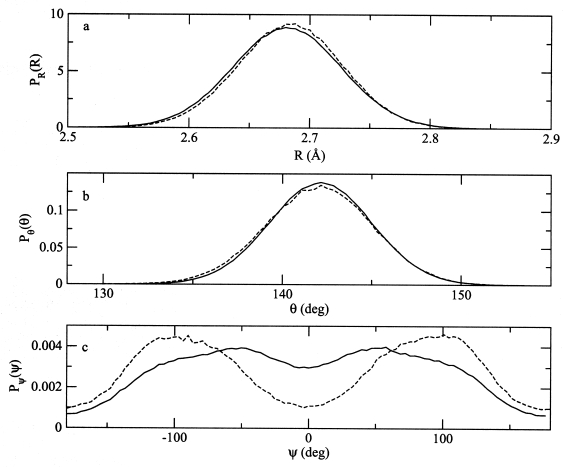
Bonded distribution functions calculated from MD simulations of the atomistic (dashed curve) and MS-CG (solid curve) model of the ion pair are presented for (a) the distribution of site A-C bond displacements, (b) the distribution of site B-A-C valence angles, and (c) the distribution of site B-A-C-E dihedral angles.
Figure 6.
Nonbonded RDFs calculated from atomistic (dashed curve) and CG (soli d curve) MD simulations of the ion pair are presented for the distributions of (a) A-A site pairs, (b) A-D site pairs, (c) D-D site pairs, and (d) E-E site pairs.
The many-body PMF was approximated by the MS-CG force field defined in Sec. 2 and included both nonbonded and bonded interactions. A point charge, QI, equal to the net charge of the atoms involved in the CG site was assigned to each site and the CG potential energy function included both short-ranged pair potentials and long-ranged Coulombic potentials for each pair of sites in distinct molecules. The CG intramolecular potential describing the interactions among the four sites within a single cation included the following terms: (1) bond-stretch potentials describing the interactions between pairs of bonded CG sites in the same cation, i.e., between E and C sites, between C and A sites, and between A and B sites; (2) bond angle potentials describing the interactions between E-C-A triples and between C-A-B triples in the same cation; and (3) a dihedral-angle potential describing the dihedral interaction between the E-C-A-B sites in the same cation. In principle, the MS-CG force field for the ionic liquid system might also include both short-ranged pair forces and long-ranged Coulombic forces among the CG sites within each cation. However, the version (2.14) of DḺPOLY employed in ensuing CG MD simulations treated nonbonded interactions (i.e., short-ranged central pair interactions and long-ranged Coulomb interactions) between pairs of sites in the same molecule equivalently to nonbonded interactions between sites in distinct molecules. Because the many-body PMF distinguishes between such types of interactions, it is likely that this approximation might introduce a significant error into the calculated MS-CG interaction potential. Consequently, these short-ranged nonbonded and long-ranged electrostatic interactions among sites within the same cation were not included in the MS-CG potential energy function for the ionic liquid system.
Analytic functional forms were not assumed in the MS-CG variational calculation of either the bonded or short-ranged nonbonded CG force field. Rather, the short-ranged nonbonded, bond-stretch, bond-angle, and bond-dihedral CG potentials were represented with discrete delta function basis functions of a single variable defined on a grid with uniformly spaced grid points as discussed in Appendix A. The short-ranged nonbonded force functions and the bond-stretch force functions were calculated as a function of intersite distance using a grid spacing of 0.04 Å. The bond-angle and bond-dihedral-angle force functions were calculated as a function of the relevant angle using a grid spacing of 1.0°. The assumed form of the CG potential and this set of basis functions determined a vector space of trial CG force fields spanned by the basis vectors {GD} that are included in Eq. 8 and discussed in Appendix B.
The coefficients defining the optimal approximation to the many-body PMF within this vector space were determined by the MS-CG variational principle according to the linear least squares problem derived in Sec. 2. For each sampled atomistic configuration, the atomistic force on each site was calculated according to Eq. (41) in Paper I as the net force on the atoms involved in the site. For each sampled configuration, the electrostatic force on each site, I, arising from the distribution of charged sites in each mapped CG configuration, , was calculated and subtracted from the total atomistic force on each site. The remaining atomistic force, , was then employed in the MS-CG residual for parametrizing the remaining force field terms in Eq. 8. The optimal MS-CG force field within this space of trial CG force fields was determined using a conjugate gradient algorithm52, 53 to iteratively minimize the MS-CG residual in Eq. 18 using the normal matrix GDD′. The matrix GDD′ was not preconditioned and after 3297 iterations the algorithm converged upon a solution with a relative error smaller than 10−12 in the residual function and .
Selected force functions, Fζi(x), in the CG force field that were parametrized by the MS-CG variational method are presented in Figs. 78. The calculated short-ranged nonbonded forces shown in Fig. 7 were smoothed using a Gaussian function to average the calculated forces over a centered window of nine consecutive data points. It is clear that these calculated pair forces are not well represented by any obvious functional form, e.g., Lennard–Jones. As shown in Fig. 7, the calculated short-ranged nonbonded interactions are mostly repulsive with weak attractive components. The attractive short-ranged nonbonded interaction between the anionic D CG sites is an exception to this trend. This interaction does not result in unphysical attraction between the anions, though, because it is overwhelmed at short intersite separation by the strong electrostatic repulsion between the anions.
Figure 7.
Short-ranged nonbonded interactions in the MS-CG force field calculated for the ionic liquid system are presented for (a) A-A site pairs, (b) A-D site pairs, (c) D-D site pairs, and (d) E-E site pairs.
Figure 8.
The analytic functional forms (solid curves) approximating the calculated MS-CG bonded interactions (dashed curves) in CG MD simulations of the ion pair are presented for the (a) the A-C bond interaction, (b) the B-A-C valence angle interaction, and (c) the B-A-C-E dihedral angle interaction.
In contrast, the calculated MS-CG bonded interactions are surprisingly well fitted by simple analytic functional forms. In particular, the calculated bond-stretch and bond-angle (dashed curves) force functions reflect strong restoring forces and are well described by harmonic forms (solid lines) as illustrated for the A-C bond stretch in panel a and for the B-A-C bond valence angle in panel b of Fig. 8. The force field for the atomistic model of the ionic liquid system involved 46 intramolecular dihedral-angle interactions among the 19 atoms in each ionic liquid cation shown in Fig. 4. Each of these dihedral-angle interactions in the atomistic model was described by a force function57 of the form A sin(mψ−ψ0) with m=2 or 3 as specified by the AMBER force field.67 The CG potential includes only one intramolecular dihedral interaction among the B-A-C-E sites and the calculated bond-dihedral-angle force function (dashed curve) is presented in panel c of Fig. 8. The calculated dihedral-angle force function is significantly weaker and also slightly more noisy than the other bonded interactions. However, it is clear from Fig. 8c that the calculated MS-CG dihedral force function is quite accurately described by the sine series (solid curve), A1 sin(ψ)+A2 sin(2ψ)+A3 sin(3ψ)+A4 sin(4ψ), using parameters that are provided in Table 3. This calculated MS-CG dihedral force function has incorporated the effects of both bonded and nonbonded interactions averaged over the local atomistic environment so that the calculated CG force field provides an optimal approximation to the many-body PMF.
Table 3.
Parameters describing the bonded MS-CG force field for the ionic liquid system. The bonded MS-CG interactions were determined without assuming any functional forms but were then approximately represented by the analytic functions described above in CG MD simulations with the DḺPOLY program (Ref. 57). The analytic functional form for each interaction and the parameters used in fitting the MS-CG interactions are presented.
| Interaction type | ζ | CG sites | Functional form | k (eV∕Å2) | ζ0 (Å) |
|---|---|---|---|---|---|
| Bond stretch | Ri | A-B | Harmonic | 17.6582 | 2.70472 |
| A-C | Harmonic | 17.4053 | 2.69201 | ||
| C-E | Harmonic | 22.8097 | 1.65874 | ||
| (eV∕rad2) | (deg) | ||||
| Valence angle | θi | B-A-C | Harmonic | 13.7542 | 142.610 |
| A-C-E | Harmonic | 5.4842 | 107.783 | ||
| Dihedral angle | ψ | B-A-C-E | |||
| F(ψ)=A1 sin(ψ)+A2 sin(2ψ)+A3 sin(3ψ)+A4 sin(4ψ) | |||||
| A1 (eV∕rad) | A2 (eV∕rad) | A3 (eV∕rad) | A4 (eV∕rad) | ||
| −0.019 498 4 | 0.030 294 1 | −0.015 229 5 | 0.016 448 3 | ||
MD simulations of the MS-CG model for the ionic liquid system were then performed with the calculated MS-CG force field using the DḺPOLY software package.57 Each tabulated short-ranged nonbonded interaction was linearly extended into the core region such that FSi(0)=FSi(Rcore+δ)+230.6 kcal mol−1 Å−1 and Rcore+δ was determined independently for each interaction form i as described for methanol. The resulting nonbonded interactions were employed as input force field files for the MD program without further smoothing, interpolation, or other modification. In principle, the tabulated MS-CG bonded forces could also be directly employed as a bonded force field for simulations of the CG model. However, in the present work, the tabulated bonded interactions were fitted to analytic functional forms that have been implemented within the DḺPOLY software package.57 These approximate representations of the bonded interactions determined by the MS-CG variational procedure were then employed as a bonded force field for simulations of the CG ionic liquid model. As demonstrated in Figs. 8a, 8b, the bond-stretch and bond-angle forces between CG sites were fitted to harmonic restoring forces with parameters provided in Table 3. As shown in Fig. 8c and discussed above, the dihedral-angle force was fitted to a sine series with parameters provided in Table 3. (The authors implemented this dihedral-angle force function and the associated potential energy function into DḺPOLY version 2.14.)
The MS-CG model for the ionic liquid system was simulated for 60.0 ns using an integration timestep of 4.0 fs in the constant NVT ensemble under the same thermodynamic conditions employed in the atomistic simulations, i.e., V=(25.0 Å)3 and T=400 K. Long-ranged electrostatic interactions between sites were computed using the Ewald method61 and both the short-ranged nonbonded interactions and the real-space contribution to the Ewald sum were truncated at 12.0 Å. The temperature was maintained using the Nose–Hoover thermostat.2, 59, 60 CG configurations were sampled from the MD trajectory every 4.0 ps. Bonded and nonbonded distribution functions were computed from these configurations and compared with the distribution functions calculated from the CG representation of the original atomistic trajectory. The CG bonded and nonbonded distributions generated by the MS-CG model are presented as the solid curves in Figs. 56 and qualitatively reproduce the distributions calculated from the CG representation of the atomically detailed configurations.
As illustrated in panels a and b of Fig. 5, the distributions of bond lengths and bond angles are nearly quantitatively reproduced in the MS-CG model. Both the center and the shape of the bond-length and bond-angle distributions generated by the MS-CG model agree very well with the distributions generated by the atomistic model. Panel c of Fig. 5 compares the dihedral-angle distribution sampled by the atomistic and MS-CG ionic liquid models. In qualititative agreement with the atomistic model, the MS-CG model generated a bimodal distribution of dihedral angles with minima at 0 and ±π. However, the agreement between the dihedral distributions generated by the atomistic and CG ionic liquid models is otherwise less satisfactory. The bimodal peaks of the dihedral distribution generated by the MS-CG model are too broad and not centered at the correct angle, while the minimum of the distribution at ψ=0 is sampled too frequently. As discussed in greater detail below, it is likely that the agreement between the atomistic and CG dihedral distributions would significantly improve if nonbonded interactions between B and E CG sites in the same cation were included in the CG potential.
The MS-CG model qualitatively reproduces the pair structure of nonbonded sites in the ionic liquid system. The positively charged ring of the amphiphilic ionic liquid cation forms an interface with the nitrate ion that facilitates aggregation of the hydrophobic cation alkyl tails.68, 69 The structure of this interface and the associated hydrophobic aggregation are described by the RDFs computed from simulations of the atomistic (dashed curves) and CG (solid curves) models that are presented in Fig. 6. As shown in panel a, the fine structure in the shoulder of the distribution for the cationic rings is lost in the CG model because the planar cationic ring and the planar nitrate anion have both been represented with spherically symmetric sites, although the CG and atomistic A-A RDFs agree quite well otherwise. The stacking of cationic rings with planar nitrate ions is described by the RDF for the A-D sites presented in panel b. It can be seen that the CG model reproduces the primary features of this interface despite the spherical symmetry of the sites. Panel c presents the RDF for pairs of anions represented by D CG sites. The planarity of the nitrate anions allows close approach between anions in the atomistic model that is sterically unfavorable for the spherical D CG sites. Similarly, the CG model also overestimates the pair distribution at R=6 Å. Finally, panel d presents the E-E site RDF, which describes the aggregation of cation alkyl tails. The MS-CG model nearly quantitatively reproduces this hydrophobic association.
In summary, the MS-CG ionic liquid model reproduces the equilibrium structure generated by the atomistic model with semiquantitative accuracy. The results shown in Figs. 5c, 6a indicate that the selected set of force field basis vectors is too restrictive to allow an approximation to the exact many-body PMF that is sufficiently accurate to quantitatively reproduce the distribution of dihedral angles or the pair distribution of planar cation rings. In particular, the results suggest that the bonded intramolecular force functions used were not sufficiently flexible to describe the intramolecular CG interactions. The MS-CG variational method has also been employed to calculate a CG potential energy function that included contributions from Coulombic interactions between B and E sites in the same cation. MD simulations of the CG model were then performed using this reparametrized and slightly more complex potential energy function. However, the agreement between the dihedral distributions sampled by the atomistic and CG models was not significantly improved. (Data not shown.) Paper I proved that, given adequate sampling, the calculated MS-CG potential energy function will become an increasingly accurate approximation to the exact many-body PMF as additional basis vectors are included in the MS-CG variational calculation. Consequently, in order to reproduce the atomistic dihedral distribution, the CG potential energy function should be extended to either include more complex bonded potential functions or contributions from non-Coulombic nonbonded interactions between B and E sites in the same cation. The effect of more complex potentials may be further investigated in future work. Nevertheless, Fig. 5 demonstrates that, despite the relatively restrictive set of basis vectors included in the present CG potential, the present MS-CG approximation to the many-body PMF is sufficiently accurate to reproduce the intramolecular bond-stretch and bond-angle distributions with nearly quantitative accuracy. Moreover, the RDFs shown in Fig. 6 demonstrate that the present MS-CG model also reproduces the primary features of the interfacial structure and hydrophobic aggregation of the ionic liquid system.
DISCUSSION
The present work applies the MS-CG theory described in Paper I to develop molecular CG models. The MS-CG variational principle has been employed to systematically parametrize both pair bonded and nonbonded interactions as well as bond-angle and dihedral-angle interactions involving three and four CG sites, respectively. Quite generally, this variational principle may be employed to parametrize interactions of arbitrary form between any number of sites. Each contribution to the CG force field has been represented with a linear combination of vector valued functions with constant coefficients that serve as force field parameters. For each D, the set of vector-valued functions {GI;D(RN)} defines a contribution to the total force on each site in any configuration, RN, and the coefficient associated with this set, ϕD, determines the magnitude of this contribution. These vector valued functions then form a basis spanning a vector space of trial CG force fields. The MS-CG force field is determined by finding the set of coefficients {ϕD} that minimize the MS-CG residual function among all CG force fields within this vector space. Assuming that the atomistic trajectory data provide an accurate surrogate for an exact ensemble average, this MS-CG force field is the closest approximation to the exact many-body PMF within the vector space of force fields defined by the given basis set. The resulting MS-CG force field then provides the optimal “match” to the atomistic force field for the sampled atomistic configurations, .
As demonstrated in Sec. 2B, the set of parameters determining this optimal approximation is obtained by numerically solving a linear least squares problem.52, 53, 55, 56 This linear least squares problem may be solved by algorithms such as conjugate gradient minimization that iteratively minimize the MS-CG residual function itself, by algorithms such as Gaussian elimination that directly solve the normal equations for the stationary point of the residual, and also by algorithms such as SVD that decompose the nonsymmetric matrix, . Methods that address the nonsymmetric matrix, , are expected to be more accurate but also more computationally expensive than methods that address the normal matrix, .52, 53 In previous applications, the computational expense of treating has been circumvented via a BA approximation.36, 37, 38, 39, 40, 41, 42, 44 The present calculations numerically validated this BA approximation for a methanol system.
Alternatively, the MS-CG force field may be determined by solving the associated set of normal equations.48, 53 The normal system of equations provide considerable insight into the MS-CG method because these equations are expressed in terms of correlation functions calculated from the CG representation of configurations sampled with the atomistic model.48 As shown in Eq. E1 in Appendix E, the quantity bD′ quantifies the correlation between the atomistic force field (more precisely, the part of the atomistic force field, , that is different from the CG electrostatic force field) and the force field basis vector, GD′, associated with the parameter ϕD′. In fact, bD′ is the projection of this force field onto the particular CG force field basis vector. However, because the ND basis vectors, {GD}, representing the CG force field describe correlated molecular interactions, this basis set is, in general, not orthonormal. The off-diagonal elements in GDD′ quantify the nonorthogonality of the basis vectors associated with distinct force field parameters ϕD and ϕD′. The MS-CG method thus constructs an effective CG force field by considering the correlations between different types of CG interactions calculated from the CG representation of sampled atomistic configurations. For systems governed by central pair potentials, the normal MS-CG equations are related to the well known Yvon–Born–Green equation70 and determine the CG pair interaction from knowledge of two- and three-body correlation functions.48 For more complex molecular systems with bonded and nonbonded interactions, the present analysis demonstrates that the MS-CG method considers not only two- and three-body correlations between nonbonded sites, but also correlations between different bonded interactions, as well as correlations between bonded and nonbonded interactions in the CG force field. By considering these complex many-body correlations, the MS-CG procedure projects the atomistic force field into the vector space of CG force fields spanned by a given set of basis vectors and, in the limit of adequate sampling, determines the optimal approximation to the CG PMF within this vector space.
The MS-CG variational principle provides considerable flexibility for the method. Rather than relying on assumed analytic functional forms for CG interactions, interactions may be represented by flexible sets of basis functions. If it is known a priori that certain interactions between CG sites are well represented by a particular functional form, then the MS-CG method may instead be employed to determine the optimal parametrization for this form. For instance, if it is known that a particular pair of sites is harmonically bonded, then the variational calculation can determine both the force constant and equilibrium displacement that provide the optimal approximation for the many-body PMF. However, functional forms that provide a good representation of interactions between atomic particles may not necessarily provide a good description of the interactions between CG sites. Furthermore, this variational principle also ensures that the MS-CG approximation to the many-body CG PMF may be systematically improved by expanding the space of trial CG force fields, for example, by introducing anisotropic,16, 71, 72 three-body,16, 34 or density-dependent nonbonded interactions.26, 51
CONCLUDING REMARKS
The MS-CG method36, 37 recently introduced by Izvekov and Voth determines an effective interaction potential for CG models through a statistical force-matching procedure that is founded on a systematic variational principle.46, 47, 48 The companion paper described a general statistical mechanical framework for the MS-CG method.46 In particular, it was proven that, if no approximations are introduced in either the representation of the CG force field or in the statistical sampling of the atomistic configuration space, the MS-CG method calculates gradients of the exact many-body PMF for the CG sites determined by an underlying atomistic model. The resulting MS-CG model will then be consistent with the atomically detailed model according to the definition developed in Paper I. However, no less significantly, this analysis also proved that, given a vector space of trial (i.e., approximate) CG force fields, the MS-CG method determines the unique force field that is closest to the exact many-body CG PMF, assuming that the atomistic configuration space has been adequately sampled.
The present work also extends the analysis introduced in Paper I for molecular CG force fields. Both bonded and nonbonded interactions may be systematically parametrized according to the present theory. Rather than relying on particular analytic functional forms, the MS-CG method can employ a flexible set of basis functions for representing CG interactions.36, 37 As long as these interactions are represented by a linear combination of basis functions, the force field parameters providing the optimal approximation to the CG PMF may be determined by solving a linear least squares problem. This linear least squares problem explicitly considers many-body correlations between different interactions in the CG force field48 and projects the atomistic force field onto the specified set of force field basis vectors. Numerical calculations for a one-site methanol model and a multisite ionic liquid model demonstrate that the MS-CG method can be highly robust, flexible, and accurate.
The combination of theory46, 48 and numerical results36, 37, 38, 39, 40, 41, 42, 43, 73 presented in this and previous work clearly establishes the MS-CG method36, 37, 47, 74 as a systematic computational method with rigorous statistical mechanical foundations. However, a number of directions for future work are suggested by the present analysis. Because the method relies on accurate sampling of the atomistic configuration space, future work may incorporate statistical inference techniques to optimize the MS-CG force field determined from limited sampling. Similarly, because the MS-CG method obtains an optimal approximation to the many-body PMF that is clearly dependent on thermodynamic condition, future work will seek to develop the principles for transferring force fields to other thermodynamic conditions and to extend the method beyond the canonical ensemble. Finally, future research will also investigate the systematic introduction of basis vectors for multisite nonbonded interactions between CG sites.
ACKNOWLEDGMENTS
This research was supported by a Collaborative Research in Chemistry grant from the National Science Foundation (CHE-0628257). W.G.N. acknowledges funding from the National Institutes of Health through a Ruth L. Kirschstein National Research Service Award postdoctoral fellowship (Grant No. 5 F32 GM076839-02). Allocations of computer time from the Lonestar supercomputer at the Texas Advanced Computing Center are gratefully acknowledged. W.G.N. gratefully acknowledges Dr. V. Krishna for many stimulating conversations and also Dr. B. Hopkins for a critical reading of the manuscript.
APPENDIX A: BASIS FUNCTIONS FOR CG INTERACTIONS
In the present work, the non-Coulombic contribution to the MS-CG potential has been decomposed into bonded and nonbonded interactions between sites. Each non-Coulombic term in the CG potential energy function, Uζi, is a function of a single collective variable, xζ, which may describe the distance between a pair of nonbonded CG sites, RIJ=∣RI−RJ∣, the displacement of a particular bond, Ri, the valence bond angle between three bonded CG sites, θi, or the dihedral angle defined by four bonded CG sites, ψi. In each case, a generalized force on the collective variable xζ, Fζi(x), may be represented by a set of basis functions of a single variable, {fζid(x)},
| (A1) |
where the coefficients of these basis functions, ϕζid, are determined through the MS-CG linear least squares problem discussed in Sec. 2B and the summation over d in Eq. A1 includes all basis functions fζid used to represent the force Fζi. In the present work, basis functions are employed to represent each interaction on a mesh of Nζi equally spaced grid points {xζid}={xζi1+(d−1)Δζi for d=1,…,Nζi}. The grid spacing, Δζi, may be chosen independently for each interaction type ζ and form i and the method may be readily generalized for grids with nonuniform spacing. For each type of interaction, appropriate boundary conditions must be enforced for the basis functions describing the interactions at the first (i.e., xζi1) and last (i.e., xζiNζi) grid points. In particular, for valence angle potentials, xζ=θ ranges from 0 to π; for dihedral-angle potentials, xζ=ψ ranges from −π to π; and in each case the periodicity of the potential must be enforced.
In the present work, three particular types of basis functions have been employed for representing interactions in the MS-CG potential. The simplest basis set is defined by a set of Nζi discrete delta functions that are defined as follows:
| (A2) |
In the discrete delta function basis, the magnitude of the generalized force is assumed constant, Fζi(x)=Fζi(xζid)=ϕζid, in the range xζid−1∕2Δζi<x⩽xζid+1∕2Δζi around each grid point, xζid. When the discrete delta basis is used to represent a force, the result of the variational calculation is a force function that is constant within the interval about each grid point, with jump discontinuities at the boundaries between these intervals.
The force Fζi may be linearly interpolated between grid points by using a set of Nζi linear spline basis functions as follows:
| (A3) |
where
| (A4) |
| (A5) |
As for the discrete delta basis, one linear spline basis function is associated with each grid point and the associated coefficient corresponds to the magnitude of the force at the given grid point. When the linear spline basis is used to represent a force, the result of the variational calculation is a force function that is linear within each interval between grid points. The derivative of the force is discontinuous at each grid point.
The force functions may also be represented by a linear combination of piecewise continuous cubic polynomials.52 This cubic spline basis set employs two types of basis functions to represent the force field at each grid point and requires 2Nζi parameters as follows:
| (A6) |
where ηd(x) is defined in Eq. A3 and
| (A7) |
is defined in terms of Ad(x) and Bd(x) defined in Eqs. A4, A5 through
| (A8) |
| (A9) |
When the cubic spline basis is used to represent a force, the result of the variational calculation is a force function that is a cubic polynomial function within each interval. The derivative of the force is discontinuous at each grid point.
In the cubic spline basis, half of the coefficients correspond to the magnitude of the generalized force at a given grid point, ϕζi(2d−1)=Fζi(xζid), while the remaining coefficients correspond to the limit of the second derivative of the force at the grid point: ϕζi(2d)=limx→xζidd2Fζi(x)∕dx2. In Eqs. A2, A3, A4, A5, A6, A7, A8, A9, the functions δd, ηd, μd, Ad, Bd, Cd, and Dd depend on the particular interaction, ζi, only through the definition of the mesh points and this dependency has been suppressed above.
APPENDIX B: BASIS VECTORS FOR CG FORCE FIELDS
In Sec. 2, the CG potential was defined as
| (B1) |
in which U(C) corresponds to long-ranged Coulomb interactions between pairs of CG sites and Uζi indicates the contribution to the CG potential from an interaction of type ζ that is described by a functional form i and that involves the set of CG sites γ. The potential Uζi is a function of a single variable xζ that is itself a function of the coordinates, {R}γ, for the sites in the given set γ. Aside from long-ranged Coulomb interactions, the present work considers potential contributions arising from short-ranged nonbonded interactions (ζ=S) between pairs of sites, bond-stretch interactions (ζ=R) between pairs of bonded sites, bond-angle interactions (ζ=θ) between triples of bonded sites, and bond-dihedral-angle interactions (ζ=ψ) between quadruples of bonded CG sites.
Short-ranged nonbonded interactions (ζ=S) are treated by classifying the N CG sites into NT distinct “types” of sites such that all sites of a given type are chemically equivalent. The combination of indices Si then identifies a particular pair of types of sites and the potentials governing the short-ranged nonbonded interactions between all pairs of sites that are of the types specified by Si have the same functional form. The combination Siγ then identifies a particular pair of sites {J,K} that are of the types specified by Si. The short-ranged nonbonded interaction between the pair of sites specified by Siγ, i.e., {J,K}, is then governed by the potential function Uζi=USi that is a function of the intersite distance
| (B2) |
The CG force field included contributions from bond-stretch potentials (ζ=R) describing the interaction between pairs of bonded CG sites. Two CG sites within a given molecule are considered to be bonded if at least one atom involved in one of the two sites is bonded to an atom that is involved in the second site. The bonds included in the CG potential are then categorized into distinct types so that all bonds of type i are chemically equivalent. The combination Riγ then identifies a particular pair of CG sites γ={J,K} that are connected by a bond of type i. The bond-stretch interaction between any pair of bonded sites γ identified by Riγ is then governed by the potential energy function Uζi=URi that is a function of the bond length
| (B3) |
The CG potential also included contributions from bond-angle (ζ=θ) interactions between triples of CG sites that are connected by two bonds and bond-dihedral-angle (ζ=ψ) interactions between quadruples of CG sites that are connected by three consecutive bonds. The bond-angle and bond-dihedral-angle interactions, i.e., ζ=θ or ζ=ψ, may be similarly categorized into types of equivalent interactions labeled ζi and each bond-angle or dihedral-angle interaction of a particular type ζi is described by a potential function of the same form. The combination ζiγ identifies a particular triple of bonded CG sites, γ={J,K,L}, or quadruple of bonded CG sites, γ={J,K,L,M}, that are involved in a particular type of interaction ζ of form i for bond-angle (ζ=θ) and bond-dihedral-angle (ζ=ψ) interactions, respectively. In the present work, the potential contributions for both of these interactions, Uζi, are functions of a single variable. Bond-angle potentials Uθi are functions of the bond angle, xζ=xθ, formed by three bonded sites,
| (B4) |
where γ={J,K,L} is a set of three sites such that sites J and L are bonded to site K and is the unit vector RJK∕∣RJK∣ where RJK=RJ−RK. Dihedral-angle potentials Uψi are functions of the dihedral angle, xζ=xψ, formed by the two planes defined by the coordinates of sites {J,K,L} and {K,L,M} as follows:
| (B5) |
where is the unit normal vector to the plane defined by the Cartesian coordinates of sites J, K, and L.
Employing the definitions in Eqs. B2, B3, B4, B5 and Eq. 9, the total force in Eq. 10 may be expanded to explicitly identify the contributions from each type of interaction as follows:
| (B6) |
In the right hand expression of Eq. B6, the second term identifies the contributions from short-ranged nonbonded interactions and the associated summation over i ranges over all pairs of site types, the third term identifies the contributions from bond-stretch interactions and the associated summation over i ranges over all bond types, the fourth term identifies the contributions from bond-angle interactions and the associated summation over i ranges over all bond-angle types, and the fifth term identifies the contributions from bond-dihedral-angle interactions and the associated summation over i ranges over all bond-dihedral-angle types. Additional and more complex interactions may be introduced into the CG force field by defining appropriate basis functions fζid and associated force field basis vectors, Gζid.
APPENDIX C: VARIATIONAL CALCULATIONS GIVEN INADEQUATE SAMPLING
As discussed in Sec. 2B, the MS-CG force field parameters are uniquely determined by a linear least squares problem when the matrix is full rank and, consequently, the associated normal matrix is full rank and positive definite. In practice, though, the given atomistic trajectory data may provide insufficient sampling to uniquely determine all of the force field parameters. In particular, if in Eq. 12 there exists some parameter ϕD′ for which for all sites I in all sampled atomistic configurations , then all of the elements of the corresponding vector are zero, and the matrix in Eq. 14 is not full rank. In this case, is independent of ϕD′ and this parameter cannot be determined from minimizing the MS-CG residual. This case may arise when the coefficient, ϕD′, corresponds to a force field parameter that is only relevant for the CG force in configurations that have not been sampled. For instance, because the atoms involved in CG sites typically generate a potential energy that is very large for small separation between the two sites, the atomistic representation of each CG site generates an excluded volume or core region. Consequently, the atomistic trajectory rarely samples configurations in which two sites are separated by a sufficiently small distance that the two sites interpenetrate into this excluded volume region. Because these small intersite distances are only infrequently sampled, the force field parameters describing the nonbonded forces at such short distances may not be uniquely determined when the data set of atomic configurations used in the variational calculation is too small. As illustrated in Sec. 3, this situation may be addressed when necessary. The present appendix further considers this situation in somewhat more detail.
If the variational problem in Sec. 2B is to be solved using a method that addresses the normal matrix , it is clearly preferable that is full rank.
If this is not the case, it is often possible to modify the basis set so that is full rank by either deleting basis functions (e.g., basis functions corresponding to very small intersite separation that have not been sampled) or using a coarser set of mesh points for constructing the force basis functions fζid of the scalar xζ and/or obtaining more simulation data.
If this modification is not performed, then some of the coefficients are not uniquely determined by the calculation. (See below for further discussion.)
If the variational problem is to be solved using a method that deals with and uses BA, it is preferable that the matrix be full rank for each block B.
If this is not the case, it may be possible to partition the data set into blocks in a different way and/or to modify the basis set so that is full rank in each block.
If this modification is not performed, then some blocks will give undetermined values for some of the coefficients. The contribution of a block to a coefficient that is not determined by the block should be omitted from the calculation of the average over blocks.
In practice, given reasonable sampling of the atomistic configuration space, problems associated with or matrices that are not full rank lead to anomalous results for the calculated CG potential only for configurations that have small population at equilibrium, e.g., for small separation of repulsive particles. Even if the matrices are full rank, there may not be enough data to determine some of the coefficients accurately, and this too can lead to anomalous results for the CG potential in these configurations. In either situation, the procedure discussed and employed in Sec. 3 can be applied to obtain adequate representations of the CG potential.
APPENDIX D: BLOCK-AVERAGING APPROXIMATION
As discussed in Sec. 2B, the MS-CG force field describing the interaction between N CG sites may be determined from nt atomistic configurations by minimizing the MS-CG residual. This residual may be minimized by methods such as iterative biconjugate gradient minimization, QR decomposition, or SVD,52, 55, 56 which involve the matrix of 3ntN rows and ND columns. Methods that treat may allow a more accurate and stable solution than methods such as iterative conjugate gradient minimization, steepest descents, direct Gaussian elimination, or LU decomposition that involve the normal matrix of ND rows and ND columns defined in Eq. 18 because .53 However, for a complex system, the MS-CG method may require significant sampling of the atomistic configuration space to determine an effective CG force field and, for sufficiently large nt, methods that manipulate the matrix may require more computational memory than is available. In this case, the MS-CG force field parameters may be approximately determined by the BA procedure36, 37 described below. The analysis in this appendix assumes that the matrix is full rank in each block. Appendix C discusses the case that is not full rank in one or more blocks.
The nt sampled atomistic configurations are partitioned into nB disjoint sets (blocks) of configurations each. Any time-averaged quantity may be expressed as an average over blocks as follows:
| (D1) |
where
| (D2) |
and is the tth atomistic configuration in block B. The rows of the matrix and the vector in Eq. 14 that are associated with each block then define a matrix and a vector for each block B. The MS-CG residual function may then be decomposed over blocks as follows:
| (D3) |
| (D4) |
| (D5) |
where and are correlation functions defined by Eqs. 16, 17, respectively, with the averages restricted to configurations partitioned into block B according to Eq. D1. For each block, B, an optimal set of force field parameters, , may be determined by minimizing . For an appropriate choice of , the matrix may be full rank so that the set of parameters determining the minimum of the residual for each block, , is unique, while the matrix remains sufficiently small that it may be stored in memory and readily addressed, e.g., by biconjugate gradient methods.53, 55, 56 The set of force field parameters determined for each block B may then be averaged over the nB blocks to determine an approximation to the true solution of the linear least squares problem for all nt configurations as follows:
| (D6) |
where is the set of parameters determining the true minimum of the MS-CG residual.
The difference between the parameters determining the true minimum and the BA approximation, , may be analytically computed as follows:
| (D7) |
where
| (D8) |
with
| (D9) |
| (D10) |
and . Equation D7 expresses the error in the BA approximation in terms of a cross-correlation function that describes the correlation of the fluctuations between blocks in the residual curvature, , with the fluctuations between blocks in the force field parameters, . Importantly, this cross-correlation function may be directly calculated without knowledge of the true minima of the residual, . However, the error in the BA approximation, , cannot be determined without inverting GDD′, which is paramount to directly solving the normal system of equations for all nt configurations. Nevertheless, it is clear from Eqs. D7, D8, D9, D10 that the BA approximation is exact when fluctuations between blocks in the curvature of the residual are statistically uncorrelated with fluctuations in the force field parameters, i.e., , for all D=1,…,ND.
In the present methanol calculations, configurations were assigned to blocks by sequential time ordering, i.e., the first ten configurations were assigned to the first block, the second ten configurations were assigned to the second block, etc. For this simple system, the numerical results of Fig. 3 indicate that the BA approximation does not introduce systematic error into the MS-CG force field. For more complex systems that undergo significant structural transitions on long-time scales, though, such a simple sequential partitioning of blocks may lead to systematic errors in the BA approximation if different blocks sample distinct regions of configuration space. However, the analysis above suggests that the BA approximation may be systematically improved by shuffling configurations between blocks to reduce the magnitude of the cross-correlation function, for all D.
APPENDIX E: MANY-BODY CORRELATIONS IN THE MS-CG METHOD
The normal MS-CG equations presented in Eq. 18 have been expressed in terms of correlation functions computed from atomistic MD simulations. These equations clearly indicate that the MS-CG method explicitly incorporates information regarding many-body correlations to determine an optimal approximation to the many-body PMF.48 The quantity bD defined in Eq. 16 is the projection of the atomistic force field (minus the CG force resulting from electrostatic interactions) onto the force field basis vector GD associated with the Dth force field parameter. If the force field basis vectors formed an orthonormal set, then GDD′=δDD′ and ϕD=bD. However, the force field basis vectors correspond to correlated molecular interactions and are not orthogonal. Consequently, the off-diagonal elements of the matrix, GDD′, play a critical role in accounting for this nonorthogonality among the basis vectors by incorporating information regarding these many-body correlations. In particular, if ϕD1=ϕζid and ϕD2=ϕζ′i′d′, then
| (E1) |
quantifies the correlation in the sampled atomistic configurations between the part of the atomistic force field, , that is not captured by the CG Coulombic force field and the CG force field basis vector, Gζid, corresponding to the dth force field parameter for the ith functional form describing CG interaction type ζ, where ζi corresponds to a particular type of nonbonded, bond-stretch, bond-angle, or dihedral-angle interaction. Similarly, the quantity
| (E2) |
quantifies the correlation in the sampled atomistic configurations between the CG force field basis vectors Gζid and Gζ′i′d′ that are associated with the types of interactions, ζi and ζ′i′, in the CG force field. The normal MS-CG equations in Eq. 18 may be expressed as
| (E3) |
for all D=1,…,ND. According to Eq. E3, the MS-CG force field, F, captures the part of the total atomistic force field that is correlated in the sampled configuration space with the basis vectors included in defining the CG force field, i.e., the MS-CG force field is the projection of the sampled atomistic force field into the space of CG force fields spanned by the set of CG force field basis vectors, {GD}, that have been included in Eq. 10. Furthermore, if the atomistic configuration space has been sampled according to the canonical equilibrium distribution, the MS-CG force field is the projection of the force field determined by the many-body PMF onto this space of trial CG force fields as follows:
| (E4) |
for all D=1,…,ND, where is the many-body CG mean force field determined by the exact many-body PMF, UPMF(RN), and pR(RN) is defined in Paper I by the atomistic equilibrium coordinate distribution, pr(rn), and the CG mapping, .46
References
- Allen M. P. and Tildesley D. P., Computer Simulation of Liquids (Oxford University Press, Oxford, 1987). [Google Scholar]
- Frenkel D. and Smit B., Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed. (Academic, New York, 2002). [Google Scholar]
- Karplus M. and McCammon J. A., Nat. Struct. Mol. Biol. 10.1038/nsb0902-646 9, 646 (2002). [DOI] [PubMed] [Google Scholar]
- Shea J. E. and Brooks C. L., Annu. Rev. Phys. Chem. 10.1146/annurev.physchem.52.1.499 52, 499 (2001). [DOI] [PubMed] [Google Scholar]
- Scott H. L., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(02)00353-6 12, 495 (2002). [DOI] [PubMed] [Google Scholar]
- Feller S. E., Curr. Opin. Colloid Interface Sci. 10.1016/S1359-0294(00)00058-3 5, 217 (2000). [DOI] [Google Scholar]
- Ganser B. K., Li S., Klishko V. Y., Finch J. T., and Sundquist W. I., Science 10.1126/science.283.5398.80 283, 80 (1999). [DOI] [PubMed] [Google Scholar]
- Simons K. and Toomre D., Nat. Rev. Mol. Cell Biol. 1, 31 (2000). [DOI] [PubMed] [Google Scholar]
- Kusumi A. and Suzuki K., Biochim. Biophys. Acta 10.1016/j.bbamcr.2005.10.001 1746, 234 (2005). [DOI] [PubMed] [Google Scholar]
- Levitt M., J. Mol. Biol. 10.1016/0022-2836(76)90004-8 104, 59 (1976). [DOI] [PubMed] [Google Scholar]
- Tozzini V., Curr. Opin. Struct. Biol. 10.1016/j.sbi.2005.02.005 15, 144 (2005). [DOI] [PubMed] [Google Scholar]
- Ayton G. S., Noid W. G., and Voth G. A., Curr. Opin. Struct. Biol. 10.1016/j.sbi.2007.03.004 17, 192 (2007). [DOI] [PubMed] [Google Scholar]
- Marrink S. J., de Vries A. H., and Mark A. E., J. Phys. Chem. B 10.1021/jp036508g 108, 750 (2004). [DOI] [Google Scholar]
- Villa E., Balaeff A., Mahadevan L., and Schulten K., Multiscale Model. Simul. 10.1137/040604789 2, 527 (2004). [DOI] [Google Scholar]
- Villa E., Balaeff A., and Schulten K., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0409387102 102, 6783 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liwo A., Czaplewski C., Pillardy J., and Scheraga H. A., J. Chem. Phys. 10.1063/1.1383989 115, 2323 (2001). [DOI] [Google Scholar]
- Levitt M. and Warshel A., Nature (London) 10.1038/253694a0 253, 694 (1975). [DOI] [PubMed] [Google Scholar]
- Tanaka S. and Scheraga H. A., Macromolecules 10.1021/ma60054a013 9, 945 (1976). [DOI] [PubMed] [Google Scholar]
- Jernigan R. L. and Bahar I., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(96)80075-3 6, 195 (1996). [DOI] [PubMed] [Google Scholar]
- Nielsen S. O., Lopez C. F., Ivanov I., Moore P. B., Shelley J. C., and Klein M. L., Biophys. J. 10.1529/biophysj.104.040311 87, 2107 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens M. J., J. Am. Chem. Soc. 10.1021/ja043611q 127, 15330 (2005). [DOI] [PubMed] [Google Scholar]
- Shih A. Y., Arkhipov A., Freddolino P. L., and Schulten K., J. Phys. Chem. B 10.1021/jp0550816 110, 3674 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink S. J. and Mark A. E., J. Am. Chem. Soc. 10.1021/ja036138+ 125, 11144 (2003). [DOI] [PubMed] [Google Scholar]
- Gohlke H. and Thorpe M. F., Biophys. J. 10.1529/biophysj.106.083568 91, 2115 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goetz R. and Lipowsky R., J. Chem. Phys. 10.1063/1.476160 108, 7397 (1998). [DOI] [Google Scholar]
- Fujitsuka Y., Takada S., Luthey-Schulten Z. A., and Wolynes P. G., Proteins 10.1002/prot.10429 54, 88 (2004). [DOI] [PubMed] [Google Scholar]
- Matysiak S. and Clementi C., J. Mol. Biol. 10.1016/j.jmb.2004.08.006 343, 235 (2004). [DOI] [PubMed] [Google Scholar]
- Praprotnik M., Delle Site L., and Kremer K., J. Chem. Phys. 10.1063/1.2714540 126, 134902 (2007). [DOI] [PubMed] [Google Scholar]
- Muller-Plathe F., ChemPhysChem 3, 754 (2002). [DOI] [PubMed] [Google Scholar]
- Lyubartsev A. P. and Laaksonen A., Phys. Rev. E 10.1103/PhysRevE.52.3730 52, 3730 (1995). [DOI] [PubMed] [Google Scholar]
- Shelley J. C., Shelley M. Y., Reeder R. C., Bandyopadhyay S., and Klein M. L., J. Phys. Chem. B 10.1021/jp010238p 105, 4464 (2001). [DOI] [Google Scholar]
- Miyazawa S. and Jernigan R. L., Macromolecules 10.1021/ma00145a039 18, 534 (1985). [DOI] [Google Scholar]
- Sippl M. J., J. Mol. Biol. 10.1016/S0022-2836(05)80269-4 213, 859 (1990). [DOI] [PubMed] [Google Scholar]
- Vendruscolo M. and Domany E., J. Chem. Phys. 10.1063/1.477748 109, 11101 (1998). [DOI] [Google Scholar]
- Kevrekidis I. G., Gear C. W., and Hummer G., AIChE J. 10.1002/aic.10106 50, 1346 (2004). [DOI] [Google Scholar]
- Izvekov S. and Voth G. A., J. Phys. Chem. B 10.1021/jp044629q 109, 2469 (2005). [DOI] [PubMed] [Google Scholar]
- Izvekov S. and Voth G. A., J. Chem. Phys. 10.1063/1.2038787 123, 134105 (2005). [DOI] [PubMed] [Google Scholar]
- Izvekov S. and Voth G. A., J. Chem. Phys. 10.1063/1.2360580 125, 151101 (2006). [DOI] [PubMed] [Google Scholar]
- Iuchi S., Izvekov S., and Voth G. A., J. Chem. Phys. 10.1063/1.2710252 126, 124505 (2007). [DOI] [PubMed] [Google Scholar]
- Wang Y. T., Izvekov S., Yan T. Y., and Voth G. A., J. Phys. Chem. B 10.1021/jp0548220 110, 3564 (2006). [DOI] [PubMed] [Google Scholar]
- Shi Q., Izvekov S., and Voth G. A., J. Phys. Chem. B 10.1021/jp062700h 110, 15045 (2006). [DOI] [PubMed] [Google Scholar]
- Zhou J., Thorpe I. F., Izvekov S., and Voth G. A., Biophys. J. 10.1529/biophysj.106.094425 92, 4289 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izvekov S., Violi A., and Voth G. A., J. Phys. Chem. B 10.1021/jp0530496 109, 17019 (2005). [DOI] [PubMed] [Google Scholar]
- Izvekov S. and Voth G. A., J. Chem. Theory Comput. 10.1021/ct050300c 2, 637 (2006). [DOI] [PubMed] [Google Scholar]
- Liu P., Izvekov S., and Voth G. A., J. Phys. Chem. B 10.1021/jp0721494 111, 11566 (2007). [DOI] [PubMed] [Google Scholar]
- Noid W. G., Chu J.-W., Ayton G. S., Krishna V., Izvekov S., Voth G. A., Das A., and Andersen H. C., J. Chem. Phys. 128, 244114 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu J.-W., Ayton G. S., Izvekov S., and Voth G. A., Mol. Phys. 10.1080/00268970701256696 105, 167 (2007). [DOI] [Google Scholar]
- Noid W. G., Chu J.-W., Ayton G. S., and Voth G. A., J. Phys. Chem. B 10.1021/jp068549t 111, 4116 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayton G. S., Noid W. G., and Voth G. A., Mater. Res. Bull. 32, 929 (2007). [Google Scholar]
- Izvekov S., Parrinello M., Burnham C. J., and Voth G. A., J. Chem. Phys. 10.1063/1.1739396 120, 10896 (2004). [DOI] [PubMed] [Google Scholar]
- Ercolessi F. and Adams J. B., Europhys. Lett. 10.1209/0295-5075/26/8/005 26, 583 (1994). [DOI] [Google Scholar]
- Press W. H., Teukolsky S. A., Vetterling W. T., and Flannery B. P., Numerical Recipes in FORTRAN: The Art of Scientific Computing (Cambridge University Press, Cambridge, 1992). [Google Scholar]
- Demmel J. W., Applied Numerical Linear Algebra (SIAM, Philadelphia, PA, 1997). [Google Scholar]
- Barrett R., Berry M., Chan T. F., Demmel J., Donato J., Dongarra J., Eijkhout V., Pozo R., Romine C., and der Vorst H. V., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. (SIAM, Philadelphia, PA, 1994). [Google Scholar]
- Paige C. C. and Saunders M. A., ACM Trans. Math. Softw. 10.1145/355984.355989 8, 43 (1982). [DOI] [Google Scholar]
- Paige C. C. and Saunders M. A., ACM Trans. Math. Softw. 10.1145/355993.356000 8, 195 (1982). [DOI] [Google Scholar]
- Forester T. R. and Smith W., DḺPOLY User Manual (CCLRC Daresbury Laboratory, Daresbury, Warrington, UK, 1995). [Google Scholar]
- Jorgensen W. L., J. Am. Chem. Soc. 10.1021/ja00214a001 110, 1657 (1988). [DOI] [PubMed] [Google Scholar]
- Nose S., Mol. Phys. 10.1080/00268978400101201 52, 255 (1984). [DOI] [Google Scholar]
- Hoover W. G., Phys. Rev. A 10.1103/PhysRevA.31.1695 31, 1695 (1985). [DOI] [PubMed] [Google Scholar]
- de Leeuw S. W., Perram J. W., and Smith E. R., Proc. R. Soc. London, Ser. A 10.1098/rspa.1980.0135 373, 27 (1980). [DOI] [Google Scholar]
- Anderson E., Bai Z., Bischof C., Blackford S., Demmel J., Dongarra J., Croz J. D., Greenbaum A., Hammarling S., McKenney A., and Sorensen D., LAPACK Users’ Guide (SIAM, Philadelphia, PA, 1999). [Google Scholar]
- Welton T., Chem. Rev. (Washington, D.C.) 10.1021/cr980032t 99, 2071 (1999). [DOI] [PubMed] [Google Scholar]
- Rogers R. D. and Seddon K. R., Science 10.1126/science.1090313 302, 792 (2003). [DOI] [PubMed] [Google Scholar]
- Yan T. Y., Burnham C. J., Del Popolo M. G., and Voth G. A., J. Phys. Chem. B 10.1021/jp047619y 108, 11877 (2004). [DOI] [Google Scholar]
- Del Popolo M. G. and Voth G. A., J. Phys. Chem. B 10.1021/jp0364699 108, 1744 (2004). [DOI] [Google Scholar]
- Cornell W. D., Cieplak P., Bayly C. I., Gould I. R., Merz K. M., Ferguson D. M., Spellmeyer D. C., Fox T., Caldwell J. W., and Kollman P. A., J. Am. Chem. Soc. 10.1021/ja00124a002 117, 5179 (1995). [DOI] [Google Scholar]
- Wang Y. T. and Voth G. A., J. Am. Chem. Soc. 10.1021/ja053796g 127, 12192 (2005). [DOI] [PubMed] [Google Scholar]
- Wang Y. T., Jiang W., and Voth G. A., in Ionic Liquids IV. Not Just Solvents Anymore, edited by Brennecke J., Rogers R., and Seddon K. (American Chemical Society, Washington, DC, 2007), pp. 272–307. [Google Scholar]
- Hansen J.-P. and McDonald I. R., Theory of Simple Liquids, 2nd ed. (Academic, New York, 1990). [Google Scholar]
- Buchete N. V. and Straub J. E., J. Chem. Phys. 10.1063/1.1561616 118, 7658 (2003). [DOI] [Google Scholar]
- Buchete N. V., Straub J. E., and Thirumalai D., Protein Sci. 10.1110/ps.03488704 13, 862 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu P. and Voth G. A., J. Chem. Phys. 10.1063/1.2408415 126, 045106 (2007). [DOI] [PubMed] [Google Scholar]
- Chu J.-W., Izvekov S., and Voth G. A., Mol. Simul. 10.1080/08927020600612221 32, 211 (2006). [DOI] [Google Scholar]