Particle size effect on diffusion in tubes with dead ends: Nonmonotonic size dependence of effective diffusion constant

Abstract

Diffusion of a spherical particle of radius r in a tube with identical periodic dead ends is analyzed. It is shown that the effective diffusion constant follows the Stokes–Einstein relation, D_eff(r)∝1∕r, only when r is larger or much smaller than the radius of the dead end entrance. In between, D_eff(r) not only deviates from the 1∕r behavior but may also even become a nonmonotonic function, which increases with the particle radius for a certain range of r.

INTRODUCTION

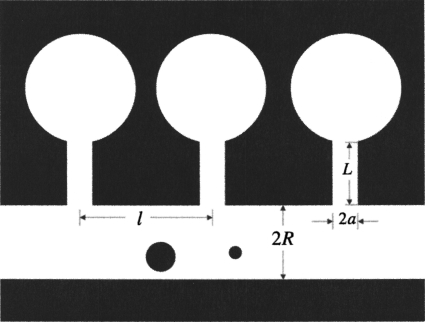
In this paper, we discuss the diffusion of spherical particles in a tube with identical periodic dead ends shown in Fig. 1. Our major focus is on the difference between particles of “finite” size and “point” particles whose size is well below the radius a of the dead end entrance. For point particles the dead ends work as reversible entropy traps,¹ which shorten the time used by the particle for diffusion along the tube. This leads to the decrease in the particle effective diffusivity compared to that in a tube without dead ends. We analyze this effect in detail in Ref. 2. Of course, a point particle is an approximation. Therefore, it seems interesting to consider how the dead end effect on diffusion depends on the particle size. This was the motivation for this work. The point particle approximation fails when the particle radius r becomes comparable with a. In particular, relatively large particles whose radius is greater than a, r>a, do not “see” the dead ends. As a consequence, their diffusivities are identical to those in a purely cylindrical tube.

Figure 1.

A tube of radius R with identical periodic dead ends separated by distance l. Dead ends are formed by cavities of volume V_cav connected to the tube by narrow channels of radius a and length L. The larger particle cannot enter the dead ends since its size exceeds the size of the dead end entrance. The smaller particle is capable of entering the dead ends that work as reversible traps for this particle, which slow down its diffusive spreading along the tube axis.

Particle size effect on diffusion in a tube with dead ends has two aspects: Depending on its size, the particle (i) sees different traps and (ii) “feels” different hydrodynamic interactions. In this note, we are concentrated on the first aspect, which is purely geometric, and mainly neglect the second aspect. It is well known that in space with no constraints the diffusion constant of a spherical particle according to the Stokes–Einstein relation is inversely proportional to the particle radius. We show that in tubes with dead ends the r-dependence of the effective diffusivity may significantly deviate from the 1∕r behavior. Moreover, the r-dependence may even be nonmonotonic. Our analysis is based on the results of our recent study of transient diffusion of point particles in tubes with dead ends,² which are briefly discussed in the next section. The major results of this note are presented in Sec. 3 and illustrated in Figs. 2345. Concluding this brief introduction, we indicate that one can find a detailed discussion of different theoretical approaches to the problem of the point particle diffusion in a tube with periodic dead ends in Ref. 2. Different objects to which the theory may be potentially applied are also mentioned in that paper.

Figure 2.

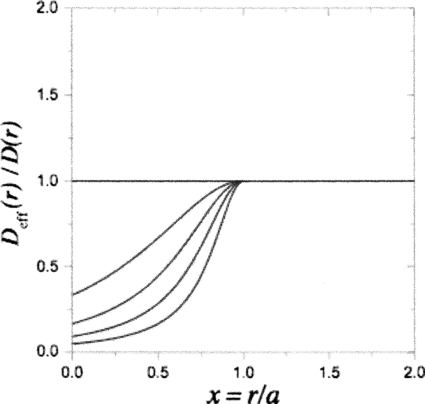
The ratio D_eff(r)∕D(r) as a function of the dimensionless particle radius, x=r∕a, for the case of dead ends with no cavities, V_cav=0. The curves from top to bottom correspond to α=0,2,5,10,20. All curves merge into one, D_eff(r)∕D(r)=1, at x>1 since D_eff(r)=D(r) at r>a.

Figure 3.

Dimensionless effective diffusion constant, D_eff(r)∕D(a), as a function of the dimensionless particle radius, x=r∕a, for the case of dead ends with no cavities, V_cav=0. The curves from top to bottom correspond to α=0,2,5,10,20. All curves merge into one, D_eff(r)∕D(a)=1∕x, at x>1 since D_eff(r)=D(r)=D(a)a∕r at r>a.

Figure 4.

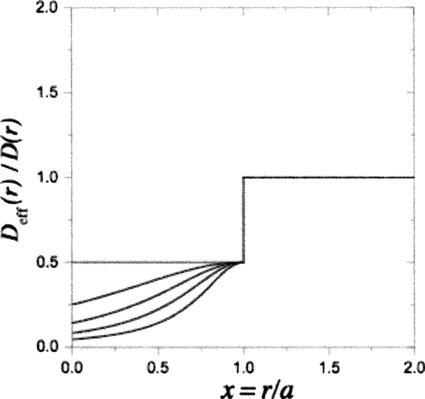
The ratio D_eff(r)∕D(r) as a function of the dimensionless particle radius, x=r∕a, for the case of dead ends with cavities of the same volume as V_tube, and β=1. The curves from top to bottom correspond to α=0,2,5,10,20. All curves merge into one, D_eff(r)∕D(r)=1, at x>1 since D_eff(r)=D(r) at r>a.

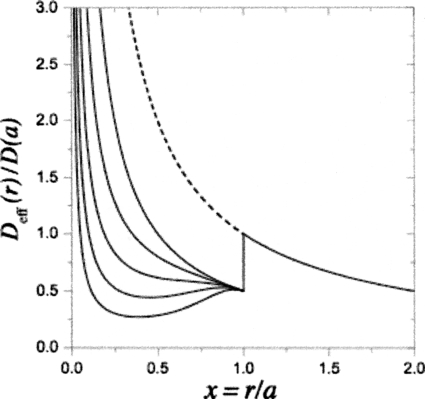
Figure 5.

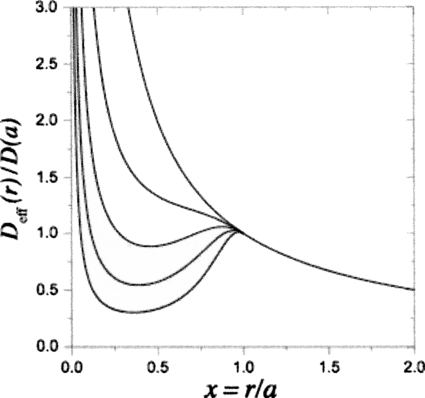
Dimensionless effective diffusion constant, D_eff(r)∕D(a), as a function of the dimensionless particle radius, x=r∕a, for the case of dead ends with cavities of the same volume as V_tube, i.e., β=1. Solid curves from top to bottom correspond to α=0,2,5,10,20. The dashed line shows the 1∕x behavior of the ratio at x<1. All curves merge into one, D_eff(r)∕D(a)=1∕x, at x>1 since D_eff(r)=D(r)=D(a)a∕r at r>a.

POINT PARTICLES IN TUBES WITH PERIODIC DEAD ENDS

Consider a tube of radius R with periodic identical dead ends separated by distance l, as shown in Fig. 1. A dead end is formed by a cavity of volume V_cav connected to the tube by a cylindrical channel of radius a and length L. We assume that the dead end entrance radius, a, is much smaller than the tube radius, R, and the period, l, a⪡R,l. About the cavity, we assume that its size, $V_{\mathrm{cav}}^{1∕3}$, is much greater than a as well, $a⪡V_{\mathrm{cav}}^{1∕3}$. In addition, we consider the case of purely cylindrical dead ends without cavities, i.e., dead ends with V_cav=0. We also consider the case of dead ends with no connecting channel, i.e., dead ends with L=0.

In Ref. 2 we analyze the transient behavior of the diffusion coefficient, D(t∣r), for point particles, r⪡a, assuming that initially, at t=0, the particles are uniformly distributed in the tube and there are no particles in the dead ends. Under these initial conditions, D(t∣r) monotonically decreases with time from D(r), which is the particle diffusion constant in the tube with no dead ends, to the effective diffusion constant, D_eff(r),

$$D_{\mathrm{eff}}\left(r\right)=\frac{V_{\text{tube}}}{V_{\text{tube}}+V_{\mathrm{de}}}D\left(r\right).$$ (2.1)

Here, V_tube=πR²l is the tube volume per one dead end and V_de is the dead end volume, V_de=V_cav+V_ch, where V_ch=πa²L is the volume of the connecting channel. Note that we neglect the size of the particle when writing V_tube and V_de since this size, r, for point particles is much smaller than all other characteristic length scales of the problem.

The transient behavior of D(t∣r) can be written in terms of the relaxation function, R(t∣r), which monotonically decreases from unity to zero as t goes from zero to infinity,

$$D(t\mid r)=D_{\mathrm{eff}}\left(r\right)+\lfloor D\left(r\right)-D_{\mathrm{eff}}\left(r\right)\rfloor R(t\mid r).$$ (2.2)

In Ref. 2, we derived an analytical solution of the Laplace transform of R(t∣r) and used it to find the relaxation time, τ_rel(r), defined as

$${\tau }_{\mathrm{rel}}\left(r\right)={\int }_0^{\infty }R(t\mid r)dt.$$ (2.3)

One of the main results of our analysis is a general expression, which gives τ_rel(r) in terms of D(r) and all geometric parameters of the problem [Eq. (3.12) from Ref. 2],

$${\tau }_{\mathrm{rel}}\left(r\right)=\frac{⟨{\tau }_{\text{tube}}\left(r\right)⟩⟨{\tau }_{\mathrm{de}}^2\left(r\right)⟩+2⟨{\tau }_w\left(r\right)⟩{⟨{\tau }_{\mathrm{de}}\left(r\right)⟩}^2}{2⟨{\tau }_{\mathrm{de}}\left(r\right)⟩(⟨{\tau }_{\text{tube}}\left(r\right)⟩+⟨{\tau }_{\mathrm{de}}\left(r\right)⟩)},$$ (2.4)

where

$$⟨{\tau }_{\text{tube}}\left(r\right)⟩=\frac{V_{\text{tube}}}{4aD\left(r\right)}=\frac{\pi R^{2}l}{4aD\left(r\right)},$$ (2.5)

$$⟨{\tau }_{\mathrm{de}}\left(r\right)⟩=\frac{V_{\mathrm{de}}}{4aD\left(r\right)}=\frac{V_{\mathrm{cav}}+\pi a^{2}L}{4aD\left(r\right)},$$ (2.6)

$$⟨{\tau }_w\left(r\right)⟩=\frac{l^2}{12D\left(r\right)},$$ (2.7)

$$⟨{\tau }_{\mathrm{de}}^2\left(r\right)⟩=2{⟨{\tau }_{\mathrm{de}}\left(r\right)⟩}^2\{1+{\left(\frac{V_{\mathrm{cav}}}{V_{\mathrm{de}}}\right)}^2+\frac{4LD\left(r\right)}{\pi a{D}_{\mathrm{ch}}\left(r\right)}[\frac{V_{\mathrm{cav}}}{V_{\mathrm{de}}}+\frac{1}{3}{\left(\frac{V_{\mathrm{ch}}}{V_{\mathrm{de}}}\right)}^2]\},$$ (2.8)

where D_ch(r) is the particle diffusion constant in the connecting channel, which may be much smaller than D(r).

FINITE SIZE PARTICLES IN TUBES WITH PERIODIC DEAD ENDS

According to Eqs. 2.1, 2.4, both D_eff(r) and τ_rel(r) depend on the particle radius, r, only through the r-dependence of the particle diffusion constant, D(r). This is an approximation, which is justifiable only for point particles, i.e., when r is much smaller than all other characteristic length scales of the problem. The approximation fails for finite size particles, whose radii may be comparable with the dead end entrance radius, a. Below we use Eq. 2.1 to analyze the r-dependence of D_eff(r) for finite size particles, assuming that r is much smaller than the tube radius, r⪡R. Based on the Stokes–Einstein relation, we take that D(r)∝1∕r.

Dead ends with no cavities, V_cav=0

A finite size particle of radius r sees a purely cylindrical dead end of radius a and length L (with no cavity) as a point particle sees a cylindrical dead end of radius a−r and length L−r. With this in mind, we can use Eq. 2.1 to write D_eff(r) for our finite size particle as

$$D_{\mathrm{eff}}\left(r\right)=\frac{D\left(r\right)}{1+\alpha {(1-\frac{r}{a})}^2(1-\frac{r}{L})H(a-r)},$$ (3.1)

where

$$\alpha =\frac{V_{\mathrm{ch}}}{V_{\text{tube}}}=\frac{a^{2}L}{R^{2}l},$$ (3.2)

and we have neglected the variation of the tube volume due to the finite size of the particle based on the fact that r⪡R. The Heaviside step function, H(a−r), entering into Eq. 3.1 takes account of the fact that particles of the radii larger than a do not enter the dead ends. Therefore, for such particles D_eff(r)=D(r).

We illustrate the deviation of D_eff(r) from D(r) in Fig. 2, assuming that the cylinder is long enough so that L⪢r. One can see that the ratio D_eff(r)∕D(r) monotonically grows with r for r<a and approaches unity as r tends to a. This ratio is equal to unity for r>a since the particles of the radii larger than a do not see the dead ends.

To analyze the r-dependence of the effective diffusion constant, consider the ratio D_eff(r)∕D(a). Assuming that L⪢r and using the relation D(r)=D(a)a∕r, we can write Eq. 3.1 as

$$\frac{D_{\mathrm{eff}}\left(r\right)}{D\left(a\right)}=\frac{1}{x[1+\alpha {(1-x)}^{2}H(1-x)]},x=\frac{r}{a}.$$ (3.3)

In Fig. 3 we show the ratio as a function of x for several values of α. This parameter defined in Eq. 3.2 determines whether the ratio is a monotonic function of x or not. The dependence is nonmonotonic when α>3. Positions of the minimum and maximum, x_min and x_max, are given by

$$x_{\min }=\frac{2}{3}-\frac{1}{3}\sqrt{1-\frac{3}{\alpha }},\alpha >3,$$ (3.4)

$$x_{\max }=\frac{2}{3}+\frac{1}{3}\sqrt{1-\frac{3}{\alpha }},\alpha >3.$$ (3.5)

Thus, when purely cylindrical dead ends are long enough the r-dependence of the effective diffusion constant is nonmonotonic. When the dead ends are not sufficiently long, the dependence is monotonic but differs from the 1∕r-dependence predicted by the Stokes–Einstein relation. We will see that this is a distinctive feature of purely cylindrical dead ends with no cavities. When dead ends have cavities, the r-dependence of the effective diffusion constant is always nonmonotonic independent of the length of the connecting channel.

Concluding this subsection, we briefly discuss the particle size effect on the relaxation time given in Eq. 2.4. For dead ends with no cavities, V_cav=0, the expressions in Eqs. 2.6, 2.8, written for point particles, simplify and take the form

$$⟨{\tau }_{\mathrm{de}}\left(r\right)⟩=\frac{\pi aL}{4D\left(r\right)},$$ (3.6)

$$⟨{\tau }_{\mathrm{de}}^2\left(r\right)⟩=2{⟨{\tau }_{\mathrm{de}}\left(r\right)⟩}^2(1+\frac{4LD\left(r\right)}{3\pi a{D}_{\mathrm{ch}}\left(r\right)}).$$ (3.7)

Accordingly, τ_rel(r) in Eq. 2.4 can be written as

$${\tau }_{\mathrm{rel}}\left(r\right)=⟨{\tau }_{\mathrm{de}}\left(r\right)⟩\frac{⟨{\tau }_{\text{tube}}\left(r\right)⟩(1+\frac{4LD\left(r\right)}{3\pi a{D}_{\mathrm{ch}}\left(r\right)})+⟨{\tau }_w\left(r\right)⟩}{⟨{\tau }_{\text{tube}}\left(r\right)⟩+⟨{\tau }_{\mathrm{de}}\left(r\right)⟩}.$$ (3.8)

To analyze the particle size effect on the relaxation time, one has to replace a by a-r in this equation and in Eqs. 2.5, 3.6 as well. After such a replacement, one can see that as r→a ⟨τ_de(r)⟩→0, ⟨τ_tube(r)⟩→∞, while ⟨τ_w(r)⟩ remains finite. Using these relations, one can find the asymptotic behavior of the relaxation time,

$${\tau }_{\mathrm{rel}}\left(r\right)=⟨{\tau }_{\mathrm{de}}\left(r\right)⟩\frac{4LD\left(r\right)}{3\pi (a-r)D_{\mathrm{ch}}\left(r\right)}=\frac{L^2}{3D_{\mathrm{ch}}\left(r\right)},r\to a.$$ (3.9)

This shows that the relaxation time diverges as r→a since D_ch(r) vanishes in this limit because of the hydrodynamic interaction.

Dead ends with large cavities, $a⪡V_{\mathrm{cav}}^{1∕3}$

When the dead ends have cavities, the expression for D_eff(r) in Eq. 3.1 must be modified. Following the same way of reasoning, which led us to Eq. 3.1, and assuming that the cavity size is much greater than a, $a⪡V_{\mathrm{cav}}^{1∕3}$, we arrive at

$$D_{\mathrm{eff}}\left(r\right)=\frac{D\left(r\right)}{1+[\beta +\alpha {(1-\frac{r}{a})}^2]H(a-r)},$$ (3.10)

where

$$\beta =\frac{V_{\mathrm{cav}}}{V_{\text{tube}}}=\frac{V_{\mathrm{cav}}}{\pi R^{2}l}.$$ (3.11)

From Eq. 3.10 one can see that when r→a, D_eff(r) tends to D(a)∕(1+β) or D(a) depending on whether the particle size, r, approaches a from below or from above, respectively. At r=a function D_eff(r) makes a step up of the height D(a)β∕(1+β). This step is a distinctive feature of the behavior of D_eff(r) in the presence of the dead end cavities. In the absence of the cavities, β=0 and the step disappears. We illustrate the step in transition of D_eff(r) to its universal behavior, D_eff(r)=D(r), at r>a in Fig. 4.

When analyzing the dependence of the effective diffusion constant on the particle radius, we again use D(a) as a scale for D_eff(r). This allows us to write Eq. 3.10 as

$$\frac{D_{\mathrm{eff}}\left(r\right)}{D\left(a\right)}=\frac{1}{x[1+{\alpha }^{\prime }{(1-x)}^{2}H(1-x)][1+\beta H(1-x)]},$$ (3.12)

$$x=\frac{r}{a},$$

where

$${\alpha }^{\prime }=\frac{\alpha }{1+\beta }=\frac{V_{\mathrm{ch}}}{V_{\text{tube}}+V_{\mathrm{cav}}}.$$ (3.13)

Equations 3.12, 3.3 are identical at x>1 since at r>aD_eff(r) demonstrates a universal behavior, D_eff(r)=D(r), which is independent of the dead end geometry. At x<1 the right-hand sides of Eqs. 3.12, 3.3 are almost identical: The former can be obtained from the latter by dividing the right-hand side of Eq. 3.3 by (1+β) and replacing their α by α^′. Parameter α^′ determines whether the ratio in Eq. 3.12 is a monotonic function of x at x<1 or not. The nonmonotonic behavior of the ratio is realized when α^′>3, with the minimum and maximum located at [cf. Eqs. 3.4, 3.5],

$$x_{\min }=\frac{2}{3}-\frac{1}{3}\sqrt{1-\frac{3}{{\alpha }^{\prime }}},{\alpha }^{\prime }>3,$$ (3.14)

$$x_{\max }=\frac{2}{3}+\frac{1}{3}\sqrt{1-\frac{3}{{\alpha }^{\prime }}},{\alpha }^{\prime }>3.$$ (3.15)

When α^′<3 the ratio in Eq. 3.12 is a monotonic function of x at x<1. However, this ratio jumps up at x=1, which makes it a nonmonotonic function. This nonmonotonic behavior of D_eff(r) at any value of α^′ is a distinctive feature of diffusion in tubes with dead ends, which have cavities. The size dependence of D_eff(r) in such tubes is illustrated in Fig. 5.

Finally, we discuss the particle size effect on the relaxation time given in Eq. 2.4, focusing on the divergence of τ_rel(r) as the particle size approaches the size of the dead end entrance, r→a. In this limiting case, one can neglect the channel volume compared to that of the cavity, V_ch⪡V_cav, and we have V_de=V_cav. With this in mind, we can write Eqs. 2.5, 2.6, 2.8 as

$$⟨{\tau }_{\text{tube}}\left(r\right)⟩\approx \frac{\pi R^{2}l}{4(a-r)D\left(r\right)},r\to a,$$ (3.16)

$$⟨{\tau }_{\mathrm{de}}\left(r\right)⟩\approx \frac{V_{\mathrm{cav}}}{4(a-r)D\left(r\right)},r\to a,$$ (3.17)

$$⟨{\tau }_{\mathrm{de}}^2\left(r\right)⟩\approx 2{⟨{\tau }_{\mathrm{de}}\left(r\right)⟩}^2[2+\frac{4LD\left(r\right)}{\pi (a-r)D_{\mathrm{ch}}\left(r\right)}],r\to a.$$ (3.18)

Using these relations and the fact that ⟨τ_w⟩⪡⟨τ_tube⟩ when r is close to a, we can write the relaxation time as

$${\tau }_{\mathrm{rel}}\left(r\right)\approx \frac{V_{\text{tube}}{V}_{\mathrm{cav}}}{V_{\text{tube}}+V_{\mathrm{cav}}}[\frac{1}{2(a-r)D\left(r\right)}+\frac{L}{\pi {(a-r)}^2{D}_{\mathrm{ch}}\left(r\right)}],r\to a.$$ (3.19)

This shows that the relaxation time diverges as 1∕(a-r) in the absence of the connecting channels, L=0, while in the presence of the channels, L≠0, this time diverges as 1∕[^(a-r)2D_ch(r)].

CONCLUDING REMARKS

In this note, we have extended our analysis of the point particle diffusion in a tube with periodic dead ends to particles of finite size. Our major focus is on the particle size dependence of the effective diffusion constant, D_eff(r). We have found that D_eff(r) follows the Stokes–Einstein relation, D_eff(r)∝1∕r, only when r⪡a and r>a and noticeably deviates from the 1∕r-dependence when r is comparable to a. Moreover, for some range of the geometric parameters of the dead ends D_eff(r) not only deviates from the 1∕r behavior but is even a nonmonotonic function of r, which increases with r at r_min<r<r_max, where r_min=ax_min and r_max=ax_max, with x_min and x_max given in Eqs. 3.4, 3.5 or 3.14, 3.15.

We have also found that the dependence D_eff(r) is sensitive to the dead end geometry, namely, whether the dead ends have cavities or not. When the dead ends have no cavities (purely cylindrical dead ends), the dependence D_eff(r) is a continuous function of r, which is nonmonotonic only when the dead ends are long enough. In the presence of the cavities, the dependence D_eff(r) is nonmonotonic at arbitrary length of the connecting channels since it always has a step at r=a.

The relaxation time, τ_rel(r), which provides a time scale characterizing relaxation of D(t∣r) from D(0∣r)=D(r) to D(∞∣r)=D_eff(r), diverges as r approaches a. The limiting behavior of τ_rel(r) is also sensitive to the dead end geometry. In the absence of the dead end cavities, τ_rel(r) diverges as 1∕D_ch(r) [recall that D_ch(r)→0 as r→a because of the hydrodynamic interaction]. In the presence of these cavities, the limiting behavior changes and τ_rel(r) diverges as 1∕(a-r), r<a, in the absence of the connecting channels, L=0, and as 1∕[^(a-r)2D_ch(r)] when L≠0.

In summary, we have shown that diffusion in tubes with dead ends has an interesting feature, namely, that there is a range of the parameters for which larger particles diffuse faster than the smaller ones. This is surprising since it is well known that in free space the larger particles always diffuse slower than the smaller ones. It turns out that this is not necessarily the case when diffusion occurs in a tube with dead ends. The reason is as follows. A larger particle, which cannot enter the dead ends, spends all the time diffusing along the tube axis, whereas the smaller particle, which is able to enter the dead ends, wastes time traveling in the dead ends and diffuses along the tube axis for only a fraction of the total observation time. This is why its effective diffusion coefficient may be smaller than that of the larger particle.