Abstract
An ability to efficiently compute the electrostatic potential produced by molecular charge distributions under realistic solvation conditions is essential for a variety of applications. Here, the simple closed-form analytical approximation to the Poisson equation rigorously derived in Part I for idealized spherical geometry is tested on realistic shapes. The effects of mobile ions are included at the Debye–Hückel level. The accuracy of the resulting closed-form expressions for electrostatic potential is assessed through comparisons with numerical Poisson–Boltzmann (NPB) reference solutions on a test set of 580 representative biomolecular structures under typical conditions of aqueous solvation. For each structure, the deviation from the reference is computed for a large number of test points placed near the dielectric boundary (molecular surface). The accuracy of the approximation, averaged over all test points in each structure, is within 0.6 kcal∕mol∕∣e∣∼kT per unit charge for all structures in the test set. For 91.5% of the individual test points, the deviation from the NPB potential is within 0.6 kcal∕mol∕∣e∣. The deviations from the reference decrease with increasing distance from the dielectric boundary: The approximation is asymptotically exact far away from the source charges. Deviation of the overall shape of a structure from ideal spherical does not, by itself, appear to necessitate decreased accuracy of the approximation. The largest deviations from the NPB reference are found inside very deep and narrow indentations that occur on the dielectric boundaries of some structures. The dimensions of these pockets of locally highly negative curvature are comparable to the size of a water molecule; the applicability of a continuum dielectric models in these regions is discussed. The maximum deviations from the NPB are reduced substantially when the boundary is smoothed by using a larger probe radius (3 Å) to generate the molecular surface. A detailed accuracy analysis is presented for several proteins of various shapes, including lysozyme whose surface features a functionally relevant region of negative curvature. The proposed analytical model is computationally inexpensive; this strength of the approach is demonstrated by computing and analyzing the electrostatic potential generated by a full capsid of the tobacco ring spot virus at atomic resolution (500 000 atoms). An analysis of the electrostatic potential of the inner surface of the capsid reveals what might be a RNA binding pocket. These results are generated with the modest computational power of a desktop personal computer.
INTRODUCTION
The utility of the electrostatic potential for gaining understanding of the function of proteins1 and nucleic acids2 has long been established.1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 Electrostatic effects can be expected to be critical to the function of viruses;15, 16 in the emerging field of nanomaterials, electrostatic properties of viral capsids have been exploited to package nonviral cargoes.17 Traditionally, methods based on numerical solutions of the Poisson–Boltzmann (PB) equation—the numerical Poisson–Boltzmann (NPB) approach—have been used to compute the electrostatic potential of biological structures. While currently these methods are arguably the most accurate among practical approaches based on the implicit solvent framework,18 the use of the NPB methodology to study electrostatic properties of biomolecules is often associated with algorithmic complexity and high computational costs, especially for large structures. For example, a 2001 pioneering NPB-based study of the ribosomal complex—a structure of nearly 100 000 atoms—required sophisticated parallel computations on 343 CPUs of the Blue Horizon supercomputer.19 Over the seven years that have passed since that landmark result, the computational costs of NPB algorithms continued to decrease,20, 21 although the computational price one has to pay for the associated accuracy is still nontrivial, as even larger atomic-resolution structures such as viral capsids move into the focus of structural biology.22
In Part I of this work, we have shown that a set of simple, closed-form expressions valid everywhere in three-dimensional (3D) space can be derived for the electrostatic potential produced by an arbitrary charge distribution inside a highly symmetrical molecular shape. Since the goal of this work is to deliver the most computationally effective implementation of the analytical approximations from Part I, we focus on the simplest of them. Should we find that the accuracy of these approximations on realistic structures is acceptable, the implementation of the analytical approximation will represent the first practical model based on the ideas presented in Part I.
The main result of Part I is a set of analytical approximations to the Poisson equation that give the electrostatic potential produced by a single point charge qi inside the molecule. The analytical potential is defined everywhere in space, both inside and outside the dielectric boundary separating the solvent from the solute,
| (1) |
| (2) |
where the proposed adaptation of the geometric parameters of the formula to realistic geometries is given in Fig. 1. In what follows, we will be using the value23 of the constant α=0.580127 for consistency with Part I. Although this value is only optimal in the specific sense discussed in Part I that pertains to perfect spherical geometry, we will see below that for real biomolecular structures of variable shapes, the “optimal” interval is very broad and includes α=0.580127.
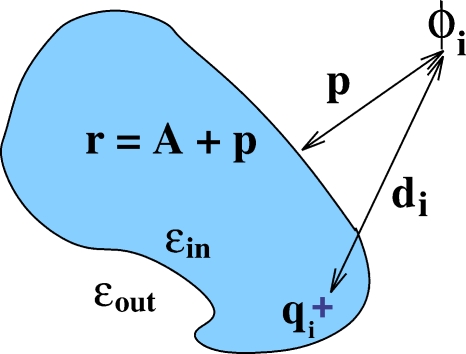
Figure 1.
Definition of the geometric parameters that enter the analytical formulas 1, 2 used to compute the electrostatic potential ϕi due to a single charge located inside an arbitrary biomolecule (in the absence of mobile ions). Here di is the distance from the source charge qi to the point of observation where ϕi needs to be computed. The distance from the point of observation to the dielectric boundary (molecular surface) is p; p<0 for points inside the boundary. The so-called effective electrostatic size of the molecule, A, characterizes its global shape and is computed analytically as described in Ref. 24. The distance from the point of observation to the “center” is then defined as r=A+p. Likewise the position of the charge, ri, is defined as A minus the distance of the charge to surface (not shown).
The above formulas represent the potential generated by a single charge qi; the total potential due to a realistic charge distribution is obtained by the superposition principle via summation over all charges inside the molecule. Note that the analytical approximation for the potential in the solvent space is nonsingular everywhere, while the analytical approximation for the inside potential diverges at every point charge.
Two additional steps are required for Eqs. 1, 2 to be useful in practice. First, the model must be adapted to incorporate the effects of nonzero ionic strength in the solvent space. Second, the accuracy of the model must be assessed for realistic biomolecular shapes. In particular, one has to identify and classify regions of space where the approximation may break down.
We begin by incorporating salt effects into the approximation given by Eqs. 1, 2. It is unclear whether the approach we used in Part I—starting from the exact infinite series solutions of the (linearized) PB equation—can preserve the appealing simplicity of these formulas in the case of κ≠0. This is because, in the κ≠0 case, the mathematical structures of the solution of the PB equation inside and outside the dielectric boundary are significantly more complex and substantially different from each other unlike in the κ=0 case. We therefore follow a different strategy: The use of a physically realistic ansatz that becomes exact in a set of limiting cases considered below. The ansatz is constructed to give the desired approximate solution in the Debye–Hückel limit. We note that this general strategy has been successfully used to adapt the generalized Born model for the case of nonzero ionic strength.25
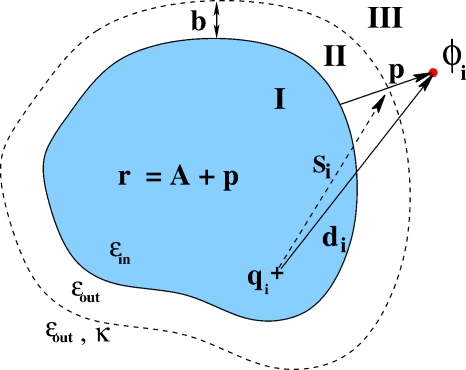
Compared to the no-salt case (Fig. 1), the space is now partitioned into three regions: Solute (region I), solvent in the immediate vicinity of molecular surface (region II), and solvent containing mobile ions (region III) (see Fig. 2). The Stern layer accounts for the effects of ion hydration, which sets a minimal distance b around the molecular surface beyond which mobile ions do not penetrate.
Figure 2.
The definition of geometrical parameters that enter Eqs. 3, 4, 5, 6, 7, 8 in the case of nonzero ionic strength of the solvent. A sharp dielectric boundary is assumed; the inside of the molecule, region I, is characterized by its constant dialectic value ϵin; the dielectric of the outside (solute, regions II and III) is also a constant, ϵout. Salt ions exist only in region III. The boundary between regions II and III—the Stern layer—is shown as a dashed line. The geometrical parameters are the same as the κ=0 case (Fig. 1) with the addition of one new parameter si, defined as the distance from the charge qi to the intersection of the Stern layer with the “distance to surface” line. The thickness of the Stern layer—distance from the surface of the molecule to the Stern layer—is denoted by b.
There are no mobile ions in regions I and II, and thus the ansatz we seek in these regions can differ from the no-salt formulas [Eqs. 1, 2] by the same additive constant. We find an approximate ansatz for electrostatic potential in the region with mobile ions (region III in Fig. 2) by noting that without mobile ions, Eq. 2 is mathematically equivalent to the sum of two point charge potentials proportional to 1∕di and 1∕r, respectively. A point charge potential in the presence of a homogeneous ionic environment has the form of a Yukawa potential: ∼e−κr∕r. Therefore, it is natural to try the following ansatz (we denote ϵin∕ϵout=β):
| (3) |
| (4) |
| (5) |
The ansatz has introduced three unknown constants, D, E, and F. The approach we take to determine the value of the constants is as follows. We assume a spherical geometry and apply a set of boundary conditions and limiting cases for which exact solutions of the PB equation are known for some simple charge configurations. The first two constants, D and E, are determined by (i) requiring that Eq. 5 becomes the exact solution of the (linearized) PB equation for a point charge at the center of a sphere and (ii) by requiring the continuity of the tangential components of the electric field at the Stern layer, . The value of constant F is chosen to ensure the continuity of the approximate potential between regions II and III,
| (6) |
| (7) |
| (8) |
with si defined in Fig. 2.
When constructing the above equations we had a choice of boundary conditions to satisfy. As discussed in Part I, the approximate solution cannot satisfy all of the boundary conditions simultaneously: In the no-salt case the continuity of dielectric displacement perpendicular to the dielectric boundary was not enforced. For consistency, we also do not enforce this condition here. As it turns out, this choice results in algebraically simpler approximate formulas. One can also check explicitly that with F, D, and E so defined, in the limit κ→0 Eqs. 3, 4, 5 reduce to the no-salt case of Eqs. 1, 2.
METHODS
Structures
The structures used to test the analytical electrostatic potential against the numerical PB reference are selected as follows. We start from the 600 representative biological molecules used for the testing purposes in earlier works.24, 26 Then, numerical PB solvers DELPHI-II (Refs. 1, 27) and MEAD (Ref. 28) with settings described in Sec. 2C below are used to generate the electrostatic potentials on a 255×255×255 cubic grid. Then, 20 of the 600 structures are excluded from the test set because either DELPHI-II or MEAD fail to output the potential map. For most of the failed cases the attempted calculation fails due to the requested memory exceeding the 1 Gbyte random access memory (RAM) capability of our PC. In addition to the above structures, we have also considered a 12 base-pair fragment of B-DNA constructed with canonical parameters. This important test case is discussed separately and is not included in the bulk statistical analysis of the above 580 structures.
The tobacco ring spot virus (TRSV) capsid is constructed from 60 identical monomers. The Protein Data Bank (PDB) file 1A6C contains the x-ray crystallographic coordinates of the single monomer at 3.50 Å resolution; the transformation matrix given in the PDB file header is used to properly rotate and align each monomer to form the complete capsid icosahedral structure.
Generation of molecular surfaces
For each of the 580 biomolecules in the test set described above, we obtain the molecular surface through the program MSMS.29 Unless otherwise specified, we use a probe radius of 2.0 Å and a triangulation density of 3.0 vertices per square Å. The molecular surface sets the boundary between the solute and solvent dielectric environments. The vertices that make up the molecular surface are then used as a basis for the sample points used to test the analytical formulas against the NPB reference. We use 2.0 Å probe radius instead of the more typical 1.5 Å as a means of mitigating the effects of differences in the surface representation used by the reference NPB solvers and MSMS.
Generation of reference NPB electrostatic potential
The reference electrostatic potential around each of the test structures is computed using DELPHI-II (Refs. 1, 27) with a 255×255×255 cubic box. The default MEAD and DELPHI-II convergence criteria are used in all cases. Grid spacing is 0.5 Å.
The following physical conditions have been used for the 580 realistic biomolecular structures. The solvent is assumed to have a dielectric constant of 80, a salt content of 0.145M, and an ion exclusion radius of 2.0 Å. The internal medium is assumed to have a dielectric constant of 4.
Sampling points
The electrostatic potential estimations provided by numerical solvers at the molecular surface—which is taken to represent the dielectric boundary in this work—are sensitive to the details of the definition of the surface. To make a connection with physical reality (finite ligand size) and to avoid artifacts related to surface definition, the points are sampled 1.5 Å away from the surface by projecting each surface vertex outward 1.5 Å along its surface normal.
For each sample point defined above, two potential values are obtained: ϕ (the analytical approximation) and ϕNPB (the numerical reference). ϕ is calculated via Eqs. 4, 5. We use κ=0.122 throughout, which corresponds to 0.145M concentration of monovalent salt in the solvent. ϕNPB is taken to be the value of the potential of the nearest finite-difference grid point.
When testing a potential field on a surface in the vicinity of the dielectric boundary, one has to make sure that all the test points lie within the intended region of interest: Either the high dielectric solvent space, regions II and III (outside the boundary), or the low dielectric solute regions I (inside the boundary) (see Fig. 1). One can check that this condition is satisfied for the set of parameters used here: NPB grid resolution R=0.5 Å, probe radius used to compute the molecular surface probe=2.0 Å, and the projection length along surface normal p=1.5 Å. In general, the condition probe radius>p+R∕2 ensure that a normal vector of length ∣p∣ that begins at the dielectric boundary remains entirely within one dielectric region. It also ensures that the NPB grid point closest to the end of that vector—where the reference potential is sampled—is also in the same region.
Visualization
The potential ϕ or ϕNPB computed at each sampling point as described above is visualized at the corresponding vertex point right on molecular surface; that is, the potential value is “projected back” on the dielectric boundary along the normal to the surface. We use a continuous color scale and the accepted color scheme, in which red corresponds to negative values of the potential, blue to positive, and white to zero. All analytical calculations and visualizations are performed by the GEM package described below.
Protonating the TRSV capsid
The standard continuum electrostatics methodology30, 31 is used to protonate the viral capsid. The full structure contains 4617 titratable groups—too many for this methodology. We therefore reduce the number of titratable groups via the following steps: We generate a subsection of the capsid surface such that one monomer unit is completely surrounded by other monomers. This results in a nine monomer (enneamer) subsection of the surface with one unit in the center and eight units surrounding it. The enneamer contains 981 titratable sites, which are still too many for the standard approach. Only the groups in the central unit are considered to be titratable in the calculations, the others are set in their standard protonation states. The total number of groups treated as titratable is therefore reduced to 125.
The AMBER (Ref. 32) set of partial atomic charges is used here for the protein charges. For the protonated states of Asp and Glu, in which the correct location of the proton is not known a priori, we use a “smeared charge” representation in which the neutralizing positive charge is symmetrically distributed: 0.45 on each carbonyl oxygen atom and 0.1 on the carbon atom. The web server H++ (Ref. 30) is used to perform the calculations with the following settings: 0.145M monovalent salt concentration, internal dielectric of 4, and external dielectric of 80. The computed pKa of the central unit are used to set its protonation state at each pH. The full capsid is then constructed from this protonated unit as described above. The biologically relevant pH interval from 4 to 9 is divided into 100 equidistant points: For each pH value we construct the full capsid in the corresponding protonation state.
Software implementation of the analytical model
Analytical formulas described in this work are implemented in a software package, GEM, freely available from the authors upon request. GEM is a tool for computing, extracting, visualizing, and outputting the electrostatic potential around macromolecules. Basic selection tools and structural representations are available. In addition, GEM supports reading and writing potential field files in the format adopted by the DELPHI-II package, reading potential field files in the format of the MEAD package, mapping electrostatic potential to the molecular surface, image output in Targa file format (TGA) format, and a graphical user interface. There is no predefined limit on the spatial resolution of the input∕output potential field maps. All electrostatic surface images used in the paper were generated through GEM. The program can either be run in batch mode or through a graphical user interface and is currently available for Linux and Macintosh OSX.
GEM performance analysis: Memory overhead
One attractive feature of GEM that sets it apart from all available packages based on NPB methodology is the ability to solve for electrostatic potential at points of interest independently from each other. NPB-based solvers must solve for the entire domain in order to provide solutions to even a single point of interest; this prerequisite is the source of extremely high memory requirements when those methods are applied to large molecules. The freedom from this limitation that GEM provides is a crucial practical advantage when analyzing the electrostatic properties of such molecules. As an example, the RAM required by GEM to store the potential map of the surface of the TRSV virus consisting of 651 544 surface grid points is only 30 Mbytes. This is an insignificant overhead for even a modest desktop computer. The corresponding requirements are orders of magnitude larger for the NPB solutions. For example, in order to store a typical finite mesh (at a typical resolution of 0.25 Å per grid point) of floating point values for a molecule of the size of TRSV virus, about 12003 (1 440 000 000) separate grid points would be needed, requiring a minimum of nearly 13 Gbytes of memory, assuming 8 byte double representation per mesh point.
GEM performance: Computational overhead
Due to the additivity of the electrostatic potential, GEM must compute the contributions from each charge in the molecule to each point of interest; without any further approximations its time complexity is O(NP), where N is the number of atoms in the molecule and P is the number of points of interest. The algorithm scales well with the number of points of interest or the number of charges in the molecule. Of course, the current implementation does not scale so well if the problem is such that the number of points of interest is a function of the number of atoms in the molecule. Work is now in progress to improve the time complexity in the worst case using standard numerical techniques such as multipole expansion.
RESULTS
Accuracy of the analytical approach
Exact solutions of the PB equation for realistic biomolecular shapes are not available in practice; we therefore resort to the accepted approximate numerical solutions to test our analytical approximations for the electrostatic potential. For testing, we use a set of 580 representative biomolecules26 (see Sec. 2).
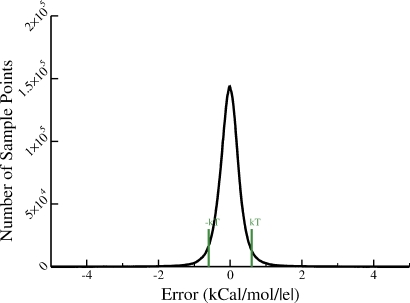
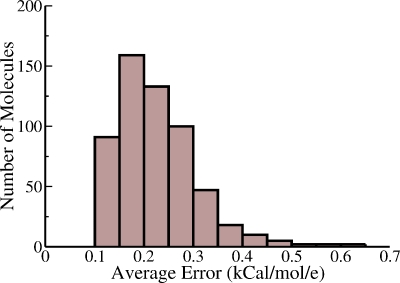
The reference numerical solutions are generated with the popular finite-difference PB solver DELPHI-II (Refs. 1, 27) using the default parameter settings. As discussed in Part I, there is no unique way of comparing two scalar fields in three dimensions. One could, for example, consider a global metric such as root-mean-square deviation (rmsd) from the reference over the entire solute space. (The metric would have to be appropriately defined to ensure convergence.) However, such a metric would likely underestimate the errors involved: Note that by construction the approximate ϕ becomes asymptotically exact far away from the charge sources. Conversely, one expects the error to increase as one approaches the molecular surface. We therefore argue that comparing the potentials at or right outside the dielectric boundary (which is defined as molecular surface) is a reasonable choice for the purposes of testing the quality of our analytical approximation ϕ. As was shown in Part I for idealized geometries, this metric is a more sensitive test of accuracy of the approximation than one based on electrostatic part of solvation free energy, which is an indirect metric. An additional argument for assessing the errors of the potential directly is that due to continuity of ϕ at the boundary, this metric will automatically test both the inside and the outside analytical approximations. Also, we shall soon see that the ability to visualize the potential at the 2D surface proves critical for investigating the performance of the approximate solutions in various regions of space. To make connection with physical reality—ligand probe of finite size—we compute the actual error not right at the dielectric boundary but at a surface located 1.5 Å outside the dielectric boundary (see Sec. 2). In this work, the error is estimated as ϕ−ϕNPB over a combined total of approximately ten million vertex points that define the sets of triangulated molecular surfaces for the test molecules. The distribution of the error is shown in Fig. 3; the deviation from the NPB reference is within kT (per unit charge ∣e∣) for the vast majority of points.
Figure 3.
The distribution of error (ϕ−ϕNPB) between the electrostatic potential values computed via the analytical approach introduced here and the standard numerical PB reference DELPHI-II. The error value is computed 1.5 Å outside the dielectric boundary, for every vertex on the corresponding molecular surface of each of the 580 representative biomolecules used as the test set. A total of 9 421 303 vertices are analyzed; to obtain the distribution, the horizontal axis is partitioned into 1000 equidistant bins. For 91.5% of the vertices, the error ∣ϕ−ϕNPB∣ lies within kT∕∣e∣. The error is within 2kT∕∣e∣ for 98.1% of the vertices.
An examination of molecular structures corresponding to the tails of the error distribution in Fig. 3—cases where the per vertex deviation from the NPB reference far exceeds kT—should give clear clues as to what one may expect from the analytical approximation in the worst case. To this end, we have identified the maximum value of the deviation ∣ϕ−ϕNPB∣ for each of the 580 structures in the test set. For a given structure, the maximum deviation was determined among all vertices on the test surface described above. The structures were then sorted down, from the worst performers to the best, according to these maximal deviations from the NPB reference. A careful analysis of 15 structures at the top of this list reveals that all of the worst performers share the same geometrical characteristic: The largest ∣ϕ−ϕNPB∣ deviation occurs in deep and narrow indentations on molecular surface. The two typical cases, actually corresponding to the first and second worst performers, are shown in Fig. 4.
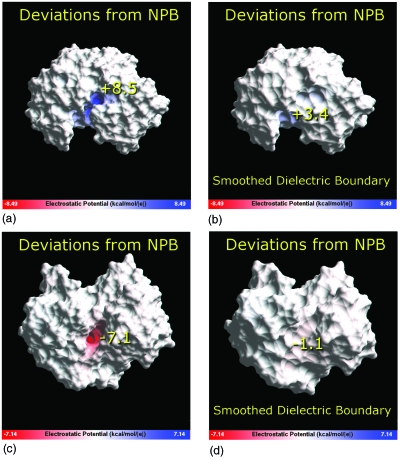
Figure 4.
The distribution of the deviation of the approximate analytical potential from the NPB reference (ϕ−ϕNPB) near the dielectric boundary of the two “worst performer” biomolecular structures. These exhibit the largest and second largest absolute deviations from the NPB reference among all the 580 molecule test set. Top: PDB ID 1BXO; bottom: 1C1D. The difference (ϕ−ϕNPB) is computed 1.5 Å outside the dielectric boundary (molecular surface) and visualized on the surface using a continuous color scale. Blue: positive values; white: zero; red: negative. The numerical value of the largest deviation for each structure, in kcal∕mol∕∣e∣, is shown on the surface near the region where it occurs. The largest deviation is reduced considerably, right panel, if a smoother dielectric boundary is used. The smoothing effect is achieved by using a larger probe radius of 3.0 Å to compute the molecular surface that represents the boundary. The GEM package is used for computing the approximate analytical potential and visualizing the deviation from the NPB reference potential computed by DELPHI-II.
Several conclusions can be made by examining the distribution of (ϕ−ϕNPB) in the near vicinity of the dielectric boundary. First, it is clear that inside some of the deepest and narrowest indentations on the dielectric boundary, the analytical approximation significantly underestimates the maximum absolute value of the reference NPB potential, by 8.5 kcal∕mol∕∣e∣ in the worst case, and by 7.1 kcal∕mol∕∣e∣ the next worst. This type of underestimation of ∣ϕNPB∣ for these regions of solvent space should not be surprising: The solutions of the Poisson equation around deep narrow regions of high dielectric are very different from that for a sphere.33 Similar deviations were observed and discussed earlier in the context of the generalized Born model.34 Note that the radius of curvature of a sphere can, in principle, range from zero to +∞ (plane) but can never be negative. The indentations shown in Fig. 4 correspond to regions of high negative curvature.
At the same time, these large deviations of the approximate potential from the NPB reference occur only at a small subset of points deep inside the narrow indentations and do not occur outside these regions of highly negative curvature. This is easily seen both from the potential maps (Fig. 4) and from the rms values of (ϕ−ϕNPB) computed over the entire test surface: For the two structures shown in the figure, the rmsds are 1.3 and 1.2 kcal∕mol∕∣e∣. Although several kcal∕mol difference with the NPB reference may seem like a very large error, we argue that most of it may not be physically realistic. Both the analytic and the NPB models are based on the linear response, continuum solvent approximation, which certainly breaks down inside the narrow crevices that can barely host a single water molecule along at least one dimension. These strongly confined water molecules are unlikely to have properties of the bulk and certainly cannot be described by a continuum dielectric of ϵ=80 used to compute the potentials. We argue that the ∣ϕ−ϕNPB∣ deviations become much smaller if one excludes regions of space where the continuum approximation is definitely inapplicable. While the exact boundaries of the applicability of the continuum model are unknown, one can get a rough idea of how the ∣ϕ−ϕNPB∣ deviation behaves as these regions are reduced. Namely, we have recalculated both potentials at the molecular surface obtained with the probe radius of 3.0 Å, which is twice the typical water radius (Fig. 4, right panel). Clearly, the analytical versus NPB deviations are now substantially reduced: For the worst performer max∣ϕ−ϕNPB∣ is 3.4 kcal∕mol∕∣e∣ and the rmsd over the entire dielectric boundary is 0.5 kcal∕mol∕∣e∣. Interestingly, the qualitative prediction of our analytical approximate model for this structure—that the potential is highly negative inside the crevice relative to the rest of the surface—appears to be consistent with the NPB result regardless of the probe radius used (results not shown). The max∣ϕ−ϕNPB∣ deviation that remains after smoothing of the dielectric boundary is even less for the second worst performer structure: 1.1 kcal∕mol∕∣e∣, with rmsd of 0.4 kcal∕mol∕∣e∣. The reduction is so significant in this case because the deep “burrow” seen in this structure in Fig. 4 has completely disappeared when the smoother dielectric boundary is used.
Having explored the relatively rare cases of large deviations from the NPB reference, we now turn our attention to the performance of the analytical approximation on structures that fall within the bulk of the error distribution in Fig. 3. Somewhat unexpectedly, even structures whose global shape deviates considerably from the perfect spherical perform quite well as judged by visual inspection (Fig. 5) and by the computed max∣ϕ−ϕNPB∣ values. In fact, for the top two structures in Fig. 5, these maximum deviations from the reference are within ∼1 kcal∕mol∕∣e∣, rmsd is less than 0.3 kcal∕mol∕∣e∣, and thus the analytical approximation is quantitatively correct for these shapes.
Figure 5.
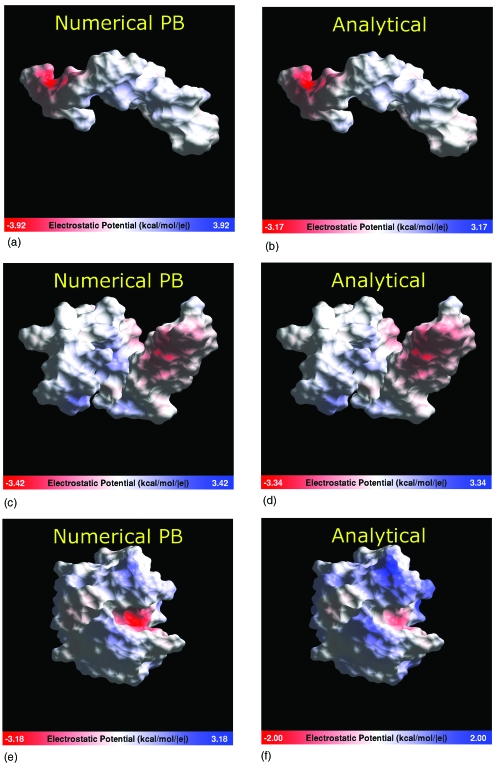
Electrostatic potential computed near the dielectric boundary of various biomolecules whose shape deviates considerably from spherical. The potential is computed 1.5 Å outside the dielectric boundary (molecular surface) and visualized on the surface using a continuous color scale. Blue: positive values; white: zero; red: negative. The range indicated on the color bar corresponds to the absolute maximum of the potential for a given structure. Left column: numerical reference. Right column: approximate analytical potential. Structures: The Alzheimer disease amyloid A4 peptide, PDB ID 1AML (top); human apolioprotein C-II, PDB ID 1I5J (middle); lysozyme, PDB ID 2LZT (bottom). The GEM package is used for the computation of the analytical potentials and the visualization.
Not surprisingly, the largest deviations are seen for the lysozyme structure that features a distinct region of negative curvature of the dielectric boundary—the enzymatic pocket. At a single point in the pocket region, ∣ϕ−ϕNPB∣ reaches 2.2 kcal∕mol∕∣e∣; however, the rmsd over the entire surface of the protein is 0.4 kcal∕mol∕∣e∣. The smoothing of the dielectric boundary, performed as described in the legend to Fig. 4, reduces the maximum deviation to 1.7 kcal∕mol∕∣e∣, and the rmsd to 0.3 kcal∕mol∕∣e∣. Unlike the very narrow indentations and deep narrow “burrows” in the dielectric boundary seen in Fig. 4, which most likely hold only highly structured water, the enzymatic pocket of lysozyme is large enough so that the continuum approximation is expected to have a reasonable degree of physical realism in this region. Thus, the deviations from the NPB reference in this case are meaningful. Exactly how significant is the ∼2 kcal∕mol∕∣e∣ maximum error relative to the NPB reference for biological function of lysozyme is less clear: This question is beyond the scope of this methodological work. One should bear in mind that the continuum solvent PB framework itself is only an approximation to the more realistic explicit solvent representation: The differences between the two are not negligible.35 Despite the quantitative deviations from the NPB, our approximate method correctly identifies the enzymatic pocket of lysozyme as the region of the highest negative electrostatic potential, relative to the rest of the structure. Thus, we conclude that the approximation provides a correct qualitative picture in this case, within the framework of the continuum model. We have also examined the accuracy of the approximation for the important case of the DNA structure. For a 12 base-pair fragment in canonical B-form, max∣ϕ−ϕNPB∣ is 1.2 kcal∕mol∕∣e∣, or 25% relative error to ϕNPB. In agreement with the conclusions made above, the deviation occurs inside the deepest part of the minor groove. The overall agreement with the NPB reference is similar to that for the proteins shown in Fig. 5, with the rmsd from the reference of 0.5 kcal∕mol∕∣e∣. We stress that both ϕ and ϕNPB used here correspond to the linearized form of the PB equation.
We have already seen that the NPB reference potential is approximated by the analytical approach within kT per unit charge for the vast majority of the points sampled from just outside the dielectric boundaries for all of the 580 test molecules. Cases of significant deviations in localized regions of space have been identified and analyzed. However, it is in principle possible that for a small subset of structures, the agreement between ϕ and ϕNPB may still be uniformly poor overall for most surface points of these few structures (although better than the local deviations seen in the worst performers in Fig. 4). Such errors would be “lost” in Fig. 3, as this particular representation does not distinguish between contributions coming from separate molecules. As a means of investigating the role that the overall molecular shape plays in the accuracy of the approximate method, we have calculated the average absolute vertex error per molecule as
| (9) |
where the summation extends over ni test surface vertices for each structure i. As seen in Fig. 6, the distribution of the average error has a finite width, and so molecular shape does indeed play a role in determining the accuracy of the method. However, no extreme outliers with average errors above kT are seen. This conclusion is consistent with the qualitative agreement between ϕ and ϕNPB on globally nonspherical shapes presented in Fig. 5.
Figure 6.
Distribution of the deviation in average potential between the analytical approximation and the NPB reference. The potentials are computed as described in Fig. 3. Horizontal axis: The average absolute error per structure ⟨∣ϕ−ϕNPB∣⟩i [Eq. 9]. Vertical axis: Number of structures corresponding to the given average error.
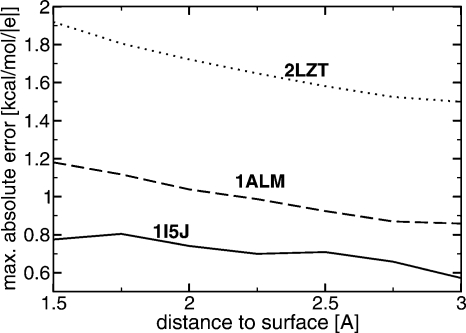
At this point, we can also provide an additional support for the statement made in the beginning of this work that the maximum errors of the analytical approximation are likely to occur in regions closest to the dielectric boundary. The claim is further substantiated by the results in Fig. 7 where the decrease of max∣ϕ−ϕNPB∣ is seen for the three very different molecular shapes shown in Fig. 5. While the origin of this behavior for large distances from the boundary is obvious—the approximate solution is asymptotically exact far away from the sources—the fact that the same result holds near dielectric boundaries of rather complex shapes may appear puzzling. While we do not have a rigorous mathematical proof for it in the case of an arbitrary surface, we note that the error bound derived in Part I for a single source charge below the spherical boundary does decrease monotonically with distance from the boundary. Presumably, this rigorous result is not far off the mark for realistic shapes that do not exhibit drastic deviations from spherical in the sense discussed above, that is, do not have regions of very high negative curvature. This may explain the low and decreasing max∣ϕ−ϕNPB∣ for 1ALM and 1I5J structures in Fig. 7. For the lysozyme (2LZT), the rigorous result is unlikely to hold, but note that the max∣ϕ−ϕNPB∣ is known to occur inside its enzymatic pocket, that is, in the region of negative curvature. As the test surface moves outside the pocket, the error is expected to decrease substantially simply because the test points move out of the region where the sphere-based approximation is less accurate compared to the rest of the space. Consistent with this explanation, the noticeable decrease in max∣ϕ−ϕNPB∣ is seen in Fig. 7 for lysozyme.
Figure 7.
The decrease of the maximum deviation max∣ϕ−ϕNPB∣ between the analytical approximate potential and the NPB reference as a function of distance to the dielectric boundary for the three structures shown in Fig. 5. The “smooth” surface (solvent probe=3 Å) is used.
We have also explored the possibility that the parameter α that enters all of our analytical formulas may not be optimal for realistic molecular shapes. Perhaps not surprisingly, we find that varying α within most of its range (0.5–0.8) resulted in virtually no change in the shape or width of the error distribution curve in Fig. 3. Thus, as long as we are looking for a single value of α optimal for an average shape relevant to biomolecular computations, the “first principles” value we derived earlier is acceptable.
The reasonable performance of our analytical approach to compute the electrostatic potential around realistic biomolecules is not completely unexpected; after all, successful use of simple shapes in a related problem—deriving approximate expressions for biomolecular solvation energy—has had a long history.24, 36, 37 Given the accuracy of our analytical approximations in the perfect spherical case, see Part I, we speculate that for some of the more spherical molecules and for some regions of space in most structures, the analytical approximations introduced here may even be closer to exact results than the corresponding NPB solutions obtained with commonly used parameter settings.
Application example: Surface potential of the TRSV viral capsid
The TRSV belongs to the Comoviridae family of the Genus Nepovirus. The TRSV virus is believed to represent a very simple (the capsid is made of single protein subunit, no lipid coat, no cleavage sites in polyproteins) precursor to the nepovirus, picornavirus, and comovirus families.38 Despite its apparent structural simplicity, the capsid is extremely selective for its RNA.39 The precise mechanism underlying the selectivity of the TRSV capsid for its RNA is still unknown, although experimental evidence suggests that it is structure based rather than sequence based.40, 41 Since electrostatic factors play a major role in protein-nucleic acid interactions, taking these effects into account is expected to be critical for solving the puzzle. In what follows we use the analytical approach presented above to compute the electrostatic potential on the surface of the TRSV capsid at full atomic resolution. We will show how the details of the potential distribution might hint at plausible mechanisms of the capsid’s puzzling selectivity for its RNA. A detailed study of the “capsid selectivity” puzzle is well beyond the scope of this purely methodological work; the analysis of the TRSV surface potential presented below should not be viewed as a rigorously justified solution of the problem, but rather as a way of demonstrating the computational potential of the proposed analytical approach.
From the structural standpoint, the capsid can be considered as serving a dual purpose, one from the exterior and one from interior. The outside interacts with the environment during the various stages of the virus’ life cycle. As the virion moves from the vertical vector to the cytoplasm of a tobacco plant cell to the plant sap, it experiences environments of different pH. As we shall see, the induced changes in the outside electrostatic potential are nearly uniform. In contrast, the inside of the capsid has a set of repeated pockets of distinct, positive electrostatic potential that persist over a wide range of pH. These areas are located at the center of a five-monomer subunit (pentamer); we will speculate that these pockets might serve as RNA binding locations.
The outer surface
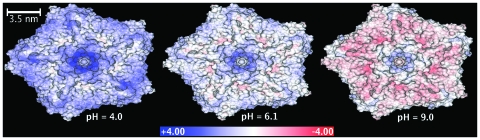
The electrostatic potential at the molecular surface of the TRSV capsid is computed for a wide range of pH values; Fig. 8 contains three representative snapshots from the range of values used. The potential appears to be nearly uniform on the outer surface and changes distinctly and uniformly with the pH of the environment. The computed isoelectric point of the capsid is at pH 7.15, and the potential is distributed uniformly across the outer surface (see Fig. 8). The surface potential is uniformly close to zero at neutral pH (Fig. 8, middle panel). The absence of strong electrostatic repulsion in the capsid leading to its structural stability in the neutral pH range makes sense biologically; the virion is known to use the sap of a healthy tobacco plant of pH 6.2 as a means for circulating through the plant in attempt to find other mechanically damaged cells to infect.42 The buildup of a fairly uniform negative charge across the capsid at high pH [Fig. 8 (right panel)] diminishes its stability due to Coulombic repulsion. This is consistent with the swelling of the capsid at pH greater than 8.0.15 In living cells, swelling might be the mechanism allowing the virion to release its RNA in cell compartments that have high pH.
Figure 8.
The outer surface of the TRSV viral capsid color-coded according to the electrostatic potential computed 1.5 Å outside the surface. Continuous color scale is used, from red (corresponding to −4.68 kcal∕mol∕∣e∣) to white (zero) to blue (+4.68 kcal∕mol∕∣e∣). The charge state of the capsid changes with the pH of the environment: The computations are performed at a constant salt concentration (0.145M) and three different pH values shown under each structure. The molecular surface of the capsid is triangulated with the resolution of 2.5 Å; the electrostatic potential is computed at the end of the outward surface normal at each vertex point via the closed-form analytical approximations of the PB equation presented in this work. The GEM package is used for all the computations.
The inner surface
In contrast to the relatively featureless outer surface potential, the inner surface reveals a distinct pocket of highly positive potential (blue region in the middle of the pentamer in Fig. 9), which is robust to pH changes in the physiologically relevant range.
Figure 9.
The inner surface of the pentamer subunit color-coded according to the computed electrostatic potential. The computations are performed at three different pH values shown under each structure with a constant salt concentration of 0.145M. A continuous color scale is used from red (corresponding to −4.00 kcal∕mol∕∣e∣) to blue (+4.00 kcal∕mol∕∣e∣). The regions of zero potential are shown in white. The proposed RNA binding pocket is seen as a bright blue spot in the center of the structure which remains distinct throughout the entire pH range. The primary source of this region of intense positive potential is a “ring” of ten arginines. Each monomer of the pentamer provides two sequential arginines (residues 453 and 454) which are in close proximity to each other in the pentamer structure. The potential is computed 1.5 Å outside molecular surface and visualized on the surface. The GEM package is used.
The source of the positive potential is two adjacent arginines (R453 and R454) in each of the five monomers that form the pentamer structure. In the assembled capsid, these 2×5=10 arginines form a “ring” of positive charges near the inner surface of the capsid. The pocket resembles a narrowing dome: Near the surface it is approximately 50 Å wide, and it narrows deeper into a more cylindrical shape with a diameter of roughly 20 Å. The entire site from top to bottom is roughly 40 Å deep. We conjecture that this pocket represents the RNA binding site and plays a role in the observed high selectivity of the TRSV capsid for its RNA. The positively charged arginine ring attracts RNA; geometry determines which RNAs are structurally compatible with the pocket.
Computational arguments alone rarely provide a definitive proof of structure-function relationships in complex systems such as TRSV. In this purely methodological work we will not pursue this issue any further, and thus our conclusions about the structure-function relationships in the TRSV capsid should be considered as conjectures. Still, we believe that the observations we have made and tools we have developed might provide useful leads and starting points for further experimental and theoretical studies of this intriguing system.
CONCLUSIONS
In Part I of this work a simple closed-form expression for calculating molecular electrostatic potentials everywhere in space was rigorously derived for an ideal spherical geometry. Here, we use a physically justified ansatz to extend the approximation to include the screening effects of mobile ions in the Debye–Hückel limit. We have tested the accuracy of the approximate potential ϕ extensively against NPB reference on a set of 580 molecular structures representing various structural classes. Among various possible accuracy metrics we chose direct deviation (ϕ−ϕNPB) computed where it is expected to be largest: Near the dielectric boundary. For each structure, (ϕ−ϕNPB) is computed under typical conditions of aqueous solvation for a large number of test points placed 1.5 Å outside the molecular surface that defines the sharp dielectric boundary. The absolute error ∣ϕ−ϕNPB∣ averaged over all test points in each structure is within 0.6 kcal∕mol∕∣e∣∼kT per unit charge for all structures tested. For 91.5% of the individual test points, the absolute deviation from the NPB potential is within 0.6 kcal∕mol∕∣e∣; the deviation is within 1.2 kcal∕mol∕∣e∣∼2kT per unit charge for 98.1% of the individual test points.
For an approximation originally derived for perfect spherical boundary, one may expect that its accuracy would decrease dramatically for structures whose global shape deviates considerable from spherical, such as structures with aspect ratio ⪢1. This, however, does not appear to be the case: We analyzed several structures that appear very nonspherical globally and found that the maximum deviations from the NPB reference are within 1 kcal∕mol∕∣e∣, with a rmsd between 0.2 and 0.4 kcal∕mol∕∣e∣. The understanding of this somewhat unexpected result came from the analysis of the absolute largest deviations from the NPB reference and regions of space where they occurred. We have identified 15 “worst performer” structures—those that exhibited the largest maximum deviations from the NPB in at least one test point near the dielectric boundary. In all 15 cases, these largest deviations of several kcal∕mol∕∣e∣ occurred only in localized pockets of highly negative curvature, that is, inside very deep and narrow indentations on the dielectric boundary. Outside of these regions, the deviations were generally within ∼1 kcal∕mol∕∣e∣. This behavior of the approximation based on a sphere is not unexpected: A spherical surface can have any curvature from zero to positive infinity (plane limit), but never a negative one. The idea that the approximation is least accurate near regions of locally highly negative curvature is supported by the fact that the maximum deviations from the NPB are reduced dramatically when the dielectric boundary is smoothed by using a larger probe radius (3 Å) to generate the molecular surface. From a practical standpoint, the above extreme cases may not be relevant though: The dimensions of the regions where these largest deviations occurred were such that they likely can host only highly constrained solvent with properties very different from the bulk dielectric continuum implied by the PB model itself. In the case of lysozyme that features a functionally important region of negative curvature (an enzymatic pocket) on its dielectric boundary, the maximum deviation of the approximate potential from the NPB reference is 2.2 kcal∕mol∕∣e∣ and is reduced to 1.7 kcal∕mol∕∣e∣ when the smoother boundary is used. The rmsd from the NPB potential for this structure is 0.4 kcal∕mol∕∣e∣. All qualitative features of the distribution of the reference NPB potential for lysozyme are preserved by the analytical approximation. The approximation behaves as expected in the case of another important structure that contains pronounced regions of negative curvature on its dielectric boundary: The DNA. For a 12 base-pair fragment in canonical B-form, the maximum deviation of 1.2 kcal∕mol∕∣e∣ or 25% relative error to NPB occurs in the deepest part of the minor groove. Outside of that spot, the agreement with the (linearized) PB is considerably closer and is similar to that for the proteins discussed above.
The computational complexity of the analytical method based on a simple formula is fundamentally lower compared to the NPB. This advantage has been exemplified by using the new approach to compute electrostatic potential on the surface of the capsid of TRSV at atomic resolution. The analysis of the electrostatic potential of the inner surface of the capsid reveals what might be a RNA binding pocket: This observation might provide a useful lead for further experimental and theoretical studies of this intriguing molecular system. All computations on this large structure—nearly half a million atoms—were performed on a desktop personal computer. In contrast, the use of the traditional numerical approach to study electrostatic properties of molecular systems of this size at atomic resolution would most likely require sophisticated algorithms and supercomputers.
From the methodological standpoint, the presented analytical approach is particularly well suited for the analysis of the electrostatic potential around very large structures. The additional computational expense associated with “zooming in” on a local region of interest is small—to increase the spatial resolution locally one needs to perform extra computations only at the positions of the added sampling points. This example highlights a fundamental difference between field-based approaches such as NPB where the potential everywhere in space is found as a solution of a partial differential equation and the source-based approaches such as the one presented here. In the latter case, the approximate Green’s function is known, and so the computational cost of computing the potential at a single point is virtually zero, whereas to obtain the single point potential using a field-based method, one would still require a much more expensive self-consistent solution over a large number of points in a finite 2D or 3D region of space.
The need for computationally facile theoretical tools for the analysis of molecular electrostatic properties exists in many areas. The general approach presented here provides an analytical approximation for the potential everywhere in space and might provide a concrete starting point for the development of other practical alternative tools to be used alongside the traditional numerical PB treatment.
ACKNOWLEDGMENTS
The authors are thankful to Sue Tolin for many helpful discussions about viral life cycles. The authors thank Grigori Sigalov, Jack Johnson, and Dave Bevan for reading the manuscript and providing valuable feedback. This work was supported by NIH Grant No. GM076121 and ASPIRES seed grant from Virginia Tech. A.T.F. acknowledges support from the NSF IGERT Grant No. DGE-0504196.
References
- Honig B. and Nicholls A., Science 10.1126/science.7761829 268, 1144 (1995). [DOI] [PubMed] [Google Scholar]
- Chin K., Sharp K. A., Honig B., and Pyle A. M., Nat. Struct. Biol. 10.1038/14940 6, 1055 (1999). [DOI] [PubMed] [Google Scholar]
- Perutz M., Science 10.1126/science.694508 201, 1187 (1978). [DOI] [PubMed] [Google Scholar]
- Davis M. E. and McCammon J. A., Chem. Rev. (Washington, D.C.) 10.1021/cr00101a005 90, 509 (1990). [DOI] [Google Scholar]
- Baker N. A. and McCammon J. A., Structural Bioinformatics (Wiley, New York, 2002). [Google Scholar]
- Warshel A. and Åqvist J., Annu. Rev. Biophys. Biophys. Chem. 10.1146/annurev.bb.20.060191.001411 20, 267 (1991). [DOI] [PubMed] [Google Scholar]
- Warshel A., Biochemistry 10.1021/bi00514a028 20, 3167 (1981). [DOI] [PubMed] [Google Scholar]
- Fersht A., Shi J., Knill-Jones J., Lowe D., Wilkinson A., Blow D., Brick P., Carter P., Waye M., and Winter G., Nature (London) 10.1038/314235a0 314, 235 (1985). [DOI] [PubMed] [Google Scholar]
- Szabo G., Eisenman G., McLaughlin S., and Krasne S., Ann. N.Y. Acad. Sci. 195, 273 (1972). [PubMed] [Google Scholar]
- Douglas T. and Ripoll D. R., Protein Sci. 7, 1083 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheinerman F. B., Norel R., and Honig B., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(00)00065-8 10, 153 (2000). [DOI] [PubMed] [Google Scholar]
- Onufriev A., Smondyrev A., and Bashford D., J. Mol. Biol. 10.1016/S0022-2836(03)00903-3 332, 1183 (2003). [DOI] [PubMed] [Google Scholar]
- Yang A. -S. and Honig B., Curr. Opin. Struct. Biol. 10.1016/0959-440X(92)90174-6 2, 40 (1992). [DOI] [Google Scholar]
- Whitten S. and Garcia-Moreno B., Biochemistry 10.1021/bi001015c 39, 14292 (2000). [DOI] [PubMed] [Google Scholar]
- ICTVdB-Management, 18.0.3.0.0.027 tobacco ringspot virus, ICTVdB—The Universal Virus Database, Version 4, 2002. (http://www.ncbi.nlm.nih.gov/ICTVdb/ICTVdB/00.018.0.03.027.htm).
- Prescott B., Sitaraman K., Argos P., and Thomas G. J., Biochemistry 24, 1226 (1985). [DOI] [PubMed] [Google Scholar]
- Douglas T. and Young M., Nature (London) 10.1038/30211 393, 152 (1998). [DOI] [Google Scholar]
- Baker N. A., Curr. Opin. Struct. Biol. 10.1016/j.sbi.2005.02.001 15, 137 (2005). [DOI] [PubMed] [Google Scholar]
- Baker N. A., Sept D., Joseph S., Holst M. J., and McCammon J. A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.181342398 98, 10037 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu B., Cheng X., Huang J., and McCammon J. A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0605166103 103, 19314 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo R., David L., and Gilson M., J. Comput. Chem. 10.1002/jcc.10120 23, 1244 (2002). [DOI] [PubMed] [Google Scholar]
- Konecny R., Trylska J., Tama F., Zhang D., Baker N. A., Brooks C. L., and McCammon J. A.,, Biopolymers 10.1002/bip.20409 82, 106 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigalov G., Scheffel P., and Onufriev A., J. Chem. Phys. 10.1063/1.1857811 122, 094511 (2005). [DOI] [PubMed] [Google Scholar]
- Sigalov G., Fenley A., and Onufriev A., J. Chem. Phys. 10.1063/1.2177251 124, 124902 (2006). [DOI] [PubMed] [Google Scholar]
- Srinivasan J., Trevathan M., Beroza P., and Case D., Theor. Chem. Acc. 10.1007/s002140050460 101, 426 (1999). [DOI] [Google Scholar]
- Feig M., Onufriev A., Lee M., Im W., Case D., and Brooks C., J. Comput. Chem. 10.1002/jcc.10378 25, 265 (2004). [DOI] [PubMed] [Google Scholar]
- Nicholls A. and Honig B., J. Comput. Chem. 10.1002/jcc.540120405 12, 435 (1991). [DOI] [Google Scholar]
- Bashford D., in Scientific Computing in Object-Oriented Parallel Environments, Lecture Notes in Computer Science, ISCOPE97 Vol. 1343, edited by Ishikawa Y., Oldehoeft R. R., Reynders J. V. W., and Tholburn M. (Springer, Berlin, 1997), pp. 233–240. [Google Scholar]
- Sanner M. F., Olson A., and Spehner J., Proceedings of the 11th Annual Symposium on Computational Geometry (ACM, Vancouver, BC, 1995), pp. 406–407.
- Gordon J. C., Myers J. B., Folta T., Shoja V., Heath L. S., and Onufriev A., Nucleic Acids Res. 33, W368 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bashford D. and Karplus M., Biochemistry 10.1021/bi00496a010 29, 10219 (1990). [DOI] [PubMed] [Google Scholar]
- Pearlman D., Case D., Caldwell J., Ross W., T.CheathamIII, DeBolt S., Ferguson D., Seibel G., and Kollman P. A., Comput. Phys. Commun. 10.1016/0010-4655(95)00041-D 91, 1 (1995). [DOI] [Google Scholar]
- Jackson J., Classical Electrodynamics, 3rd ed. (Wiley, New York, 1999). [Google Scholar]
- Mongan J., Svrcek-Seiler W. A., and Onufriev A., J. Chem. Phys. 10.1063/1.2783847 127, 185101 (2007). [DOI] [PubMed] [Google Scholar]
- Swanson J. M. J., Adcock S. A., and McCammon J. A., J. Chem. Theory Comput. 10.1021/ct049834o 1, 484 (2005). [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G., J. Chem. Phys. 10.1063/1.1749489 2, 351 (1934). [DOI] [Google Scholar]
- Havranek J. J. and Harbury P. B., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.96.20.11145 96, 11145 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekar V. and Johnson J. E., Structure (London) 6, 157 (1998). [DOI] [PubMed] [Google Scholar]
- Buzayan J. M., McNinch J. S., Schneider I. R., and Bruening G., Virology 160, 95 (1987). [DOI] [PubMed] [Google Scholar]
- Passmore B. and Bruening G., Virology 197, 108 (1993). [DOI] [PubMed] [Google Scholar]
- Singh S., Rothnagel R., Prasad B., and Buckley B., Virology 213, 472 (1995). [DOI] [PubMed] [Google Scholar]
- Johnstone G. R. and Wade G. C., Aust. J. Bot. 22, 437 (1974). [Google Scholar]