Using Triplet Periodicity of Nucleotide Sequences for Finding Potential Reading Frame Shifts in Genes

Abstract

We introduce a novel approach for the detection of possible mutations leading to a reading frame (RF) shift in a gene. Deletions and insertions of DNA coding regions are considerable events for genes because an RF shift results in modifications of the extensive region of amino acid sequence coded by a gene. The suggested method is based on the phenomenon of triplet periodicity (TP) in coding regions of genes and its relative resistance to substitutions in DNA sequence. We attempted to extend 326 933 regions of continuous TP found in genes from the KEGG databank by considering possible insertions and deletions. We revealed totally 824 genes where such extension was possible and statistically significant. Then we generated amino acid sequences according to active (KEGG's) and hypothetically ancient RFs in order to find confirmation of a shift at a protein level. Consequently, 64 sequences have protein similarities only for ancient RF, 176 only for active RF, 3 for both and 581 have no protein similarity at all. We aimed to have revealed lower bound for the number of genes in which a shift between RF and TP is possible. Further ways to increase the number of revealed RF shifts are discussed.

1. Introduction

Mutations in DNA sequences appear as a result of base substitution or deletions, insertions and DNA sequence inversion.¹ At the level of amino acid sequences, substitutions of DNA bases may lead to substitutions of amino acids, i.e. single nucleotide substitution changes one amino acid or none. In this sense, deletions, insertions and inversions of DNA coding regions are more dramatic events for genes because such mutational alteration may lead to a reading frame (RF) shift and to modification of the extensive region of amino acid sequence. Substitution frequencies are well investigated, whereas RF shifts in genes are less studied, which is due to the difficulty in their identification. However, the investigation of the influence of RF shifts in genes on protein structure is of great interest. A single DNA base substitution may result in only one change of amino acid in a protein, whereas an RF shift causes the change of all amino acids coded downstream of the shift point in a gene. If after this the protein does not lose its function, then it is supposed that a frame shift has occurred in a functionally insignificant site or that the RF shift generates functionally similar amino acid sequences. But if after RF shift the protein has changed its function, then it is of great interest to understand how changes in amino acid sequence determine the protein's new function.

Answers for these questions can probably be found after a detailed investigation of RF shift statistics. To that end, we need a method for finding RF shifts in existing genes. Currently, general methods for finding RF shifts and inversions comprise the search for similarities between amino acid sequences through the BLAST program or its analogues.^2,3 When using such procedures for finding RF shifts, we should in some way mark out the gene region where the RF shift is expected to be found. Then we recode this region of nucleotide sequence into that of the amino acid according to the new RF, thus obtaining the hypothetic amino acid sequence as a result. Thereafter, we run a similarity search for a hypothetic amino acid sequence in UniProtKB/Swiss-Prot databank. If statistically significant similarities are found, then we can be sure that the gene contains an RF shift, i.e. we see that sequences related to the hypothetic a amino acid sequence do exist. This method has allowed us to find, so far, several hundred genes in which the RF shift has really taken place.^2,3

However, this scheme of finding RF shifts and inversions has some limitations. First, we have to choose a gene, using some criterion, where an RF shift is supposed to exist, and after that, find the probable site of RF shift and inversion in it. A full-scale search for RF shifts in all genes would require very powerful computational facilities that are not always available, although modern computer systems have made such search possible.² Second, even if we solve the first task, then the UniProtKB/Swiss-Prot databank will be necessary to contain the amino acid sequence having a statistically significant similarity to the hypothetical amino acid sequence. But it is possible that such a sequence will not be found due to the limitation of the UniProtKB/Swiss-Prot databank and because of too great an evolutional dissimilarity accumulated between amino acid sequences. Therefore, the concerned approach can reveal only some RF shifts accumulated to date in existing genes.

In order to reveal RF shifts and inversions in genes in a more reliable way, some new approach to seeking RF shifts should be developed instead of searching for similarities between hypothetic and real amino acid sequences. As shown in this work, a search for uniform triplet periodicity (TP) within the nucleotide sequence of gene's coding regions may be used as such an approach. Triplet organization of protein coding DNA sequences is a general feature of all presently known live systems.^4–12 The reason for this lies not only in the structure of genetic codes, which is virtually the same either for prokaryotes or for eukaryotes, but also in the saturation of proteins by certain amino acids.^13–16 If an RF shift occurs in genes in the presence of TP, then it will be revealed because a shift between TP and RF will also occur (Fig. 1). Since TP in a DNA sequence is unlikely to be changed by a small number of base substitutions,¹⁷ then such shift will exist for a long period of time. The presence of such a shift between the TP of a nucleotide sequence and RF may serve as an indication of an RF shift in the concerned gene.

Figure 1.

Influence of one nucleotide deletion on TP of nucleotide sequence. Numbers above sequence S1 show positions of nucleotides in RF. Twenty-fifth base has been deleted from sequence S1. Consequently, sequence S1 can be presented as two sequences—S2 and S3, i.e. S1 = S2aS3. In S2 and S3 sequences, TP (matrices M2 and M3) will be the same, but in sequence S3, there will be cyclical shifts by one base relative to sequence S2 and to RF in sequence S1. This means that first column of matrix M2 corresponds to third column of matrix M3, second column of matrix M2 corresponds to first column of matrix M3, third column of matrix M2 corresponds to second column of matrix M3. After summing sequences S2 and S3 and formation of sequence S4, TPM (M4 matrix) comes out from addition of first column of matrix M2 to first column of matrix M3 and so on, that leads to merging of non-identical columns and considerably decreases statistical significance of TP in sequence S4. By accounting deletions, we get sequence S4 that has TPM (M4 matrix) in which matrices M2 and M3 are merged in consideration of cyclic permutation. Finding and accounting deletions considerably increases statistical significance of TP in sequence S4.

Currently, some methods have been developed that reveal TP by using regularity in symbol preferences over different triplet positions in the DNA sequence. They use Fourier transformation, hidden Markov chains and other statistical methods based on position-dependent preferences for nucleotides in coding sequences as a mathematical apparatus.^18–23 The methods are aimed at revealing DNA coding sequences and their separation from non-coding regions. A later, method of information decomposition to find TP ^17,24 allows the introduction of the term of a TP class (TPC) as a 3 × 4 matrix. In this matrix, columns represent period positions and rows represent nucleotides.

In the current work, two problems were set. First, we wanted to find all genes where RF shifts can be identified by using TP. For each gene from the KEGG-29 databank, analysed²⁵ we extracted a region with TP having maximal statistical significance calculated by information decomposition without allowing any deletions or insertions of nucleotides.^17,24 Then we built a corresponding matrix of TP which was linked to the existing RF of the given DNA region. This meant that the first column of the TP matrix (TPM) corresponded to the first base of ORF presented in the DNA region having TP. Then we searched for a statistically significant extension of the TP region in the same gene in the presence of insertions and deletions of nucleotides by using modified profile analysis (Fig. 1). More than 800 genes contained a statistically significant shift between TP and ORF, which points to the presence of mutations in genes originating from the RF shift.

Second, we wished to check whether hypothetical amino acid sequences translated by using the RF of TP have homology with sequences from UniProtKB/Swiss-Prot databank (http://www.uniprot.org/). We made such a check for the genes that had mismatches between the gene's RF and TP. We confirmed the existence of such shifts for a part of the genes, since we found similarities between hypothetical amino acid sequences and amino acid sequences from the UniProtKB/Swiss-Prot databank.

2. Materials and methods

2.1. Searching for TP in genes by method of information decomposition

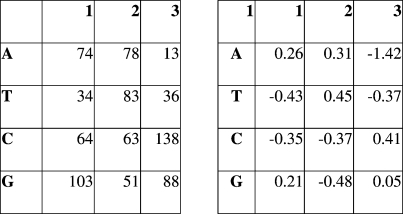
For each nucleotide sequence S = {s(i), i = 1, 2, … , L}, we carried out a search for a region having maximally expressed TP by the method of information decomposition.^17,24 Let s(i) be letters of the alphabet A = {a,t,c,g}, A(1) = a, A(2) = t, A(3) = c and A(4) = g. Then we also make an artificial periodic sequence U = {u(i), i = 1, 2, … , L} of the same size as nucleotide sequence S. In artificial sequence, u(i) = 1 for i = 1 + 3n, u(i) = 2 for i = 2 + 3n, u(i) = 3 for i = 3 + 3n, where n = 0, 1, 2, … . Then we choose coordinates L₁ and L₂ starting from the beginning of nucleotide sequence and fill the matrix M^4,3 for selected subsequence. Element of matrix m(k,j) shows how many times symbol A(k) in nucleotide subsequence from L₁ to L₂ matches the number j in artificial periodical sequence U. Each column j of the matrix M(k,j) shows number of bases a, t, c and g that occur in positions i = j + 3n of a sequence S, where n = 0, 1, 2, … . We calculate mutual information as²⁶

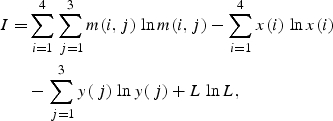1

where x(i) and y(j) are the frequencies of nucleotide occurrences in sequence S and of numbers 1, 2 and 3 occurrences in artificial sequence, correspondingly.

We used gene sequences from KEGG-29 databank as source sequences S. All analysed sequences represent coding region (CDS) of genes without introns. That is why, when L₁−1 and L₂ are set to a multiple of 3 while defining sequences S and U, then first, second and third columns of matrix M for any values of L₁ and L₂ will always contain nucleotides corresponding to first, second and third bases of the gene's codon, respectively. In other words, matrix M is linked to RF, which exists in the analysed gene.

Doubled mutual information 2I has χ² distribution with six degrees of freedom. This allows us to estimate statistical significance of the periodicity found. We can reduce I to standard normal distribution:²⁷

2

Conformity of 2I to χ² distribution with six degrees of freedom and of value Z to standard normal distribution are reached in the case of sufficiently large size of statistical data sample, i.e. sufficiently large length of a sequence S. In order to determine the minimal length of a sequence S that makes possible the usage of function χ² as approximation for 2I value distribution, we tested conformity of 2I to χ² distribution for various lengths of sequences S. We produced a set of nucleotide sequences for each length in the range from 30 to 1000 nucleotides by using a random number generator. Each of these sets contained 10 000 sequences. Thereafter, mutual information was calculated for each sequence from each set. For each set the histogram showing distribution of 2I value was also built. We compared this histogram with the theoretical distribution by χ² criteria. It was found that for sequences of length over 60 bp, 2I distribution conformed to χ²(6) with a probability more than 99%. All sequences with TP, which were found in the current work, were longer than 60 bp. This allows using χ² distribution for statistical estimations of hitting 2I into interval from some threshold value 2I₀ to infinity.

For sequence S, we calculated the values of 2I for all possible values of L₁ and L₂ (L₁ < L₂ ≤ L) and chose the pair (L₁,L₂) for which the value of mutual information was maximal. Let us refer to the nucleotide sequence found in such a way as T.

If the value of Z was >5.0 for sequence T, then we considered that the region with TP has been found. The value of Z >5.0 ensures the probability of incidental TP revealing in DNA sequence to be <10⁻⁶. Thereafter, we saved the found maximal sequence for the given gene, its coordinates in the given gene and periodicity matrix M, which shows the type of TP found. We chose a threshold level Z > 5.0 for finding TP in order to keep the number of incidentally found TPs near 1% of all detected regions with TP found in genes from the 29th release of the KEGG databank. To choose a threshold value for Z, we generated a set of random DNA sequences with the same size and sequence length distribution as for genes from the 29th release of KEGG databank. For Z > 5.0, the number of found random sequences was 7200, which is ∼1.5% of found regions with TP (see below). For Z > 6.0, we found 172 such sequences, and for Z > 7.0, we found no such sequences. We intentionally chose the level of Z > 5.0 in order to find the most complete extension of TP regions (see Section 2.2) that exist in various genes. The point is that gene's TP can be split up by insertions and deletions into several sections that may have rather low level of Z, but which is greater than 5.0. However, matrices M for each such section in gene will be identical or very similar, but cyclically shifted against each other (Fig. 1). In this case, consequent joining of these sections into a single one can considerably increase the statistical significance of a joined region that can be found by making an alignment against matrix M (see Section 2.3). Therefore, using a relatively low threshold value of Z will allow to not miss TP regions in genes separated into several sections by insertions and deletions.

2.2. Algorithm of TP region extension in genes from KEGG databank

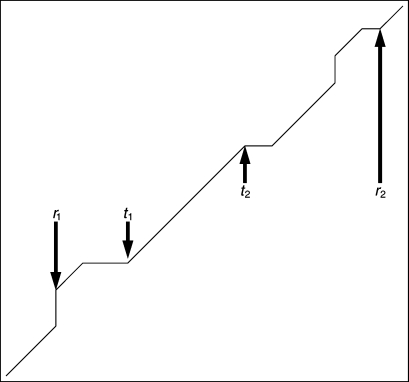
We applied this algorithm for those DNA sequences in which we have revealed TP without insertions and deletions by the method of information decomposition. Let S = {s(i), i = 1, 2, … , L} be the analysed nucleotide sequence from KEGG databank and t₁ and t₂ be coordinates of the left and right borders of a region T with continuous TP in sequence S. For region T, we determined TPM and used this matrix to extend the TP region by considering possible nucleotides’ insertions and deletions. Then we carried out local alignment of examined DNA sequence against weight matrix w introduced on the basis of TPM. Let the coordinates of start and end of found local alignment R be r₁ and r₂. Under extension of TP region T, we mean those R such that r₁ < t₁ or r₂ > t₂. Our goal is to choose from the KEGG databank only the genes that contain statistically significant extension of the TP region T. To find statistically significant extensions, we carried out global alignment of sequence S against weight matrix w and determined the values ΔF_T = F(t₂) − F(t₁) and ΔF_R = F(r₂) − F(r₁), where F is the value of similarity function on path of global alignment (Fig. 2). We selected only those genes that had ΔF₁ = ΔF_R − ΔF_T > 0. Thereafter, we have to determine whether the value of ΔF₁ is statistically significant. To do this, we used the Monte Carlo method. We generated a set of random nucleotide sequences Q on which the region T was left unchanged and the regions of sequence S within the range from 1 to t₁ and from t₂ to L were shuffled in a random way. The set Q contained 10⁶ sequences. For each sequence from the set Q, we built global alignment and determined the value ΔF_R − ΔF_T. Then we calculated such value ΔF₀ that the probability of ΔF_R − ΔF_T ≥ ΔF₀ for the set of sequences Q was ∼10⁻⁵. We chose the value ΔF₀ as a threshold and considered that if ΔF₁ > ΔF₀, then we found statistically significant extension of the region with continuous TP up to the bounds of region R via considering possible insertions and deletions of nucleotides. We analysed ∼3 × 10⁵ genes in such a way, and detected from 0 to 8 cases of region T extension due to accidental factors with a discovering probability of the given interval equal to 95%. As we revealed more than 750 genes with extension of the TP region T, then the fraction of genes with extension of region T due to merely accidental factors is ∼1.1% which is a relatively small value.

Figure 2.

Example of alignment against weight matrix obtained from TPM. Here, t₁ and t₂ are coordinates of region with continuous TP found by information decomposition (T region) and r₁ and r₂ are coordinates of extended region with TP found by dynamic programming (R region). Points r₁ and r₂ on optimal alignment path have the coordinates (i₀,j₀) and (i_m,j_m) in matrix, respectively (see Section 2.3).

Also, we estimated statistical significance Z_R of alignment R by the Monte Carlo method in a way we described earlier.^28,29 Thereto, we generated a set of sequences QR in which the region R was randomly shuffled. Then for each of these random sequences from QR set, we built global alignment and for each alignment we determined the values ΔG = G(r₂) − G(r₁). G is the similarity function for global alignment R, and it is calculated as we do for function F. For a set of ΔG values, we determined mean value 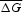and D(ΔG), where D(ΔG) is the dispersion of ΔG. Then we determined the value of Z_R as:

3

where ΔG₀ = G(r₂) − G(r₁) for original sequence R.

2.3. Implementation of local and global alignment of nucleotide sequence against TPM

During carrying out local and global alignment, we used matrices of TP M obtained for regions T of each gene from 29th release of KEGG databank. Using the matrix M, we built corrected position-specific matrix of the base weights as we suggested earlier:^28,29

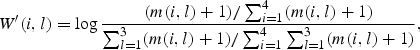4

where w′(i,l) is the uncorrected weight of the base a_i at position l of profile. Corrected weight matrix W was calculated as:

5

where 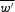is the mean value of the uncorrected weight matrix. We added unity to each position of matrix m(i,l) to eliminate the influence of zero elements in matrix M on the weights w′(i,l). The value of C was selected for each matrix M using the QV sequences (see Section 2.4). Thereto, we varied C from interval [−6,+6] with a step equal to 0.2. For each value of C from the interval, we determined alignments for N sequences from QV set, N = 100. For each alignment, we estimated Z_T (the statistical significance of T region alignment) by the Monte Carlo method (similar to Section 2.2). Thereto, we generated a set of sequences QT (for each sequences from QV set) in which the region T was randomly shuffled. Then we built a global alignment for each random sequence from QT set, and for each alignment, we determined the values ΔG(T) = G(t₂) − G(t₁). G(T) is the similarity function for global alignment of region T for DNA sequences from QT set. For a set of ΔG(T) values, we determined the mean value 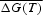and D(ΔG(T)), where D(ΔG(T)) is the dispersion of ΔG(T). Then we determined the value of Z_T as:

6

where ΔG(T)₀ = G(t₂) − G(t₁) for original sequence T from QV set. Then we calculated:

7

We take the sum in Equation (7) for N sequences from QV set. As a result, we have a set of X_C where each C from interval [−6,+6] has one X_C. We used for further calculation a value of C that has a maximum of X_C. We did the selection of C value for each matrix M.

Transition to weight matrix ensures assignment of higher weight to infrequent bases when they have high frequency in the given position of profile and, vice versa, assignment of lower weight for such bases having low frequency in the given position. To build optimal alignment of sought sequence against profile, we also introduced the weight for opening insertion or deletion ν_do and weight ν_dc for their continuation. Thereby the correlation in the formation of adjacent insertions or deletions is taken into account.

On the basis of introduced weights, we can find the optimal alignment, between analysed sequence and profile, i.e. we find such their subsequences for alignment, that maximise the similarity function. Let S = {s(j), j = 1, 2, … , L} be the analysed sequence. Let us create a profile matrix q(i,j) of size L as:

8

where i shows the row number, i = 1, 2, 3, 4, and j the column index of a matrix q, j = 1, 2, … , L.

To find local optimal alignment of sequence s(j) against profiles q(i,j), we applied the method of dynamic programming.³⁰ We iteratively calculated similarity function F according to the following equation:³¹

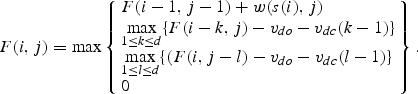9

Here, the index i stands for nucleotide in sequence s(i) and index j for the column number in profile matrix q. Initial values for similarity function F are specified as:

10

11

12

where d is the maximal number of insertions or deletions allowed. For calculations on triplet matrix, d equals 2. During building the local alignment, we determine the maximal value of the similarity function F coordinates (i_m,j_m) corresponding to this maximal value. Then we determine the path from points (i_m,j_m) to (i₀,j₀), where the value of the similarity function becomes zero for the first time. According to the path made, we built alignment between sequence S and profile matrix q. For building alignment, nucleotides of sequence S and numbers l = mod3(j) indicating columns of matrix w [Equation (5) were used].

We used Equation (9) for carrying out the global alignment but without using zero in the right part of the equation. All other parameters were the same as in the case of the local alignment. Initial values for similarity function F for global alignment are specified as:³¹

13

14

15

2.4. Choosing values for v_do and v_dc

We chose values ν_do to prohibit the optimal path in local and global alignments from moving round the nucleotide having minimal weight in matrix w(i,j) because of two sequential insertions. On this basis, we chose 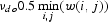At the same time, it was important to make the alignment able to find region T revealed by the method of information decomposition (Section 2.1) without any insertions and deletions. In order to choose the corresponding coefficient ν_do for each gene from KEGG databank, we generated a set of random sequences QV, where regions of sequence S in the range from 1 to t₁ and from t₂ to L were shuffled in a random manner. The region of sequence S in the range from t₁ to t₂ was constructed by TPM M. Then matrix M was transformed to M′ as (see also Section 2.1):

16

Then we generated in a random manner three nucleotide sequences S1(k), k = 1, 2, … , y(1), S2(k), k = 1, 2, … , y(2) and S3(k), k = 1, 2, … , y(3). Nucleotide probabilities in sequence S1 are equal to probabilities m′(i,1), nucleotide probabilities in sequence S2 are equal to probabilities m′(i,2) and nucleotide probabilities in sequence S3 are equal to probabilities m′(i,3). Index i varies from 1 to 4. Thereafter, nucleotides of sequence S1 took positions k = t₁, t₁ + 3, … , t₂ − 2; nucleotides of sequence S2 took positions k = t₁ + 1, t₁ + 4, … , t₂ − 1 and nucleotides of sequence S3 took positions k = t₁ + 2, t₁ + 5, … , t₂. This algorithm was used for the generation of 1000 random sequences contained in QV.

Selection procedure of the ν_do value for each gene from the KEGG databank from which region T was extracted is described below. First, we chose the value for 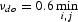and ν_dc = 0.25 ν_do. Then we made alignments for the set of random sequences QV and determined the number of sequences having insertions or deletions within the region from t₁ to t₂. If the fraction of sequences in set QV having at least one insertion or deletion within region from t₁ to t₂ exceeded 1%, then we increased the value of ν_do by 0.1 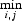and calculated ν_dc = 0.25 ν_do again. Alignments of sequences from set QV were also built again using these new parameters. If the fraction of sequences with insertions or deletions was under 1%, then the process was stopped and the obtained value ν_do was used for finding the extended region R by local alignment (Sections 2.2 and 2.3). If the fraction of sequences with insertions or deletions was over 1%, then we increased ν_do and ν_dc again as shown earlier and alignments of sequences from set QV were built again.

3. Results and discussion

3.1. Finding extensions of the regions with TP for genes accumulated in KEGG databank

We analysed 578 868 genes accumulated in 29th release of the KEGG databank (http://www.genome.ad.jp/kegg/). We found 472 288 regions having continuous TP in 457 333 genes. These data indicate that 79% of genes have regions with TP. These results conform to earlier works on TP detection by either using informational methods or other techniques.^4–13,32 From these 472 288 regions containing continuous TP, we selected only those the lengths of which were significantly less than that of a gene. This means that the distance from the left and right edges of the TP region to the start and end of the gene was more than 30 bp. This criterion was satisfied for 326 933 TP regions. Then we aligned nucleotide sequences of corresponding genes against TPM (see Sections 2.2 and 2.3), which were revealed in the gene by the method of information decomposition (Section 2.1).

We revealed totally 824 genes in which TP regions were extended by using alignment against TPM. General information describing all these sequences can be found in the Section Supplementary data. Details including periodicity alignment and found protein similarities can be found in online databank installed at http://victoria.biengi.ac.ru/pertails/.

3.2. Finding protein similarities for the products obtained using active and ancient gene RFs

Let us consider those genes in which the region of continuous TP was extended by taking into account nucleotide insertions and deletions (see Section 2.2). Further, we will discuss nucleotide sequences with coordinates from r₁ to t₁ and from t₂ to r₂ (Fig. 2). Let us call these sequences T1 and T2 (the region of continuous TP was earlier referred to as T). In sequences T1 and T2, we found TP with insertions and deletions that were very similar to continuous TP T. This is the reason why we found statistically significant alignment from r₁ to r₂ in sequence S against the weight matrix constructed on the basis of TPM M. We suppose that TP found in sequences T1 and T2 is a trace of some ancient RF that existed in these nucleotide sequences earlier. First column of the matrix M corresponds to the first codon base in sequence S, whereas due to insertions and deletions of nucleotides, in subsequences T1 and T2 matrix M corresponds to alternative ancient RF which may not match the actual RF there. Let us refer to RF specified by matrix M as ‘ancient RF’. We suppose that it is possible to reveal similarity between amino acid sequences obtained by ancient RF from nucleotide sequences T1 and T2 and amino acid sequences accumulated in modern databanks like UniProtKB/Swiss-Prot. Such an assumption is based on the idea that if a gene responsible for the same genetic function existed in several genomes, then insertion or deletion of nucleotides in this gene within one genome does not ultimately lead to analogous changes in another genome. It is important that these sequences should be now known and should not have accumulated many evolutional alterations. This will allow us to see their similarity. We conducted such an investigation within the scope of the present work. Sequences of regions T1 and T2 were translated to amino acid sequences in accordance with the RF existing in the gene and in accordance with ancient RF's revealed by TPM M. For all amino acid sequences obtained in such a way, we searched for their similarities with sequences accumulated in UniProtKB/Swiss-Prot databank³³ by using BLAST program.³⁴ Totally we found 824 T regions in genes that were extended via joining regions T1 and/or T2. Sixty-four of TP regions T had protein similarities with regions T1 and/or T2 only by ancient the RF constructed on the basis of matrix M (see above). At the same time, for 176 T regions, protein similarities in regions T1 and/or T2 were found only for the active RF of a gene, and in three cases, for both RFs. Five hundred and eighty-one T regions have no protein similarities in regions T1 and/or T2 for amino acid sequences constructed either by the existing gene's RF or by the ancient RF constructed on the basis of matrix M.

Let us consider an example of continuous TP extension in a putative dehydratase gene (locus ‘SMa0056’ in KEGG databank). This gene has a length of 1134 bp and contains the region of continuous TP from 16th to 840th nucleotide. TPM for region T and weight matrix w(i,j) is of the form that is shown in Fig. 3. We extended the found TP region T by adding region T2 that leads to the appearance of TP in this gene from the 840th to 1134th nucleotides. Statistical significance Z_R of the found alignment R was equal to 17.7. The value ΔF₀ equalled 10.25, whereas the value ΔF₁ equalled 13.85. This provides the probability of incidental addition of region T2 to region T at a level <10⁻⁵.

Figure 3.

TPM M and position-specific weight matrix w(i,j) built for T region from 16th to 840th nucleotides of the locus ‘SMa0056’ (KEGG databank). For the calculation of weight matrix, we used C = − 0.3,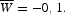

During alignment of the sequence relative to found continuous TP, we revealed the insertion of the nucleotide at position 841 (nucleotide t) of the locus (Fig. 4). This means that after the 840th nucleotide (towards first nucleotide), a shift occurs between TP and RF. Thus, the first codon base in sequence T2 corresponds to the third column of matrix M, whereas in sequence T, the first codon base T2 corresponds to the first column of matrix M (Fig. 4). We suppose that in the past this gene existed without insertion of the nucleotide t in position 841 (towards first nucleotide of a gene) and mutations could not blur the TP existing in this region (Fig. 5). To check this hypothesis, we recoded T2 region to amino acid sequence by the actual gene's RF and by the ancient RF (Fig. 4). Then we searched for similarities with these two amino acid sequences in UniProtKB/Swiss-Prot databank. Consequently, we found five cases of similarities for hypothetic sequence only, i.e. for the amino acid sequence obtained by RF specified by TPM M (Fig. 4). At the same time, amino acid sequence constructed by RF specified in KEGG had no similarities at all (Fig. 4). Similarities for hypothetical amino acid sequence were found to dehydratases. Match ratio was >30% (e-value in range from 10⁻¹² to 10⁻⁷), i.e. found similarity is evolutionally distant and statistically significant. All found similarities can be accessed at http://victoria.biengi.ac.ru/pertails/perinfo.php?perid=270869.

Figure 4.

Sequence of ‘SMa0056’ gene from 818th to 877th nucleotide (1) aligned against weight matrix w(i,j). Insertion of 841st nucleotide (nucleotide t) is shown by asterisk. Further under gene, the consensus sequence for TP (2) is shown, which is constructed by matrix М and also by RF existing in gene (3) and RF specified by TPM М named as ancient RF (4). Below translated fragments of the nucleotide sequences are shown. Translation is made according to RF existing in gene (5) and to ancient RF (6). Regions having RF shift are marked in bold.

Figure 5.

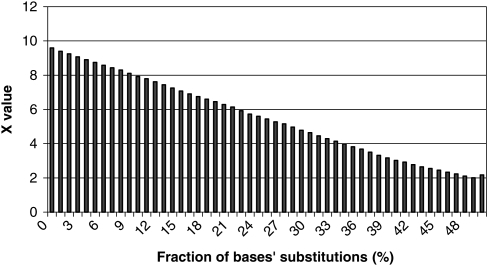
Resistance of sequence T with continuous TP of gene ‘mlr4742’ to nucleotides' substitutions. We selected a base in sequence T in a random manner and then substituted it, also in a random manner, by one of the nucleotides a, t, c or g (with probability of each being equal to 0.25). Thereafter, we estimated statistical significance of obtained sequence according to Equation (2). As follows from figure, statistical significance of TP decreases relatively slow during mutations' accumulation. For example, 10% difference from the original sequence still allows revealing TP at statistically significant level.

It is also of great interest to point out that the amino acid sequence corresponding to the gene ‘SMa0056’ from the KEGG databank has similar amino acid sequences in the UniProtKB/Swiss-Prot databank. This amino acid sequence is designated as ‘Q931B9_RHIME’ in the UniProtKB/Swiss-Prot databank. Similarity is observed from the start of the protein to the 280th amino acid. This is true for a set of different mandelate racemase/muconate lactonizing enzymes and glucarate dehydratases (e.g. ‘Q024C0_SOLUE’, ‘A9FRR8_SORC5’). This set also contains five amino acid sequences (‘GUDH_STRCO’, ‘GUDX_ECOLI’, ‘GUDH_ECO57’, ‘GUDH_ECOLI’ and ‘GUDH_PSEPU’), where we found similarity to amino acid sequence produced from 842nd to the end of the gene by the ancient RF. Therefore, it can be assumed that these five sequences existed before the insertion of the 841st or independently of it. These sequences have similarity to the sequence ‘Q931B9_RHIME’ from 1st to 280th ±10 amino acids for the gene's (KEGG) RF and from 281st to 378th amino acids for ancient RF.

3.3. Discussion

In this work, we managed to show that investigation of shifts between TP and RF can reveal possible mutations via RF shift in a gene. We found 824 such genes in which there existed some single-type TP regions separated by deletions or insertions of nucleotides. They account for ∼0.2% of the total number of analysed genes. We suppose that in the past RF and TP in these regions were explicitly linked to each other and shifts between them appeared only after deletions or insertions of nucleotides. Such relatively small fractions of genes in which an RF shift can potentially occur can be explained by the following reasons. First, we searched only for relatively short deletions or insertions having lengths up to 2 nucleotides (d = 2). We confined ourselves to small deletions and insertions because while the length of deletion and insertion increases, the value of function F decreases [see Equation (6)]. Costs of deletion and insertion can be too high; in this case, the value ΔF₁ will be statistically insignificant. Thus, the current method will miss the major part of genes containing long deletion and insertion of nucleotides. Second, the technique used works well for the small number of regions where deletions or insertions of nucleotides occurred. If density of deletions and insertions is more than one deletion and insertion for several tens of nucleotides (∼50), then the accurate placement of deletions and insertions using this algorithm will be difficult. This will lead to the statistically insignificant value of ΔF₁ for such a gene.

In general, in this work, we aimed to reveal the lower bound for the number of genes in which a shift between RF and TP is possible. Actually, there can be much more such genes. These values are also confirmed by data in work² where the number of genes with RF shift obtained by BLAST program is >1%.

The technique used to find shifts between TP and RF and to reveal mutations via RF shift in genes seems to be more preferable than the usage of BLAST program for finding possible similarities. The current method of revealing mutations via an RF shift in the gene does not require finding similarities in the databank of amino acid sequences. Owing to the limited size of the databank, there will always exist a chance that similarities will not be found, although actually mutation via RF shift will exist. We suppose that complete revealing of mutations via an RF shift in genes is possible by the integration of these two techniques. That is, we also have to investigate genes having 0 ≤ ΔF₁ ≤ ΔF₀ and to consider that we found mutations via an RF shift if regions T1 and T2 have statistically significant similarities. In this case, the TP just indicates the possibility of an RF shift and the fact of such mutations can be considered to be proved only after revealing similarities with regions T1 and T2. On the other hand, enhancement of the algorithm used in the current work can facilitate the use of more perfect algorithms for finding TP, such as Markov models. This probably will allow us to reveal RF shifts induced by a set of nucleotides insertions and deletions in various gene regions.

From the functional point of view, mutations via RF shift seem to be events that are able to cardinally change the gene function. This fact can explain the relatively small number of such events found during investigations in the past and in the current works.^2,3,35 They can make a great contribution to the formation of new genes by copying known genes and generating mutations via an RF shift^2,3,35 in them. However, the genetic code has to be adapted for this event in some way,³⁶ and the new amino acid sequence has to possess some biological function. Otherwise, overrun of mutational events for the creation of the new gene's function can be too great, and impossible within reasonable evolutional time.

In the light of these assumptions, TP can be some kind of test to check the gene's integrity. If the gene was duplicated in the genome, then its new copy may fail the check, which opens up possibilities for evolutional changes of the gene's copy via the RF shift and for the creation of a new gene with a new biological function as a result.

Supplementary data

Supplementary data are available online at www.dnaresearch.oxfordjournals.org.

Funding

This work was supported by Russian Academy of Sciences.