Simulations of nucleation and elongation of amyloid fibrils

Abstract

We present a coarse-grained model for the growth kinetics of amyloid fibrils from solutions of peptides and address the fundamental mechanism of nucleation and elongation by using a lattice Monte Carlo procedure. We reproduce the three main characteristics of nucleation of amyloid fibrils: (1) existence of lag time, (2) occurrence of a critical concentration, and (3) seeding. We find the nucleation of amyloid fibrils to require a quasi-two-dimensional configuration, where a second layer of β sheet must be formed adjunct to a first layer, which in turn leads to a highly cooperative nucleation barrier. The elongation stage is found to involve the Ostwald ripening (evaporation-condensation) mechanism, whereby bigger fibrils grow at the expense of smaller ones. This new mechanism reconciles the debate as to whether protofibrils are precursors or monomer reservoirs. We have systematically investigated the roles of time, peptide concentration, temperature, and seed size. In general, we find that there are two kinds of lag time arising from two different mechanisms. For higher temperatures or low enough concentrations close to the disassembly boundary, the fibrillization follows the nucleation mechanism. However, for low temperatures, where the nucleation time is sufficiently short, there still exists an apparent lag time due to slow Ostwald ripening mechanism. Consequently, the lag time is nonmonotonic with temperature, with the shortest lag time occurring at intermediate temperatures, which in turn depend on the peptide concentration. While the nucleation dominated regime can be controlled by seeding, the Ostwald ripening regime is insensitive to seeding. Simulation results from our coarse-grained model on the fibril size, lag time, elongation rate, and solubility are consistent with available experimental observations on many specific amyloid systems.

INTRODUCTION

Deposition of amyloid fibrils is associated with a variety of neurodegenerative diseases, including Alzheimer’s, Huntington’s, and prion diseases.^{1, 2} Identifying the key steps in the formation of amyloid fibrils may reveal important information for inhibition or reversal of fibril formation. Furthermore, recent reports suggested that the toxicity of Aβ and other amyloidogenic proteins is not due to mature fibrils but rather prefibrillar oligomers.^{3, 4} Therefore, an understanding of the detailed molecular mechanism of amyloid fibrillogenesis is desirable.

Despite little sequence homology, all amyloidogenic proteins exhibit fibrillar morphology and share a common cross-β sheet structure,⁵ with β strands perpendicular to and interstrand hydrogen bonds parallel to the fibril axis. The morphologies of amyloid fibrils are typically unbranched fibrils of 10 nm in width and of 0.1–10 μm in length.⁶ The x-ray fiber diffraction showed that the cross-β structure is characterized by two lengths at 0.5 and 1.0 nm, corresponding, respectively, to the interstrand (intrasheet) hydrogen bonding (H bonding) and intersheet distances.⁵ Although the generic cross-β structure of amyloid fibrils at larger length scales is robust, details of peptide configurations at atomistic resolution are rich. Many structural models have been proposed which can be roughly classified into two major categories: (1) ribbonlike model such as polar zippers,⁷ continuous zippers,⁸ pair-of-sheets steric zipper,⁹ and double-layered β sheets;¹⁰ (2) helical model such as water-filled nanotubes,¹¹ double helix,¹² and helical array of β sheets.¹³ Unfortunately, even for the ribbonlike model alone, whether intrasheet neighboring strands are parallel or antiparallel⁵ is still uncertain. The relative importance of van der Waals,⁹ hydrophobic,¹⁰ π-π aromatic stacking,¹⁴ and interdigitation⁸ forces behind the intersheet interactions continues to be investigated. This situation is further exemplified by the fact that two entirely different models have been proposed for exactly the same diffraction data.^{8, 11} From the above analysis, it is evident that there is no universal atomistic-level structure model for all amyloid fibrils.⁶ The only consensus we can reach now is that they all form the fibrillar morphology with the cross-β structure, where the intersheet interactions are always weaker than the intrasheet H-bonding interactions. This consensus will serve as the basis for our above-molecular-level coarse-grained model in the present paper.

It has been widely accepted that formation of amyloid fibrils is a nucleation phenomenon. Three criteria as evidence of nucleation were proposed:^{15, 16} (1) There exists a critical protein concentration below which no aggregation occurs. (2) Above this critical concentration by a small amount, there exists a lag time before fibrillization occurs. (3) The lag time can be reduced or even eliminated by adding a preformed fibril, which is known as the “seeding” phenomenon. These three criteria were indeed confirmed by numerous experiments.^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26} However, the exact nature of the nucleus is yet to be determined. The nucleus might possibly be a micelle,²⁷ a colloidal aggregate,²⁸ one turn of a helix,¹⁵ or even a folded monomer.²⁹ Another mystery lies in how these amyloid nuclei grow after the nucleation stage. Although transient appearance of protofibril oligomers has been identified at the early stage of fibrillogenesis, their function has not been determined: protofibrils might act as an off-pathway reservoir in rapid equilibrium with monomers, the latter of which slowly assemble into fibrils, or protofibrils are on-pathway precursors of the mature fibrils.^{30, 31} Even if protofibrils are indeed on-pathway precursors, it is still unclear about whether the protofibril-to-fibril transition is dominated by sequential addition of monomers or by coalescence of protofibrils (end-to-end association or lateral attachment).³¹ There has recently been an attempt³² to fit the aggregation kinetics data in terms of empirical reaction rate equations. The present paper aims to shed new light on both nucleation and growth processes. In view of the very large length scales of the fibrillar morphologies we are seeking to address and because it is now impossible to execute a full simulation with all atomic details for such large structures, we introduce a coarse-grained model capable of addressing the most salient global features of amyloid growth.

In the context of our goal of generating a coarse-grained model, it is to be noted that high-resolution microscopy has revealed that amyloid protofibrils have a beadlike structure (∼5 nm in height), where young protofibrils appear as dimers, trimers, and oligomers of these beads.^{28, 33, 34, 35}In situ observations also demonstrated that protofibril elongation occurs by aggregation of these beads from solution.^{34, 35} Here we take this bead as the primary assembly unit in our model. The molecular details inside the bead and conformational changes accompanying aggregation are omitted and only anisotropic interactions between beads are assumed. The origin of the anisotropy of the interactions among the building blocks lies in the stronger intrasheet H bonding relative to the weaker intersheet interactions.

The coarse-grained lattice model presented here is complementary to several coarse-grained models reported already in the literature. The latter models have focused primarily on the nucleation stage and the potential important roles played by intermediate conformational states. In the leading lattice model,³⁶ effects of external conditions such as the protein concentration, temperature, pH, salt concentration, and dimer seeds were studied on the polymerization mechanisms. Based on simulations of a relatively small number of polypeptides and their sequences, a rich phase diagram of possible ordered morphologies was identified. Based on a lattice model³⁷ for two chains each with 64 residues, the role of sequences on the nature of polymerization was investigated. In an off-lattice model^{38, 39, 40} where the protein structure is of intermediate resolution, molecular dynamics simulations were carried out for tens of 16-mer chains which showed that an amorphous aggregate is a precursor to the fibrillization. In a more recent off-lattice Langevin dynamics simulation,⁴¹ self-assembly and chirality of the fibrillar aggregates from β sheet forming short peptides were studied based on a coarse-grained united atom model. The influence⁴² of intermediate states and reversibility of the polymerization process were addressed and it was shown⁴³ that the propensity of intermediates depends on the relative stability of β prone conformational state. In contrast to these simulation models, our attempt here is to probe the later stages of nucleation of fibrils and their competitive growth. Since our model uses coarse-grained building blocks with their internal conformational degrees of freedom reflected only by effective surface free energies, we are able to explore very large length and time scales so as to explore competitive growth of multiple fibrils. Although this idea of aggregation of prefolded proteins has already been introduced in the literature,⁴⁴ our focus here is to understand the phenomena of nucleation and competitive growth in the context of amyloid fibrillization.

The rest of the paper is organized as follows. The details of our model are presented first. Morphologies, fibril sizes, lag time, and elongation rates are studied next in comparison with experiments as functions of time, temperature, peptide concentration, and seed size for both single-fibril and multifibril cases. Finally, mechanisms of nucleation and competitive growth of fibrils are discussed.

MODEL AND SIMULATION ALGORITHM

In view of the goal to address the large length scale and long time scale features associated with the growth of the fibrils, we represent each of the monomers as a cuboid. Each cuboid may represent an extended peptide, a folded peptide, a pair of peptides, or even a beadlike nanoaggregate of peptides discussed in Sec. 1 depending on the particular amyloid system. The intrinsic degrees of freedom responsible for forming the building blocks are integrated out in the present model, and we keep the building blocks to be identical elementary units for a given system. Any conformational change in the building block that might accompany the attachment of a monomer at the growth front is ignored. However, all conformational changes, both enthalpic and entropic, prior to the attachment are effectively accounted for. The chemical attributes of the forces emanating from each of the building blocks are parametrized in terms of three surface energy parameters, corresponding to the three pairs of opposite sides of the cuboid. Indeed we choose these three parameters in such a way that the interaction energy between cuboids in the intrasheet H-bonding direction is sufficiently attractive, that in the intersheet direction is only weakly attractive, and that in the direction parallel to the peptide is repulsive in order to capture the anisotropy of the aggregation process. Our model shares some features with other models used in simulations of grain growth⁴⁵ and crystal growth.⁴⁶

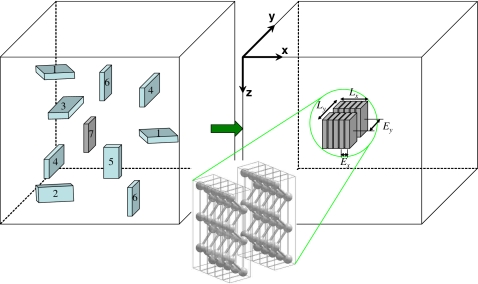
Two slightly different algorithms are employed in the present paper: one is for multiple fibrils; the other is for a single fibril. The general setup is as follows. The elementary cuboidal building unit in our model is shown in Fig. 1. The interactions between units are different along the x, y, and z directions, as designated by E_x, E_y, and E_z. As already pointed out, each cuboid represents a particular peptide structure corresponding to the smallest building unit depending on the nature of the amyloid. As an example, an extended peptide is illustrated in Fig. 1 to be represented by each cuboid. For specificity, by taking polyglutamine D_2Q15K₂ as an example, the typical size of a cuboid in our model is 0.48 nm thick (H-bonding intrasheet distance), 0.83 nm wide (intersheet distance), and 7 nm long (length of the extended peptide).⁸ Simulations of peptide aggregation are all performed in a cuboidal simulation box with lengths B_x, B_y, and B_z under periodic boundary conditions. The lattice spacing is assumed to be comparable to the spatial dimension of the building block, which in turn is system dependent. Other choices for lattice spacing can be made which would result in an overall scale factor for the Monte Carlo time. Typical values for B_x,y,z range from 50 to 500. The simulation box is further discretized into B_x×B_y×B_z cubic lattice cells. Each cubic lattice cell is assigned a state from seven possible states, as illustrated in Fig. 1: state S₀, solvent lattice cell (invisible area in the box); states S₁ and S₂, the x-oriented peptide with its wider lateral sides facing the z and y directions, respectively; states S₃ and S₄, the y-oriented peptide facing z and x, respectively; states S₅ and S₆, the z-oriented peptide facing y and x, respectively. For the single-fibril case, an additional state S₇ (with the same orientation as S₆) is introduced to serve as a seed nucleus.

Figure 1.

Coarse-grained model of amyloid fibril formation. Peptide solutions for amyloid fibril formation are mapped onto a 3D array of lattice sites. The elementary building block is modeled as a cuboid and the internal energetics of the building unit is manifested through the interfacial energies between the cuboids. As an example, each cuboid mimics an extended peptide chain, as sketched. The number of cuboids in the simulation box, which are initially randomly distributed, depends on the initial peptide concentration. Each cuboid undergoes a random walk and randomly changes its orientation (among states S₁–S₆) and aggregates with other peptides when having the same orientation. The solvent (state S₀) is represented by empty lattice sites. For the single-fibril case, an additional state S₇ (same orientation as S₆) is introduced to serve as the seed nucleus. The fibril thus formed has length L_x, width L_y, intrasheet H-bonding interaction E_x, and intersheet interaction E_y.

The simulation procedure for multiple fibrils is given first as follows. Initially, a specific number (B_x×B_y×B_z×C, where C is the initial peptide concentration) of peptides with random orientations (S_1–6) are put at random locations in the simulation box. The rest of lattice cells are assigned to the solvent state (S₀). Next, one peptide is selected randomly. It is then allowed to undergo a random walk to any of its six nearest neighbors and at the same time change its orientation randomly. If the immediate walking direction is blocked by another peptide present in the next cell, the walk is stopped and another peptide is selected randomly for the next iteration. The energies of the peptide before (E₀) and after (E₁) such a random walk are computed. Only the free monomers are allowed to undergo the random walk. The walk is accepted with the probability as in the classical Metropolis algorithm:⁴⁷

$$P=\{\begin{array}{cc}1& \text{when}\Delta E\le 0\\ \text{exp}\left(\frac{-\Delta E}{kT}\right)& \text{when}\Delta E>0,\end{array}\phantom{\}}$$ (1)

where the energy change ΔE=E₁−E₀, k is the Boltzmann constant, and T is the absolute temperature. The above procedure is repeated for several billion times. The number of iterations is given in units of Monte Carlo step (MCS). At 1 MCS, the number of attempted random walks is equal to the total number of peptides in the simulation box (the time needed on an average for each of the peptide chains to make a random walk). As is conventional for Monte Carlo simulations, all temperatures are given as kT with units of energy rather than just temperature. Based on their physical meanings, the random walks can be classified into four different categories: diffusion (E₀=0, E₁=0), adsorption (E₀=0, E₁<0), desorption (E₀<0, E₁=0), and rearrangement within the fibril (E₀<0, E₁<0).

The energy setting in the current paper is as follows. The Hamiltonian for the simulation is calculated as the sum of interaction energies between each peptide i and its nearest-neighbor peptide j (if any exist):

$$H=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^{6}E\left(q_i,q_j\right),$$ (2)

where the change in the total Hamiltonian, ΔH, is equivalent to the local ΔE in Eq. 1 for each random walk, N is the total number of peptides, q is the state∕orientation of the peptide (i.e., S₁–S₆), and E(q_i,q_j) is the interaction energy between neighboring peptides in arbitrary units of energy and is a function of the states of the two neighboring peptides. It should be noted that the interaction energy is defined differently along the x, y, and z directions. As an example, let us consider the case of Fig. 1 (right panel), where aggregated peptides are z oriented and x faced. To illustrate the multifibril case first, we assume that they are temporarily in state S₆. For each individual peptide in the state q_i=S₆, the total interaction energy with its six nearest neighbors, ${\sum }_{j=1}^{6}E\left(q_i,q_j\right)$, is counted according to the following five rules: if there is any peptide with the same orientation (q_j=q_i) in its two nearest neighbors along the x direction, they will form stronger intrasheet H bonds (E_x<0); if there is any equal-oriented peptide in its y neighbors, they will form weaker intersheet attractive interaction (E_y<0); if there is any equal-oriented peptide in its z neighbors, they are not allowed to grow along z to form a “β sheet” structure so that a repulsive interaction is set to avoid its formation (E_z>0); if there is any peptide with different orientations (q_j≠q_i) in its six nearest neighbors along the x, y, or z directions, such a configuration is unstable and impractical (the nonparallel energy E_n is set to be repulsive, E_n>0); the interaction with solvent is always set to zero so that the solvent acts like an empty site. Since only the dimensionless ratio ΔE∕kT controls the acceptance probability of random walks, we reduce E_y to −1 and determine an appropriate range of kT values by trial and error. Different magnitudes of E_x=−1 to −15 have been tried and a good fibrillar morphology is obtainable only when E_x≤−10. The magnitudes of E_n and E_z do not affect the “cross-β” fibril formation as long as certain repulsion exists to avoid forming nonparallel configurations or the β sheet structure. A typical large value E_n=E_z=+10 is chosen to ensure this. It is to be noted that the above setting of E_x,y,z,n is only concerned with z-oriented and x-faced peptides (q_i=S₆). For peptides with other orientations (q_i=S_1–5), the interaction energies E_x,y,z,n have to be redefined in a corresponding way.

The preceding setting is devoted to the multifibril algorithm. For the single-fibril algorithm, several modifications are implemented. First, a seed nucleus (S₇) with dimension n_x×n_y is put at the origin of the simulation box in the very beginning. In order to form a single fibril, the interactions between freely diffusing peptides (S_1–6) are disabled. Only the interactions with the seed peptides (S₇) are considered. The free peptide (S_1–6) has to diffuse to the vicinity of the seed peptide (S₇) to get adsorbed, thus converting its own state to S₇. The once-adsorbed peptide (S₇) has the probability P=exp(−ΔE∕kT) to desorb (becoming free peptides S_1–6) or rearrange within the fibril at a later time. However, the initial seed is fixed throughout the simulation. For details, a step-by-step procedure is given for a similar system in our previous paper.⁴⁶

It is to be stressed that our model has several limitations and approximations. First, the collective movement of two or more assembly units is ignored, i.e., only one assembly unit is moved at a time. This essentially ignores the movement of protofibrils (including dimers, trimers, and one-layer oligomers) and fibrils (two or more layers of β sheets), and therefore omits the end-to-end and lateral attachments of protofibrils∕fibrils. However, as pointed out in Ref. 31, the end-to-end association is unlikely due to the difficulty associated with the diffusion and proper alignment of protofibril ends. More importantly, the collective diffusion dynamics of protofibrils∕fibrils is much slower than the diffusion dynamics of single monomers. As will be demonstrated below, even without considering the collective diffusion, time evolution of fibril size distributions in our simulations matches very well with experimental results, suggesting that lateral attachment and end-to-end association might contribute little to the growth kinetics.

Another advantage in allowing only single-unit movement is the convenience to incorporate the entropic contribution arising from any precursor states of the monomer. Unlike the extended peptide shown in Fig. 1, the monomer may assume a random-coil configuration in solution, undergo structural change and transform into an extended or folded peptide before aggregation (pay entropic penalty), and then attach on the preformed protofibril∕fibril end (gain energy). So the free energy terms E_x,y in our simulations can be assumed to be the net result of enthalpic gain minus entropic loss during the amyloid aggregation. Alternatively, if conformational change in monomers occurs before aggregation and after disaggregation but not concurrently with the aggregation∕disaggregation processes, our model is still applicable. However, the precise partitioning of E into enthalpic and entropic parts is not addressed here and E is taken only as a free energy parameter.

The other limitation is that our simulations are performed in discrete lattice space. Because the smooth ribbonlike fibrils are often observed in experiments, suggesting that the peptides within and between the β sheets are aligned perfectly to maximize the enthalpic gain, we expect that relaxing the lattice constraint into continuum space will not alter our main results at least for ribbonlike amyloid fibrils.

In spite of the simplicity of our coarse-grained model, the cuboid-stacking scenario is supported by direct observation of striations perpendicular to the Aβ_11–25 fibril axis, with 0.48 nm spacing between striations.⁴⁸ Our model can naturally apply to the case of flat-ribbonlike amyloid fibrils,^{19, 22, 49, 50, 51} with possible extension to twisted ribbons^{6, 24, 35, 50, 51, 52} or coiled helical structure with constant interacting regions [Fig. 6(a) of Ref. 53]. The stacking configuration of neighboring strands can be parallel or antiparallel for extended peptides⁵ or can be face to face¹⁰ or side by side⁸ for hairpin peptides. In short, our coarse-grained generic model omits molecular details inside the aggregation unit and merely focuses on kinetics of amyloid fibrillogenesis by utilizing the classical Metropolis algorithm with a simple assumption, ∣E_x∣>∣E_y∣.

RESULTS AND DISCUSSION

Single fibril

Energy ratio versus length ratio

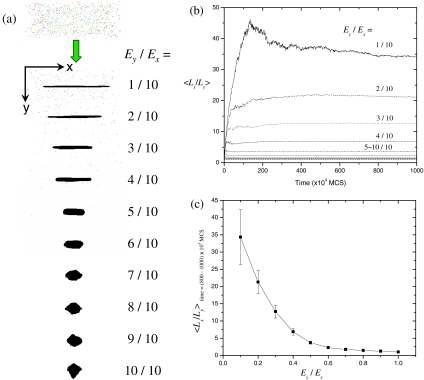
Aggregation of diffusing peptides is driven by the reduction in the total energy via forming more and more peptide-peptide interfaces (E_x,y<0), and the kinetics of this process is determined by two ratios: E_x∕kT and E_y∕E_x. First we fix kT to be a constant value kT=1.0 to see how the energy ratio E_y∕E_x influences the fibril morphology. To achieve various energy ratios, we fix E_x=−10 and vary E_y from −1 to −10. The simulation box is initially populated with random peptides and a single seed nucleus at the center. As time elapses, diffusing peptides adsorb and grow on the seed, exhibiting distinct eventual morphologies for different energy ratios [Fig. 2a]. As the energy setting along the x and y directions becomes more anisotropic, the shape of the aggregate becomes more anisotropic too, leading to a fibrillar shape at large energy ratios. The length ratio L_x∕L_y (defined in Fig. 1) is observed to increase with time and then reach equilibrium in the late stage [Fig. 2b]. The equilibrium values of L_x∕L_y (as obtained from the last 200 data sets covering over 2×10⁶ MCS) are plotted against E_y∕E_x in Fig. 2c. It turns out that the length ratio varies significantly from 1∕1 to 35∕1 when the energy ratio varies from 1∕1 to 1∕10. So Fig. 2c provides a rough way to estimate the relative magnitude of peptide interactions from its morphology. For example, a ribbonlike fibril of 10 nm in width and 350 nm in length can be estimated to have an energy ratio of 1:10 between the inter- and intrasheet interactions. In the following context, for simplicity, the energy ratio is fixed to 1:10. This particular choice for the energy ratio is not expected to affect our general results on the kinetics of fibrillization.

Figure 2.

Dependence of the shape anisotropy (L_x∕L_y) on the energy ratio (E_y∕E_x). The size of the initial seed nucleus is 1 [almost invisible in (a)]; the simulation box is with B_x=250 and B_y=B_z=100; temperature kT=1.0; the initial peptide concentration C=0.0005; the total simulation time t_max=10⁷ MCS. (a) Initial and final morphologies for various energy ratios. (b) Time evolution of L_x∕L_y which is averaged over 50 independent simulation runs with different random-number seeds. Error bars are omitted for clarity. (c) L_x∕L_y vs E_y∕E_x. L_x∕L_y is averaged over t=(800–1000)×10⁴ MCS in (b).

Nucleation and growth

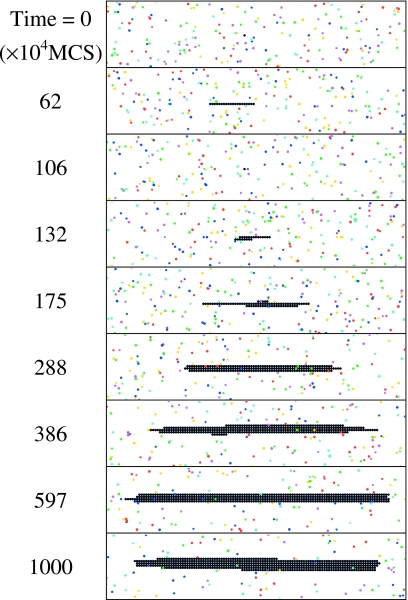
A typical process of nucleation and growth of a single fibril is shown in Fig. 3, where the black beads (used here to represent the cuboids constituting the fibril for the sake of clarity) represent the seed and subsequently grown fibril and colored beads stand for free peptides with different orientations. Starting from a single seed at t=0, the freely diffusing peptides tend to land on the seed and grow linearly along the x direction. The initial growth is thermodynamically unfavorable,^{15, 18} as manifested by the fluctuations in the size of the protofibril. In the current context, all single-layer structures are termed interchangeably as protofilaments and protofibrils, and two or more layer structures are termed as fibrils. Also, oligomers are referred to as short protofilaments∕protofibrils. Due to the nature of the coarse graining in our model, we do not encounter the protofibrils⁴² seen in experiments which are presumably less ordered than fibrils. However, as will be shown in the following sections, the temporal behavior of single-layer structures shares that of the experimentally observed protofibrils. In view of this, we are using the terms protofilament and protofibril interchangeably in the current paper and it is hoped that this does not cause any confusion. The one-dimensional (1D) protofibril grows [t=62 (×10⁴ MCS)] and shrinks (t=106) back and forth until its size is large enough to overcome an apparent nucleation barrier. In particular, a second layer of beads (t=132) seems to help stabilize the structure. Once the stable nucleus has been formed, subsequent growth (t>132) becomes thermodynamically favorable. The lateral side surface of the final fibril is quite smooth, generating a ribbonlike morphology. Presumably it is because the peptides which are attached on the lateral sides have less binding energy (E_y=−1) than the peptides which are attached on the fibril ends (E_x=−10). It is noteworthy that nucleation appears only within narrow ranges of temperature and concentration. At lower kT or higher C, the fibril growth is spontaneous so that the nucleation behavior is nonexistent.

Figure 3.

Nucleation and growth of a single fibril. The seed size is 1; kT=1.17; C=0.001. All subsequent simulations on single fibrils are under the conditions B_x=500, B_y,z=50, and t_max=10⁷ MCS. In the rest of the paper, the default energy settings are E_x=−10, E_y=−1, and E_z,n=+10.

Fibril size and lag time

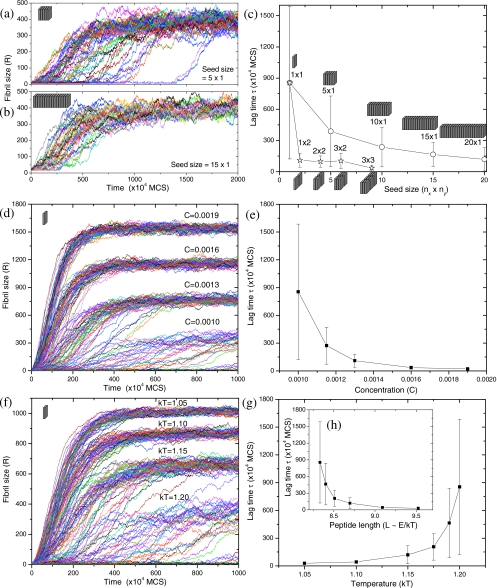
To quantify the above observations, we monitor the time evolution of the fibril size R by counting the number of beads in the fibril, as shown in Fig. 4. In agreement with numerous experiments,^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26} the fibril growth exhibits the characteristic sigmoidal curve which can be divided into three stages: (1) nucleation stage, where the fibril grows and redissolves back and forth until its size exceeds a critical nucleus size, i.e., R>R_c; (2) growth stage, where R is found to increase linearly with time; and (3) equilibrium stage, where R reaches a plateau as the free peptides in the simulation box are exhausted. The duration of the nucleation stage, called “lag time” τ, can be obtained from the R-t curves. For convenience of discounting wild fluctuations in the fibril size during the nucleation stage, we calculated the lag time as the time at which R reaches 50. This choice of the cutoff value is not expected to affect our general results. In rare cases, where the size fluctuation is larger than 50, we recorded the correct lag time manually. It is evident from Fig. 4a that nucleation is a stochastic process.²⁶ Under identical conditions, simulation runs with different random-number seeds produce quite different lag times. The distribution of lag times is found to be lognormal (data not shown). A comparison between Fig. 4a for the 5×1 seed and Fig. 4b for the 15×1 seed shows that the lag time is significantly influenced by the seed size. The average value of lag times is plotted in Fig. 4c as a function of the seed size. Apparently, the lag time is reduced significantly by increasing the seed size, which is related to the seeding phenomenon.^{15, 18} Similarly, Harper et al.⁵⁴ noted that the fibril formation can be seeded by the addition of (bigger) fibrils but not by (smaller) protofibrils. Consistent with our previous argument regarding the second layer of cuboids, the double-layer seed is more effective in seeding than the single-layer seed (τ for the 1×2 seed is even shorter than τ for the 10×1 seed), the reason for which will be discussed in a later section. Another characteristic of nucleation is the existence of a “critical concentration,” below which fibrillization cannot occur.¹⁵ This effect is illustrated in Figs. 4d, 4e. The lag time increases sharply with decreasing the peptide concentration,^{20, 21, 22, 23, 24, 25, 26} tending to diverge at a finite concentration (critical concentration).

Figure 4.

Time evolution of the fibril size (R) and the corresponding lag time (τ) as functions of the initial seed size (n_x×n_y), the initial peptide concentration (C), the temperature (kT), and the peptide length (L). (a) Smaller 5×1 seed. (b) Larger 15×1 seed. Different curves in (a) and (b) correspond to 50 independent simulation runs. (c) The average lag time vs the seed size. (a)–(c) are under the conditions C=0.001 and kT=1.2. (d) Fibril growth at various concentrations. (e) Lag time vs concentration. (d) and (e) are under the conditions kT=1.2 and the seed size of 1. (f) Fibril growth at various temperatures. (g) Lag time vs temperature. (h) Lag time vs the peptide length which is assumed to be proportional to the peptide interaction energies E_x and E_y. (f)–(h) are under the conditions C=0.001 and the seed size of 1.

Although the effect of temperature on fibril formation has rarely been investigated experimentally, we have considered the role of temperature in our simulations. As the temperature is raised, the desorption probability [P=exp(−ΔE∕kT)] increases so that intuitively the fibril growth should become more difficult, thus leading to a longer lag time, as shown in Figs. 4f, 4g. There are only a few experimental results available,^{20, 21, 25, 55} which show that the lag time decreases with increasing temperature, in contradiction to the intuitively obvious results from Figs. 4f, 4g. It is to be noted that the available experimental results^{20, 21, 25, 55} on the temperature dependence are in the context of multiple fibrils and within a very narrow temperature range (∼15–45 °C). As will be demonstrated in a later section, our simulations for multiple fibrils at lower temperatures show the same trend as in the experiments.

Since the temperature appears only through the dimensionless parameter, E_x,y∕kT, lowering of temperature is equivalent to an increase in E_x,y. If the peptide length (L) is larger, then the effective value of E_x,y is also higher. We use this aspect in addressing an important phenomenological result relating the age of onset of Huntington’s disease (i.e., the lag time for fibril growth) to the peptide length of polyglutamine.^{56, 57, 58, 59} The result presented in Fig. 4h provides an explanation. For extended peptides, it is a natural assumption that the interaction between neighboring peptides is proportional to the peptide length, i.e., E∝L. In our model, it is recalled that only the ratio E∕kT matters, where E represents the absolute value of E_x or E_y. To mimic the effect of doubling the peptide length L, one way is to fix kT=1.0 and then double the energy setting (E_x,E_y) from (−10,−1) to (−20,−2). An alternative way is to keep the energy setting unchanged but reduce kT from 1.0 to 0.5. Either way will lead to the same simulation results. In this sense, L∝E∝1∕kT. Therefore, the data in Fig. 4g can be replotted in Fig. 4h, with 10∕kT being the abscissa. In other words, although in reality we fix E=10 and vary kT from 1.05 to 1.20 to study effects of temperature [Fig. 4g], we can equivalently regard kT as a constant (kT=1.00) and assume that E varies from 10∕1.05 to 10∕1.20 to study effects of the peptide length [Fig. 4h], as illustrated by the following equation:

$$\frac{E}{kT}=\frac{10}{1.05}\sim \frac{10}{1.20}=\frac{9.52}{1.00}\sim \frac{8.33}{1.00}.$$ (3)

The length dependence of lag time in Fig. 4h agrees with the experimental results very well:^{56, 57, 58, 59} the lag time (or equivalently the age of onset of the disease) decreases exponentially with increasing the peptide length; the lag time is stochastic in nature so that there is a large variability in the lag time even for the same peptide length; such variability (the size of error bars) is larger for the shorter peptide length; there exists a critical peptide length below which the disease would not occur. Although the above result is appealing, caution must be exercised. The molecular basis of the onset of diseases is not completely understood, although relationships between the in vitro measured lag times, the peptide length, and the onset of Huntington’s disease exist. Since the building block in our model does not explicitly account for the internal degrees of freedom such as changes in conformational entropy, the direct proportionality between the peptide length and E_x,y is only an approximation.

Multiple fibrils

So far, the results we presented only involve the single-fibril case, which tries to mimic heterogeneous nucleation on a specific number of preset heterogeneous seeds (e.g., heterogeneous nucleation of Aβ_26–40 on Aβ_26–43,¹⁷ where homogeneous nucleation of Aβ_26–40 is unable to occur under the same conditions). When homogeneous nucleation occurs and an unspecific number of multiple fibrils are formed, the interactions or competitions between multiple fibrils are expected to play an important role, thus possibly leading to distinctly different kinetics from the single-fibril case. We present some key simulation results for the homogeneous nucleation and growth of multiple fibrils. It turns out that the results from our simple simulation model are qualitatively analogous to the experimental results in Ref. 33.

Time evolution

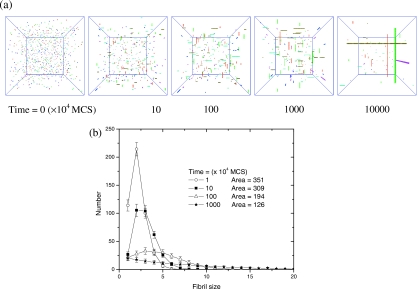
Time evolution of morphologies and fibril size distributions are presented in Fig. 5. As seen in Fig. 5a, the simulation box is initially populated with randomly oriented and unaggregated peptides. The diffusing peptides quickly aggregate into many short protofibrils. Then the short protofibrils elongate gradually into longer protofibrils and eventually ribbonlike fibrils (two or three layers of β sheets). The histogram of the number count for different protofibril sizes is plotted as a frequency distribution in Fig. 5b. The population of longer protofibrils increases while the population of shorter protofibrils decreases with time. The total number of protofibrils decreases with time too, which is evident from Fig. 5b where the total number of fibrils, “area,” decreases from 351 to 126 as time elapses. The most probable fibril size increases with time. These simulation results are remarkably similar to those observed experimentally (Fig. 2 of Ref. 33) despite the simplicity of the present model.

Figure 5.

Time evolution of morphologies and fibril size distributions for multifibril assembly. C=0.001; kT=0.8; the simulation box is with length B_x,y,z=100. (a) Morphologies. (b) Number count for each fibril size. The integrated area represents the total number of protofibrils (monomers with size of 1 are excluded from integration). Distributions in (b) are averaged over 50 runs.

In addition to reproducing the experimentally observed features, our simulations provide insight into the mechanism controlling the growth process. In contrast to the view that the elongation of amyloid fibrils is irreversible,^{60, 61} we note that adsorbed peptides can reversibly desorb into free space during the elongation process, i.e., a protofibril may undergo 120 adsorption and 100 desorption events in order to grow 20 cuboids longer. In conformity with the prevalent view in the literature, it appears that all fibrils are in fast, dynamic exchange with the peptide solution (free diffusing peptides dissolved in free space). The fibril growth is not uniform either: some protofibrils grow faster; some grow slower; some disappear soon; some initially grow and shrink later. It frequently occurs that relatively bigger fibrils can gain more peptides than smaller ones during both their exchanges with the peptide solution presumably due to the relatively lower desorption probability for the bigger fibrils. So it appears as if the peptides on smaller fibrils are gradually transferred onto bigger fibrils by a diffusion process. In fact, this phenomenon is widely known as the “Ostwald ripening,”⁶² where bigger objects grow at the expense of smaller ones via an evaporation-condensation mechanism. During the Ostwald ripening, the whole system is driven from a nonequilibrium state to an equilibrium state by minimizing the total interfacial energy. Ideally the equilibrium state is reached when there is only one gigantic fibril left in the simulation box, which is indeed seen in our simulations for very long times (not shown). We expect this phenomenon to be robust even if the fibrils themselves are allowed to undergo diffusion in addition to the monomers.

The above observations are further supported by already reported experimental results. The atomic force microscopy movies from experiments³⁵ revealed a highly dynamic and reversible process for assembly of protofibrils, where beadlike monomers can diffuse, align transiently forming chains and then move apart again, or elongate directly into longer protofibrils. The elongation can be unidirectional or bidirectional. Real-time monitoring of fibril growth by fluorescence microscopy⁶³ also revealed that the elongation rates for different protofibrils are not uniform. They vary significantly from one protofibril to another. The measurements by size exclusion chromatography^{31, 51} revealed that the amount of oligomers first increases and then decreases, while the amount of monomers∕dimers decreases monotonically with time, consistent with our morphologies and distributions in Fig. 5. For example, in Fig. 5b, the number of protofibrils with size of 5 first rises and then diminishes, while the number of monomers∕dimers with size of 1 or 2 decreases monotonically with time. Interestingly, the debate as to the role of protofibrils^{30, 31} can be reconciled in the context of the Ostwald ripening (bigger fibrils eat smaller ones). Protofibrils can be either on-pathway precursors or off-pathway monomer reservoirs depending on their relative sizes.

Effects of concentration and temperature

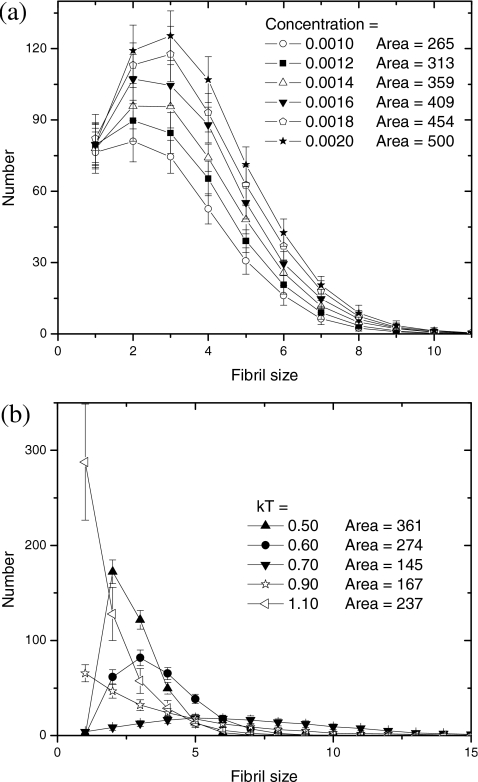
We have performed extensive simulations of the competitive assembly of multiple fibrils by varying concentration and temperature. Typically, the fibril length (monitored at a fixed time) increases with increasing the initial peptide concentration. Analogous to the discussion of Fig. 5b, the histogram of the number of fibrils with a given size is given in Fig. 6a for six different concentrations, all in the early stage of growth. As expected intuitively, more peptides should produce more fibrils, as is evident from the distributions in Fig. 6a (area increases from 265 to 500). It appears that the shape of the distribution is insensitive to concentration.

Figure 6.

(a) Concentration dependence of fibril size distribution. kT=0.9;t=10⁵ MCS. (b) Temperature dependence of fibril size distribution.C=0.001; t=10⁷ MCS.

In terms of temperature effects, our simulations show that an increase in temperature results in longer and fewer fibrils. This result is in agreement with Refs. ^{33, 64}. However, we find from our simulations that the opposite behavior can occur at higher temperatures due to the disassembly of the fibrils. Thus, a nonmonotonic dependence of the fibril length on temperature is predicted. This is more evident from the fibril size distributions in Fig. 6b, where the distribution shifts to bigger fibril sizes and then shifts back to smaller sizes with increasing temperature. Similarly, the total number of fibrils (area) drops and rises (361→145→237) with increasing temperature. It appears that the fibril growth is most favorable in the intermediate temperature range, below or above which the fibril growth is hindered. Inspection of our simulation movies shows that, at lower temperatures all peptides are frozen on numerous short protofibrils due to their low desorption probability. At higher temperatures, on the contrary, all peptides diffuse vigorously in the solution and less likely to adsorb on fibrils due to their high desorption probability. So the two extremes at low and high temperatures can be regarded as “frozen” and “disassembled” states, respectively.

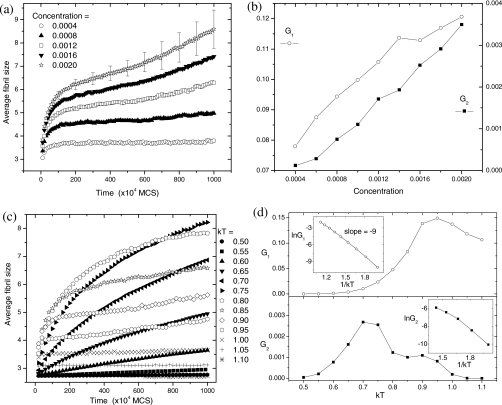
In order to compare with experiments (Ref. ³³) more quantitatively, time evolution of the average fibril size is plotted as functions of concentration and temperature in Fig. 7. As noted by Harper et al.,³³ there is approximately 10- to 20-fold reduction in elongation rates by comparing initial rate over 4 h to subsequent growth over the next 2 days. Our data in Fig. 7a also show two different growth rates. Both the initial growth rate (G₁) and the late-stage growth rate (G₂) are proportional to the initial peptide concentration [Fig. 7b].³³ In terms of temperature effects [Fig. 7c], the average fibril size is invariant at low kT=0.50, increases quickly with time at intermediate kT=0.75, and diminishes again at high kT=1.05. In the low-T region (kT=0.5–0.9 for G₁ and kT=0.5–0.7 for G₂), both G₁ and G₂ increase exponentially with temperature [Fig. 7d]. The logarithm of both the initial and late growth rates in the low-T region, ln G₁ and ln G₂, are indeed roughly proportional to 1∕kT.³³ However, as the temperature is increased further, both G₁ and G₂ decrease. As seen in Fig. 7d, the growth rates exhibit a bell shape as a function of temperature. Although this nonmonotonic G−T dependence was not found in Ref. 33 presumably due to the narrow temperature range (3–37 °C), insulin amyloid fibrillization over a broad temperature range (37–140 °C) exhibits a nonmonotonic G−T dependence.⁶⁵

Figure 7.

(a) Time evolution of the average size of fibrils (based on all fibrils with size≥2) at various initial concentrations. kT=0.9. For clarity, only a few error bars of standard deviation are shown. (b) Concentration dependence of the fibril growth rates: G₁ at early stage for t=(0–10)×10⁴ MCS; G₂ at late stage for t=(500–1000)×10⁴ MCS. (c) Time evolution of the average size of fibrils (size≥2) at various temperatures. C=0.001. (d) Temperature dependence of the fibril growth rates: G₁ at early stage for t<100×10⁴ MCS; G₂ at late stage for t=(600–1000)×10⁴ MCS. The insets use only the low-T data.

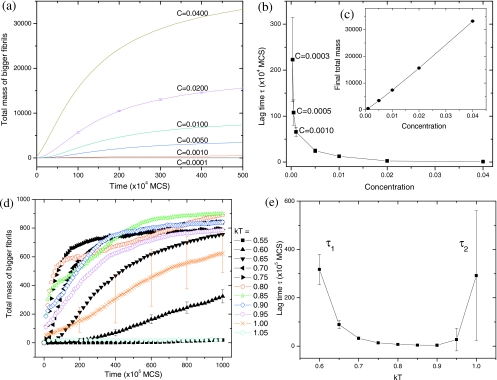
In experiments, it is not always possible to track the fibril length individually. More commonly, the overall degree of fibrillization is monitored⁶⁶ by thioflavin T (ThT) fluorescence, turbidity, etc. It is believed that the ThT intensity is proportional to the amount of dye bound to all amyloid fibrils, which in turn is positively correlated with their total length. So the total intensity should be proportional to the total mass (or total length) of all fibrils. In addition, it was found that during the lag time the oligomeric protofibrils (observed by transmission electron microscopy) are too short to be detected by ThT fluorescence.⁵¹ Based on these two considerations, we monitor the time evolution of the total mass of all bigger fibrils whose size≥10 in Fig. 8. Different cutoff sizes (5, 15, 20) have been tried, but the general trends remain unaltered. As depicted in Fig. 8a, the fibril growth exhibits a sigmoidal shape for this new characterization method. To observe distinct lag times (from τ→∞ to τ=0), a broad concentration range (C=0.0001–0.04) is required. The lag time increases sharply with decreasing concentration [Fig. 8b]. The large variation of τ is observable only within a narrow concentration range (C=0.0001–0.001), above which τ varies little over a broad concentration range (C=0.001–0.04). This observation reconciles the debate as to whether τ is sensitive¹⁵ or insensitive²⁵ to the change in concentration. The critical concentration, below which there is no evidence of fibril growth even until t=10⁸ MCS, is estimated as C^*≈0.0001 for the present condition (kT=0.8). Similar to the results in Fig. 7b, both the initial growth rate (not shown) and the final equilibrium value [Fig. 8c] are linear functions of the initial peptide concentration, consistent with ThT measurements.^{66, 67}

Figure 8.

(a) Time evolution of the total fibril mass (based on all fibrils with size≥10) as a function of the initial peptide concentration. kT=0.8. (b) The corresponding lag time vs concentration. (c) The total mass at t=500×10⁴ MCS vs concentration. (d) Time evolution of the total mass as a function of temperature. C=0.001. (e) The corresponding lag time vs temperature. Each curve is an average of 50 simulation runs. For clarity, only a few error bars are shown for (a) and (d).

The temperature effect on the total fibril mass is more complex. We find two types of lag time: τ₁ at low temperatures and τ₂ at high temperatures. As seen from the slow fibril elongation rate at low temperatures in Fig. 8d, τ₁ corresponds to a slow Ostwald ripening process, where the desorption probability is so low that all protofibrils are frozen and hindered from monomer exchanges between fibrils. On the other hand, τ₂ corresponds to a nucleation process, where the desorption probability is so high that all protofibrils are disassembled and undergo large size fluctuations, waiting for the time when the size happens to be larger than the critical nucleus size. We notice that the time-mass curves of 50 simulation runs are similar for all temperatures except kT=1.00, where the lag time differs significantly from one run to another. So the averaged curve for kT=1.00 in Fig. 8d is actually unreliable because the original sigmoidal shape for each individual run [like Fig. 4a] is smoothed out by averaging along the y axis. The corresponding lag time is plotted in Fig. 8e as a function of temperature. We find that the τ-T curve exhibits an inverse-bell shape [opposite to the bell-shaped G−T curve in Fig. 7d]: τ₁ decreases with T, whereas τ₂ increases with T. The larger error bar for τ₂ is attributed to the stochastic nature of nucleation.²⁶ The smaller error bar for τ₁ is attributed to the cumulative nature of Ostwald ripening. It appears that large variation of lag times due to nucleation (τ₂) occurs only at high temperatures [kT=0.95–1.05 in Fig. 8e] or low concentration [C=0.0001–0.001 in Fig. 8b], i.e., in the vicinity of the disassembly boundary. At low temperatures [kT=0.55–0.65 in Fig. 8e] and intermediate concentration (C=0.001), the lag time caused by slow Ostwald ripening (τ₁) dominates. Hitherto, lag time was often seen to decrease with increasing temperature^{20, 21, 25, 55} presumably because most experiments were performed at physiological temperatures (low-T) and intermediate concentration. If temperature is very high or concentration is very low, we predict that the lag time increases with temperature.

Another point requiring explanation is why the peptide-length dependence of age of disease onset does not exhibit an inverse-bell shape for the multifibril case [recall that the length effect is inverse to the kT effect for the single-fibril case in Figs. 4g, 4h]. In other words, if peptides are very long [corresponding to very low kT in Fig. 8e] and have strong binding energy, they may be frozen into numerous short protofibrils, exhibiting the lag time behavior due to slow Ostwald ripening (τ₁). However, τ₁ is cumulative in nature and these accumulated short protofibrils (too short to be detected by ThT fluorescence) may be still toxic.^{3, 4} In this sense, age of disease onset is not always equivalent to the lag time in our model. Assuming that only τ₂ (due to nucleation) corresponds to a truly disease-free state, the age of disease onset should decrease with the peptide length monotonically.^{56, 57, 58, 59}

Seeding

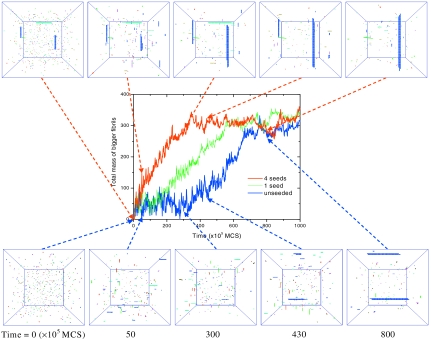
The seeding phenomenon, i.e., lag time being reduced or eliminated by adding preformed fibrils, has been regarded as the key evidence of the nucleation mechanism for amyloid.^{15, 16} As shown above, we observe two different mechanisms (slow Ostwald ripening and nucleation) responsible for the lag time. Although it is natural for the nucleation time to be reduced by seeding, it is not known whether the lag time associated with the slow Ostwald ripening mechanism (at lower temperatures and intermediate concentration) is also reduced by seeding. In view of this, we have systematically studied the growth kinetics at different temperatures and with added seeds of different sizes. After trying various temperatures in the low-T region (slow Ostwald ripening region), seed sizes, and seed concentration, to our best effort, we could not reproduce the seeding behavior. It appears that the growth of preadded seeds parallels the formation and growth of endogenous seeds (formed by homogeneous nucleation). The monomers not only land on the preadded seeds but also form their own seeds and continue to grow. So the curve of the total fibril mass versus time appears to shift only vertically upward (but keeping the same sigmoidal shape) after the addition of seeds. Instead of observing the typical sigmoidal-to-logarithmic (S-to-L) shape transition after adding seeds, we only observe the sigmoidal-to-sigmoidal shape.

On the other hand, in the high-T region (nucleation region), we are able to observe the S-to-L transition by adding seeds, as shown in Fig. 9. Note that the disassembly temperature kT_m=0.97 for C=0.0005 (no evidence of growth up to t=10⁸ MCS) so that kT=0.90 is in the high-T region. In this case, only preadded seeds can grow immediately, whereas the endogenously formed seeds cannot grow immediately because they are below the critical nucleus size. For the unseeded case in Fig. 9 (lower part), the monomers quickly aggregate into many short protofibril seeds within t=5 (×10⁵ MCS). However, the morphology remains the same from t=5 to 300, i.e., during the lag time. The fibril formation has to wait until the size fluctuations happen to be large enough to overcome the nucleation barrier. At t=330, a double-layer structure is formed and turns into a stable seed. After this step, the time-mass curve enters the growth region. At t=430, the second stable seed starts to form, while the first stable seed has grown into a longer fibril. Eventually, two big fibrils are formed at t=800 when the total mass reaches equilibrium. In contrast, for the seeded case in Fig. 9 (upper part), the only difference at t=0 is that four 20×2 seeds are added in the solution at random locations with random orientations. Because these seeds are already larger than the critical nucleus size at the present conditions, they start to grow immediately. At t=300, they have grown into big fibrils and the total mass almost reaches equilibrium, in contrast to the unseeded case where it is still within the lag time. After t=350, although the total mass remains the same, the underlying Ostwald ripening still goes on (the morphology changing from four fibrils to two bigger ones during the equilibrium stage of the total mass). Similar results were observed in experiments,⁵¹ where changes in fibril morphology could still be seen in the solutions from day 4 to day 7 even though the fluorescence signal had essentially reached a plateau on day 4. The fact that the total mass has entered the final equilibrium stage does not necessarily guarantee that the fibril growth has stopped. The above S-to-L shape transition in the time-mass curve is typical of results observed in numerous experiments.^{17, 18, 19, 22, 23} In addition, the effect of the seed concentration is also reproduced in Fig. 9, where increasing the number of seeds results in a shorter lag time.^{26, 29, 68, 69} Our simulations show vivid details of molecular mechanism behind the seeding phenomenon in addition to capturing the essential aspects of experimental observations.

Figure 9.

Effects of seeding and seed concentration on fibril growth. Time evolution of the total fibril mass (based on all fibrils with size≥10) is monitored for the unseeded, one-seed, and four-seed cases. The corresponding morphologies for the unseeded and four-seed cases are given at t=0, 50, 300, 430, and 800 (×10⁵ MCS). The size of each seed is 20×2. C=0.0005; kT=0.9. The mass contribution due to added seeds was subtracted (Refs. ¹⁸, ²²). Due to the stochastic nature, only one typical run is given for the time-mass curve. The average lag time of 50 simulation runs, however, indeed decreases with increasing the seed concentration: τ=171, 74, and 3 (×10⁵ MCS) for the unseeded, one-seed, and four-seed cases, respectively.

Disassembly upon dilution

Finally, we have monitored the kinetics of disassembly of the already formed fibrils (under the conditions C=0.002, kT=0.9, simulation box length of 100) by putting them in a bigger simulation box with length of 300 (27-fold dilution). The time evolution of the average fibril size was followed by monitoring all fibrils with size≥2. The average fibril size is observed to decrease very rapidly, reaching a plateau around t=750×10⁴ MCS. During this course, the average fibril size decreases from the initial value of 8.7 to 3.9, 3.1, and 2.6, respectively, at t=2.5×10⁶, 5×10⁶, and 2×10⁷ MCS. The rate of decrease in fibril length is much faster over the first 2.5×10⁶ MCS (size=8.7→3.9) as compared to the subsequent 2.5×10⁶ MCS (size=3.9→3.1). The fibril density also decreases as time elapses. These observations are consistent with Fig. 4 of Ref. 33.

Mechanism of nucleation and growth

Size-dependent binding energy

One of the puzzles regarding nucleation of amyloid fibrils is how an apparently 1D object suffers from a nucleation barrier.¹⁵ According to the classical nucleation theory, the free energy change of forming a three-dimensional (3D) spherical nucleus of radius R is

$$\Delta F=-\frac{4}{3}\pi R^3\Delta \mu +4\pi R^2\sigma ,$$ (4)

where Δμ is the bulk free energy gain, and σ is the surface energy penalty. By setting ∂ΔF∕∂R=0=−4πR²Δμ+8πRσ, the critical nucleus size is obtained as

$$R_c=\frac{2\sigma }{\Delta \mu }.$$ (5)

For R<R_c, the surface energy term dominates and ΔF increases with increasing R (the growth is thermodynamically unfavorable); for R>R_c, the bulk energy term dominates and ΔF decreases with increasing R (the growth is thermodynamically favorable); at R=R_c, ΔF reaches maximum. So a free energy barrier is formed. In order to grow, the 3D object has to wait until its size fluctuation happens to be larger than R_c so that the free energy barrier is overcome. For two-dimensional (2D) growth of a square of side R, there is a nucleation barrier with R_c given by the same Eq. 5. A similar argument for 1D situation shows that there is no critical size for nucleation to occur. Even for a uniform cylinder of length R and fixed radius r growing in one dimension, the free energy of formation is

$$\Delta F=-\left(\pi r^2\right)R\Delta \mu +\left(2\pi r\right)R\sigma ,$$ (6)

where σ is the lateral surface energy. There is also an additional constant surface energy term representing the two end faces. Since both terms in Eq. 6 are linearly proportional to R, there is no critical length for nucleation. If 2σ>rΔμ, the cylinder does not grow. If 2σ<rΔμ, the growth of cylinder will occur spontaneously.

However, the experimental data on amyloid fibrils exhibit the earmarks of nucleation, viz., sigmoidal growth curves and the seeding phenomenon. In order to couch the experimental data within “1D nucleation” framework, one turn of a helix has been proposed as a stable nucleus (with R_c corresponding to the number of peptides required to form exactly one turn of a helix).¹⁵ In contrast, our observation is that the amyloid fibril is not really a 1D object but rather a semi-2D object. As seen in our simulations, monomers can aggregate into dimers, trimers, one-layer protofibrils, or two- or three-layer fibrils. These fibrils all undergo frequent adsorption∕desorption events, i.e., they are in dynamic exchange with monomers in the solution. Here the building blocks in the middle parts of the fibril are almost impossible to desorb due to high binding energies with their neighbors. So we focus only on the adsorption∕desorption of peptides on the fibril ends. Although the adsorption probabilities are the same for all fibrils, the desorption probabilities are different for different fibril sizes because the binding energy of end peptides is a function of the number of layers in the fibril. For example, at kT=1.0, the desorption probability of an end peptide for a one-layer fibril is P_d1=exp(−10∕1.0)=4.5×10⁻⁵, three times larger than that for a two-layer fibril, P_d2=exp(−11∕1.0)=1.7×10⁻⁵ (where 11 is the sum of the intrasheet energy of 10 and the intersheet energy of 1). Under certain conditions (high T or low C), if the adsorption probability happens to be within this range 1.7×10⁻⁵<P_a<4.5×10⁻⁵, the two-layer fibril can grow (P_a>P_d2) while the one-layer fibril cannot grow (P_a<P_d1). Thus the fibril growth has to wait until the size fluctuations happen to form a second layer to overcome the nucleation barrier. The critical nucleus size R_c now corresponds to the size of a two-layer fibril. This idea is consistent with the mass-per-length (MPL) measurements in experiments,^{35, 51} where MPL=21, 31, and 42 kDa∕nm, corresponding to two-, three-, four-layer fibrils, indicating that the one-layer fibril is more unstable. Note that the binding energy will saturate and approach a limiting value, 12, with increasing the number of layers. The stability difference between one- and two-layer fibrils is larger than the stability difference between two- and multilayer (even 100-layer) fibrils in our model. This idea is also supported by Fig. 4c, where the reduction in τ becomes less significant with increasing the number of layers from 1 to 2 and then to 3.

Once the nucleation barrier is overcome, Ostwald ripening starts to dominate. As seen from the unseeded case in Fig. 9, one nucleus forms earlier, while another nucleus forms later. When they grow bigger, they have different sizes. For example, one is a two-layer fibril, and the other is a three-layer fibril. The desorption probability of end peptides in a three-layer fibril is P_d3=exp(−11.33∕1.0)=1.2×10⁻⁵, where 11.33 is the average binding energy for its end peptides [(11+12+11)∕3]. As the monomer reservoir becomes exhausted (C becomes lower), the adsorption probability should also become smaller. Under certain conditions, if the adsorption probability happens to drop into the range 1.2×10⁻⁵<P_a<1.7×10⁻⁵, the three-layer fibril can grow (P_a>P_d3) while the two-layer fibril starts to shrink (P_a<P_d2). Thus it looks as if the three-layer fibril grows at the expense of the two-layer fibril. So the size-dependent binding energy is also the reason for Ostwald ripening. As time goes by, the free monomers become exhausted, and the nucleation barrier is essentially lifted (we will show later that R_c increases with lowering C) so that smaller fibrils tend to disaggregate while bigger fibrils tend to grow. In this sense, Ostwald ripening can be regarded as “competitive nucleation.”

Pure 1D single fibril

To test our idea of a semi-2D growth of fibrils, we modified the energy setting to E_x=−10 and E_y,z,n=+10, which ensured that the fibril growth is purely 1D. The fibril can either grow immediately or never grow. The lag time can be either zero or infinity. There is no finite lag time. The sigmoidal curve is not observable (scrutinized at kT=1.10,1.11,…,1.15). This agrees with the classical nucleation theory in that a pure 1D growth has no nucleation barrier.

Because the pure 1D growth is simpler, we can analyze its kinetics more quantitatively. For pure 1D growth, there are only two growth fronts on both ends. The probability of adsorption per end per MCS is equal to the probability that one monomer happens to be in the end site (1∕V) times the total number of monomers (n),

$$P_a=\frac{n}{6V}=\frac{C}{6},$$ (7)

where V is the box volume, C is the instantaneous monomer concentration, and 1∕6 represents the fact that only one of six possible orientations leads to a successful adsorption. The probability of desorption per end per unit time is

$$P_d=\text{exp}\left(-E∕kT\right),$$ (8)

where the binding energy E=10 for the 1D case. So the elongation rate per end is

$$G=P_a-P_d=\frac{C}{6}-\text{exp}\left(\frac{-E}{kT}\right).$$ (9)

For the initial concentration C₀=0.001 and kT=1.0, Eq. 9 predicts that the number of grown peptides within the first 10⁵ MCS is [0.001∕6−exp(−10∕1.0)]×10⁵×2×(5∕6)=20.2, where 2 represents two ends and (5∕6) represents the fact that one of six directions for adsorption∕desorption is blocked by the preformed fibril end. Simulation results of 50 independent runs give an average value of 19.2±4.6, which is very close to the theoretical value. On the other hand, the elongation rate is zero when the fibril growth reaches equilibrium at late stage. By setting G=0 in Eq. 9, the equilibrium solubility is obtained as

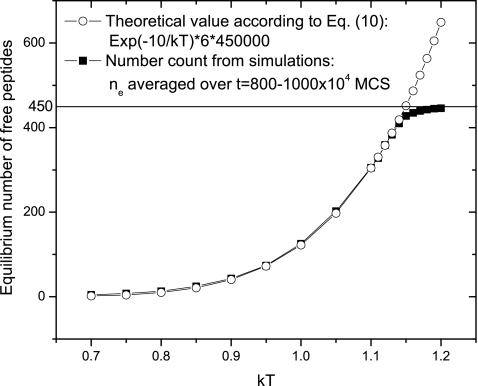
$$C_e=6\text{exp}\left(-E∕kT\right).$$ (10)

So the equilibrium number of monomers is n_e=VC_e=6V exp(−E∕kT), where the box volume V=500×30²=450 000. As shown in Fig. 10, the number count from simulations shows an exact match with the theoretical predictions. The deviation above kT=1.15 is because the maximum number of peptides (VC₀=450) is reached. The elongation rate is also zero when the disassembly temperature is reached. Similar to Eq. 10, the disassembly temperature follows

$$C_0=6\text{exp}\left(-E∕k{T}_m\right).$$ (11)

This predicts kT_m=−E∕ln(C₀∕6)=−10∕ln(0.001∕6)=1.15, which is consistent with our simulation results.

Figure 10.

Comparison of equilibrium solubilities between theoretical predictions and actual values counted from simulations. The error bars are smaller than the signs.

Semi-2D single fibril

For the semi-2D single-fibril case, the above analysis still applies. The initial elongation rate G and n_e counted from simulations are between the two theoretical values obtained by using E=10 and 11 with Eqs. 9, 10 (data not shown). According to Eq. 10, the slope in the plot of ln C_e versus 1∕kT should give us an estimate of the binding energy for end peptides. It turns out that E=11 (data not shown), consistent with the final morphology at t=1000×10⁴ MCS in Fig. 3, where the majority of end peptides have binding energy of 11. Setting E=11 in Eq. 11 predicts the disassembly temperature kT_m=−11∕ln(0.001∕6)=1.26, which is higher than the value (kT_m=1.15) for the pure 1D case and consistent with the observations in Fig. 4f.

For the pure 1D case, E in Eq. 9 is a constant so that either G<0 or G>0 will occur for the fixed C and T. For the semi-2D case, however, E is not a constant but a variable of the fibril size E(R) so that it is possible G<0 initially while G>0 afterwards when the size fluctuations happen to increase R and consequently E(R). Namely, for the semi-2D case with a nonconstant E(R), nucleation and sigmoidal curves become feasible. Assuming G=0 in Eq. 9 at the critical nucleus size, we obtain E(R_c)=kT ln(6∕C). Because E correlates positively with R, for simplicity, we assume that E=10+R∕20. Then we get R_c=20kT ln(6∕C)−200, suggesting that R_c increases with increasing kT or lowering C. We also note that the lag time τ depends on the relative magnitudes of the seed size R₀ and the critical nucleus size R_c: τ=0 if R₀>R_c and τ>0 if R₀<R_c. As already pointed out, the effect of the peptide length L is inverse to the effect of kT in Figs. 4g, 4h. In summary, the lag time is a function of four factors, τ[R₀,R_c(C,T,L)], conforming to the following dependencies:

$$R_0\downarrow ,C\downarrow ,T\uparrow ,L\downarrow \Rightarrow \tau \uparrow .$$ (12)

This explains the four simulation results in Fig. 4. In addition to the three criteria of nucleation [(1) existence of lag time, (2) existence of critical concentration, and (3) seeding],^{15, 16} we can add two more criteria: (4) critical temperature above which fibril growth cannot occur and (5) critical peptide length below which there is no fibril growth. In contrast to the traditional view that nucleus (critical nucleus size) is an invariant entity corresponding to a specific conformation or number,^{15, 27, 28, 29} we believe that R_c(C,T) is a variable depending on the experimental conditions [the degree of supersaturation kT ln(C∕C_e)]. Under a specific condition, it is possible that a two-layer fibril cannot grow while a three-layer fibril can grow so that R_c corresponds to the size of a three-layer fibril, although this condition might be difficult to locate (e.g., in a very narrow C₀ range). However, Ostwald ripening itself is a good example showing how R_c increases with time as C becomes exhausted. In fact, for a pure 2D system in a separate paper,⁴⁶ we have derived a phase diagram showing how R_c increases with increasing kT or lowering C.

Semi-2D multiple fibrils

For the multifibril case, the competition between fibrils makes the analysis difficult. Although Eq. 9 explains the linear concentration dependence of growth rates, it fails to take into account the low-T behavior (G decreases with decreasing T). At low temperatures, the protofibril elongation and ripening are frozen by the low desorption probability. The more desorption events occur, the more exchanges with monomers occur, with the consequence of faster Ostwald ripening (and faster growth of the fibrils). In the low-T region, it is possible that G is proportional to the desorption rate, i.e., G∝exp(−E∕kT). This would explain the linear dependence of ln G on 1∕kT in Fig. 7d, where the slope happens to be −9. However, there is no solid foundation for the above reasoning. Due to the low-T ripening, relation 12 should be modified to

$$R_0\downarrow ,C\downarrow ,T\uparrow \downarrow ,n\left(R_0\right)\downarrow \Rightarrow \tau \uparrow ,$$ (13)

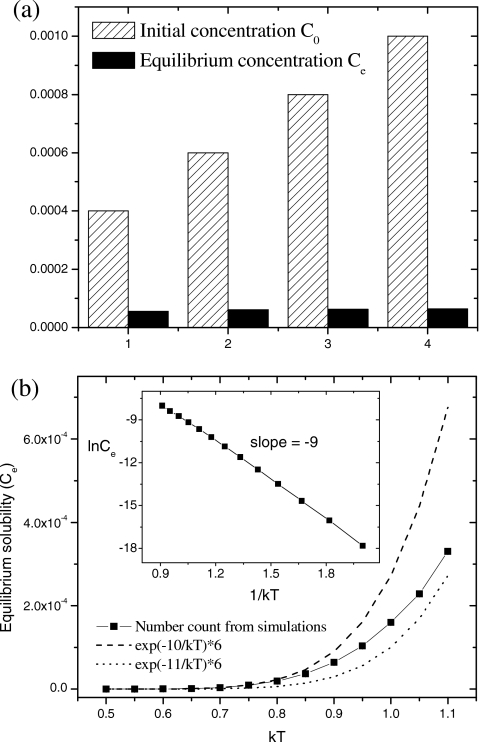
where n(R₀) is the seed concentration. This corresponds to the simulation results in Figs. 89. In Fig. 9, if smaller seeds are added, the seeding is less effective or even unsuccessful (not shown). In all aspects, nucleations for the multi- and single-fibril cases are quite similar. The disassembly upon dilution can be explained by the sudden unbalance of Eq. 9, where the adsorption term becomes suddenly smaller than the desorption term upon dilution. Equation 10 predicts that the equilibrium solubility C_e should be independent of the initial monomer concentration C₀,^{16, 70} which is confirmed by simulation results in Fig. 11a. Equation 10 also predicts that increasing the peptide length (E∝L) should result in lower C_e, in accordance with the experimental finding that the final solubility of β_26–43 is 12-fold lower than that of β_26–40.⁷¹ The equilibrium solubility counted from simulations is between the two theoretical values, as shown in Fig. 11b. According to Eq. 10, the plot of ln C_e versus 1∕kT gives an estimate of the binding energy E. Because the low-T data are closer to the theoretical line of E=10, and the high-T data are closer to the theoretical line of E=11, the inset of Fig. 11b estimates a lower slope E=9 [the same as the slope in Fig. 7d], reflecting a cooperative crossover behavior. Nevertheless, it provides a rough way to estimate the molecular binding energy by simply measuring the temperature dependence of equilibrium solubility of peptides in solutions. Interestingly, setting E=9 for Eq. 11 leads to the disassembly temperature kT_m=−9∕ln(0.001∕6)=1.03, which is consistent with what we find in Fig. 8d.

Figure 11.

(a) Independence of the equilibrium solubility C_e on the initial concentration of monomers C₀. kT=0.9. (b) Temperature dependence of C_e obtained from simulations and theoretical calculations. C₀=0.001. In both figures, C_e is averaged over t=(800–1000)×10⁴ MCS. Error bars are too small to be shown.

CONCLUSION

We have composed a simple coarse-grained lattice model for the nucleation and growth of amyloid fibrils. By employing the classical Metropolis algorithm, we have studied the mechanism of the fibrillization in terms of peptide concentration, temperature, peptide length, and seed size. Two scenarios of growth of an isolated fibril and multiple fibrils are considered. The simulation results from our model are consistent with various experimental observations reported in the literature on many specific systems. Furthermore, vivid details of the various contributing factors for the mechanisms of fibril formation are provided, in addition to fresh predictions.

The main findings are summarized as follows. (1) We have provided physical mechanism and morphological details accompanying the unseeded and seeded fibril formations. (2) We propose that nucleation of amyloid fibrils is due to its semi-2D nature, i.e., nucleation cannot occur without the existence of intersheet interactions. It is confirmed that a pure 1D growth does not require nucleation and does not exhibit sigmoidal growth curves. The importance of the second layer of β sheet is stressed. The mechanism of nucleation is explained by the size-dependent binding energy and desorption rate. (3) We propose that Ostwald ripening (bigger fibrils growing at the expense of smaller ones) is the mechanism of amyloid fibril growth. Ostwald ripening dominates at high concentrations or low temperatures (away from the disassembly boundary, where there is no nucleation) and also during the late-stage growth after nucleation (close to the disassembly boundary). Ostwald ripening mechanism reconciles the debate as to whether protofibrils are precursors or monomer reservoirs. (4) We propose that there are two types of lag times. Their differences are summarized below.^**

• τ₁: due to slow Ostwald ripening, present at low T and intermediate C, decreases with T, cumulative in nature, and cannot be seeded.

• τ₂: due to nucleation, present at high T or low C, increases with T, stochastic in nature, and can be seeded.

(5) The lag time due to nucleation is shown to be a function of five factors τ[n(R₀),R_c(C,T,L)]. Increasing the seed size R₀ or the seed concentration n(R₀) results in shorter τ. The two-layer seed is more effective in seeding than the one-layer seed. τ increases sharply with decreasing the peptide concentration C, diverging at the critical concentration C^*. Critical temperature (T^*) and critical length (L^*) can be added to the three existing criteria of nucleation (lag time τ, seeding R₀, critical concentration C^*). It is stressed that the critical nucleus size (R_c) is not a constant but a variable depending on the experimental conditions. (6) The elongation rate G (obtained either from the average fibril size or from the total mass) increases linearly with the initial peptide concentration. The relation ln G∼1∕kT is observed at lower temperatures. In general, G depends on T nonmonotonically due to the relative importance of desorption and adsorption rates. (7) For each individual fibril, the elongation rate per end is found to be G=C∕6−exp(−E∕kT). Based on this equation, the equilibrium solubility is shown to be independent of the initial peptide concentration but depends on the peptide length, and the plot of ln C_e versus 1∕kT provides a rough way to estimate the intrasheet H-bonding interaction. On the other hand, the length ratio (morphology) of a ribbonlike fibril may provide a rough way to estimate the ratio between the intrasheet and intersheet interactions.

Structure (molecular conformation and morphology), interactions, and kinetics (nucleation and growth) are three key issues in amyloid studies.⁶ The amyloid fibrils, although formed from a variety of protein precursors with different conformations and specific molecular interactions, share a common cross-β structure and a similar fibrillization process. The present generic model, by parametrizing the molecular details into coarse-grained building blocks, provides a promising tool to investigate the common features of large-scale morphologies and kinetics for all amyloid fibrils.