Abstract
We have studied a charge-insertion process that models the deprotonation of a histidine side chain in the active site of cytochrome c oxidase (CcO) using both the continuum electrostatic calculations and the microscopic simulations. The group of interest is a ligand to CuB center of CcO, which has been previously suggested to play the role of the proton pumping element in the enzyme; the group is located near a large internal water cavity in the protein. Using the nonpolarizable Amber-99 force field in molecular dynamics (MD) simulations, we have calculated the nuclear part of the reaction-field energy of charging of the His group and combined it with the electronic part, which we estimated in terms of the electronic continuum (EC) model, to obtain the total reaction-field energy of charging. The total free energy obtained in this MDEC approach was then compared with that calculated using pure continuum electrostatic model with variable dielectric parameters. The dielectric constant for the “dry” protein and that of the internal water cavity of CcO were determined as those parameters that provide best agreement between the continuum and microscopic MDEC model. The nuclear (MD) polarization alone (without electronic part) of a dry protein was found to correspond to an unphysically low dielectric constant of only about 1.3, whereas the inclusion of electronic polarizability increases the protein dielectric constant to 2.6–2.8. A detailed analysis is presented as to how the protein structure should be selected for the continuum calculations, as well as which probe and atomic radii should be used for cavity definition. The dielectric constant of the internal water cavity was found to be 80 or even higher using “standard” parameters of water probe radius, 1.4 Å, and protein atomic radii from the MD force field for cavity description; such high values are ascribed to the fact that the standard procedure produces unphysically small cavities. Using x-ray data for internal water in CcO, we have explored optimization of the parameters and the algorithm of cavity description. For Amber radii, the optimal probe size was found to be 1.25 Å; the dielectric of water cavity in this case is in the range of 10–16. The most satisfactory cavity description, however, was achieved with ProtOr atomic radii, while keeping the probe radius to be standard 1.4 Å. In this case, the value of cavity dielectric constant was found to be in the range of 3–6. The obtained results are discussed in the context of recent calculations and experimental measurements of dielectric properties of proteins.
INTRODUCTION
The most computationally efficient treatments of electrostatic interactions and estimation of pKa values in proteins are based on the continuum models,1, 2, 3 in which the effective dielectric constants for the protein are used. The results obtained with such models are very sensitive to the value of the dielectric constant; however, the optimal value of this parameter for a particular protein is difficult to choose or justify. In fact, the protein dielectric constant εp is not a universal constant but rather a parameter that depends on the model used.4 Thus, it has been suggested5 that εp>20 should be used in macroscopic models, instead of a low dielectric εp∼4 observed in the experiments on dry protein powders6, 7 and supported by some simulations.8, 9, 10 For example, Miyashita et al. found reasonable agreement with experiment when the dielectric constant of the protein εp was assumed to be 10–20.11 Furthermore, Muegge et al. suggested that when charged groups are considered, the protein dielectric constant should be as high as 40 or even higher.12 Schutz and Warshel have pointed out,4 however, that one needs to use large εp only when both the reaction-field energy and protein field (Coulomb interaction) energies are described with the same value of εp. Once the restriction that the same εp is used for both effects is removed (as it was first proposed by Krishtalik et al.13), the reaction-field energy is reproduced most consistently with εp between 2 and 8 (Refs. 4, 14, 15, 16, 17, 18, 19) (depending on the protein, charge insertion site, and the semimacroscopic model used); whereas, the protein field term is reproduced with εp∼1.13, 15
Additional reason for variation of εp in different systems is that proteins are inhomogeneous, different parts may have different dielectric properties. One of the sources of inhomogeneity is internal water, which is expected to increase the dielectric polarizability of the protein.6, 7 Since different proteins have different amounts of internal water, it is not surprising that the resulting effective dielectric “constant” of proteins can vary significantly.
Here, we use microscopic molecular dynamics simulations to probe the dielectric parameters of cytochrome c oxidase (CcO), an enzyme which has been the subject of many recent experimental and theoretical studies because of its central role in energy metabolism in aerobic cells and its intriguing proton pumping function.20, 21 In CcO, there are a lot of internal water molecules which significantly affect the functionality of the enzyme and its dielectric properties.
The previous studies of CcO were exclusively based on the continuum models, in which the internal water cavities, the protein itself, the membrane, and the external solvent are described by different dielectric constants. The values of such parameters are often different in different studies, which is one of the reasons for the differences in the pKa calculations of the enzyme.3, 21, 22 The key parameter appears to be the dielectric constant of the enzyme water cavities εcav, about which very little is known. Although it is well recognized that different cavities may have different dielectric properties (e.g., size dependent), it is important to know typical magnitudes of their dielectric relaxation parameters.
The upper limit for the dielectric constant of water cavities found in the literature corresponds to the dielectric constant of the bulk solvent (εcav=80). However, according to experimental observations,6, 7 the movement of water molecules inside of the protein is more restricted than in the bulk; therefore, the polarizability of the internal water should be lower than that of the bulk. At the other extreme, the lowest limit of εcav is the dielectric constant of “dry” proteins itself, which is assumed to be around 4. This empirical value is supported by experimental data on the lysozyme hydrated powder.6 For different proteins or different hydration levels, such as CcO, however, this value may be even lower than 4. Thus, one cannot avoid the conclusion that the protein dielectric parameters are ill-defined and likely not transferable from one protein to another.
Here, we use detailed microscopic simulations to determine the corresponding continuum phenomenological parameters of CcO which best reproduce the charging free energies obtained by molecular dynamics (MD) simulations. A similar approach was used earlier to study dielectric relaxation in several other proteins.10, 14, 15, 17, 23, 24, 25 We apply this strategy to examine deprotonation of His291 ligand of CuB metal center of CcO (in bovine heart cytochrome c oxidase). This residue is a key element of a recently proposed proton pumping mechanism of the enzyme.3, 21 The dielectric constant of the protein εp and that of an important water cavity εcav in the vicinity of the catalytic center (see Fig. 1) are determined as adjustable parameters which reproduce the microscopic reaction-field energy of charging (or deprotonation) obtained in MD simulations of the dry protein and the protein with internal water.
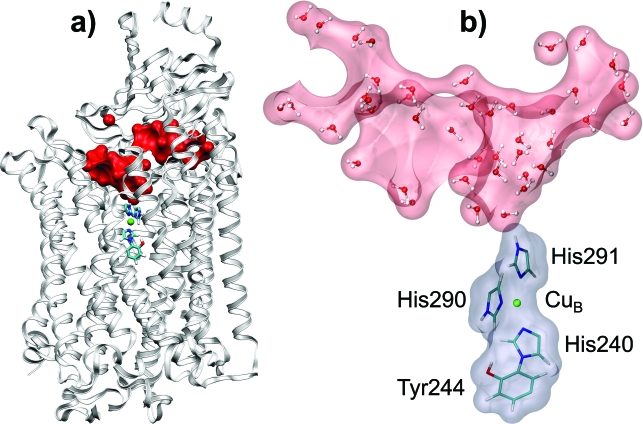
Figure 1.
Simulated model of CcO. (a) The model for MD simulations: Only two subunits A and B are considered, tubes and ball stand for the QM system, the red surface represents the internal water, white ribbons represent the protein. (b) The continuum model: Rose and gray surfaces represent the continuum water cavity and QM system region, respectively; the protein region is not shown here.
The parametrization of the continuum models employing microscopic simulations as a reference has been explored by many authors before.4, 10, 13, 23, 25, 26, 27 One of the difficulties that one encounters here is related to the issue of electronic polarization in microscopic simulations. The conventional force fields [e.g., AMBER99 (Refs. 28, 29) and OPLS-CHARMM (Ref. 30)] are nonpolarizable. In low-dielectric environments, such as interior of a protein, the standard MD approach produces poor results; therefore, the missing electronic polarization, the cause of the problem, needs to be treated explicitly.31, 32, 33 Another problem is that in many cases, especially when the polarizable medium includes water, the microscopic dielectric response (or relaxation) of the system can be nonlinear16, 23, 24, 27, 34 while the continuum models assume linearity of the dielectric response. The computation analysis presented in this work addresses both of the above problems.
The plan of the paper is as follows. The theoretical background for the microscopic model is discussed in the following section. The results, including the computation scheme, are represented next. The discussion and conclusions are given in the last section of the paper. Additional computational details are given in Appendixes A, B.
FORMALISM
The protonation∕deprotonation energy of an ionizable group in a protein can be divided into two parts: The inner-sphere part, which represents the internal energy changes of the group, and the outer-sphere part, which is due to interactions of the group with the surrounding medium. The CuB center of CcO with imidazole rings of ligated residues His290, His291 (protonatable group), and His240 cross-linked to Tyr244 (see Fig. 1) will be referred to as a QM system; following the solvation theory terminology, the QM system will also be called a solute. To determine the dielectric properties of the polarizable medium (protein and solvent) surrounding the QM system, the calculation of only the outer-sphere electrostatic free energy change (charging free energy) is required.
General theory for charging free energy simulations
The charging free energy ΔG will be calculated by the thermodynamic integration method
| (1) |
Here, λ is a coupling parameter chosen in such a way that H0≡H(λ=0) and H1≡H(λ=1) correspond to the Hamiltonian of our system in the initial (protonated) and final (deprotonated) states, respectively; ⟨∂H(λ)∕∂λ⟩λ is the derivative averaged over the equilibrium ensemble for a given parameter λ. If the Hamiltonian functional H(λ) is constructed as H(λ)=H0+λ(H1−H0), then the derivative ∂H(λ)∕∂λ for a given molecular configuration is written as follows:
| (2) |
Here, are atomic positions of the system; N is total number of atoms; indices i,j run over all atoms of the QM system, and μ runs over all atoms of the surrounding medium; and are interatomic distances; , where and are the initial and final partial charges of the ith QM atom, respectively; and Qμ denotes partial charges of the medium atoms. One should keep in mind that according to standard force fields (e.g., AMBER99), the interactions between 1–2 and 1–3 neighbors should be illuminated from the sum [Eq. 2] or scaled on the factor 1∕1.2 for 1–4 neighbors.
The second term in Eq. 2 is the electrostatic energy change of the QM system itself. This term should be excluded from the derivative [Eq. 2] since it contributes only to the “inner-sphere” free energy change of the QM system, whereas we are interested in the “outer-sphere” one, i.e., free energy change due to polarization of the medium surrounding the QM system. We drop this term throughout the formalism below. Thus, part of our interest is given by the following expression:
| (3) |
where
Here, Vi is the electrostatic potential at the position ofith solute atom induced by the medium; ⟨Vi⟩0 and Φi(λ) represent the protein and reaction field, respectively, at the position of ith solute atom. Substitution of Eq. 3 to Eq. 1 gives
| (4) |
Here, ΔGprot and ΔGrf are the so-called protein field and reaction-field free energy term, respectively. Thus, the free energy change due to introduced charges consists of two parts: The protein field term, representing the work needed to transfer charges Δqi from infinity to the corresponding atomic positions of the solute at fixed (equilibrium) nuclear positions of the latter, and the reaction-field term, representing the free energy change due to the relaxation of the equilibrium atomic positions in response to the introduced charges. In the literature, ΔGprot and ΔGrf are also called as the protein field and Born term,3, 21, 35, 36 static and relaxation term,14, 15, 17 or as the interaction and self-energy terms,4, 25, 27 respectively.
In this paper, we will be interested only in ΔGrf term which reflects the dielectric relaxation of the protein medium.
Assuming small atomic displacements in the medium, we will use the following approximation: ⟨1∕riμ⟩λ=1∕⟨riμ⟩λ, which is correct up to quadratic Taylor extension terms of the function over the small parameter , where is the fluctuation of the interatomic vector . Substitution of these relations to Eq. 3 gives
| (5) |
Here, ∂H(r;λ)∕∂λ denotes exactly the same derivative ∂H(λ)∕∂λ as in Eqs. 1, 2, 3, 4, with just explicitly specified dependence of the function on the molecular configuration; is average molecular configuration for a given λ. Equation 5 opens a way to estimate ⟨∂H(r;λ)∕∂λ⟩λ value in only single calculation of the function ∂H(r;λ)∕∂λ based on the average molecular configuration ⟨r⟩λ and avoid the cumbersome averaging over the configuration ensemble.
Linear response approximation
If the derivative ⟨∂H(λ)∕∂λ⟩λ is a linear function of the coupling parameter λ (the linear response approximation), the integration in Eqs. 1, 4 can be done analytically, and the solvation free energy changes can be expressed in terms of ⟨∂H∕∂λ⟩ in the initial and final states
| (6) |
In the linear response approximation, the reaction-field energy can be related to fluctuations of ∂H∕∂λ using the Kubo relation37
| (7) |
Here, ⟨δ(∂H∕∂λ)δ(∂H∕∂λ)⟩ is the square variation of the value ∂H∕∂λ; kB and T are the Boltzmann constant and temperature, respectively; and Δλ is the change of Kubo’s “generalized force” corresponding to the transition from the initial to final state, in-out case Δλ=1. The λ value for which the fluctuations should be calculated is not specified in Eq. 7 because in the linear response approximation the fluctuations should not depend on λ.
Equations 6, 7 provide two computationally independent methods for the reaction-field energy estimation. Expressions 6, 7 are not computationally identical since statistical precisions of their evaluation are quite different in the MD simulations. Keeping the terminology used in Refs. 38, 39, we refer to the method based on Eq. 6 as algorithm I and one based on the Eq. 7 as algorithm II. As it was shown in Refs. 38, 39, algorithm I is computationally more reliable than the algorithm II. Nevertheless, algorithm II can be useful for the result comparison, as a statistical consistency test for a given simulation.
The electronic polarization and MDEC model
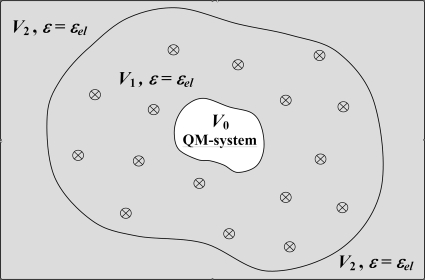
The molecular dynamics electronic continuum (MDEC) model employed in this paper for accounting for electronic polarization in MD simulations is discussed in detail in Ref. 33. This model suggests that the charging free energy ΔGrf can be calculated both in high- and low-dielectric media by combining MD simulations with an explicit treatment of electronic polarization in terms of the electronic continuum (EC) approximation. In this approximation, all charges are considered to be immersed in the electronic continuum of dielectric constant εel. The key result of the model is the expression for charging free energy
| (8) |
where is the reaction-field energy obtained with standard nonpolarizable MD simulations, and is the electronic part of the reaction-field energy. The latter is estimated by using phenomenological EC model shown in Fig. 2. The QM system is represented by a set of point charges located inside the QM cavity; inside the cavity, the dielectric constant ε is set to be unity, while outside ε=εel. The charging energy is found by solving the Poisson equation, as done, e.g., in Ref. 40. Some caveats of calculation are discussed in Appendix B. The factor 1∕εel in Eq. 8 reflects the electronic screening of interaction of the charges on the QM system that undergoes charging and the charges of the surrounding protein medium.
Figure 2.
Illustration of the molecular∕continuum MDEC model. V0 is the region of the QM system; V1 is the region of explicit treatment of the polarizable medium (ε=εel), where crossed circles stand for the protein and internal water particles considered in MD; and V2 is the protein exterior region (ε=εel, since in our case there are no particles, but the electronic continuum should be present for the consistency with the nonpolarizable force-field parametrization). In this model, we approximately assigned the same value of εel for both the protein and internal water.
In high-dielectric media, such as water, the above expression produces results which are very close to those of the standard MD approach; the latter does not consider electronic polarization energy at all and assumes . For example, for a spherical ion of radius R, the total charging energy in high-dielectric medium is approximately Q2∕2R. It is this value that the standard MD simulations should reproduce; therefore, . The electronic energy, on the other hand, is . Thus, in this, case Eq. 8 predicts , as in the standard approach.
In the low-dielectric media, however, the solvation energy is mainly due to electronic polarization; the standard nonpolarizable MD will produce in this case a negligible contribution . Equation 8 predicts in this case , as expected. Equation 8 can therefore be considered as interpolation between high- and low-dielectric cases.
Successful simulations of hydration free energies of ions,32 dielectric constants of neat alcohols and alkanes,33 as well as nonequilibrium reorganization energies in water,41, 42 dichloroethane,41, 42 tetrahydrofuran,41 and supercritical carbon dioxide41 solvents indicates that the MDEC model is expected to work well both in high- and low-dielectric media. The justification of MDEC model and further details can be found in Ref. 33.
COMPUTATIONAL PROCEDURES AND RESULTS
The system
His291 residue is a ligand of CuB metal center of CcO; to estimate the electrostatic response of the protein to charge insertion onto this group, we define a QM system as CuB center together with imidazole rings of ligated residues His290, His291, and His240 cross-linked to Tyr244, see Fig. 1. During the charging process, the partial charges of QM system determined in ab initio quantum-chemical calculation are changing from to ; here, i index runs over all solute atoms. The two charge distributions correspond to protonated and deprotonated states of His291 δ-N, respectively.
Cytochrome c oxidase is modeled by only subunits A and B with cofactors CuA and heme a in oxidized state, while heme a3 and CuB are reduced, which correspond to the so-called OORR state of Ref. 35. Simulations are done for two different water contents in CcO: The dry protein (with no explicit water) and protein with 42 explicit, internal water molecules (see Appendix A for details). In the following, we describe the calculation of the free energy associated with dielectric response of CcO protein to charge redistribution on the QM system.
The computation scheme
For convenience, we summarize here the computational procedures of the paper. The reaction-field energy and the values of dielectric constants for the protein and its internal water cavity were carried out in following steps.
-
(1)
The standard MD simulations are performed from which the reaction-field energies of the charge transfer process are obtained. The free energy simulation is done for two systems: For dry protein CcO (no internal water) and for the protein with internal cavity filled by water molecules; see Secs. 3C, 3D and Appendix A.
-
(2)
The charging reaction-field energy of the electronic polarization is estimated by solving Poisson-Boltzmann (PB) equation, as described in Appendix B, for the continuum model shown in Fig. 2. In this calculation (the continuum calculations were carried out for variable probe and atomic radii to investigate the sensitivity of the results to definition of dielectric boundary; see Sec. 3F), the dielectric constant of the solute region is set to 1, whereas, dielectric of the protein and protein exterior region is set to εel, see Sec. 3E Appendixes A, B.
-
(3)
The total charging reaction-field energy is evaluated using Eq. 8 of the MDEC model. and terms are taken from the steps (1) and (2), respectively. See Sec. 3E.
-
(4)
The continuum PB calculations were performed to adjust the dielectric parameter εp of the protein to reproduce the total microscopic reaction-field energy obtained for the dry protein. In the present work, the continuum calculations were carried out for three structures rcs, ⟨r⟩0, and ⟨r⟩1 of the dry protein (the protonated crystal structure and the initial and final average structures, respectively). See Secs. 3E, 3F.
-
(5)
Finally, in the continuum PB calculation, the dielectric parameter εcav is adjusted to reproduce the total microscopic reaction-field energy obtained in step (3) for the protein with internal water. The cavity is defined by the positions of experimentally observed water molecules, see Secs. 3E, 3F. The protein dielectric parameter εp is taken from step (4). The continuum calculations were carried out for three structures rcs, ⟨r⟩0, and ⟨r⟩1 of the protein.
MD simulations of dry CcO
First, using MD, we evaluated profiles of the derivative ⟨∂H∕∂λ⟩λ and corresponding microscopic solvation free energies for dry CcO. Three MD models with different atomic constraints were examined to check reliability of the results. In the first constraint model (A), all alpha carbons (total number of Cα atoms is 741) and metal centers CuA and Mg2+ are fixed. In the second model (B), only external (protein exterior exposed) Cα atoms remain fixed (number of external α carbons is 316). The third MD model (C) has no constrained atoms except Na+ and atoms belonging to the QM system, which are kept fixed in all simulation models. The details of MD simulations are given in Appendix A.
An example of ⟨∂H∕∂λ⟩λ profile as a function of λ calculated with the MD model (A) is shown in Fig. 3. It is reminded that only the polarization energy of the protein outside the QM system is calculated here, i.e., without energy of the QM itself; the latter can be calculated accurately only quantum mechanically. In the MD calculations, the internal energy of the QM system (−86.5 kcal∕mol) was subtracted from the total energy.
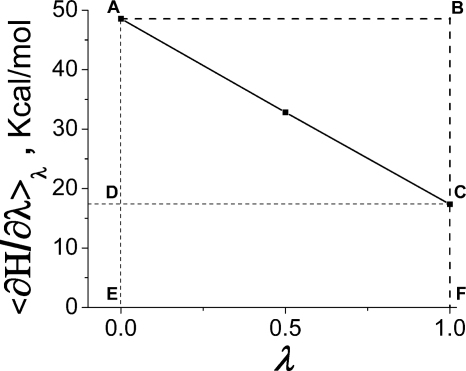
Figure 3.
⟨∂H∕∂λ⟩λ profile obtained for the constraint model (A) of the dry CcO. Only outer-sphere part is shown.
The total free energy, Eq. 1, is the area under the ⟨∂H∕∂λ⟩λ curve—in Fig. 3, the area of EACF figure, whereas the protein field energy and the absolute value of the reaction-field energy are given by the areas of EABF and ABC figures, respectively. In the following, we focus only on the reaction-field energy that characterizes the magnitude of protein relaxation. As seen in Fig. 3, the profile ⟨∂H∕∂λ⟩λ for dry protein is remarkably linear in λ; hence, the condition of the linear response approximation is satisfied with high precision.
The reaction-field energy calculations were done in two different ways: First using average values ⟨∂H∕∂λ⟩0 and ⟨∂H∕∂λ⟩1 (algorithm I), Eq. 6, and second via fluctuation of the value ∂H∕∂λ (algorithm II), as given by Eq. 7. Results are summarized in Table 1. The comparison of values obtained by algorithms I and II is a test for statistical consistency of simulations.39 It is seen in Table 1 that reaction-field energies calculated by algorithms I and II coincide within 3 kcal∕mol for the each simulation model. This is remarkable agreement because the values obtained via fluctuations are very sensitive to details of simulation. For example, a significant disagreement between the results obtained with algorithms I and II is observed (the last line of the Table 1) if the cutoff radius of 15 Å is applied. Thus, the agreement between the two algorithms indicates that simulations of the dry CcO (using no cutoff) are statistically consistent, the long-range electrostatic interaction is treated satisfactory, and the condition of linear response approximation is remarkably satisfied.
Table 1.
Reaction-field energies of charging obtained in MD simulations of the “dry” CcO, values are in kcal∕mol.
| Constraint model | Algorithm I | Algorithm II | |
|---|---|---|---|
| λ=0 | λ=1 | ||
| A | −15.7 | −15.3 | −15.5 |
| B | −18.2 | −19.1 | −17.8 |
| C | −15.2 | −18.1 | −13.7 |
| A, cutoffa | −13.3 | −1052 | −1051 |
The cutoff radius is 15 Å.
The comparison of simulations with different types of constraints of the atoms [simulation models (A), (B), and (C)] showed that the reaction-field energy is reasonably insensitive to the applied constraints. Therefore, for the following simulations, we chose the (technically) simplest simulation model (A). In this model, the protein relaxation time is shorter which allows for obtaining converged results on shorter trajectories.
MD simulations of CcO with internal water
Simulations for the same charging process of the CuB site were carried out in CcO with internal water (42 explicit molecules taken from x-ray data, see Appendix A). Half of these water molecules constitute the main closed cavity located in the vicinity of His291 residue, whereas another half form two possible proton exit channels36 (Fig. 1).
The obtained profile (of the outer-sphere part) of ⟨∂H∕∂λ⟩λ is shown in Fig. 4. In contrast to dry protein, Fig. 3, the dependence on λ is nonlinear. Obviously, the nonlinearity is caused by water. The nonlinear effects in the medium which include water were observed in many earlier studies.16, 23, 24, 27, 34, 38 In our system, the effect is mainly due to reorientation of one particular water molecule located between the two propionates of heme a3; this water molecule forms different types of hydrogen bonds with His291 in its protonated and deprotonated states, and in the process of charging needs to change orientation. The orientation flipping of that water molecule occurs around λ=0.75, which apparently breaks the linearity of the response, see Fig. 4.
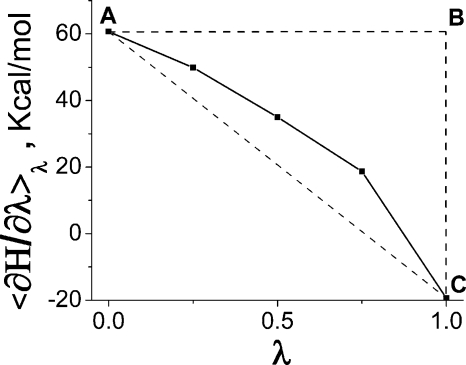
Figure 4.
⟨∂H∕∂λ⟩λ profile obtained for the constraint model (A) of the CcO with internal water. Only outer-sphere part is shown.
In this nonlinear case, the reaction-field energy calculated by Eq. 4 (the negative area of the ABC∕solid curve figure in Fig. 4) is −29.6 kcal∕mol, whereas the linear response approximation (negative area of ABC∕dashed line in Fig. 4), Eq. 6, gives value of −40.0 kcal∕mol. Thus, the relative error in due to the linear response assumption would be ∼30%; however, the error in the total reaction-field energy [Eq. 8] would not be as dramatic, as we show later. The inconsistency of the linear response assumption inherent to the macroscopic continuum model with the actual nonlinear dielectric response is discussed in the Sec. 4.
The continuum calculations
We now wish to see which phenomenological parameters of the fully continuum electrostatic model can reproduce the charging reaction-field energies obtained in the microscopic simulations. However, before we switch over to the continuum calculations, we need to clarify the question of which molecular configuration should be used for the continuum model.
Choosing the protein structure for continuum calculations
The continuum model (discussed in the next section) needs as an input the protein structure. However, the protein continuously fluctuates around some equilibrium position due to the thermal motions of its atoms. A characteristic deviation of the value ∂H∕∂λ from the equilibrium value ⟨∂H∕∂λ⟩λ due to the protein fluctuations is about 4 kcal∕mol for the dry protein and 5–8 kcal∕mol for the protein with internal water. This means that depending on a particular choice of the instant protein configuration, the electrostatic energy is expected to fluctuate around the average by several kcal∕mol. Such a precision is not satisfactory for most of the continuum applications.
Earlier, Simonson et al.14, 15, 17 dealt with this problem by averaging the results of PB calculations over multiple (∼100–200) structures taken from the molecular dynamics simulation. In the present work, we suggest much simpler approach. We notice that when structural fluctuations of the protein are small, the average value of ∂H(r)∕∂λ over the equilibrium configuration ensemble for a given λ is approximately equal to ∂H(⟨r⟩λ)∕∂λ, see Eq. 5. In this case, the average structure ⟨r⟩λ reflects the equilibrium protein polarization corresponding to a given λ.
To verify the applicability of the above approximation for our system, we recalculated all ⟨∂H∕∂λ⟩λ values via single average configurations. The difference between the results given by Eq. 5 and those of straightforward averaging procedure is within 0.5 kcal∕mol for the dry CcO and within 1 kcal∕mol for the protein with internal water. Moreover, the uncertainty in determination of the reaction-field term is much lower (∼0.1 kcal∕mol) than that of the protein term. Such a remarkable precision does not exceed the statistical uncertainty of simulations.
In principle, the problem with above approach can arise when internal water is considered. Water can diffuse within the protein; hence, the fluctuations around average can be large. Such effect was observed for CcO with internal water: A water molecule located between propionates of heme a3 was seen to exchange with other water molecules in the cavity. This problem was resolved by reordering water molecules in the MD trajectory before the averaging procedure.
The average configurations ⟨r⟩λ quite accurately describe the protein polarization; therefore, it is a reasonable choice as the input for the PB calculations. However, it is not a priori clear which λ (protonation state) should be chosen for estimation of the dielectric constant. In the linear approximation, any λ should result in the same reaction-field energy. The continuum PB calculations are typically carried out using the crystal structure of the protein,43 disregarding the fact that equilibrium protein structures can be different in protonated and deprotonated states. To examine the difference of using different structures, we performed PB calculations for three protein structures: rcs, ⟨r⟩0, and ⟨r⟩1, where rcs denotes the crystal structure43 with optimized hydrogen positions, and ⟨r⟩0 and ⟨r⟩1 denote average configurations of the initial (protonated His291) and final (deprotonated His291) equilibrium states of the protein.
Standard continuum model
The reaction-field energies of charging CuB site in CcO obtained in the MD simulations [constrain model (A), Secs. 3C, 3D) are −15.7 and −29.6 kcal∕mol for dry protein and the protein with internal water, respectively. We now wish to calculate the corresponding reaction-field energies using continuum models based on the PB equation. In such continuum calculations, we use the two adjustable parameters: The dielectric constant of the protein εp and that of the water cavity εcav. By the comparison of the charging reaction-field energies obtained in MD and in the continuum model, we want to find most appropriate values of these parameters.
A key step in the continuum calculations is to define the shape of the molecule and the boundaries of the internal water cavities. To this end, we first use the procedure adopted in MEAD program3, 21, 40, 44, 45 with “standard” parameters of the probe radius 1.4 Å and the protein atomic radii from the MD force field29 (van der Waals radii). The details of this calculation are in Ref. 21 and briefly summarized in Appendix A. This model is further referred to as standard.
(a) Matchingfor a dry protein. The first set of continuum calculations involved dry CcO. Here, we calculated the charging reaction-field energy of the protein by the continuum model and adjusted the value of the protein dielectric constant so as to reproduce the microscopic reaction-field energy of the dry protein obtained in MD (uncorrected with the effects of electronic screening discussed in Sec. 2C). The obtained εp values are 1.4, 1.3, and 1.4 for the structures rcs, ⟨r⟩0, and ⟨r⟩1, respectively. Similar estimate of 1.5 of the protein dielectric constant for most internal region of cytochrome c was reported in earlier work of Simonson and Perahia18 and elsewhere.8 The reason for such a low polarization response is now well recognized: The conventional MD simulations with nonpolarizable force fields do not yield the total protein polarization energy, but only its nuclear part,16, 17, 31, 32, 33, 39, 42, 46 exaggerated by the factor εel. To obtain the correct result, one needs first to calculate the total solvation free energy correctly, as discussed in Sec. 2C, and only then match it with a continuum model.
(b) Matchingusing Eq. 8. We now correct by the factor 1∕εel and add the corrected value of the nuclear polarization energy to the electronic part , according to Eq. 8. The electronic part is estimated using the continuum model. The electronic dielectric is taken to be 2. The electronic polarization energy is −37.8 kcal∕mol. The total is −45.6 kcal∕mol for the dry CcO. Note that the magnitude of reaction-field energy calculated by the standard nonpolarizable MD technique is almost three times lower than one of the total reaction-field free energy calculated by the MDEC model. Such a qualitative difference unambiguously demonstrates that the conventional MD approach does not take into account the energy of electronic polarization; therefore, the latter should be added explicitly. Indeed, matching to the continuum free energy yields εp=1.3 for the dry CcO (see above subsection), which is unphysically low for the static dielectric constant for a condensed phase; indeed, it is even lower than pure electronic polarizability εel∼2. In contrast, MDEC approach leads to physically reasonable estimations that are in line with results of other authors47 (see Sec. 4). The results of matching the MDEC total polarization energy thus obtained are presented in Table 2.
Table 2.
Dielectric properties of CcO obtained in conventional Poisson calculations. Reaction-field energies are given in kcal∕mol.
| CcO structure | Dry CcO | CcO with water cavity | |||||
|---|---|---|---|---|---|---|---|
| εp | εcav | ||||||
| rcs | 2.62 | 79 | |||||
| ⟨r⟩0 | −37.8 | −15.7 | −45.6 | 2.57 | −29.6 | −52.5 | Infinitya |
| ⟨r⟩1 | 2.70 | 14 | |||||
The actual adjusted value is 105.
For a dry protein, all three examined geometries produce approximately the same protein dielectric constant εp in the range of 2.6–2.7, with corresponding uncertainty in the reaction-field energy about 1 kcal∕mol. This constant includes both electronic and nuclear polarizability of the protein.
For water cavity, however, the results are not as robust and strongly depend on the geometry used. As seen from Table 2, the obtained dielectric constants of the water cavity are completely different for different molecular configurations; moreover, εcav>80 obtained for configuration ⟨r⟩0 is not realistic at all. The values obtained for configurations rcs and ⟨r⟩1 are in the range of physical possibility, yet are quite different to be considered as satisfactory. The encountered problem is examined below.
Optimization of the parameters for continuum calculations
There are two factors that contribute to sensitivity of the results for water cavity to minor structural changes: The volume of the cavity and the position of its boundary with respect to the QM system. The cavity volume is known to be highly sensitive to the probe and atomic radii48 and hence to protein structure; different studies suggest different parameters to be optimal.49 The problem is partially due to the fact that the boundaries between different dielectric regions of the protein are modeled using hard spheres. Given the same polarization energy, different volumes will produce different effective dielectric constants of the cavity. This underscores the phenomenological nature of the dielectric parameters that we are trying to establish. Even more significant is the fact that in our case the cavity is located very closely to the QM system hence the position of its boundary becomes a critical issue.
In order to examine sensitivity of the results to the parameters involved, we recalculated dielectric constants of the protein and water cavity using different probe and protein atomic radii. Also, a modified algorithm for cavity definition was implemented to make sure that the water molecules seen in x-ray data, and those used in our MD study, are completely embraced by the continuum cavity. This is not always the case with the standard MEAD procedure, because in cases when there is an overlap between the protein atomic sphere and water molecule represented by the probe sphere, MEAD gives preference to atoms of the protein—we call this algorithm exclusive. In a modified algorithm, the cavity is defined in such a way that the experimentally observed water molecules are always completely included in the cavity; i.e., the preference is given to water molecules inside the cavity. The modified algorithm is called therefore inclusive, to contrast it with the exclusive algorithm of MEAD program. For more details on the procedure, see Appendix A.
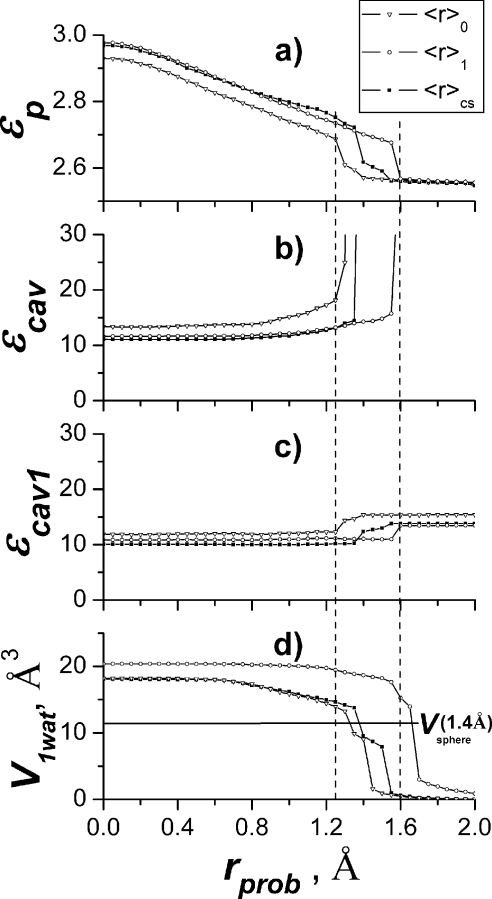
Optimal probe radius for Amber atomic radii
In Fig. 5, the results are shown for variable probe radius, while the protein atomic radii are fixed as in the standard model, i.e., at the values corresponding to the position of the minimum of van der Waals potential given by the Lennard-Jones parameters from the MD force field. The calculations were done for all three examined protein geometries.
Figure 5.
Dependency of result on the probe radius. (a) Protein dielectric constant, (b) dielectric constant of internal water cavity obtained with “exclusive” cavity definition, (c) dielectric constant of internal water cavity obtained with “inclusive” cavity definition, and (d) the volume of the critical part of the continuum water cavity with “exclusive” definition.
Figure 5a shows the behavior of the protein dielectric constant εp, which has a relatively minor systematic variation for probe radius less than roughly 1.2 Å in the range from 2.7 to 2.9. The drift is due to the fact that volume of the empty cavities of the protein (including the one we are studying in this paper) is increasing with decrease of the probe radius, thus decreasing the volume of the polarizable protein medium. The smaller polarizable volume requires higher dielectric constant to reproduce the same polarization energy. The steplike behavior for probe around 1.4 Å will be explained below.
Figure 5b shows the behavior of the dielectric constant of the cavity εcav using MEAD “exclusive” algorithm. For the probe radius below roughly 1.2 Å, εcav essentially does not change, staying in the range 11–15, depending on the geometry used; however, as the probe radius increases up to 1.3–1.6 Å, the unstable behavior is observed, and the dielectric constant of the cavity is sharply increasing. It is this region that corresponds to the standard continuum protocol considered earlier.
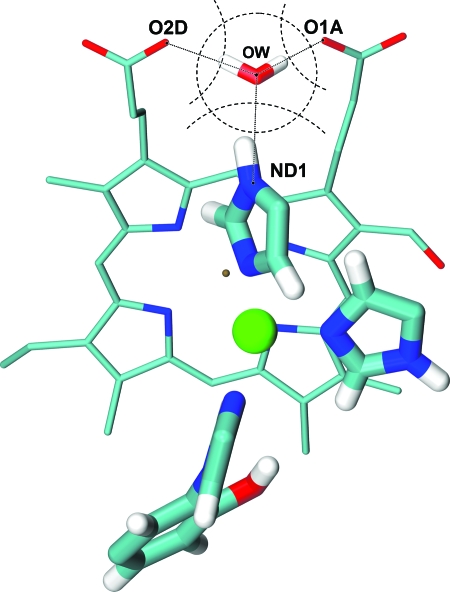
The reason for such a behavior was recognized to be due to sensitivity of the dielectric constant of the cavity to the position of the cavity boundary in the most critical region—close to the protonation site. This region, together with one critical water molecule of the cavity, the nearest one to the protonation site (δ nitrogen of the His291), is shown in Fig. 6. The cavity has a small pocket between two propionates of heme a3, where one water molecule resides. This water molecule is observed in the x-ray data of the protein. Since the solute charge redistribution mainly takes place on the protonatable group, this water molecule contributes significantly to the polarization effect of the water cavity; thus, continuum result is very sensitive to the protein∕solvent boundary in this region.
Figure 6.
The buffering water molecule located between propionate oxygens (O1A and O2D) of heme a3 and protonatable nitrogen (ND1) of His291. Larger tubes and ball represent the QM system. Dotted lines stand for hydrogen bonds; dashed arcs and circle represent atomic and probe sphere contours, respectively.
It turns out that the critical cavity pocket between the propionates that accommodate the water molecule nearest to the protonation site, see Fig. 6, sharply disappears as the probe radius becomes higher than 1.3–1.6 Å. Slightly different geometries would have different critical radius, but in all cases the probe sphere is eventually expelled from the region between the propionates, resulting in a dramatic change of the position of the boundary of the cavity in the region closest to QM system. In addition, the overall volume of the cavity also sharply decreases as the probe radius becomes larger. The smaller polarizable volume of water cavity requires significantly higher polarizability to reproduce the microscopic polarization energy , thus the dramatic increase of the dielectric parameter of the cavity.
The effect of the sharp decrease of volume of the cavity pocket between the propionates as the probe radius becomes larger is demonstrated in Fig. 5d, where the volume of the overlap of the MEAD cavity and a sphere of radius of 1.8 Å centered at the position of the water molecule between two propionates is shown as a function of probe radius used to calculate the cavity. The volume of the pocket decreases sharply when the probe radius becomes larger roughly 1.2 Å.
In order to avoid the decrease of the volume of the cavity beyond its ability to accommodate the experimentally observed water molecules, we used a modified algorithm for cavity definition. In this inclusive algorithm, the cavity boundary is defined by water atomic spheres centered at the position of experimentally observed water molecules (see Appendix A for details). For a sufficiently large radius of water atomic spheres (e.g., 1.8 Å), the volume of the cavity is always larger than the minimum volume needed to accommodate all water molecules. Thus, the cavity dielectric constant obtained with the modified cavity definition can be considered as a lower limit of the result for a given set of probe and atomic radii of the QM system. The behavior of the dielectric constant of the cavity for this modified algorithm is shown in Fig. 5c.
It is important that the results for dielectric constant for probe radius below 1.2 Å are stable for both the MEAD and the modified algorithms (for small probe radii, the two algorithms are essentially identical), and the hence the obtained value can be considered as a reasonable well-defined phenomenological parameter of the model.
As seen from Figs. 5b, 5c, for probe radius below roughly 1.2 Å, the dielectric constant of the cavity becomes a well defined property, determined in a stable computational procedure, with the value in the range of 10–15. The too small values of the probe radius, however, have little physical meaning because the probe sphere models a solvent molecule which cannot be significantly smaller than 1.4 Å. Therefore, for a given set of atomic radii (Amber99), the appropriate (maximum) value of the probe radius can be taken to be 1.25 Å. The same optimal value for the parameter was obtained in morphological study of cavities in globular proteins.48 For this set of continuum parameters, the protein dielectric constant for all protein structures used in calculations is approximately 2.7 [Fig. 5a]. The cavity dielectric constant is varied from 11 to 16 depending on the average structure and cavity definition algorithm [see Figs. 5b, 5c]. The value is 10–13 if the crystal structure is used.
Optimal atomic radii for a standard probe radius
As shown previously, the combination of the probe, 1.25 Å, and standard protein atomic radii results in a stable computational procedure for determining the phenomenological dielectric parameters of the protein and water cavity that reproduce microscopic polarization free energies. It is recognized, however, that the determined values still depend on the protein atomic radii used for the modeling. This dependence reflects the phenomenological nature the continuum model. In a meaningful phenomenological description, the dependence of the results on the parameters of the model is expected to be reasonably slow, yet the dependence itself always remains. (In the above calculations, we were able to determine the range of parameters where the dependence on the probe radius is relatively slow, and thus acceptable for phenomenological description.) As shown below, the use of standard atomic radii, even in combination with probe 1.25 Å, although acceptable computationally, is not entirely satisfactory on the physical grounds; we therefore further explored optimization of the atomic radii of the protein.
The problem with standard radii can be recognized in the details of the structure shown in Fig. 6. According to the Amber99 force field, the van der Waals radius of the histidine δ nitrogen is 1.82 Å, while the equilibrium distance between observed water oxygen and the protonatable nitrogen is only 2.85 Å. Hence, the maximum size of probe sphere centered at the position of experimentally observed water should be about 1.0 Å. Recognizing that the probe sphere represents real water molecules in the protein, such a small radius is not consistent with its physical meaning.
More generally, one finds that for the commonly used continuum parameters,3, 21, 40, 44 the sum of the probe and atomic radius significantly exceeds the equilibrium interatomic distance between given protein atom and water oxygen observed in the x-ray data. The reason for this is that internal water molecules form strong hydrogen bonds with protein structure,6, 7 but commonly used parameters do not properly take into account this effect. The conventional probe radius of 1.4 Å corresponds to approximately the half of average oxygen-oxygen distance in the bulk water, whereas water in proteins may form stronger hydrogen bonds and approach closer to protein atoms. Thus, to model such effects, either the probe radius should be decreased, as we did earlier, or protein atomic radii should be decreased. The latter possibility seems to be physically more reasonable and, hence, is explored next.
The probe radius is now fixed at 1.4 Å, while the atomic radii are varied by the scaling factor kvdW as R=kvdWRvdW, where R and RvdW are atomic and van der Waals radii (minimum position of the Lennard-Jones atomic potential), respectively. Thus, the atomic radii with kvdW=1 correspond to commonly used definition of the atomic radii.3, 21, 40, 44
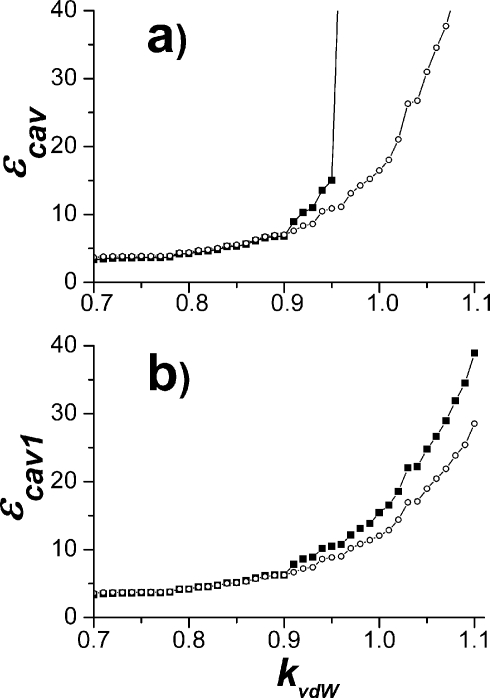
The obtained behavior of the dielectric constant of the cavity εcav and εcav1 as a function of the parameter kvdW is shown in Fig. 7. The dielectric parameter of the protein εp (not shown) remains approximately the same in the range of the parameters of interest. First of all, it is observed that for smaller protein radii, scaling factor kvdW<0.9, the dependence on the radii is relatively slow, as expected. The divergent behavior for kvdW>0.9 again reflects the fact the probe sphere of 1.4 simply does not fit in the pocket between propionates shown in Fig. 6. For smaller protein radii, the results are almost the same for both algorithms, again as expected, but the slow dependence remains.
Figure 7.
The dependency of cavity dielectric constant on atomic radii obtained with the probe radius 1.4 Å based on ⟨r⟩0 structure: (a) The exclusive cavity definition and (b) the inclusive cavity definition. The line with filled boxes represents calculations when atomic radii of all atoms are uniformly scaled by the parameter kvdW (see text). The line with open circles was obtained in calculations when radius of the δ nitrogen of His291 was only varied by the parameter kvdW; while the ProtOr value (Ref. 50) 1.28 Å is assigned for the radius of two closest propionate oxygens (Fig. 6), atomic radii of the rest correspond to van der Waals radii (Amber99).
The remaining slow dependence of the dielectric of the cavity on the protein radii is mainly determined by how closely the cavity boundary approaches the protonation site of the QM system—in our case δ-N of His291, see Fig. 6. The open circle data in Fig. 7 show that indeed this is the case. The dielectric constant of the cavity is changing now in the range of 3–6. This remaining dependence on the boundary position cannot be eliminated. Naturally, for smaller atomic radii, the cavity is bigger, and therefore the corresponding dielectric constant is smaller. As seen from Fig. 7, the combination of probe, 1.4 Å, and reduced protein radii, with parameter kvdW in the range from 0.7 to 0.9, is another acceptable set from the computational standpoint (i.e., dielectric constant is relatively slowly varying function here).
If one takes the scaling parameter 0.8, however, the radius of the protonatable nitrogen of His291, Fig. 6, becomes equal to 1.45 Å (instead of original 1.82 Å) which is exactly the value needed to place the probe sphere of radius 1.4 Å at the distance 2.85 Å—the distance between N and the water oxygen seen in the x-ray data.
It is interesting to note that this value of N radius determined from the x-ray data is almost identical to that from the ProtOr (Ref. 50) parameter set for hydrogen bonded atoms, 1.48 Å; for propionate oxygens, the ProtOr value is 1.28 Å, which also fits the 1.4 Å water sphere in the critical cavity pocket (Fig. 6). The ProtOr parameters have been derived by intermolecular distance analysis of large number of organic compounds, and appear to be reasonable choice since these atomic radii account for hydrogen bonding of the atomic groups which are clearly present in our case. The seemingly small values of the dielectric constant for water cavity determined here, and in the previous section, are discussed in the next section.
CONCLUSIONS AND DISCUSSION
We have analyzed the charge insertion process that models deprotonation of His291 residue of CuB catalytic center of CcO. MD simulations of the enzyme with different water content have been carried out and compared with the results of the continuum calculations.
The pure MD charging free energy (nonpolarizable force field is used, and no electronic polarization included explicitly) is reproduced by the standard continuum model with unphysically low protein dielectric constant εp=1.3. It is recognized that such a small dielectric constant reflects the fact that nonpolarizable force field describes only the nuclear part of polarization. The same effect was observed in other studies.8, 16, 17, 39, 46 When the electronic polarization (εel=2.0) energy is added explicitly to nuclear part obtained in MD (MDEC method), for dry protein the continuum model reproduces microscopic reaction-field energy with dielectric constant εp=2.6–2.8. These values are significantly lower than 4—a value commonly assigned for the protein dielectric constant in PB calculations.3, 21, 40, 44, 45 Given the discrepancy, one should bear in mind that the “true” value of the dry protein medium is not known with certainty experimentally; on the other hand, our MD simulations (trajectories of tens of ns long) by no means cover long time-scale dielectric relaxation processes of the protein which can extend to microsecond or even to millisecond range (for dielectric relaxation time-scale discussion, see Refs. 51). The quantitative contribution of such structural relaxation processes to dielectric properties of proteins is unknown.
Several earlier theoretical studies18, 19 have shown that the dielectric relaxation near the protein surface of the protein can be significantly larger than in the protein interior; the fairly large (15–40) overall effective dielectric constant arises mainly from the motion of charged side chains. On the other hand, it has been also shown that when the contributions of ionized side chains on the surface are excluded (i.e., they are considered as a part of the solvent), the rest of the protein behaves as a low-dielectric medium with the dielectric constant 2–4.18, 19 For example, for the enzyme aspartyl-tRNA synthase, the dielectric constant of the protein was found to be in the range 3–6,14 using similar method as in this paper. The obtained relaxation dielectric constants are varied depending on the exact charge insertion site and the nature of the ligand. Our results are in a qualitative agreement with these simulations since the CuB–His291 site is located right in the middle of the enzyme where the protein polarizability is lower. Besides, the surface residues in our case are mostly neutral (i.e., they are not in the so-called standard state), as was determined previously from self-consistent field calculations, Ref. 35. The distribution of titratable residues for our model of CcO is close to that for the “ionized” protein model47 of cytochrome c for which the estimation εp=2.9 remarkably correlates with our result.
Our low dielectric results are also consistent with dielectric measurements on several other systems. For example, dry collagen fibers have a static dielectric constant of 2–3 (for solvent contents of 15%–20%).52 Very dry powders of ovalbumin (less than 10% water) have a static dielectric constant of 2–4.53 A dielectric constant of about 2 was reported for lysozyme powders with solvent contents below 10%.54 Although, another measurement (assuming a reasonable value of 2–2.5 for the high-frequency dielectric constant) gave a higher estimate of about 3.5–4.6 Linear fits of experimentally determined redox potentials for cytochrome b5 mutants were best reproduced with dielectric constants 2–4.55
Summarizing, the low dielectric constant 2.6–2.8 obtained in our calculations for the dry protein is consistent with other previous theoretical and experimental studies which also find that the dielectric constant of dry proteins is lower than 4.
When the large water cavity located near His291 site is filled with water, the nonlinear polarization response was observed. The significant nonlinearity (∼10% of the total response) reflects the microscopic details of the nonlinear medium dynamics, and cannot be accurately described in terms of a linear continuum model. That means that the continuum model parameters adjusted to reproduce the microscopic reaction-field energy will not precisely reproduce the microscopic electrostatic potential at the atomic positions of the QM system.
The effective dielectric constant of the water cavity εcav in the continuum model was determined as a parameter that best reproduces the polarization (reaction-field) energy of microscopic simulations. The value of this dielectric parameter can be strongly model dependent. The problem arises mainly due to hard-sphere simplistic modeling of the protein cavities.
Thus standard parameters (Amber van der Waals radii and probe 1.4 Å) give, in our case, inconsistent values for dielectric of the cavity in the wide range from 14 to infinity (depending on the molecular configuration used) because this parametrization gives unphysically small cavities. The volume of the water cavity generated by the standard MEAD procedure turns out to be several times smaller than one required to accommodate all experimentally observed water molecules in the cavity. Due to smaller volume of the cavity, larger values of dielectric constant of the cavity were required to reproduce the microscopic polarization energy.
To determine more physically relevant and well-defined values of εcav, we have optimized the parameters of the continuum model. With Amber atomic radii, a satisfactory cavity size and convergence for all three examined structures (the protonated crystal structure43 and the initial and final state average structures) is only achieved using probe radius as small as 1.25 Å. The same optimal value for the parameter was obtained in morphological study of cavities in globular proteins.48 The cavity dielectric constant in this case is 11–16 depending on the average structure and cavity definition algorithm used and 10–13 if the crystal structure is used.
To reproduce physically more realistic cavity size and shape, the atomic radii were optimized, and the best agreement with experimental data was found for radii similar to the ProtOr atomic set,50 which accounts for hydrogen bonding. The continuum procedure with ProtOr (Ref. 50) radii of protein atoms in the critical water pocket (Fig. 6) and conventional probe size 1.4 Å appears to represent the most appropriate continuum model. The value of cavity dielectric constant determined with this parametrization is in the range 3–6 depending only on the parameter of His291 δ-nitrogen. If ProtOr parameter is also accepted for this protonatable nitrogen, the cavity dielectric property is converged on the value of 4. Such an unexpectedly low polarizability of the internal water, although counterintuitive, in fact, is supported experimentally.6, 7 According to interpretation of Bone and Pethig,6, 7 the internal water molecules bounded to the protein structure by two or more hydrogen bonds are tightly incorporated into the vibrating protein structure and have similar polarization properties as the dry protein itself. Such a tight hydrogen binding is consistent with the requirement that water molecule inside the protein has lower free energy than in a bulk, where each water molecule forms four hydrogen bonds.56
Summarizing, we have clearly demonstrated the difficulties involved in the parametrization of the continuum electrostatic models of proteins. The question arises whether the continuum models should be abandoned due to these problems. Unfortunately, the fully microscopic pKa calculations on a system with several (typically over a hundred) coupled titratable sites2, 35 are not feasible at present. The continuum electrostatics, despite all its phenomenological character and uncertainties discussed in this paper, is still needed, because this is the only practical way to perform such calculations; obviously, more studies of this challenging problem are needed. Apparently, more accurate treatment of water molecules that are hydrogen bonded to the protonation site is needed by including them into the QM system. Also, the long time-scale (order of milliseconds) dielectric relaxation processes should be somehow accounted for in the simulation.
ACKNOWLEDGMENTS
This work has been supported in part by the NSF Grant No. PHY 0646273 and NIH GM054052. We would like to thank our colleagues Motomichi Tashiro and Dragan Popovic for providing data for cytochrome c oxidase; we also thank Dragan Popovic for his help with continuum electrostatic calculations.
APPENDIX A: COMPUTATIONAL DETAILS
The system
The cytochrome c oxidase structure and topology are mainly the same as in Ref. 57. The dry CcO is modeled by only subunits A and B taken from the fully reduced bovine heart cytochrome c oxidase structure (Tsukihara et al.,43 PDB code 1V55) and initially protonated according to the standard protonation state of the residues.58 The partial charges of the redox centers, heme a, heme a3, CuA, and CuB, were obtained by fitting the electrostatic potential in a Hartree-Fock calculation with the 6-31G* basis set. The calculations were separately performed for each of the redox centers together with their respective ligating residues. Thus, His61A and His378A were included to the heme a group, and His376A was included to the heme a3 group. For the binuclear CuA center, Cys196B, Cys200B, His161B, and His204B were calculated together with two copper atoms, and for the CuB complex (QM system), imidazole rings of His290A, His291A, and His240A cross-linked to Tyr244A were calculated with a copper atom, for all centers maintaining the geometry of the crystal structure. The truncated carbon atoms were substituted by methyl groups. In these calculations, CuA and heme a were oxidized and heme a3 and CuB were reduced. The protonation states of the titratable residues were then determined by the electrostatic continuum method of Popovic and Stuchebrukhov.35 The titratable residues with a proton occupancy larger than ∼0.3 were treated as fully protonated, while all others as deprotonated, so as to make the system electrostatically neutral and to avoid partial proton occupancies which cause ambiguities in the MD simulations. The titration states of the important residues are as follows: All the propionates of hemes a and a3 are deprotonated, Arg438A and 439A are protonated, Asp364A and Glu242A are protonated, and His290A and His291A are protonated in the δ position. (The partial charges of the redox centers are available in the supporting information of the work.57) The charge distribution of the CuB center (QM system) corresponding to deprotonated His291 was also found in the Hartree-Fock calculation. The structure and topology of the CcO with internal water were obtained exactly in the same way as for the dry CcO with only the difference that 42 water molecules were added to the system. Residue numbers of the oxygen atoms forming the internal water, according to the crystal structure order,43 are as follows: 10, 15, 16, 17, 19, 20, 22, 23, 24, 31, 32, 33, 34, 35, 38, 40, 41, 42, 44, 46, 48, 54, 55, 63, 111, 165, 179, 220, 221, 228, 258, 326, 369, 371, 642, 683, 684, 702, 716, 2004, 2288, and 2574. The internal water, in fact, does not correspond to a single continuous cavity. Half of these 42 water molecules constitute the main closed cavity located right above the QM system, whereas another half form two possible proton exit channels.36 Though only few of these 42 molecules considerably contribute to the water polarization effect, the rest of the water is necessary to avoid serious deviation of the system from the crystal structure geometry.
MD simulations
For our simulations, we used the GROMACS molecular dynamics package59 with the Amber force fields ported by Sorin and Pande.60 A prior computational test has shown that all energy terms calculated by the MD package AMBER7 (Ref. 58) and GROMACS (Ref. 59) for the same configuration of the dry CcO coincide with high precision. The TIP3P model was used for the internal water.
The initial configurations for MD runs were obtained by the position minimization of all released atoms in accord with applied constraints. Three different constraint models [(A), (B) and (C)] were tested (see Sec. 3C). All simulations were done in vacuum with no periodic boundary condition. The Berendsen thermostat with reference temperature of 298 K and coupling constant of 0.2 ps was applied. Covalent bonds to hydrogens were constrained with SHAKE algorithm and the time step was 2 fs.
All simulations were carried out with no cutoff (all “nonbonded” interactions are taken into account), except for only one test simulation with cutoff 15 Å. Due to a long protein relaxation time and the need for careful long-range interaction treatment, the equilibration of our systems was done in few stages. First, 20–25 ns MD run was carried out for the structure relaxation for each system in the initial (protonated) state. To equilibrate long-range electrostatic interactions for all intermediate λ including the final (deprotonated) state of the system, the MD run of 5–15 ns was done starting from the relaxed configuration. Then 5 ns trajectories were collected for analysis.
Continuum calculations
To analyze charge insertion with the continuum model, finite-difference Poisson calculations were performed for three structures (the protonated crystal structure and the initial and final average structures) for each system. The protonated crystal structures, rcs, were obtained by minimization of the hydrogen positions in the systems. The average structures ⟨r⟩0 and ⟨r⟩1 were obtained by MD simulations of the systems in the initial and final states, respectively. Both atomic charges and radii were taken from the force field parametrization used in MD simulations. Thus, atomic radii were defined via Lennard-Jones parameters [AMBER99 (Ref. 29)] as minimum positions of the van der Waals interaction. As described in Appendix B, only charge differences of the QM system are necessary for calculations of the reaction-field free energy term. The molecular surfaces were constructed using variable probe and atomic radii (see Secs. 3E, 3F). The Poisson equation was solved by a three-step grid focusing procedure40, 61 with the finest grid spacing of 0.25 Å.
Calculations for the dry protein were done by the SOLINPROT program which is part of the MEAD package.40 For continuum calculations of the protein with water cavity, we modified the original SOLINPROT code in order to independently vary the dielectric constant of the specified cavity. The modified code enables one to describe the system by four different dielectric constants defining polarizabilities of the QM system, protein, cavity, and external solvent. Two alternative procedures for the cavity definition were implemented. In fact, both of them determine which grid points of the finite-difference procedure are inside of atomic spheres preset by radii and positions of explicit water atoms. However, they differently treat grid points belonging at once to both the protein region and water atomic spheres. These grid points are treated as a protein in the first procedure but as a cavity in the second procedure, i.e., such grid points are excluded from the cavity region in the first procedure but included into the cavity region in the second one. In the present work, these two different ways of cavity definition are referred to as the exclusive and inclusive cavity definition algorithms, respectively. The van der Waals radius of 1.8 Å of TIP3P model and water oxygen positions of examined structures were used for the definition of water spheres. It should be noted here that, according to the original SOLINPROT code, the grid points which do not belong to the QM-system region as well as the protein region are treated as the external solvent with the dielectric constant value εext. Hence, the modified PB procedure based on the “exclusive” cavity definition algorithm exactly corresponds to the original SOLINPROT program at the value of the cavity dielectric constant εcav=εext. Thus, the exclusive algorithm corresponds to the conventional way of the internal cavity definition and referred in the paper also as a “standard” algorithm.
In all continuum calculations, a dielectric constant of 1 was specified for the QM system, and the value of the MDEC parameter εel for the external solvent εext=εel. For estimation of the electronic polarization effect , the value of εel was assigned also for the protein and cavity dielectric constants, i.e., in this case the value of the electronic dielectric constant was specified for the whole space, except the QM-system region. The value of 2.0 estimated for cytochrome c (Ref. 10) was accepted for the dielectric constant of the electronic continuum εel. The protein and cavity dielectric constants were variable parameters in calculations of the total reaction-field free energy (see Secs. 3E, 3F).
APPENDIX B: REACTION-FIELD ENERGY CALCULATION IN THE CONTINUUM MODEL
The reaction-field energy of charging is given by Eq. 4. In the linear response approximation, one can explicitly perform the integration over lambda to obtain the following:
| (B1) |
where Φi(λ=1) is reaction field in the final state [see Eq. 3] at the position of ith solute atom, Φi(λ=1)=∑jKijΔqj, and Kij is a medium susceptibility to introduced charges Δqi. In terms of the microscopic model of the polarizable medium, the susceptibility is expressed via fluctuations of the reaction field,37 whereas, in terms of the continuum model, Kij is a complicated function of dielectric constants and parameters defining dielectric boundaries. Important point is that the energy of our interest is quadratic in charge increments Δqi.
On the other hand, the total solvation energy G of a QM system with charges {qi} in the continuum model has the following form:
| (B2) |
Here, q stands for a full set of the solute atomic partial charges {qi}; Qμ is charge of the polarizable medium (protein and solvent), where μ runs over all atoms of the medium; Giμ is Green’s function of the Poisson differential equation at positions of the atom i and μ, ; and the susceptibilities Kiμ and Kij are determined by solving Poisson equation and define the polarizable medium response on the protein and solute charges, respectively. If the external charges Qμ are absent, only the last term in Eq. B2 remains, which is identical to the reaction-field energy of our interest, Eq. B1, if charges {qi} are formally assigned values {Δqi}. This provides an easy calculation method of the reaction-field energy of charging by using standard PB packages, which typically evaluate expression shown in B2. Namely, the continuum ΔGrf energy is obtained as the reaction-field term of continuum PB calculation with solute partial charges set up to {Δqi}.
It is worth noticing that the reaction-field energy of charging [Eq. B1] is not equivalent to a difference of the reaction-field energies for the QM system in the final and the initial charge states. Indeed, the solvation free energy difference is
| (B3) |
Here, q0 and q1 stand for the initial and final charge sets ( and ) of the solute, respectively; Δq stands for the set of solute charge differences {Δqi}. One can see that even when the external charges Qμ are absent, i.e., there is no permanent protein field, the difference in solvation energies contains a linear term [second term in Eq. B3] in addition to the term of our interest [the third term in Eq. B3].
References
- Warwicker J. and Watson H., J. Mol. Biol. 10.1016/0022-2836(82)90505-8 157, 671 (1982); [DOI] [PubMed] [Google Scholar]; Davis M. E. and McCammon J. A., Chem. Rev. (Washington, D.C.) 10.1021/cr00101a005 90, 509 (1990); [DOI] [Google Scholar]; Gunner M. R. and Honig B., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.88.20.9151 88, 9151 (1991); [DOI] [PMC free article] [PubMed] [Google Scholar]; Honig B. and Nicholls A., Science 10.1126/science.7761829 268, 1144 (1995); [DOI] [PubMed] [Google Scholar]; Beroza P. and Case D. A., J. Phys. Chem. 10.1021/jp9623709 100, 20156 (1996). [DOI] [Google Scholar]
- Bashford D. and Karplus M., Biochemistry 10.1021/bi00496a010 29, 10219 (1990). [DOI] [PubMed] [Google Scholar]
- Popovic D. M., Quenneville J., and Stuchebrukhov A. A., J. Phys. Chem. B 109, 3616 (2005). [DOI] [PubMed] [Google Scholar]
- Schutz C. N. and Warshel A., Proteins 10.1002/prot.1106 44, 400 (2001). [DOI] [PubMed] [Google Scholar]
- Antosiewicz J., McCammon J. A., and Gilson M. K., J. Mol. Biol. 10.1006/jmbi.1994.1301 238, 415 (1994). [DOI] [PubMed] [Google Scholar]
- Bone S. and Pethig R., J. Mol. Biol. 10.1016/0022-2836(82)90477-6 157, 571 (1982). [DOI] [PubMed] [Google Scholar]
- Bone S. and Pethig R., J. Mol. Biol. 10.1016/0022-2836(85)90096-8 181, 323 (1985). [DOI] [PubMed] [Google Scholar]
- Gilson M. K. and Honig B. H., Biopolymers 10.1002/bip.360251106 25, 2097 (1986). [DOI] [PubMed] [Google Scholar]
- Sharp K. and Honig B., Annu. Rev. Biophys. Biophys. Chem. 10.1146/annurev.bb.19.060190.001505 19, 301 (1990); [DOI] [PubMed] [Google Scholar]; Simonson T. and Brooks C. L., J. Am. Chem. Soc. 10.1021/ja960884f 118, 8452 (1996). [DOI] [Google Scholar]
- Simonson T. and Perahia D., J. Am. Chem. Soc. 10.1021/ja00135a018 117, 7987 (1995). [DOI] [Google Scholar]
- Miyashita O., Onuchic J. N., and Okamura M. Y., Biochemistry 42, 11651 (2003). [DOI] [PubMed] [Google Scholar]
- Muegge I., Schweins T., Langen R., and Warshel A., Structure (London) 4, 475 (1996). [DOI] [PubMed] [Google Scholar]
- Krishtalik L., Kuznetsov A., and Mertz E., Proteins 28, 174 (1997). [DOI] [PubMed] [Google Scholar]
- Archontis G. and Simonson T., J. Am. Chem. Soc. 10.1021/ja010716+ 123, 11047 (2001). [DOI] [PubMed] [Google Scholar]
- Simonson T., Archontis G., and Karplus M., J. Phys. Chem. B 10.1021/jp991354j 103, 6142 (1999). [DOI] [Google Scholar]
- Simonson T., Carlsson J., and Case D., J. Am. Chem. Soc. 10.1021/ja039788m 126, 4167 (2004). [DOI] [PubMed] [Google Scholar]
- Archontis G. and Simonson T., Biophys. J. 10.1529/biophysj.104.055996 88, 3888 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonson T. and Perahia D., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.92.4.1082 92, 1082 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonson T., J. Am. Chem. Soc. 10.1021/ja980071m 120, 4875 (1998); [DOI] [Google Scholar]; Simonson T., Int. J. Quantum Chem. 73, 45 (1999); [DOI] [Google Scholar]; Pitera J., Falta M., and Van Gunsteren W., Biophys. J. 80, 2546 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wikstrom M., Curr. Opin. Struct. Biol. 10.1016/S0959-440X(98)80127-9 8, 480 (1998); [DOI] [PubMed] [Google Scholar]; Gennis R. B., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.95.22.12747 95, 12747 (1998); [DOI] [PMC free article] [PubMed] [Google Scholar]; Michel H., Behr J., Harrenga A., and Kannt A., Annu. Rev. Biophys. Biomol. Struct. 27, 329 (1998); [DOI] [PubMed] [Google Scholar]; Bloch D., Belevich I., Jasaites A., Ribacha C., Puustinen A., Verkhovsky M. I., and Wikstrom M., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0306036101 101, 529 (2004); [DOI] [PMC free article] [PubMed] [Google Scholar]; Ruitenberg M., Kannt A., Bamberg E., Fendler K., and Michel H., Nature (London) 417, 99 (2002); [DOI] [PubMed] [Google Scholar]; Gennis R. B., Front. Biosci. 9, 581 (2004). [DOI] [PubMed] [Google Scholar]
- Popovic D. M. and Stuchebrukhov A. A., FEBS Lett. 566, 126 (2004). [DOI] [PubMed] [Google Scholar]
- Fadda E., Chakrabarti N., and Pomes R., J. Phys. Chem. B 109, 22629 (2005); [DOI] [PubMed] [Google Scholar]; Olsson M. H. M., Sharma P. K., and Warshel A., FEBS Lett. 579, 2026–2034 (2005). [DOI] [PubMed] [Google Scholar]
- Simonson T., Perahia D., and Brunger A. T., Biophys. J. 59, 670 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- King G., Lee F., and Warshel A., J. Chem. Phys. 10.1063/1.461760 95, 4366 (1991). [DOI] [Google Scholar]
- Sham Y., Muegge I., and Warshel A., Biophys. J. 74, 1744 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frohlich H., Theory of Dielectrics (Clarendon, Oxford, 1949); [Google Scholar]; Warshel A., Russell S. T., and Churg A. K., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.81.15.4785 81, 4785 (1984); [DOI] [PMC free article] [PubMed] [Google Scholar]; Simonson T., Rep. Prog. Phys. 10.1088/0034-4885/66/5/202 66, 737 (2003); [DOI] [Google Scholar]; Smith P., Brunne R., Mark A., and van Gunsteren W. F., J. Phys. Chem. B 97, 2009 (1993); [Google Scholar]; Nakamura H., Q. Rev. Biophys. 29, 1 (1996). [DOI] [PubMed] [Google Scholar]
- Sham Y. Y., Chu Z. T., and Warshel A., J. Phys. Chem. B 10.1021/jp963412w 101, 4458 (1997). [DOI] [Google Scholar]
- Cornell W., Cieplak P., Bayly C., Gould I., Merz K., Ferguson D., Spellmeyer D., Fox T., Caldwell J., and Kollman P., J. Am. Chem. Soc. 10.1021/ja00124a002 117, 5179 (1995). [DOI] [Google Scholar]
- Wang J., Cieplak P., and Kollman P. A., J. Comput. Chem. 21, 1049 (2000). [DOI] [Google Scholar]
- Jorgensen W. L. and Tirado-Rives J., J. Am. Chem. Soc. 10.1021/ja00214a001 110, 1657 (1988); [DOI] [PubMed] [Google Scholar]; Mackerell A. D., Bashford D., Bellott M., Dunbrack R., Evanseck J., Field M., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., W. E.ReiherIII, Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., and Karplus M., J. Phys. Chem. B 10.1021/jp973084f 102, 3586 (1998). [DOI] [PubMed] [Google Scholar]
- Leontyev I. V., Vener M. V., Rostov I. V., Basilevsky M. V., and Newton M. D., J. Chem. Phys. 10.1063/1.1605944 119, 8024 (2003). [DOI] [Google Scholar]
- Vener M. V., Leontyev I. V., and Basilevsky M. V., J. Chem. Phys. 10.1063/1.1605945 119, 8038 (2003). [DOI] [Google Scholar]
- Leontyev I. V. and Stuchebrukhov A. A., J. Chem. Phys. 130, 085102 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Buono G., Figueirido F., and Levy R., Proteins 20, 85 (1994); [DOI] [PubMed] [Google Scholar]; Smith P. and van Gunsteren W. F., J. Chem. Phys. 10.1063/1.466975 100, 577 (1994); [DOI] [Google Scholar]; Dejaegere A. and Karplus M., J. Phys. Chem. 10.1021/jp952332+ 100, 11148 (1996); [DOI] [Google Scholar]; Hummer G., Pratt L., and Garcia A., J. Am. Chem. Soc. 10.1021/ja971148u 119, 8523 (1997). [DOI] [Google Scholar]
- Popovic D. M. and Stuchebrukhov A. A., J. Am. Chem. Soc. 126, 1858 (2004). [DOI] [PubMed] [Google Scholar]
- Popovic D. M. and Stuchebrukhov A. A., J. Phys. Chem. B 109, 1999 (2005). [DOI] [PubMed] [Google Scholar]
- Kubo R., Toda M., and Hashitsume N., Statistical Physics II: Nonequilibrium Statistical Mechanics (Springer-Verlag, Berlin, 1991), p. 146. [Google Scholar]
- Vener M. V., Leontyev I. V., Dyakov Y. A., Basilevsky M. V., and Newton M. D., J. Phys. Chem. B 10.1021/jp021396z 106, 13078 (2002). [DOI] [Google Scholar]
- Leontyev I. V. and Tachiya M., J. Chem. Phys. 10.1063/1.2423026 126, 064501 (2007). [DOI] [PubMed] [Google Scholar]
- Bashford D., in Scientific Computing in Object-Oriented Parallel Environments, edited by Ishikawa Y., Oldehoeft R. R., Reynders J. V. W., and Tholburn M. (Springer, Berlin, 1997), Vol. 1343, p. 233. [Google Scholar]
- Vener M. V., Tovmash A. V., Rostov I. V., and Basilevsky M. V., J. Phys. Chem. B 10.1021/jp061069h 110, 14950 (2006). [DOI] [PubMed] [Google Scholar]
- Leontyev I. V., Tovmash A. V., Vener M. V., Rostov I. V., and Basilevsky M. V., Chem. Phys. 10.1016/j.chemphys.2005.03.037 319, 4 (2005). [DOI] [Google Scholar]
- Tsukihara T., Shimokata K., Katayama Y., Shimada H., Muramoto K., Aoyama H., Mochizuki M., Shinzawa-Itoh K., Yamashita E., Yao M., Ishimura Y., and Yoshikawa S., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.2635097100 100, 15304 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson W. H., Peng C., Bashford D., Noodleman L., and Case D. A., Int. J. Quantum Chem. 61, 207 (1997); [DOI] [Google Scholar]; Li J., Nelson M. R., Peng C. Y., Bashford D., and Noodleman L., J. Phys. Chem. A 10.1021/jp980753w 102, 6311 (1998); [DOI] [Google Scholar]; Li J., Fisher C. L., Konecny R., Bashford D., and Noodleman L., Inorg. Chem. 10.1021/ic980731o 38, 929 (1999). [DOI] [PubMed] [Google Scholar]
- Ullmann G. M., Noodleman L., and Case D. A., JBIC, J. Biol. Inorg. Chem. 7, 632 (2002). [DOI] [PubMed] [Google Scholar]
- Vorobyov I. V., Anisimov V. M., and MacKerell A. D., J. Phys. Chem. B 10.1021/jp053182y 109, 18988 (2005); [DOI] [PubMed] [Google Scholar]; Anisimov V. M., Vorobyov I. V., Roux B., and A. D.MacKerell, Jr., J. Chem. Theory Comput. 3, 1927 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muegge I., Qi P. X., Wand A. J., Chu Z. T., and Warshel A., J. Phys. Chem. B 10.1021/jp962478o 101, 825 (1997). [DOI] [Google Scholar]
- Hubbard S. J., Gross K.-H., and Argos P., Protein Eng. 7, 613 (1994). [DOI] [PubMed] [Google Scholar]
- Connolly M. L., Int. J. Pept. Protein Res. 28, 360 (1986); [DOI] [PubMed] [Google Scholar]; Rashin A. A., Iofin M., and Honig B., Biochemistry 10.1021/bi00360a021 25, 3619 (1986); [DOI] [PubMed] [Google Scholar]; Eriksson A. E., Baase W. A., Zhang X.-J., Heinz D. W., Blaber M., Baldwin E. P., and Matthews B. W., Science 10.1126/science.1553543 255, 178 (1992); [DOI] [PubMed] [Google Scholar]; Eriksson A. E., Baase W. A., Wozniak J. A., and Matthews B. W., Nature (London) 10.1038/355371a0 355, 371 (1992). [DOI] [PubMed] [Google Scholar]
- Tsai J., Taylor R., Chothia C., and Gerstein M., J. Mol. Biol. 10.1006/jmbi.1999.2829 290, 253 (1999). [DOI] [PubMed] [Google Scholar]
- Song X., Chandler D., and Marcus R., J. Phys. Chem. 10.1021/jp960887e 100, 11954 (1996); [DOI] [Google Scholar]; Xu D., Phillips J. C., and Schulten K., J. Phys. Chem. 10.1021/jp960076a 100, 12108 (1996); [DOI] [Google Scholar]; Jordanides X., Lang M. S., and Fleming G., J. Phys. Chem. B 10.1021/jp9910993 103, 7995 (1999); [DOI] [Google Scholar]; Medvedev E. S., Kotelnikov A. I., Barinov A. V., Psikha B. L., Ortega J. M., Popovic D. M., and Stuchebrukhov A. A., J. Phys. Chem. B 112, 3208 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigera J. R., Vericat F., Hallenga K., and Berendsen H. J. C., Biopolymers 10.1002/bip.1979.360180105 18, 35 (1979). [DOI] [Google Scholar]
- Takashima S. and Schwan H. P., J. Phys. Chem. 69, 4176 (1965); [DOI] [PubMed] [Google Scholar]; Gascoyne P. and Pethig R., J. Chem. Soc., Faraday Trans. 10.1039/f19817701733 77, 1733 (1981). [DOI] [Google Scholar]
- Harvey S. C. and Hoekstra P., J. Phys. Chem. 10.1021/j100665a011 76, 2987 (1972). [DOI] [PubMed] [Google Scholar]
- Lippard S. J. and Berg J. M., Principles of Bioinorganic Chemistry (University Science Books, New York, NY, 1994), see Fig. 12.7, pg. 365, http://books.google.com/books?id=zGJtXzPINAUC&lpg=PA362&dq=Fe4S4+redox+potential&source=web&ots=gBK2N-tmA&sig=U76iNN3BQWb_ZoPeTb1LZwqBdXo&hl=en&sa+X&oi=book_result&resnum=10&ct=result#PPA365,M1; [Google Scholar]; Rodgers K. K. and Sligar S. G., J Am. Chem. Soc. 113, 9419 (1991). [Google Scholar]
- Head-Gordon T. and Johnson M. E., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0510593103 103, 7973 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tashiro M. and Stuchebrukhov A. A., J. Phys. Chem. B 109, 1015 (2005). [DOI] [PubMed] [Google Scholar]
- Case D. A., Pearlman D. A., Caldwell J. W., T. E.CheathamIII, Wang J., Ross W. S., Simmerling C. L., Darden T. A., Merz K. M., Stanton R. V., Cheng A. L., Vincent J. J., Crow-ley M., Tsui V., Gohlke H., Radmer R. J., Duan Y., Pitera J., Massova I., Seibel G. L., Singh U. C., Weiner P. K., and Kollman P. A., AMBER 7 Users’ Manual (University of California, San Francisco, 2002). [Google Scholar]
- van der Spoel D., Lindahl E., Hess B., van Buuren A. R., Apol E., Meulenhoff P. J., Tieleman D. P., Sijbers A. L. T. M., Feenstra K. A., van Drunen R., and Berendsen H. J. C., Gromacs User Manual, version 3.3, www.gromacs.org, 2006.
- Sorin E. J. and Pande V. S., Biophys. J. 10.1529/biophysj.104.051938 88, 2472 (2005); [DOI] [PMC free article] [PubMed] [Google Scholar]; http://chemistry.csulb.edu/ffamber/
- Bashford D. and Gerwert K., J. Mol. Biol. 10.1016/0022-2836(92)91009-E 224, 473 (1992). [DOI] [PubMed] [Google Scholar]