In situ Mechanical Properties of the Chondrocyte Cytoplasm and Nucleus

Abstract

The way in which the nucleus experiences mechanical forces has important implications for understanding mechanotransduction. Knowledge of nuclear material properties and, specifically, their relationship to the properties of the bulk cell can help determine if the nucleus directly experiences mechanical load, or if it is signal transduction secondary to cell membrane deformation that leads to altered gene expression. Prior work measuring nuclear material properties using micropipette aspiration suggests that the nucleus is substantially stiffer than the bulk cell (Guilak et al., 2000), whereas recent work with unconfined compression of single chondrocytes showed a nearly one-to-one correlation between cellular and nuclear strains (Leipzig and Athanasiou, 2008). In this study, a linearly elastic finite element model of the cell with a nuclear inclusion was used to simulate the unconfined compression data. Cytoplasmic and nuclear stiffnesses were varied from 1 to 7 kPa for several combinations of cytoplasmic and nuclear Poisson’s ratios. It was found that the experimental data were best fit when the ratio of cytoplasmic to nuclear stiffness was 1.4, and both cytoplasm and nucleus were modeled as incompressible. The cytoplasmic to nuclear stiffness ratio is significantly lower than prior reports for isolated nuclei. These results suggest the nucleus may behave mechanically different in situ than when isolated.

Introduction

How mechanical forces are experienced by the nucleus has important consequences for understanding mechanotransduction (Wang et al., 1993). Mechanotransduction is the process by which mechanical loads induce changes in the gene expression profile of a cell, which can ultimately alter cellular physiology and homeostasis. It has also been shown that alterations in the physical dimensions of the nucleus, resulting from an applied load on the tissue (Buschmann et al., 1996) or single cell (Leipzig and Athanasiou, 2008), correlate with changes in gene regulation. Previous investigation into mechanical characteristics of isolated nuclei suggest they behave like a viscoelastic material and are significantly stiffer than the cell as a whole (Guilak et al., 2000; Caille et al., 2002). However, these results are possibly influenced by the fact that the nuclei were removed from their in situ environment. The nuclear lamina, the framework for nuclear structure, is intimately linked to intermediate filaments positioned throughout the cytoplasm (Maniotis et al., 1997). Thus, mechanical properties of the nucleus may change when these connections are disrupted and the nucleus undergoes structural reorganization.

In this study, a finite element modeling approach was employed to obtain cytoplasmic and nuclear stiffness values which best match previously reported cellular and nuclear axial and lateral strains obtained during unconfined compression of single attached chondrocytes (Leipzig and Athanasiou, 2008). Based on the nearly one-to-one correlation of cellular and nuclear strains observed in that study, we hypothesized the in situ nuclear stiffness is similar to that of the cytoplasm. Further, effects of changing both cytoplasmic and nuclear Poisson’s ratios were explored to investigate the validity of the commonly used assumption of cellular incompressibility.

Materials and Methods

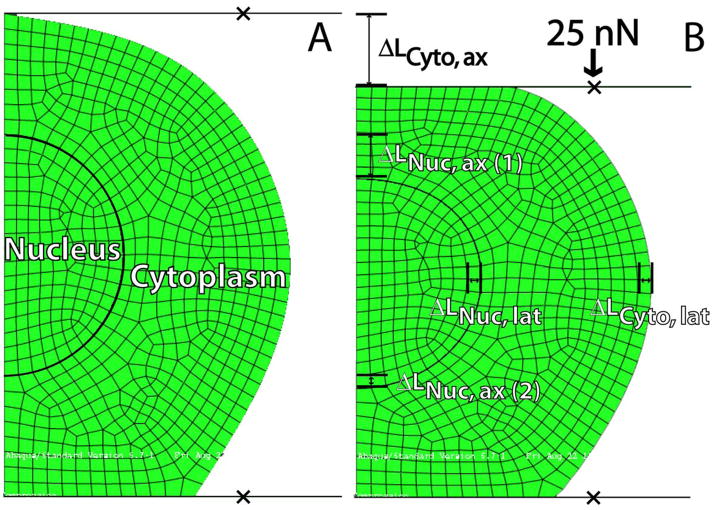
An axisymmetric model of the chondrocyte (height = 10 μm, width = 12 μm) with a nuclear inclusion (radius = 2.5 μm) was created using ABAQUS 6.7.1 (Fig. 1). The aforementioned geometric parameters were chosen to closely resemble an attached chondrocyte seeded for 3 hours (Leipzig and Athanasiou, 2005; Koay et al., 2008). Both nucleus and cytoplasm were modeled as isotropic linearly elastic solids. This elastic model was chosen since the experimental data for cytoplasmic and nuclear strains were reported at equilibrium (Leipzig and Athanasiou, 2008), corresponding to long-time behavior of a viscoelastic solid (Leipzig and Athanasiou, 2005). Along the cell bottom, 4 μm of membrane was placed in frictionless contact with a rigid substrate. Preliminary analysis showed substrate adhesiveness had no effect on the cytoplasmic and nuclear mechanical properties determined. Finally, the cell membrane was placed in frictionless contact with the compression platen. A reference point was created for the platen to which a 25 nN load was applied. The cytoplasm and nucleus consisted of 522 and 144 axially symmetric four node reduced integration continuum elements (CAX4R), respectively. This was determined sufficient for convergence, as a model containing 2123 and 561 elements (cytoplasm and nucleus, respectively) yielded identical results.

Figure 1.

Axisymmetric finite element depiction of a chondrocyte, with distinct nuclear and cytoplasmic regions, undergoing unconfined compression. In its undeformed state (A), the cell is considered to be 10 μm tall and 12 μm wide, with a spherical nuclear inclusion of radius 2.5 μm. The lateral and axial deformations of both the cytoplasm and nucleus were measured in response a 25 nN load applied onto the cell (B). The linear elastic mechanical properties of the cytoplasm and nucleus were varied parametrically, and a cost function (δ_RMS) value was calculated for each case in comparison to known experimental data (Leipzig and Athanasiou, 2008). (ax = axial; lat = lateral)

To determine the combination of cytoplasmic and nuclear stiffnesses and Poisson’s ratios that best matched observed cytoplasmic and nuclear strains (Leipzig and Athanasiou, 2008), a root-mean-square difference cost function was used, defined as:

$${\delta }_{\mathit{RMS}}=\sqrt{\begin{array}{l}{({\epsilon }_{\mathit{Axial}}^{\mathit{Model}}(\mathit{Nuc})-{\epsilon }_{\mathit{Axial}}^{\mathit{Experimental}}(\mathit{Nuc}))}^2+{({\epsilon }_{\mathit{Axial}}^{\mathit{Model}}(\mathit{Cyto})-{\epsilon }_{\mathit{Axial}}^{\mathit{Experimental}}(\mathit{Cyto}))}^2\\ +{({\epsilon }_{\mathit{Lateral}}^{\mathit{Model}}(\mathit{Nuc})-{\epsilon }_{\mathit{Lateral}}^{\mathit{Experimental}}(\mathit{Nuc}))}^2+{({\epsilon }_{\mathit{Lateral}}^{\mathit{Model}}(\mathit{Cyto})-{\epsilon }_{\mathit{Lateral}}^{\mathit{Experimental}}(\mathit{Cyto}))}^2\end{array}}$$

δ_RMS was calculated for each combination of material properties. Lower values of δ_RMS indicate model output more closely matched the previously reported data.

Briefly, as reported by Leipzig and Athanasiou (Leipzig and Athanasiou, 2008), cytoplasmic and nuclear strains were measured experimentally through analysis of immunocytochemistry of cells fixed under a 25 nN compressive load. Cytomechanical testing was performed using a previously validated creep cytoindentation apparatus (Leipzig and Athanasiou, 2005; Leipzig et al., 2006; Shieh and Athanasiou, 2006; Eleswarapu et al., 2007; Shieh and Athanasiou, 2007), which applies controlled compressive loads onto single adherent cells. Cell to platen contact was determined by a 5 nN preload, followed by compression to 25 nN. At equilibrium deformation, chondrocytes were fixed with paraformaldehyde. After fixation, a phalloidin stain was applied for the cytoskeleton and a Hoescht’s stain was applied for the nucleus. Both loaded and unloaded (control) cells were imaged with a confocal microscope, followed by 3-dimensional image reconstructions. The use of fluorescent staining to examine cellular and nuclear deformations and strains has been previously described in the literature (Knight et al., 1998; Knight et al., 2002).

In an initial coarse search, cytoplasmic and nuclear Young’s moduli were varied parametrically at 0.5 kPa increments from 1 to 7 kPa for combinations of Poisson’s ratios shown in Table 1. These search parameters were guided by literature values for Poisson’s ratios and cellular stiffness (Freeman et al., 1994; Leipzig and Athanasiou, 2005; Shieh and Athanasiou, 2006; Trickey et al., 2006; Leipzig and Athanasiou, 2008), as well as preliminary analyses confirming Young’s moduli less than 1 kPa and Poisson’s ratios less than 0.3 yielded higher δ_RMS values.

Table 1.

Effect of Poisson’s ratio combinations on cytoplasmic and nuclear stiffnesses for the initial coarse search. In the coarse search, cytoplasmic and nuclear stiffness values were each varied parametrically from 1 to 7 kPa, resulting in 169 different stiffness combinations for each set of Poisson’s ratio values. In the coarse search, it was observed that the ν_Cyto = ν_Nuc = 0.5 combination best fit the experimental data with the lowest cost function value, resulting in E_Y^Cyto = 3.5 kPa, E_Y^Nuc = 5 kPa. The similarity of “best fit” stiffnesses and cost function demonstrate that Poisson’s ratio had little effect on the ratio of cytoplasmic to nuclear stiffness.

Poisson’s Ratio		“Best fit” Stiffness
Cytoplasm	Nucleus	Cytoplasm (kPa)	Nucleus (kPa)	δRMS
0.3	0.3	4	4.5	0.03770
0.3	0.4	4	4.5	0.03360
0.4	0.3	3.5	5	0.03357
0.4	0.4	3.5	5	0.03018
0.4	0.5	4	4.5	0.02595
0.5	0.4	3.5	5	0.02627
0.5	0.5	3.5	5	0.02279

Based on results from the coarse search, Young’s moduli were refined to increment 0.25 kPa from 3 to 5.5 kPa for ν_Cyto = ν_Nuc = 0.5 and ν_Cyto = 0.4, ν_Nuc = 0.5. Simulations were also performed for the cell without a nuclear inclusion to examine the contribution of the nucleus. For these cases, the cell was considered to be an isotropic linearly elastic solid with the same initial physical dimensions as before. For the cell model, cost function values were calculated using only cytoplasmic axial and lateral strains.

Due to the inherent variability in any cell mechanics technique and analysis, the finite element model was examined for its sensitivity to slight changes in the experimental data of Leipzig and Athanasiou (Leipzig and Athanasiou, 2008). The following three cases were studied: 1) increased axial and lateral cytoplasmic strains by 5%; 2) decreased axial and lateral nuclear strains by 5%; 3) increased cytoplasmic strains by 5% and decreased nuclear strains by 5%. Finite element analysis was performed on the aforementioned cases for ν_Cyto = ν_Nuc = 0.5 to yield stiffness values for the cytoplasm and the nucleus.

Results

Table 1 shows minimum values computed from the cost function for each combination of Poisson’s ratios, and the values of cytoplasmic and nuclear Young’s moduli for which the minimum was obtained. From the initial coarse search, the ratio of cytoplasmic to nuclear stiffness was either ~1.4 (E_Y^Cyto = 3.5 kPa, E_Y^Nuc = 5 kPa) or ~1.1 (E_Y^Cyto = 4 kPa, E_Y^Nuc = 4.5 kPa) depending upon Poisson’s ratios used. The minimum δ_RMS, or case most closely matching the experimental data, occurred for ν_Cyto = ν_Nuc = 0.5, i.e., both cytoplasm and nucleus incompressible. Figure 1 shows the cell in its undeformed and deformed states for this minimum δ_RMS case. Comparing cases where cytoplasmic and nuclear Poisson’s ratios were held equal, there was little effect of Poisson’s ratio on δ_RMS, though the ν_Cyto = ν_Nuc = 0.3 case had different “best fit” Young’s moduli than the ν_Cyto = ν_Nuc = 0.4 or ν_Cyto = ν_Nuc = 0.5 cases.

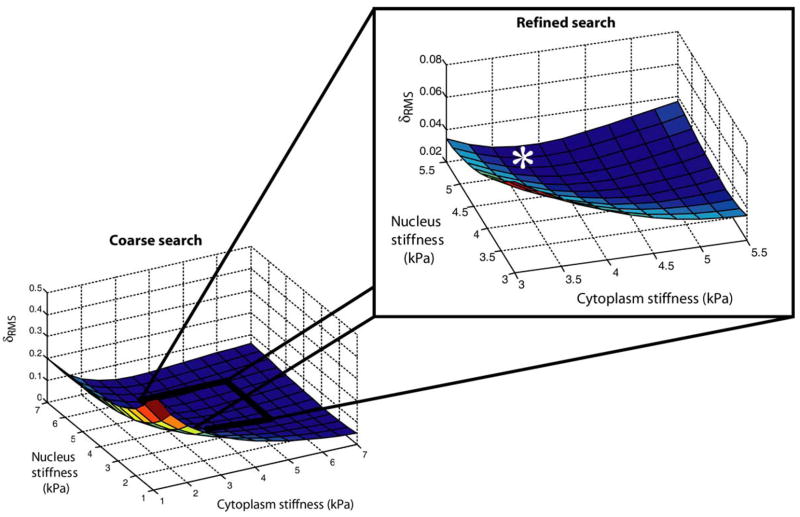
Figure 2 shows a 3-D plot of δ_RMS as a function of E_Y^Cyto and E_Y^Nuc for ν_Cyto = ν_Nuc = 0.5. In this refined search, the minimum Young’s moduli were determined to be E_Y^Cyto = 3.75 kPa and E_Y^Nuc = 5.25 kPa, with δ_RMS = 0.02276. In the refined search for ν_Cyto = 0.4 and ν_Nuc = 0.5, minimum Young’s moduli were determined to be E_Y^Cyto = 4.0 kPa and E_Y^Nuc = 4.75 kPa, with δ_RMS = 0.02572. Without a nuclear inclusion, E_Y^Cell = 4.25 kPa, which did not change for ν_Cell = 0.4 or 0.5.

Figure 2.

Cost function (δ_RMS) plots for the case of ν_Cyto = ν_Nuc = 0.5. In the initial coarse search, the elastic moduli of the cytoplasm and nucleus were varied from 1 kPa to 7 kPa, at 0.5 kPa increments. In the exploded view, the search was refined to range from 3 kPa to 5.5 kPa, at 0.25 kPa increments. A global minimum for δ_RMS was observed at E_Y^Cyto = 3.75 kPa, E_Y^Nuc = 5.25 kPa (indicated by the asterisk).

Finally, experimental strains were varied to ascertain the effects of the experimental measurements on the ratio of cytoplasmic to nuclear stiffnesses. Slight changes in the experimental data of Leipzig and Athanasiou (Leipzig and Athanasiou, 2008) did not yield substantial differences in the calculated stiffness for the cytoplasm and nucleus. In the case where the experimentally measured axial and lateral cytoplasmic strains were increased by 5%, the Young’s moduli were determined to be E_Y^Cyto = 3.0 kPa and E_Y^Nuc = 5.5 kPa. In the alternative case, where the experimentally measured axial and lateral nuclear strains were decreased by 5%, the Young’s moduli were determined to be E_Y^Cyto = 3.5 kPa and E_Y^Nuc = 6.0 kPa. Finally, when the cytoplasmic strains were increased by 5% and nuclear strains decreased by 5%, the Young’s moduli were determined to be E_Y^Cyto = 3.0 kPa and E_Y^Nuc = 6.0 kPa, yielding a nuclear to cytoplasmic stiffness ratio of 2.0.

Discussion

Using a finite element approach, this study investigated in situ mechanical properties of the nucleus. Young’s moduli and Poisson’s ratio were parametrically changed for the cytoplasm and nucleus, and predicted cellular and nuclear strains were compared to known experimental results during unconfined cytocompression (Leipzig and Athanasiou, 2008). It was found that the experimental data were best matched when E_Y^Cyto = 3.75 kPa, E_Y^Nuc = 5.25 kPa, and both cytoplasm and nucleus were incompressible. These results suggest the ratio of nuclear to cytoplasmic stiffness is less than previously reported for single cells (Guilak, 2000; Caille et al., 2002). Moreover, changing Poisson’s ratio had little effect on the model.

Examining nuclear mechanical properties is an important step toward understanding cellular mechanotransduction. Nuclear physical characteristics change in response to an applied load on native tissue (Guilak et al., 1995) or tissue engineered constructs (Lee et al., 2000). Enclosed within the nucleus, chromatin is organized by the nuclear lamina (Aebi et al., 1986). Due to cellular deformations, mechanical linkages between cytoskeleton and nuclear lamina may lead to changes in chromatin conformation/alignment and/or 3-D spatial orientation of transcription factors. Thus, understanding how the nucleus senses and responds to forces provides insight into possible gene regulatory mechanisms.

The results presented in this study have applicability to current finite element models of cell – matrix interactions. These models predict the local mechanical environment of chondrocytes under various loading conditions (Guilak and Mow, 2000; Wu and Herzog, 2000; Breuls et al., 2002; Wang et al., 2002). When considering the cell without a nuclear inclusion, cellular Young’s modulus was minimally greater than the cytoplasm itself. Moreover, the in situ difference between cytoplasmic and nuclear stiffnesses during compression is small, and variations in Poisson’s ratio had little effect on Young’s moduli (i.e. E_Y^Cyto = 3.75 kPa, E_Y^Nuc = 5.25 kPa for ν_Cyto = ν_Nuc = 0.5 versus E_Y^Cyto = 4 kPa, E_Y^Nuc = 4.75 kPa for ν_Cyto = 0.4, ν_Nuc = 0.5). These results suggest that assumptions of cellular homogeneity and incompressibility may be valid simplifications for theoretical models describing chondrocytes. Supporting these simplifications, no volume change has been measured experimentally in single chondrocytes subjected to unconfined compression at strain levels below ~30–35% (Koay et al., 2008).

Several explanations exist for why our results differ from previously reported nuclear and cellular stiffnesses. We observed a nuclear to cytoplasmic stiffness ratio of ~1.1 or ~1.4 depending on the assumed combination of Poisson’s ratios, whereas prior results from micropipette aspiration testing of chondrocytes and isolated nuclei suggest this ratio is 3 to 4 (Guilak et al., 2000). However, in comparison to the free-floating state in micropipette aspiration, cytoskeletal rearrangements during cell attachment for unconfined cytocompression may cause alterations in nuclear structure and decreased stiffness. Moreover, when tested in situ, connections between the nuclear lamina and cytoskeleton are intact, resulting in a more integrated mechanical framework between the cytoplasm and nucleus. Further, the cellular stiffness under compression is greater than previous micropipette aspiration results with single chondrocytes (Trickey et al., 2000), in which tensile forces dominate. Prior literature has confirmed that cell stiffness is greater during bulk cell compression than during local aspiration of the cell membrane (Trickey et al., 2000; Bader et al., 2002; Shieh and Athanasiou, 2006).

It is further important to note that the stiffness values for single chondrocytes calculated in this study coincide with measurements obtained by Knight and Bader (Knight et al., 2002) for cells compressed within alginate constructs. In both unconfined cytocompression and cell compression within constructs, single cells must withstand compressive forces applied onto the whole cell, and thus a similar mechanical response is expected. Additionally, the predicted stiffness value of the overall cell using our model is 2 to 3 times greater than previous unconfined compression results for single chondrocytes (Leipzig and Athanasiou, 2005; Shieh and Athanasiou, 2006). Since our finite element model represents the cell as an ellipsoid, which more accurately resembles the geometry of attached chondrocytes than a cylinder (Shieh et al., 2006), the increased stiffness is likely an effect of modeling the changing contact surface area. The contact area between the cell (represented by our geometry) and the platen in the compressed state at equilibrium is 28% of that obtained assuming the entire cell’s cross-section is in contact under compression (cylindrical geometry). Thus, for the same applied force, the stress experienced by our cell would be approximately 3.6 times greater than that of a cell with an assumed cylindrical geometry. Smaller contact area results in increased stress and, hence, greater cell stiffness.

Several assumptions were made for this model which could limit its representation of physical reality. First, the assumption of a spherical nucleus can potentially affect the resultant properties of the cytoplasm and nucleus. Changes in nucleus size, morphology, uniformity, and connections with the cytoplasm may alter the stress distributions applied on the nucleus, thereby changing the calculated stiffness of the nucleus. For instance, a larger contact area between the nucleus and cytoplasm could decrease the stress in the nucleus, resulting in a lower nuclear stiffness. In addition, preferential interactions between the nucleus and cytoskeleton could result in nonuniform nuclear deformations, changing the calculated stiffness values. In this study, we choose to assume a simple spherical geometry because previous finite element modeling (Vaziri and Mofrad, 2007) and experimental data (Guilak, 1995) have used or suggested, respectively, a spherical nucleus. An additional limitation is that the cell is assumed to be in frictionless contact with the platen, which is inherently difficult to verify experimentally. This may result in variations in cell stiffness and, thus, different cytoplasmic to nuclear stiffness ratios. However, as mentioned in the previous paragraph, the high cell stiffness reported in this study may also be due to a more accurate representation of cellular geometry (Koay et al., 2008). Finally, this model assumed both the cytoplasm and nucleus to be isotropic materials. Differences in the Poisson’s ratio between principal directions can alter the axial and lateral strains and, thus, the calculated mechanical material properties. However, the experimental results presented by Leipzig and Athanasiou (Leipzig and Athanasiou, 2008) suggest a deviation from isotropy only at loads 50 nN or greater. At the 25 nN load case, examined in this study, the experimental Poisson’s ratio values for the cell and nucleus were 0.45 and 0.42, respectively. These values have been confirmed with other experimental testing modalities, generally yielding Poisson’s ratios between 0.3 and 0.5 (Freeman et al., 1994; Shieh and Athanasiou, 2006; Trickey et al., 2006). Thus, based on previous experimental work at the low loads and strains examined in our model anisotropy was not considered. In the future, this model can be adapted to include consideration of varying nuclear morphologies, cytoskeletal and nuclear interactions, frictional contact between the cell and the compressing platen, and anisotropies.

In conclusion, this study elucidated a combination of chondrocyte cytoplasmic and nuclear stiffnesses and Poisson’s ratios which simulated previous results for unconfined cytocompression. In situ, nuclear stiffness was determined to be 40% more than the cytoplasm, which is lower than previously reported (Guilak et al., 2000; Caille et al., 2002). Moreover, little effect of Poisson’s ratio on the model’s behavior was observed, and the incompressible case best matched the prior experimental data. These results have implications in understanding the basis of cellular mechanotransduction.