Abstract
Studying the Brownian motion of a system driven by an external control from one macroscopic state to another macroscopic state, this paper presents the derivation of a nonlinear fluctuation-dissipation theorem (FDT). The new FDT relates the nonequilibrium work to the equilibrium free-energy difference in a very simple manner. It is valid wherever the Brownian dynamics is applicable. It recovers the well-known Crooks fluctuation theorem (CFT) within the quasiequilibrium regime where the dissipative work is nearly zero. It will also be shown that the CFT’s fundamental assumption of microscopic reversibility is not obeyed in experiments such as mechanically unfolding biological molecules, in which the external driving forces depend on the system’s coordinates.
The bridge from the nonequilibrium work to the equilibrium free-energy difference has been a subject of much interest in recent years. Such a bridge is necessary to relate the experimental data of forces and displacements to the intrinsic properties of the system in the unfolding studies of proteins and nucleic acids.1 It also serves as an effective and efficient method in the computations of free energy.2 In the current literature, Jarzynski equality3 (JE) and the undergirding Crooks fluctuation theorem4 (CFT) are taken as the bridge while questions have been raised5, 6, 7 about their applicability and range of validity. The self-consistency check of the CFT has suggested8 that the CFT and JE are valid only in the quasiequilibrium or linear response regime. In this paper, I will present the derivation of a new fluctuation-dissipation theorem (FDT) without invoking any assumption beyond the Brownian dynamics. I will also show that the assumption of microscopic reversibility, on which the CFT is based, is generally invalid outside the quasiequilibrium regime. This will establish that the CFT and JE are applicable only within the quasiequilibrium regime where the dissipative work is nearly zero. However, the new FDT is valid wherever the Brownian dynamics is applicable.
Let us start with the Langevin equation for the Brownian dynamics as follows:9
| (1) |
Here mi and xi are the atomic mass and coordinate of the ith degree of freedom, respectively. γ is the damping (frictional) constant. V is the potential energy of the system that is a function of all coordinates. ξi is the stochastic force acting on the ith degree of freedom. It is assumed to be Gaussian with the following characteristics:
| (2) |
Here kB is the Boltzmann constant. T is the absolute temperature. δij is the Kronecker delta and δ(t−t′) is the Dirac delta function. Fi is the external force component acting on the ith degree of freedom. The external force drives the system from state A at time t=0 to state B at time t=τ. For example, in a mechanical unfolding experiment, the two terminus atoms are subject to the external forces that are functions of the atomic coordinates and time. In general, Fi=Fi(x,t), where x={xi} is the collection of the atomic coordinates.
Now, we divide the time interval [0,τ] into N equal slices of width dt=τ∕N. In this, we have tn=ndt with n=0,1,…,N. For clarity, we omit the index for the degree of freedom and denote xn≜xi(tn), ∂Vn≜∂V(x(tn))∕∂xi, and Fn≜Fi(x(tn),tn). Then the discrete form of the Langevin equation 1 is
| (3) |
Noting the statistical characteristics of the stochastic term on the right hand side of Eq. 3, we have the transition probability between state xn at time tn and state xn+1 at time tn+1, namely, the probability for the system to be in state xn+1 at time tn+1 given that it is in state xn at time tn as follows:
| (4) |
Here the normalization factor Ω=(2kBTdt∕mγ)1∕2, which is independent of the system’s coordinates. Note that the Ito scheme is adopted in this paper for the discrete form of the Langevin equation in Eq. 3. If the Stratonovich scheme were adopted, Ω would have a very complex dependence on the coordinates through ∂Vn+1 and Fn+1. When that complex dependence is correctly accounted for, the Stratonovich scheme should agree exactly with the Ito scheme.9
Considering the dynamics of the system is Markovian, we have the probability for transition along a given path (x(t))=(x0,x1,…,xN) from state A (x0=xA) to state B (xN=xB) as follows:
| (5) |
where pe(xA)=exp(−βV(xA))∕ZA is the equilibrium probability distribution of the system when it is constrained to the macroscopic state A. ZA=exp(−βGA) is the partition function and GA is the free energy of that macroscopic state. β≜1∕kBT. The system is driven from state A to state B by the external force (F(t))=(F0,F1,…,FN).
The following question has been asked but not answered correctly in the current literature: What is the probability for the system to take the exact reverse path if the external driving force is tuned backward in time, ? Answering this question correctly requires particular attention to the subtle stochastic nature of the Brownian dynamics. Resembling exactly Eq. 4, the transition probability between state xN−n at time tn and state xN−n−1 at time tn+1 is
| (6) |
The probability for transition along the reverse path is
| (7) |
where pe(xB)=exp(βGB−βV(xB)) is the equilibrium probability of the system when constrained to the macroscopic state B. The relationship between the probabilities along the forward and reverse paths will become clear once we substitute the dummy index n in the sum on the second line of Eq. 7, l=N−n−1. Then,
| (8) |
Note that the indices are in different order than those of Eq. 5. The ratio between the two probabilities can be found as
| (9) |
In deriving the above equation, we made use of the fact that dt is infinitesimal so that
| (10) |
Examining the differentials in the exponent on the right hand side of Eq. 9, we note that the internal force ∂V terms lead to the potential energy differences between states A and B as follows:
| (11) |
However, the external driving forces are not conservative and their terms have to be dealt with explicitly. Now we have
| (12) |
Here ΔG≜GB−GA is the free-energy difference between the macroscopic states A and B.
| (13) |
is the work done to the system along the transition path (x(t))=(x0,x1,…,xN) and
| (14) |
is the work done to the system along the transition path , which is the exact reverse of (x(t)). Now we see that the probability for a given path is related to that for the exact reverse path in a very simple formula
| (15) |
Integrating both sides of Eq. 15 with respect to all coordinates x0,x1,…,xN at all time points, we find a new formula that relates the nonequilibrium work to the equilibrium free-energy difference
| (16) |
Here WA→B(B→A) denotes the work done to the system when it is driven from state A to state B (driven back from state B to state A). The angular brackets in the numerator represent the statistical mean among all the forward paths (from state A to state B), and their counterparts in the denominator represent the same among the reverse paths (from state B to state A). This new FDT is valid as long as the Brownian dynamics is applicable because its derivation does not require any additional assumptions.
The microscopic reversibility required by the CFT assumes that
| (17) |
When this is valid or a good approximation, Eq. 15 can be rearranged into the following form:
| (18) |
Multiplying the two sides of Eq. 18 with an arbitrary but finite function f(W[x0,x1,…,xN]), integration over coordinates at all times immediately leads to the CFT in the following form:
| (19) |
At this point, it is appropriate briefly look into the CFT’s self-consistency. Choosing f(W)=1, Eq. 19 gives the free-energy difference through exp(−βΔG)=1∕⟨exp(−βWB→A)⟩R. Choosing f(W)=e−βW, it leads to the well-known JE, exp(−βΔG)=⟨exp(−βWA→B)⟩F. The self-consistency and thus the validity of the CFT and JE demand that
| (20) |
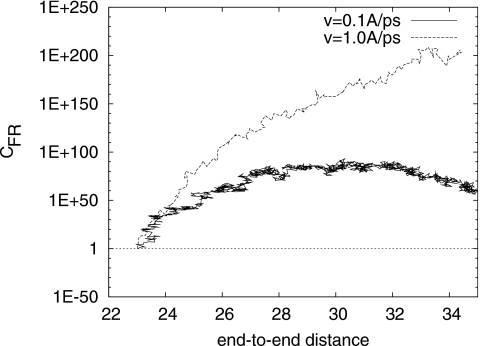
Equation 20 is a very strong constraint and therefore severely limits the CFT’s applicability. It has been shown8 that, for near-equilibrium processes, Eq. 20 is simply the linear FDT. For processes that are not near equilibrium; the self-consistency requirement, Eq. 20, is far from being satisfied. I have done in silico experiments of unfolding titin (1TIT) in vacuum. The CHARMM27 force fields are used for the interatomic interactions. NAMD∕SMD (Ref. 10) is used for the numerical undertakings. I sampled ten unfolding and ten refolding paths to compute the consistency factor CFR defined in Eq. 20. The consistency CFR is plotted in Fig. 1 as a function of the end-to-end distance for two unfolding∕refolding speeds. As expected, CFR is closer to 1 for the speed of 0.1 Å∕ps than for the speed of 1.0 Å∕ps. Even in the case of 0.1 Å∕ps, though, CFR is still very far from 1, which means CFT is not self-consistent for these far nonequilibrium processes.
Figure 1.
The self-consistency factor CFR vs the distance (Å) between the terminus N atom (that is fixed) and the terminus C atom (that is pulled at constant velocity v).
Now it is time to examine whether or not the assumption of microscopic reversibility is valid. From the definition of work, we have
| (21) |
The assumption of microscopic reversibility means that the right hand side of Eq. 21 is equal to zero. Now one might be attempted to conclude that the right hand side of Eq. 21 vanishes as dt→0 because (xn+1−xn)∼dt and (Fn+1−Fn)∼dt. But that conclusion is invalid. In fact, it does not vanish as long as the external force F(x,t) is not independent of the system’s coordinates. In general, we have
| (22) |
where ∂Fn≜∂F(x(tn),tn)∕∂xi. The right hand side of Eq. 22 would be zero if (xn+1−xn)2 were proportional to dt2, but the stochastic nature of the system makes (xn+1−xn)2 proportional to dt instead of dt2. Therefore the right hand side of Eq. 22 does not vanish in the dt→0 limit. It is equal to twice the dissipative work instead. This means that the CFT and JE are invalid unless the dissipative work is vanishingly small.
Now one more question needs to be asked: What about the case when the external force is independent of the system’s coordinates? In such a case, the right hand side of Eq. 22 does vanish. However, with such kind of external forces, the system may not transition from state A to state B because of the stochastic nature of its dynamics. In the experiments of mechanically unfolding biological molecules at constant speed, the forces acting on the system are indeed functions of the coordinates of the terminus atoms attached to the tips of the atomic force microscope or the optical tweezers. CFT and JE are inapplicable to those experiments unless the pulling speeds are slow enough that the system is always near equilibrium.
In summary, a new FDT has been derived from the Brownian dynamics without invoking any assumption. This new FDT is valid in the near-equilibrium or far nonequilibrium regime, wherever the Brownian dynamics is valid. It is also shown that the CFT and the JE are valid only in the near-equilibrium regime where the dissipative work is nearly zero.
Acknowledgments
The author thanks Robert Buckley for a critical reading of the manuscript. He acknowledges support from a NIH grant (Grant No. SC3 GM084834) and the Texas Advanced Computing Center.
References
- See, for example, Liphardt J., Onoa B., Smith S. B., I.Tinoco, Jr., and Bustamante C., Science 10.1126/science.1058498 292, 733 (2001) [DOI] [PubMed] [Google Scholar]; Hummer G. and Szabo A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.071034098 98, 3658 (2001) [DOI] [PMC free article] [PubMed] [Google Scholar]; Park S., Khalili-Araghi F., Tajkhorshid E., and Schulten K., J. Chem. Phys. 10.1063/1.1590311 119, 3559 (2003) [DOI] [Google Scholar]; Imparato A. and Peliti L., Phys. Rev. E 10.1103/PhysRevE.72.046114 72, 046114 (2005) [DOI] [PubMed] [Google Scholar]; Collin D., Ritort F., Jarzynski C., Smith S. B., Tinoco I., and Bustamante C., Nature (London) 10.1038/nature04061 437, 231 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ytreberg F. M., Swendsen R. H., and Zuckerman D. M., J. Chem. Phys. 10.1063/1.2378907 125, 184114 (2006). [DOI] [PubMed] [Google Scholar]
- Jarzynski C., Phys. Rev. Lett. 10.1103/PhysRevLett.78.2690 78, 2690 (1997). [DOI] [Google Scholar]
- Crooks G. E., Phys. Rev. E 10.1103/PhysRevE.61.2361 61, 2361 (2000). [DOI] [Google Scholar]
- Cohen E. G. D. and Mauzerall D., Mol. Phys. 10.1080/00268970500151536 103, 2923 (2005). [DOI] [Google Scholar]
- Kosztin I., Barz B., and Janosi L., J. Chem. Phys. 10.1063/1.2166379 124, 064106 (2006). [DOI] [PubMed] [Google Scholar]
- Vilar J. M. G. and Rubi J. M. F., Phys. Rev. Lett. 10.1103/PhysRevLett.100.020601 100, 020601 (2008). [DOI] [PubMed] [Google Scholar]
- Chen L. Y., J. Chem. Phys. 10.1063/1.2978949 129, 091101 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risken H., The Fokker-Planck Equation (Springer-Verlag, New York, 1989). [Google Scholar]
- Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kale L., and Schulten K., J. Comput. Chem. 10.1002/jcc.20289 26, 1781 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]