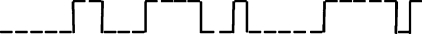Maximum Caliber: A variational approach applied to two-state dynamics

Abstract

We show how to apply a general theoretical approach to nonequilibrium statistical mechanics, called Maximum Caliber, originally suggested by E. T. Jaynes [Annu. Rev. Phys. Chem. 31, 579 (1980)], to a problem of two-state dynamics. Maximum Caliber is a variational principle for dynamics in the same spirit that Maximum Entropy is a variational principle for equilibrium statistical mechanics. The central idea is to compute a dynamical partition function, a sum of weights over all microscopic paths, rather than over microstates. We illustrate the method on the simple problem of two-state dynamics, A↔B, first for a single particle, then for M particles. Maximum Caliber gives a unified framework for deriving all the relevant dynamical properties, including the microtrajectories and all the moments of the time-dependent probability density. While it can readily be used to derive the traditional master equation and the Langevin results, it goes beyond them in also giving trajectory information. For example, we derive the Langevin noise distribution rather than assuming it. As a general approach to solving nonequilibrium statistical mechanics dynamical problems, Maximum Caliber has some advantages: (1) It is partition-function-based, so we can draw insights from similarities to equilibrium statistical mechanics. (2) It is trajectory-based, so it gives more dynamical information than population-based approaches like master equations; this is particularly important for few-particle and single-molecule systems. (3) It gives an unambiguous way to relate flows to forces, which has traditionally posed challenges. (4) Like Maximum Entropy, it may be useful for data analysis, specifically for time-dependent phenomena.

INTRODUCTION

While the theoretical foundations of statistical mechanics of the equilibrium state are well established,¹ there seems to be no unique and generally accepted formulation of the nonequilibrium state.^{2, 3, 4} Rather, there are various well-understood approaches to nonequilibrium statistical mechanics, each of which is plagued by some deficiencies. For example, master-equation methods give differential equations that can be solved for time-dependent probabilities of states. However, in systems having only small numbers of particles, dynamical fluctuations can be so large that mean probabilities, which are smooth, continuous, and differentiable quantities, are not the natural language for the dynamics. Moreover, probability distribution-based methods do not give information about individual particle trajectories. The Langevin equation, on the other hand, does give trajectory information, but it is usually restricted in various ways. Analytical Langevin modeling is challenged by nonlinear dynamical problems² and is usually based on assuming noise that is white and uncorrelated or Gaussian. Hence, as a matter of principle, it would be useful to have a single unified approach to nonequilibrium statistical mechanics (a) from which both distribution-based or trajectory-based approaches can be derived, (b) which is not restricted to near equilibrium, to linear systems, or simple kinds of noise, and (c) from which the properties of fluctuations can be derived rather than assumed. Furthermore, it is desirable to have a variational principle for dynamics that would serve the same role that Maximum Entropy and the Second Law serve for problems of equilibrium.

Here, we explore such a variational approach, called Maximum Caliber. It was originally suggested by Jaynes⁵ as a generalization of his Maximum Entropy Formulation. To illustrate its full range of predictions, we apply this approach to one of the simplest problems of dynamics, the two-state system, A↔B. Caliber may ultimately be useful for systems, such as in biology, nanotech, and single-molecule experiments, where the numbers of particles is small and where there is some interest in knowing the distribution of trajectories.^{6, 7}

In this paper, we focus on dynamics, not statics. However, our strategy follows so closely the derivation of the Boltzmann distribution law of equilibrium statistical mechanics of Jaynes^{8, 9, 10} that we first show the Jaynes treatment of equilibria, called Maximum Entropy (MaxEnt). To derive the Boltzmann law, MaxEnt starts from a given set of equilibrium microstates j=1,2,3,…,N that are relevant to the problem at hand. We aim to compute the probabilities p_j of those microstates in equilibrium. We define the entropy, S, of the system as

$$S\left(\left\{p_j\right\}\right)=-k_B\sum _{j=1}^N{p}_j\text{ln}{p}_j,$$ (1.1)

where k_B is Boltzmann’s constant. The equilibrium probabilities, $p_j=p_j^{*}$, are those values of p_j that cause the entropy to be maximal, subject to two constraints:

$$\sum _{i=1}^N{p}_j=1,$$ (1.2)

which is a normalization condition that insures that the probabilities p_j sum to one, and

$$⟨E⟩=\sum _j{p}_j{E}_j,$$ (1.3)

which says that the energies, when averaged over all the microstates, sum to the macroscopically observable average energy. This is equivalent to the statement that the temperature is constant. Introducing Lagrange multipliers μ and β to enforce constraints 1.2, 1.3, we maximize the function

$$S\left(\left\{p_j\right\}\right)=-k_B\sum _{j=1}^N{p}_j\text{ln}{p}_j+\mu \sum _{j=1}^N{p}_j-\beta \sum _{j=1}^N{p}_j{E}_j,$$ (1.4)

which leads to the equilibrium probabilities

$$p_j^{\ast }=\frac{e^{-\beta E_j}}{Q},$$ (1.5)

where Q=∑_je^−BE_j is the partition function. By using the thermodynamic expression d⟨E⟩=TdS with 1.1, 1.3, we readily obtain β=1∕k_BT. This MaxEnt derivation of the Boltzmann distribution law provides a simple, compact, and transparent variational principle for computing the equilibrium probabilities of the microstates. The basic idea is that, by maximizing Eq. 1.4, we select the distribution with the greatest multiplicity that agrees with the given information 1.2, 1.3.

Following this idea, the generalization of MaxEnt to time-dependent problems is—at least in principle—a straightforward matter.^{5, 11, 12} In this case we have some time-dependent quantities A_n with averages

$$⟨A_n\left(t\right)⟩=\sum _j{p}_j\left(t\right)A_{nj}.$$ (1.6)

Instead of the equilibrium probability p_j of a microstate in Eq. 1.4, the p_j(t) now denote the probability of a microtrajectory, e.g., a specific single-particle trajectory. As a consequence, the resulting entropy ∝∑_jp_j(t)ln p_j(t) will be a functional or path integral¹³ of the {p_j(t)}. In direct analogy to the equilibrium case [Eq. 1.4], we construct the quantity

$$\mathcal{C}\left(t\right)=-\sum _j{p}_j\left(t\right)\text{ln}{p}_j\left(t\right)+\mu \sum _j{p}_j\left(t\right)+\sum _n{\lambda }_n\sum _j{p}_j\left(t\right)A_{nj},$$ (1.7)

where Lagrange multipliers μ and λ_n enforce that the distribution is normalized and that the averages 1.6 are satisfied. Jaynes called this quantity “Caliber,” since it refers to the cross sectional area of a tube, which partly determines the flow in a dynamic process.⁵ To find the weights of the individual dynamical paths, p_j(t), we maximize the Caliber 1.7 by setting δC∕δp_j=0. This gives for the path weights

$$p_j\left(t\right)=Q_{\text{d}}^{-1}\text{exp}\left\{{\lambda }_1{A}_{1j}+\cdots +{\lambda }_L{A}_{Lj}\right\},$$ (1.8)

where Q_d=∑_jexp{λ₁A_1j+⋯+λ_LA_Lj} denotes the dynamical partition function. In complete analogy to MaxEnt, by maximizing Eq. 1.7, we select the path distribution $\left\{p_j^{*}\left(t\right)\right\}$ with the greatest multiplicity that agrees with the given information 1.2, 1.6. This path distribution then determines the time evolution of all time-dependent observables of the system.

Here is how Caliber is applied to a given dynamical problem. First, we are given a set of trajectories (for example, from a model) and a set of values, A_nj, characterizing the property A_n for trajectory j. We take as given (for example, from experiments) L first-moment quantities A_n. Maximizing the Caliber via δC∕δp_j=0 gives L equations that can be solved for the L unknowns λ_n. Finally, substituting these quantities λ_n into Eq. 1.8 gives the dynamical partition function Q_d and the trajectory populations p_j. Those quantities, in turn, can then be used to obtain all the other dynamical distribution properties of interest.

This derivation makes no assumptions that a system is near equilibrium, or about separations of time scales, or about the linearity or nonlinearity of relationships between forces and flows, or about the nature of distributions of noise or fluctuations. The Caliber method is quite general in principle, although for many problems, similar to equilibrium statistical mechanics, analytical solutions will not be possible and it may be necessary to resort to numerical methods of solution. The approach has been subject to some formal study,^{11, 12, 14, 15} but practical applications and tests of it have been largely unexplored. Only recently, the principle of Maximum Caliber has been experimentally verified for the problem of nanodiffusion^{16, 17} and for a single bead trapped in a double well potential.¹⁸ In this work, we illustrate the Caliber approach more specifically through application to two-state dynamical systems.

THE DYNAMICAL PARTITION FUNCTION

Definition

Consider a Brownian-driven classical two-state system A↔B. Consider, first, the trajectory of a single particle (Fig. 1). We divide time into discrete units Δt. Each possible trajectory has N time steps, so the time duration of each trajectory is t=NΔt.

Figure 1.

One possible trajectory of a single particle that alternates stochastically between states A and B as a function of time.

There are four rate quantities that are of interest: N_abj, the number of transitions (over the full course of the N time intervals from time 0 to t, of one particular trajectory j) that have occurred from state B to state A; N_baj, the number of transitions from A to B along trajectory j; N_aaj, the number of “transitions” from state A to state A; and N_bbj, the number of transitions from B to B during a trajectory. Once the populations p_j of the individual trajectories are known, the average numbers of such transitions can be computed from

$$⟨N_{ab}⟩=\sum _j{p}_j{N}_{abj},⟨N_{ba}⟩=\sum _j{p}_j{N}_{baj},$$ (2.1)

$$⟨N_{aa}⟩=\sum _j{p}_j{N}_{aaj},⟨N_{bb}⟩=\sum _j{p}_j{N}_{bbj}.$$

Hence, quantities such as ⟨N_ab⟩∕N are rates; these are the numbers of such transitions per unit time. Other quantities are obtainable from these. For example, for a trajectory having N time steps, the fraction of time that the system spends in state A can be expressed as ⟨N_A∕N⟩=⟨(N_aa+N_ab)∕N⟩. In our present simple example, we consider steady-state situations in which each such average rate is a fixed number and is not, itself, a time-varying quantity. However, as we show below (see Sec. 4C), the Caliber method is general and can treat arbitrary time dependencies.

For the two-state system, the path weights are given by Caliber [Eq. 1.8],

$$p_j\left(t\right)=Q_{\text{d}}^{-1}\text{exp}\left\{{\lambda }_1{N}_{abj}+{\lambda }_2{N}_{baj}+{\lambda }_3{N}_{aaj}+{\lambda }_4{N}_{bbj}\right\}=Q_{\text{d}}^{-1}{\gamma }_{ab}^{N_{abj}}{\gamma }_{ba}^{N_{baj}}{\gamma }_{aa}^{N_{aaj}}{\gamma }_{bb}^{N_{bbj}},$$ (2.2)

where, to keep the notation as simple as possible, we have converted to different variables, γ_ab=e^λ₁, γ_ba=e^λ₂, γ_aa=e^λ₃, and γ_bb=e^λ₄. The dynamical partition function

$$Q_{\text{d}}\left(t\right)=\sum _j{\gamma }_{ab}^{N_{abj}}{\gamma }_{ba}^{N_{baj}}{\gamma }_{aa}^{N_{aaj}}{\gamma }_{bb}^{N_{bbj}}$$ (2.3)

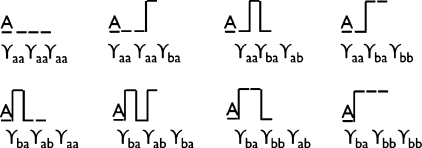
is a sum over the dynamical weights of all the trajectories. Each dynamical weight is a product of factors describing that trajectory: γ_ba is the probability that during the time interval Δt, the system was in state A and switches to state B, γ_ab is the probability that the system was in state B and switches to state A, γ_aa is the probability that the system was in state A and stays in state A, and γ_bb is the probability of staying in state B. Without loss of generality, we will consider trajectories that start at time t=0 in state A. To illustrate, in a simple system involving only three time steps (N=3), there are eight possible paths, giving the following partition sum over those path weights:

$$Q_{\text{d}}\left(t=3\Delta t\right)={\gamma }_{aa}^3+{\gamma }_{aa}{\gamma }_{ab}{\gamma }_{ba}+{\gamma }_{ab}{\gamma }_{ba}{\gamma }_{aa}+{\gamma }_{ab}{\gamma }_{bb}{\gamma }_{ba}+{\gamma }_{ba}{\gamma }_{aa}^2+{\gamma }_{ba}^2{\gamma }_{ab}+{\gamma }_{ab}{\gamma }_{bb}{\gamma }_{ba}+{\gamma }_{bb}^2{\gamma }_{ba};$$

these paths and their weights are illustrated in Fig. 2.

Figure 2.

All the possible two-state trajectories of N=3 time steps for a system starting in state A, with their corresponding statistical weights.

Collecting up the results above into a more compact matrix notation gives

$$Q_{\text{d}}\left(t=N\Delta t\right)=\left(\begin{array}{cc}1& 1\end{array}\right){\mathbf{G}}^N\left(\begin{array}{c}1\\ 0\end{array}\right),$$ (2.4)

with initial state $\left(\genfrac{}{}{0ex}{}{1}{0}\right)$ (start in A) and final state $\left(\genfrac{}{}{0ex}{}{1}{1}\right)$ (end in A or B) and where

$$\mathbf{G}=\left(\begin{array}{cc}{\gamma }_{aa}& {\gamma }_{ab}\\ {\gamma }_{ba}& {\gamma }_{bb}\end{array}\right)$$ (2.5)

is the matrix of transition probabilities between the two states. Of these four variables, note that only two are independent because of the conservation relationships:

$${\gamma }_{aa}+{\gamma }_{ba}=1,$$ (2.6)

$${\gamma }_{bb}+{\gamma }_{ab}=1.$$

That is, for example, if the particle is in state A at time t, then at time t+Δt, the particle must be either in state A or B.

What are the probabilities P_A(t) and P_B(t) that the system is in state A or state B, respectively, at time t? We can readily obtain these probabilities from the dynamical partition function. Suppose the system starts in state A at time t=0 with probability P_A(0) and in B with probability P_B(0). To compute the state populations at time t, we multiply by the propagator matrix G for each of the N time steps to get

$$\left(\begin{array}{c}{P}_A\left(t\right)\\ P_B\left(t\right)\end{array}\right)={\mathbf{G}}^N\left(\begin{array}{c}{P}_A\left(0\right)\\ P_B\left(0\right)\end{array}\right).$$ (2.7)

Since P_A(t)+P_B(t)=1, it follows from Eq. 2.7 that the partition function is normalized,

$$Q_{\text{d}}\left(t\right)=P_A\left(t\right)+P_B\left(t\right)=1.$$ (2.8)

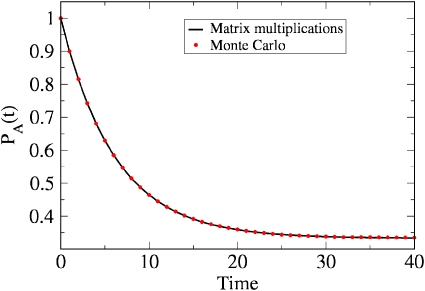
As an illustration, Fig. 3 shows the time evolution of P_A(t), given that γ_ba=1∕10 and γ_ab=1∕20. As expected, P_A(t) decays at a rate γ_ab+γ_ab=3∕20.

Figure 3.

Time evolution of population probability P_A(t) as obtained from Eq. 2.7, starting from state A and assuming transition probabilities γ_ba=k_a=1∕10 and γ_ab=k_b=1∕20 for illustration. The system relaxes with a decay rate of γ_ab+γ_ab=3∕20 and approaches equilibrium, P_A(∞)=1−⟨N_B⟩_eq∕N=γ_ab∕(γ_ba+γ_ab)=1∕3, as expected. Also shown is the result of a dynamical Monte Carlo simulation (dotted line), which agrees well with the matrix multiplication method (solid line), when 10⁶ trajectories are employed.

Another quantity of interest is the conditional probability, P_A(t₂∣t₁), that the system is in state A at time t₂, given that it was in state A at time t₁:

$$P_A\left(t_2\mid t_1\right)=\left(\begin{array}{cc}1& 0\end{array}\right){\mathbf{G}}^{N_2-N_1}\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right){\mathbf{G}}^{N_1}\left(\begin{array}{c}{P}_A\left(0\right)\\ P_B\left(0\right)\end{array}\right)=P_A\left(t_2-t_1\right)P_A\left(t_1\right).$$ (2.9)

Some properties are derivatives of the dynamical partition function

It is readily verified from Eq. 2.3 that various average quantities and higher moments can be calculated as derivatives of the partition function. For example, we can get the average number of switching transitions, N_ba, from

$$⟨N_{ba}⟩=\frac{\partial \text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{ba}},⟨{\left(N_{ba}\right)}^2⟩-{⟨N_{ba}⟩}^2=\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{ba}^2}$$ (2.10)

(and similarly for the other quantities N_ab, N_aa, and N_bb; see Appendix A). In the equilibrium limit, we can readily derive closed-form expressions for the moments. For example, N_B∕N=(N_ba+N_bb)∕N is the fraction of the time NΔt that the system spends in state B. Appendix A shows that in this limit, as N→∞, we have

$$\frac{{⟨N_B⟩}_{\text{eq}}}{N}=\frac{{⟨N_{ba}+N_{bb}⟩}_{\text{eq}}}{N}=\frac{{\gamma }_{ba}}{{\gamma }_{ba}+{\gamma }_{ab}},$$ (2.11)

$$\frac{{⟨N_B^2⟩}_{\text{eq}}-{⟨N_B⟩}_{\text{eq}}^2}{N}=\frac{2{\gamma }_{ba}{\gamma }_{ab}}{{\left({\gamma }_{ba}+{\gamma }_{ab}\right)}^3}-\frac{{\gamma }_{ba}{\gamma }_{ab}}{{\left({\gamma }_{ba}+{\gamma }_{ab}\right)}^2}.$$ (2.12)

It is worth noting that these equations imply detailed balance, i.e., ⟨N_B⟩_eqγ_ab=⟨N_A⟩_eqγ_ba.

Other derivatives of the dynamical partition function are also useful—mixed moments, for example. Central to equilibrium thermodynamics is the set of reciprocal relationships known as Maxwell’s relations, which involve equalities among mixed second derivatives of the partition function. The importance of Maxwell’s relations lies in the fact that we often want to know the quantity on one side of such equalities, but we are only able to measure the quantity on the other side. Here, we show that Caliber gives similar mixed second derivative equalities, except here it is for dynamical properties rather than for equilibria. For example,

$$\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{bb}\partial \text{ln}{\gamma }_{ba}}=\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{ba}\partial \text{ln}{\gamma }_{bb}}.$$ (2.13)

Perhaps expressions such as Eq. 2.13 will be useful for dynamics in the same way that Maxwell’s relations are for equilibria.

A chemical fluctuation theorem

Of much interest in nonequilibrium statistical mechanics are fluctuation theorems.^{15, 17, 19, 20} A fluctuation theorem relates the probability P_f of a forward trajectory to the probability P_r of the corresponding reverse trajectory in a dynamical system. From Caliber, we can readily calculate such ratios for our two-state system. The dynamical partition function 2.3 gives the ratio of the populations of forward to reverse trajectories as

$$\frac{P_{\text{f}}}{P_{\text{r}}}=\frac{{\gamma }_{aa}^{N_{aa}}{\gamma }_{ab}^{N_{ab}}{\gamma }_{ba}^{N_{ba}}{\gamma }_{bb}^{N_{bb}}}{{\gamma }_{aa}^{N_{aa}}{\gamma }_{ab}^{N_{ab}+1}{\gamma }_{ba}^{N_{ba}-1}{\gamma }_{bb}^{N_{bb}}}=\frac{{\gamma }_{ba}}{{\gamma }_{ab}},$$ (2.14)

where we have assumed, for the purpose of calculation, that the forward trajectory starts in state A and ends in state B. Employing Eq. 2.11 for the equilibrium populations P_A(t)=1 and P_B(∞) gives

$$\frac{{\gamma }_{ba}}{{\gamma }_{ab}}=\frac{P_B\left(\infty \right)}{P_A\left(\infty \right)}=e^{S_A-S_B},$$ (2.15)

where S_A and S_B denote the entropies over the populations of states A and B, respectively. This simple derivation gives the fluctuation theorem for the two-state system,

$$\frac{P_{\text{f}}}{P_{\text{r}}}=e^{S_A-S_B},$$ (2.16)

showing the more favorable routes are exponentially more populated than their reverse trajectories.

Other dynamical quantities can be obtained from the dynamical partition function

Other properties that are not simple derivatives of Q_d can also be obtained from the dynamical partition function. One such property is the probability P(N_B,t) that the particle has spent exactly N_B time steps in state B over the time course from time t^′=0 to t. Another example is the probability P(N_ba,t) that the particle has had exactly N_ba switches during the trajectory. Or, because of its relationship to the equilibrium constant K=N_B∕N_A, we may be interested in the dynamical distribution of the quantity P(N_B∕N_A,t). Computing these properties requires a way to “pick out” certain specific trajectories from the partition sum. Expressed in terms of Kronecker delta functions, these are

$$P\left(N_B,t\right)=\sum _j{p}_j\left(t\right){\delta }_{N_B,N_{Bj}},$$ (2.17)

$$P\left(N_{ab},t\right)=\sum _j{p}_j\left(t\right){\delta }_{N_{ab},N_{abj}},$$ (2.18)

$$P\left(N_B∕N_A,t\right)=\sum _j{p}_j\left(t\right)\delta \left[\left(N_B∕N_A\right)-\left(N_{Bj}∕N_{Aj}\right)\right].$$ (2.19)

Recalling from Eq. 2.2 that the path weights p_j depend on the variables N_abj, N_baj, N_aaj, and N_bbj, we can calculate, say, P(N_ab,t), by simply summing over all the particular paths j that take on the particular value of interest, N_abj=N_ab:

$$P\left(N_{ab},t\right)=\sum _{N_{baj},N_{aaj},N_{bbj}}{g}_j{\gamma }_{ab}^{N_{abj}}{\gamma }_{ba}^{N_{baj}}{\gamma }_{aa}^{N_{aaj}}{\gamma }_{bb}^{N_{bbj}},$$ (2.20)

where g_j=g(N_abj,N_baj,N_aaj,N_bbj) denotes the multiplicity of paths j that have these particular values of the four quantities.

Although the direct enumeration of paths is straightforward in principle, it becomes cumbersome for large N, since the number of paths grows exponentially with the length of the trajectory. In these cases, such averages can be obtained using a dynamical Monte Carlo scheme instead.^{21, 22, 23} In a direct generalization of standard equilibrium Monte Carlo, we can sample the nonequilibrium dynamics by comparing the rates of individual time steps with random numbers (see Ref. 23 for a recent review). For example, the Gillespie algorithm describes a random walk in state space that reproduces the correct distribution of the master equation of the process.²¹ For our single-particle two-state system, we can use a particularly simple dynamical Monte Carlo scheme. At each time step, we draw a random number r, which is compared to the transition probability γ_ba (when the system is in state A) or γ_ab (when it is in state B). If the transition probability is larger than r, the system makes a transition to the new state; otherwise, the system stays in its previous state. Figure 3 shows that the Monte Carlo approach gives good agreement with the matrix multiplication method, when 10⁶ trajectories are employed.

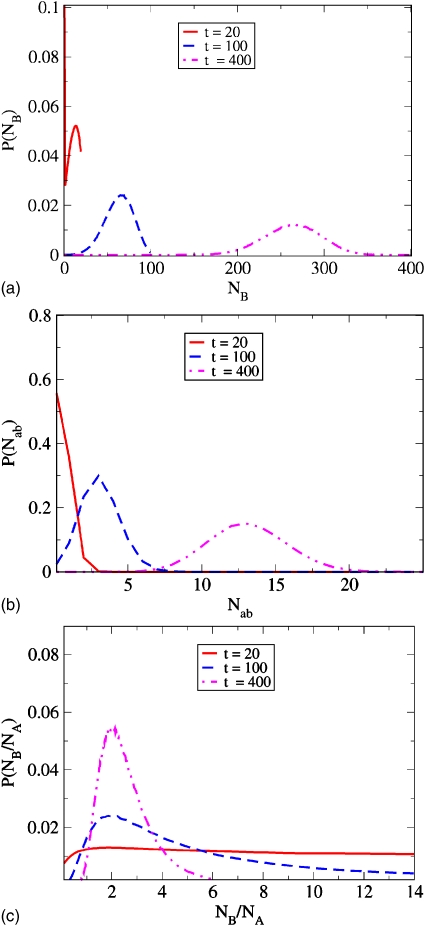
Adopting again our simple example with γ_ba=1∕10 and γ_ab=1∕20, Fig. 4 shows how the distributions P(N_B,t), P(N_ba,t), and P(N_B∕N_A,t) begin sharply peaked when the system is initiated in state A, and remain asymmetrical as they shift with time toward their equilibrium distributions (t≳400). Interestingly, we find a nonzero third moment of these distributions, even in the limit of long times. This implies that they are not exactly Gaussian, as the corresponding Langevin modeling would normally assume (although the deviation is quite small). For example, we obtain ⟨(N_ba−⟨N_ba⟩)⟩³∕N=0.006 86 and 0.006 91 from Eq. A15 and the Monte Carlo simulations. At long times, we find that P(N_B∕N_A,t) peaks at the expected equilibrium coefficient value, N_B∕N_A=2.

Figure 4.

Time evolution of distributions P(N_B,t) (top), P(N_ab,t) (middle), and P(N_B∕N_A,t) (below).

DERIVING EQUATIONS OF MOTION FROM CALIBER

Our premise in this paper is to use Caliber as a foundational principle from which we can derive dynamical properties. A standard way to treat dynamics is through master equations and Langevin equations.

Master equation

Master equations are among the most common modeling approaches in nonequilibrium statistical mechanics. These are differential equations that express the governing dynamics of state probabilities, such as P_A(t) or P_B(t) in the two-state system. Here, we show how to derive the master equation for this problem from Caliber’s trajectory-based dynamical partition function. We aim to compute quantities such as dP_A∕dt and dP_B∕dt. For the single time step Δt=1 from t to t+1, Caliber Eq. 2.7 gives

$$\frac{\text{d}{P}_A}{\text{d}t}=P_A\left(t\right)-P_A\left(t-1\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)\left({\mathbf{G}}^t-{\mathbf{G}}^{t-1}\right)\left(\begin{array}{c}{P}_A\left(0\right)\\ P_B\left(0\right)\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)\left(\mathbf{G}-1\right){\mathbf{G}}^{t-1}\left(\begin{array}{c}{P}_A\left(0\right)\\ P_B\left(0\right)\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)\left(\mathbf{G}-1\right)\left(\begin{array}{c}{P}_A\left(t-1\right)\\ P_B\left(t-1\right)\end{array}\right).$$ (3.1)

Converting from the γ notation to the more familiar rate-coefficient notation, k_a and k_b, gives

$$\mathbf{G}-\mathbf{1}=\left(\begin{array}{cc}{\gamma }_{aa}-1& {\gamma }_{ab}\\ {\gamma }_{ba}& {\gamma }_{bb}-1\end{array}\right)\equiv \left(\begin{array}{cc}-k_a& k_b\\ k_a& -k_b\end{array}\right),$$ (3.2)

leading to the well-known master equation for this problem

$$\frac{\text{d}{P}_A}{\text{d}t}=-k_a{P}_A+k_b{P}_B,$$ (3.3)

$$\frac{\text{d}{P}_B}{\text{d}t}=+k_a{P}_A-k_b{P}_B,$$

where P_A and P_B on the right-hand side represent the state populations at time t−1 in the discrete time notation. While chemical master equations such as these are well-understood standard fare, they are limited; they do not give information about the underlying system trajectories. Thus, it is not straightforward to compute the distribution of dynamical quantities, which can be measured, e.g., in single molecule experiments. The advantage of the Caliber approach above is that it gives a deeper vantage point from which we can derive the dynamical properties of both the trajectories and the state densities, all within a single framework.

Switching from one-particle to multiple-particle systems

In the sections above, we have considered one particle that switches between states A and B. Now we generalize and treat a system of M particles. Each particle can switch stochastically between states A and B. We treat the case of independent particles to show how the dynamical partition function method simplifies such problems. Because of the particle independence, the dynamical partition function Q_d,M for the total system factorizes into M single-particle partition functions Q_d,1:

$$Q_{\text{d},M}=Q_{\text{d},1}^M.$$ (3.4)

Hence, for the M-particle system, we obtain directly

$${\left[P_A\left(t\right)+P_B\left(t\right)\right]}^M=\sum _{n=0}^M\left(\begin{array}{c}M\\ n\end{array}\right)P_A^n\left(t\right)P_B^{M-n}\left(t\right)=\sum _{n=0}^M{P}_n\left(t\right),$$ (3.5)

which gives

$$P_n\left(t\right)=\left(\begin{array}{c}M\\ n\end{array}\right)P_A^n\left(t\right)P_B^{M-n}\left(t\right),$$ (3.6)

where $\left(\genfrac{}{}{0ex}{}{M}{n}\right)$ denotes the binomial coefficients and P_n(t) is the probability that n of the M particles are in state A at time t.

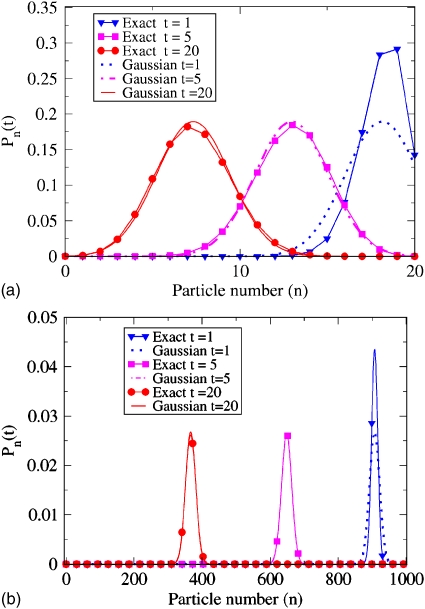
Here are some examples of how Eq. 3.6 can be useful. First, Eq. 3.6 gives the diffusional dynamics of the M-particle system (see Fig. 5). It is clear from the substantial width of this curve for M=20 particles that the mean value, P_A(t)=(1∕M)∑_n=1,MnP_n(t)=⟨n⟩∕M, provides only a limited description of the time evolution of the system. The copy numbers of proteins inside biological cells are often not much greater than this, so such dynamical variance quantities will be important in such cases. Assuming M=1000 particles, on the other hand, the distributions are well localized at their mean values.

Figure 5.

Time evolution of probability distribution P_n(t) of number of particles, n, in state A, assuming k_a=1∕10, k_b=1∕20, and initial condition P_n(0)=δ_n,M. For various times, the exact binomial distribution is shown in solid lines along with the Gaussian distribution drawn with broken lines. In the upper panel M=20 total particles are considered, in the lower M=1000.

Second, Eq. 3.6 gives a simple way to derive the Poisson-like distribution for the M-particle equilibrium. At long times, we have P_A(∞)=k_b∕(k_a+k_b)=1−P_B(∞). Substituting these relationships into the right-hand equality in Eq. 3.6 and defining the equilibrium constant as K=k_b∕k_a gives the Poisson-like distribution²

$$P_n\left(\infty \right)\propto \frac{K^n}{n!(M-n)!}.$$ (3.7)

which is expected for independent particles at equilibrium; the proportionality constant is a function of M.

Third, Eq. 3.6 gives a simple way to derive the master equation for the M-particle τ_B reaction. We calculateP_n(t+Δt)−P_n(t) using Eq. 3.6 and expand to first order in the rate coefficients k_a and k_b to get the M-particle master equation

$$\frac{\text{d}{P}_n}{\text{d}t}=+k_a\left(n+1\right)P_{n+1}-k_{a}n{P}_n+k_b\left(M-\left[n-1\right]\right)P_{n-1}-k_b\left(M-n\right)P_n,$$ (3.8)

which accounts for the gains and losses in the n-particle “bin” to and from the adjacent n+1 and n−1 bins. Here again, this master equation is well-known; the virtue of this Caliber derivation is simply in showing that the state-population dynamics can be derived from a single unified framework that also gives trajectory properties.

Deriving the chemical Langevin equation from Caliber

Master equations describe quantities that are already integrated over the microscopic trajectories. The standard way to recapture information about dynamical trajectories is to use a Langevin equation instead. In the Langevin approach, the left-hand side of an expression, for example, is a differential equation for average forces, velocities, or rates for a particular dynamical problem. On the right-hand side is a fluctuating noise quantity, which is assumed to have certain statistical properties. Typically, the noise is assumed to be uncorrelated and white, or to obey a Gaussian distribution. Such approaches are known to fail, however, in various circumstances, such as when the dynamics is nonlinear.² There is currently no deeper analytical approach that prescribes the nature of the noise when setting up a Langevin equation for complex problems. Here, we illustrate how to derive the chemical Langevin equation, for the two-state model, from Caliber, giving a principled way of treating the noise. We begin with the full trajectory distribution given by Caliber and show how to derive the appropriate fluctuations for the corresponding Langevin equation from it.

In Langevin terminology, for our two-state problem, let n(t) represent the instantaneous number of particles in state A at time t. Correspondingly, M−n(t) is the instantaneous number of particles in state B. Formally, the Langevin approach asserts that the fluctuating trajectory quantity n(t) can be expressed in terms of a differential equation²

$$\frac{dn}{dt}=-k_{a}n+k_b\left(M-n\right)+F_t,$$ (3.9)

where F_t is a fluctuating noise quantity that has particular properties.²⁴ First, it is assumed that the average noise is zero, ⟨F_t⟩=0, so that averaging over trajectories recovers the correct macroscopic expression for the mean dynamics,

$$\frac{d}{dt}⟨n⟩=-k_a⟨n⟩+k_b⟨\left(M-n\right)⟩.$$ (3.10)

Since ⟨n⟩=MP_A(t) and ⟨M−n⟩=MP_B(t), this step of averaging over trajectories just recovers the master equation for this system. Now, rearranging Eq. 3.9 and replacing the derivative on the left side with the single time-step (Δt=1) quantity, n(t+1)−n(t), gives

$$n\left(t+1\right)-n\left(t\right)+k_{a}n\left(t\right)-k_b\left[M-n\left(t\right)\right]=F\left(t\right).$$ (3.11)

Our aim here is to derive from Caliber the nature of this fluctuating quantity, F(t), rather than to assume that it is a Gaussian distribution, as is often done in Langevin modeling. We want to determine the various statistical moments of F(t). To do this, we need the joint probability distribution P(n(t+1),n(t)). Using the notation n(t+1)=m and n(t)=n, P(n(t+1),n(t)) can be expressed as

$$P\left(m,n\right)=P_n\left(t\right)\left[\sum _i\left(\begin{array}{c}n\\ i\end{array}\right)\left(\begin{array}{c}M-n\\ m-n+i\end{array}\right){\gamma }_{ba}^i{\gamma }_{aa}^{n-i}{\gamma }_{bb}^{M-m-i}{\gamma }_{ab}^{m-n+i}\right],$$ (3.12)

where P_n(t) is given by Eq. 3.6. This expression contains two types of terms. First, given n particles in state A at time t, this sums over the trajectories in which i of them jump to state B at time t+1 (hence, n−i of them stay in state A). Second, given M−n particles in state B at time t, this sums over trajectories in which m−n+i of them jump into state A at time t+1 (so, M−m−i remain in state B).

Based on this joint distribution, Appendix B derives the first three moments of the distribution over trajectories. For the first moment, Caliber gives ⟨F(t)⟩=0, as expected. For the second moment, we obtain

$$⟨F{\left(t\right)}^2⟩=M\left(k_a{P}_A\left(t\right)+k_b{P}_B\left(t\right)\right).$$ (3.13)

Clearly, since P_A and P_B are time dependent, this second moment is also time dependent. However, in the limit as t→∞, the second moment reduces to

$$⟨F{\left(\infty \right)}^2⟩=\frac{2M{k}_a{k}_b}{k_a+k_b}$$ (3.14)

via the substitution of P_A(∞)=k_b∕(k_a+k_b)=1−P_B(∞) into Eq. 3.13. Correspondingly, the third moment is (in first order of k_a and k_b, see Appendix B)

$$⟨F{\left(t\right)}^3⟩=M\left(P_B\left(t\right)k_b-P_A\left(t\right)k_a\right),$$ (3.15)

which is time dependent and goes to zero in the limit of long times, ⟨F(∞)³⟩=0. Since the third moment is nonzero for short times, the standard assumption in Langevin modeling that the noise is Gaussian-distributed is not exact, but becomes an increasingly good approximation for long times. Also as a matter of principle, the implication of this derivation is that for more complex Langevin modeling, Caliber may provide a general way to derive the appropriate noise distributions, when the Gaussian assumption is known to fail.

Finally, to complete the Caliber derivation of the Langevin approach, we integrate Eq. 3.9 to put it into the form

$$n\left(t\right)=⟨n\left(t\right)⟩+{\int }_0^{t}d{t}^{\prime }{e}^{-\left(k_a+k_b\right)\left(t-t^{\prime }\right)}{F}_{t^{\prime }},$$ (3.16)

where ⟨n(t)⟩=MP_A(t). Next, we note that the underlying distribution P_n(t) is given by the binomial distribution Eq. 3.6, which we approximate as a Gaussian,

$$P_n\left(t\right)=\frac{1}{\sigma \left(t\right)\sqrt{2\pi }}\text{exp}\left\{-\frac{{\left[n-⟨n\left(t\right)⟩\right]}^2}{2{\sigma }^2\left(t\right)}\right\},$$ (3.17)

where

$${\sigma }^2\left(t\right)=⟨n^2\left(t\right)⟩-{⟨n\left(t\right)⟩}^2={\int }_0^{t}d{t}_2{\int }_0^{t}d{t}_1{e}^{-\left(k_a+k_b\right)\left(2t-t_2-t_1\right)}⟨F\left(t_2\right)F\left(t_1\right)⟩=M{P}_A\left(t\right)\left[1-P_A\left(t\right)\right].$$ (3.18)

This derivation shows how, starting from Caliber, we recover the standard Langevin model assumption of Gaussian noise. Figures 5a, 5b show that the Gaussian curves accurately mimic the binomial distribution, and that the Gaussian differs from the exact P_n(t) only at very short times. Interestingly, the exact result shows that the width of the distribution is time dependent at short times. This, of course, is not recovered by the usual Langevin treatment.

CONSTRAINTS

How to choose constraints for Caliber modeling

What is the justification for the Caliber approach? Statistical mechanics is about making models. For dynamics, a model is a statement of a set of possible microscopic routes and some chosen set of microscopic parameters (the statistical weights, not known in advance), the number of which will typically be much smaller than the number of different trajectories. The Caliber strategy is simply a way to determine the values of those statistical weight parameters so as to satisfy the observable average flux quantities, and so as to otherwise assign no further favoritism to any one trajectory over any other. The essential idea is that all trajectories are equivalent intrinsically and are only weighted differently by virtue of the resultant statistical weight factors. Caliber then predicts other dynamical moments. If those other dynamical moments were then found to disagree with experiments, it would imply the need for a different model.

This raises the question of what types of constraints are appropriate in Eq. 1.7, 1.6, 2.1. In this regard, the Maximum Caliber approach to dynamics bears close resemblance to the Maximum Entropy approach to equilibrium, which involves satisfying constraints, such as Eq. 1.3, on certain equilibrium averages. In applying either Caliber to problems of dynamics or MaxEnt to problems of equilibrium, we are not at liberty to choose constraints arbitrarily. For example, for the two-state model of interest in this paper, there are many possible quantities that could have served as the “observables” of our trajectories, including ⟨N_ab−N_ba⟩, $⟨N_B^2⟩$, and $⟨N_{ab}^3∕N_B⟩$, or an infinite number of others. The resulting dynamical distribution function that would have been predicted from those various choices can differ depending on what constraints are chosen. So, what are the “right” constraints?

First, in physical problems, some quantities, like energy, momentum, mass, particle numbers, or volume, are conserved. They are extensive, or first-order homogeneous functions. In equilibrium thermodynamics, you can only predict a state of equilibrium if you maximize the entropy S(U,V,N) that is a function of extensive variables; you cannot predict equilibrium by maximizing the function S(T,V²,N∕U) of intensive variables, such as temperature, or other non-conserved quantities. Similarly, for dynamics, the constraints used in Caliber are only fluxes, such as ⟨N_ab⟩, which are time derivatives of conserved first-moment quantities, not higher moments of fluxes. Second, any linear combination of flux quantities would also lead to the same prediction for the p_j’s: hence, substituting ⟨N_A⟩=⟨N_aa⟩+⟨N_ab⟩ for the quantities ⟨N_aa⟩ or ⟨N_ab⟩, for example, would give the same trajectory populations. Hence, there is freedom to choose among linear combinations of flux constraints those that are most convenient.

Third, what is the right number of constraints? In our present model, we have two, corresponding traditionally, say, to an equilibrium constant and a forward rate coefficient. In a two-state system of independent particles having stationary dynamics and no memory, this may be sufficient to account for bulk experiments. However, modern single-molecule measurements can also give the higher moments.^{17, 18, 25, 26} In those cases, it is found that no further statistical weight parameters are needed. If some additional microscopic process were operative that caused a further preference of some trajectories over others, additional measurements (constraints) would be needed to fix the values of the additional parameters required. In the sections below, we illustrate how Caliber can be applied to other conserved quantities (time, rather than flux), to time-dependent constraints, and to memory effects.

Constraining the time rather than the flux

An alternative way to describe the two-state system is through the waiting time distribution rather than through the flux distribution. Caliber can treat time distributions as simply as it can treat flux distributions. Often measured in single-molecule experiments are the waiting times τ_A and τ_B, i.e., the number of time steps the system spends in state A or B until it switches to the other state. The mean waiting time in state A is ⟨τ_A⟩=∑_jp_j(t)τ_Aj. Now, switching from constraints on average fluxes to constraints on average times, this time-based Caliber formulation gives the path weights $p_j=Q_{\mathrm{d}}^{-1}{e}^{-\lambda \tau A_j}$, where Q_d is a dynamical partition sum over all the possible waiting times,

$$Q_{\text{d}}={\int }_0^{\infty }{e}^{-\lambda {\tau }_A}\text{d}{\tau }_A=1∕\lambda .$$ (4.1)

Hence, we obtain for the average waiting time

$$⟨{\tau }_A⟩=Q_{\text{d}}^{-1}{\int }_0^{\infty }\tau e^{-\lambda {\tau }_A}\text{d}{\tau }_A=\frac{1∕{\lambda }^2}{1∕\lambda }=1∕\lambda .$$

The average waiting time ⟨τ_A⟩=1∕k_a is an observable, equal to the inverse of the rate constant. Hence, from this observable, we obtain λ, leading also to the well-known Poisson waiting time distribution for this system,

$$p_j=k_a{e}^{-k_a{\tau }_{Aj}}.$$ (4.2)

This simple derivation shows how a constraint on the mean waiting time gives, through the Caliber approach, the full waiting time distribution. Also, since the same holds independently for the waiting time distribution in state B, we obtain from these two constraints the weights

$$p_j\propto e^{-k_a{\tau }_{Aj}}{e}^{-k_b{\tau }_{Bj}}.$$ (4.3)

In short, there can be different ways to choose constraints for Caliber. We have shown the equivalence of fixing two flux quantities such as N_ab and N_aa or fixing, instead, two mean waiting times, for states A and B. One advantage of the latter is that the waiting times are decoupled and independent [Eq. 4.2], while the former quantities are interdependent and must be combined, as indicated in this paper, to give a proper distribution.

Time-dependent constraints

Consider now a two-state process, A↔B, in which the energy minima and barrier height vary with time. Now, the constraint quantities, such as ⟨N_ab(t)⟩, will depend on time, as does the dynamical partition function Q_d. The Caliber formulation remains the same;^{5, 11, 12} here is an illustration of how it is implemented in this case. First, consider a discrete piecewise time variation, whereby an observable A takes on a fixed value for some time interval, and a different value over the next time interval, τ≤t:

$$⟨A\left(\tau \right)⟩=\sum _j{p}_j\left(N\right)A_j\left(\tau \right).$$ (4.4)

By fixing ⟨A(τ)⟩ for a number of times τ=τ₁,…,τ_K, we obtain the Caliber function

$$\mathcal{C}\left(t\right)=\sum _j{p}_j\left(t\right)\text{ln}{p}_j\left(t\right)+\mu \sum _j{p}_j\left(t\right)+\sum _j{p}_j\left(t\right)\sum _{\tau }{\lambda }_{j\tau }{A}_j\left(\tau \right).$$ (4.5)

It is clear that by taking the limit of small time intervals, this procedure can accommodate any arbitrary time dependence.

As an illustration, suppose the two-state system has two different rate constants over two different time regimes:

$$k_n\left(t\right)=\{\begin{array}{cc}{k}_n^{\left(1\right)}& \text{if}0\le t\le t_1,\\ k_n^{\left(2\right)}& \text{if}{t}_1\le t\le t_2.\end{array}\phantom{\}}$$ (4.6)

This corresponds to the time-dependent constraints

$$⟨N_{ab}\left(t_1\right)⟩=\sum _j{p}_j\left(N\right)N_{abj}\left(t_1\right),$$ (4.7)

$$⟨N_{ab}\left(t_2\right)⟩=\sum _j{p}_j\left(N\right)N_{abj}\left(t_2\right),$$

and similarly for the other flux quantities. As a consequence, each term in Eq. 2.20 is replaced by a double sum, e.g.,

$$\sum _{N_{abj}}{\gamma }_{ab}^{N_{abj}}\to \sum _{N_{abj}\left(t_1\right)}{\gamma }_{ab}^{N_{abj}\left(t_1\right)}\sum _{N_{abj}\left(t_2\right)}{\gamma }_{ab}^{N_{abj}\left(t_2\right)}.$$ (4.8)

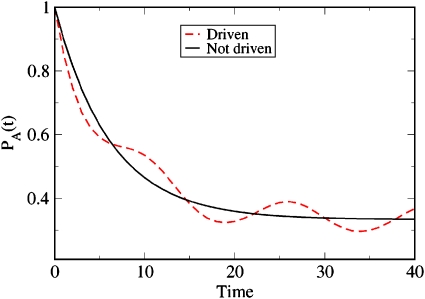
Figure 6 shows a calculation for a periodically forced two-state system. In this case, we use γ_ab(t)=γ_ab[1+0.5 cos(4γ_abt)]. To compute the dynamical properties of the system, we discretize the values of γ_ab(t) for each time interval Δt and substitute each such value into its own G matrix, which we then multiply together to get the time-dependent partition function [see Eqs. 2.5, 2.6, 2.7]. The figure shows how the computed value of the population of A, P_A(t), oscillates in time in this case.

Figure 6.

Time evolution of P_A(t) for a periodically driven two-state system (dashed line) compared to the stationary nondriven case (solid line) treated previously.

Memory effects

The Caliber approach also allows us to treat dynamics that is non-Markovian and involves memory effects. To account for the time history, we can make the substitution³

$$-k_n{P}_n\left(t\right)\to -{\int }_0^{\infty }d{t}^{\prime }{K}_n\left(t^{\prime }\right)P_n\left(t-t^{\prime }\right)$$ (4.9)

in master Eq. 3.3, where K_n(t) (n=A,B) is the memory function that accounts for the non-Markovian behavior of the system. A common form is K_n(t)=c_ne^−t∕τ_n, where τ represents the memory time.

There are different ways to treat memory effects in the Caliber formulation. First, consider the memory function

$$K_n\left(t\right)=k_n\delta \left(t-t_n\right),$$ (4.10)

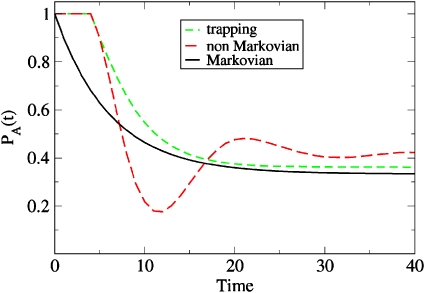
which describes a system that gets trapped in state n=A,B for t_n time steps before it can exit. For this simple case, we again get the dynamical partition function 2.3 but augmented with the additional conditions that N_aaj≥t_B and N_bbj≥t_B. Figure 7 shows the Caliber prediction for t_A=t_B=4. Starting in state A at t=0, we obtain P_A(t)=1 for t≤4 by construction. For longer times, P_A(t) looks similar to the Markovian case, although the system needs to wait each time it arrives at state A or B for at least four time steps.

Figure 7.

Two-state dynamics showing P_A(t) in two systems having memory: The system gets trapped in state A for four cycles [light dashed line, Eq. 4.10] or is trapped with an exponential memory decay [dark dashed line, Eq. 4.12], both compared to simple Markovian relaxation (solid line).

Let us now consider the case that there are only first-neighbor effects in time. Hence, we need to go beyond P_A(t) and P_B(t) and consider the joint probabilities: P_AA(t)=P(A,t∣A,t−Δt) that the system is in state A at time t given that it was in state A at time t−Δt; P_AB(t)=P(A,t∣B,t−Δt) that the system is in state A at time t given that it was in state B at time t−Δt; etc. The only modification required of the simpler Caliber treatment above is now the need for a larger transition matrix G:

$$\vec{P}\left(t\right)=\left(\begin{array}{c}{P}_{AA}\\ P_{AB}\\ P_{BA}\\ P_{BB}\end{array}\right)\to G^N\vec{P}={\left(\begin{array}{cccc}{\gamma }_{aaa}& {\gamma }_{aab}& 0& 0\\ 0& 0& {\gamma }_{aba}& {\gamma }_{abb}\\ {\gamma }_{baa}& {\gamma }_{bab}& 0& 0\\ 0& 0& {\gamma }_{bba}& {\gamma }_{bbb}\end{array}\right)}^N\left(\begin{array}{c}{P}_{AA}\\ P_{AB}\\ P_{BA}\\ P_{BB}\end{array}\right),$$ (4.11)

where γ_ijk denotes the transition probability to state j from i, given that the system was in state k before. Instead of four numbers N_A, N_B, N_ab, N_ba to characterize the occurrences of the four transition probabilities γ_aa, γ_ab, γ_ba, γ_bb along a path of the Markovian two-state system, we now need eight statistical weights. As in Eq. 2.6, each column of transition matrix G in Eq. 4.11 sums up to one. In general, to treat longer memory processes, Caliber simply requires increasingly large G matrices, and additional statistical weights that characterize those variations.

As an example, Fig. 7 shows a memory process that combines trapping and exponential decay. Here, we take

$$K_n\left(t\right)=k_n\Theta \left(t-t_n\right)e^{-\left(t-t_n\right)∕{\tau }_n}$$ (4.12)

with t_n=τ_n=4. The calculation requires the construction of a G matrix according to Eq. 4.11 including M=4 memory steps. Again we find that the population P_A(t) gets stuck in state A for t≤4. For longer times, however, the combination of trapping and exponentially decaying memory function results in an oscillatory decay of P_A(t), until equilibrium is reached.

CONCLUSIONS

We have described the Maximum Caliber approach to nonequilibrium statistical mechanics, applied to a simple dynamical two-state system, A↔B. In this approach, experimentally observable average rates are taken as input to determine microscopic dynamical statistical weight quantities. This is done using a dynamical partition function, Q_d, which is a sum over microscopic paths, resembling the way that equilibrium partition functions are sums over microstates. Caliber is quite general: It gives both the time evolution of density- or population-based quantities, as master equations do, but it also gives trajectory quantities, as Langevin models do. Analytical Langevin models require assumptions about the nature of noise distributions and are typically limited to linear dynamics. In contrast, Caliber gives a deeper foundation from which those noise distributions can be derived and is not limited to linear systems. Also, in principle, Caliber is not limited to applications near equilibrium.

While this work has been restricted to two-state dynamics, several generalizations of the Caliber formulation are obvious. First, we have shown here that Caliber can readily treat more complex dynamics, for example, in which the energy landscape itself varies in time or involving non-Markovian memory. Hence, we can also describe nonequilibrium situations with a persisting external perturbation. Second, it is straightforward to extend the theory to a general N-state system, simply by increasing the dimensionality of the G matrix. In a similar vein, standard diffusion or random walk problems can be expressed through a G matrix and subsequently treated by Caliber. Finally, we can generalize from a discrete state space (e.g., states A and B) to a continuous state space (e.g., position space x). We obtain for the continuous time evolution of a continuous state variables x(t) the path probability p[x(t)] as a functional of the path x(t), and the dynamical partition function is given by the functional integral¹³$Q_{\mathrm{d}}\left(t\right)={\int }_0^{t}p\left[x\left(\tau \right)\right]\mathrm{d}x\left(\tau \right)$, which sums up all continuous paths x(t) that start from x(0).

One of the main motivations for the Caliber approach is that it can treat single-molecule or few-particle systems, where it is of interest to know the dynamical distributions over trajectories. Also, in the same way that the MaxEnt method has found applications beyond equilibrium statistical mechanics, in signal and image processing applications, we believe that Maximum Caliber may be similarly useful for the analysis of dynamical data.

APPENDIX A: ANALYTICAL RESULTS FOR THE TWO-STATE PROBLEM

We wish to derive analytic expressions for the first moments of the distributions P(N_B,t) [Eq. 2.17] and P(N_ab,t) [Eq. 2.18], where N_B∕N is the part of the time the system spends in state B and N_ab denotes the number of switches from state B to state A. To this end, we diagonalize transition matrix G given in Eq. 2.5 in order to obtain a closed expression of the dynamical partition function Q_d in Eq. 2.4. We denote the eigenvalues of G by λ₁ (larger) and λ₂ (smaller) and the corresponding eigenvectors as (e_1a,e_1b) and (e_2a,e_2b). Thus, upon inserting the complete set we can write Q_d of Eq. 2.4 as

$$Q_{\text{d}}\left(t=N\Delta t\right)=\left(\begin{array}{cc}1& 1\end{array}\right)\left(\begin{array}{c}{e}_{1a}\\ e_{1b}\end{array}\right){\lambda }_1^N\left(\begin{array}{cc}{e}_{1a}& e_{1b}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)+\left(\begin{array}{cc}1& 1\end{array}\right)\left(\begin{array}{c}{e}_{2a}\\ e_{2b}\end{array}\right){\lambda }_2^N\left(\begin{array}{cc}{e}_{2a}& e_{2b}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(e_{1a}+e_{1b}\right)e_{1a}{\lambda }_1^N+\left(e_{2a}+e_{2b}\right)e_{2a}{\lambda }_2^N.$$ (A1)

In the limit of long times, we can approximate Eq. A1 as

$$\text{ln}{Q}_{\text{d}}\left(t=N\Delta t\right)\simeq N\text{ln}{\lambda }_1,$$ (A2)

$$\lambda \equiv {\lambda }_1=\frac{{\gamma }_{aa}+{\gamma }_{bb}}{2}+\frac{1}{2}\sqrt{{\left({\gamma }_{aa}-{\gamma }_{bb}\right)}^2+4{\gamma }_{ba}{\gamma }_{ab}},$$ (A3)

that is, the partition function Q_d depends only on the largest eigenvalue for t→∞. We note that this approximation of the equilibrium partition function is equivalent to the transfer matrix method, which is usually employed to solve Ising models.²⁷ The corresponding eigenvector (e_1a,e_1b) can be written as

$$e_{1a}\left(\lambda -{\gamma }_{aa}\right)=e_{1b}{\gamma }_{ab}.$$ (A4)

Therefore, we can express the mean flows in terms of γ_aa, γ_bb, γ_ab, and γ_ba as

$$⟨N_{ba}⟩=\frac{\partial \text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{ba}}\simeq N\frac{\partial \text{ln}\lambda }{\partial \text{ln}{\gamma }_{ba}},$$ (A5)

$$⟨N_{ab}⟩=\frac{\partial \text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{ab}}\simeq N\frac{\partial \text{ln}\lambda }{\partial \text{ln}{\gamma }_{ab}},$$ (A6)

$$⟨N_{aa}⟩=\frac{\partial \text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{aa}}\simeq N\frac{\partial \text{ln}\lambda }{\partial \text{ln}{\gamma }_{aa}},$$ (A7)

$$⟨N_{bb}⟩=\frac{\partial \text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{bb}}\simeq N\frac{\partial \text{ln}\lambda }{\partial \text{ln}{\gamma }_{bb}}.$$ (A8)

With ⟨N_A⟩=⟨N_aa⟩+⟨N_ab⟩ and ⟨N_B⟩=⟨N_bb⟩+⟨N_ba⟩, we obtain explicit expressions for the flows at t→∞:

$$\frac{⟨N_A⟩}{N}=\frac{{\gamma }_{ab}}{{\gamma }_{ab}+{\gamma }_{ba}},\frac{⟨N_B⟩}{N}=1-\frac{⟨N_A⟩}{N}=\frac{{\gamma }_{ba}}{{\gamma }_{ba}+{\gamma }_{ab}},$$ (A9)

$$\frac{⟨N_{ab}⟩}{N}=\frac{⟨N_{ba}⟩}{N}=\frac{{\gamma }_{ab}{\gamma }_{ba}}{{\gamma }_{ab}+{\gamma }_{ba}}.$$ (A10)

To derive similar results for the second moments, we use Eq. 2.3 to derive the expressions

$$\frac{⟨N_B^2⟩-{⟨N_B⟩}^2}{N}=\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\left({\gamma }_{bb}\right)}^2}+\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\left({\gamma }_{ba}\right)}^2}+2\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial \text{ln}{\gamma }_{bb}\partial \text{ln}{\gamma }_{ba}},$$ (A11)

$$\frac{⟨{\left(N_{ba}\right)}^2⟩-{⟨N_{ba}⟩}^2}{N}=\frac{{\partial }^2\text{ln}{Q}_{\text{d}}}{\partial {\left(\text{ln}{\gamma }_{ab}\right)}^2}.$$ (A12)

Using the same strategy as described above, we then obtain

$$\frac{⟨N_B^2⟩-{⟨N_B⟩}^2}{N}=\frac{2{\gamma }_{ba}{\gamma }_{ab}}{{\left({\gamma }_{ba}+{\gamma }_{ab}\right)}^3}-\frac{{\gamma }_{ba}{\gamma }_{ab}}{{\left({\gamma }_{ba}+{\gamma }_{ab}\right)}^2},$$ (A13)

$$\frac{⟨{\left(N_{ba}\right)}^2⟩-{⟨N_{ba}⟩}^2}{N}=\frac{{\gamma }_{ba}{\gamma }_{ab}}{{\gamma }_{ba}+{\gamma }_{ab}}\left[\frac{{\gamma }_{ab}^2+{\gamma }_{ba}^2}{{\left({\gamma }_{ba}+{\gamma }_{ab}\right)}^2}-\frac{{\gamma }_{ba}{\gamma }_{ab}}{{\gamma }_{ba}+{\gamma }_{ab}}\right].$$ (A14)

Similarly, the third moments can be calculated by taking the appropriate derivatives of the partition sum. Here we report the third moment of the stochastic variable N_ba,

$${⟨\left(N_{ba}-⟨N_{ba}⟩\right)⟩}^3=\frac{{\gamma }_{ab}{\gamma }_{ba}}{{\gamma }_{ab}+{\gamma }_{ba}}-3\frac{{\gamma }_{ab}^2{\gamma }_{ba}^2}{{\left({\gamma }_{ab}+{\gamma }_{ba}\right)}^2}-6\frac{{\gamma }_{ab}^2{\gamma }_{ba}^2}{{\left({\gamma }_{ab}+{\gamma }_{ba}\right)}^3}+2\frac{{\gamma }_{ba}^3{\gamma }_{ab}^3}{{\left({\gamma }_{ba}+{\gamma }_{ab}\right)}^3}+6\frac{{\gamma }_{ab}^3{\gamma }_{ba}^3}{{\left({\gamma }_{ab}+{\gamma }_{ba}\right)}^4}+12\frac{{\gamma }_{ab}^3{\gamma }_{ba}^3}{{\left({\gamma }_{ab}+{\gamma }_{ba}\right)}^5}.$$ (A15)

APPENDIX B: NOISE DISTRIBUTION OF THE CHEMICAL LANGEVIN MODEL

Consider a single time step, Δt=1. In order to calculate the moments of Langevin noise 3.11, we first evaluate the distribution P(m,n) defined in Eq. 3.12. In leading order, only jumps with m=0,±1 are considered, which leads to

$$P\left(m,n\right)=P_n\left(t\right)\{\begin{array}{l}n{\gamma }_{aa}^{n-1}{\gamma }_{ba}{\gamma }_{bb}^{M-n},\text{if}m=n-1,\\ \left[{\gamma }_{aa}^n{\gamma }_{bb}^{M-n}+n\left(M-n\right){\gamma }_{ba}{\gamma }_{aa}^{n-1}{\gamma }_{bb}^{M-n-1}{\gamma }_{ab}\right],\text{if}m=n,\\ \left(M-n\right){\gamma }_{ab}{\gamma }_{aa}^n{\gamma }_{bb}^{M-n-1},\text{if}m=n+1,\end{array}\phantom{\}}$$ (B1)

where P_n(t) is given by Eq. 3.6. Using γ_aa=1−γ_ba, γ_bb=1−γ_ab, γ_ba=k_a, γ_ab=k_b, and expanding to first order in k_a and k_b, we obtain

$$P\left(m,n\right)=P_n\left(t\right)\{\begin{array}{l}n{k}_a,\text{if}m=n-1,\\ \left(1-n{k}_a-\left(M-n\right)k_b\right),\text{if}m=n,\\ \left(M-n\right)k_b,\text{if}m=n+1.\end{array}\phantom{\}}$$ (B2)

Insertion in Eq. 3.11 gives for the second moment of F(t)

$$⟨F{\left(t\right)}^2⟩=\sum _n{P}_n\left(t\right)\left\{{\left(n\left(k_a+k_b\right)-M{k}_b-1\right)}^{2}n{k}_a+{\left(n\left(k_a+k_b\right)-M{k}_b\right)}^2\left(1-n{k}_a-M{k}_b+n{k}_b\right)+{\left(n\left(k_a+k_b\right)-M{k}_b+1\right)}^2\left(M-n\right)k_b\right\}.$$ (B3)

Using $P_n\left(t\right)=\left(\genfrac{}{}{0ex}{}{M}{n}\right)P_A^n{\left(1-P_A\right)}^{M-n}$, this simplifies to

$$⟨F{\left(t\right)}^2⟩=⟨\left(M{k}_b-n{k}_b+n{k}_a\right)⟩-⟨{\left(M{k}_b-n{k}_a-n{k}_b\right)}^2⟩=M\left(k_a{P}_A+k_b{P}_B\right).$$ (B4)

In the last line we used that ⟨n⟩=MP_A and $⟨n^2⟩=M{P}_A{P}_B+M^2{P}_A^2$ and kept only terms to first order in k_a and k_b. Since P_A(∞)=k_b∕(k_a+k_b)=1−P_B(∞), we obtain at long times

$$⟨F{\left(\infty \right)}^2⟩=\frac{2M{k}_a{k}_b}{k_a+k_b}.$$ (B5)

In complete analogy to the above derivation, we can also calculate higher moments of F(t) from Eq. B2. For example, the third moment reads

$$⟨F{\left(t\right)}^3⟩=⟨{\left(n\left(k_a+k_b\right)-M{k}_b+1\right)}^3\left(\left(M-n\right)k_b\right)⟩+⟨{\left(n\left(k_a+k_b\right)-M{k}_b-1\right)}^3\left(n{k}_a\right)⟩+⟨{\left(n\left(k_a+k_b\right)-M{k}_b\right)}^3\left(1-n{k}_a-\left(M-n\right)k_b\right)⟩.$$

In leading order we then obtain

$$⟨F{\left(t\right)}^3⟩=⟨\left(M-n\right)⟩k_b-⟨n⟩k_a=M\left(P_B\left(t\right)k_b-P_A\left(t\right)k_a\right),$$ (B6)

which vanishes in the limit of long times

$$⟨F{\left(\infty \right)}^3⟩=M\left(P_B\left(\infty \right)k_b-P_A\left(\infty \right)k_a\right)=0.$$ (B7)