Probing the mechanisms of fibril formation using lattice models

Abstract

Using exhaustive Monte Carlo simulations we study the kinetics and mechanism of fibril formation using lattice models as a function of temperature (T) and the number of chains (M). While these models are, at best, caricatures of peptides, we show that a number of generic features thought to govern fibril assembly are captured by the toy model. The monomer, which contains eight beads made from three letters (hydrophobic, polar, and charged), adopts a compact conformation in the native state. In both the single-layered protofilament (seen for M⩽10) and the two-layer fibril (M>10) structures, the monomers are arranged in an antiparallel fashion with the “strandlike” conformation that is perpendicular to the fibril axis. Partial unfolding of the folded monomer that populates an aggregation prone conformation (N^*) is required for ordered assembly. The contacts in the N^* conformation, which is one of the four structures in the first “excited” state of the monomer, are also present in the native conformation. The time scale for fibril formation is a minimum in the T-range when the conformation N^* is substantially populated. The kinetics of fibril assembly occurs in three distinct stages. In each stage there is a cascade of events that transforms the monomers and oligomers to ordered structures. In the first “burst” stage, highly mobile oligomers of varying sizes form. The conversion to the N^* conformation occurs within the oligomers during the second stage in which a vast number of interchain contacts are established. As time progresses, a dominant cluster emerges that contains a majority of the chains. In the final stage, the aggregation of N^* particles serve as a template onto which smaller oligomers or monomers can dock and undergo conversion to fibril structures. The overall time for growth in the latter stages is well described by the Lifshitz–Slyazov growth kinetics for crystallization from supersaturated solutions. The detailed analysis shows that elements of the three popular models, namely, nucleation and growth, templated assembly, and nucleated conformational conversion are present at various stages of fibril assembly.

INTRODUCTION

The link between aggregation of proteins and a number of neurodegenerative diseases has spurred many experimental^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and theoretical studies.^{11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23} Aggregation rates depend not only on protein sequence but also on the concentration of proteins and external conditions (temperature, pH, presence of crowding agents, etc.). The observation that many proteins that are unrelated by sequence and structure can aggregate and form fibrils¹⁰ with similar morphologies (albeit under different growth conditions) suggests that certain generic aspects of oligomerization and subsequent fibril growth can be gleaned from toy models. Toward this end, a number of lattice models^{11, 24, 25} have been introduced to probe the fibril formation mechanism. Here, following the important studies by Hall and co-workers,¹¹ we use a three-dimensional lattice model that is, in part, inspired by all-atom simulations of oligomer formation of the peptide fragment Aβ_16–22,¹⁶ to provide insights into mechanism of fibril formation.

Soluble (S) monomeric polypeptide chains can be either random coil-like (Aβ peptides or α-synuclein) or folded (transthyretin). Typically, fluctuations or denaturation stress can populate one of several aggregation-prone conformations (N^*). Because of conformational variations in N^*, fibrils with differing molecular structure can form starting from the same sequence. However, the growth mechanism starting from N^* to the fibril state is not fully understood. Three mechanisms for fibril assembly have been proposed. In the nucleation-growth (NG) mechanism,^{26, 27} the first step is the oligomerization of a sufficient number of N^* particles that form a critical nucleus, which is a free-energetically uphill process. Upon forming ${\mathbf{N}}_n^{*}$ (with n>the size of the critical nucleus n_c), S monomers can rapidly add to the oligomer resulting in their growth and eventual fibril assembly. The templated-assembly (TA) process^{28, 29, 30} suggests that preformed ${\mathbf{N}}_n^{*}$ complex, with presumably n>n_c, serves as a template onto which S or N^* can dock and undergo the needed structural rearrangement to lock onto the template. Based on kinetic data on prion formation in yeasts, the nucleated conformational conversion (NCC) model^{1, 31} has been proposed. In the NCC model, it is envisioned that S forms mobile disordered oligomers. The monomers in the oligomer undergo S→N^* conversion to form nuclei ${\mathbf{N}}_n^{*}$. The species ${\mathbf{N}}_n^{*}$ can serve as a template and incorporate other (less structured) oligomers or monomers to rapidly form ordered fibrils. The important feature of NCC is that structural rearrangement S→N^*→N_fib (N_fib is the monomer structure in the fibril) occurs within the molten oligomer. In many cases, the structures of N^* and N_fib are similar.

In this paper, we study the mechanism of fibril assembly using a simple lattice model for which extensive simulations can be performed. The analysis reveals a complex scenario for protofilament and fibril assembly that has the elements of all three growth models. The dependence of fibril formation time τ_fib on the number of monomers reveals that late stages of growth have a lot in common with crystallization in supersaturated solutions. These findings arise from detailed Monte Carlo (MC) simulation studies using a toy lattice model in which each chain has N=8 beads of three types, namely, hydrophobic (H), polar (P), and charged (see Sec. 2). Our simulations show that the overall assembly of ordered protofilaments and fibrils occur in three distinct stages. The smallest time scale is associated with a fast “burst phase” during which highly mobile oligomers form. During this stage there is a distribution of oligomers of varying sizes. Because we are forced to simulate a finite number of chains, we cannot quantify the nature of the size distribution. The second stage is the transformation of the burst phase structures into a disordered but compact oligomer in which about half of the interpeptide contacts form. It is likely that the conformational transition from S→N^* takes place during this stage, as envisioned in the NCC model. The longest time scale corresponds to the final stage of fibril formation. In this stage, the large clusters grow by incorporating the small clusters. The structural transitions here are best described by a dock-lock mechanism that requires the presence of a template. Thus, even in the toy model there are complex structural transitions that take place in each stage of assembly. It appears that elements of NG, TA, and NCC are operative at different stages of fibril formation.

METHODS

Model

Each chain consists of N connected beads that are confined to the vertices of a cube. The simulations are done using M identical chains with N=8. The sequence of a chain is +HHPPHH−, where + and − are charged beads. The assignment of chemical character and the nature of interactions between the beads should be viewed as a caricature of polypeptide chains and are not a realistic representation of amino acids. Despite such a drastic simplification, it has been shown that lattice models are useful in providing insights into protein folding mechanisms.^{32, 33, 34}

The inter- and intrachain potentials include excluded volume and contact (nearest neighbor) interactions. Excluded volume is imposed by the condition that a lattice site can be occupied by only one bead. The energy of M chains is

$$E=\sum _{l=1}^M\sum _{i<j}^N{e}_{sl\left(i\right)sl\left(j\right)}\delta (r_{ij}-a)+\sum _{m<l}^M\sum _{i,j}^N{e}_{sl\left(i\right)sm\left(j\right)}\delta (r_{ij}-a),$$ (1)

where r_ij is the distance between residues i and j, a is the lattice spacing, sm(i) indicates the type of residue i in the mth peptide, and δ(0)=1 and zero, otherwise. The first and second terms in Eq. 1 represent intrapeptide and interpeptide interactions, respectively.

The contact energies between the H beads e_HH is −1 (in the units of k_BT). The propensity of polar (including charged) residues to be “solvated” is mimicked by using e_Pα=−0.2, where α=P, + or −. “Salt-bridge” formation between oppositely charged beads is accounted for by a favorable contact energy e₊₋=−1.4. All other contact interactions are repulsive. The generic value for repulsion e_αβ is 0.2. For a pair of like-charged beads, the repulsion is stronger, i.e., e₊₊=e₋₋=(0.7). The chains were confined to the vertices of the three-dimensional hypercube. For example, when M=10 the length of the hypercube is 10a. Therefore, the volume fraction occupied by the peptides is 0.08, and the concentration corresponds to 250 mM. This is about three orders of magnitude denser than that used in typical experiments.

Simulation details

The simulations were performed by enclosing M chains in a box with periodic boundary conditions. We use MC algorithm to study the kinetics of amyloid formation. At the beginning of each MC cycle, a peptide is selected at random. Then one of the two types of MC moves, global or local, is randomly chosen. The acceptance probabilities of global and local moves are 0.1 and 0.9, respectively. Global moves correspond to either translation of a peptide by a in a randomly chosen direction or rotation by 90° around one of the randomly chosen coordinate axes. The direction of rotation as well as the type of global move are selected at random. A local move corresponds to tail rotation, corner flip, and crankshaft rotation.³⁵ Given the condition that a local move is accepted with 0.9 probability, we used the same relative probabilities for selecting the particular types of local moves as described elsewhere.³⁶ We measure time in units of MC steps (MCS). The combination of local and global moves constitutes one MCS.

For interacting chains, which leads to complex formation, care must be taken to ensure that move sets are efficient enough so that on the simulation time scale equilibrium is established.³⁷ Our previous work²⁵ on lattice model for aggregation showed that the relative rotation of chains, in a complex, is a slow process. Thus, we explicitly allowed for such moves and global translation. The acceptance rates were adjusted to ensure that chain disassociation occurs. Multiple association and disassociation of chains from transiently formed oligomers assures us (but does not prove) that for M=16 we have approached equilibrium at long times. In addition, the kinetic simulations lead to the ordered structure that is identical to the one obtained by an independent simulated annealing protocol.

Structural probes

The contacts in the aggregated state (oligomer or fibrils) are divided into two categories; intrapeptide and interpeptide. If two nonbonded beads (i.e., those that are not covalently linked) of a given chain are near neighbors, then they form an intrachain contact. An interpeptide contact in an ordered conformation is one that is (i) formed between beads belonging to different peptides, and (ii) the associated peptide bonds are in the ordered state. All interpeptide contacts in the fibril structure satisfy condition (ii), although this is not generally the case for an arbitrary oligomeric structure. The numbers of intrapeptide and interpeptide fibril contacts in an arbitrary conformation are denoted as Q_m and Q_f with Q_m,0 and Q_f,0 being their values in the fibril state. In what follows, quantities with the subscript 0 correspond to the fibril structure.

In order to probe the growth of the fibril, we obtained the distribution of the fibril clusters in a given oligomer conformation. A fibril cluster is computed by selecting a pair of fibril contacts and adding adjacent fibril contacts whose peptide bonds are parallel or antiparallel to the bonds associated with the original fibril contact pair. The growth of the fibril cluster continues until no more fibril contacts can be added to the cluster in any direction. A typical oligomer contains several fibril clusters of different sizes that are measured by the number of incorporated fibril contacts. The number of fibril contacts in the largest cluster is denoted by Q_fc. In the fibril structure, a single fibril cluster consumes all of the residues and chains, and hence Q_fc=Q_f.

We have also computed the number of interpeptide contacts (of any type) C_out, which describes the formation of the aggregated state. Aggregation of chains is also monitored by computing the distribution of oligomers. An oligomer is defined as a group of aggregated chains. Two oligomers are distinct if none of the chains from one oligomer interacts with any chain from the other. A given multichain conformation may contain several oligomers, and their number N₀ is useful to characterize the process of aggregation. In addition, the number of peptides in the largest oligomer N_p is computed. As aggregation progresses, N_p approaches M.

Kinetics of assembly

To follow the kinetics of aggregation, an initial distribution of M random peptide structures is generated and equilibrated at high temperature (T=3.0) for 10⁵ MCS. The resulting distribution of chains is used as a starting point for initiating fibril assembly which begins by quenching the temperature to T_s (<3.0). Each MC trajectory starts with a unique distribution of chains. The total number of MC trajectories N_MC for a given T_s varies from 100 to 400. The first instance, when the fraction of intrapeptide and interpeptide fibril contacts exceed 0.85, is associated with the first passage time τ_fib,i for fibril assembly for a trajectory i. The condition Q(=0.85), which is the fraction of intra- and interchain fibril contacts, was chosen empirically by analyzing numerous MC trajectories. The mean time of fibril assembly is computed by fitting the yield of the fibril structure P_f(t) in the pool of N_MC independent MC trajectories.

Rapid nucleation of fibril structure was analyzed as follows. For each trajectory, we considered an interval of 10⁶ MCS immediately preceding τ_fib,i and computed various quantities associated with fibril formation as described above. In addition, within the time interval, τ_fib,i−10⁶<t<τ_fib,i, we considered the subset of fibril contacts in the largest fibril cluster Q_fc, which satisfy two conditions,^{38, 39} namely, (i) that these fibril contacts are formed at the time of fibril assembly, τ_fib,i, and (ii) that apart from short lived disruptions they remain stable within the interval (t,τ_fib,i). The disruptions of fibril contacts must not exceed t=2000 MCS. The results do not depend on the specific value of t when it is varied by ±1000 MCS. The fibril contacts satisfying these two conditions are referred to as “nucleation” fibril contacts and their number is denoted as Q_nfc.

RESULTS AND DISCUSSION

Monomeric and fibril structures

Monomer

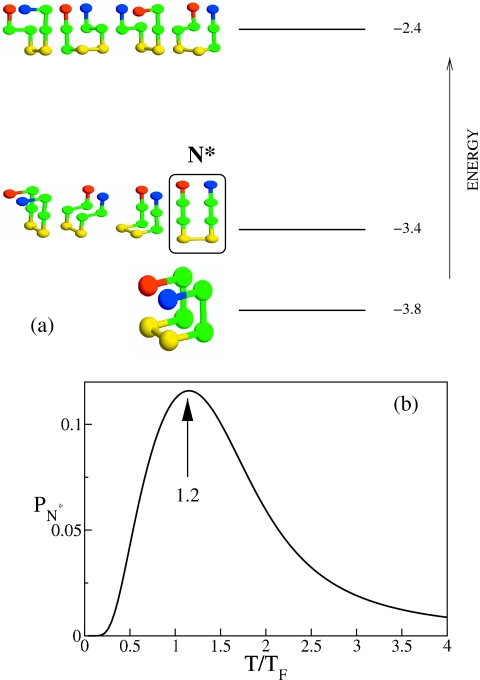
The exact enumeration of all possible conformations of the monomer of eight beads shows that there are 18 energy levels. The three lowest levels in the spectrum are presented in Fig. 1. The monomeric native state is compact, and it has the lowest energy E=−3.8. It should be noted that the conformation of the chain in the fibril state is not compact, and it belongs to the first excited state (label N^* in Fig. 1) which is fourfold degenerate. Fluctuations in the monomer conformations has to populate the structure with E=−3.4 for oligomerization to start. Such fluctuations, under condition when the native structure is stable, can occur spontaneously or through interchain interactions. Clearly, suppression of fluctuations at low temperatures would slow down the process of ologimerization. The toy model captures the well-accepted proposition that aggregation requires partial unfolding of the native conformation.⁴⁰

Figure 1.

(a) Energies and structures of some of the conformations of the monomer using exact numeration. Hydrophobic, polar, positively, and negatively charged beads are shown in green, yellow, blue, and red, respectively. There are a total 1831 possible conformations that are spread among 18 possible energy values. The nondegenerate native conformation is separated from degenerate higher energy conformations. The structure enclosed in the box is the one that the chain adopts in the fibril, and is referred to as N^*. The second highest energy structures are also fourfold degenerate. (b) The probability P_N^* of populating the aggregation-prone structure N^* as a function of T. The arrow indicates the temperature at which P_N^* is maximum.

Ensemble of peptides

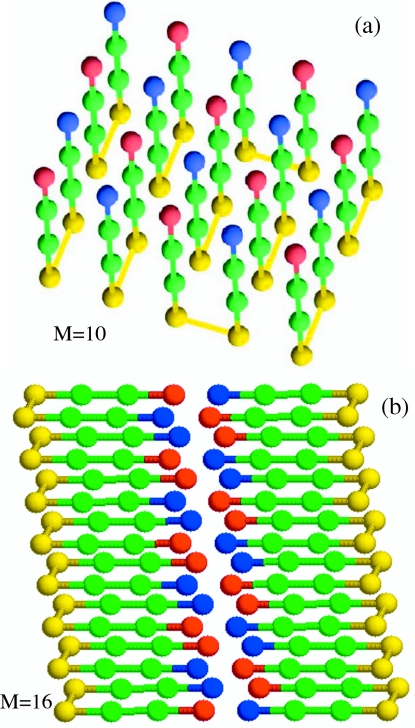
When multiple chains are present in the unit cell, aggregation is readily observed, and in due course they form ordered structures (Fig. 2). Exact enumeration of all the conformations for multichain systems is not possible so the structure of the lowest energy has to be determined using simulations. We used the MC annealing protocol, which allows for the exhaustive conformational search, to find the lowest energy conformation. In the ordered protofilament (M=10) and fibril (M=16) structures, the chains adopt an antiparallel arrangement (Fig. 2).

Figure 2.

(a) The lowest energy structure for ten monomers (M=10). The chains are arranged in an antiparallel manner. The structure of the monomer is the same as the N^* conformation in Fig. 1a. Beads are colored in the same manner as in Fig. 1a. This single-layer structure is a protofilament. (b) The double-layer structure of M=16. As in fibrils of polypeptides the “β-sheet-like” monomers are arranged perpendicular to the fibril axis which lies parallel to the salt-bridge plan (contact between blue and red). Thus, the protofilament and the fibril are stabilized by hydrophobic interactions and salt bridges.

The nature of ordering changes depending on M, and hence the concentration. For M⩽10 the chains are arranged in a single layer, while for M>10 the fibril state has a double-layer arrangement (Fig. 2). Just as noted, using all-atom molecular dynamics simulations,⁴¹ the organization of the chains in the fibril satisfies the principles of amyloid self-assembly (PASA) which states that the fibril structures are determined by maximizing the number of salt bridges and hydrophobic contacts.⁴¹ In accord with PASA, we found that the organization of the lowest energy structure demonstrates a remarkable order, leading to the maximization of favorable electrostatic and hydrophobic interactions (Fig. 2). All H (in green) beads located at the core of the fibril are sandwiched between exposed layers of P (in yellow) and charged beads (in blue and red). More importantly, all of the peptides adopt an in-registry antiparallel mutual orientation, which implies that for all bond vectors connecting nearest neighbor pairs of residues (i,N−i+1) and $(i+1,N-i){\vec{r}}_{i,i+1}^m=-{\vec{r}}_{N-i,N-i+1}^l$, where m and l are the peptide indices. The antiparallel arrangement is enforced by favorable electrostatic interactions. Figure 2 shows that the nearest neighbors of all negatively charged terminals (in red) are positively charged beads (in blue).

For M=10, there are in all 84 interpeptide fibril contacts and 30 intrapeptide contacts, and the entire protofilament structure in Fig. 2a comprises a single layer. This implies that a given interpeptide antiparallel in-registry arrangement of the chains is translated across the entire volume of the fibril in all directions. It is interesting that all intrapeptide contacts are also found in the native conformation of the monomer [lowest energy conformation in Fig. 1a] and the N^* structure [Fig. 1a]. Due to different possible distributions of peptides within the volume of a fibril, the lowest energy fibril structure has nonzero entropy.

The fibril contains both interpeptide and intrapeptide interactions. The structure of the monomer in the ordered fibril coincides with one of the structures that is higher in energy than the native monomer conformation (conformation N^* in Fig. 1). Because the fibrils are associated with aggregation of unfolded structures (here the first excited state in the spectrum of allowed monomer conformation), it is logical that other morphologies, which nucleate from different unfolded conformations, can form. By scanning the sequences for N=8, we could not produce fibrils starting from one of the high energy monomer conformations which highlights one of the limitations of the lattice model. This observation suggests that as long as the peptide sequence contains hydrophobic patches and oppositely charged residues distributed along the sequence, the fibril structure is likely to include a mixture of inter- and intrapeptide interactions. A combination of inter- and intrapeptide contacts maximizes the number of hydrophobic and salt bridges thus satisfying the PASA.

There are superficial similarities between structures in Fig. 2 and the model proposed for Aβ_1–40, whose sequence is interspersed with charged and hydrophobic residues. The amyloidgenic Aβ peptide contains two hydrophobic regions (central hydrophobic cluster and the C-terminal), as well as charged residues. The proposed fibril model for Aβ_1–40 is based on the assumption that an Aβ_1–40 monomer contains a turn, which brings the two hydrophobic regions in proximity and facilitates the formation of a salt bridge.⁴²

Time scales for monomer folding and fibril assembly

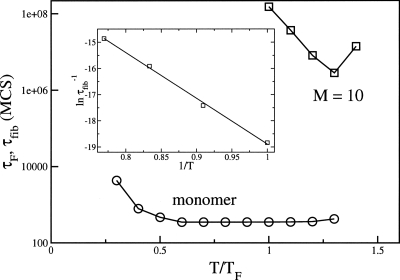
The short chain (N=8) allows us to compute the times τ_F for monomer folding as a function of temperature. The decay of the population of unfolded conformations is best described using a single exponential (data not shown), which is a characteristic of well-designed sequence. The folding time τ_F is well below 10³ MCS (Fig. 3) over a wide temperature range. In contrast, the temperature-dependent time for fibril formation τ_fib is dramatically different (Fig. 3). There are two striking observations about τ_fib. First, τ_fib is about four to six orders of magnitude larger than τ_F. Clearly, the sizes of the monomer and the fibril can cause the vastly greater value of τ_fib compared to τ_F. The effect of the system size can be roughly rationalized using the approximate dependence of τ_F on N.⁴³ It has been shown that ${\tau }_F\approx {\tau }_{F0}{e}^{1.1\sqrt{N}}$.⁴⁴ Assuming that τ_F0 does not change significantly and taking into account that the fibril in our model is ten times larger, then the monomer size alone would yield τ_fib∕τ_F∼10³. In addition, the formation of fibril (or protofibrils) also requires collective fluctuation (e.g., formation of nucleus), which requires that several monomers access the N^* structure in the first excited state of the isolated monomer (Fig. 1). There are barriers associated with such processes that also increase τ_fib. The relative values τ_fib∼(10⁴–10⁶)τ_F is not inconsistent with experimental observations. Typical values of τ_F for small proteins is about 1–100 ms. Thus, our simulations would suggest τ_fib∼10²–10⁴ s if τ_F∼10 ms.

Figure 3.

The temperature dependence of monomeric folding time τ_F (open circles) and the time for protofilament assembly τ_fib (squares) for M=10. Temperature is given in the units of the monomer folding temperature T_F=0.5. This value of T_F is obtained using the condition ⟨Q(T_F)⟩=0.5, where ⟨Q(T_F)⟩ is the fraction of native contacts. The inset shows ${\tau }_{\mathrm{fib}}^{-1}$ at low temperatures as a function of 1∕T for M=10.

The most striking aspect of Fig. 3 is the dramatic differences in the T-dependence of τ_F(T) and τ_fib(T). The temperature independence of τ_F(T) in the 0.3T_F⩽T⩽1.3T_F is typical of well-designed monomer sequences for which T_F≈T_θ, where T_θ is the collapse transition temperature.⁴⁵ In contrast, τ_fib(T) changes drastically as T varies. In the narrow temperature range (T_F⩽T⩽1.4T_F), τ_fib varies by almost two orders of magnitude. At the temperature T≈1.3T_F (Fig. 3), when τ_fib is the smallest, the native structure is less stable than the unfolded ensemble. The structures of the partially unfolded conformations at T≈1.3T_F shows that the probability of the “salt bridges” (intramolecular contact between + and − beads) being in contact exceeds 0.5. At T≈1.3T_F there is a substantial probability of populating the aggregation-prone monomer [Fig. 1b], which acts as a seed for nucleation and growth. At T≈1.3T_F, the fibrils form in the smallest time with 100% yield, whereas at T=T_F the yield of the fibril drops to 0.42 during the simulations lasting 10⁸ MCS.

The observation that partial unfolding of the native state is a necessary condition for oligomerization and fibril growth is consistent with experimental observations that many nonhomologous protein sequences assemble into amyloid fibrils under denaturing conditions.⁴⁶ Although the formation of fibrils is apparently a generic feature of polypeptide sequences, our simulations suggest that for a given sequence, there may be only a narrow window of external conditions that favor rapid fibril assembly. Besides requiring that the native monomer partially unfolds for aggregation to begin, the denaturing conditions must also be relatively mild. Under these conditions, aggregation-prone structures with intramolecular native interactions that are moderately stable can be populated. In our model, the conformation that nucleates and grows (Fig. 1) is homogeneous, which results in a unique fibril structure. Denaturing conditions that favor its formation, with intact salt bridges results in the most rapid assembly (Fig. 1). In polypeptide chains, there may be a collection of conformations that can lead to fibrils. The differences in fibril morphology is probably linked to the variations in the initial conformations of the monomer.

Fibril assembly occurs in three major stages

Formation of protofilaments

To provide microscopic details of fibril assembly, we generated multiple MC trajectories for M=10 at T_s=0.65=1.3T_F at which τ_fib is the smallest (Fig. 3). In all, 100 MC trajectories starting from random initial conditions were generated. The length of the MC trajectories (8×10⁷ MCS) at T_s was sufficiently long to observe ordered structure formation in each trajectory. Figure 4 displays several quantities averaged over 100 trajectories and normalized to vary from 1 (at t=0) to 0 (the equilibrium value). The averaging over the ensemble of trajectories is indicated by angular brackets ⟨ ⟩. The time scales from exponential fits to these functions describe the kinetics of fibril formation. The analysis of the various time dependent quantities and the inspection of the structures sampled enroute to the final fibril gives an intuitive picture of assembly and growth.

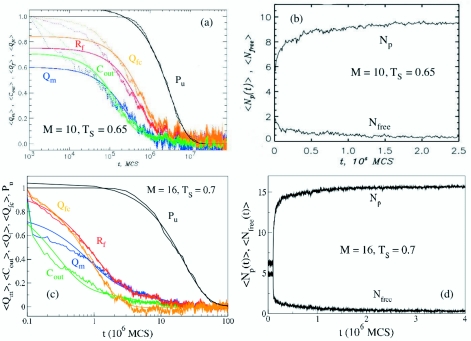
Figure 4.

(a) Time dependence of structural quantities probing the formation of fibril structure. The number of intrapeptide fibril contacts ⟨Q_m(t)⟩, the number of interpeptide contacts ⟨C_out(t)⟩, the number of fibril contacts ⟨Q_f(t)⟩, and the number of fibril contacts in the largest fibril cluster ⟨Q_fc(t)⟩ are shown in blue, green, red, and orange, respectively. The data are averaged over 100 trajectories, and smooth lines represent the biexponential fits to the data. The fraction of trajectories in which the fibril structure is still not reached, P_u(t), is shown in black. (b) The time dependence of the number of peptides in the largest oligomer ⟨N_p(t)⟩ and the number of free peptides ⟨N_free(t)⟩. (c) Same as in (a) except the results for M=16. (d) Same as (b) but for M=16.

Immediately after the temperature quench to T_s, the chains are randomly distributed in the unit cell. The numbers of intra- and interpeptide fibril contacts are negligible, and there are relatively few interchain interactions. The largest oligomer contains, on average, four chains (N_p=4). Within a short time, the interchain interactions trigger the formation of oligomers, which represent the growth stage in the route to fibrils. Figure 4b shows that the average number of free chains ⟨N_free⟩ (i.e., those which do not make interpeptide contacts) is less than 1 in ≈0.03×10⁶ MCS or 0.01τ_fib. Almost concurrently, the number of peptides in the largest oligomer ⟨N_p(t)⟩ exceeds 9. Thus, already in the initial stage, the chains interact and cooperatively form fluidlike oligomers. Indeed, ⟨N_p(t)⟩ grows on the time scale of 0.06×10⁶ MCS or 0.02τ_fib, and approaches its equilibrium value of 9.8. Therefore, virtually all of the chains are incorporated in a single burst phase leading to mobile oligomer formation.

The second stage in fibril assembly is associated with the formation of intra- and interpeptide interactions, which transforms the mobile oligomer formed in the first stage into a compact disordered oligomer. During this stage, structural rearrangement and conversion from S→N^* take place, as shown by a number of quantities. The intrapeptide fibril contacts ⟨Q_m(t)⟩ [data in blue in Fig. 4a] are formed on the time scale of 0.1τ_fib. On a similar time scale, the number of interpeptide contacts ⟨C_out(t)⟩ (data in green) approaches the equilibrium value of approximately 67. Interestingly, the number of distinct clusters ⟨N_fc(t)⟩ reaches a maximum during this stage of fibril assembly (data not shown). We surmise that the disordered oligomer contains as many as four distinct fibril clusters, the largest of which already comprises roughly 50% of the entire protofilament. Figure 4a further demonstrates that at t≈0.1τ_fib the distribution of the volume of fibril clusters extends from predominantly small clusters (Q_fc⩽14) to larger ones (15⩽Q_fc⩽28). The total number of fibril contacts is still relatively small in the disordered oligomer (⟨Q_f(0.2τ_fib)⟩≈30=0.36Q_fc,0). Therefore, disordered oligomers are characterized by a nascent single-layer protofilamentlike structure [Fig. 2a], which emerges in the oligomer volume as a distribution of disjoint fibril clusters of varying sizes.

The transformation of disordered oligomers to an ordered structure occurs during the third stage of fibril assembly. It follows from Fig. 4a that the time scale for the formation of interpeptide fibril contacts ⟨Q_f(t)⟩ is 0.5×10⁶ MCS or ≈0.2τ_fib (data in red). Importantly, on the same time scale, the dominant fibril cluster grows as shown by ⟨Q_fc(t)⟩ (data in orange). This result indicates that the formation of the fibril structure occurs via the growth of the largest fibril cluster at the expense of small clusters. The winner-take-all scenario of fibril growth is further described below. The number of fibril clusters ⟨N_fc(t)⟩ decreases to less than 3 in the time interval of 0.2τ_fib<t<τ_fib. On the other hand, the maximum in the kinetic distribution of the fibril structure among the clusters shifts to the right, signaling the emergence of large clusters (43⩽Q_fc⩽70). By assigning weight in proportion to the size of fibril clusters, we find that the dominant fibril cluster comprises of almost the entire fibril structure. In accord with this conclusion, we found that the number of fibril contacts (i.e., the degree of fibril structure) in the largest clusters is 43⩽Q_fc⩽70 (results not shown). It is clear that at t>0.4τ_fib more than 80% of ordered structure is localized in a single large fibril cluster. Because on these time scales ⟨N_fc(t)⟩≈2, the remaining 10%–20% of fibril contacts are found in a much smaller satellite fibril cluster.

The formation of a dominant cluster containing the protofilament also follows from the calculations of thermodynamic quantities. The thermal averages of the number of fibril contacts ⟨Q_f⟩ and the number of fibril contacts in the largest fibril cluster ⟨Q_fc⟩ are 52 and 47, respectively. Thus, ⟨Q_fc⟩=0.90 ⟨Q_f⟩. After the dominant fibril cluster appears at t≈0.4τ_fib its further growth and consolidation continues until it reaches its equilibrium size (about 60% of all fibril contacts). This kinetic phase can be described by additional time scale with a small amplitude. Due to this additional fibril ordering, the final fibril assembly takes place only at τ_fib=3.3×10⁶ MCS. Thus, long after the formation of the largest cluster, structural reorganization continues until the ordered stable fibril forms. The slow TA within the large cluster is reminiscent of the lock phase.

Mechanism of fibril assembly

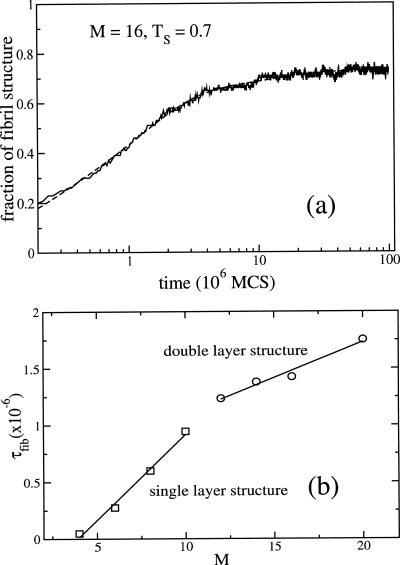
In order to probe the mechanism of fibril formation [two-layer structure in Fig. 2b] at T_s=0.7, we generated 100 trajectories with each being 10⁸ MCS. The mean time for fibril formation is τ_fib≈2×10⁷ MCS. These long runs ensure that the fully ordered state is reached in each trajectory. Qualitatively, the fibril formation kinetics is the same as in the M=10 case, i.e., it follows three-stage kinetics. However, there are a few quantitative differences. In the protofilament formation case, the interpeptide contacts ⟨C_out(t)⟩, and intrapeptide fibril contacts ⟨Q_m(t)⟩ [Fig. 4b] are formed on the same time scale. For M=16 [Fig. 4c] ⟨C_out(t)⟩ approaches the value of 0.5 earlier. A fit of ⟨C_out(t)⟩ using a sum of three-exponential functions gives τ₁=0.15×10⁶ MCS≈0.01τ_fib, τ₂≈10⁶ MCS≈0.05τ_fib and τ₃≈11.2×10⁶ MCS≈0.5τ_fib. Thus, τ₁ is a characteristic time scale of the burst phase in which fluidlike clusters form. On this time scale, only a few interpeptide fibril contacts Q_f (≈0.6% of total contacts) are formed and the largest oligomer contains, on average, only five peptides (N_p=5). Using the three-exponential fit and data presented in Fig. 5a, one can show that the formation of the largest cluster occurs on a time scale of ≈0.02τ_fib. The number of peptides in this cluster approaches 15 [Fig. 4d], whereas the number of free peptide becomes 0. Almost simultaneously, the number of distinct fibril clusters ⟨N_fc(t)⟩ reaches a maximum (data not shown).

Figure 5.

(a) Time dependence of the fraction of fibril structure for M=16 and T=0.7. The dashed curve corresponds to fit of the simulated data using a sum of three exponentials. (b) Dependence of τ_fib as a function of M. The change in the slope for M>10 corresponds to the transition from profilament (single layer) to fibrils (double layer).

The second stage of fibril assembly, in which the burst phase oligomer is transformed into a compact disordered oligomer, takes place on the times scale τ₂≈0.05τ_fib. Due to the larger value of M, this time is larger than for M=10. At this stage, 50% of the equilibrium values of the intra- (Q_m) and interpeptide (Q_f) fibril contacts are formed. Contrary to the M=10 case, fibril contacts in the largest cluster Q_fc are formed earlier than the total Q_f. This is probably due to the increasing role of the satellite clusters as the number of monomers increases. On long time scales, we have more than two and less than two such clusters for M=16 and 10, respectively. The “winner-take-all scenario” is also valid for the M=16 system because for t>0.2τ_fib the largest cluster contains ≈75% of the fibril contacts. These observations are made quantitative by using the dependence of τ_fib∼M (see below).

As seen from Fig. 5a, the three exponentials (f(t)=f₀−f₁ exp(−t∕τ₁)−f₂ exp(−t∕τ₂)−f₃ exp(−t∕τ₃)) fit the data well (dashed line). Here, we have three different time scales τ₁≈0.17×10⁶, τ₂≈1.24×10⁶, and τ₁≈12.18×10⁶ MCS (the partitions of these phases are f₁≈0.19, f₂≈0.46, and f₃≈0.1). Experiments on the fibril growth kinetics of Aβ-peptides,²⁸ which is fit using a sum of two exponential functions, have been interpreted in terms of a template-assisted “dock-lock” mechanism. From the perspective of the present studies, we conclude that such a mechanism is probably valid during the second and third stages of fibril growth. The lock phase, during which in-registry arrangement of the chains takes place, clearly occurs only during the last part of stage three in the fibril growth process. The early stages of growth reveal a much more complex set of events in which the physical processes described in NG and NCC are manifested (see also the Sec. 4).

Dependence of fibril formation time on number of monomers: Lifshitz–Slyozov growth law

In order to obtain the dependence of τ_fib on the number of monomers, we fixed the monomer concentration and computed τ_fib for each system at T_s. The fibril formation time scales linearly with the number of monomer [Fig. 5b], τ_fib∼M but with different slopes for M⩽10 and M>10. This is probably related to the difference between protofilament and fibril formation [see Figs. 2a, 2b]. The linear dependence of τ_fib on M supports the template-assisted mechanism in which monomers are added one by one to preformed ordered structures (protofibrils or fibrils), provided that the number of these monomers exceeds the size of the critical nucleus. Thus, the linear dependence characterizes growth only during the late stages of ordered assembly. Our results agrees with the experimental findings of Kowalewski and Holtzman⁴⁷ who studied the aggregation of Alzheimer’s β-amyloid peptides on hydrophilic mica and hydrophobic graphite surfaces, as well as with the results obtained by Collins et al.⁴⁸ for the amyloidogenic yeast prion protein Sup35.

Interestingly, the dependence of τ_fib on M for such a complicated process as fibril assembly seems to follow the well-known Lifshitz–Slyzov (LS) law. Since M∼L³, where L is a typical size of the ologimer, we obtain τ_fib∼L^1∕3 which is the LS law⁴⁹ describing the growth of a cluster in a supersaturated solution. The finding in Fig. 5b further supports the “winner-take-over” scenario for oligomer growth because the LS law is based on the assumption that the largest cluster grows at the expense of smaller ones.

The evidence for the LS growth law is based on MC simulations involving multiple chains. Although the simplicity of the system permits us to perform exhaustive simulations that gives us confidence that we repeatedly reach the ordered state at long times (for both M=10 and M=16), the effect of the move sets used on the predicted LS law has to be assessed. This is particularly important because in a careful analysis Deeds et al.³⁷ argued that move sets in systems that involve transient complex formation have to be carefully taken into account to ensure approach to equilibrium. The theoretical analysis of LS is based on the assumption that large oligomers devour smaller ones by diffusion which is mimicked here by MC simulations. Thus, LS theory shows L³≈Dt, where D is an effective multiparticle diffusion constant. If one was to vary the move sets in a MC simulations we suspect that only D would be renormalized with the LS growth law remaining intact.

CONCLUDING REMARKS

We have used a lattice model to elucidate the generic features of fibril assembly mechanisms in proteins. Using this toy model, many aspects of the transitions from the monomer to fully formed fibrils can be monitored. The examination of the kinetics of the assembly process reveals that several aspects of a complex set of transitions seen in the simple model is also qualitatively observed in experiments.

• (1)The ordered fibrils form as the number of chains becomes greater than a critical value. In our system, we find that for M=16 a stable two-layer fibril is formed, which is perhaps the minimum replicating unit in the infinite fibril. For smaller M [Fig. 2a], ordered protofilaments are the lowest energy conformation. It is likely that there are substantial internal rearrangements of the chains as the number of monomers increases so that stable fibrils can be populated. Although we did not carry out systematic calculations to infer the size of the critical nucleus, it appears both from the temperature dependence of protofilament formation as well as the ease of fibril production for M=16 that the size of the nucleus has to be less than 10.
• (2)The kinetics of fibril formation occurs broadly in three distinct stages. In the initial stage, the chains rapidly partition into clusters of varying sizes. Because of finite size limitations, we are unable to determine the precise distribution of cluster sizes. The chains within each cluster is mobile and fluidlike. There are, in all likelihood, substantial conformational fluctuations within each cluster. In the second stage, the chains in the clusters form a number of intra- and interchain contacts that lead to the disordered oligomers. During this stage, bigger clusters grow at the expense of smaller ones. In the process, protofibrils in which many peptides adopt the eventual conformation in the fibrils form. In the third postnucleation stage, the chains add to the largest (single) cluster. In this stage, which is captured in experiments, the addition of a monomer occurs by a lock-dock mechanism. Thus, a cascade of events, starting from conformational fluctuations in the monomer that populate the aggregation-prone conformation [Fig. 1a] through a series of interpeptide interaction-driven conformational changes, results in fibril assembly.
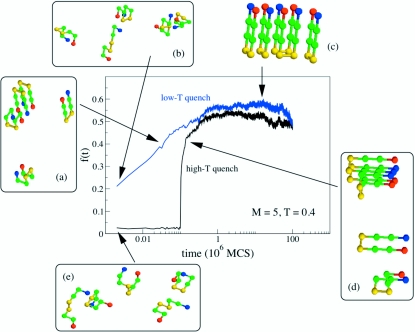
• (3)The growth kinetics depends on the depth of the quench ΔT=(T_i−T_s), where T_i is the initial temperature at which the chains are brought at equilibrium. When the depth of the quench is large, there appears to be a lag-time before the fibrils are populated. In this case, the ordered structures form in a highly cooperative manner. In contrast, when the growth process is initiated by equilibrating the monomers at the final growth temperature (ΔT=0), the fibril growth occurs in a continuous manner and is less cooperative (Fig. 6). Because the aggregation-prone structure is unique in the toy model, we do not observe variations in the morphology of the final fibril structure. This is surely an artifact of the lattice model.
• (4)The temperature dependence of ${\tau }_{\mathrm{fib}}^{-1}$ for M=10 shows Arrhenius behavior with ${\tau }_{\mathrm{fib}}^{-1}\sim \exp (-E_A∕k_{B}T)$ (see inset in Fig. 3). This is in qualitative agreement with experiments.^{50, 51} In addition, the collective rearrangements of several chains from the S to the N^* structure that occurs within the oligomer become slower at low temperatures. These two factors contribute to the barrier that leads to a substantial increase in τ_fib as T is lowered.
• (5)The mechanism of assembly of fibrils even in this toy model is highly complex. While the overall growth kinetics can be summarized using a three-stage growth, the events that transpire in the distinct stages involve large structural transitions. In the initial burst phase loosely bound clusters form in which the chains are essentially “noninteracting.” In the second stage, stable clusters with considerable interparticle interactions form. There is a distribution of oligomers. Due to the finite size of the simulations, the nature of the distribution is unclear. It is within these oligomers, in which the chains are in a mixture of S-like and the aggregation prone N^*-like states, that the conversion from S to N^* takes place. These transitions result in the formation of large-enough ordered oligomers that can serve as templates for the conversion of additional monomers or oligomers to form mature fibrils. It is the last stage that is best described by the dock-lock mechanism.
• (6)Strikingly, the growth of mature fibrils in the third stage occurs by the LS mechanism in which the largest clusters grow at the expense of smaller ones. The proposed mechanism supports the physical picture that the S→N^* transition occurs either in the oligomers (NCC model) or upon addition to preformed ordered template (dock-lock mechanism). Thus, we find that the elements of the three models (NG, TA, and NCC) are found in each assembly stage. This conclusion also supports a detailed study of fibril growth in an off-lattice model of polyalanine⁵² in which multiple routes to fibril formation were found, even in the final stages of the incorporation of ordered structures or disordered monomers. Finally, the proposed LS growth law strongly suggests that seeding with a preformed fibrils should lead to rapid growth because such large structures can incorporate disordered oligomers on time scales that vary linearly with peptide concentration.

Figure 6.

Dependence of the fibril fraction f(t) for the pentamer (M=5) at T=0.4 (<T_F). The initial conformations for the high T-quench were generated by equilibrating the pentamer for 10⁵ MCS at T=2.0. Subsequently assembly of the fibril fragment is initiated by quenching the temperature to T_s=0.4. In the low-T quench regime the initial configurations were generated in the same way but equilibration was done at T=0.4. Typical snapshots at various times during the fibril growth are shown.