Abstract
Widely different time scales are common in systems of chemical reactions and can be exploited to obtain reduced models applicable to the time scales of interest. These reduced models enable more efficient computation and simplify analysis. A classic example is the irreversible enzymatic reaction, for which separation of time scales in a deterministic mass action kinetics model results in approximate rate laws for the slow dynamics, such as that of Michaelis–Menten. Recently, several methods have been developed for separation of slow and fast time scales in chemical master equation (CME) descriptions of stochastic chemical kinetics, yielding separate reduced CMEs for the slow variables and the fast variables. The paper begins by systematizing the preliminary step of identifying slow and fast variables in a chemical system from a specification of the slow and fast reactions in the system. The authors then present an enhanced time-scale-separation method that can extend the validity and improve the accuracy of existing methods by better accounting for slow reactions when equilibrating the fast subsystem. The resulting method is particularly accurate in systems such as enzymatic and protein interaction networks, where the rates of the slow reactions that modify the slow variables are not a function of the slow variables. The authors apply their methodology to the case of an irreversible enzymatic reaction and show that the resulting improvements in accuracy and validity are analogous to those obtained in the deterministic case by using the total quasi-steady-state approximation rather than the classical Michaelis–Menten. The other main contribution of this paper is to show how mass fluctuation kinetics models, which give approximate evolution equations for the means, variances, and covariances of the concentrations in a chemical system, can feed into time-scale-separation methods at a variety of stages.
INTRODUCTION
Systems of chemical reactions are usually described by deterministic mass action kinetics (MAK) models comprising ordinary differential equations that approximately track the expected concentrations of the constituent chemical species. When both fast and slow reactions are present, the slow dynamics that typically dominate experimental observations can be often described by a smaller number of state variables than in the original description. This issue has received wide attention since the early days of chemical kinetics.1, 2 A classic example is the irreversible enzymatic reaction, for which separation of time scales in an MAK model results in approximate rate laws for the slow dynamics, such as that of Michaelis–Menten. Exploiting separation of time scales in deterministic models continues to be important in modern applications to biochemical systems,3, 4, 5, 6, 7 not just to reduce the computational burden but also to facilitate analysis and understanding.
At the small volumes and concentrations of many biological systems, models that capture the probabilistic nature of chemical reactions can be significantly more informative and accurate than MAK models. These probabilistic models tend to be much more elaborate and computationally expensive than their deterministic counterparts, and thus can greatly benefit from model reduction. While model reduction through separation of time scales has played a pivotal role in deterministic models of chemical reactions, it is only recently that such techniques have been developed for the stochastic formulation.8, 9, 10, 11, 12, 13, 14, 15, 16
The most widely used stochastic model for both analytical and simulation studies of chemical kinetics is the chemical master equation (CME). The Markov model underlying the CME is the basis for the Gillespie stochastic simulation algorithm17 and its extensions, for example, the algorithm of Gibson and Bruck.18 Sparked by the papers of Rao and Arkin10 and of Haseltine and Rawlings,9 different authors9, 10, 12, 13 have presented methods for obtaining separate reduced CMEs for the slow and fast system variables when time-scale separation is present. The reduced CMEs, although approximate, are amenable to simpler analysis and enable more efficient simulation, as demonstrated in the above papers and in this paper.
The approach by Rao and Arkin10 is based on assumptions that were subsequently justified in a more fundamental way by Cao et al.12 and by Goutsias,13 though the justifications ignored the effects of slow reactions on the fast variables; their resulting time-scale-separation methods and results therefore end up somewhat different from that of Rao and Arkin.10 Haseltine and Rawlings14 later described a unifying framework that, under appropriate conditions, can give rise to their previously proposed method9 or to the results of Cao et al.12 and Goutsias.13 Other papers11, 15, 19 exploit the fact that the CME is a linear time-invariant operator using eigenvector methods to exploit time-scale separation for model reduction. Our paper presents a modified time-scale-separation method that is related to the approaches in Refs. 10, 12, 13, 15 but that can, for a broad class of systems, better account for the effects of the slow reactions on the fast subsystem, thereby extending the validity and improving the accuracy of the resulting reduced models.
This paper, which builds from Ref. 20, is structured as follows. Section 2 provides some background on stochastic models for systems of chemical reactions and on separation of time scales. Section 3 describes how to systematically identify conserved, slow and fast variables in chemical systems, given a set of slow and fast reactions. The identification of slow and fast variables is at the heart of time-scale model reduction methods. Some recent works21, 22, 23 have successfully identified slow and fast variables in the stochastic models of specific chemical systems with the purpose of model reduction through time-scale separation. Our procedure (elaborated in Appendix A) is related to that of Heinrich and Schuster24 and provides a general and systematic approach to both deterministic and stochastic models.
Section 4 of this paper shows how to exploit the identification of slow and fast variables to obtain reduced slow and fast CMEs. The reduced CMEs we obtain are expected to be more accurate than previously published ones for systems where the rates (propensities) of the slow reactions that modify the slow variables are independent of the slow variables themselves. Importantly, many biological systems of interest, such as the irreversible enzymatic reaction discussed later or more elaborate enzymatic networks,3, 4, 6, 7 fall within this class. For other systems, which of the approximate methods is more accurate will be system specific (see Appendix C). Our reduced-order slow and fast CMEs are close to those of Rao and Arkin10 but more tightly justified and more fully exploited.
The reduced CMEs obtained by time-scale separation are often used for stochastic simulation. Typically, however, a great deal of information is carried by the time evolution of the means, variances, and covariances of the state variables. It is therefore noteworthy that recent studies25, 26, 27 have shown how to obtain approximate evolution equations of complexity not much greater than that of MAK for these first and second moments; we refer to these as models for mass fluctuation kinetics (MFK). Section 4 includes a description of how the MFK approach can feed into time-scale-separation methods at a variety of stages.
We illustrate our proposed separation-of-time-scales method in Sec. 5 (with supplementary details in Appendix B) by obtaining and evaluating a new reduced slow CME and associated MFK model for the irreversible enzymatic reaction. The MFK model here is a natural generalization of the deterministic total quasi-steady-state approximation (tQSSA),28 which in turn generalizes the Michaelis–Menten or quasiequilibrium approximation. We conclude with a discussion of our results and of some recent related work29 in Sec. 6.
BACKGROUND
Systems of chemical reactions consist of n chemical species X1,…,Xn interacting in a volume ν through L reactions labeled R1,…,RL. Reaction Rℓ may be specified by
| (1) |
where and are the numbers of molecules of species Xi that are consumed and produced, respectively, on every firing of the reaction. The consumed species are referred to as reactants. The parameter kℓ in Eq. 1 is the rate constant of the reaction; its role is described later.
We let xi and yi be the number of molecules and the concentration, respectively, of species Xi, more generically we shall refer to the quantities xi, or equivalently yi, as the system variables. Molecule numbers are normalized by the system size, given by Ω=Aν where A is Avogadro’s number, to yield concentrations in moles per unit volume, so that yi=xi∕Ω. Let x be the column vector of molecule numbers (with the ith component {x}i=xi), referred to as the species population vector. A firing of reaction Rℓ changes x instantaneously to x+sℓ, where is the stoichiometric coefficient of species Xi in reaction Rℓ, and sℓ is referred to as the reaction’s stoichiometry vector. The vector y is defined as the vector of concentrations, with {y}i=yi.
Models
Under appropriate conditions, a continuous-time discrete-state Markov process model30 of the time evolution of x provides a good stochastic description of the system of chemical reactions above. Let the probability that reaction Rℓ occurs in a small time interval with duration dt be approximately equal to aℓ(x)dt; the quantity aℓ(x) is the propensity of reaction Rℓ and is proportional to the rate constant kℓ. The probability distribution of the state x at time t, conditioned on an initial state x(to)=xo, will simply be denoted by P(x), suppressing the time argument t for notational simplicity. This distribution P(x) satisfies the CME (see, e.g., Ref. 31), namely,
| (2) |
This is simply the forward Kolmogorov equation for the Markov process.30
The MFK equations, which are derived from the CME in Eq. 2, constitute an approximate model for the time evolution of the means, variances, and covariances of the concentrations of all species in the system.25, 26, 27 The exact evolution of these moments is typically a function of higher-order moments; MFK models are approximations because they eliminate this dependence through various approaches, such as setting all higher-order central moments to zero.25, 26 Let μ be the (column) vector of mean species concentrations, with the ith entry {μ}i=μi=E[yi]. Denote the concentration covariance matrix by V, with the (i,j)th entry {V}ij=σij=E[(yi−μi)(yj−μj)]. The MFK equations25 are then given by
| (3) |
| (4) |
(The symbol ′ denotes the vector or matrix transpose.) Here S is the stoichiometry matrix; its ℓth column is the stoichiometry vector sℓ of reaction Rℓ. The column vector r denotes the effective reaction rate. Its ℓth entry {r}ℓ, the effective rate Rℓ of reaction Rℓ, is given by
| (5) |
where the microscopic reaction rate ρℓ(y) is the propensity of the reaction Rℓ normalized by Ω and expressed as a function of y instead of x:
| (6) |
The quantity ρℓ(μ) is also known in metabolic control theory24 as the reaction flux. The matrix diag(r) has the entries of r on its diagonal and 0 everywhere else. Define the vector ρ to have the ℓth entry {ρ}ℓ=ρℓ; then M=S[dρ(μ)∕dμ], where dρ(μ)∕dμ is a Jacobian matrix. See Ref. 25 or 26 for more on the derivation and application of the MFK equations. Note that when variances and covariances are negligible, the evolution of the mean in Eq. 3 reduces to MAK.
Time scales and model reduction
Reduced approximate models based on time-scale separation have been widely studied for deterministic systems of ordinary differential equations in the context of singular perturbation theory (e.g., see Ref. 32). Two key conditions enable the model reduction. The first requires a separation of state variables into two sets, perhaps made apparent only after a coordinate transformation,24, 33 such that the initial rates of change in the variables in one set (the slow variables) are much smaller in magnitude than those of the variables in the other set (the fast variables). This condition results in a fast initial transient of the fast variables. The second condition requires that the fast subsystem settles to the neighborhood of a quasistatic equilibrium within the fast time scale, and subsequently remains there as the slow subsystem varies (over longer time scales).
The fast variables will thus quasiequilibrate at the end of the initial transient, after which their rates of change are small, driven only by the slow variables. This allows one to construct a good reduced model on the time scale of the slow variables. If the fast transient is of interest, it too can be determined from a reduced model in which the slow variables are frozen at their initial values. (Appendix C briefly elaborates on this description.)
In the (deterministic or) stochastic chemical kinetics context, having slow and fast reactions—which we define to be reactions with small and large initial propensities, respectively—can also result in slow and fast subsystems for which reduced models can be obtained; this is the focus of the rest of the paper. The process begins with identification of the slow and fast variables in the system; we develop a method that serves this purpose in Sec. 3. Section 4 describes how to obtain reduced models for the slow and fast subsystems under the additional assumption that the fast subsystem settles to a quasiequilibrium condition within the fast time scale and subsequently remains there as the slow subsystem varies (over longer time scales). We finally illustrate the approach in detail in Sec. 5 on a widely used and important example.
IDENTIFYING SLOW AND FAST VARIABLES
The starting point of our separation-of-time-scales method is the specification of a set of slow and fast reactions. Reactions will be classified as slow or fast depending on whether their initial propensities are, respectively, small or large. Classification on the basis of reaction rates rather than reaction rate constants is characteristic of the tQSSA approach5, 6 in deterministic chemical kinetics. Given an initial set of slow and fast reactions, stoichiometry considerations alone suffice for the identification of slow and fast variables at this initial time. Our identification of slow and fast variables will indeed guarantee an initial transient during which the fast and slow subsystems will evolve rapidly and slowly, respectively. (A subsequent assumption on the rapid settling of these fast variables to a quasiequilibrium allows the initial separation into slow and fast variables to be maintained beyond the initial time.) The slow and fast system variables are molecule numbers (or equivalently, concentrations) of the different chemical species in the system or are integer linear combinations of these.
Our procedure can also be applied in the deterministic case to identify slow and fast variables simply by using reaction rates rather than propensities to classify reactions as slow or fast. The procedure is related to that of Heinrich and Schuster,24 which was developed for the deterministic case, but our approach is more directly and simply described. The results of our procedure for the identification of slow and fast variables are also consistent with previous studies of specific stochastic chemical kinetics models.21, 22, 23
A prototypical example
The example we examine in this subsection has three types of variables according to their dynamical time scales: conserved, slow, and fast. This example is discussed by Liu and Vanden-Eijnden34 and by Gillespie et al.35 and comprises the following reactions:
| (7) |
Let x=[x1x2x3x4]′ denote the column vector of the species molecule numbers.
Suppose we know that reactions R1 (producing X3 from X2) and R2 (producing X2 from X3) have propensities that are much smaller in magnitude than those of the other reactions at the initial time to, as provided by the assumptions regarding the reaction rate constants and initial molecule numbers in Gillespie et al.35 (Note that propensities are determined by both rate constants and molecule numbers. It is therefore possible to have reactions with disparate initial propensities even when the rate constants are comparable; what is needed in that case is to have big enough differences in the initial molecule numbers of the species that determine the various propensities.) Reactions R1 and R2 are accordingly termed slow and the others fast. The corresponding stoichiometry matrix is given by
| (8) |
where the partitioning separates the columns Ss corresponding to slow reactions from the columns Sf corresponding to fast reactions.
We might expect that this partitioning of reactions into slow and fast gives rise to variables evolving at slow and fast time scales depending, respectively, on whether they get modified only by slow reactions or by both fast and slow reactions. However, for the example system here all species have fast components to their dynamics as they are all modified by at least one fast reaction.
It turns out that there actually are slow variables in this system, defined by appropriate linear combinations of the species molecule numbers, but identifying these combinations requires considering linear transformations of the original coordinates. We describe the process in some more detail next, both to illuminate the discussion of this example by Liu and Vanden-Eijnden34 and by Gillespie et al.35 and because it serves to illustrate our proposed approach in identifying slow and fast variables in the general case.
Consider the variable xα=αx, where α is a four-component row vector with integer entries. Every time reaction Rℓ occurs, xα immediately changes by αsℓ, a number that may be thought of as the stoichiometry coefficient of the linear combination xα in reaction Rℓ. We now consider the stoichiometry of xα for different choices of α.
First consider xα=xo=x1+x2+x3+x4, obtained when α=αo=[1 1 1 1]. The change in xo is exactly zero for all reactions because αo lies in the left null space of S (i.e., αoS=0). The variable xo is thus a conserved variable that does not change throughout the experiment; the reason is that every reaction in this example involves creating one molecule of some species while destroying one molecule of another. Since the left null space of S has dimension equal to 1, there is no other vector α in this null space that is linearly independent of αo, and hence no other independent conserved variable.
Conserved variables are unchanged by all reactions, i.e., they have stoichiometry coefficients that are zero regardless of what the propensities are and can immediately be used to reduce the order of the system model, as is well known. In our example, the conservation relation implies, for instance, that x4 can be written in terms of x1, x2, and x3, so the latter three variables suffice to describe the dynamic state of the system.
Going beyond conserved variables, we are now interested in finding (combinations of) variables with slow dynamics; these will correspond to quantities conserved on the fast time scale. We therefore focus only on the fast reactions, shutting off slow ones, which gives us
| (9) |
Now define slow variables via the quantities conserved in these fast reactions, i.e., via linear combinations of x whose stoichiometry coefficients are zero for all fast reactions. By inspection, it is evident that x1+x2 and x3+x4 are both conserved in the fast reactions, so these would be candidate slow variables. However, we can only select one of them for our transformed description, for example, xs=x1+x2, because the other would then be dependent on the selected one plus the previously obtained conservation relation:
| (10) |
This shows that the system actually has exactly one slow variable.
There must now be exactly two fast variables to complete the system description. These can be any two linear combinations of the xi that are independent of those combinations we have already picked, e.g., xf1=x2 and xf2=x3. The new system of coordinates is then related to the old via , where
| (11) |
so the new stoichiometry matrix governing changes in is
| (12) |
where the first two columns still correspond to the slow reactions. This transformed stoichiometry matrix Q has a very particular structure. The row corresponding to the conserved quantity has only zeros as its entries. The row of the slow variable has only zeros in the columns corresponding to fast reactions but is not zero in the remaining columns (else it would correspond to a conserved variable). Similarly, the matrix block corresponding to the fast variables and the fast reactions has full row rank (else there would be additional conserved or slow variables). What we have now accomplished is an identification of slow and fast variables based on the initial separation of reactions into slow and fast.
It is precisely because the particular choice of slow and fast reactions in the example in Eq. 7 leads to fast and slow variables that a meaningful separation-of-time-scales approximation, such as that by Gillespie et al.,35 can be developed. The very same system may lack an appropriate partitioning into slow and fast variables if the reactions separate some other way into slow and fast ones. For example, consider now the case where the slow reactions in this system are given instead by R1, R3, and R5. We still have the same conservation relation as before, but focusing now on only fast reactions results in
| (13) |
which gives no further conserved quantities. Any linear combination of the molecule numbers x1, x2, x3, and x4, other than the conserved combination xo, gets changed by a fast reaction. The original system therefore has no slow variables, just one conserved quantity and three fast variables.
General systems
The analysis of the preceding example can be generalized. As in the example, we assume that at the start of the experiment at time to, a subset of the reactions, termed slow reactions, have propensities that are much smaller in magnitude than those of the remaining reactions, which are termed fast reactions. We emphasize again that propensities are determined by both rate constants and molecule numbers. Thus, significant differences in the magnitudes of the reaction propensities can arise from significant differences in molecule numbers rather than from differences in the magnitudes of the rate constants. Label the slow reactions by R1,…,RLs, with Ls⩽L; the remaining Lf=L−Ls reactions are the fast reactions.
Given a set of slow and fast reactions, we again consider a linear change in coordinates to identify conserved, slow, and fast variables in the system. This identification is embodied in a transformation of the form , with A nonsingular and of dimensions n×n. The rows α of A will define linear combinations αx that have the desired characteristics. Before describing the construction in matrix terms, we outline the overall idea.
-
(1)
First identify a maximally independent set of (integer) linear combinations of the original variables that are conserved no matter which reactions are running. These correspond to independent choices of α for which αS=0. The number nc of such conserved variables is therefore given by the dimension of the left null space of S.
-
(2)
Note that the preceding combinations will all be conserved even if only the fast reactions are running. However, there may be additional linear combinations of these original variables, independent of those found in step 1, that are conserved when only the fast reactions are running. Find a maximally independent set of such additional combinations; these are the slow variables in the transformed system. These correspond to new independent choices of α for which αSf=0. The number ns of such slow variables will be the difference between the dimensions of the left null space of Sf and the left null space of S, where Sf denotes the columns of S corresponding to the fast reactions.
-
(3)
Finally, find an additional set of linear combinations of the original variables, independent of those found in steps 1 and 2, that—taken together with the conserved variables and slow variables—provide an equivalent description to the original set of variables. These additional linear combinations will be the fast variables in the transformed description; more accurately, they are the nonslow variables because they have fast components (possibly along with slow components). These correspond to further independent choices of α that fill out A to a square invertible matrix. The number of such fast variables is given by n−nc−ns.
The original system can now be described as a function of only the new variables using the relation to express the old variables as functions of the new ones and using the matrix Q=AS instead of the original stoichiometry matrix S. By construction, Q has the form shown in the following equation:
| (14) |
The matrices Qfs and Qff have nf rows, while Qss has ns rows. Importantly, our construction ensures that Qss and Qff have full row rank, which guarantees that no further conserved or slow variables can be exposed by such linear transformation. The pattern of zeros in Q makes evident that the state of the conserved variables is unmodified by any reaction, while the state of the slow variables can only be modified by slow reactions. (Note that it is possible for certain columns of Qss to be zero while still satisfying the above conditions; such columns correspond to slow reactions that do not affect the slow variables.) These structural features enable the direct model reduction in Sec. 4. The matrix A above can be constructed systematically by standard methods, see Appendix A.
Since the first nc entries of are constant at their initial values, it suffices to keep the slow and fast variables as the dynamic state variables of the system. The system state therefore comprises the last ns+nf components of . To simplify the notation, we revert to our earlier symbols and refer to this state of the system simply as x in what follows; we accordingly denote the slow and fast variables, which are typically linear combinations of the molecule numbers of the original species, by xs and xf, respectively. Similarly, we shall denote simply by S the stoichiometry matrix for the transformed slow and fast variables, though the matrix actually comprises the last ns+nf (block-triangular) rows of Q. We shall also denote the submatrix [QfsQff] of Q by Sϕ later in the paper, when we write the MFK equations for the fast CME.
OBTAINING REDUCED SLOW AND FAST CME MODELS THROUGH TIME-SCALE SEPARATION
We assume as above that at the start of the experiment at time to, the first Ls⩽L reactions are slow (i.e., have small propensities), and the remaining Lf=L−Ls reactions are fast (i.e., have large propensities). Then the CME in Eq. 2 can be written as
| (15) |
where the first summation is over the slow reactions and the second over the fast reactions. Further assume that the analysis in the previous section has been performed, resulting in a state vector with only slow and fast variables. To obtain the desired approximate system descriptions, partition the state vector x and the stoichiometry vector sℓ of every reaction Rℓ in the system into their slow and fast components:
| (16) |
Here ssℓ and sfℓ are the changes in the slow and fast variables xs and xf, respectively, with one occurrence of reaction Rℓ. The goal of this section is to derive approximate models for the time evolution of the marginal probability distribution P(xs) of the slow variables, and of the conditional distribution P(xf∣xs) of the fast variables given the values of the slow variables. These two distributions jointly specify the full distribution P(x) via
| (17) |
Note from Eq. 17 that
| (18) |
an equation that will be useful in developing the reduced CMEs.
The slow CME
We start by substituting Eq. 16 into the CME in Eq. 15 and then summing both sides of the equation over all possible values of the fast variables xf. The result, after some algebra, is the exact expression
| (19) |
Equation 19 resembles the CME in Eq. 2 but with two important differences: it describes the probability distribution of just the slow variables xs and it requires the conditional propensity of each reaction Rℓ, which is the average of aℓ over the time-dependent distribution of the fast variables xf at time t, conditioned on the slow variables at time t:
| (20) |
However, despite the formal similarity of Eq. 19 to a CME, it cannot be used to solve for P(xs) without knowledge of the P(xf∣xs) required in Eq. 20. In the next subsection, we will derive an approximate fast CME for P(xf∣xs) and use this fast CME’s quasi-steady-state solution to evaluate Eq. 20. Employing the resulting conditional propensities in Eq. 19, or more precisely in Eq. 21 below, will then result in an approximate slow CME for P(xs).
Equations 19, 20 were obtained by Frankovicz et al.8 for systems with two variables. Rao and Arkin10 later obtained these equations for general chemical systems as an approximate expression, but Goutsias13 subsequently showed that Eq. 19 is exact.
The summation in Eq. 19 is over all reactions, both slow and fast. However, note that terms for which ssℓ=0 drop out of the summation. We know that ssℓ=0 for all fast reactions, since by definition (and construction, using our procedure in Sec. 3) slow variables are not changed by fast reactions. In addition, we will have ssℓ=0 for those slow reactions that only modify fast variables; these correspond to having columns of Qss in Eq. 14 equal to zero. The terms of the summation in Eq. 19 corresponding to the fast reactions therefore drop out, resulting in the following equation, which depends only on the slow reactions:
| (21) |
(Those slow reactions for which ssℓ=0 will drop out of the sum above too.) Note that all the conditional propensities appearing in Eq. 21 are small because they involve averages of the propensities of only slow reactions. Note also the relation of Eq. 21 to Eq. 15. We now turn to the development of the fast CME.
The fast CME
Our aim in this subsection is to develop a new reduced fast CME that approximately governs the conditional density of the fast variables P(xf∣xs). This CME is also needed to specify the slow CME, since the conditional propensities are a function of P(xf∣xs). As argued later, the fast CME we obtain is expected to be more accurate than previously published ones for systems where the small propensities that modify the slow variables are independent of the slow variables themselves. Importantly, many biological systems of interest, such as the irreversible enzymatic reaction discussed later or more elaborate enzymatic networks,3, 4, 6, 7 fall within this class. For other systems, which of the approximate methods is more accurate will be system specific [see Appendix C, particularly the discussion around Eqs. C11, C12, C13].
Since the right side of Eq. 21 only involves the small propensities corresponding to the slow reactions, P(xs) indeed varies slowly on the time scale of the transients in the fast variables, so we can write
| (22) |
over the duration of the fast transient. Using Eqs. 17, 18, 22 in the full CME in Eq. 2 then results in
| (23) |
In order to obtain an approximate fast CME from Eq. 23, previous papers12, 13, 14, 15 drop the terms corresponding to all the slow reactions from the above summation, reasoning that these terms are relatively negligible because of the small propensities of slow reactions. However, it is possible to obtain an approximate fast CME while still retaining the slow reactions provided that for every reaction Rℓ
| (24) |
For reactions that satisfy ssℓ=0, namely, all the fast reactions and those slow reactions that only modify fast variables, the two sides of Eq. 24 are actually exactly equal, so the assumption only pertains to the slow reactions that modify slow variables. For such reactions (which must exist whenever there are slow variables), it is typically the case that most of the entries in ssℓ are zero except for one or two that are small integers, so the approximation in Eq. 24 holds if the product P(xs,⋅)aℓ(xs,⋅) is relatively insensitive to small changes in the argument xs.
Substituting expression 24 into Eq. 23 and dividing by P(xs) results in the fast CME, given by
| (25) |
where the summation is over all reactions and not only over the fast ones as in Refs. 12, 13 and (in effect) in Ref. 15. Note that xs here is a parameter of the distribution (i.e., a constant) and not a dynamic variable.
The required approximation in Eq. 24 can be simplified if
| (26) |
For example, the two sides of Eq. 26 would actually be equal if the propensities of the slow reactions that modify slow variables are independent of the slow variables, i.e., if aℓ(xs,xf) is actually not a function of xs. When Eq. 26 holds, Eq. 24 reduces to
| (27) |
which only requires that the probability distribution of the full state varies slowly in the slow variables (specifically, that any two states separated by a single slow reaction have similar probabilities). We expect this condition to hold when the support of the probability distribution P(xs,xf) over the slow variables is broad relative to the magnitudes of the entries in ssℓ. The magnitude of the discrepancy between the two sides of Eq. 27, summed over all values of xs and xf, is in the worst case bounded by 2, and the corresponding error incurred on the right side of Eq. 25 is therefore still only on the order of the small propensities.
Systems that satisfy Eq. 26 include protein interaction networks and networks of enzymatic reactions, such as the irreversible enzymatic reaction system discussed later in this paper and the covalent modification cycle analyzed by Gomez-Uribe.20 In these systems, the catalytic reactions that convert enzyme-substrate complexes into product plus enzyme are typically the slow reactions, while the binding and∕or unbinding of substrates with enzymes are fast reactions. As a consequence, the concentrations of enzyme-substrate complexes are typically the fast variables, while the concentrations of bound plus unbound (i.e., total) substrates are the slow variables. Since only catalytic reactions (i.e., slow reactions) modify the slow variables and have propensities that are functions of the concentrations of only the complexes (i.e., of the fast variables), condition 26 is actually satisfied with equality.
To the extent that Eq. 24 is satisfied, our fast CME is more accurate than previously published ones because no terms have been dropped in Eq. 23. (A similar improvement over standard slow∕fast reduction is obtained by the analog of our approach in a class of deterministic singularly perturbed, linear, time-invariant systems. Appendix C briefly develops the analogy for the simplest such case, as it adds some insight and validation to our CME reduction approach.) Otherwise, our fast CME can be more accurate or less accurate than those previously published,12, 13, 14, 15 depending on the actual system parameters, because it is then not a priori clear that our approximation of the small terms in Eq. 23 leads to better results than simply setting these terms to zero.
We demonstrate in Sec. 5 on a specific example that our fast CME in Eq. 25 can indeed result, via its use in Eq. 20, in a significantly more accurate slow CME than alternative versions that ignore slow reactions. Rao and Arkin10 also used Eq. 25 but assumed it rather than deriving it as we do here. Furthermore, they did not take advantage of an MFK model to obtain the conditional propensities, as we do in Sec. 4C below, but instead obtained an assumed functional form for these propensities by invoking approximations obtained in the deterministic context.
Obtaining the conditional propensities
We can now complete the specification of the slow CME in Eq. 21 by using the fast CME in Eq. 25 to evaluate the conditional propensities in Eq. 20. The fast CME is guaranteed by our selection of fast variables in Sec. 3 to be driven by large (and possibly small) reaction propensities, so its dynamics are initially much faster than those of the slow CME in Eq. 21. We now assume that the fast CME is sufficiently stable that the distribution of the fast variables, conditioned on the slow ones, essentially attains a quasistationary form on the fast time scale and remains quasistatic during the subsequent slow behavior. This assumption is at the heart of time-scale reduction approaches and appears explicitly or implicitly in virtually all the literature on slow∕fast CMEs, for example, in Refs. 9, 10, 12, 13, 14, 15. With this assumption, we can set
| (28) |
in analyzing the slow CME beyond the (small) initial settling time of the fast CME. The fast CME in Eq. 25 may accordingly be assumed at steady state beyond this settling time, resulting in
| (29) |
The steady-state distribution P(xf∣xs) can be obtained from this equation numerically if not analytically and used in Eq. 20 to obtain the conditional propensities needed for the slow CME in Eq. 21. Note that these conditional propensities will now be functions of only the slow variables, not functions of time, because of the stationarity assumption in Eq. 28. Equations 21, 20, 29 together fully specify our approximate CME for the slow variables, the slow CME.
Approximate CMEs for the slow variables are typically used to obtain sample trajectories for the slow variables as a function of time through Monte Carlo simulation via the Gillespie algorithm17 or its later variants such as the algorithm of Gibson and Bruck.18 The difference between our resulting slow CME and those in Refs. 10, 12, 13, 14 is only in the expressions for the conditional propensities. The costs of evaluating these conditional propensities for our method and the various cited methods are comparable, and simulation is in any case not dominated by these evaluations. Consequently, the computational cost of generating sample trajectories for the slow variables as a function of time in our model is comparable to the costs of the methods in the cited papers, as will be illustrated in Sec. 5. Note that all these reduced models have simulation times significantly less than that of the full model due to the fact that the running time is proportional to the total number of reactions over the simulation interval; the full model requires simulating each occurrence of every fast (hence frequent) reaction in addition to each occurrence of every slow (hence infrequent) reaction, while the slow models only require simulating the slow reactions that modify the slow variables.
Since propensities are typically at most quadratic in the fast species (in systems of at most bimolecular reactions), computing just the steady-state means, variances, and covariances of the fast species relative to the steady-state distribution P(xf∣xs) often suffices to specify the conditional propensities. These steady-state moments may actually be obtained more directly through the MFK model of the fast CME in Eq. 25, as we describe in the next subsection. (MFK models of the fast CME may also be used to approximate conditional propensities that are more general nonlinear functions of the fast variables by Taylor expanding such propensities around the means, keeping up to second-order terms, and then taking expectations, resulting in expressions that depend only on the steady-state means, variances, and covariances of the fast species.)
Using MFK models with fast and slow CMEs
Fast MFK models
The fast MFK model is specified by equations analogous to Eqs. 3, 4 but for the conditional mean concentration and conditional covariance matrix of the fast species; the slow species concentration is simply a parameter. Letting yf=xf∕Ω and ys=xs∕Ω denote the fast and slow concentrations, respectively, the resulting MFK equations are
| (30) |
| (31) |
where μf=E[yf∣ys] and Vf=E[(yf−μf)(yf−μf)′∣ys] are the conditional mean and variance of the fast species concentrations. The matrix Sϕ, defined earlier in Sec. 3B, has L columns, one for each reaction; its ℓth column is sfℓ, the change in the fast species from one reaction Rℓ. The effective reaction rate r is defined as in Eq. 5 but keeping in mind that the slow species now have fixed concentrations. That is, ρℓ is now the microscopic reaction rate evaluated at (yf,ys)=(μf,ys), and
| (32) |
where yfi denotes the ith fast species concentration and Vf,ij the entry in row i and column j of Vf. Similarly, Mf is just the Jacobian of Sϕρ with respect to the fast species concentrations evaluated at (μf,ys). The diagonal matrix Λ is the same as before, with the effective rates as its diagonal entries.
Checking that the fast MFK model reaches a steady state and remains close to stationary in the fast time scale may serve as proxy for checking the stability assumption on the fast CME that led to Eq. 28. The steady-state form of these MFK equations may then be solved for the steady-state μf and Vf, which can then be used to obtain the conditional propensities . (One could also, as was done by Cao et al.,36 use these means and variances to generate samples of the fast variables, if this was of interest.) In Sec. 5 we illustrate concretely on an example how to use this fast MFK model.
Slow MFK models
As noted earlier, approximate CMEs for the slow variables are typically used to obtain sample trajectories for the slow variables as a function of time through Monte Carlo simulation via the Gillespie algorithm.17 It is often desired to compute slow-variable statistics, particularly means, variances, and covariances. While these statistics may be obtained through Monte Carlo simulation, the computational cost may still be prohibitive even for the reduced model. An alternate and often more efficient approach, when just the means, variances, and covariances of the slow variables suffice, is to work with an MFK model of the slow variables.
Such a model may be obtained by two different approaches. The first uses the MFK model corresponding to the slow CME in Eq. 21. This model, like the slow CME itself, involves only the slow reactions and slow variables of the full system, with reaction propensities given by rather than aℓ, and with stoichiometry matrix equal to the block of the full-system stoichiometry matrix corresponding to the slow-variable rows and slow-reaction columns [i.e., Qss in Eq. 14]. The model describes the time evolution of the mean vector and covariance matrix of the slow-variable concentrations. These MFK equations can then be solved numerically to obtain approximations for the time evolution of the means, variances, and covariances of the slow variables.
The second approach starts from the MFK model of the full unreduced CME in Eq. 2 and carries out the separation of time scales in the full MFK model directly, for example, by using standard results of singular perturbation theory; we shall not elaborate on this approach here, but see Ref. 20. The two stages involved in each of these approaches, namely, separation of time scales and moment truncation, need not be commutative, so the resulting MFK models obtained from the two approaches are generally slightly different.
A SLOW-TIME-SCALE MODEL FOR THE IRREVERSIBLE ENZYMATIC REACTION
We now illustrate our proposed time-scale reduction approach on the irreversible enzymatic reaction system. As the same system was analyzed by Cao et al.,36 Goutsias,13 and Rao and Arkin,10 this example allows us to explicitly compare the different methods. Our analysis of this system is guided by concepts developed for its classical (or deterministic) counterpart, in particular, the tQSSA,28, 33 which results in a rate law of wider validity than the Michaelis–Menten rate law.
Enzymatic reactions are pervasive in chemistry and biology. They are prototypically modeled through the reactions
| (33) |
where E, S, C, and P respectively denote the enzyme, substrate, enzyme-substrate complex, and product; the symbols ki denote the rate constants of the reactions. The standard setup assumes initial nonzero concentrations of enzyme and substrate, and zero concentrations for the complex and product.
Slow and fast variables
Simple inspection reveals the following two conservation relations in the system:
| (34) |
where a subscript denotes the species (e.g., xc is the molecule number of species C), except for xeo and xso, which are constants determined by the initial conditions, namely, the initial total number of enzyme molecules and of substrate molecules, respectively. Analysis of the stoichiometry matrix as in Sec. 3 reveals that there are no additional conserved quantities beyond the two listed in Eq. 34. This implies, for our four-species system, that only two variables are needed to describe the dynamics of the system.
Let xt=xs+xc be the total substrate. The propensity functions for the reactions are then given by
| (35) |
Now suppose that at the initial time we have a3⪡max(a1,a2), which in terms of the initial concentrations, denoted by y, is equivalent to
| (36) |
after some rearrangement. Then R3 is a slow reaction and R1 or R2 (or both) are fast reactions.
To find the slow variables, we shut off the slow reactions (R3 and perhaps R1 or R2) and note that the total substrate xs+xc=xt is the only additional conserved quantity independent of the two in Eq. 34. The total substrate is then a slow variable since it only gets modified by a slow reaction. (We could equivalently choose the product xp=xso−xt as a slow variable, and we do so in our discussion of the deterministic models, since this has often been the slow variable of choice in the deterministic MAK context. In the stochastic context, however, we choose the total substrate xt instead, as has been done in the previous literature on the tQSSA.)
The remaining variable, which must be linearly independent of the total substrate and of the conservation relations, is now a fast variable. The number of enzyme-substrate complex molecules xc satisfies the required independence condition and is chosen as the fast variable. An analogous argument, using concentrations instead of molecule numbers and reaction rates instead of propensities, results in the same identification of slow and fast system variables in the deterministic MAK model of the system.
Deterministic models
The usual MAK model of the system consists of the following two coupled nonlinear ordinary differential equations for the mean concentrations of the fast and slow variables, respectively:
| (37) |
along with the conservation relations in Eq. 34, which can be written in terms of mean concentrations simply by replacing all x in Eq. 34 by μ. The conservation relations serve to determine μe and μs from the dynamic variables μc and μp in Eq. 37.
For a range of rate constants and initial conditions, the mean complex concentration μc in typical reactions of this type has much faster dynamics than the mean product concentration μp, resulting in an approximate description with the single slow dynamic variable μp, obtained through separation of time scales. Setting the rate of change in μc to zero (to capture the quasi-steady-state of this fast variable that follows its rapid initial transient) results in the tQSSA:28
| (38) |
where is the steady-state concentration of the complex, which satisfies the relation
| (39) |
where
| (40) |
Here μt is the concentration of the total substrate, defined as μt=μs+μc=μso−μp, and Km=(k2+k3)∕k1 is the Michaelis–Menten constant.
When r⪡1, which is, for example, the case when either the enzyme is scarce (i.e., μt+Km⪢μeo) or the substrate is scarce (i.e., μeo+Km⪢μt), the expressions above simplify to
| (41) |
which is known as the first-order tQSSA. Under conditions of substrate excess, the first-order tQSSA in Eq. 41 reduces to the Briggs–Haldane rate law,37 which is the Michaelis–Menten rate law when k3⪡k2.1, 2 The tQSSA models have been quite successful at describing systems with enzymatic reactions since they are more accurate and more generally valid than the Michaelis–Menten approximation.3, 4
We will show next that applying the reduced CMEs presented in Sec. 4 to the stochastic model of the enzymatic reaction 33 results in a more general approximation analogous to the tQSSA model 38, 39, 40, where other methods10, 13, 36 result in expressions related to the Briggs–Haldane or Michaelis–Menten rate laws.
The stochastic model and slow approximation
Assuming still that condition 36 holds at the initial time, the total substrate is a slow variable since it is unchanged by the fast reaction(s). Similarly, since R1 and R2 or both are fast reactions by assumption, the complex xc is a fast variable since it is modified by at least one fast reaction. Additionally, the propensity of the slow reaction R3 that modifies the slow variable is not a function of the slow variable itself, thereby falling within the class of systems where our approach is expected to be more accurate than previous ones.
Note that the condition in Eq. 36 is certainly true when k3⪡k2, an inequality that has been often assumed in previous works. But the condition is also true more generally, for example, when μc(to)=0, or when the initial concentrations of total enzyme and total substrate are sufficiently different from one another (i.e., when either μeo⪡μt or μt⪡μeo at t=to), since the complex concentration can never be more than min(μeo,μt). Both these situations are commonly of interest.
The CME of the full system describing Eq. 33 is given in Appendix B. Letting xs=xt and xf=xc denote the slow and fast variables of the system, Eq. 21 gives the approximate slow CME for the total substrate:
| (42) |
Equation 42 requires a single conditional propensity, namely, , which is fully specified by , the conditional mean of the complex, since by definition
| (43) |
The fast CME for this system is in Appendix B. The MFK model corresponding to it (rewritten in terms of molecule numbers rather than concentrations) results in the following evolution equations for and :
| (44) |
| (45) |
Note that xt functions as a parameter in these equations. Assuming these equations reach a quasi-steady-state in the fast time scale and remain quasistatic in the subsequent slow dynamics, they may be solved (numerically) to obtain the quasi-steady-state values of and . Instead, we here pursue a simple approximation to draw a parallel to the classical approximations for the deterministic case.
At the quasi-steady-state following the fast transient, Eq. 44 gives a quadratic expression for the steady-state of , which can be solved to obtain
| (46) |
where
| (47) |
and is the steady-state variance of the complex C. Note the similarity of these expressions to Eqs. 39, 40, obtained for the deterministic case.
A sequence of further approximations helps connect the stochastic results presented here with the deterministic tQSSA results for the enzymatic system. As in the deterministic model, suppose that r⪡1 and further assume that . Equation 46 then becomes
| (48) |
Substituting this expression into Eq. 43 and using the resulting conditional propensity in Eq. 42 fully specifies a first approximation for the CME of the total substrate xt.
Letting μt and denote the mean and variance of the total substrate concentration, the MFK model for the reduced slow CME specified by Eqs. 42, 43, 48 results in the evolution equations
| (49) |
| (50) |
These equations are the stochastic generalization of the deterministic tQSSA. Note that in the absence of fluctuations (when ), the equations above reduce to the deterministic tQSSA in Eq. 41. The equations above may be used instead of the deterministic rate law to describe enzymatic reactions in small volumes where stochastic effects may be important.
The methods by Cao et al.,36 Goutsias,13 and Rao and Arkin10 result in CME expressions identical to Eqs. 42, 43 for the total substrate in the system, but they all obtain different expressions for the complex , and therefore for the conditional propensity in Eq. 43. Cao et al.36 and Goutsias13 both ignored the slow reaction (R3) in the fast system. Cao et al. ended up with an expression for identical in form to Eq. 46, but with K instead of Km and with assumed negligible. Goutsias also ignored the slow reaction in the fast system and after another assumption obtained the approximation ; this approximation is equivalent to assuming that the minority species is in saturation. As further analysis reveals,5 this approximation is valid when ∣xt−xeo∣⪢KmΩ. Lastly, Rao and Arkin10 did keep the slow reactions in the fast system, but instead of working with the fast part of the stochastic system to obtain , they relied on the macroscopic deterministic Michaelis–Menten approximation to set , which has been shown to be valid38 only when xt+KmΩ⪢xeo.
Comparison of the different approximations
Our reduced model in Eqs. 42, 43, 46, and with the assumption that , results in better accuracy over a wider range of conditions than the other models discussed above. We demonstrate this next with numerical simulations, all performed on an iMac computer with an Intel 2 GHz dual core processor. In this subsection, both the exact and approximate traces are obtained by Monte Carlo simulation using the Gillespie algorithm,17 the exact from the full system and the approximate from the approximation under evaluation. The statistics of interest (e.g., the average or standard deviation of the total substrate) are obtained from evenly spaced samples taken from the start of the experiment until the time when the average total substrate equals 1% of its initial value.
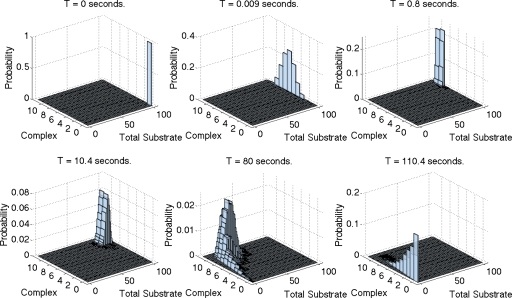
For certain parameter ranges, the assumptions of all the different approximations are satisfied: excess substrate, negligible catalytic reaction (k3⪡k2), and saturation of the minority species. In these cases all the different approximations are reasonably accurate. Figure 1 shows the distribution P(xt,xc) obtained by Monte Carlo simulation of the full CME in Eq. B1 at various time points for one such example, where we used the same parameters as in Fig. 1(a) of Goutsias.13 The top three plots correspond to time points within the initial fast transient, where the distribution moves mostly along the axis corresponding to the fast variable (i.e., the complex). The lower three plots correspond to the slow motion following the initial transient, where the distribution over the fast variable remains quasistatic as the support of the distribution moves along the axis corresponding to the slow variable (i.e., the total substrate).
Figure 1.
Empirical probability distribution P(xt,xc) obtained from 20 000 realizations of the full CME in Eq. B1 via the Gillespie algorithm (Ref. 17) at six different time points. We used Ω=k1=k2=1, k3=0.1 and initial enzyme and total substrate equal to 10 and 100 molecules, respectively.
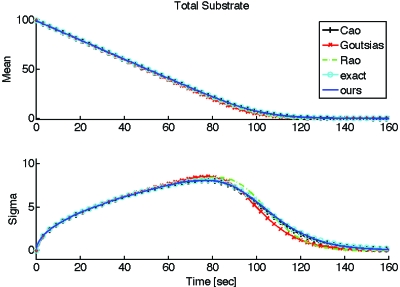
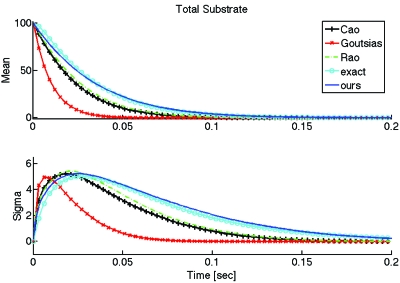
To compare the previously discussed approximate models to each other and to the full solution, Fig. 2 shows the average and standard deviation of the total substrate as a function of time, obtained from Monte Carlo simulation of the full CME, and of the different approximate slow CMEs. All the approximate methods took comparable computation times as expected, ranging from 6.77 to 7.02 s for 10 000 simulations, while simulation of the full system required around 107 s. As already noted, the reduction in simulation time between the full and approximate models is due to the fact that the full model requires simulating each occurrence of every fast (hence frequent) reaction in addition to each occurrence of every slow (hence infrequent) reaction, while the slow models only require simulating the slow reactions that modify the slow variables.
Figure 2.
Mean and standard deviation of the total substrate xt computed from 10 000 realizations for each of the stochastic descriptions considered. The realizations were all obtained from Monte Carlo simulation using the Gillespie algorithm. All parameters are the same as those in Fig. 1. In this case, all approximate methods work well but require only 6.77–7.02 s of computation, vs 107 s for simulation of the full (“exact”) model.
For the particular choice of parameters shown in Fig. 2, the different reduced models result in rather good approximations for the evolution of the average and standard deviation of the total product. To quantitatively assess the overall accuracy of an approximation, we define the (“root mean square” or rms) error between an exact and an approximate time trace (of a mean or standard deviation), denoted by f and , respectively, by
| (51) |
where fi and respectively denote the ith sample of the exact and approximate time traces and m is the number of samples. The (rms) errors for the mean total substrate in Fig. 2, where initially there were 100 substrate molecules, are less than 2 molecules for each of the approximations. Similarly, the errors for the total substrate standard deviation are less than 0.5 molecules.
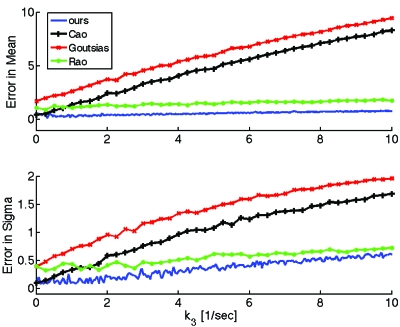
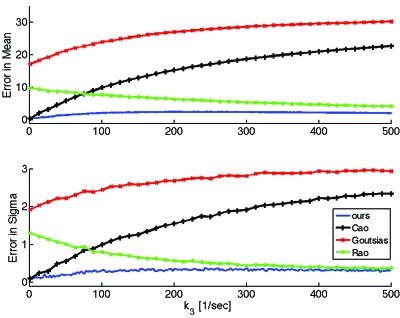
In Fig. 3 we quantify the errors of the different approximations as a function of k3 for the example of Fig. 2. For each value of k3 we first obtain time traces for the mean and standard deviation of the total substrate by Monte Carlo simulation (up to the time when the mean equals 1% of the initial substrate) and then compute the error of the mean and of the standard deviation of each approximation as in Eq. 51.
Figure 3.
Errors of the mean and standard deviation of the total substrate xt vs k3 for the different approximations discussed here. Except for k3, we used the same parameters as in Fig. 2. We used 2000 Monte Carlo realizations for the smallest value of k3 and increased the number of realizations linearly, working with 20 000 realizations for the largest value of k3 shown; this was done to maximize accuracy for the available computational power. Our method is uniformly more accurate as k3 is varied.
As expected, the errors of the approximations proposed by Goutsias13 and Cao et al.36 grow quickly as k3 increases because the conditions for which their approximations were developed (e.g., k3⪡k2 in Goutsias13) are violated for large k3. The approximation proposed by Rao and Arkin,10 on the other hand, does better than the previous ones as k3 increases. This is again expected, since Rao and Arkin did not ignore slow reactions in the fast system and also because for this example the substrate is at excess, as they assumed. However, for a wide range of k3 values, the most accurate approximation is clearly the one proposed in this paper.
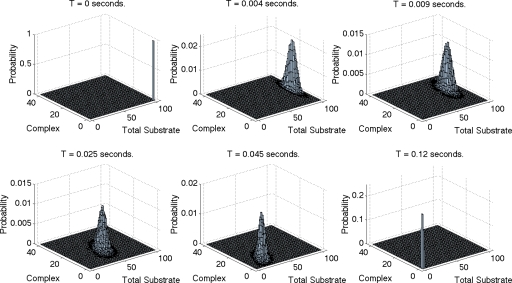
Figure 4 shows the probability distribution P(xt,xc) at various time points for another choice of parameters in which the conditions for the accuracy of the approximations by Goutsias13 and Cao et al.36 are again not satisfied. Here xt=xeo, violating the saturation assumption Goutsias made for this example, and k2=k3, violating the requirements of Goutsias13 and Cao et al.36 The top plots in Fig. 4 correspond to time points within the initial fast transient and the lower plots to time points within the slower motion. Note that the separation of time scales in this example is not as extreme as that of the example in Fig. 1.
Figure 4.
Empirical probability distribution P(xt,xc) obtained from 120 000 realizations of the full (nonapproximate) CME in Eq. B1 via the Gillespie algorithm at six different time points. The system parameters are Ω=k1=1, k2=k3=100, and initial enzyme and total substrate both equal to 100. Note that the separation of time scales in this example is not as extreme as that of the example in Fig. 1.
Figure 5 shows the average and standard deviation of the total substrate as a function of time, obtained from the different models previously discussed for the choice of parameters in Fig. 1. Here again all the approximate methods took comparable computation times, ranging from 6.18 to 6.37 s for 10 000 simulations, while simulation of the full system required around 21 s. Note that the reduction in computation time is less here than in the previous example because the time-scale separation here is not as large. As expected, the models of Goutsias13 and Cao et al.36 do not perform so well for this example. Our approach, however, still results in a good approximation to the exact solution.
Figure 5.
Mean and standard deviation of the total substrate xt computed from 10 000 realizations for each of the stochastic descriptions considered for the system parameters of Fig. 4. The realizations were all obtained from Monte Carlo simulation using the Gillespie algorithm. Our method produces more accurate solutions than the other approximate methods shown.
Figure 6 plots the errors of the different models for the same example for a large range of k3 values. Our approach performs well throughout this range. For values of k3 much less than k2 (=100), the approach of Cao et al. works well, while that of Goutsias does not because of violation of his saturation assumption. Interestingly, the error of the approximation of Rao and Arkin10 decreases as k3 increases, although it is never smaller than the error of our approximation. The reason for this dependence is that their approximation assumes low enzyme numbers in the form of xeo⪡xt+KmΩ. As k3 increases, so does Km, making their assumption more reasonable and their approximation more accurate.
Figure 6.
Errors of the mean and standard deviation of the total substrate xt vs k3 for the different approximations discussed here. Except for k3, we used the same parameters as in Fig. 5. We used 1000 Monte Carlo realizations for the smallest value of k3 and increased the number of realizations linearly, working with 10 000 realizations for the largest value of k3 shown; this was done in order to maximize accuracy for the available computational power. Our method is uniformly better as k3 is varied.
CONCLUDING REMARKS
We have described here a systematic method to identify slow and fast variables in a system of slow and fast chemical reactions and have developed reduced CMEs for these variables, starting from a CME for the full system. We have also illustrated on a canonical example the potential for significantly increased accuracy over a wide range of parameters and with a computational burden that is comparable to related reduction schemes.10, 12, 13
The identification of slow and fast variables is at the heart of time-scale decomposition methods but has typically not been addressed systematically, particularly in the stochastic case. Our approach, which is related to that of Heinrich and Schuster,24 is quite transparent and generalizes what has previously been observed and exploited in particular examples.21, 22, 23
Our slow CME is distinct in its retention of the effects of slow reactions on the fast subsystem. The resulting model reduction method should be particularly useful in systems where the slow reactions that modify the slow variables are independent of the slow variables, as occurs in many biological systems of interest, such as enzymatic reaction or protein interaction networks. We have also highlighted the value of MFK models, with their tracking of means, variances, and covariances, as adjuncts to this model reduction process.
A recent paper by Barik et al.29 developed a method similar to ours to identify slow and fast variables in stochastic chemical systems and used it to obtain an approximate master equation for the slow variables. These authors demonstrated, as we do here, that retaining slow reactions in the fast subsystem results in better approximations for the specific systems they considered. However, they did not isolate the feature of their examples that is key for their good results, namely, that for their protein interaction networks the slow propensities that modify the slow variables are not a function of the slow variables. As we have pointed out, such gain in accuracy need not be attained for systems where the slow propensities that modify the slow variables do depend on the slow variables. Additionally, Barik et al. obtained the conditional propensities from the deterministic steady-state MAK model, which ignores fluctuations in the fast variables, in contrast with the MFK-based approach proposed here.
Numerical experiments with our reduced CME model for the slow variables in a canonical example—the irreversible enzymatic reaction—have demonstrated consistently and predictably better results than other stochastic treatments of this example in the literature. Furthermore, our reduced MFK model for the slow system in this example specializes in the large-volume (low-fluctuation) limit to familiar deterministic total quasi-steady-state models that are more accurate and more broadly applicable than traditional Michaelis–Menten models.
It is worth noting that Goutsias13 and Haseltine and Rawlings9, 14 work with a different coordinate system than that used here, specifying the state to be the degree of advancement of the reactions (i.e., the number of reactions of each kind that have occurred since the start of the experiment). This alternate state is particularly useful when reactions are not instantaneous but rather change the molecule numbers in the system only after a specified amount of time since the beginning of the reaction has passed; Goutsias,13 for instance, has a detailed explanation. However, the expressions here can be adapted quite straightforwardly to their model.
Recent papers by Peleš et al.15 and MacNamara et al.19 directly exploited the linearity and time invariance of the CME operator by using eigenvector methods to carry out time-scale decomposition. Although we have found it useful to interpret the results in this paper using the framework of Peleš et al., we omit such interpretations here due to space constraints. Finally, considerable work remains to be done to bridge the more informally justified time-scale reduction methods developed here and in related literature, with more rigorous treatments such as that in Ball et al.39 for models of interest in stochastic chemical kinetics.
ACKNOWLEDGMENTS
C.A.G.-U. gratefully acknowledges the support of an MIT-Merck Graduate Fellowship and the MIT EECS∕Whitehead∕Broad Training Program in Computational Biology (Grant No. 5 R90 DK071511-01 from the NIH). G.C.V. is grateful to Professor Thomas Kailath at Stanford University for support on many dimensions. A.R.T was partially supported by an NIH grant (R01 GM 49039).
APPENDIX A: ALGORITHM FOR EXPOSING SLOW AND FAST VARIABLES
One way to obtain the matrix A in Eq. 14 is as the product T2T1 of two matrices, where T1 is an integer matrix embodying row operations chosen to transform Sf to the form
where Qff has full row rank. In the process S gets modified to the form
Now T2 is chosen as
with I being an identity matrix and being an integer matrix again embodying row operations to transform to the form
where Qss has full row rank. The net effect is to obtain the decomposition in Eq. 14.
APPENDIX B: THE FULL CME AND FAST CME OF THE ENZYMATIC SYSTEM
The CME for the full system is given by
| (B1) |
Similarly, the approximate fast CME for the fast variables, Eq. 25, takes the form
| (B2) |
APPENDIX C: CONNECTION TO DETERMINISTIC SINGULAR PERTURBATION THEORY
Singular perturbation theory provides a very useful framework for model reduction via separation of time scales in systems of ordinary differential equations. The standard deterministic singular perturbation model starts with the evolution equations of the slow and fast variables of a system, respectively denoted by xs and xf:
| (C1) |
| (C2) |
where t denotes time and ϵ⪡1 is a small parameter, and the functions f( ) and g( ) are O(1) in ϵ. These conditions guarantee an initial transient where the rates of change in the slow and fast variables have small and large magnitudes, respectively. Under appropriate conditions on the stability of the fast subsystem, this subsystem settles rapidly to a quasi-steady-state; its settling transient can be approximated by replacing xs in Eq. C2 by the constant vector xs(to) corresponding to its value at the starting time to. The slow variables can then be approximated by replacing xf in Eq. C1 by a quasi-steady-state value. The resulting slow subsystem is
| (C3) |
where h(t,xs) is a steady-state solution of the fast subsystem in Eq. C2 for ϵ=0:
| (C4) |
The approximation has an error of order ϵ (see Ref. 32, for example).
The model reduction method we suggest in this paper is similar to the standard singular perturbation result cited above, the difference being that we do not set ϵ to zero on the right side of the evolution equation for the fast system. We accordingly solve
| (C5) |
rather than Eq. C4 to obtain the quasi-steady-state values of the fast variables as a function of the slow ones. The potential benefit of the idea can be more readily seen in the context of a simple linear, time-invariant, two-time-scale system, which we briefly discuss next.
Consider the dynamic system
| (C6) |
where all entries are scalars and where the entries in the matrix depend on a small parameter ϵ as follows:
| (C7) |
The derivatives of xs and xf comprise a sum of terms, some that depend on ϵ (these correspond to the slow-reaction rates in our analogy to chemical kinetics) and some that do not (which correspond to the fast reactions). The slow variable xs typically evolves more slowly than the fast variable xf since the derivative of the former only involves slow reactions while that of the latter is a combination of slow and fast reactions.
To obtain an approximate description of the slow variables in this system, one would set the rate of change in the fast variable to zero (assuming that the fast subsystem is stable and has quickly settled) and then solve for the quasi-steady-state expression of xf in order to substitute it into the evolution equation for xs. The method we propose would do so without setting ϵ to zero in dxf∕dt, in contrast to the standard singular perturbation approach. This method then results in
| (C8) |
while standard singular perturbation yields
| (C9) |
To gauge which approximation is more accurate, suppose for simplicity that the goal of the approximation is to capture the time scale of the slow system accurately. The time constants of a linear, time-invariant system are simply the inverses of (the real parts of) its eigenvalues, so we shall simply compare eigenvalues. For the full system given by Eqs. C6, C7, these eigenvalues are given by
| (C10) |
where we use the fact that ∣a4∣⪢∣a1∣,∣a2∣, which follows from our specification C7 when ϵ is small, to obtain the second equation, which is correct up to second order in ϵ. Ignoring terms in powers of ϵ higher than 2, the eigenvalue corresponding to the slow time scale of the full system is then
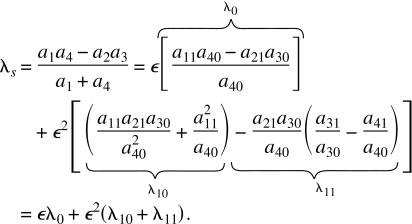 |
(C11) |
The eigenvalues of our approximations in Eq. C8 and the standard approximation in Eq. C9 may be read directly from those equations. They are respectively given by
| (C12) |
where the second equality ignores higher-order terms in ϵ, and
| (C13) |
Comparing Eqs. C12, C13 to Eq. C11 reveals that the approximations in Eqs. C8, C9 are quite accurate since they both capture the slow eigenvalue to first order in ϵ. Neither in general captures the eigenvalue correctly to second order in ϵ. However, our approach does capture the second-order term in ϵ correctly for systems where a1=0 so that λ10=0, i.e., where the slow reactions that modify the slow variables are not functions of the slow variables. This is the case of most interest for the approach of this paper.
References
- Henri V., Lois Générales de l’Action des Diastases (Hermann, Paris, 1903). [Google Scholar]
- Michaelis L. and Menten M., Biochem. Z. 49, 333 (1913). [Google Scholar]
- Ciliberto A., Capuani F., and Tyson J. J., PLOS Comput. Biol. 3, e45 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez-Uribe C., Verghese G. C., and Mirny L. A., PLOS Comput. Biol. 3, e246 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzafriri A. R. and Edelman E. R., Biochem. J. 402, 537 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersena M. G., Bersani A. M., and Bersani E., Bull. Math. Biol. 10.1007/s11538-006-9136-2 69, 433 (2007). [DOI] [PubMed] [Google Scholar]
- Del Vecchio D., Ninfa A. J., and Sontag E. D., Mol. Syst. Biol. 4, 161 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankowicz M., Moreau M., Szczȩsny P., Tòth J., and Vicente L., J. Phys. Chem. 10.1021/j100111a029 97, 1891 (1993). [DOI] [Google Scholar]
- Haseltine E. L. and Rawlings J. B., J. Chem. Phys. 117, 6959 (2002). [Google Scholar]
- Rao C. and Arkin A., J. Chem. Phys. 118, 4999 (2003). [Google Scholar]
- Roussel M. R. and Zhu R., J. Chem. Phys. 10.1063/1.1802495 121, 8716 (2004). [DOI] [PubMed] [Google Scholar]
- Cao Y., Gillespie D. T., and Petzold L. R., J. Chem. Phys. 122, 14116 (2005). [DOI] [PubMed] [Google Scholar]
- Goutsias J., J. Chem. Phys. 10.1063/1.1889434 122, 184102 (2005). [DOI] [PubMed] [Google Scholar]
- Haseltine E. L. and Rawlings J. B., J. Chem. Phys. 123, 164511 (2005). [DOI] [PubMed] [Google Scholar]
- Peleš S., Munsky B., and Khammash M., J. Chem. Phys. 10.1063/1.2397685 125, 204104 (2006). [DOI] [PubMed] [Google Scholar]
- Mastny E. A., Haseltine E. L., and Rawlings J. B., J. Chem. Phys. 10.1063/1.2764480 127, 094106 (2007). [DOI] [PubMed] [Google Scholar]
- Gillespie D. T., J. Phys. Chem. 10.1021/j100540a008 81, 2340 (1977). [DOI] [Google Scholar]
- Gibson M. and Bruck J., J. Phys. Chem. A 10.1021/jp993732q 104, 1876 (2000). [DOI] [Google Scholar]
- MacNamara S., Bersani A., Burrage K., and Sidje R., J. Chem. Phys. 129, 95105 (2008). [DOI] [PubMed] [Google Scholar]
- Gomez-Uribe C., Ph.D. thesis, Massachusetts Institute of Technology, 2008. [Google Scholar]
- Bundschuh R., Hayot F., and Jayaprakash C., Biophys. J. 84, 1606 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren P. B., Tanase-Nicola S., and ten Wolde P. R., J. Chem. Phys. 10.1063/1.2356472 125, 144904 (2006). [DOI] [PubMed] [Google Scholar]
- Morelli M. J., Allen R. J., Tanase-Nicola S., and ten Wolde P. R., J. Chem. Phys. 10.1063/1.2821957 128, 045105 (2008). [DOI] [PubMed] [Google Scholar]
- Heinrich R. and Schuster S., The Regulation of Cellular Systems, 1st ed. (Chapman and Hall, London, 1996), pp. 112–134. [Google Scholar]
- Gómez-Uribe C. A. and Verghese G. C., J. Chem. Phys. 126, 024109 (2007). [DOI] [PubMed] [Google Scholar]
- Goutsias J., Biophys. J. 92, 2350 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A. and Hespanha J., in Proceedings of the 45th IEEE Conference on Decision and Control, 2006. (unpublished).
- Tzafriri A. R., Bull. Math. Biol. 10.1016/S0092-8240(03)00059-4 65, 1111 (2003). [DOI] [PubMed] [Google Scholar]
- Barik D., Paul M. R., Baumann W. T., Cao Y., and Tyson J. J., Biophys. J. 95, 3563 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallager R., Discrete Stochastic Processes (Springer, New York, 2001). [Google Scholar]
- Gillespie D. T., Physica A 10.1016/0378-4371(92)90283-V 188, 404 (1992). [DOI] [Google Scholar]
- Khalil H., Nonlinear Systems (Prentice-Hall, Englewood Cliffs, NJ, 2002). [Google Scholar]
- Borghans J. A., de Boer R. J., and Segel L. A., Bull. Math. Biol. 10.1007/BF02458281 58, 43 (1996). [DOI] [PubMed] [Google Scholar]
- E W., Liu D., and Vanden-Eijnden E., J. Chem. Phys. 10.1063/1.2109987 123, 194107 (2005). [DOI] [PubMed] [Google Scholar]
- Gillespie D. T., Petzold L. R., and Cao Y., J. Chem. Phys. 10.1063/1.2567036 126, 137101 (2007); [DOI] [PubMed] [Google Scholar]; Gillespie D. T., Petzold L. R., and Cao Y., J. Chem. Phys. 10.1063/1.2567071126, 137102 (2007). [DOI] [PubMed] [Google Scholar]
- Cao Y., Gillespie D. T., and Petzold L. R., J. Chem. Phys. 10.1063/1.2052596 123, 144917 (2005). [DOI] [PubMed] [Google Scholar]
- Briggs G. E. and Haldane J. B. S., Biochem. J. 19, 339 (1925). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segel L. A., Bull. Math. Biol. 10.1016/S0092-8240(88)80057-0 50, 579 (1988). [DOI] [PubMed] [Google Scholar]
- Ball K., Kurtz T. G., Popovic L., and Rempala G., Ann. Appl. Probab. 16, 1925 (2006). [Google Scholar]