Lattice kinetic Monte Carlo simulations of convective-diffusive systems

Abstract

Diverse phenomena in physical, chemical, and biological systems exhibit significant stochasticity and therefore require appropriate simulations that incorporate noise explicitly into the dynamics. We present a lattice kinetic Monte Carlo approach to simulate the trajectories of tracer particles within a system in which both diffusive and convective transports are operational. While diffusive transport is readily accounted for in a kinetic Monte Carlo simulation, we demonstrate that the inclusion of bulk convection by simply biasing the rate of diffusion with the rate of convection creates unphysical, shocklike behavior in concentrated systems due to particle pile up. We report that elimination of shocklike behavior requires the proper passing of blocked convective rates along nearest-neighbor chains to the first available particle in the direction of flow. The resulting algorithm was validated for the Taylor–Aris dispersion in parallel plate flow and multidimensional flows. This is the first generally applicable lattice kinetic Monte Carlo simulation for convection-diffusion and will allow simulations of field-driven phenomena in which drift is present in addition to diffusion.

INTRODUCTION

The kinetic Monte Carlo (KMC) method has been applied extensively to the study of nonequilibrium, stochastic phenomena in materials science, biology, and physics. Diverse applications include dynamics of λ phage infection of E. coli,¹ multicomponent aggregation fragmentation,² defect diffusion in metals and semiconductors,³ and crystal growth.⁴ A common element in these applications is that the system dynamics are driven by stochastic events (e.g., molecular reaction and∕or diffusion) that occur on time scales much larger than the microscopic dynamics of individual atoms or molecules.

Although the KMC approach is well established for purely diffusive or reactive systems,⁵ it has generally not been applicable to situations in which convective transport (drift) by fluid flow, or any other globally applied field that introduces drift, is also operational. In fact, recent work has shown that accounting for both diffusion and drift in Monte Carlo simulations can be challenging under certain conditions, even for a single particle.⁶ Enabling KMC simulations of convective-diffusive transport offers the possibility to study stochastic behavior in such systems, investigate the morphology of particle aggregates formed under complex transport conditions, and even provide an alternative solution approach in cases where numerical difficulties are problematic in partial differential equation-based continuum models. While methods such as lattice Boltzmann⁷ and dissipative particle dynamics⁸ are highly suited for simulating particle motion in a fluid, these methods also solve for the fluid flow, which can limit the scale of problems that can be addressed. Moreover, the KMC approach offers established avenues for coarse graining^{9, 10} and acceleration.¹¹

The primary input into the KMC algorithm is a rate database for all possible events. These rates may be precomputed¹² or computed during¹³ the simulation. In general, restricting a KMC simulation onto a fixed lattice greatly reduces the dimensionality of the state space and leads to a highly efficient approach known as lattice KMC (LKMC). While it is natural to employ a lattice for simulations of diffusion in a crystalline solid, for example, the lattice in general does not need to reflect any underlying crystalline order but rather serves to simplify the calculation of rates for the various possible events. One limiting example is the case of diffusion of noninteracting solute particles in a stationary fluid. In this situation, the rate of each “hop” between adjacent lattice sites is the same and is given by the diffusivity of the particles in the stagnant fluid medium.

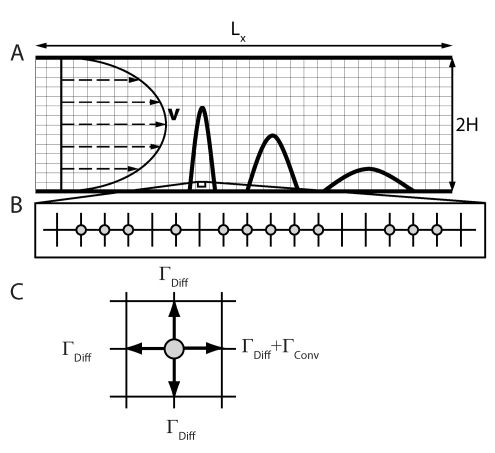
The aim of this paper is to present and analyze mathematically a new approach for performing LKMC simulations where an external flow field (or force field in the overdamped limit) is applied to a system of diffusing particles and where the flow field (force field) is not backcoupled to the time-dependent solute particle distribution. The well-known phenomenon of Taylor dispersion¹⁴ is first used to develop and analyze the convective LKMC algorithm. We consider a collection of solute particles in a fluid contained between two impermeable parallel plates, as shown in Fig. 1a. Under a pressure gradient in the x-direction and assuming no slip at the plate surfaces, the steady-state, fully developed fluid flow profile is given by

$$v\left(y\right)=\frac{3}{2}{v}_{\text{avg}}\left(1-\frac{y^2}{H^2}\right),$$ (1)

where v_avg is the average fluid velocity and 2H is the parallel plate separation distance. A pulse of solute is introduced into the channel at x=0 in which the particle distribution is given by a one-dimensional (1D) Gaussian distribution in the x-direction, with a height of 0.5 and unit standard deviation of σ²=1. The continuum governing equation describing the transport of solute is generally given by

$$\frac{\partial C}{\partial t}+\nabla \cdot \left(vC\right)=D\frac{{\partial }^{2}C}{\partial x^2}+D\frac{{\partial }^{2}C}{\partial y^2},$$ (2)

where C(x,y) is the solute concentration and D is solute diffusivity. Assuming that the solute particles are much larger than the fluid molecules, the solute particle diffusivity can be determined from the Stokes–Einstein relation as D=k_BT∕6πηa, where T is the temperature of the fluid, a is the radius of the particle, and η is the fluid viscosity. For long times, the moment analysis of Aris¹⁵ predicts that the solute pulse broadening can be described by

$$\frac{\partial \overline{C}}{\partial t}=K\frac{{\partial }^2\overline{C}}{\partial x^2},$$ (3)

where K is the dispersivity and $\overline{C}=\left(1∕A\right)\int CdA$ is the cross-sectional average of the concentration profile. For the geometry considered here, the dispersivity is given by K=D(1+(2∕105)Pe²), where the Peclet number is given by Pe≡v_avgH∕D.¹⁶

Figure 1.

(a) Two-dimensional rectangular domain discretized with lattice spacing h_x and h_y. The flow field, represented by v, can be any externally applied flow. (b) Blowup of a region of high concentration from panel (a) showing the blocking that occurs with multiple particles. (c) Transition rates for an isolated particle with flow toward the right.

LATTICE KINETIC MONTE CARLO SIMULATION OF TAYLOR DISPERSION

In order to perform LKMC simulations of Taylor dispersion, the domain shown in Fig. 1a was discretized using a uniform rectangular grid with N_x and N_y grid points in the x and y directions, respectively, with corresponding lattice spacing h_x=L_x∕(N_x−1) and h_y=2H∕(N_y−1). In the present work, solute particles are assumed to be noninteracting except for same-site exclusion. Under zero flow conditions (v_avg=0), the particles exhibit purely diffusive motion, and on a discrete lattice, the timescale of a diffusive hop between nearest-neighbor sites is given by τ_diff=h²∕D. The rate Γ for a diffusive event therefore is given by

$${\Gamma }_{\text{diff}}\equiv \frac{1}{{\tau }_{\text{diff}}}=\frac{D}{h^2}.$$ (4)

In the LKMC algorithm, a specific event i with rate Γ_i is picked with probability P_i=Γ_i∕Γ_tot, where Γ_tot is the total rate for all possible (in this case, diffusive) events at a given time. The simulation clock is updated following each event by the time increment τ=−ln U∕Γ_tot, where U is a uniformly distributed random number in the interval [0,1]. The cross-sectional average of the solute pulse diffusion profile obtained from LKMC and solution of Eq. 2 with v_avg=0 in Eq. 1 are compared in Fig. 2 (inset) for several times, demonstrating excellent agreement at timescales that are long relative to individual hops.

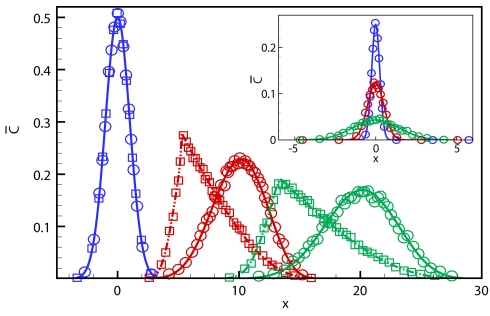
Figure 2.

Temporal evolution of the cross-sectional average of solute concentration in parallel plate flow with an initial Gaussian solute pulse (zero mean and unit standard deviation). Simulation conditions, Pe=100 (v_avg=1000, H=0.1, D=1), and uniform LKMC grid (h_x=0.01, h_y=0.002). From left to right the simulation times are t=0 (blue), t=0.01 (red), and t=0.02 (green). Solid line: COMSOL solution of Eq. 2. Dash-dotted line: COMSOL solution of Eq. 2 with concentration dependent velocity from Eq. 8. Squares: SBA-LKMC. Circles: PFA-LKMC. Inset: evolution of a 1D Gaussian solute pulse with maximum of 0.25 and standard deviation of 0.25 with zero convection computed with (a) COMSOL [Eq. 2] (solid lines) and (b) LKMC (circles). The three curves represent t=0 (blue), t=1 (red), and t=10 (green).

Consider next the case where v_avg≠0 and solute particles are transported by both diffusion and convection. In the simple 1D flow example described in Fig. 1a, the grid in the x-direction is aligned with the flow streamlines and the timescale for convection over one lattice spacing is given by τ_conv=h_x∕v, where v is the local velocity. The rate for a “convective move” along the velocity vector therefore is given by Γ_conv=v∕h_x. At first glance, the simplest approach to include convection into an LKMC simulation would be to augment the diffusive rates by Γ_conv along the direction of the velocity vector [in this case, the positive x-direction as shown in Fig. 1c]. The rates normal to and against the velocity vector are unchanged. This algorithm is henceforth referred to as the simplest biasing algorithm (SBA).

The evolution of the Gaussian solute pulse with the SBA for Pe=100 (v_avg=1000, H=0.1, D=1) and a uniform LKMC grid (h_x=0.01, h_y=0.002) is shown in Fig. 2 (square symbols). The particle evolution is clearly nondiffusive, whereby the trailing edge of the particle distribution becomes steeper while the leading edge exhibits a long tail. Also shown in Fig. 2 is the numerical solution of Eq. 2 with the velocity profile in Eq. 1, computed using a commercial finite element method software (COMSOL Multiphysics™, Burlington, MA) (solid line), which demonstrates the expected diffusive spreading of the solute pulse. In the context of Taylor dispersion, the Aris analysis gives a constant value of K=191 at long times, which is in excellent agreement with the numerically extracted value of K=191 at t=0.02 from the COMSOL solution of Eq. 2. Not only is the SBA-LKMC prediction of the pulse shape evolution incorrect, but it also underpredicts the average velocity of the solute particles. With more dilute solute pulses, these discrepancies become smaller, but the SBA-LKMC method does not provide satisfactory results until the solute particle concentration approaches zero everywhere.

The errors in the SBA-LKMC results arise from the combination of single-particle moves inherent in the LKMC method and particle-particle blocking due to the site exclusion interaction. Note that site exclusion is required if morphological information (e.g., aggregate shape) is to be preserved. Particles that have nearest neighbors in the direction of the flow are blocked and are subject to zero convective (and diffusive) hopping rates [Fig. 1b]. As a result of convective blocking, the sum of the rates in the system at any given time is underestimated. Moreover, the fact that the probability of such an occurrence increases with the solute concentration leads to a concentration-dependent rate of convection.

We report that the effect of global convection can be accurately captured in a standard LKMC simulation simply by identifying nearest-neighbor connected chains in the direction of the local flow and passing forward to the leading particle the convective rates of all blocked particles. For the 1D flow profile in Fig. 1a, the total convective rate associated with a particle that is located at the front of a linearly connected chain of s particles (i.e., the rightmost particle for the situation shown in Fig. 1) is then given by

$${\Gamma }_{\text{conv}}\left(s\right)=s{\Gamma }_{\text{conv}}.$$ (5)

We denote this algorithm as the pass forward algorithm or PFA. The rate modification in Eq. 5 effectively reintroduces the blocked convective rates into the overall dynamics of the LKMC algorithm and leads to a time update correction of the form

$$\tau =\frac{-\text{ln}U}{{\Gamma }_{\text{tot}}^{\prime }+{\Gamma }_{\text{blocked}}},$$ (6)

where ${\Gamma }_{\mathrm{tot}}^{\prime }$ is the total rate computed using SBA-LKMC and Γ_blocked is the total convective rate of all blocked particles in the system at a given configuration (i.e., ${\Gamma }_{\mathrm{tot}}={\Gamma }_{\mathrm{tot}}^{\prime }+{\Gamma }_{\text{blocked}}$). The theoretical basis for this approach is presented later in this section.

The transient solute particle distribution using PFA-LKMC is shown in Fig. 2 (circle symbols). The agreement with the continuum COMSOL solution (solid line) now is excellent for all times and a dispersivity of 202.0±2.8 averaged from t=0.19 to t=0.20 is obtained, which is in very good agreement with both the analytic and continuum numerical solution values. However, there is some small additional algorithm dispersion that arises from discretization, which is discussed in Sec. 4. Similar agreement between the PFA-LKMC and continuum solution results is obtained at other values of Pe ranging from 1≤Pe≤1000 (data not shown).

PFA-LKMC is the only rate passing algorithm for single-particle moves that can correct for the errors in SBA-LKMC as will be shown below. Concerted moves of linearly connected particles do resolve the blocking problem to some extent but lead to significant errors when the convective field varies over the length of the average chain. The validity of the PFA-LKMC and the source of the error in the SBA-LKMC can be established mathematically. Consider particles moving on a 1D lattice, with grid spacing h and a number density distribution, C(x). For simplicity, here we assume that the fluid velocity is constant with magnitude v and that there is no diffusive transport. For a single move, the velocity of the chosen particle is therefore h∕τ, where τ is the time step increment at a given system configuration. The velocities of all other particles over that time interval are zero. The average velocity of a particle over many LKMC moves therefore is given by

$$⟨v_{\text{particle}}⟩=P_{\text{particle}}⟨\frac{h}{\tau }⟩=\frac{⟨{\Gamma }_{\text{particle}}⟩h}{⟨{\Gamma }_{\text{tot}}⟩⟨\tau ⟩}=⟨{\Gamma }_{\text{particle}}⟩h,$$ (7)

where P_particle is the probability of picking a particular particle to move. In order to make the particle average velocity equal to the average fluid velocity v, Eq. 7 requires that ⟨Γ_particle⟩=Γ_conv=v∕h, which is satisfied only when no particles are blocked. In the SBA-LKMC algorithm, this can only be ensured at infinite dilution. For finite particle concentration, particle blocking leads to a decrease in the average particle velocity.

The extent of the velocity decrease in SBA-LKMC can be estimated. Consider a particle at position x where the local particle density is C(x). Assuming that the local particle density is constant over one lattice spacing, the probability that a particle can move in the direction of the flow in an SBA-LKMC simulation is (1−C(x)). Therefore, the average transport rate of a particle at a position x in the SBA-LKMC simulation is ⟨Γ_particle(x)⟩_SBA=(1−C(x))Γ_conv, which leads to a spatially dependent velocity,

$${⟨v_{\text{particle}}\left(x\right)⟩}_{\mathrm{SBA}}=\left(1-C\left(x\right)\right)v.$$ (8)

The SBA-LKMC results were compared directly to a numerical solution of Eq. 2 with the velocity given by Eq. 8 (dashed line); as shown in Fig. 2 the agreement is excellent, confirming the validity of the preceding analysis, even when diffusion is present. The 1D form of Eq. 2 with the concentration dependent velocity from Eq. 8 is related to the Burgers equation,¹⁷ which was originally proposed to understand turbulence and has applications in traffic flow,¹⁸ surface growth dynamics,¹⁹ sedimentation,²⁰ and other traveling shock phenomena. However, it is important to note that the shock behavior seen in SBA-LKMC arises from an artificial bias in the algorithm and does not correspond to a physically relevant phenomenon, because no hydrodynamic interactions between particles are considered in this work. Moreover, the concentration-dependent bias introduced in SBA-LKMC causes particles to lose the momentum that is being transferred to them from the fluid, a process that violates the basic physics of the model.

The PFA-LKMC algorithm removes the concentration dependence of the velocity by modifying the probability of picking a specific particle by the probability that the particle is at the front of a connected chain, where the front is defined by the flow direction. These probabilities can be estimated using 1D percolation theory²¹ in the limit that the concentration gradient is small relative to the average chain length. In this limit, the probability of finding a specific isolated chain of s connected particles that includes site x is given by sC(x)^s(1−C(x)⁾². Given that site x is occupied, the probability that it is at the front of the chain therefore is

$${\eta }_s\left(x\right)=C{\left(x\right)}^{s-1}{\left(1-C\left(x\right)\right)}^2.$$ (9)

The average drift rate of a particle located at position x is given by the weighted average of rates due to all possible chains terminating at that position, i.e.,

$${⟨{\Gamma }_{\text{particle}}\left(x\right)⟩}_{\text{PFA}}=\sum _s{\eta }_{s}s{\Gamma }_{\text{conv}}={\Gamma }_{\text{conv}}{\left(1-C\left(x\right)\right)}^2\sum _{s}sC{\left(x\right)}^{s-1}={\Gamma }_{\text{conv}},$$ (10)

and the velocity of a particle at position x for the PFA is therefore equal to the local fluid velocity, i.e.,

$$v_{\text{PFA}}\left(x\right)=v.$$ (11)

In other words, by passing the rates of blocked particles forward to the first available particle, the correct velocity is obtained at every position in the system.

EXTENSION OF PFA-LKMC TO TWO-DIMENSIONAL FLOWS–EXPANSION FLOW

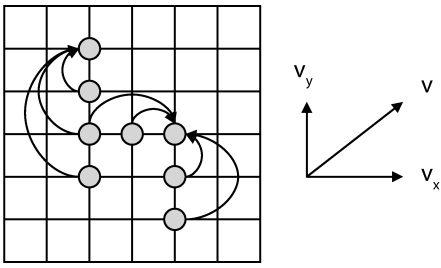
The PFA-LKMC method can be extended readily to situations with multidimensional flows that are not necessarily aligned with the grid by simply decomposing the local velocity vector into its components along the LKMC grid. Generally, a velocity field in the Cartesian coordinate system employed in Fig. 1a is given by $\overline{v}={\overline{e}}_x{v}_x+{\overline{e}}_y{v}_y$, where e_i is the unit vector in the ith direction. In order to apply the PFA-LKMC algorithm to this two-dimensional velocity field, the component convective rates are passed to the front particle of connected chains in both the x and y directions, as shown in Fig. 3.

Figure 3.

Schematic of PFA-LKMC algorithm in two-dimensional flows. Arrows denote the passing of convective rates to the front of connected chains defined in the directions of the components of a generalized velocity v.

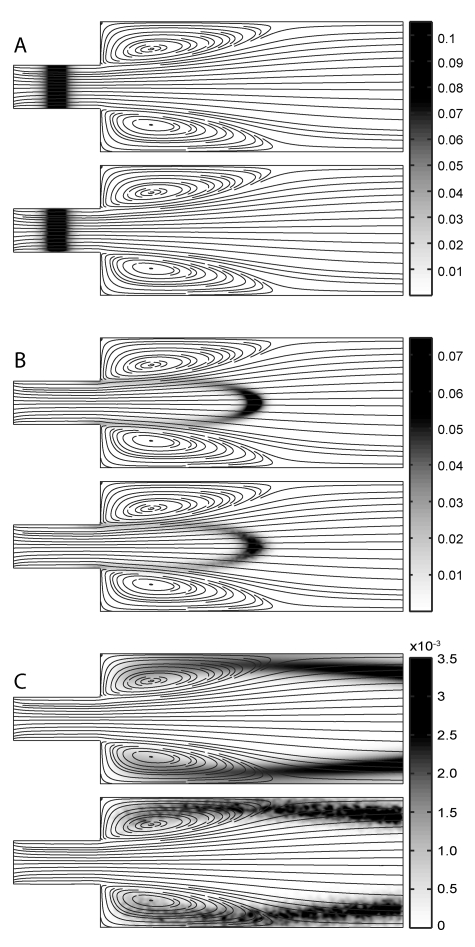
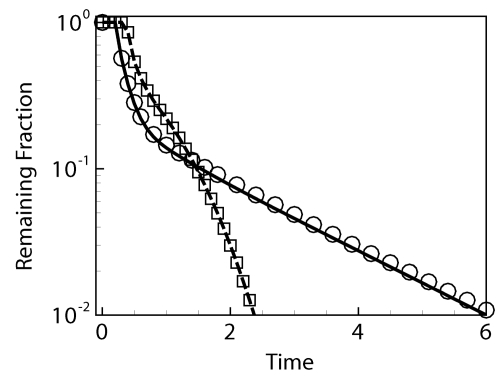
The two-dimensional version of the PFA-LKMC algorithm is tested using a parallel plate, 3:1 expansion-flow geometry, which leads to the formation of vortices in the region immediately following the expansion (see Fig. 4). The evolution of a Gaussian (in the x-direction) solute pulse as a function of time, computed by numerical solution of Eq. 2, and with PFA-LKMC, is shown in Fig. 4. The vortices serve as reservoirs for the solute and continue to leach solute out of the cell long after the primary pulse has been convected out of the domain. Figure 5 shows the fraction of solute remaining in the expansion-flow domain, which shows the lag time before the primary pulse exits the domain, then the rapid loss of solute, and the long-time leaching of solute from the vortices. For comparison, the remaining solute fraction as a function of time for a straight channel is also shown in Fig. 5. Excellent agreement is demonstrated in Fig. 5 between the continuum and the PFA-LKMC predictions for the fraction of solute remaining for both expansion-flow and straight channel geometries.

Figure 4.

Solute pulse evolution as a function of time in a two-dimensional laminar expansion flow. The narrow channel width is 1 dimensionless unit and the wide channel width is 3 units. The lengths of the narrow and wide channels are 2 and 7 units, respectively. Each panel shows a comparison between numerical solution of Eq. 2 (upper) and PFA-LKMC (lower) with the color bar representing dimensionless concentration for both the numerical solution and PFA-LKMC. The velocity profile, denoted by streamlines, was computed with COMSOL with Pe=413 (v_avg=41.3, D=0.1) and Re=41.3 (ρ=1, μ=1) at the inlet. (a) t=0, (b) t=0.1, and (c) t=0.6.

Figure 5.

Fraction of solute remaining within the simulation domain from Fig. 4 as a function of (dimensionless) time. Lines: numerical solution of Eq. 2 with COMSOL. Solid line represents expansion flow geometry and dashed line represents straight-channel geometry. Symbols: PFA-LKMC. Circles represent expansion-flow geometry and squares represent straight-channel geometry. The straight-channel geometry has the same overall length of the expansion-flow domain shown in Fig. 4 and the same height as the wide region. The flow parameters are the same at the outlet of each channel.

ERROR ANALYSIS FOR CONVECTIVE LATTICE KINETIC MONTE CARLO

While the PFA-LKMC algorithm effectively corrects for particle blocking on a lattice, the algorithm nevertheless does exhibit some error, which is apparent in the increased dispersivity (K=202 versus 191) within the Taylor–Aris analysis in Sec. 2. The error appears to increase with fluid velocity and with particle concentration, but decreases with finer lattice spacing. We analyze mathematically this effect using a 1D system of N diffusionless particles subject to constant velocity v on a uniform lattice with spacing h using PFA. The particle positions at time t are given by a distribution X(t)={x₁(t),x₂(t),⋯,x_N(t)}, which evolves from an initially Gaussian distribution X(0) with mean and variance of μ₀ and ${\sigma }_0^2$, respectively. It follows that the distribution of particle positions given that exactly m LKMC steps have occurred has mean μ_x∣m+μ₀ and variance ${\sigma }_{x\mid m}^2+{\sigma }_0^2$, where μ_x∣m and ${\sigma }_{x\mid m}^2$ are the change in the mean and variance of X, respectively. The step number m is itself a random Poisson variable with mean and variance, ${\mu }_m={\sigma }_m^2=t{\Gamma }_{\mathrm{tot}}$, where Γ_tot=Nv∕h for the diffusionless system under consideration. For m>10, m can be approximated by a normal distribution with the same mean and variance,²² i.e., $m=⟨m⟩\pm {\sigma }_m=t{\Gamma }_{\mathrm{tot}}\pm \sqrt{t{\Gamma }_{\mathrm{tot}}}$.

The true mean of X(t), μ_x+μ₀, is given by the conditional expectation formula²²

$${\mu }_x=⟨{\mu }_{x\mid m}⟩=⟨m⟩\Delta x=tv,$$ (12)

where Δx=h∕N is the change in μ_x∣m due to a single move and the expressions for ⟨m⟩ and Γ_tot given above were applied. The true variance of the distribution X(t), ${\sigma }_x^2+{\sigma }_0^2$, is derived in a similar fashion based on the conditional variance formula,²²

$${\sigma }_x^2=⟨{\sigma }_{x\mid m}^2⟩+\text{var}\left({\mu }_{x\mid m}\right),$$ (13)

where $\mathrm{var}\left({\mu }_{x\mid m}\right)={\sigma }_m^2{\left(\Delta x\right)}^2=tvh∕N$ is the variance of μ_x∣m. To determine ${\sigma }_{x\mid m}^2$, we consider the change in the variance of the particle position distribution due to a single move at position x_k, i.e., ${\sigma }_{x\mid m=1}^2=\left({⟨x^2⟩}_f-{⟨x^2⟩}_i\right)-\left({⟨x⟩}_f^2-{⟨x⟩}_i^2\right)$, where the indices f and i refer to the final and initial states, respectively. The change in the first moment of the particle position distribution is given by

$$\left({⟨x⟩}_f^2-{⟨x⟩}_i^2\right)={\left({⟨x⟩}_i+\frac{h}{N}\right)}^2-{⟨x⟩}_i^2=\frac{h}{N}\left(2{⟨x⟩}_i+\frac{h}{N}\right).$$ (14)

The contribution to the change in the moments from all stationary particles is zero, therefore the change in the second moment of the particle position distribution, which is only due to the particle at position x_k, is

$$\left({⟨x^2⟩}_f-{⟨x^2⟩}_i\right)=\frac{x_k^2{\mid }_f-x_k^2{\mid }_i}{N}=\frac{{\left(x_k+h\right)}^2-x_k^2}{N}=\frac{h}{N}\left(2x_k+h\right).$$ (15)

Equations 14, 15 directly lead to

$${\sigma }_{x\mid m=1}^2\left(x_k\right)=\frac{2h}{N}\left(x_k-⟨x⟩\right)+\frac{h^2\left(N-1\right)}{N^2}.$$ (16)

At finite concentration, particle blocking in the flow direction leads to a systematic bias in the selection process–only particles at the leading edge of connected chains can be selected. For a single chain, the front particle is s∕2−1∕2 lattice units away from the mean of that chain. Averaged over all possible chain lengths, the resulting local systematic bias is given by (x_k−⟨x⟩)=(⟨s⟩−1)h∕2, where ⟨s⟩ is the mean chain length at the local concentration, C(x_k), which is given by²¹

$$⟨s⟩=\frac{{\sum }_s{s}^2{\eta }_s}{{\sum }_{s}s{\eta }_s}=\left(\frac{1+C\left(x_k\right)}{1-C\left(x_k\right)}\right).$$ (17)

For small m, C(x_k) is approximately constant and Eq. 16 can be expressed as

$${\sigma }_{x\mid m}^2\left(x_k\right)=m\left(\frac{h^2}{N}\frac{1+C\left(x_k\right)}{1-C\left(x_k\right)}-\frac{h^2}{N^2}\right).$$ (18)

Finally, the probability that a site at position x_k is chosen at any given time is C(x_k)∕N, which leads to the result that

$$⟨{\sigma }_{x\mid m}^2⟩=⟨m⟩\left(\frac{h^2}{N}f\left(C\right)-\frac{h^2}{N^2}\right),$$ (19)

where $f\left(C\right)=\int \left(\frac{C\left(x\right)}{N}\right)\left[\frac{(1+C\left(x\right))}{(1-C\left(x\right))}\right]dx$, which is evaluated over the entire domain. Inserting this result into Eq. 13 gives

$${\sigma }_x^2=tvhf\left(C\right).$$ (20)

Because C(x) is approximately constant in time over a small number of steps, f(C) is also constant, so Eq. 20 is linear in time and therefore may be represented by a numerical dispersion coefficient of the form

$$K_{err}\equiv \frac{{\sigma }_x^2}{2t}=\frac{vh}{2}f\left(C\right).$$ (21)

This analysis was tested by comparing the apparent dispersion coefficient obtained from a PFA-LKMC simulation of a Gaussian solute pulse in straight-channel plug-flow with the result in Eq. 21. The apparent dispersion coefficient in the LKMC simulations was obtained by computing the difference between the initial and final variance of the solute pulse concentration over a short time interval. Two types of runs were performed. In the first, particles were assumed to be nondiffusive and any measured dispersion therefore can be attributed to algorithm error. In the second case, particles with finite diffusivity D were simulated and the dispersive error was defined by

$$K_{err}=\frac{{\sigma }_x^2}{2t}-D.$$ (22)

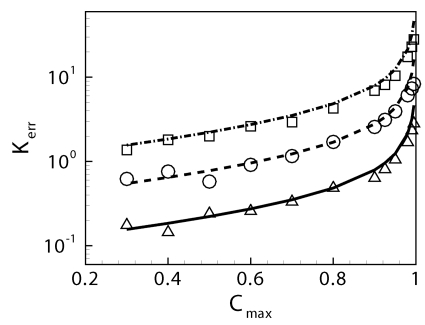
As shown in Fig. 6, the simulated [Eq. 22, open symbols] and calculated [Eq. 21, lines] diffusive errors are in excellent quantitative agreement for variations in concentration, velocity, grid spacing, and grid Peclet number, vh∕D. The error scales linearly with h, so it may be understood as a discretization error that is amplified by the presence of connected chains of particles. The fact that the calculated error in Eq. 21 accounts for all excess algorithm dispersion indicates that this is the dominant error in the algorithm.

Figure 6.

Diffusive∕dispersive error associated with the evolution of a Gaussian pulse (σ=1) in a 1D plug flow velocity profile as a function of peak concentration, C_max. The lines represent numerical evaluations of Eq. 21 and the corresponding symbols are the results from PFA-LKMC over a short time interval, Δt=10⁻⁴. The triangles∕solid line are with h=0.002, v=100, and D=0 (vh∕2=0.1, Pe=∞). The circles∕dashed line are with h=0.007, v=100, and D=0 (vh∕2=0.35, Pe=∞). The squares∕dashed dot line are with h=0.002, v=1000, and D=0.4 (vh∕2=1, Pe=5).

CONCLUSIONS

A new approach for incorporating convective transport of particles into LKMC simulations was developed and validated. The method is applicable to systems of tracer solute particles that do not affect the fluid flow and do not interact hydrodynamically. It was shown that a straightforward addition of local convective rates to the diffusive rates of particles leads to shocklike propagation behavior, along with an artificial reduction in the average particle transport rate, because of particle blocking. These artifacts were fully corrected with an algorithm whereby the blocked convective rates are passed forward to particles at the front of nearest-neighbor connected chains defined along the direction of flow. The validity of this approach was established mathematically for 1D systems. The PFA-LKMC method was also shown to be directly extensible to general two (and higher) dimensional flows using an expansion flow geometry.

The LKMC rates used in the present work are subject to some inaccuracies that will be addressed in detail in a future publication. First, they do not quantitatively satisfy the single-particle first passage problem in one-dimension that was applied to derive Monte Carlo moves for drift-diffusion systems.^{6, 23} However, our analysis demonstrates clearly that, over a wide range of Peclet numbers, the dominant error in the systems considered here arises from particle blocking due to same site exclusion. There also exists an inherent discretization error that scales as the vh∕2, associated with the application of LKMC to drift-diffusion systems at any concentration, which can be reduced arbitrarily by refining the lattice spacing. Second, the LKMC rates applied here only strictly satisfy detailed balance at low to moderate values of the grid Peclet number; however, this issue is generally not critical for the highly nonequilibrium situations encountered in flow-driven aggregation.

The method presented here enables the application of LKMC simulation to systems in which both convective and diffusive transport modes are operational. This approach enables stochastic simulation of diverse problems in systems biology, microfluidics, and nanomaterials processing, which span molecular to macroscopic length scales and manifest their complexity in the presence of convection. In future work, we seek to apply the generality of the formulation to the consideration of external fields such as magnetic, electric, or gravitational fields.