The multinomial simulation algorithm for discrete stochastic simulation of reaction-diffusion systems

Abstract

The Inhomogeneous Stochastic Simulation Algorithm (ISSA) is a variant of the stochastic simulation algorithm in which the spatially inhomogeneous volume of the system is divided into homogeneous subvolumes, and the chemical reactions in those subvolumes are augmented by diffusive transfers of molecules between adjacent subvolumes. The ISSA can be prohibitively slow when the system is such that diffusive transfers occur much more frequently than chemical reactions. In this paper we present the Multinomial Simulation Algorithm (MSA), which is designed to, on the one hand, outperform the ISSA when diffusive transfer events outnumber reaction events, and on the other, to handle small reactant populations with greater accuracy than deterministic-stochastic hybrid algorithms. The MSA treats reactions in the usual ISSA fashion, but uses appropriately conditioned binomial random variables for representing the net numbers of molecules diffusing from any given subvolume to a neighbor within a prescribed distance. Simulation results illustrate the benefits of the algorithm.

INTRODUCTION

The idea of treating a spatially inhomogeneous chemically reacting system as a collection of smaller interacting subsystems has appeared in literature since the 1970s under a few names, notably the “Reaction Diffusion Master Equation”¹ (RDME) and the “Multivariate Master Equation.”² The theory was explored by Nicolis and Prigogine.² The reaction-diffusion approach has been confirmed against results obtained by direct simulation Monte Carlo³ and reactive hard sphere molecular dynamics.⁴ Widespread awareness of the multivariate master equation approach was achieved through its inclusion in the classic texts of Gardiner⁵ and Van Kampen.⁶

At this mesoscopic level of description, a system consists of a list of molecular species, and reactions which couple them as reactants or products. The system state, x, is given by the number of molecules of each species. It evolves from the initial condition through the firing of reactions, whose stochastic rates are known as propensity functions. The forward Kolmogorov equation governing the flow of probability from one state to another in time is called the Master Equation.

The Stochastic Simulation Algorithm^{7, 8} (SSA) is the technique commonly used to sample the Chemical Master Equation (CME), which governs the evolution of homogeneous, or well-stirred, systems. There exist several implementations of the exact SSA, for example, the direct method, the first reaction method,⁸ and the next reaction method.⁹ Much effort has gone into developing approximations to the exact SSA, e.g., τ-leaping¹⁰ and the Slow Scale SSA.¹¹

In the inhomogeneous setting, a system is divided into subvolumes, each of which is assumed to be homogeneous. Reactions occur in each subvolume as in the homogeneous case, and the populations in neighboring subvolumes are coupled by diffusive transfers, treated as unimolecular reactions.^{1, 12, 13} The probability of the system being in any given state at any time is then given by the MME^{2, 3} or RDME.¹ We call the SSA as applied to the inhomogeneous setting the “Inhomogeneous SSA” (ISSA). Analogously to the SSA, the ISSA can also be implemented in different ways. An implementation based on the Next Reaction Method was used by Isaacson and Peskin,¹⁴ the Next Subvolume Method was developed by Elf and co-workers,^{15, 16} and the null process technique was developed by Hanusse and Blanche.¹⁷ However, even optimized versions of the ISSA can be prohibitively slow for some systems and, in particular, in the presence of fast diffusion.

In this paper we present the Multinomial Simulation Algorithm (MSA), which is designed to outperform the ISSA in just this type of scenario: when diffusive transfers greatly outnumber reaction events. The MSA is a stochastic-stochastic hybrid method which is based on separating chemical reactions, which are treated in the usual SSA way, from diffusive transfers, which are treated by an approximate stochastic process. The MSA computes the net diffusive transfer from each subvolume to its neighbors in a given time step. In this sense it is similar to the τ-leaping method, but with some important differences. In τ-leaping, each reaction channel which consumes a given species fires independently of the other channels consuming that species, so it is possible that the sum of the molecules of a species removed by all channels which consume it will be greater than the number of molecules that were present in the beginning of the time step. That is to say, in τ-leaping the number of molecules of a given species which are available to be consumed by a given event in a given time step is not adjusted as a result of the firing of other events which consume that species in that time step. The MSA has the important property that it conserves the total number of molecules across subvolumes by reducing the number of molecules of a given species available to be consumed by a given event in a given time step by the number of molecules of that species already consumed by other events in that time step.

A number of authors^{18, 19, 20} proposed deterministic-stochastic hybrid methods in which diffusion is treated deterministically everywhere, and reactions are treated stochastically. These methods are applicable when the diffusing species are present everywhere in large population, but often this is not the case. The MSA is capable of obtaining spatial resolution even in the low population case.

The MSA is different from the Gillespie Multi-Particle (GMP) method of Rodriguez et al.,²¹ another stochastic-stochastic hybrid method, in two ways. First, although the MSA also relies on a type of operator splitting to separate reactions and diffusive transfers, it interleaves reactions and diffusions differently from the GMP method. We feel that our approach is better justified theoretically, and possibly more accurate. Second, the GMP method uses Chopard’s multi-particle method²² to simulate diffusion. According to this method, molecules from one subvolume are uniformly randomly distributed among the immediately neighboring subvolumes at each diffusion step, and the macroscopic diffusion equation is recovered in the limit λ→0, where λ is the subvolume’s side length. In the MSA, molecules from one subvolume are also distributed among the neighboring subvolumes, but the probabilities used for that are multinomial.

Rossinelli et al.²⁰ presented two methods: Sτ-leaping is a stochastic algorithm which employs a unified step for both the reaction and diffusion processes, while the hybrid Hτ-leaping method combines deterministic diffusion with τ-leaping for reactions. As in homogeneous τ-leaping,²³ the difficulty in spatial τ-leaping is choosing a time step that simultaneously satisfies the leap condition, i.e., that the propensities do not change substantially during the leap (an accuracy condition), but also has a low likelihood of causing the population to become negative. The choice of diffusion time step for the MSA is also limited by an accuracy condition, but the way in which the jump probabilities are conditioned eliminates the problem of negative population.

Jahnke and Huisinga²⁴ noted the role of multinomial random variables in their paper on the analytical solution of the CME for closed systems which include only monomolecular reactions. Our treatment of diffusion (which is indeed a monomolecular problem) in the MSA is based on an exact multinomial solution of the master equation for diffusion, although in the interest of efficiency we truncate that solution.

Finally, the same stochastic process theory which forms the early steps of the derivation of the MSA appears in a nonspatial context in Rathinam and El Samad’s paper on the Reversible-equivalent-monomolecular τ (REMM-τ) method.²⁵ REMM-τ is an explicit τ-leaping method, which approximates bimolecular reversible reactions by suitable unimolecular reversible reactions, and considers them as operating in isolation during the time step τ. The MSA and REMM-τ apply to distinctly different physical systems, but they share a common mathematical foundation, namely, an exact, time-dependent stochastic solution for the reversible isomerization reaction set S₁⇌S₂. In the present work we generalize that solution to the reaction set S₁⇌S₂⇌⋯⇌S_n, for n>2, and we also develop approximations to make the calculations practical. The n=2 solution expresses the instantaneous populations of the species as linear combinations of statistically independent binomial random variables. Our n>2 generalization takes the form of linear combinations of statistically independent multinomial random variables, hence the name of the MSA.

The remainder of this paper is organized as follows: In Sec. 2 we develop multinomial diffusion for one species in one dimension in the absence of any reactions. In Sec. 3 we extend this to an arbitrary number of species, and add reactions to obtain the MSA; we then present simulation results and evaluate the algorithm’s performance in one dimension. In Sec. 4 we describe the algorithm for two dimensions and present some simulation results. We conclude with a discussion of how the algorithm can be used as part of a larger adaptive simulation strategy.

DIFFUSION IN ONE DIMENSION

Theoretical foundations

In this subsection we derive the foundations of the MSA. For simplicity we do this for a one-dimensional (1D) system.

Suppose we have a 1D system of length L which contains only one chemical species. Consider n subvolumes of equal size, l=L∕n, which we index from left to right 1,2,…,n. Initially, subvolume i contains k_i molecules of a given chemical species, distributed randomly and uniformly. Now suppose that κ is defined as follows:

$$\kappa dt\equiv \text{the}\text{probability}\text{that}\text{a}\text{molecule}\text{will}\text{jump}\text{to}\text{an}\text{adjacent}\text{cell}\text{in}\text{the}\text{next}\text{infinitesimal}dt.$$ (1)

This parameter is taken to be κ=D∕l², where D is the usual diffusion coefficient of the chemical species, because then, in the limit l→0, the master equation for discrete diffusion becomes the standard diffusion equation. In this diffusion equation, D is the phenomenologically defined diffusion coefficient, and its solution has a Gaussian form whose variance grows as 2Dt.

Then define the probabilities,

$$p_{ij}^{\left(n\right)}\left(t\right)\equiv \text{the}\text{probability}\text{that}\text{a}\text{randomly}\text{chosen}\text{molecule}\text{in}\text{cell}i\text{at}\text{time}0\text{will}\text{be}\text{found}\text{in}\text{cell}j\text{at}\text{time}t>0,(i,j=1,2,\dots ,n).$$ (2)

Since these n² probabilities satisfy the n relations,

$$p_{i,1}^{\left(n\right)}+p_{i,2}^{\left(n\right)}+\dots +p_{i,n}^{\left(n\right)}=1(i=1,2,\dots ,n),$$ (3)

only n(n−1) of them will be independent.

To find these probabilities, note that in an infinitesimal time dt there will be effectively zero probability of more than one molecule jumping between adjacent cells. If the boundaries of our system are reflective (i.e., diffusive jumps between subvolumes 1 and n are not allowed), then the addition and multiplication laws of probability yield

$$p_{i1}(t+dt)=p_{i1}\left(t\right)[1-\kappa dt]+p_{i2}\left(t\right)\kappa dt,$$ (4)

$$p_{ij}(t+dt)=p_{i(j-1)}\left(t\right)\kappa dt+p_{ij}\left(t\right)[1-2\kappa dt]+p_{i(j+1)}\left(t\right)\kappa dt(j=2,\dots ,n-1),$$

$$p_{in}(t+dt)=p_{i(n-1)}\left(t\right)\kappa dt+p_{in}\left(t\right)[1-\kappa dt].$$

The first line in Eq. 4 means the probability that a molecule will be in subvolume 1 at time t+dt given that it was in state i at time 0 is equal to the sum of the probability that the molecule was in subvolume 1 at time t, given that it was in subvolume i at time 0 and it did not jump away from subvolume 1 in the next dt, plus the probability that the molecule was in subvolume 2 at time t, given that it was in subvolume i at time 0 and it jumped from subvolume 1 to subvolume 2 in the next dt. All other routes to subvolume 1 at time t+dt from a subvolume other than 1 or 2 at time t will be second order in dt (and will thus make no contribution when Eq. 4 is later converted to an ordinary differential equation).

If the boundaries of our system are periodic (i.e., subvolumes 1 and n communicate), then we have

$$p_{i1}(t+dt)=p_{in}\left(t\right)\kappa dt+p_{i1}\left(t\right)[1-2\kappa dt]+p_{i2}\left(t\right)\kappa dt,$$ (5)

$$p_{ij}(t+dt)=p_{i(j-1)}\left(t\right)\kappa dt+p_{ij}\left(t\right)[1-2\kappa dt]+p_{i(j+1)}\left(t\right)\kappa dt(j=2,\dots ,n-1),$$

$$p_{in}(t+dt)=p_{i(n-1)}\left(t\right)\kappa dt+p_{in}\left(t\right)[1-2\kappa dt]+p_{i1}\left(t\right)\kappa dt.$$

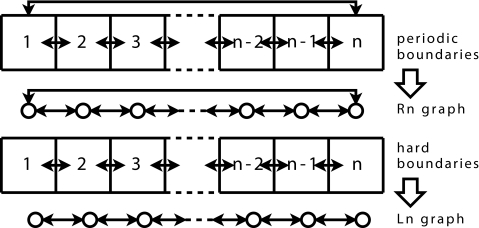
The discussion which follows can be made independent of boundary condition by using the concept of the Laplacian matrix of a graph. There is an isomorphism between the discretization of our system into subvolumes, and a directed graph (a collection of vertices and directed edges). Each subvolume of our system can be represented by a vertex. We can then connect with a directed edge those vertices which correspond to allowable diffusive transfers. The resulting graph G is just another representation of our original system, with vertices denoting the possible locations of molecules, and edges denoting the possible transitions (diffusive jumps) between those locations. When our system has n subvolumes and periodic boundary conditions, then the resulting graph is R_n, the so-called ring graph with n vertices; a system with n subvolumes and reflecting boundary conditions yields L_n, the line graph (see Fig. 1).

Figure 1.

Boundary conditions and the resulting graphs. The solid arrows show the allowed diffusive jumps.

Equations 4, 5 both lead to the general set of differential equations

$$\frac{d\mathit{p}\left(t\right)}{dt}=-\kappa {\mathfrak{L}}_{\mathit{G}}\mathit{p}\left(t\right),$$ (6)

where

$$\mathit{p}\left(t\right)=\left(\begin{array}{c}{p}_{i1}\left(t\right)\\ p_{i2}\left(t\right)\\ \dots \\ p_{in}\left(t\right)\end{array}\right)$$ (7)

and L_G is the so-called Laplacian matrix of the graph G∊{L_n,R_n}, with entries

$${\mathfrak{L}}_G(i,j)=\{\begin{array}{l}\text{number}\text{of}\text{neighbors}\text{of}i\text{if}i=j\\ -1\text{if}i\ne j,\text{and}i\text{is}\text{adjacent}\text{to}j\\ 0\text{if}i\ne j,\text{and}i\text{is}\text{not}\text{adjacent}\text{to}j.\end{array}\phantom{\}}$$ (8)

For the initial condition p(0), the solution to Eq. 6 is

$$\mathit{p}\left(t\right)=\mathit{V}\cdot e^{-\lambda \kappa t}\cdot {\mathit{V}}^{-1}\cdot \mathit{p}\left(0\right),$$ (9)

where V is the matrix of eigenvectors of L_G, and

$$e^{-\lambda \kappa t}\equiv \left(\begin{array}{cccc}{e}^{-{\lambda }_1\kappa t}& 0& \dots & 0\\ 0& e^{-{\lambda }_2\kappa t}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & e^{-{\lambda }_n\kappa t}\end{array}\right),$$ (10)

where λ_i (i=1,…,n) is the ith eigenvalue of L_G.

Now we introduce the random variables

$$M_{ij}^{\left(n\right)}(k_i,t)\equiv \text{the}\text{number}\text{of}\text{the}{k}_i\text{molecules}\text{in}\text{subvolume}i\text{at}\text{time}0\text{that}\text{will}\text{be}\text{in}\text{subvolume}j\text{at}\text{time}t,(i,j=1,2,\dots ,n).$$ (11)

These n² random variables satisfy the relations

$$M_{i1}^{\left(n\right)}(k_i,t)+M_{i2}^{\left(n\right)}(k_i,t)+\cdots +M_{in}^{\left(n\right)}(k_i,t)=k_i$$ (12)

$$(i=1,2,\dots ,n)$$

so only n(n−1) of them will be independent. We choose the independent variables to be $M_{ij}^{\left(n\right)}(k_i,t)$ for i≠j. There will be n such statistically independent sets.

Consider first the (n−1) variables $M_{1j}^{\left(n\right)}(k_i,t)$ for j=2,…,n. These are statistically independent of the (n−1)² variables $M_{ij}^{\left(n\right)}(k_i,t)$ for i,j=2,…,n because individual molecules move independently of each other, but the $M_{ij}^{\left(n\right)}(k_i,t)$ are not statistically independent of each other.

Denote the joint probability density function of the (n−1) subvolume 1 random variables by

$$P_{2,\dots ,n}^{(1;n)}(m_{12},m_{13},\dots ,m_{1n};k_1,t)\equiv \mathrm{Prob}\{M_{1j}^{\left(n\right)}(k_1,t)=m_{1j}\text{for}j=2,\dots ,n\}.$$ (13)

From the addition and multiplication laws of probability we have

$$P_{2,\dots ,n}^{(1;n)}(m_{12},m_{13},\dots ,m_{1n};k_1,t)=\frac{k_1\text{!}}{m_{12}\text{!}{m}_{13}\text{!}\dots m_{1n}\text{!}(k_1-m_{12}-m_{13}-\cdots -m_{1n})}\times [{\left(p_{12}^{\left(n\right)}\left(t\right)\right)}^{m_{12}}{\left(p_{13}^{\left(n\right)}\left(t\right)\right)}^{m_{13}}\cdots {\left(p_{1n}^{\left(n\right)}\left(t\right)\right)}^{m_{1n}}{(1-p_{12}^{\left(n\right)}\left(t\right)-p_{13}^{\left(n\right)}\left(t\right)-\cdots -p_{1n}^{\left(n\right)}\left(t\right))}^{k_1-m_{12}-m_{13}-\dots -m_{1n}}].$$ (14)

The second factor on the right-hand side is the probability that, of the k₁ molecules in subvolume 1 at time 0, a particular set of m₁₂ of them will wind up in subvolume 2 at time t, and a particular set of m₁₃ of them will wind up in subvolume 3 at time t, and so on, with the remaining k₁−m₁₂−m₁₃−⋯−m_1n molecules remaining in subvolume 1 at time t. The first factor on the right-hand side of Eq. 14 is the number of ways of choosing groups of m₁₂,m₁₃,…,m_1n molecules from k₁ molecules. The joint probability function 14 implies that the random variables $M_{1i}^{\left(n\right)}$ for i=2,…,n, are multinomially distributed. We now observe that Eq. 14 is algebraically identical to

$$P_{2,\dots ,n}^{(1;n)}(m_{12},m_{13},\dots ,m_{1n};k_1,t)=\frac{k_1\text{!}}{m_{12}\text{!}(k_1-m_{12})\text{!}}{\left(p_{12}^{\left(n\right)}\left(t\right)\right)}^{m_{12}}{(1-p_{12}^{\left(n\right)}\left(t\right))}^{k_1-m_{12}}\times \frac{(k_1-m_{12})\text{!}}{m_{13}\text{!}(k_1-m_{12}-m_{13})\text{!}}{\left(\frac{p_{13}^{\left(n\right)}\left(t\right)}{1-p_{12}^{\left(n\right)}\left(t\right)}\right)}^{m_{13}}{(1-\frac{p_{13}^{\left(n\right)}\left(t\right)}{1-p_{12}^{\left(n\right)}\left(t\right)})}^{k_1-m_{12}-m_{13}}\times \cdots \times \frac{(k_1-m_{12}-\cdots -m_{1(n-1)})\text{!}}{m_{1n}\text{!}(k_1-m_{12}-\cdots -m_{1n})\text{!}}{\left(\frac{p_{1n}^{\left(n\right)}\left(t\right)}{1-p_{12}^{\left(n\right)}\left(t\right)-\cdots -p_{1(n-1)}^{\left(n\right)}\left(t\right)}\right)}^{m_{1n}}\times {\left(\frac{p_{1n}^{\left(n\right)}\left(t\right)}{1-p_{12}^{\left(n\right)}\left(t\right)-\cdots -p_{1(n-1)}^{\left(n\right)}\left(t\right)}\right)}^{k_1-m_{12}-\cdots -m_{1n}}.$$ (15)

The significance of Eq. 15 is that it immediately implies the conditioning

$$P_{2.\dots ,n}^{(1;n)}(m_{12},m_{13},\dots ,m_{1n};k_1,t)=P_2^{(1;n)}(m_{12};k_1,t)P_{3\mid 2}^{(1;n)}(m_{13}\mid m_{12};k_1,t)\times \cdots \times P_{n\mid 2,\dots ,(n-1)}^{(1;n)}(m_{1n}\mid m_{12},\dots ,m_{1(n-1)};k_1,t),$$ (16)

where

$$P_2^{(1;n)}(m_{12};k_1,t)={\mathbb{P}}_{\mathcal{B}}(m_{12};p_{12}^{\left(n\right)}\left(t\right),k_1),$$ (17)

$$P_{3\mid 2}^{(1;n)}(m_{13}\mid m_{12};k_1,t)={\mathbb{P}}_{\mathcal{B}}(m_{13};\frac{p_{13}^{\left(n\right)}\left(t\right)}{1-p_{12}^{\left(n\right)}\left(t\right)},k_1-m_{12}),$$ (18)

⋯

$$P_{n\mid 2,\dots ,(n-1)}^{(1;n)}(m_{1n}\mid m_{12},\dots ,m_{1(n-1)};k_1,t)={\mathbb{P}}_{\mathcal{B}}(m_{1n};\frac{p_{1n}^{\left(n\right)}\left(t\right)}{1-p_{12}^{\left(n\right)}\left(t\right)-\cdots -p_{1n}^{\left(n\right)}\left(t\right)},k_1-m_{12}-\cdots -m_{1n})$$ (19)

with P_B the binomial probability distribution function

$${\mathbb{P}}_{\mathcal{B}}(m;p,n)=\frac{n\text{!}}{m\text{!}(n-p)\text{!}}{p}^m{(1-p)}^{n-m}.$$

The physical interpretation of this result is as follows: the number m₁₂ of the k₁ molecules in subvolume 1 at time 0 that will be found in subvolume 2 at time t, irrespective of the fates of the other (k₁−m₁₂) molecules, can be chosen by sampling the binomial distribution with parameters $p_{12}^{\left(n\right)}\left(t\right)$ and k₁. Once the number m₁₂ has been selected in this way, the number m₁₃ of the remaining (k₁−m₁₂) molecules that will be found in subvolume 3 at time t can be chosen by sampling the binomial distribution with parameters$p_{13}^{\left(n\right)}\left(t\right)∕(1-p_{12}^{\left(n\right)}\left(t\right))$ and (k₁−m₁₂). This procedure can be repeated to generate the remaining m_1i for i=4,…,n as samples of the binomial distribution with parameters given by Eq. 19.

Equations 17, 18, 19 show how to generate the time t fates of the molecules that are in subvolume 1 at time 0. The time t fates of the k_i molecules in subvolume i at time 0, for i=2,…,n, are independent of those in any other subvolume, and the procedure for determining them is analogous.

Some additional approximations

At this point it may seem that we have specified an algorithm for generating the number m_ij of molecules moving from subvolume i to subvolume j in time t for all i≠j. However this algorithm has a serious drawback, which renders it practically unusable: it requires O(n²) samples of the binomial distribution per time step. Generating O(n²) binomial samples is likely to be a prohibitive computational burden, even for modest n. Furthermore, each (n−1) of the samples are dependent, limiting any speedup that may be obtainable by parallelizing the binomial sample generation.

In this section we take three steps to obtain an algorithm which does not have this quadratic complexity disadvantage. First, to obtain linear complexity, we limit the distance any molecule can diffuse in a single time step. Second, to maintain accuracy in spite of this approximation, we impose an upper limit on the time step. Third, to scale the algorithm to large system sizes, we approximate the diffusion probabilities of systems of arbitrary size n by those of a small, finite system of size $\widehat{n}$.

Step 1: Ideally, rather than O(n²), we would prefer to generate only O(n) binomial samples per time step. This can be achieved if we restrict where molecules can go: if a molecule, rather than having n choices of destination subvolume, instead only has a constant number of choices, then only O(n) binomial samples per time step will be required. By neglecting subvolumes outside a radius s of the subvolume of origin, we reduce the number of binomial samples required from (n−1)² (with each (n−1) dependent) to 2sn (with each 2s dependent).

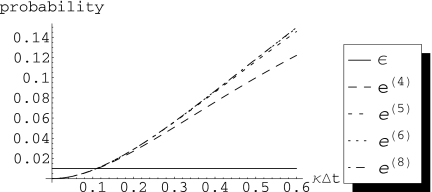
Step 2: For an algorithm based on a limited diffusion radius to be accurate, the size of the time step must be restricted. The time step restriction should satisfy the following condition: the probability of a molecule jumping from subvolume i to any subvolume beyond a radius of s subvolumes away from i in time Δt, should be less than or equal to a given ε. This probability per molecule per time step represents the error from “corralling” the molecules within a radius of s subvolumes from their subvolume of origin in any given time step. We will denote this error $e_i^{\left(n\right)}$, where the subscript i refers to the subvolume of origin, and the superscript (n) refers to the total number of subvolumes in the system. In the case of a periodic system, the subscript i can be dropped (as it will be in Fig. 2) since the diffusion probabilities, and therefore the error, are identical for all origin subvolumes. Generally (for both periodic and reflective boundaries) the probability that a molecule will, in time Δt, diffuse more than s subvolumes away from its original subvolume i is

$$e_i^{\left(n\right)}(s,\Delta t)=1-\sum _{j∊J(i,s)}{p}_{ij}^{\left(n\right)}\left(\Delta t\right),$$ (20)

where J(i,s) is the set of subvolumes within a radius of s subvolumes from i (including i).

Figure 2.

A plot of $e_i^{\left(n\right)}$ (s=1,t) vs κΔt, for a system with periodic boundaries, and different values of n. The horizontal black line indicates error per molecule per time step ε=1%. Note that increasing the system size does not appreciably change the error.

Thus, if we are willing to incur $e_i^{\left(n\right)}(s,\Delta t)⩽\epsilon$ error in probability per molecule per time step, we can restrict the distance a molecule can travel from subvolume i in time Δt, to s subvolumes from i in either direction by taking the time step Δt to be less than or equal to Δt_max, where Δt_max is given by the solution to $e_i^{\left(n\right)}(s,\Delta t_{\max })=\epsilon$.

The elements p_ij(t) of p(t) [Eq. 9] are probabilities which are always functions of the product κt, where κ depends on the diffusion coefficient of the molecular species. Thus, in practice, the maximum time step Δt_max will always be a function of κ.

Step 3: We have shown how to reduce the complexity of the algorithm by limiting the diffusion radius to s, and how to ensure that a level of accuracy ε is satisfied by limiting the time step Δt. However up to this point our analysis has depended on the system size n. We will next show how the dependence on the system size n can be dropped, allowing the algorithm to be applied to systems of arbitrary size.

For t⩽Δt_max it is possible to find a system size $\widehat{n}$, such that the probabilities $p_{ij}^{\left(n\right)}\left(t\right)$, for j∊J(i,s), are nearly indistinguishable for all $n>\widehat{n}$. The error, being a function of these probabilities [see Eq. 20], will also be indistinguishable for all $n>\widehat{n}$. To illustrate this, consider four systems with periodic boundary conditions and n=4, 5, 6, and 8 subvolumes. Figure 2 shows the probability of going past a radius s=1, i.e., the error $e_i^{\left(n\right)}(s=1,t)$, for these systems. These probabilities were obtained analytically using MATHEMATICA to solve Eq. 9. A series expansion (again, performed using MATHEMATICA) reveals that for all n=4,5,6,8, $e_i^{\left(n\right)}(s=1,t)={\left(\kappa \Delta t\right)}^2+O\left({\left(\kappa \Delta t\right)}^3\right)$. Thus for small κΔt we do not expect these probabilities to have significantly different values. Indeed, for probability ⩽1% (horizontal black line), there is almost no visible difference in the error if we compare these systems; for n past $\widehat{n}=4$, the error does not appreciably increase with increasing n.

The same pattern holds for the probabilities $p_{11}^{\left(n\right)}\left(t\right)$ and $p_{12}^{\left(n\right)}\left(t\right)$, individually. As t→∞, $p_{ij}^{\left(n\right)}\left(t\right)\to 1∕n$, i.e., the probabilities tend to a uniformly random distribution. When we perform a series expansion, we see that, for all n, the$p_{11}^{\left(n\right)}\left(t\right)$ share a leading term which is O(1), the $p_{12}^{\left(n\right)}\left(t\right)$ share a leading term which is O(κΔt), and so on. Thus, for small κΔt, consistent with ε=1%, these probabilities, which we will use directly in the algorithm, are also indistinguishable for $n>\widehat{n}=4$.

This observation suggests a way to scale the algorithm to arbitrary system sizes, given a desired per molecule per time step error of ε=1% (horizontal black line): since for all n>4, $e_i^{\left(n\right)}(1,t)\approx e_i^{\left(4\right)}(1,t)$ for κΔt consistent with ε, then the probabilities with superscript $\widehat{n}=4$, corresponding to a system with four subvolumes, can be used in place of the probabilities of any larger system.

In addition, the observation that $e_i^{\left(4\right)}(1,t)\approx {\left(\kappa \Delta t\right)}^2$ suggests that for s=1 we can choose a conservative maximum time step consistent with a level of error less than or equal to ε by satisfying

$$\Delta t⩽\sqrt{\epsilon }∕\kappa .$$ (21)

This gives a formula for choosing the time step.

To summarize, the steps that must be followed in order to obtain a practical algorithm from the theory of the previous section are as follows:

• 1.choose a diffusion radius s, and a given level of error ε;
• 2.choose Δt_max to satisfy $e_i^{\left(n\right)}(s,\Delta t_{\max })=\epsilon$, as a function of κ [for s=1, use Eq. 21; for s>1, similar formulas exist];
• 3.find $\widehat{n}$ which satisfies $e_i^{\left(n\right)}(s,\Delta t)\approx e_i^{\left(\widehat{n}\right)}(s,\Delta t)$, $\forall n>\widehat{n}$ and Δt⩽Δt_max.

Implementation of the algorithm

There is one practical consideration in the implementation of the algorithm which we have not yet addressed. Because the sum total of the probabilities of the events which can occur in the simulation must be unity, the probability $e_i^{\left(n\right)}(s,\Delta t)$ of going beyond the diffusion radius must be reassigned to an event which can occur during the simulation. Where should we reassign this probability?

According to our tests, two different strategies work best in two distinct cases. If the subvolume of origin i is an interior subvolume, the best accuracy is achieved by adding $\frac{1}{2}{e}_i^{\left(n\right)}(s,\Delta t)$ to the two probabilities of going as far away as possible from i in either direction. In a periodic system, all subvolumes fall in this category.

For reflective boundary systems, we have found that if the subvolume of origin i has a boundary close to it, the best accuracy is achieved by adding $e_i^{\left(n\right)}(s,\Delta t)$ to the probability of staying in subvolume i.

This distinction makes it clear that we need a shorthand notation for the probabilities we will use in the implementation of the algorithm. Thus we define

$${\widehat{p}}_{ij}(t;s,\Delta t)\equiv \text{the}\text{system}\text{-}\text{size}\text{independent}\text{probability}\text{that}\text{a}\text{single}\text{molecule}\text{which}\text{was}\text{in}\text{subvolume}i\text{at}\text{time}0,\text{will}\text{be}\text{in}\text{subvolume}j\text{at}\text{time}t,\text{as}\text{it}\text{will}\text{be}\text{used}\text{in}\text{the}\text{algorithm}\text{with}s\text{and}\Delta t.$$ (22)

For example, for an interior subvolume i and diffusion radius s=1, the formulas are given by

$${\widehat{p}}_{i,(i+1)}(t;1,\Delta t)={\widehat{p}}_{i,(i-1)}(t;1,\Delta t)\equiv p_{i,(i+1)}^{\left(\widehat{n}\right)}\left(t\right)+\frac{1}{2}{e}_i^{\left(\widehat{n}\right)}(1,\Delta t).$$ (23)

For a subvolume directly abutting a reflective boundary on one side, we modify the probability of staying in that subvolume, yielding the formula

$${\widehat{p}}_{ii}(t;1,\Delta t)\equiv p_{ii}^{\left(\widehat{n}\right)}\left(t\right)+e_i^{\left(\widehat{n}\right)}(1,\Delta t),i=1,n.$$ (24)

We are now ready to give the procedure for approximate multinomial diffusion for a system with n subvolumes, each of length l, and a single species X with diffusion coefficient D. The algorithm first computes the 2sn values of the variables ΔX_ij, for i=1,…,n and j=i±1,…,i±s, giving the number of molecules which will move from subvolume i to a subvolume j, to the right (j=i+1,…,i+s) or to the left (j=i−1,…,i−s) of i. A second loop then applies these population changes to the state X_i, i=1,…,n, and finally the time is incremented. The function B(p,n) generates random numbers distributed according to the binomial distribution with parameters p and n [Eq. 20]. For the sake of simplicity, we will present the algorithm for s=1.

Algorithm 1.

. Diffusion in one dimension with diffusion radius s=1

Choose s and ε
Calculated Δtmax as a function of ε, s, and κ=D∕l2
Choose Δt⩽Δtmax
whilet⩽tfinaldo
fori=1 to ndo
$\Delta X_{i(i+1)}=\mathcal{B}({\widehat{p}}_{i(i+1)}\left(\Delta t\right),X_i)$
$\Delta X_{i(i-1)}=\mathcal{B}(\frac{{\widehat{p}}_{i(i-1)}\left(\Delta t\right)}{1-{\widehat{p}}_{i(i+1)}\left(\Delta t\right)},X_i-\Delta X_{i(i+1)})$
end for
fori=1 to ndo
Xi=Xi−ΔXi(i+1)−ΔXi(i−1)+ΔX(i+1)i+ΔX(i−1)i
end for
t=t+Δt
end while

Error analysis for s=1

Of the three steps outlined in Sec. 2B, steps 1 and 3 represent approximations, and each one introduces some error to our simulation. We can gain some intuition about the relative magnitude of the two errors by revisiting Fig. 2. The error from the restriction of the diffusion radius to s (step 1) is given by the $e^{\left(\widehat{n}\right)}$ curve. The error from the approximation of the probabilities of an arbitrary-sized system by the probabilities of a $\widehat{n}$-sized system (step 3) is given by the difference between the $e^{\left(\widehat{n}\right)}$ curve and the e⁽ⁿ⁾ curves with $n>\widehat{n}$. In this example $\widehat{n}=4$. While the step 1 error is plainly large (but less than ε), the step 3 error is negligible by comparison.

We have already pointed out that the error per molecule per time step due to the restriction of the diffusion radius (step 1), for a system with periodic boundaries and s=1, is O((κΔt)²). The case of reflective boundaries is a little more difficult to analyze, but the answer turns out to be the same.

In a system with reflective boundaries, and s=1, we recognize that we will have to consider three “classes” of subvolumes. Class 1 contains the two subvolumes closest to the boundary (subvolumes 1 and n); class 2 contains the two subvolumes which are one subvolume removed from the boundary [2 and (n−1)]; class 3 contains the remaining subvolumes (subvolumes i with 3⩽i⩽(n−2)), which we shall call “interior” subvolumes. Where the subscript i on the error $e_i^{\left(n\right)}$ previously denoted the subvolume of origin, we will now parenthesize ($e_{\left(i\right)}^{\left(n\right)}$, i=1,2,3) it to denote the class of subvolume.

The probabilities of diffusing away from each class of subvolume are given by different formulas. The interior subvolumes [indexed 3,…,(n−2)] are assumed to be sufficiently far from the boundary so that they do not “feel” its effect. Their diffusion probabilities will be taken to be those from a periodic system. Figure 2 has already shown us that $\widehat{n}=4$ for a periodic system. Thus, for class 3 (interior) subvolumes of a reflective boundary system we have error

$$e_{\left(3\right)}^{\left(4\right)}=1-p_{11}^{\left(R4\right)}-2p_{12}^{\left(R4\right)}=p_{13}^{\left(R4\right)},$$ (25)

where the superscript R4 denotes that the probabilities are taken from a periodic system (R stands for “ring”) with four subvolumes. We have already detailed in Sec. 2B that this error is O((κΔt)²), and that to achieve an error level ε we must satisfy Eq. 21.

To decide on a value for $\widehat{n}$ for class one and class two subvolumes, we need to consult the error from reflective boundary systems with n=4 and n=6 subvolumes. These can be obtained analytically in the same way that we obtained the periodic boundary probabilities, using MATHEMATICA to solve Eq. 9. Class 1 errors (for subvolumes indexed 1 and n) are given by

$$e_{\left(1\right)}^{\left(4\right)}(1,\Delta t)=1-p_{11}^{\left(L4\right)}-p_{12}^{\left(L4\right)}=p_{13}^{\left(L4\right)}+p_{14}^{\left(L4\right)},$$ (26)

$$e_{\left(1\right)}^{\left(6\right)}(1,\Delta t)=1-p_{11}^{\left(L6\right)}-p_{12}^{\left(L6\right)}=p_{13}^{\left(L6\right)}+p_{14}^{\left(L6\right)}+p_{15}^{\left(L6\right)}+p_{16}^{\left(L6\right)},$$ (27)

where the superscripts L4 and L6 represent probabilities from the reflective boundary system (L stands for “line”) with 4 and six subvolumes, respectively. Performing a series expansion on these errors gives

$$e_{\left(1\right)}^{\left(4\right)}(1,\Delta t)=\frac{1}{2}{\left(\kappa \Delta t\right)}^2-\frac{2}{3}{\left(\kappa \Delta t\right)}^3+\frac{7}{12}{\left(\kappa \Delta t\right)}^4-\frac{2}{5}{\left(\kappa \Delta t\right)}^5+\frac{41}{180}{\left(\kappa \Delta t\right)}^6+O\left({\left(\kappa \Delta t\right)}^7\right),$$ (28)

$$e_{\left(1\right)}^{\left(6\right)}(1,\Delta t)=\frac{1}{2}{\left(\kappa \Delta t\right)}^2-\frac{2}{3}{\left(\kappa \Delta t\right)}^3+\frac{7}{12}{\left(\kappa \Delta t\right)}^4-\frac{2}{5}{\left(\kappa \Delta t\right)}^5+\frac{11}{48}{\left(\kappa \Delta t\right)}^6+O\left({\left(\kappa \Delta t\right)}^7\right).$$ (29)

Two things are notable. First, the errors differ in the sixth and higher order terms. This means that they are practically indistinguishable, and that we can take $\widehat{n}=4$. Second, the leading term is O((κΔt)²), as it was for class three, but the coefficient is $\frac{1}{2}$, i.e., half that of the error for class 3. We could have foreseen that using the following reasoning, molecules from class 1 subvolumes have half as many opportunities to leave their subvolume of origin as do molecules from interior subvolumes. From this observation we conclude that the error in class 1 subvolumes, being approximately half that of class 3 subvolumes, will not impose a further limitation on the time step.

Our reasoning for class 2 subvolumes [indexed 2 and (n−1)] is completely analogous. The errors for n=4 and n=6 are

$$e_{\left(2\right)}^{\left(4\right)}(1,t)=1-p_{22}^{\left(L4\right)}-p_{21}^{\left(L4\right)}-p_{23}^{\left(L4\right)}=p_{24}^{\left(L4\right)}=\frac{1}{2}{\left(\kappa \Delta t\right)}^2+O\left({\left(\kappa \Delta t\right)}^3\right),$$ (30)

$$e_{\left(2\right)}^{\left(6\right)}(1,t)=1-p_{22}^{\left(L6\right)}-p_{21}^{\left(L6\right)}-p_{23}^{\left(L6\right)}=p_{24}^{\left(L6\right)}+p_{25}^{\left(L6\right)}+p_{26}^{\left(L6\right)}=\frac{1}{2}{\left(\kappa \Delta t\right)}^2+O\left({\left(\kappa \Delta t\right)}^3\right).$$ (31)

Since they differ in higher order terms, we shall use $\widehat{n}=4$. Since the leading term in the error is half that of class three subvolumes, it will not restrict the time step further.

Stability analysis for s=1

The per molecule per time step error due to the diffusion radius restriction is a local error. In this section we show that the global error (i.e., the error at any given time in a fixed interval as Δt→0) in the simulation mean is bounded and O(κΔt).

The expected value of a binomial random variable B(p,n) is np. Given x molecules in a subvolume, and probabilities $\widehat{p}\left(\Delta t\right)$ of jumping either left and right in time Δt, we can say the following: The number of molecules that will jump to the right in the next Δt is $\mathcal{B}(\widehat{p}\left(\Delta t\right),x)$. This implies that the mean number jumping to the right in the next Δt is $\widehat{p}\left(\Delta t\right)x$. If we are given that r of the x molecules do jump to the right, then the number of the (x−r) remaining molecules that will jump to the left in the next Δt is $\mathcal{B}(\widehat{p}\left(\Delta t\right)∕(1-\widehat{p}\left(\Delta t\right)),x-r)$. This implies that the mean number of the x molecules that jump to the left, given that r of those x molecules have jumped to the right, is $[\widehat{p}\left(\Delta t\right)∕(1-\widehat{p}\left(\Delta t\right))][x-r]$. We can eliminate this conditioning by using the iterated expectation formula (E(X)=E(E(X∣Y))). Then the mean number of molecules jumping to the left, unconditionally, reduces to $\widehat{p}\left(\Delta t\right),x$, the same as jumping to the right, unconditionally.

Extending this idea to the full system, we can obtain an update formula for the mean population evolving through multinomial diffusion with s=1. The condensed form of the update formula is

$${\mathit{X}}_{N+1}=(\mathit{I}+\mathit{B}){\mathit{X}}_N,$$ (32)

where X_N is the state (as a column vector) at time step N, I is the identity matrix, and B is the matrix with elements: $-({\widehat{p}}_{i,(i+1)}\left(\Delta t\right)+{\widehat{p}}_{i,(i-1)}\left(\Delta t\right))$ on the ith row of the diagonal; ${\widehat{p}}_{(i-1),i}\left(\Delta t\right)$ on the (i,(i−1)) subdiagonal positions; ${\widehat{p}}_{(i+1),i}\left(\Delta t\right)$ on the (i,(i+1)) superdiagonal positions; and zeros everywhere else.²⁶

The next-nearest neighbor diffusion probabilities${\widehat{p}}_{i,(i+1)}\left(\Delta t\right)$ and ${\widehat{p}}_{i,(i-1)}\left(\Delta t\right)$ can be series expanded, and shown to be κΔt+O((κΔt)²). Update formula 32 can then be written as ${\mathit{X}}_{N+1}=(I+\Delta t\widehat{\mathit{B}}+O\left({\left(\kappa \Delta t\right)}^2\right)){\mathit{X}}_N$, where

$$\widehat{\mathit{B}}=\kappa \left(\begin{array}{ccccccc}-1& 1& 0& \dots & 0& 0& 0\\ 1& -2& 1& \dots & 0& 0& 0\\ ⋮& & & \ddots & & & ⋮\\ 0& 0& 0& \dots & 1& -2& 1\\ 0& 0& 0& \dots & 0& 1& -1\end{array}\right).$$ (33)

As shown in the previous section, the error per molecule per time step is O((κΔt)²). Thus the mean population satisfies a forward-time, centered-space approximation to the diffusion equation, as we would expect. Standard results from the numerical analysis of partial differential equation (Ref. ²⁷) yield stability as Δt→0 on a fixed time interval, and convergence to accuracy O(κΔt). The stability criterion for forward-time centered-space solution of the diffusion equation is Δt∕(Δx)²⩽1∕2D. In our case, this criterion is automatically satisfied due to the accuracy condition 21.

Diffusion radius s=2

Thus far we have mainly discussed the situation in which the diffusion radius is s=1. Increasing the radius to s=2 subvolumes on either side of the subvolume of origin, while maintaining same error e_i(2,Δt)⩽1%, will yield a longer κΔt_max≈0.4. For s=2, ε=1%, and periodic boundaries, we have $\widehat{n}=6$, and $e^{\left(6\right)}\left(\Delta t\right)=\frac{1}{3}{\left(\kappa \Delta t\right)}^3+O\left({\left(\kappa \Delta t\right)}^4\right)$. For reflective boundaries, there are four classes of subvolumes, numbered in increasing order from the closest to the boundary (class one) to the interior subvolumes (class four). Class four subvolumes again dominate the error and determine the step-size restriction.

Because the choice s=2 doubles the number of binomial samples required for a single time step, it will also increase the computational time required per time step, by a factor of 2. In a diffusion-only setting, the s=2 algorithm will take one quarter as many steps as the s=1 algorithm, and will require half as much computational time. However, as we will show in Sec. 3B, once reactions are added to the mix, the computational and accuracy advantages of the s=2 algorithm will only manifest themselves in situations where reactions are spaced overwhelmingly farther apart than diffusive transfers.

REACTION-DIFFUSION IN ONE DIMENSION

The algorithm

Our stated goal was to create an algorithm which will be faster than the ISSA for systems in which diffusion is much faster than reaction, and still accurately represent small population stochastic phenomena. We are now ready to describe this algorithm, which we call the MSA. It incorporates Algorithm 1 for diffusion in one dimension as one element, while its other element is the firing of reactions according to the usual SSA scheme.

The system is divided into the usual n subvolumes of length l, but now contains more than one species. The state is given by the matrix X, where X_ij is the population of the jth species in the ith subvolume. The diffusion coefficient of the jth species is D_j. The reaction propensity functions α_ir give the propensity of the rth reaction in the ith subvolume, and a₀ is the total reaction propensity ${\alpha }_0={\sum }_{i=1}^n{\sum }_{r=1}^R{\alpha }_{ir}$. The variable U represents a uniform random number in the interval (0, 1). The time to the next reaction is given by τ, while the maximum time step for diffusion is given by Δt_max.

Algorithm 2.

. Reaction-diffusion in one dimension

Choose s and ε

Calculate Δtmax as function of ε, s, and maxi{κi=Di∕l2}

whilet⩽tfinaldo

Calculate total reaction propensity ${\alpha }_0={\sum }_{i=1}^n{\sum }_{r=1}^R{\alpha }_{ir}$

Pick time to next reaction as τ=−ln(U)∕α0

Pick indices i (subvolume) and j (reaction) of next reaction as in the SSA

if (t+τ)⩽tfinal

Remove reactants of reaction j in subvolume i

reacted=True

else

τ=tfinal−t

end if

tmp=0

while (τ−tmp)⩾Δtmax

Take a Δtmax diffusion jump for all species (see Algorithm 1)

tmp=tmp+Δtmax

end while

Take a (Δt=τ−tmp) diffusion jump for all species (see Algorithm 1)

if reacted is True

Add products of reaction j in subvolume i

reacted=False

end if

t=t+τ

end while

Unlike the GMP method,²¹ which performs diffusion steps at time points which are completely decoupled from the times at which reactions fire, the MSA couples the diffusion and reaction time steps. First, the time τ to the next reaction, as well as the type and location of the reaction, is chosen. Then the reactants are immediately removed, and diffusive steps are taken until time τ is reached. Then the products of the reaction appear. This may seem somewhat strange, but it is the least complicated and most accurate strategy we have found. In our tests we have found that the alternative of both removing the reactants and producing the products at the beginning of the reaction step is less accurate. The alternative of doing both at the end of the step is not an option, as there is no guarantee that the reactants will still be at the same location after diffusion has occurred.

Simulation results and error analysis

We have three goals in this section: (a) to establish that the multinomial method gives qualitatively correct results, (b) to quantify the performance of the multinomial method compared to the ISSA, and (c) to quantify the error between the multinomial method and the ISSA.

The MSA and ISSA codes on which the results in this paper are based are written in ANSI C, and the two methods are driven by a common problem description file. The ISSA implementation is based on the direct method, with only the most obvious optimizations: avoiding the recalculation of diffusion propensities for species which did not change in the previous time step, and of reaction propensities in subvolumes which were not touched in the previous time step. We use the shorthand MSA(s) for the MSA with diffusion radius set to s.

We have already laid out the logic by which the probabilities ${\widehat{p}}_{ij}(t;s=1,\kappa \Delta t)$ were derived. The s=2 probabilities were chosen completely analogously. These diffusion probabilities depend on the elements p_ij(t) of the matrix p(t) from Eq. 9, which we obtained analytically using MATLAB’s symbolic computation toolkit.

The A+B annihilation problem

The A+Bannihilation problem, which has been previously used as a test problem for two implementations of the ISSA,¹⁵ is given by the reaction

$$A+B\stackrel{k}{\to }\varnothing .$$

We consider a 1D domain of length L=40, with reflective boundaries at the ends, subdivided into n=100 subvolumes. We set k=10. Initially 1000 molecules of species A are evenly distributed across the system, while 1000 molecules of species B are located in the leftmost subvolume. Both species have diffusion coefficient D=5. The maximum time step is chosen to be consistent with error ε=1%, i.e., such that (D∕l²)Δt_max=0.1 for the MSA(1), and (D∕l²)Δt_max=0.4 for the MSA(2). We run ensembles of 1000 simulations to final time t_f=100.

Figure 3 shows the population means for species A and B, versus time and space, of 1000 simulations of the A+B annihilation problem. The plots correspond to the ISSA (top), the MSA(1) (middle), and the MSA(2) (bottom). Recall that in this problem B molecules in the left end of the system diffuse to the right and annihilate the uniformly distributed A molecules. It is plain to see that the qualitative agreement between the ensemble means of the methods is good.

Figure 3.

Mean population of 1000 runs vs time for the annihilation problem. The methods are, from top to bottom, the ISSA, MSA(1), and MSA(2). The units are molecules per subvolume.

To quantitatively assess the error between ISSA and MSA results, we use the Kolmogorov distance. For two cumulative distribution functions, F₁(x) and F₂(x) the Kolmogorov distance is defined as

$$K(F_1,F_2)=\underset{\text{all}x}{\max }\mid F_1\left(x\right)-F_2\left(x\right)\mid$$ (34)

and it has units of probability.

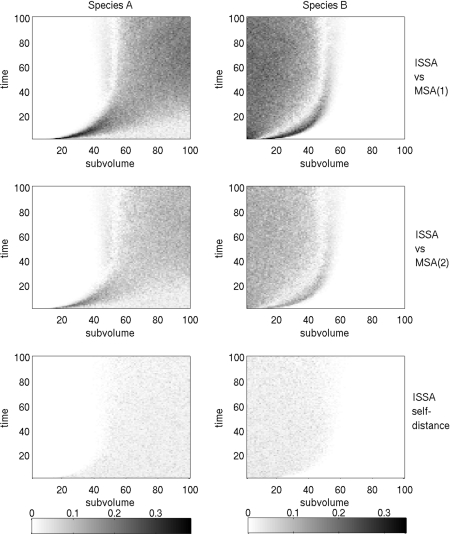
Figure 4 shows the Kolmogorov distance in space and time. The bottom plot gives what is known as the ISSA “self-distance,”²⁸ which is the amount of “noise” we expect to see in an ensemble of a given size (here 1000 realizations) due to the natural fluctuations in the system. This is found by calculating the Kolmogorov distance between two ISSA ensembles of the same size which were run with different initial seeds.

Figure 4.

The Kolmogorov distance (units of probability) between ISSA and MSA(1) (top), ISSA and MSA(2) (middle), and the ISSA self-distance (bottom), for the annihilation problem.

It is interesting to note that the error is highest at the location of the wave front of B first coming in contact with and annihilating A. That is where reactions are happening the fastest, in response to the molecules that have managed to diffuse the farthest. The MSA “corrals” molecules closer to their subvolume of origin, introducing an error in the location of the molecules. However it also introduces another error by decoupling reaction from diffusion in a way that makes reactions happen later than they would by the ISSA. In the ISSA, molecules can move into a neighboring subvolume and begin being considered as reaction partners to the other molecules in that subvolume much earlier than in the MSA, according to which molecule transfers between subvolumes are lumped together into groups of preferably more than 10 (for s=1) or 20 (for s=2).

The Fisher problem

The Fisher problem, which has been used as a test problem for the Sτ- and Hτ-leaping methods,²⁰ is given by the reversible reaction

$$X\underset{B}{\overset{A}{\rightleftharpoons }}X+X.$$

X can represent, for example, an advantageous gene, in which case the Fisher equation models its spread. We initially place a total of X₀ molecules of species X in the left 10% of a reflective boundary system. If the reaction rate coefficients A and B are balanced with the diffusion coefficient D of X, then the system displays a wave front which moves to the right. We use A=0.01, B=0.000 81, and D=50 000. The time step is again chosen to achieve ε=1% level for both MSA methods.

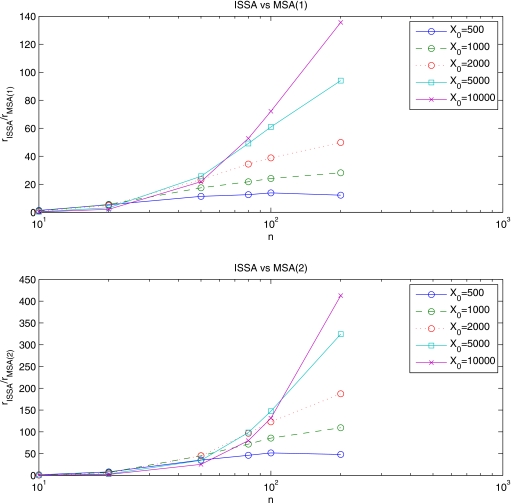
The ratio r_method=[diffusive steps (MSA) or jumps(ISSA)]∕(reactions) is very informative. When we consider r_ISSA, corresponding to an ISSA simulation, we can get a sense of, on average, how much more frequent diffusive jumps are than reactions for a given problem. The MSA works by lowering the number of algorithmic steps necessary to perform diffusion, i.e., collecting many diffusive jumps into a single diffusive step. Thus the ratio r_MSA(s) for a MSA simulation will be much smaller than for the corresponding ISSA simulation, and r_ISSA∕r_MSA(s) is approximately proportional to the speedup we expect to see when going from an ISSA simulation to an MSA simulation. Figure 5 gives this ratio for simulations of the Fisher system at varying initial populations X₀ and subvolume number n.

Figure 5.

The ratio r_ISSA∕r_MSA(s), where r_method=(diffusive steps or jumps)∕(reactions), for the Fisher problem. The top plot gives r_ISSA∕r_MSA(1), while the bottom plot gives r_ISSA∕r_MSA(2). We vary the initial population X₀ and number of subvolumes n.

The speedup observed in a MSA simulation compared to the corresponding ISSA simulation is computed as the ratio (CPU time taken for the ISSA simulation)∕(CPU time taken for the MSA simulation). Figure 6 shows the speedup for the Fisher problem. Note that the diffusion∕reaction ratio of Fig. 5 is a good predictor of the speedup. For the MSA(1), the diffusion∕reaction ratio is approximately ten times larger than the speedup. For the MSA(2), they differ by about a factor of 20. [The 20:10 ratio between the MSA(1) and MSA(2) is exactly as expected, since the MSA(2) requires the generation of twice as many binomial samples]. This means that the computational cost of performing a single multinomial diffusion step is approximately equal to the computational cost of performing 10 or 20 ISSA diffusive jumps. Thus we expect to see an improvement in performance due to using the MSA in cases where diffusive jumps outnumber reactions by more than an order of magnitude.

Figure 6.

Speedup over the ISSA of MSA(1) (top) and MSA(2) (bottom), for the Fisher problem.

It is straightforward to compute the Kolmogorov distance between the ensemble distributions of a given species, in a given subvolume, at a given time. However, it is often the case that we need the distance between the ensemble distributions of a given species, at a given time, but over the entire spatial domain. In this case the random variable is a vector with as many elements as there are subvolumes. For this purpose we “average” the Kolmogorov distance over the spatial domain according to the formula

$${⟨K(F_1\left(\mathbf{x}\right),F_2\left(\mathbf{x}\right))⟩}_n=\frac{1}{n}\sum _{i=1}^{n}K(F_1\left(x_i\right),F_2\left(x_i\right)),$$ (35)

where n is the number of subvolumes. This average Kolmogorov distance satisfies two desirable properties: first, it has units of probability; second, it can be used for comparing across results for the same system with a different spatial discretization.

In Fig. 7 we plot the space-averaged Kolmogorov distance [Eq. 35] for the ISSA (bottom), the MSA(1) (top), and the MSA(2) (middle). The simulations are of the Fisher problem, for increasingly fine discretization (i.e., increasing number of subvolumes n) and initial population density X₀. We note that the error of the MSA(1) is approximately twice that of the MSA(2). We also note that, although the speedup from using the MSA is monotonically increasing as the number of subvolumes and the initial population increases (Fig. 6), the space-averaged error presents no such monotonic behavior. In fact, based on the top plot, corresponding to the s=1 method, one could argue that the error increases up to a point, and then shows a downward trend. This inflection point, the peak of the error curves, appears to be correlated with a population density per subvolume of about 50–100 molecules, for the s=1 method.

Figure 7.

The space-averaged Kolmogorov distance between ISSA and MSA(1) (top), ISSA and MSA(2) (middle), and the ISSA self-distance (bottom), for the Fisher problem. These results are based on ensembles of size 1000, varying the number of subvolumes n and initial population X₀.

REACTION-DIFFUSION IN TWO DIMENSIONS

We have also implemented the MSA(1) for two-dimensional (2D) systems. The MSA(2) is considerably more complicated than the MSA(1) in two dimensions, so we did not implement it.

The test problem we used was a 2D version of the A+B annihilation problem. We considered a system with 30×30 subvolumes of side length l=0.04, reaction rate k=10, and the diffusion coefficients of A and B taken to be D=2. The time step was chosen to satisfy the usual error level of ε=1%. The system was initialized with 9000 uniformly distributed A molecules, and 9000 B molecules placed in the lower left subvolume. Ensembles of 500 simulations were run to final time t_f=0.2.

Figure 8 shows the qualitative agreement in the mean of the ISSA and MSA(1) ensembles at the final time. Figure 9 shows the (nonspace averaged) Kolmogorov distance, a measure of error in the top plot and noise in the bottom plot, also at the final time.

Figure 8.

The mean of ensembles of 500 simulations of the annihilation problem in two dimensions at t_f=0.2, obtained via the ISSA (top) and the 2D MSA(1) (bottom). Recall that species A is uniformly distributed throughout the volume, while B is injected at the lower left hand corner, and diffuses throughout the volume. The units are molecules per subvolume.

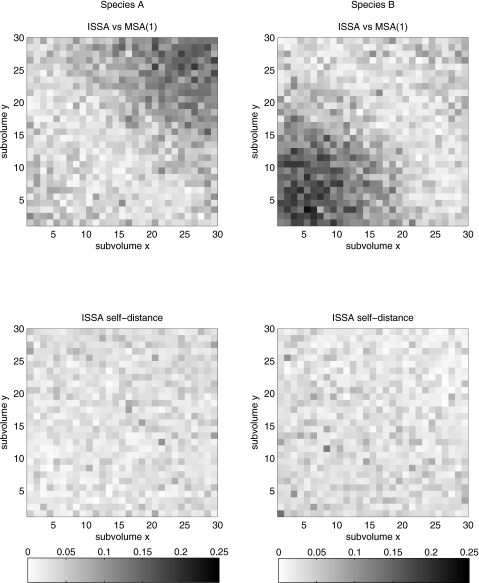
Figure 9.

The (non-space-averaged) Kolmogorov distance between ensembles of size 500, for the annihilation problem in two dimensions. The top plot gives the error between the ISSA and MSA(1), while the bottom plot gives the ISSA self-distance. The units are probability.

DISCUSSION

We have introduced a new method for efficient approximate stochastic simulation of reaction-diffusion problems. Where diffusion alone is concerned, the multinomial method has two sources of error: (a) the error from the truncation of the diffusion radius of molecules (step one), and (b) the error from the approximation of transition probabilities for systems of arbitrary size by the transition probabilities for systems of finite size (step three). The second source of error is negligible compared to the first, which for s=1, is O((κΔt)²).

When coupled with reactions, the multinomial method yields the MSA. The MSA has an additional source of error, which is similar to that observed in τ-leaping methods. Like τ-leaping methods, the MSA assumes that for specific intervals of time, while diffusion is, in fact, still occurring, the propensities of reactions are not changing. This is clearly an approximation. While τ-leaping methods constrain the size of their time step via the “leap condition” in a way that ensures that the error from this approximation is below a certain level, the MSA has no such condition. In fact, the MSA’s computational efficiency hinges on leaping over as many diffusive transfers as possible. If those transfers are occurring in a system near diffusional equilibrium, the efficiency comes at no cost in accuracy. If, however, the diffusive transfers are contributing to the smoothing out of a sharp gradient, whose species can participate in reactions, then the MSA will incur an error from the assumption that, between the time when the reaction propensity is calculated and the time, location, and type of the next reaction are decided, and the time at which that reaction fires, reaction propensities have not changed. The A+B annihilation problem and the Fisher problem were chosen because they represent this most challenging scenario for the MSA, as they do for partial differential equation simulation methods which depend on operator splitting.

The derivation of a 2D version of MSA(2), three-dimensional (3D) versions of MSA(1) and MSA(2), and versions of the MSA for more complicated spatial decompositions, is, in principle, straightforward. One must simply substitute the appropriate Laplacian matrix into Eq. 6. However, our implementation of 1D MSA(1) and MSA(2) and 2D MSA(1), as discussed in this paper, hinged on obtaining an analytical solution of Eq. 9 via MATHEMATICA. Solving Eq. 9 analytically becomes more difficult as the size of the Laplacian increases. Thus, this hand-crafted approach for obtaining the probability functions on which the MSA depends was neither efficient nor practical enough to pursue for 2D MSA(2) and 3D MSA(1) and MSA(2). Since the method has now been shown to work, we intend to devote some time to finding the best way to implement it for arbitrary dimensionality and diffusion radius.

The MSA is efficient in situations where diffusive transfers substantially outnumber reaction events. The likelihood of this condition being satisfied can be easily assessed by comparing the magnitudes of the total diffusion propensity and the total reaction propensity. This simple criterion can serve as a reliable indicator for when the MSA should be used in an adaptive MSA-ISSA code.