Statolith Sedimentation Kinetics and Force Transduction to the Cortical Endoplasmic Reticulum in Gravity-Sensing Arabidopsis Columella Cells^,

Abstract

The starch statolith hypothesis of gravity sensing in plants postulates that the sedimentation of statoliths in specialized statocytes (columella cells) provides the means for converting the gravitational potential energy into a biochemical signal. We have analyzed the sedimentation kinetics of statoliths in the central S2 columella cells of Arabidopsis thaliana. The statoliths can form compact aggregates with gap sizes between statoliths approaching <30 nm. Significant intra-aggregate sliding motions of individual statoliths suggest a contribution of hydrodynamic forces to the motion of statoliths. The reorientation of the columella cells accelerates the statoliths toward the central cytoplasm within <1 s of reorientation. During the subsequent sedimentation phase, the statoliths tend to move at a distance to the cortical endoplasmic reticulum (ER) boundary and interact only transiently with the ER. Statoliths moved by laser tweezers against the ER boundary experience an elastic lift force upon release from the optical trap. High-resolution electron tomography analysis of statolith-to-ER contact sites indicate that the weight of statoliths is sufficient to locally deform the ER membranes that can potentially activate mechanosensitive ion channels. We suggest that in root columella cells, the transduction of the kinetic energy of sedimenting statoliths into a biochemical signal involves a combination of statolith-driven motion of the cytosol, statolith-induced deformation of the ER membranes, and a rapid release of kinetic energy from the ER during reorientation to activate mechanosensitive sites within the central columella cells.

INTRODUCTION

Plants can sense and redirect their growth in response to gravity (Darwin, 1907). The sites of gravity perception in plant roots are columella cells. These specialized sensory cells function as statocytes, which are cells that can both detect and respond to the gravitational force (Sack, 1991; Sievers et al., 1991; Kiss, 2000; Boonsirichai et al., 2002). The columella cells are the only cells in roots that exhibit structural polarity with respect to gravity and can transmit the sensory information related to the gravitational force to the root elongation zone (Driss-Ecole et al., 2003). In columella cells, statoliths, specialized starch-containing plastids (amyloplasts), primarily respond to the force of gravity. The relatively high particle density of starch drives statolith sedimentation, which is the sinking of the statoliths under the opposing forces of gravitation and buoyancy. According to the starch statolith hypothesis (Haberlandt, 1900; Nĕmec, 1900), displacement of the statoliths in the gravitational field provides a means for converting the gravitational potential energy into sensor-activating kinetic energy, which then gives rise to a biochemical signal.

How the gravity-induced displacement of statoliths triggers the initial biochemical signal has remained an enigma for over 100 years. It has been suggested that actin filaments transmit the force generated by the movements of statoliths to mechanosensitive sites in the plasma membrane or the cortical endoplasmic reticulum (ER) through direct connections (Sievers et al., 1991; Baluška and Hasenstein, 1997) or through a tensegrity-based mechanism with no direct physical links of the statoliths to actin (Yoder et al., 2001). The mechanoreceptor(s) in columella cells are still unknown, and there is no evidence for force transduction via actin filaments. Indeed, the actin-based models for force transduction (Sievers et al., 1991; Yoder et al., 2001) have been undermined by the findings that actin-disrupting drugs do not inhibit gravitropism for both stems and roots (Yamamoto and Kiss, 2002; Hou et al., 2003, 2004) and that gravity sensing during seed germination requires statoliths but not a fully developed actin cytoskeleton (Ma and Hasenstein, 2006). These results indicate that actin is not directly involved in statolith-mediated force transduction.

It also has been suggested that direct statolith interactions with the cortical ER could induce calcium transients (Volkmann and Sievers, 1979; Sack and Kiss, 1989; Belyavskaya, 1996; Sinclair and Trewavas 1997; Chen et al., 1999, 2002; Perbal and Driss-Ecole, 2003). Intracellular Ca²⁺ is thought to be an important second messenger for sensing and responding to gravity (reviewed in Plieth, 2005). The concept that statoliths initiate transient Δ[Ca²⁺]_c gravitropic signals via interactions with the ER is attractive because the ER of columella cells is confined to the cell cortex (Zheng and Staehelin, 2001) and is therefore in a position to facilitate directional sensing and signaling and because the ER serves as a major [Ca²⁺] storage compartment in plants (Sievers and Volkmann, 1972; Sack, 1997; Persson and Harper, 2006). Calcium is a well-known mediator of cell signaling responses, and intracellular free or cytosolic [Ca²⁺]_c is affected by almost any stimulus, including mechanical stimuli such as gravity (Fasano et al., 2001; Yang and Poovaiah, 2003; Plieth, 2005). However, the lack of direct supporting evidence and kinetic data has precluded the development of a mechanistic understanding of the role of [Ca²⁺] in gravitropism. Recently, an increase in [Ca²⁺]_c upon reorientation of Arabidopsis thaliana seedlings in the gravitational field has been measured (Plieth and Trewavas, 2002; Toyota et al., 2008). The observed fast, biphasic [Ca²⁺]_c response provides support for the hypothesis that [Ca²⁺]_c is part of the initial gravitropic signaling response. However, to date, no correlation between the sedimentation of statoliths and changes in [Ca²⁺]_c has been established due to the lack of measured [Ca²⁺]_c signals from the columella cells and the lack of correlative information on the movements of the statoliths.

In this study, we applied differential interference contrast (DIC) microscopy, an imaging technique that generates minimal photodamage during real-time observations (Danuser et al., 2000), and laser tweezers, a noninvasive technique to apply controlled forces inside living cells (Ashkin and Dziedzic, 1989; Leitz et al., 1995), to analyze the movements of statoliths in relation to the cortical ER interface in columella cells of intact Arabidopsis seedlings. In addition, we applied high-pressure freezing and electron tomography to characterize the statolith-induced changes in ER membrane structure with nanometer resolution in Arabidopsis, Nicotiana tabacum, and Medicago sativa. A critical advantage of using Arabidopsis for live cell imaging instead of maize (Zea mays) roots as in previous studies (Sack et al., 1985, 1986; Yoder et al., 2001) is that the roots are relatively small and transparent and therefore do not require sectioning to image the statoliths in columella cells. The use of intact plants reduces the possibility that changes in osmotic pressure, shear stress, and other wound-induced artifacts affect the columella cells. Indeed, we could not verify previously published data about statolith sedimentation kinetics in response to 180° root reorientation derived from sectioned maize roots (Yoder et al., 2001) for intact Arabidopsis roots (data not shown). The organization of the Arabidopsis columella cells in distinct cell tiers S1 to S3 further allows that the sedimentation of statoliths can be accurately correlated to their position in the root cap. In particular, we have analyzed the response of statoliths to the gravitational force in the centrally located columella cells in the S2 cell layer. The importance of the central S2 columella cells for plant gravity sensing has been shown previously by selective cell destruction using a laser microbeam (Blancaflor et al., 1998) and localization of the auxin efflux carrier At PIN3 to the central S2 columella cells (Friml et al., 2002). At PIN3 is involved in the initial movement of auxin to the root elongation zone (Ottenschläger et al., 2003). This relatively slow hormonal response is preceded by a fast ionic response mediated by cytoplasmic Ca²⁺ and pH (Scott and Allen, 1999; Fasano et al., 2001; Plieth and Trewavas, 2002). Changes in membrane potential, reflecting altered ion fluxes of root statocytes, have been measured as early as 2 s after the onset of stimulation through gravity (Sievers et al., 1984). This and other observations led to the proposal that the perception time for plant gravity sensing is shorter than 1 s (Hejnowicz et al., 1998; Perbal et al., 2002; Perbal and Driss-Ecole, 2002).

We present experimental data derived from the central S2 columella cells that reconcile these extremely fast perception times with the sedimentation kinetics of statoliths. The initial response of statoliths to reorientation is dominated by an instantaneous movement of the statoliths away from the cortical ER toward the central cytoplasm, suggesting that the cortical ER network is a flexible and elastic platform capable of responding to gravity-induced statolith movements within <1 s. The subsequent sedimentation of statoliths is governed by aggregate formation, intra-aggregate statolith movements, and transient interactions of the statoliths with the peripheral ER. We show that the force of gravity on the mass of statoliths is sufficient to locally deform the cortical ER membranes, which indicates that ER membrane deformation is a potential mechanism underlying force transduction during channel gating in columella cells.

RESULTS

The Arabidopsis root is well suited for live cell microscopy due to its small size, transparency, and simple pattern of cellular organization. The statoliths (amyloplasts) are micron-sized particles inside columella cells located in the root cap. The columella cells are organized in three horizontal tiers, S1 through S3, with four cells in each tier, two central and two peripheral cells (Figure 1). In wild-type plants, the statoliths have sufficient mass to be displaced by gravity, and this has been correlated with the ability of plants to sense changes in the gravity vector. We have focused our studies on the response of statoliths to the gravitational force in the central tier (S2) cells of growing roots reoriented up to angles of 135°. The findings reported here are representative of the light microscopic recordings of >50 roots and on the analysis of ∼20 roots preserved by high-pressure freezing for electron microscopy. The main emphasis was on the analysis of statolith sedimentation after 90° reorientation of the root.

Figure 1.

Arabidopsis Root Cap.

DIC micrograph of a root cap from Arabidopsis ecotype Wassilewskija (Ws) showing the organization of the columella tissue region in three distinct cell tiers, S1 to S3, with four cells in each tier. Bar = 10 μm.

Statoliths in the Central Columella Cells Respond as an Aggregate to Root Reorientation

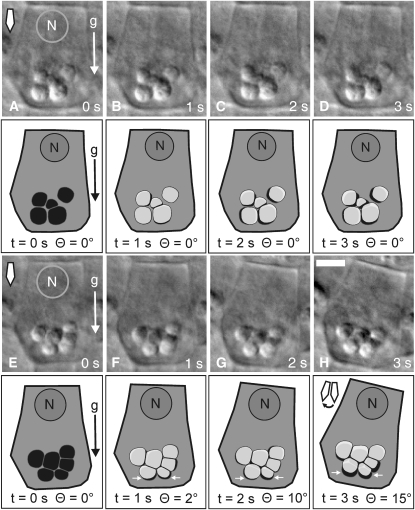
In vertically oriented, downward-growing roots, the statoliths settle as a group onto the ER network at the distal end of the columella cells, and since this ER network is relatively wide there (Figure 2A), the statoliths settle at a distance of several microns from the cell wall (Figures 2C and 2D). Reorientation of the roots causes the statoliths to initially move away from the previously distal ER interface (Figures 2E and 3A) and then progress in a downward-oriented movement toward the newer lower cell wall/ER interface (Figures 2F to 2H, 3A, and 3D; see Supplemental Movie 1 online). During sedimentation, the statoliths typically remained in close physical contact for up to several minutes, and the distances for cooperative statolith motions extended up to several microns. The micrographs and movies document the persistence of statolith aggregates during sedimentation after 90° (Figures 2E to 2L; see Supplemental Movie 1 online) and 130° (Figures 4B to 4F; see Supplemental Movie 2 online) reorientation. In both experiments, the statoliths reached a new equilibrium state in ∼10 min, and the statoliths settled into a spread-out configuration along the new lower cell wall (Figures 2L and 4F; see Supplemental Movies 1 and 2 online). The observed pattern of statolith sedimentation was independent of the initial root orientation. The statoliths also sedimented as an aggregate when a previously horizontally oriented root was subsequently turned upwards or downwards into a vertical position (Figures 4G to 4N and 5D to 5F). Individual statoliths, predominantly near the rear end of a sedimenting aggregate, were occasionally observed to separate from the aggregate, progress independently as single statoliths through the cytoplasm, and then rejoin the aggregate (data not shown). However, the bulk of the statoliths always remained associated with an aggregate.

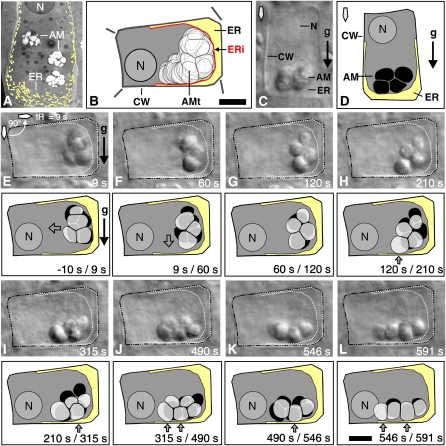
Figure 2.

Statolith Sedimentation Kinetics Relative to the Cortical ER.

(A) The cortical ER (highlighted in light yellow) visualized by electron microscopy in a vertically oriented Arabidopsis (Ws) columella cell.

(B) The cortical ER (highlighted in light yellow) as delineated by motion analysis in a horizontally oriented central S2 columella cells of Arabidopsis (Ws).

(C) to (L) Sedimentation kinetics of statoliths in relation to the cortical ER boundary at various time points (s) after 90° root reorientation. The columella cell immediately before reorientation, shown as DIC micrograph (C) and traced image (D) with the statoliths (black) resting above the ER interface (light yellow).

(E) to (L) Sedimentation of statoliths as aggregates after 90° reorientation in relation to the cortical ER boundary; shown are the DIC micrographs (top images) with the ER interface projected into the image (white dotted line) and the corresponding motion analysis (bottom images) with the ER interface (light yellow), the preceding statolith positions (black), and overlaid with the current statolith position (transparent gray). AM, amyloplasts; AM_t, traced positions of statoliths; ERi, ER interface; n, nucleus; tR, duration of reorientation in seconds (s); CW, cell wall. Arrows indicate direction of statolith movement (transparent arrows), statolith contact with the cortical ER (gray arrows), direction of gravity (black arrow), and orientation of root tip (diamond-shaped arrow). Bars = 5 μm.

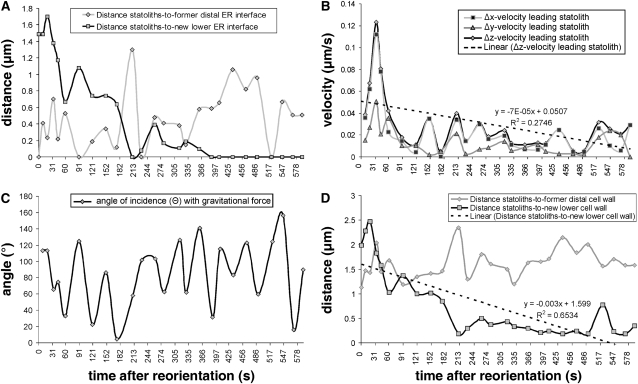
Figure 3.

Statolith Sedimentation Kinetics in a Central S2 Arabidopsis Columella Cell after 90° Root Reorientation (Detailed Analysis of the Micrograph Series Shown in Figure 2).

(A) Minimum separation distances (μm) of the aggregated statoliths to the former distal and new lower ER interface.

(B) Minimum velocities (μm s⁻¹) of the leading statolith in the horizontal (Δx), the vertical (Δy), and in the direction of the resultant vector (Δz); dashed line = trend line (Δz).

(C) Angle of incidence (Θ) of the leading statolith with the gravitational force.

(D) Distances (μm) of the statolith aggregate to the former distal and new lower cell wall; dashed line = trend line (distance to new lower cell wall). The time after reorientation is given in seconds.

Figure 4.

Statolith Sedimentation Kinetics in a Central S2 Arabidopsis Columella Cell after 130° and 180° Root Reorientation.

(A) Position of the statoliths immediately before reorientation.

(B) to (F) Series of DIC micrographs showing the sedimentation of statoliths as aggregates at various time points after a 130° reorientation. The gravity vector (g), the orientation of the root tip (diamond-shaped arrow), and the position of the cell nucleus (N) at the proximal end of the columella cell are as indicated. The time is given in seconds after the completion of root reorientation. tR, duration of reorientation (s). Bar = 5 μm.

(G) Settled position of the statoliths in close proximity to the lateral cell wall several minutes after 90° reorientation and immediately before a second 90° reorientation (overall reorientation is for 180° with the root tip turned upwards). This image was digitally turned (by 90°) to facilitate the comparison of the position of statoliths before and after reorientation. The actual orientation of the root is horizontally with the statoliths settled at the lateral cell wall.

(H) to (N) Series of DIC micrographs showing the sliding motion of a single, relative large statolith (indicated by a star) through an aggregation of statoliths at various time points after 90° reorientation. The gravity vector (g), the orientation of the root tip (diamond-shaped arrow), and the position of the cell nucleus (N) at the proximal end of the columella cell are as indicated. The time is given in seconds after the completion of the second 90° root reorientation. tR, duration of reorientation (s). Bar = 5 μm.

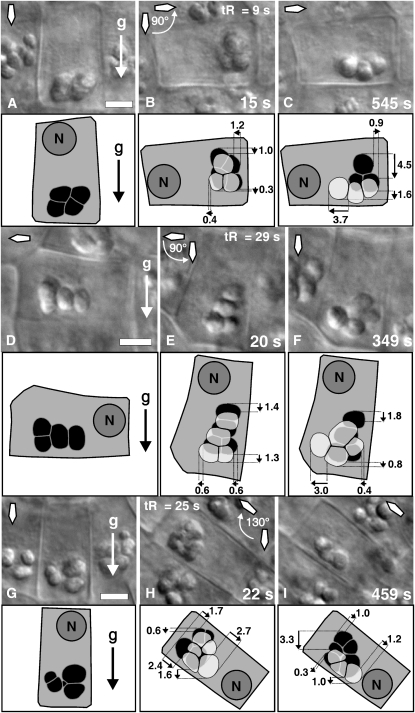
Figure 5.

Comparative Distances Covered by the Statoliths in the Central S2 Columella Cells from Arabidopsis within a Few Seconds (15 to 22 s) Relative to Longer (345 to 545 s) Time Intervals after Reorientation.

(A) Position of statoliths (black) immediately before reorientation.

(B) Displacement of the statoliths (transparent gray) 15 s after 90° root reorientation superimposed on the position of the amyloplasts before reorientation (black).

(C) Displacement of the statoliths 545 s after reorientation superimposed on the position of statoliths 15 s after reorientation; duration of reorientation tR = 9 s.

(D) Position of statoliths (black) in a horizontally oriented root immediately before reorientation.

(E) Position of statoliths (transparent gray) 20 s after 90° downward-directed reorientation superimposed on the position of the amyloplasts before reorientation (black).

(F) Displacement of the statoliths 349 s after reorientation superimposed on the position of statoliths 20 s after reorientation; duration of reorientation tR = 29 s.

(G) Position of statoliths (black) immediately before reorientation.

(H) Position of statoliths (transparent gray) 22 s after 130° reorientation superimposed on the position of statoliths before reorientation (black).

(I) Statolith displacement 459 s after reorientation superimposed on the position of statoliths 22 s after reorientation; duration of reorientation tR = 25 s.

DIC micrographs are shown above the corresponding models. Small black arrows indicate the direction of movement, and numbers display distances in microns. The gravity vector (g), the position of the cell nucleus (N), and the orientation of the root (diamond-shaped arrow) within the gravity field are as indicated. tR, duration of reorientation (s). Bars = 5 μm.

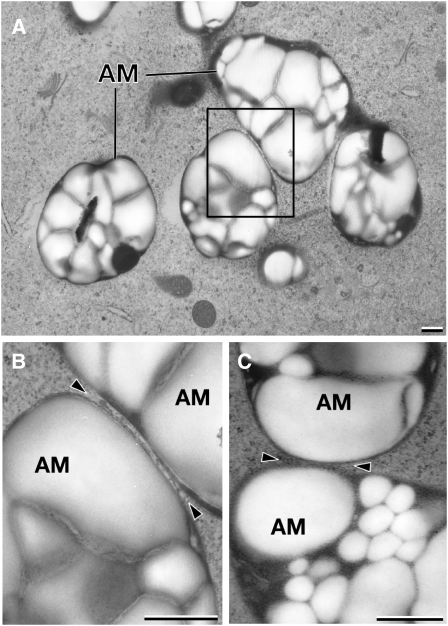
Statoliths Clustered in an Aggregate Can Approach Each Other to within ∼30 nm

Statoliths were considered aggregated when no separation or gap between adjacent statoliths could be resolved by light microscopy imaging. The gap size between statoliths is an important factor to evaluate the interfacial forces that govern aggregate formation; we therefore analyzed the contact region between statoliths in cells preserved by high-pressure freezing/freeze substitution techniques. These preparation methods provide for a highly accurate structural preservation of cells and allow for precise measurements of distances between organelles and other cellular structures by electron microscopy analysis. Figure 6A illustrates a group of aggregated amyloplasts in a high-pressure frozen columella cell. Due to the thinness of the section, only some of the contact regions between the amyloplasts of the aggregate are evident. Approximately 80% of the amyloplast volume is occupied by polygonal-shaped, tightly packed, and lightly stained starch granules, which are surrounded by more darkly stained stroma material. Imaging the statolith-statolith contact regions at higher magnification demonstrates that the outer membranes of the amyloplasts (statoliths) can approach each other to within <30 nm (Figures 6B and 6C). This proximity excludes other cytoplasmic structures, such as ribosomes and actin filaments, from the contact regions and suggests that the interacting amyloplasts are separated by a thin Newtonian liquid interface. An intervening layer of fluid between statoliths should facilitate intra-aggregate statolith movements by a sliding motion between statoliths. The subsequent image series shows the sliding motion of a single, relative large statolith through an aggregation of statoliths (Figures 4G to 4N). The comparatively large volume of the sliding statolith suggests that this movement is predominantly driven by the force of gravity on the mass of the statolith. The intimate contact to neighboring statoliths and frequent changes of the shape and orientation of the statolith suggest that the amyloplasts are to some extent flexible. The tomographic analysis confirmed that the statoliths do not touch and that the surfaces of the amyloplasts can be deformed to maximize the surface area in close contact (Figures 6A and 6B).

Figure 6.

Electron Micrographs of High-Pressure Frozen and Freeze-Substituted Columella Cells from Tobacco and Arabidopsis.

(A) The amyloplast (statolith) volumes are occupied by polygonal-shaped, tightly packed, and lightly stained starch granules, which are surrounded by more darkly stained stroma material.

(B) Higher-magnification view of the boxed area in (A). The adjacent statoliths from N. tabacum are separated by an ∼30-nm gap, and the surface of one of the amyloplasts appears deformed at the contact site (arrowheads).

(C) The adjacent statoliths from Arabidopsis are separated by an ∼30-nm gap (arrowheads). AM, amyloplast. Bars = 500 nm.

Statolith Aggregates Move Fastest during the First 30 s after Reorientation

We traced the position of individual statoliths over time and measured the distances traveled to quantify the movement of statoliths within seconds and several minutes after root reorientation. The vertical-mounted rotary stage often required recentering and refocusing of the cells at higher magnifications when reorientation angles exceeded 30° due to the eccentricity of the stage. Together with variations in the speed of rotation, this recentering led to variations in the interval between the onset of rotation and the recording of the first in-focus images after reorientation (see Methods). In Figure 5, three representative examples of statolith positions within 15 to 22 s after reorientation are compared with the statolith positions after an extended time period of 349 to 545 s after reorientation during which the statoliths were still in progressive motion but had not yet reached their new equilibrium state. In all of the examples shown, the relatively large distances traveled within the first 15 to 22 s after reorientation (Figures 5B, 5E, and 5H) indicated a significant slowdown in sedimentation velocities as the statoliths further approached or moved along the new lower cell wall during the subsequent time periods from 349 to 545 s (Figures 5C, 5F, and 5I). We therefore measured the velocity of the leading statolith at various time intervals after 90° reorientation and the distances of the aggregated statoliths to the cell wall, since the presence of cell walls or finite boundaries exerts a retarding effect on the sedimentation of particles in a viscous medium (Guyon et al., 2001). These measurements confirmed a relatively high initial velocity of the aggregated statoliths within the first 30 s after root reorientation and the tendency of the statoliths to initially move away from the cell wall after reorientation (Figures 3B and 3D). The sedimentation velocity of the leading statolith reached a peak of ∼0.1 μm s⁻¹ at ∼30 s after reorientation (Figure 3B) and then declined rapidly to the average velocity for single statoliths ∼0.025 μm s⁻¹ as it approached the new lower cell wall (Figures 3B and 3D).

The Cortical ER Interface Can Be Delineated in Living Columella Cells by Retracing Statolith Positions during Cell Reorientation

One of the defining structural features of columella cells is the confinement of the ER cisternae to the cell cortex where they are organized in the form of a continuous membrane network that is anchored to the cell periphery through connections to plasmodesmata (Figure 2A). This organization frees up the interior of the cell and enables the statoliths to sediment without interference by transcellular strands of ER. The spacing of the ER tubules within the cortical network is below the resolution of the light microscope. However, because the cortical ER network excludes the statoliths and prevents them from interacting directly with the plasma membrane (Zheng and Staehelin, 2001), it is possible to define this cortical ER zone by tracing the positions of individual statoliths and mapping their closest approach to the cell wall during sedimentation (Figure 2B). For this purpose, the cells were imaged by DIC microscopy, a very planar imaging technique, which facilitated the tracing of the statoliths and the cell wall after reorientation (see Methods). The validity of this technique for delineating the cortical ER boundary in living cells can be evaluated by comparing the distribution of this ER system in electron micrographs of cryofixed cells with the exclusion zone derived from the statolith tracing (cf. Figures 2A and 2D). This comparison demonstrates that it is possible with both methods to distinguish between a wider ER region along the distal cell wall and thinner regions along the lateral walls as seen in the electron micrograph. Thus, this approach appears to be a suitable method for delineating the central cytoplasm boundary of the cortical ER network in living columella cells.

The Statoliths Interact Transiently with the Peripheral ER during Downward-Oriented Sedimentation

The delineation of the ER interface as described above provided a means to monitor the interactions of individual statoliths with the surface of the cortical ER network in living cells. This motion analysis indicated that the statoliths do not continuously retain contact with the ER interface. Instead, the statoliths only interact transiently with the ER as they sediment (Figures 2E to 2L and 3A; see Supplemental Figure 1 online). The micrograph series also shows that statolith aggregates are dynamic multiparticle clusters, and intra-aggregate sliding motions contribute significantly to the kinetics of individual statoliths. The statoliths can slide along each other, move in and out of the focal plane, and frequently change direction while remaining in an aggregated state. For this reason, the angle of incidence of the leading statolith with the gravitational force Θ showed considerable fluctuations, and pure downward-oriented movements in the direction of the gravity vector Θ = 0° were seldom observed within the time intervals of ∼30 s (Figure 3C). A consequence of these intra-aggregate statolith movements was that displacements of individual peripheral statoliths toward the cortical ER resulted in only transient short-lived contacts or close proximities (<0.4 μm) between the statoliths and the cortical ER membranes until the statoliths reached a new equilibrium state (Figures 2E to 2L and 3A; see Supplemental Figure 1 online). The first direct physical contact of the statolith aggregate with the former distal ER interface was observed ∼90 s after reorientation (Figure 3A). This motion analysis also shows that the statoliths are in a continuous downward-oriented movement toward the new lower cell wall for up to 210 s after reorientation until the first physical contact with the new lower ER interface is made (Figures 2H, 3A, and 3D). Subsequently, a dynamically stable interaction of the statoliths with the cortical ER was reached at ∼370 s after reorientation (Figure 3A).

The Initial Response of Statoliths to Reorientation Is a Rapid Translocation Away from the Cortical ER Interface toward the Central Cytoplasm

The initial response of the statoliths to reorientation is a rapid displacement away from the peripheral ER interface (Figures 2E, 3A, and 7H; see Supplemental Figure 2 online). Because the angle of incidence with the gravitational force remained above Θ > 90° while this movement occurred (Figure 3C), it is likely that an elastic lift force exerted from the cortical ER contributed to this initial kinetic response. In the following example, we traced the outlines of statoliths in the central S2 columella cells and superimposed the retraced statolith positions before reorientation (Figures 7A to 7D) and during the rotation (Figures 7E to 7H) at 1-s time intervals (t = 1, 2, and 3 s; transparent light-gray statoliths) on the starting position of the statoliths (t = 0 s; black statoliths) using the cell walls as reference structures for cell alignment. This motion analysis indicated that the aggregated statoliths responded in <1 s to the reorientation of the plants within the gravity field. In particular, the statolith aggregate did not remain stably pressed against the underlying cortical ER after the onset of rotation; instead, it nearly instantaneously bounced off the surface of the ER network (Figures 7E to 7H). Superimposed on this rotation-induced displacement of the statoliths away from the ER interface are saltatory statolith movements (Figures 7A to 7D; see Supplemental Movie 3 online) that are comparatively shorter and signified by random direction.

Figure 7.

Saltatory Statolith Movements and Rapid Response of Statoliths Displayed at 1-s Time Intervals during Reorientation up to 15° in Arabidopsis (Ws).

(A) to (D) Statoliths exhibiting short-range, randomly oriented saltatory movements. Shown are the DIC micrographs of a central S2 columella cell (top images) and the retraced cell (bottom images). The time-resolved positions of the statoliths (transparent gray) during 1-s time intervals (t) without root reorientation (Θ = 0°) are superimposed on the starting position of the statoliths (t = 0 s; black).

(E) to (H) Statolith aggregates show an instantaneous response within <1 s to short-range reorientations. Shown are the DIC micrographs of a central S2 columella cell (top images) and the retraced cell (bottom images). The time-resolved positions of the statoliths (transparent gray) during 1-s time intervals (t) up to an angle of incidence Θ = 15° with the gravitational force are superimposed on the position of the statoliths before reorientation (t = 0 s; black). The net movement of statoliths (white arrows) is away from the ER interface toward the central cytoplasm. The gravity vector (g), the orientation of the root tip (diamond-shaped arrow) within the gravity field, and the position of the cell nucleus (N) at the proximal end of the columella cell are as indicated. Bar = 5 μm.

To further quantify the initial response of statolith aggregates, we analyzed the vector-valued position and velocity of single statoliths moving in the plane in response to short-range root reorientations. Root reorientations at higher magnifications in general require subsequent x–y repositioning of the microscope stage and/or refocusing of the sample mainly due to the eccentricity of the rotation device. To circumvent this problem, we analyzed the immediate response of statoliths to fast reorientations (<8 s) and short angles of reorientation up to 35°, which did not require refocusing of the sample. For these experiments, the roots were imaged by a high numerical aperture objective lens (numerical aperture = 1.4), and the rotation was recorded at 250-ms intervals to increase the spatial and temporal resolution. The columella cells were typically subjected to a small amount of lateral and vertical displacement up to 15 μm (on average 3.87 μm in the horizontal and 2.96 μm in the vertical direction) during rotation. This type of noncentric rotation is characteristic of virtually all root reorientation experiments reported in the literature, which typically involve the reorientation of whole Petri dishes with growing seedlings.

In a first approach, we analyzed the movements of statoliths in vertically oriented, stationary, and reoriented central S2 columella cells. Each data value in the first sample (non-reoriented cells) was linked to a data value in the second sample (reoriented cells); in this case, the link was due to the fact that the data values were before and after reorientation of the columella cells and measurements were from the same statoliths (n = 30). In particular, we analyzed the minimum velocity (ν_min) of the statoliths and the angle of incidence (Θ) with the gravitational force at 1-s intervals immediately before and at the onset of reorientation (see Methods). The statoliths in the non-reoriented (stationary) columella cells moved at an average velocity of ν_min = 0.10 ± 0.028 μm s⁻¹ (α = 0.01, sd = 0.059, n = 30) at an average angle Θ = 111.7 ± 17.97° (α = 0.01, sd = 38.22, n = 30). When the statoliths were subjected to cell reorientation, they moved at an average velocity of ν_min = 0.24 ± 0.063 μm s⁻¹ (α = 0.01, sd = 0.134, n = 30) at an angle Θ = 93.8 ± 19.06° (α = 0.01, sd = 40.52, n = 30). The average reorientation for these samples was 8°, and the cells were shifted for a mean distance of 5.9 μm in the horizontal and 5.6 μm in the vertical direction. We performed a paired Student's t test that proved that there was a significant difference [t (29) = 3.92, P < 0.0005] in statolith velocities between the control and the reference samples. In a second approach, we analyzed larger sample sizes by retracing the positions of statoliths in stationary and reoriented columella cells at various 1-s intervals. In contrast with the former analysis, statolith positions were also traced at consecutive 1-s time intervals. In the stationary cells, statoliths were traced up to 3 s and in the reoriented cells up to 35° and 8 s after the beginning of reorientation. The average cell reorientation of these samples was 15.90°, and the cells were shifted for a mean distance of 3.87 μm in the horizontal direction and 2.96 μm in the vertical direction. The statoliths in the stationary columella cells moved at an average velocity of ν_min = 0.09 ± 0.014 μm s⁻¹ (α = 0.01, sd = 0.062, n = 140) and an average angle Θ = 102.17 ± 10.87° (α = 0.01, sd = 49.94, n = 140). The velocity of the statoliths subjected to cell reorientation was ν_min = 0.27 ± 0.032 μm s⁻¹ (α = 0.01, sd = 0.145, n = 140) at Θ = 92.97 ± 9.57° (α = 0.01, sd = 43.98, n = 140). The difference in the mean statolith velocities between the control (saltatory movements) and the reference (reorientation induced plus saltatory movements) was significant [t (139) = 3.56, P < 0.0005; Student's t test]. The data indicate a more than twofold increase in statolith velocities upon reorientation with no directional preference toward the direction of gravity (Θ = 0°). Moreover, using analysis of variance (ANOVA), we did not find significant differences in the statolith movements between individual vertically oriented, stationary roots [ANOVA; F (3, 114) = 1.02, P > 0.05] or between reoriented roots [ANOVA; F (2, 52) = 2.43, P > 0.05].

We subsequently retraced the position of the leading and trailing statolith in 25 central S2 columella cells from 20 roots before and after 90° root reorientation to evaluate the movement of statolith aggregates after extended time periods for larger angles of reorientation (see Supplemental Figure 2 online). The duration of the 90° root reorientations was within a range from 5 to 49 s (average = 27 s), and statolith positions were retraced 1 to 10 s (average = 5.8 s) after completion of the reorientation. The leading and trailing statoliths were displaced for a mean distance of 0.85 ± 0.15 μm (α = 0.01, sd = 0.40, n = 50) toward the central cytoplasm at an average angle of incidence Θ = 56.3 ± 11.9° (α = 0.01, sd = 32.60, n = 50) to the gravitational force. These measurements indicate a significant displacement of the statoliths toward the central cytoplasm within <10 s after completion of the 90° reorientation. The lower angle of incidence with the gravitational force (Θ) is likely due to an increased sedimentation of the statoliths.

Statoliths Can Transmit Their Kinetic Energy through Membrane Deformation to the Cortical ER Network

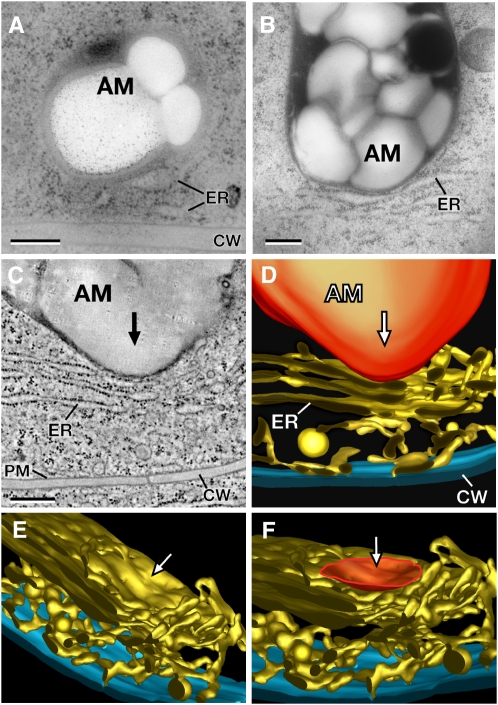
The rapid displacement of the statoliths away from the cortical ER interface during root reorientation (Figures 7E to 7H) suggested that the cortical ER network could represent an elastic and deformable platform and that this deformation could provide a means for producing a gravitational signal (e.g., a Ca²⁺ flux) since the ER is a potential site for mechanosensitive channels. To determine if the force of gravity on the mass of statoliths is sufficient to deform the ER membranes, we high-pressure froze root tips that had been allowed to gravitationally equilibrate in the freezing holders for 5 to 10 min prior to high-pressure freezing. This equilibration period was designed to allow the statoliths in the columella cells to sediment and then settle onto the surface of the cortical ER network prior to cryofixation after previously being subjected to a period of constantly changing gravity vectors during loading of the roots into the freezing holders. The cryofixation techniques used can provide high-resolution and reliable information on transient events inside cells because the cells are stabilized within milliseconds (Gilkey and Staehelin, 1986; Kiss and Staehelin, 1995). As documented in the thin section electron micrographs (Figures 8A and 8B) and in the tomographic image and models (Figures 8C to 8F), sedimented statoliths in columella cells of Arabidopsis, N. tabacum, and M. sativa have enough mass to deform the membranes of the cortical ER network. In contrast with the N. tabacum and M. sativa images (Figures 8B and 8C), which depict sheet-like peripheral ER membranes, the statolith-induced ER deformation is more difficult to discern in Arabidopsis (Figure 8A). The reason for this is that the peripheral ER in Arabidopsis is primarily composed of tubular ER that stains less strongly than cross-sectioned, sheet-like ER membranes. At the statolith-induced ER indentation sites, the statoliths approach the ER membrane to within ∼30 nm, and the depth of the indentations can reach ∼200 nm (Figures 8A to 8C). Because the area of ER membrane deformation is highly localized and closely matches the region of interaction between the two organelles, one can calculate the amount of localized ER membrane expansion associated with this type of deformation to be in the order of 15 to 20%. These deformations of ER membranes affect both tubular (Figure 8A) and sheet-like ER membrane domains (Figures 8B and 8C), thereby indicating that the force exerted by the sedimenting statoliths is sufficient to deform any domain of the cortical ER in columella cells. Furthermore, it is likely that additional forces can be generated through mass coupling of several statoliths. An example of mass coupling of several statoliths to an individual statolith contacting the cortical ER is shown in Figure 2K. In this example, three statoliths were held together in a v-shaped configuration, while only one statolith remained in direct physical contact with the ER interface (arrow). This v-shaped configuration of the statoliths remained stable for over 30 s, and it is therefore probable that this or similar arrangements of statoliths (Figure 2H) can significantly increase the pressure on a relatively small membrane area.

Figure 8.

Electron Micrographs, a Tomographic Slice Image, and Tomographic Reconstructions of the Cortical Cytoplasm of High-Pressure Frozen and Freeze-Substituted Columella Cells from Arabidopsis, N. tabacum, and M. sativa.

(A) and (B) Electron micrographs of statoliths (amyloplasts) in close physical contact with cortical ER cisternae in columella cells of Arabidopsis (A) and N. tabacum (B). Note the deformation of the ER membranes in the contact region.

(C) Tomographic slice image of a statolith (amyloplast) that has deformed an ER cisterna of the cortical ER network adjacent to the cell wall in a columella cell from M. sativa.

(D) to (F) The tomographic models show the tubules and cisternae of the cortical ER network and the statolith-induced deformation of the ER membrane from different viewing angles. The deformed ER region (F) is highlighted (orange), and the arrows ([C] to [F]) indicate the direction of the statolith impact. AM, amyloplast; PM, plasma membrane; CW, cell wall. Bars = 300 nm.

Statoliths Moved by Laser Tweezers against the Cortical ER Network of Arabidopsis Columella Cells Elastically Rebound from the ER Interface upon Release from the Optical Trap

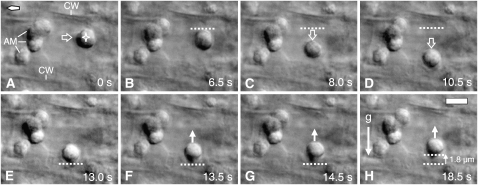
To further validate that the ER network can respond elastically to statolith impacts, we applied a localized force to the cortical ER membranes using statoliths as intracellular probes held and moved by optical forces. Single statoliths were stably trapped by laser tweezers and then pushed against the ER boundary by laser beam steering while the columella cell itself remained stationary and the beam propagation axis was perpendicular to the gravitational force (Figure 9; see Supplemental Figure 3 online). We subsequently traced the movement of the statoliths after release from the optical trap. In particular, we probed the ER along the side wall and the wider ER area within the tip of columella cells (Figures 2A and 2D) by two different types of experiments. In the first approach, a single statolith was separated from an aggregate and then moved downwards toward the cell periphery in a horizontally oriented root (Figures 9A to 9D). The laser beam was turned off after the statolith reached close proximity to the cell wall boundary (Figure 9E). The statolith subsequently moved (bounced) upwards against the gravitational force at a relative high initial velocity of ∼1.2 μm s⁻¹ as soon as it was released from the optical trap (Figures 9E to 9H). In other experiments involving vertically oriented roots, the laser tweezers were not turned off; instead, the laser beam was continuously moved downwards across the wide cortical ER at the distal end of the columella cell and further across the cell wall boundary into the space of the adjacent cell (see Supplemental Figure 3 online). The statolith escaped from the optical trap at a considerable distance (2.2 μm) away from the cell wall boundary (see Supplemental Figure 3E online), which suggests that an increased resistance against the optical displacement caused by a compression of the cortical ER network facilitated the escape of the statolith from the optical trap. The released statolith immediately started to move upwards against the gravitational force (see Supplemental Figures 3E to 3H online). Motion analysis of the position of the aggregated statoliths within this columella cell confirmed that the released statolith not only moved upwards for a distance of ∼1.7 μm after it escaped from the optical trap but also that the elastic force driving the statolith upwards was strong enough to also displace nearby statoliths against the gravitational force.

Figure 9.

Elastic Rebound of a Statolith (Amyloplast) Moved by Optical Force against the Cortical ER Boundary in a Gravity-Sensing Arabidopsis Columella Cell.

(A) A single statolith (indicated by a star in panel A) is separated from a group of statoliths by optical force using laser beam steering to move the statolith through the cytoplasm (the wide arrow indicates the direction of movement). The root is positioned at 90° with respect to the gravity vector. The diamond-shaped arrow points toward the root tip. AM, amyloplasts; CW, cell wall.

(B) to (D) The statolith is moved by optical force toward the cortical ER/cell wall boundary (the wide arrow indicates the direction of movement). The dashed line indicates the original position of the upper statolith boundary before the downward movement.

(E) to (H) The laser beam is turned off after the statolith has reached close proximity to the cell cortex, effectively releasing the statolith from the optical trap. This release causes an upward movement (white arrow) of the statolith against the gravitational force (g). The dashed line indicates the original position of the statolith before the upward movement ([E] to [H]) and the end position (H). The time is given in seconds. Bar = 5 μm.

DISCUSSION

The columella cells at the root apex are mechanosensory cells that respond to force. The external force of gravity acts throughout the cell volume, whereas internal or contact forces can be regarded as acting on an element of volume through its bounding surface (Aris, 1989). In columella cells, this transition from an external to an internal force is mediated by the statoliths, which are accelerated by the gravitational force. The mechanisms of force transduction also require an element or structure that is directly altered by the applied force (Janmey and Weitz, 2004). We therefore analyzed the motion of statoliths in relation to the cortical ER, which is a potential site for lipid bilayer–mediated mechanosensing in columella cells.

Statoliths Are Subject to Attractive Van der Waals and Repulsive Electrostatic Forces

The statoliths in the central columella cells sedimented as dynamic aggregates in response to root reorientations of 90° and 130° (Figures 2, 4, and 5). The formation of statolith aggregates also has been observed in cells of sectioned maize roots (Sack et al., 1986; Yoder et al., 2001), in plants grown in microgravity (Perbal and Driss-Ecole, 1989; Smith et al., 1997), and in inflorescence stems (Saito et al., 2005). The formation of compact statolith aggregates is indicative of particle–particle contacts as well as contact forces that contribute to the transient binding between statoliths and act over relatively short distances. The boundary of amyloplasts is formed by two envelope membranes, and if the outer membranes come in close physical contact, they are subjected to intermembrane forces such as van der Waals and electrostatic forces (Boal, 2002). The van der Waals force depends on geometry rather than on surface chemistry and increases with surface contact area (Autumn et al., 2002). Long-range van der Waals attractive forces have been detected between microscopic particles across water at distances up to 200 nm (Bevan and Prieve, 1999). As shown in Figure 6, the amyloplasts can approach each other to within 30 nm, and at the sites of interaction, the surfaces can be deformed to maximize the surface area in close contact. These observations support the view that adhesion between statoliths is the result of van der Waals forces and indicate that the adhesion energies are large enough to influence the shape of the amyloplasts. The combination of attractive van der Waals forces and repulsive electrostatic forces due to overlapping electric double layers forms the basis for the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory for colloidal stability (Derjaguin and Landau, 1941; Verwey and Overbeek, 1948). The statoliths suspended in the cytoplasm also can be regarded as a colloidal system, a multiphase system in which a dispersed phase or colloid (statoliths) is distributed throughout a dispersion medium (cytoplasm). The term colloidal usually refers to particles in the size range from a few nanometers to 50 μm (Pashley and Karaman, 2004). Strong attractive van der Waals forces, which hold particles in close physical contact, can increase the average settling velocities of suspensions (Davis and Acrivos, 1985), and it has been shown for other systems that particle aggregates can settle faster than predicted by Stokes' law (Li and Logan, 1997; Li and Yuan, 2002). However, aggregate velocities are also affected by an increase in drag force due to the larger effective hydrodynamic diameter and wall effects on the sedimentation.

Hydrodynamic Forces Contribute to the Motion of Statoliths

We have provided evidence that the amyloplasts are separated by a thin Newtonian liquid interface (Figures 6B and 6C); therefore, the aggregates can be defined as composite entities comprising amyloplasts adhering to each other and entrained fluid. The DLVO theory describes the forces between surfaces interacting through a liquid medium; however, the aggregates have no frozen-in structure since the individual amyloplasts are always in motion. At very low Reynolds numbers (Re << 1), which is the regime for statolith movements, lubrication forces are the dominant hydrodynamic force. Lubrication forces arise from the pressure necessary to replace the liquid within the gap between two approaching amyloplasts and, in principle, particles do not touch in this regime (Davis et al., 2003). The intervening layer of fluid between the surfaces can eliminate contact friction and facilitate amyloplast movements relative to each other through a sliding motion. The sliding motions between statoliths within an aggregate, the formation of such aggregates, and the relatively high initial velocities of the leading statolith in a reoriented columella cell (Figures 2E to 2L, 3B, and 4G to 4N) are difficult to reconcile with the idea that the statoliths are tethered via actin filaments to ER or plasma membranes (Sievers et al., 1991) or suspended in a cross-linked actin network (Yoder et al., 2001).

Statolith Sedimentation Kinetics Are Affected by the Boundaries of Columella Cells

The presence of the cell wall parallel or normal to the motion of the falling statoliths increases the corresponding frictional effects because the Stokes force is very sensitive to the presence of such boundaries (Guyon et al., 2001). The cell wall or other finite boundaries exert a retarding effect on the sedimentation of particles in a viscous medium and can introduce an asymmetry in the drag force (Vogel, 1994; Brenner, 1999; Lin et al., 2000; Kuusela et al., 2004). These so-called wall effects will significantly affect statolith velocities and the relative motion of statoliths and, therefore, statolith membrane interactions and consequently gravitropic signaling events. The tendency of the statoliths to move toward the central cytoplasm and the significant slowdown of the aggregated statoliths upon approaching or moving close to the ER/cell wall boundary (Figures 3A, 3B, 3D, and 5) can be attributed to wall drag effects. When a particle falls toward the ER/cell wall region, it slows down because of the increasing effect of viscosity. Therefore, as the separation between the particle and the cell wall tends toward zero, the velocity also approaches zero (Guyon et al., 2001). At low Reynolds numbers, this drag on the statoliths by the wall is substantially increased 100 or more body-diameters away (Vogel, 1994) and therefore will have an effect throughout the entire cell volume. The cortical ER network keeps the statoliths at a distance from the cell wall, and an elastic lift force exerted by the ER could also be an effective mechanism to push the statoliths away from the cell wall, thus avoiding impeding wall effects on the velocity. In particular, since the ER network is wider along the distal end of the columella cell (Figures 2A and 2D), this could facilitate the initial movement of statoliths out of their normal steady state position in downward growing roots.

The Force of Gravity on the Mass of Statoliths Is Sufficient to Locally Deform the Cortical ER Membranes and thereby Activate Mechanosensitive Ion Channels

The ER membrane system of columella cells is directly accessible to physical impacts from the statoliths; it is also a major [Ca²⁺] storage compartment in plants (Persson and Harper, 2006; Urbina et al., 2006). The ER is therefore a potential source for Ca²⁺ release into the cytoplasm; however, the mechanosensitive channels and receptors have not been identified, and it is also possible that tension of the plastid envelope membranes releases Ca²⁺ stored within the amyloplasts (Kikuyama and Tazawa, 2001). The ER is confined to a thin layer in the columella cell cortex and forms a relatively compact membrane network of interconnected tubular and cisternal ER domains capable of excluding amyloplasts, Golgi stacks, and vacuoles (Figures 2 and 8). The previously described nodal ER domains (Zheng and Staehelin, 2001) have so far not been found in columella cells of Arabidopsis, and it is therefore likely that these structures are not directly involved in the gravity sensing of roots. The applied electron microscope analysis showed that the force of gravity on the statoliths is sufficient to locally deform the underlying cortical ER membranes (Figure 8). At these statolith-induced ER indentation sites, the statoliths approach the ER to within ∼30 nm, and the depth of the indentation can reach ∼200 nm, thereby causing a significant amount of local membrane bending that is limited to the region of close contact between the two organelles and will likely also depend on Van der Waals and electrostatic interactions (Dean and Horgan, 2006). This finding provides direct mechanistic evidence of how the force of sedimenting statoliths could activate mechanosensitive ion channels in the ER (Yoshimura et al., 2004). Many mechanosensitive channels are activated by changes in intrabilayer pressure gradients generated through membrane curvature and do not depend on interactions with the cytoskeleton (Hamill and Martinac, 2001; Perozo et al., 2002). The MscL channel of Escherichia coli, for example, is gated by membrane tension in the lipid bilayer alone (Sukharev et al., 1994).

The Kinetics of Statolith Interactions with the Cortical ER Can Potentially Trigger Mechanosensation within Less Than a Second of Root Reorientation

The statoliths showed a biphasic response to the reorientation of columella cells. The initial response starts within <1 s of the onset of reorientation and is marked by the rapid displacement of statoliths away from the distal ER interface (Figure 7; see Supplemental Figures 1 and 2 online). The ER micrographs suggested that the statoliths can compress the ER, and the exerted force is likely to increase through mass coupling of the statoliths (Figures 2H and 2K). The elastic potential energy that is stored in such a compressed ER network and possible adjacent cytoskeletal elements can be rapidly converted into kinetic energy, thereby lowering the threshold to induce a signal. The rebound of statoliths from the ER induced by optical trapping and the more than twofold increase in statolith velocities upon reorientation at an average angle of Θ = 92.97° support the hypothesis that the released kinetic energy is sufficient to move statoliths against the gravitational force and trigger initial [Ca²⁺]c transients or other mechanosensory signals within columella cells (Figures 9 and 10B; see Supplemental Figure 3 online). During the subsequent sedimentation phase, which lasted ∼370 s, the statoliths tended to move at a distance to the ER boundary and make only transient contacts with the cortical ER (Figures 2 and 3) until they reached a new equilibrium state (∼600 s after reorientation) and settled along the cortical ER adjacent to the new, lower cell wall (Figures 2L and 4F). The high fluctuations of the angle of incidence with the gravitational force for the leading statolith in the range of Θ = 0° to 180° during sedimentation (Figure 3C) are indicative of significant isotropic movements, statolith–statolith interactions, velocity gradients induced by the presence of boundaries at all times, and the overall complexity of statolith dynamics. The observed fast initial and slower transient statolith-to-ER interactions could give rise to a biphasic [Ca²⁺]c response within columella cells since statolith-induced Δ[Ca²⁺]_c transients will exhibit, as most Ca²⁺-based signaling events, a typical, unique time course (Plieth, 2005), which will be closely correlated to the statolith dynamics. An initial [Ca²⁺]c spike and subsequent shoulder signals were reported for whole Arabidopsis seedlings after reorientation; however, the observed biphasic Ca²⁺ responses were not derived from root columella cells (Plieth and Trewavas, 2002; Toyota et al., 2008). There is currently no direct evidence for Ca²⁺ responses in root gravitropism. The tomographic analysis (Figures 8D to 8F) provided structural evidence that tension in the ER membrane is one mode of mechanosensation within columella cells; however, it is not known which membrane proteins are affected by these conformational changes, and it is probable that other factors contribute to the energetics of channel gating and trigger different receptors for signaling at the ER and/or plasma membrane.

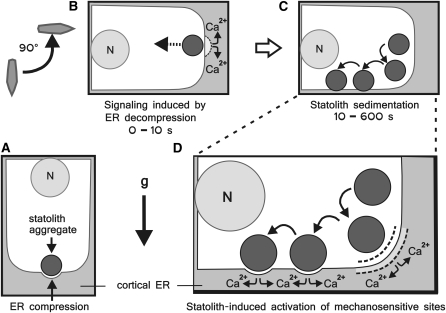
Figure 10.

Schematic Diagram of the Statolith-Mediated Force Transduction to the Cortical ER in Gravity-Sensing Columella Cells.

(A) Before reorientation the ER is compressed by the weight of the statoliths.

(B) Reorientation leads to a rapid displacement of the statoliths away from the ER interface toward the central cytoplasm. This elastic rebound can potentially trigger an initial Ca²⁺ or other signal within the columella cell.

(C) The statoliths sediment driven by the gravitational force (g) until contact with the cortical ER adjacent to the new lower cell wall is reestablished.

(D) During the sedimentation phase, the statoliths interact transiently with the cortical ER through direct physical impacts and constantly through a cytosol-mediated action at a distance (dashed line), which may also reach the subtending plasma membrane. These mechanisms are postulated to activate mechanosensitive sites in the ER and/or at the plasma membrane—here exemplary shown is a Ca²⁺ response. N, nucleus.

Saltatory Statolith Movements Are Superimposed on the Sedimentation of Statoliths

The signaling within columella cells will also be affected by saltatory movements (Sack et al., 1986). The saltatory movements are rapid (<1 s), randomly oriented, and short-range (<1 μm) statolith motions (Figures 7A to 7D; see Supplemental Movie 3 online) that are superimposed on the gravity-driven sedimentation of statoliths. These statolith movements are thought to be caused by actin-dependent forces and possible weak Brownian motions. The cytoplasm of columella cells contains short randomly oriented actin filaments (Driss-Ecole et al., 2000; Yoder et al., 2001). It has also been suggested that the actin filaments are oriented toward the cell center to explain the movement of statoliths toward the cell center in microgravity (Perbal et al., 2004). However, we attribute this movement (not driven by molecular motors) to the combined effect of microgravity and the viscoelasticity of the cytoplasm since a viscoelastic fluid exerts an aggregative power resulting in the attraction of nearby bodies (Joseph et al., 1994). The average angle of incidence with the gravitational force for saltatory statolith movements Θ = 102.17° (n = 140) is signified by a high variance (sd = 49.94; variance = 2494), a random process and therefore a constant source of noise inherent to columella cells. The magnitude of these fluctuations sets the fundamental limit for the ability of columella cells to detect the signals generated by the sedimentation of statoliths. In this context, it is conceivable that the response of columella cells undergoes resonance-like behavior as a function of the noise level. The addition of random noise can enhance information-carrying signals through stochastic resonance (Douglass et al., 1993; Hänggi, 2002; Ma and Hasenstein, 2006). Moreover, saltatory statolith movements could help maintain the cortical ER in a dynamic, responsive state, since they will affect the time-dependent recovery of membrane extensional deformations caused by the gravity-driven statolith impacts on the ER membranes.

The Sedimentation of Statoliths Instantaneously Causes Motion of the Cytosol at a Distance

The rapid rebound of the statoliths away from the cortical ER corresponds to a perception time of <1 s and therefore can provide a physical basis for the fast electrical and ion flux responses reported previously (Hejnowicz et al., 1998; Perbal and Driss-Ecole, 2002; Blancaflor and Masson, 2003). The elastic rebound of the ER membranes could allow the columella cells to reset and possibly resensitize their gravity-sensing systems; however, it is unlikely that this initial response provides significant directional cues for the gravitropic growth response. Considering that it takes ∼3.5 min for the statoliths to reach the ER interface along the new, lower cell wall after a 90° reorientation (Figures 3A and 3D), the question arises as to the sensing mechanism that enables the plant to set the directional growth response prior to the statoliths making contact with the lower ER interface. The observed time lines for statolith-to-ER impacts and the impeding effect on statolith velocity imposed by the cell boundaries suggest that a statolith-mediated action at a distance, which does not require direct physical contact between the amyloplasts and the ER, also contributes to mechanosensing (Figure 10D).

During sedimentation, the statoliths will produce a velocity field around them in the cytosol, which, at low Reynolds numbers, decays as r⁻¹ where r is the distance from the particle center (Brenner, 1999; Kuusela et al., 2004). Along the cytosol-statolith interface, the velocity of the immediately adjacent cytosol will be the same as that of the moving statolith, the cytosol tends to move with the statolith, and further away a velocity gradient with respect to distance extends as a consequence of the no-slip boundary condition (Vogel, 1994, 2003; Pickard, 2003). This velocity field influences the motion of other statoliths at considerable distances similar to the way the presence of the cell wall affects the moving statoliths. The wide field of affected flow that accompanies the sedimentation of statoliths will interact instantaneously with the cortical ER network and the plasma membrane as long as the statoliths are in motion. There is molecular evidence that the plasma membrane is a potential site for mechanosensing in plants (Hayashi et al., 2006; Nakagawa et al., 2007; Zhang et al., 2007).

Based on these considerations, we suggest that direct physical impact forces of the statoliths on the ER as well as a cytosol-mediated action at a distance on the ER and plasma membrane induced by the movement of statoliths contribute to mechanosensing in columella cells (see schematic diagram presented in Figure 10). This hypothesis is consistent with a fast, actin-independent mechanism for force transduction in plant gravity sensing and encompasses a mechanism for real-time sensing of the plants orientation within the gravitational field. Our results indicate that columella cells have the ability to respond rapidly to even small changes in the gravity vector and that columella cells, as most mechanosensory cells (Gillespie and Walker, 2001), are optimized for speed and sensitivity.

METHODS

Plant Material and Culture Conditions

Plant seeds of wild-type Arabidopsis thaliana ecotypes Wassilewskija (Ws) and Landsberg erecta (this ecotype was used for the image series showing the response to 135° root reorientation), alfalfa (Medicago sativa), and tobacco (Nicotiana tabacum) were sterilized by vapor-phase sterilization using 25 mL NaOCl (bleach) supplemented with 1 mL concentrated HCl for 5 to 6 h. Surface-sterilized seeds were germinated and grown on 0.6% agar-solidified quarter-strength Murashige Minimum Organics Medium (Invitrogen). The seedlings were subsequently grown in vertical orientation with a 12-h light-dark cycle at 21°C in a microprocessor-controlled low-temperature incubator.

Sample Preparation

After 4 to 5 d, seedlings with primary root lengths between 10 and 15 mm were transferred gently to microscope slides onto a thin layer of 2% agarose (Invitrogen). The samples were suspended in a small droplet of 0.25 liquid Murashige Minimum Organics Medium and covered with a 22 × 22-mm cover glass. To minimize mechanical impacts, small droplets of petroleum jelly (Vaseline) were applied as a spacer at each corner of the cover glass

Vertical Stage Microscopy

Light microscopy was performed at room temperature 21 ± 1°C on an upright Axioskop microscope (Zeiss) mounted on a 0.6 × 0.6-m optical breadboard (Melles Griot). The breadboard was mounted in vertical orientation on an optical table with vibration isolation (Technical Manufacturing Corporation). The plant roots were imaged by DIC using a Plan Neofluar 40/0.75 DIC objective and a green glass filter in the transmitted light path. Images were recorded by a digital camera (XCD-SX900; Sony Electronics) that was connected by an IEEE 1394-interface to a computer (Precision 350; Dell) and controlled by Fire-i software (Unibrain). Alternatively, a Plan Neofluar 40/1.30 oil DIC objective was used and images were recorded with a CoolSnap HQ CCD camera (Roper Scientific) that was controlled by MetaMorph software (Universal Imaging).

Laser Tweezers

The laser tweezers system integrated dual optical traps into the vertical stage microscope (see previous section) to exert forces on statoliths perpendicular to the gravitational force. The trapping laser consisted of a fiber-coupled, diode-pumped, solid-state Nd:YVO₄ laser system (T-Series Z-106C; Spectra Physics), which delivered continuous-wave output up to 10 W at 1064 nm in TEM₀₀ mode. The linearly polarized trapping beam was expanded by a high-energy beam expander mounted on a five-axis kinematic stage (CVI Laser and New Focus) and subsequently split into two beams by a broadband polarizing beamsplitter cube (CVI Laser) to create two independently adjustable laser traps in the object plane. The power ratio of the two beams was controlled by a rotatable half-wave plate (λ/2; Thorlabs), and the intensity of the main trapping laser by a compensated attenuator (M-925B; Newport). One laser beam was conceived as a stationary optical trap in the center of the field of view and the other laser beam as a moveable laser trap controlled by a motorized gimbal-mounted mirror (SL series, Newport; Z612B, Thorlabs) mounted on a crossed roller bearing XY stage (OptoSigma) and a motorized telescope lens system (linear actuators 850F and motion controller MM2000; Newport). The trapping lasers were subsequently recombined by a second polarizing beamsplitter cube mounted on a three-axis prism table (CVI Laser and OptoSigma). The laser beam was subsequently directed into the microscope via a set of kinematic steering mirrors, lenses mounted on three-axis translators (Thorlabs and Siskiyou Design Instruments), and two made-to-order dichroic mirrors (Omega Optical). A green laser at 532 nm (World Star Tech.) was used as a pilot laser to indicate the position of the trapping laser. The optical traps were controlled by a computer program developed through graphical programming using LabView (National Instruments). This software interface controlled the speed and direction of the trap movement in the object plane and allowed the setting of several waypoints or a sequence of movements that were then executed. The program further controlled the motorized telescopes (z axis), the laser output power, and two shutters (Uniblitz VS14 with shutter drivers VMM-T1 and VMM-D1; Vincent Associates) to time and control the two traps independently. The positions of the optical traps were indicated by markings overlaid onto the image display, and these were continuously updated as the trap moved in the object plane. In addition, important experimental data like the laser power, the image time stamp, and the gating of the shutters were saved in a separate (metadata) file to be subsequently embedded in each of the acquired images.

Plant Reorientation

For reorientation of the plant seedlings, a manual rotating and centering stage with 360° graduation was mounted on the microscope (Z150 with AK3; Märzhäuser). The rotating stage was modified with beryllium-copper shims added to the inner rim of the rotating platform to improve rotational movement. The Z150 rotating stage was centered on the optical axis of the microscope and the root cap aligned to the center of the field of view by the AK3 object guide. Roots were then rotated to the angles Θ = 90° and Θ = 135° ± 5°, or for short-range reorientations, up to Θ = 35° with reference to the gravity vector. For roots reoriented up to angles of 90°, it was often possible to keep the central columella cells in the field of view during rotation; however, higher magnifications, larger angles of reorientation, or faster reorientation times of <10 s in general required x-y repositioning and refocusing of the samples. This often led to variations in the time interval between the completion of rotation and the recording of the first in focus images after reorientation. The corresponding error terms that reveal the performance limitations for rotational motion are quantified as wobble and eccentricity. For a rotary stage, eccentricity is a linear displacement of the mechanical center of the stage from the axis of rotation, and wobble is the unintentional tilting of the axis about which the device is rotating.

Image Analysis

Images of statolith sedimentation were digitally recorded at 0.25- or 1-s intervals and further analyzed using image processing and graphics software (MetaMorph, Universal Imaging; CorelDraw Graphics Suite, Corel). Photo plates were prepared using Adobe Photoshop (Adobe Systems) and CorelDraw Graphics Suite. For control measurements and distance calibration, a digital caliper and a stage micrometer (Zeiss) were used. For motion analysis, selected digital images were imported into the CorelDraw graphics program and converted to a three-dimensional stack of images. The time-resolved positions of individual statoliths were determined by retracing the outline of the statoliths and cell wall boundaries in individual images using the object and line tools of the software. To compensate for any object drift and position the target cell in the same position, the top layer image was made partially transparent and aligned with the underlying image by repositioning the image. In addition, several line drawings, mainly of cell wall intersections, were used as fixed reference points throughout the root cap. The microscopy images were subsequently deleted and the graphical data from individual image series were superimposed onto each other to correlate the position of the statoliths within the columella cell at different time points and/or angles of incidence with the gravitational force. The motions of statoliths were further analyzed by measuring the displacements of the leading and trailing statoliths over time. For this quantitative analysis, the horizontal displacement (Δx) and the vertical displacement (Δy) of statoliths were measured tangentially to the circumferences of the statoliths by overlaying the retraced position of the statoliths at different time points (t) within one graphical image. These linear measurements were done with the dimension tool of the CorelDraw Graphics software at a 1:4 scale and then converted to microns. The shortest possible paths of the statoliths were calculated using the trigonometric function Δz = 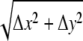. Since the resultant vector (Δz) represents the shortest path the statoliths could have taken, calculated velocities therefore represent the minimum statolith velocities ν_min = Δz/t. The statistical analysis and calculations of the angles of incidence with the gravitational force Θ = 90° − arcsin (A) and sin (A) = Δx/Δz were done using MSExcel software (Microsoft). The confidence interval for a population mean at a specific significance level (α), the standard deviation (sd) of the population, and the sample size (n) are given. The probability (P) associated with a Student's t test and variance analysis using the ANOVA function was used for further data analysis. The cortical ER interface was determined by retracing the outer edge of statoliths closest to the cell wall during sedimentation from ∼1500 single images at 1-s intervals of a central columella during rightward and leftward reorientation.

Electron Microscopy, Tomography, and Modeling

The contact region between adjacent amyloplasts and between amyloplasts and the cortical ER was analyzed by electron microscopy in high-pressure frozen and freeze-substituted roots from Arabidopsis, N. tabacum, and M. sativa as described by Zheng and Staehelin (2001). For electron tomographic analysis, images of the cortical ER and statoliths from four consecutive 300-nm-thick sections were taken at ×12,000 from +60° to −60° with 1.5° increments around two orthogonal axes. The images were collected with a Gatan Megascan 795 digital camera covering 4.096 × 4.096 μm² (pixel size 2.0 nm) (Gatan). Dual-axis tomograms were calculated using the etomo interface of the IMOD software package (MCD Biology). Tomogram display and analysis were performed with the 3dmod graphic module of the IMOD software package. ER membrane, plasma membrane, and the statoliths were traced and converted into three-dimensional models as described by Otegui et al. (2001). The deformed ER region in Figure 8 was delineated by highlighting the ER membrane domain pressed down by the statolith from an imaginary plane straightly extended from the neighboring flat ER surface.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure 1. Statolith Sedimentation Kinetics Relative to the Cortical ER Interface in a Central S2 Arabidopsis Columella Cell.

• Supplemental Figure 2. Motion Analysis of the Initial Response of Statoliths in Central S2 Arabidopsis Columella Cells after 90° Root Reorientation.

• Supplemental Figure 3. Elastic Rebound of a Statolith Moved by Optical Force against the Distal Cortical ER Boundary in Central Arabidopsis Columella Cells.

• Supplemental Movie 1. Statolith Sedimentation Kinetics in a Central S2 Arabidopsis Columella Cell after 90° Root Reorientation.

• Supplemental Movie 2. Statolith Sedimentation Kinetics in a Central S2 Arabidopsis Columella Cell after 130° Root Reorientation.

• Supplemental Movie 3. Saltatory Statolith Movements in a Central S2 Arabidopsis Columella Cell.