Abstract
Aptamers are nucleic acid molecules selected in vitro to bind a particular ligand. While numerous experimental studies have examined the sequences, structures, and functions of individual aptamers, considerably fewer studies have applied bioinformatics approaches to try to infer more general principles from these individual studies. We have used a large Aptamer Database to parse the contributions of both random and constant regions to the secondary structures of more than 2000 aptamers. We find that the constant, primer-binding regions do not, in general, contribute significantly to aptamer structures. These results suggest that (a) binding function is not contributed to nor constrained by constant regions; (b) in consequence, the landscape of functional binding sequences is sparse but robust, favoring scenarios for short, functional nucleic acid sequences near origins; and (c) many pool designs for the selection of aptamers are likely to prove robust.
Keywords: Aptamer, RNA, Bioinformatics, In vitro selection
Introduction
Nucleic acid molecules that perform a wide range of functions such as binding (e.g., aptamers) and catalysis (e.g., ribozymes) can be selected from random sequence pools (Ulrich 2006; Joyce 2004; Tuerk and Gold 1990; Ellington and Szostak 1990). Aptamers are typically selected from a random sequence pool flanked by two constant regions necessary for enzymatic manipulation, such as in vitro transcription and PCR. The random regions of aptamers typically range from 20 to 200 nucleotides in length, while the constant regions are generally from 18 to 30 nucleotides long (Lee et al. 2004). Aptamers can be selected to bind a wide range of target ligands with high affinities and specificities, and typically fold into compact secondary and tertiary structures (Carothers et al. 2004; Ellington 1994). While aptamers have a variety of biotechnological applications (Davidson and Ellington 2005; Ulrich 2006; Issacs et al. 2006; Lee et al. 2006), the process and products of in vitro selection experiments also allow basic questions in origins and evolutionary biology to be addressed (Joyce 2000; Schultes and Bartel 2000; Hughes et al. 2004).
One means of determining the topology of nucleic acid fitness landscapes is to determine how function varies relative to the pool used for selection. For example, theoretical proposals and empirical research suggest that pools with greater structural diversity (Gevertz et al. 2005; Kim et al. 2007), modified nucleotide compositions (Knight and Yarus 2003), and/or different lengths (Coleman and Huang 2002, 2005; Legiewicz et al. 2005) can increase the efficiency with which functional aptamers and ribozymes may be selected.
An alternative way to examine the influence of these variables on function is to use bioinformatics approaches. Some researchers have focused on using secondary structure as a surrogate for function, and either have carried out selections in silico (Patzel 2004; Hall et al. 2007) or have analyzed the secondary structures of aptamers following selection (Connell et al. 1993; Majerfeld and Yarus 1998; Lozupone et al. 2003; Huang and Szostak 2003; Carothers et al. 2004; Sayer et al. 2004; Dey et al. 2005).
We have now examined the sequence, rather than structural, constraints on selected binding species. In particular, it has previously been observed that the constant regions of aptamer sequences can participate in their functional secondary structures (Connell et al. 1993; Majerfeld and Yarus 1998; Ellington et al. 2000; Louzupone et al. 2003). If this were a general phenomenon, then it would greatly influence which aptamers are selected from random pools because functional aptamer sequences whose structures exploit the constant regions may be more prevalent in a pool and predominate during the selection process.
To determine the extent to which the constant regions influenced the function of selected aptamers, we examined how constant regions influenced the folding of more than 2000 aptamer sequences selected to bind 141 unique target ligands. We find that, in general, constant regions are only minimally involved in the overall structures of selected aptamers. These results have important implications for both evolution and biotechnology, in that it is clear that function predominates over the ‘tyranny of short motifs.’
Materials and Methods
Aptamer Database
We examined the secondary structures of the selected aptamers in the Aptamer Database (http://www.aptamer.icmb.utexas.edu [Lee et al. 2004]). The Aptamer Database is a manually curated collection of RNA aptamers that have been selected to bind a wide variety of target molecules, ranging from small molecules (e.g., vitamin B12) to large proteins (e.g., lyoszyme) to whole organisms (e.g., E. coli). We examined every aptamer species in the database for which the primer sequences were also included, giving a sample size of n = 2040 aptamer sequences, covering 141 unique target ligands.
RNA Folding Algorithms
RNA molecules fold into secondary structures (“shapes”) that are scaffolds for functional tertiary structures and are strongly conserved for most natural functional RNA molecules (Doudna 2000). The formation of secondary structures is relatively well understood and can be rapidly predicted using thermodynamic minimization (Hofacker et al. 1994; Mathews et al. 1999; Zuker and Stiegler 1981; Zuker 1989). We used the Vienna RNA folding software (version 1.6.3) to predict the lowest free energy shapes of sequences in the Aptamer Database (Hofacker et al. 1994). We used the default parameter set with the following exceptions: (i) we included thermodynamic interactions between adjacent helices (the ‘dangles’ variable was set to 2), and (ii) we excluded single-base-pair stacks (the ‘noLonelyPairs’ variable was enabled).
Measuring Structural Distances
To measure the structural differences between two RNA secondary structures, we used the Hamming distance metric. The Hamming distance is calculated by first converting each RNA secondary structure to a parenthetical notation in which paired bases are represented by pairs of parentheses, whereas unpaired bases are represented by dots (e.g., (((....))) is a simple hairpin structure). The Hamming distance is then simply the number of positions at which the parenthesized RNA secondary structures differ. For example, the shapes (((....))) and ((......)) would have a Hamming distance of 2; the Hamming distance considers all types of structural differences, and does not simply count the number of base pairs.
Measuring Thermodynamic Stabilities
We used the Boltzmann probability of the ground-state shape as a measure of the thermostability of an aptamer (Ancel and Fontana 2000). Wuchty et al. (1999) extended the standard thermodynamic folding algorithms to predict all shapes that are thermodynamically similar to the ground-state shape. This approach permits the rapid computation of the partition function , where ΔGs is the free energy of shape s, K is the Boltzmann constant, and T is the absolute temperature (McCaskill 1990). The Boltzmann probability p of a shape s is then ps = e(−ΔGS/KT)/Z, assuming thermodynamic equilibration and no kinetic barriers to transitioning between alternative structures.
Results
Aptamers are commonly selected from a pool consisting of a “random region” flanked by two constant regions used for enzymatic manipulation, such as PCR amplification and in vitro transcription (Fig. 1). The distribution of the aptamers in the Aptamer Database was heavily skewed toward shorter random regions, of the order of 20–40 residues in length (Fig. 2A), and toward constant regions that were each generally from 20 to 30 residues long (Fig. 2B). We ensured that the lengths of the random regions and the lengths of the constant regions were independent of one another (Pearson correlation coefficient R = −0.09, p = 0.795).
Fig. 1.
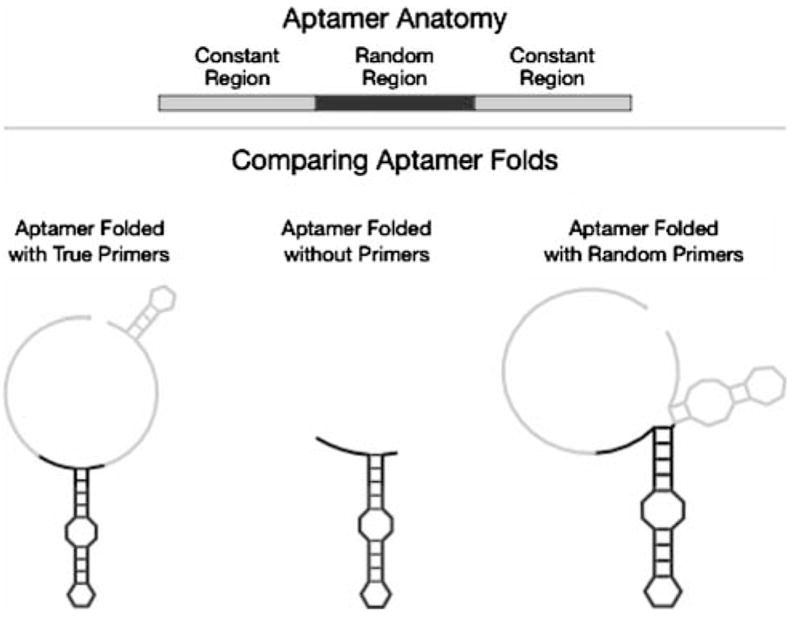
Cartoon schematic of the anatomy of an aptamer sequence. Top: Aptamer sequences consist of a random region (black rectangle) that is flanked by two constant regions (gray rectangles). The random region undergoes most evolution during in vitro selection, whereas the constant regions serve for amplifying the aptamers during the selection process. Bottom: Comparison of different folded strcutures used in the present study. This structure of the random region (black) is robust to the absence of constant regions or the presence of randomized constant regions (gray)
Fig. 2.
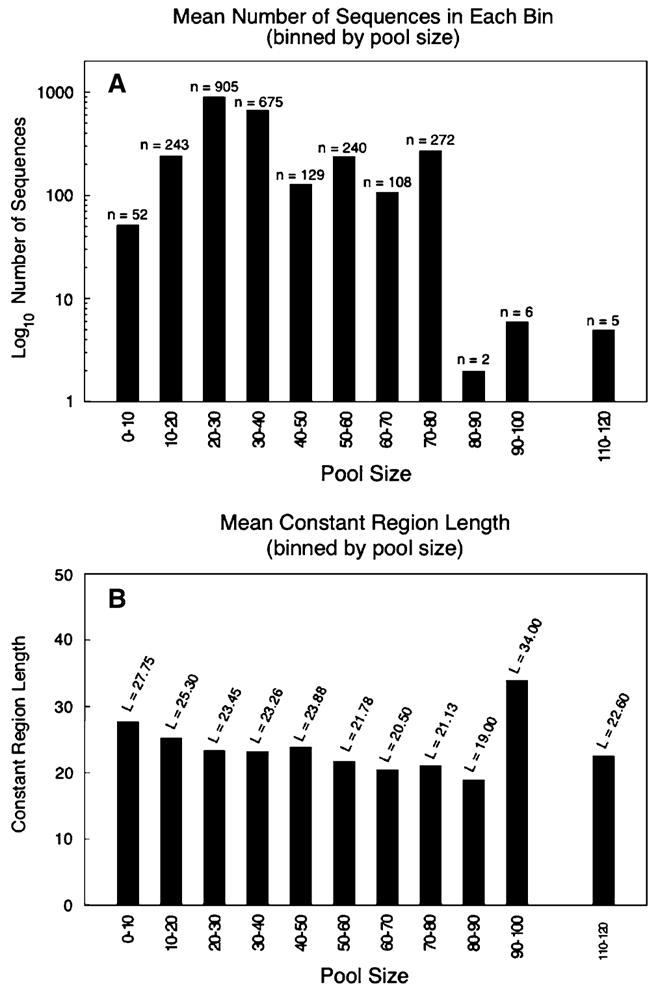
(A) Distribution of the number of aptamers in the database at each pool size. (B) Distribution of the number of aptamers in the database at each constant region length. In both (A) and (B), we only include aptamers in which the entire sequence (random and constant regions) is contained in the Aptamer Database (Lee et al. 2004)
Structural Participation by Constant Regions
We sought to determine the general extent to which constant regions participate in the secondary structure of an aptamer. We propose that if the constant regions are intimately involved in the aptamer structure, then the random region will fold very differently in the presence of constant regions than in their absence. As an example, Fig. 1 shows an aptamer sequence in which the random region (in black) folds into the same shape regardless of whether it is flanked by true constant regions, randomized constant regions, or no constant regions whatsoever.
We therefore measured the Hamming distances between the secondary structures of aptamer random regions folded with constant regions and the secondary structures of the aptamer random regions folded without constant regions. We refer to this structural difference as the ‘participation’ of the constant regions. We express participation relative to the length of the random regions, to permit comparison across the range of pool sizes. For example, if the participation is 0.50, this means that 50% of the positions in an aptamer’s random region differ when the random region is folded alone relative to when it is folded in the presence of its constant regions.
As a control, we randomized the constant regions 1000 times for each aptamer, preserving the base composition of each constant region. We then measured the difference between the secondary structures of the random regions folded in the presence of the randomized constant regions and the secondary structures of the random regions folded in the absence of the constant regions. We take the mean participation over the 1000 randomized constant regions as a single measurement for the participation by randomized constant regions, and use this value for comparison with the actual constant regions.
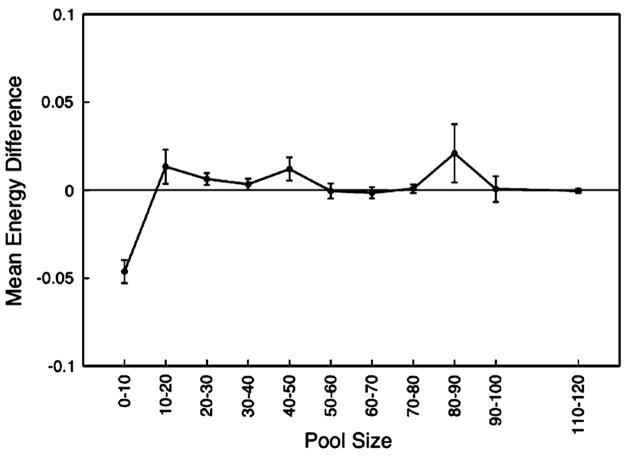
Figure 3A shows that the secondary structures calculated in the presence of constant regions generally differ from those calculated in the absence of constant regions. The mean participation by the actual constant regions (dark line, stars) ranges from approximately 0.2 to 0.5; the participation values at the upper end of this range may not be significant, however, because the longer pool sizes (at least 80 nucleotides) are represented by relatively few aptamer sequences resulting in greater error in our measurements. Constant regions generally participated more in shorter pools than in longer pools, as might be expected given that the amount of information available to form functional secondary structures is smaller in the random sequence regions of smaller pools.
Fig. 3.
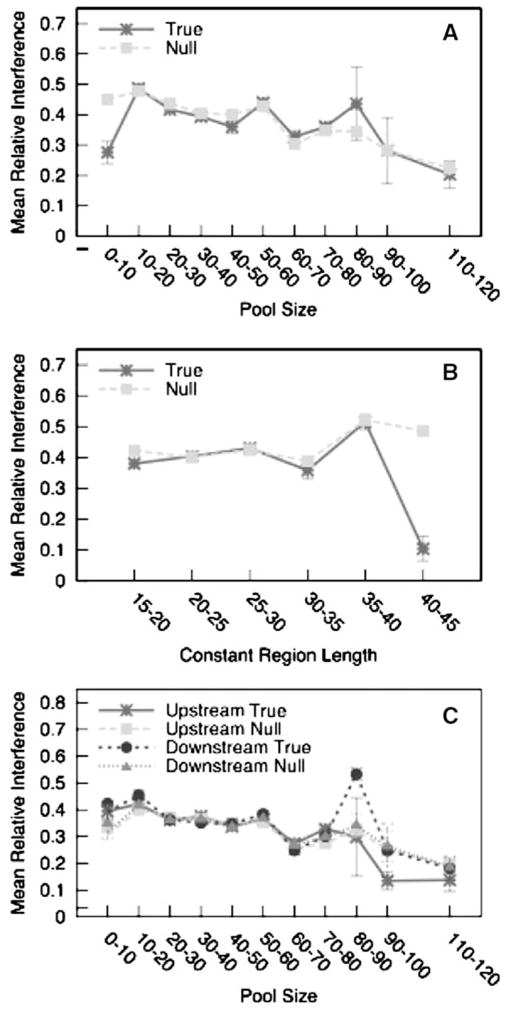
The relative interference caused by constant regions (A) over the range of pool sizes, (B) across the range of constant region sizes, and (C) by the individual constant regions. In (A) and (B), the dark lines (stars) show the interference caused by the true constant regions, whereas the light lines (squares) show the interference from randomized constant regions. In (C), the dark lines (stars, circles) depict the interference caused by the true constant regions, and the light lines (squares, triangles) depict interference caused by randomized constant regions. We normalized the distance to the length of the random region to facilitate comparison across the range of pool sizes. Error bars depict one standard error about the mean
Interestingly, though, the observed participation by true constant regions was typically no greater than that of the randomized constant regions (gray line, squares) (Fig. 3A). The sole exceptions were in the shortest pools (0–10 residues in length) and perhaps in pools whose random regions were 40–50 residues long. In both of these cases, the randomized constant regions counter intuitively appeared to participate more in the aptamer structures than did the true constant regions. To the extent that these exceptions are real, the alternative explanation is obviously that the random regions have evolved to avoid interference by the constant regions in their functional structures, rather than to utilize their constant regions to form functional structures.
In greater detail, across the range of constant region lengths, the effect of the constant regions was found to be relatively consistent, with the exception of the longest and shortest constant regions (Fig. 3B). At these two extremes, it again appears as though the aptamers fold in a manner that buffers their structures against interference from the constant regions. We note, however, that this apparent phenomenon may merely reflect a deviation from the norm due to the relatively small numbers of aptamers that have individual constant regions 40–45 nucleotides long.
Contributions by Individual Constant Regions
While overall there does not appear to be significant participation by constant regions in aptamer structures, it was possible that a more detailed analysis would reveal interactions that were missed in evaluating the data as a whole. To this end, we investigated whether either the 5′ or the 3′ constant regions participated more in functional aptamer structures. Our approach was similar to that described above, in that we measured the amount of structural difference between the random regions folded alone and the random regions folded with one or the other of the two constant regions. We compared the participation by the true constant regions to that caused by randomized constant regions (preserving base composition). Figure 3C suggests that, on average, the random sequences do not preferentially pair with only one or another constant region.
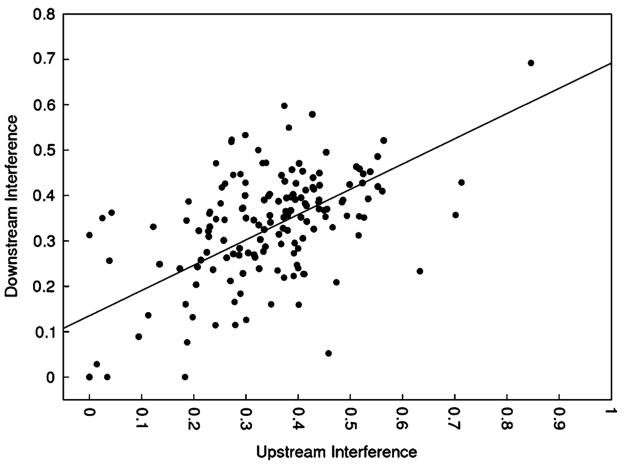
In Fig. 4, we plot the participation of upstream (5′) constant regions as a function of the participation of the downstream (3′) constant regions. The relationship between these two measurements appears to be linear (r2 = 0.38, p < 2.2 × 10−16). Interestingly, the slope of the regression line is 0.55 (p < 2.2 × 10−16), which suggests that the upstream constant regions participate roughly twice as much in functional structures as the downstream constant regions. In contrast, when this comparison is made using randomized constant regions, the correlation is 0.81, much closer to the unbiased value of 1.0 (not shown).
Fig. 4.
A regression of upstream constant region-induced interference on downstream constant region-induced interference. The slope of the regression line is 0.55 (p < 2.2 × 10−16)
The finding that the two constant regions differentially participate in aptamer structure would at first glance seem to contradict the finding that the true constant regions participate no more than do randomized constant regions. To explain this apparent discrepancy, we examined the sequence compositions of the constant regions. Interestingly, we found that the upstream constant regions were significantly enriched in the fraction of guanosine and adenosine residues relative to the downstream constant regions. The most significant enrichment was in the fraction of guanosine (29.5% upstream vs 24.5% downstream). Guanosine forms the most stable base-pair stacking interactions of any of the four nucleotides, and therefore it most powerfully affects the formation of RNA secondary structures, irrespective of whether it is found in a true or randomized constant region. The enriched guanosine fraction in the upstream constant regions significantly increases the likelihood of forming continuous purine stacks, which are significantly more stable than stacks composed of both purines and pyrimidines (Mathews et al. 1999), and are therefore favored by the folding algorithms.
Effect of Random Sequences on Predicted Aptamer Stabilities
Thermodynamic stability is an important property of the secondary structures of functional RNAs because it helps determine their robustness to the environment and mutation (Ancel and Fontana 2000; Meyers et al. 2004). In the previous section, we showed that constant regions exerted minimal effects on the secondary structures of aptamer sequences. We now turn our attention to the thermodynamic stabilities of the aptamer structures formed by the random regions themselves.
We measured the thermodynamic stability of an aptamer structure using the Boltzmann probability of the ground-state shape. The Boltzmann probability is an approximate measure of the fraction of time an aptamer sequence spends folded into a particular shape (Ancel and Fontana 2000). The ground-state structure always has the largest Boltzmann probability of any shape a sequence may assume. This probability can be small, however, in which case an RNA molecule is not expected to stably fold into its ground-state shape. On the other hand, if the Boltzmann probability of a sequence’s ground-state shape is large, then that sequence is expected to stably assume its ground-state shape most of the time.
We measured the Boltzmann probability of each complete aptamer sequence, as described under Materials and Methods. We compared the “true” Boltzmann probability to the Boltzmann probabilities of 100 sequences in which the random region was shuffled, preserving base composition. Specifically, we calculated the mean difference between the Boltzmann probability of the true aptamer sequence and the Boltzmann probabilities of the 100 randomized sequences. If the mean difference should turn out to be small, this would suggest that the random regions do not significantly contribute to the overall thermostabilities of aptamer structures. If the difference should turn out to be large, this means that the particular sequences of the selected random regions may be significantly stabilizing (or destabilizing).
Surprisingly, Fig. 5 shows that, across the range of pool sizes, the random regions generally do not significantly contribute to the thermostability of the aptamer structures. The mean differences among the Boltzmann probabilities differ on average by only approximately 0.5%. The possible exception occurs in the shortest random regions, which appear to exert a significant destabilizing effect on aptamers. Combined with the fact that constant regions appear to participate more in the secondary structures of aptamers derived from short random regions (above), this again means that functional secondary structures for aptamers derived from short random regions are produced by a collaboration between random and constant regions.
Fig. 5.
Contribution of random regions to thee thermostability of aptamer structures. The Boltzmann probability of the ground-state structure for each true aptamer is compared to the Boltzmann probabilities of 100 sequences in which the random region is shuffled. Data points below the zero line represent aptamers in which the randomized sequences are more thermostable, on average, than the true aptamer sequences. Error bars depict one standard error about the mean
Discussion
We have carried out a bioinformatic analysis of the effects of constant regions on the formation of functional secondary structures in selected nucleic acid aptamers. To perform this study, we relied on the Aptamer Database, which currently offers the largest compiled and curated set of aptamer sequences (Lee et al. 2004). Our study included more than 2000 different aptamer sequences selected to bind 141 unique ligands.
Our results show that, in general, aptamers are not particularly dependent on their constant regions to assume functional structures. Our results also suggest that the selected sequences are not, on average, of greater (or lesser) thermostability than shuffled versions of the selected sequences. These results agree with our previous observations, which show that aptamers do not evolve significant thermostability (Meyers et al. 2004).
The finding that, over many different aptamers, the constant regions seem to contribute little to functional aptamer structures is quite surprising. It has previously been both hypothesized (Jhaveri et al. 1997; Sabeti et al. 1997) and shown experimentally (Bartel and Szostak 1993; Salehi-Ashtiani and Szostak 2001; Legiewicz et al. 2005) that short, functional motifs will readily emerge from selection experiments, a tendency that has been dubbed “the tyranny of short motifs” (Jhaveri et al. 1997; Ellington et al. 2000). To the extent that this hypothesis is true, then it is reasonable to speculate that constant regions should frequently play a role in the formation of functional aptamer secondary structures, as the participation of constant regions would greatly favor shorter, less information-rich random tracts during selection. Indeed, it has previously been noted that antiarginine aptamers selected from short random sequence pools (25 random sequence positions) relied heavily on their constant regions for structure and function (Connell et al. 1993; Ellington et al. 2000). In addition, studies in which anti-isoleucine aptamers were selected from a variety of pool lengths (Lozupone et al. 2003 Lozupone et al. 2005) found greater participation of constant regions in the structures of those aptamers isolated from pools with fewer random sequence positions. Even aptamers selected from longer pools (50 random sequence positions) can sometimes utilize their constant regions for structure formation (Majerfeld and Yarus 1998).
There are several explanations for why constant regions do not seem to more generally participate in aptamer structures. The most obvious reason is that the most functional aptamer sequences and structures in a population will only rarely require the arbitrary sequence provided by a constant region. The plethora of information-poor structures formed with constant regions does not in general predominate over the information-rich structures formed from random regions alone. On this basis, it can be inferred that the information-rich structures are more functional, and thus that directed evolution experiments in general avoid the previously predicted ‘tyranny of short motifs.’ Another possibility (that does not require speculation as to the relative functional capacities of aptamers with different information contents) is that constant regions may only be able to participate in a limited number of structural motifs because they are located at the ends of the aptamers.
A more mechanistic explanation for why constant regions do not participate in aptamer structures stems from their role in amplification. Typically aptamers are amplified by molecular biology methods, which require that oligonucleotide primers bind to the constant regions. Aptamers in which the random region strongly interacts with the constant region may therefore be at a selective disadvantage for primer binding and amplification. Over multiple rounds of selection and amplification, this selective disadvantage in fecundity might overshadow any selective advantages due to numerical representation in the population or any functional advantages due to the ready formation of stable aptamer secondary structures. Interestingly, Legiewicz et al. (2005) found that more structured constant regions gave rise to fewer antileucine aptamers than less structured constant regions, and attributed this to the statistical underrepresentation of a common aptamer motif in pools with the more structured constant regions. However, the disparity predominated at all pool sizes, contradicting purely statistical predictions which suggested that both unstructured and structured constant regions should readily yield the isoleucine-binding motif at pool lengths of ≥50. The simplest explanation for the latter result is that the aptamers with the structured constant regions (and therefore structured primers) were more difficult to amplify and, thus, led to a decrease in the probability of finding aptamers in pools of any length.
Furthering this analysis, it can be argued not only that constant regions do not participate in aptamer structures, but that selected aptamers actively avoid interference by their constant regions. There is some anecdotal information to support this hypothesis. Bartel and coworkers found that extending previously selected ribozymes with a longer, random sequence region resulted in a general depression of activity (Sabeti et al. 1997). When individual clones from these extended libraries were examined the median depression was approximately fivefold. Similarly, Burke and coworkers found that extending selected aptamers with new constant regions resulted in a general depression of activity. When thioester-synthesizing ribozymes were selected from a mixture of pools, the longer pools were at a large competitive disadvantage relative to shorter pools in terms of both replication and misfolding (Coleman and Huang 2002, 2005). While the latter study did not explicitly examine the impact of constant regions, it nonetheless speaks to the potential for sequences outside of a selected motif to interfere with function.
Our results have interesting implications for the nature of nucleic acid fitness landscapes and perhaps for the evolution of a putative RNA world. Fitness landscapes can be inferred to be relatively rugged, with information-rich peaks functionally differentiated from information-poor regions. However, the functional peaks are not so rare as to be unobtainable even in typical selection experiments in which the random sequence library does not fully encompass the available sequence space. While it is of course difficult to generalize these results to natural selection, given that the relative complexity, length, and functionality of sequences in a putative RNA world are unknown, it can nonetheless be speculated that the early, short, and abundant functional motifs may not have greatly constrained the later evolution of longer, more functional RNAs with entirely different sequences. Studies have suggested that extensive neutral paths can greatly facilitate evolution from abundant initial motifs to less common, functionally superior RNA structures (Schuster et al. 1994).
Our results also have useful implications for biotechnology. The fact that constant regions do not feature prominently in overall aptamer structures greatly simplifies issues of pool and primer design. Almost any primer sequences (and corresponding constant regions) that are generally suitable for PCR are predicted not to interfere unduly with the probability of aptamer selection or with the functions of selected aptamers.
References
- Ancel L, Fontana W. Plasticity, modularity and evolvability in RNA in vitro. Exp Zool. 2000;288:242–283. doi: 10.1002/1097-010x(20001015)288:3<242::aid-jez5>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Bartel DP, Szostak JW. Isolation of new ribozymes from a large pool of random sequences. Science. 1993;261:1411–1417. doi: 10.1126/science.7690155. [DOI] [PubMed] [Google Scholar]
- Carothers JM, Oestreich SC, Davis JH, Szostak JW. Informational complexity and functional activity of RNA structures in vitro. Am Chem Soc. 2004;126:5130–5137. doi: 10.1021/ja031504a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coleman TM, Huang F. RNA-catalyzed thioester synthesis. Chem Biol. 2002;9:1227–1236. doi: 10.1016/s1074-5521(02)00264-8. [DOI] [PubMed] [Google Scholar]
- Coleman TM, Huang F. Optimal random libraries for the isolation of catalytic RNA. RNA Biol. 2005;2:129–136. doi: 10.4161/rna.2.4.2285. [DOI] [PubMed] [Google Scholar]
- Connell GJ, Illangesekare M, Yarus M. Three small ribooligonucleotides with specific arginine sites. Biochemistry. 1993;32:5497–5502. doi: 10.1021/bi00072a002. [DOI] [PubMed] [Google Scholar]
- Davidson EA, Ellington AD. Engineering regulatory RNAs. Trends Biotechnol. 2005;23:109–112. doi: 10.1016/j.tibtech.2005.01.006. [DOI] [PubMed] [Google Scholar]
- Dey AK, Griffiths C, Lea SM, James W. Structural characterization of an anti-gp120 RNA aptamer that neutralizes R5 strains of HIV-1. RNA. 2005;11:873–884. doi: 10.1261/rna.7205405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doudna JA. Structural genomics of RNA. Nature Struct Biol. 2000;7:954–956. doi: 10.1038/80729. [DOI] [PubMed] [Google Scholar]
- Ellington AD. RNA selection. Aptamers achieve the desired recognition. Curr Biol. 1994;4:427–429. doi: 10.1016/s0960-9822(00)00093-2. [DOI] [PubMed] [Google Scholar]
- Ellington AD, Szostak JW. In vitro selection of RNA molecules that bind specific ligands. Nature. 1990;346:818–822. doi: 10.1038/346818a0. [DOI] [PubMed] [Google Scholar]
- Ellington AD, Khrapov M, Shaw CA. The scene of a frozen accident. RNA. 2000;6:485–498. doi: 10.1017/s1355838200000224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gevertz J, Gin HH, Schlick T. In vitro RNA random pools are not structurally diverse: a computational analysis. RNA. 2005;11:853–863. doi: 10.1261/rna.7271405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall B, Hesselberth JR, Ellington AD. Computational selection of nucleic acid biosensors via a slip structure model. Biosens Bioelectron. 2007;22:1939–1947. doi: 10.1016/j.bios.2006.08.019. [DOI] [PubMed] [Google Scholar]
- Hofacker IF, Fontana W, Stadler BF, Bonhoeffer S, Tacker M, Schuster P. Fast folding and comparison of RNA secondary structures. Monatshefte Chemie. 1994;125:167–188. [Google Scholar]
- Huang Z, Szostak JW. Evolution of aptamers with a new specificity and new secondary structures from an ATP aptamer. RNA. 2003;9:1456–1463. doi: 10.1261/rna.5990203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes RA, Robertson MP, Ellington AD, Levy M. The importance of prebiotic chemistry in the RNA world. Curr Opin Chem Biol. 2004;8:629–633. doi: 10.1016/j.cbpa.2004.09.007. [DOI] [PubMed] [Google Scholar]
- Isaacs FJ, Dwyer DJ, Collins JJ. RNA synthetic biology. Nature Biotechnol. 2006;24:545–554. doi: 10.1038/nbt1208. [DOI] [PubMed] [Google Scholar]
- Jhaveri SD, Hirao I, Bell S, Uphoff KW, Ellington AD. Landscapes for molecular evolution: lessons from in vitro selection experiments with nucleic acids. Annu Rep Comb Chem Mol Divers. 1997;1:169–191. [Google Scholar]
- Joyce GF. RNA structure: ribozyme evolution at the crossroads. Science. 2000;289:401–402. doi: 10.1126/science.289.5478.401. [DOI] [PubMed] [Google Scholar]
- Joyce GF. Directed evolution of nucleic acid enzymes. Annu Rev Biochem. 2004;73:791–836. doi: 10.1146/annurev.biochem.73.011303.073717. [DOI] [PubMed] [Google Scholar]
- Kim N, Gan HH, Schlick T. A computational proposal for designing structured RNA pools for in vitro selection of RNAs. RNA. 2007;13:478–492. doi: 10.1261/rna.374907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight R, Yarus M. Analyzing partially randomized nucleic acid pools: straight dope on doping. Nucleic Acids Res. 2003;31:e30. doi: 10.1093/nar/gng030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JF, Hesselberth JR, Meyers LA, Ellington AD. Aptamer Database. Nucleic Acids Res. 2004;32:D95–D100. doi: 10.1093/nar/gkh094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JF, Stovall GM, Ellington AD. Aptamer therapeutics advance. Curr Opin Chem Biol. 2006;10:282–289. doi: 10.1016/j.cbpa.2006.03.015. [DOI] [PubMed] [Google Scholar]
- Legiewicz M, Lozupone C, Knight R, Yarus M. Size, constant sequences, and optimal selection. RNA. 2005;11:1701–1709. doi: 10.1261/rna.2161305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lozupone C, Changayil S, Majerfeld I, Yarus M. Selection of the simplest RNA that binds isoleucine. RNA. 2003;9:1315–1322. doi: 10.1261/rna.5114503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majerfeld I, Yarus M. Isoleucine: RNA sites with associated coding sequences. RNA. 1998;4:471–478. [PMC free article] [PubMed] [Google Scholar]
- Mathews DH, Sabina J, Zuker M, Turner DH. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure in vitro. Mol Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- McCaskill JS. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1109. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
- Meyers LA, Lee JF, Cowperthwaite MC, Ellington AD. The robustness of naturally and artificially selected nucleic acid secondary structures in vitro. Mol Evol. 2004;58:618–625. doi: 10.1007/s00239-004-2590-2. [DOI] [PubMed] [Google Scholar]
- Patzel V. In silico selection of functional RNA molecules. Curr Opin Drug Disc Dev. 2004;7:360–369. [PubMed] [Google Scholar]
- Sabeti PC, Unrau PJ, Bartel DP. Accessing rare activities from random RNA sequences: the importance of the length of molecules in the starting pool. Chem Biol. 1997;4:767–774. doi: 10.1016/s1074-5521(97)90315-x. [DOI] [PubMed] [Google Scholar]
- Salehi-Ashtiani K, Szostak JW. In vitro evolution suggests multiple origins for the hammerhead ribozyme. Nature. 2001;414:82–84. doi: 10.1038/35102081. [DOI] [PubMed] [Google Scholar]
- Sayer NM, Cubin M, Rhie A, Bullock M, Tahiri-Alaoui A, James W. Structural determinants of conformationally selective, prion-binding aptamers. J Biol Chem. 2004;279:13102–13109. doi: 10.1074/jbc.M310928200. [DOI] [PubMed] [Google Scholar]
- Schultes EA, Bartel DP. One sequence, two ribozymes: implications for the emergence of new ribozyme folds. Science. 2000;289:448–452. doi: 10.1126/science.289.5478.448. [DOI] [PubMed] [Google Scholar]
- Schuster P, Fontana W, Stadler P, Hofacker I. From sequences to shapes and back: a case study in RNA secondary structures. Proc Roy Sci Lond B. 1994;255:279–284. doi: 10.1098/rspb.1994.0040. [DOI] [PubMed] [Google Scholar]
- Tuerk C, Gold L. Systematic evolution of ligands by exponential enrichment: RNA ligands to bacteriophage T4 DNA polymerase. Science. 1990;249:505–510. doi: 10.1126/science.2200121. [DOI] [PubMed] [Google Scholar]
- Ulrich H. RNA aptamers: from basic science towards therapy. Handbk Exp Pharmacol. 2006;173:305–326. doi: 10.1007/3-540-27262-3_15. [DOI] [PubMed] [Google Scholar]
- Wuchty S, Fontana W, Hofacker IL, Schuster P. Complete suboptimal folding of RNA and the stability of secondary structures. Biopolymers. 1999;49:145–165. doi: 10.1002/(SICI)1097-0282(199902)49:2<145::AID-BIP4>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- Zuker M. On finding all suboptimal foldings of an RNA molecule. Science. 1989;244:48–52. doi: 10.1126/science.2468181. [DOI] [PubMed] [Google Scholar]
- Zuker M, Stiegler P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 1981;9:133–148. doi: 10.1093/nar/9.1.133. [DOI] [PMC free article] [PubMed] [Google Scholar]