The Ability of Actinic Light To Modify the Bacteriorhodopsin Photocycle Revisited: Heterogeneity vs Photocooperativity^,

Abstract

In 1995, evidence both for photocooperativity and for heterogeneity as possible explanations for the ability of actinic light to modify the kinetics and pathways of the bacteriorhodopsin (BR) photocycle was reviewed (Shrager, R. I., Hendler, R. W., and Bose, S. (1995) Eur. J. Biochem. 229, 589–595). Because both concepts could be successfully modeled to experimental data and there was suggestive published evidence for both, it was concluded that both photocooperativity and heterogeneity may be involved in the adaptation of the BR photocycle to different levels of actinic light. Since that time, more information has become available and it seemed appropriate to revisit the original question. In addition to the traditional models based on all intermediates in strict linear sequences, we have considered both homogeneous and heterogeneous models with branches. It is concluded that an explanation based on heterogeneity is more likely to be the true basis for the variation of the properties of the photocycle caused by changes in actinic light intensity. On the basis of new information presented here, it seems that a heterogeneous branched model is more likely than one with separate linear sequences.

A long standing observation, that the photocycle of bacteriorhodopsin is markedly altered by the strength of actinic light, has not been adequately explained (1). The initial and primary illustration of the phenomenon is that the fraction of M-fast (M_f) to total M (M_tot) starts high at low laser pulse strength and smoothly decreases with increasing strength (2). In addition, M_f decays through the N and O intermediates to BR,¹ whereas M-slow (M_s) does not (3,4). For the 25 years since Ohno clearly demonstrated the ability of light to regulate the ratio of M_f/M_s, there have been two different possible explanations for the phenomenon. One, based on a homogeneous photocycle and photocooperativity, proposes that the fundamental target, a trimer of BR molecules, when hit by a single photon decays through the M_f route, whereas when two or three photons strike the target, decay includes the M_s route. The other explanation proposes that there are different ground states (BR) that proceed through different photocycles. Recently (4), one of us (R.W.H.) reviewed evidence published both prior to and since the earlier review on the question of a photocooperative-homogeneous vs heterogeneous parallel cycles. A group of publications were cited which could be explained by parallel photocycles but not by single homogeneous cycles. Evidence for the existence of different ground states was presented. Minimal criteria were specified that should be met before any proposed kinetic model be seriously considered. The model must provide a solution to the equation A = DY, where D is a matrix containing all absolute spectra for the intermediates and Y is a matrix containing time courses for each component in D. The time courses in Y are made up of a mixture of all of the exponentials involved in each discrete transition specified by the model. Rate constants for these exponentials must be provided, and when the model is expressed using a Jacobian matrix J, that J must yield eigenvalues which equal the observed kinetic macro constants obtained by fitting exponentials to the experimental data. When the matrix D is obtained from the raw data by the operation D = A/Y, where /Y is the pseudo inverse of Y, the derived absolute spectra must correspond to those found in other laboratories using independent procedures. Parallel cycle models were shown to meet all of these criteria under nine different combinations of temperature and pH. In contrast, not a single proposed photocooperative–homogeneous model has yet been shown to do the same.

At neutral pH and T near 20 °C, two different cycles have been identified (3,4).

$$\begin{array}{l}\text{BR}\to {\text{L}}_{\text{f}}\to {\text{M}}_{\text{f}}\to \text{N}\to \text{O}\to \text{BR}\\ \text{BR}\to {\text{L}}_{\text{s}}\to {\text{M}}_{\text{s}}\to \text{BR}\end{array}$$

It is important to resolve the issue and define precisely the steps in the photocycle(s?) in order to link the electrogenic steps of proton transport to specific transitions between known intermediates. In 1995, two of the current authors (R.I.S. and R.W.H.) concluded that both possibilities could be successfully mathematically modeled and that there was evidence that could be interpreted in favor of both (1). At the time, it appeared that perhaps both cooperativity and heterogeneity may be involved in the adaptation of the photocycle to actinic light.

Now, almost 12 years later, in the face of additional information (briefly summarized above), and with newer, more extensive experimental data (included here) we are able to arrive at a more definitive resolution of the issue, namely, that a model based on heterogeneity is more likely to be true than one based on homogeneity and photocooperativity.

EXPERIMENTAL PROCEDURES

1. Preparation of Purple Membrane (PM)

PM was isolated from the ET1001 strain of Halobacterium salinarum by the procedure of Oesterhelt and Stoeckenius (5) as modified by Mukhopadhyay et al. (6). For kinetic studies, 0.5 mg of BR in PM was suspended in 3 mL of 50 mM potassium buffer at pH 7.2 and 21 °C. The container was a 4 cm × 1 cm × 1 cm clear plastic optical cuvette.

2. Optical Data Collection

Time-resolved multichannel data were collected as previously described (7). Light adaptation was obtained and maintained by constant illumination from the monitoring light source operated at 80 mW (Proton Technology International (PTI) 75 W xenon arc lamp model A1010, powered by a PTI LPS 220). There was no evidence of any significant amount of dark-adapted photocycle, such as the peak for BR being blue-shifted or the presence of an intermediate with a decay time constant near 30 ms. The fitted kinetic constants we obtained are in agreement with those published in the literature by other laboratories (8–11). Actinic photostimulation of the sample was achieved by directing the 532 nm second harmonic output of a single selected pulse (5 ns at 10 pulses per second) from a Continuum SureLite I, 10 Hz, Nd:YAG laser through a series of lenses and filters to the sample at right angles from the monitoring light beam. Repetition rates for successive cycles were at 0.2 Hz (i.e., every 5 s). With a 1.11 kV setting, the laser delivered 29 mJ to a 2 cm² surface of the optical cuvette at a right angle to the monitoring beam. Neutral density (ND) filters with nominal absorbances of 0.2, 0.5, 1.0, and 1.5 A, calibrated for their transmissions at 532 nm were used to attenuate the strength of the laser. For the next-to-highest laser strength, no ND filter was used at the 1.11 kV generated laser pulse. The highest intensity laser pulse (49 mJ) was obtained at a 1.20 kV setting of the laser. The table below shows the mJ irradiation per 2 cm² and the corresponding number of turnovers averaged. One turnover is the completion of a full photocycle initiated by a laser flash. The number of turnovers was increased as the strength of the laser was decreased and also for the two highest laser strengths in order to better establish the plateau level for maximum turnover.

mJ	turnovers
1.2	300
3.5	150
9.9	100
17.7	100
29	200
49	200

3. Optical Data Analysis

A. Determination of Kinetic Constants

The column space of the raw data matrix contains spectra taken at different times while the row space contains amplitudes for absorbance at each wavelength as a function of time. The singular (orthonormal) eigenvectors of the column space were separated, in a matrix U, from the corresponding row space vectors, in a matrix V^T, by singular value decomposition (12) (SVD). The first five vectors of the V-matrix were determined to contain all of the relevant kinetic information. It is important to note that the individual V-vectors do not correspond to individual kinetic constants and that they each contain kinetic information contributed by all of the kinetic constants present. These were simultaneously fitted to the six kinetic constants known to be present in the photocycle at pH near 7 and temperature near 20 °C (3, 4). Table 1 shows statistics for fitting these data as well as quality-of-fit criteria which includes standard errors as well as dependency values which guard against using more than the minimum number of exponentials (13). The possible presence of superfluous exponentials is indicated by dependency values >10.

Table 1.

Statistics of Fitting^a

laser mJ [ ]b	k (ms−1)	error (ms−1)	dependency	tau (ms)
49 [100]	8.8429e1	2.7799e0	1.2026e0	1.1308e–2
	1.4685e1	3.1963e–1	2.3928e0	6.8097e–2
	4.3393e0	4.2349e–1	5.8882e0	2.3045e–1
	3.17789e0	2.8463e–1	5.1584e0	3.1457e–1
	4.8610e–1	1.9553e–3	1.4634e0	2.0572e0
	2.1259e–1	2.8190e–4	1.1779e0	4.7039e0
49 [100]	9.4224e1	3.5690e0	1.2211e0	1.0613e–2
	1.5505e1	3.7743e–1	2.5031e0	6.4497e–2
	5.1153e0	2.5066e–1	3.5972e0	1.9549e–1
	2.7423e0	1.1898e–1	2.7566e0	3.6465e–1
	4.8307e–1	1.9449e–3	1.4864e0	2.0701e0
	2.1495e–1	2.8470e–4	1.1964e0	4.6523e0
29 [100]	9.1284e1	2.8195e0	1.2261e0	1.0955e–2
	1.4460e1	2.9735e–1	2.4893e0	6.8214e–2
	4.6460e0	2.7468e–1	4.2485e0	2.1524e–1
	2.8514e0	1.4562e–1	3.4660e0	3.5070e–1
	4.8256e–1	1.7857e–3	1.5037e0	2.0723e0
	2.1628e–1	2.6377e–4	1.1924e0	4.6236e0
29 [100]	9.5425e1	3.0105e0	1.2160e0	1.0479e–2
	1.4788e1	2.8584e–1	2.4767e0	6.7623e–2
	4.8965e0	1.5745e–1	3.2463e0	2.0423e–1
	2.4364e0	7.4879e–2	2.4219e0	4.1044e–1
	4.4054e–1	1.5405e–3	1.4986e0	2.2699e0
	1.9730e–1	2.2568e–4	1.2014e0	5.0684e0
17.7 [100]	9.9408e1	4.9492e0	1.2562e0	1.0060e–2
	1.6084e1	4.5855e–1	2.5086e0	6.2175e–2
	5.6684e0	1.9148e–1	2.8387e0	1.7642e–1
	2.2849e0	7.1768e–2	2.0986e0	4.3766e–1
	4.6937e–1	2.1338e–3	1.5456e0	2.1305e0
	2.1004e–1	3.0801e–4	1.1825e0	4.7611e0
9.9 [100]	8.7493e1	2.4350e0	1.2187e0	1.1429e–2
	1.4259e1	2.6437e–1	2.4263e0	7.0132e–2
	3.9970e0	3.0559e–1	5.6502e0	2.5019e–1
	2.7987e0	1.9688e–1	4.8647e0	3.5731e–1
	4.6086e–1	1.8026e–3	1.4976e0	2.1698e0
	2.1832e–1	3.1676e–4	1.2523e0	4.5805e0
3.5 [150]	8.6413e1	2.4525e0	1.2241e0	1.1572e–2
	1.3507e1	2.3345e–1	2.3487e0	7.4033e–2
	3.3459e0	4.5574e–1	8.8950e0	2.9888e–1
	2.7029e0	3.4553e–1	8.2116e0	3.6997e–1
	4.5829e–1	2.0708e–3	1.5206e0	2.1820e0
	2.2540e–1	4.2307e–4	1.3091e0	4.4365e0
1.9 [300]	1.0774e2	1.4924e1	1.2808e0	9.2818e–3
	1.7044e1	9.9961e–1	2.4936e0	5.8672e–2
	5.7043e0	2.7446e–1	2.5834e0	1.7531e–1
	1.5640e0	7.8352e–2	2.0305e0	6.3939e–1
	4.7584e–1	5.5495e–3	1.7205e0	2.1015e0
	2.2981e–1	1.0045e–3	1.2872e0	4.3514e0

^aThe numbers are presented in exponential notation where the digit following e designates the power of 10. For example, 1e1 is 10 and 1e–1 is 0.1.

^b[ ] designates the number of single turnovers used for the error analysis.

B. Determination of Amounts of M_f and M_s

From the exponential time course described by each fitted kinetic constant, one can obtain the unique, associated transitional difference spectrum. For example, the difference spectrum for the M_f transition shows the loss of the spectrum for M accompanied by the rise of the spectrum for O, whereas the difference spectrum for the M_s transition shows the loss of M accompanied by a rise in BR (7). The M-intermediate has a characteristic peak absorbance near 412 nm. The changes in absorbances for the wavelength range from 400 to 429 nm were fitted to a cubic polynomial, and the amplitude at the wavelength nearest to 412 nm was taken as the amount of M which turned over during the photocycle. It has been established that at pH near 7 and temperature near 20 °C, M_f disappearance occurs in the transition with tau near 2 ms and that M_s disappearance occurs during the transition with tau near 5 ms (3, 4). Table 2(Results) shows the fitted changes in absorbance for both M-intermediates at all levels of laser intensity, as well as the absorbance of the data point at the same wavelength, and the standard errors.

Table 2.

Amounts of M_f and M_s Turning Over

laser mJ [ ]a	M	fitted valueb (OD)d	actual value (OD)d	errorc (OD)d
49 [100]	Mf	2.3104e–2	2.3087e–2	4.0465e–5
	Ms	3.0395e–2	3.0128e–2	8.2184e–5
49 [100]	Mf	2.3795e–2	2.37991e–2	3.7668e–5
	Ms	3.0915e–2	3.0633e–2	8.6689e–5
29 [100]	Mf	2.1648e–2	2.1630e–2	5.9365e–5
	Ms	2.7609e–2	2.7363e–2	8.6794e–5
29 [100]	Mf	2.1807e–2	2.1788e–2	4.6648e–5
	Ms	2.8837e–2	2.8586e–2	8.1184e–5
17.7 [100]	Mf	2.0529e–2	2.0517e–2	3.2833e–5
	Ms	2.3915e–2	2.3692e–2	6.7274e–5
9.9 [100]	Mf	1.8115e–2	1.8103e–2	3.8129e–5
	Ms	1.8791e–2	1.8611e–2	5.6760e–5
3.5 [150]	Mf	1.2001e–2	1.2011e–2	1.5898e–5
	Ms	9.0985e–3	8.9872e–3	3.1633e–5
1.9 [300]	Mf	6.1405e–3	6.1560e–3	3.2518e–5
	Ms	3.5891e–3	3.5329e–3	2.33291e–5

^a[ ] designates the number of single turnovers used for the error analysis.

^bValues obtained by fitting to a 4th degree polynomial as described above.

^cStandard error for the data point near 412 nm.

^dThe numbers are optical density changes in absorbance units.

C. Determination of Monomers per Trimer That Cycle

If 100% of the total BR turns over, then all 3 monomers per trimer are cycling. If only 1 monomer per trimer can cycle, then 33% of the total BR turns over. All of the BR which turns over is recovered in the transitions that occur with a tau near 5 ms (3, 4). This includes the decays of both O and M_s intermediates to the ground state. The positive absorbance change that is seen for the isolated BR component in this transition difference spectrum, obtained from SVD-based least-squares, provides us with the absorbance value for BR that has cycled. In order to express this in terms of the percent of turnover, we must obtain an accurate value for the total absorbance for all of the BR that is present. When BR is present in a water suspension of PM, there is no aggregation and light scattering is at a minimum. The amount of apparent absorption due to scattering steadily decreases with increasing wavelength and reaches zero at wavelengths close to 700 nm. The extinction coefficient at near 570 nm is 63000 M⁻¹ cm⁻¹ (14). But even this extinction coefficient contains some contribution from light-scattering. In buffer, aggregation of the PM fragments is enhanced so that more of the measured absorbance is due to light-scattering. If not corrected for, there will be an overestimation of total BR and an underestimation of the percent turnover. The value obtained for BR turnover from the SVD-derived transition difference spectrum is totally free of light-scattering because only time-related changes are recorded and the light-scattering background is constant. Another possible cause for error in a single beam spectrophotometer is that the cuvette for the blank and the cuvette for the sample may not be perfectly matched. In a split-beam spectrophotometer, it is possible to counteract any such imbalance electronically. We have been able to correct both for any possible contributions from light-scattering and for offsets to the baseline. Our spectrophotometer consists of two separate spectrometers, each containing 46 diodes. One is normally set to cover the region from 391 to 521 nm, and the other covers the region 541 to 675 nm. This allows good coverage for all of the intermediates in the photocycle and provides a gap from 521 to 541 nm to protect the photodiodes from oversaturation from the 532 nm laser flash. The spectrum of ground-state BR contributes little below 440 nm. The ground-state absorbance in the wavelength range from 391 to 440 nm is due entirely to light-scattering. Our correction procedure for light-scattering requires that we obtain data in the higher wavelength region beyond the absorption spectrum for BR. To accomplish this, we acquired another spectrum with the wavelength region covered by the second spectrometer extended to cover a range up to 735 nm. We blended the extended range of the spectrum for BR with that of the spectrum that ended at 675 nm in order to obtain a full spectrum out to 735 nm. This extended spectrum labeled CBR is shown in Figure 1 (panel A). The absorption spectrum for BR is preceded and followed by regions where only light-scattering is present. Two reference wavelengths, 400 and 440 nm, delimited the low wavelength region, and two, well beyond the absorbance range of BR, at 715 and 735 nm, delimited the high wavelength region. A cubic polynomial function with four coefficients was used to connect the two extreme regions and form a continuous background curve, labeled Cbg in Figure 1 (panel A). Subtraction of Cbg from CBR produced the corrected spectrum for BR shown in Figure 1 (panel B). This correction procedure was used for the kinetic data reported in this paper in which the PM suspension was subjected to increasing levels of actinic laser energy. The spectrum labeled BR in panel C extends to a maximum wavelength of 675 nm. The Cbg spectrum shown in Figure 1 (panel A) was vertically adjusted to coincide with the light-scattering region in the low wavelength region of the acquired BR spectrum. The BR spectrum is seen to meet the high wavelength, light-scattering region of the Cbg curve in Figure 1 (panel C). Subtraction of the Cbg curve from the acquired BR curve produced the corrected BR spectrum shown in Figure 1 (panel D).

Figure 1.

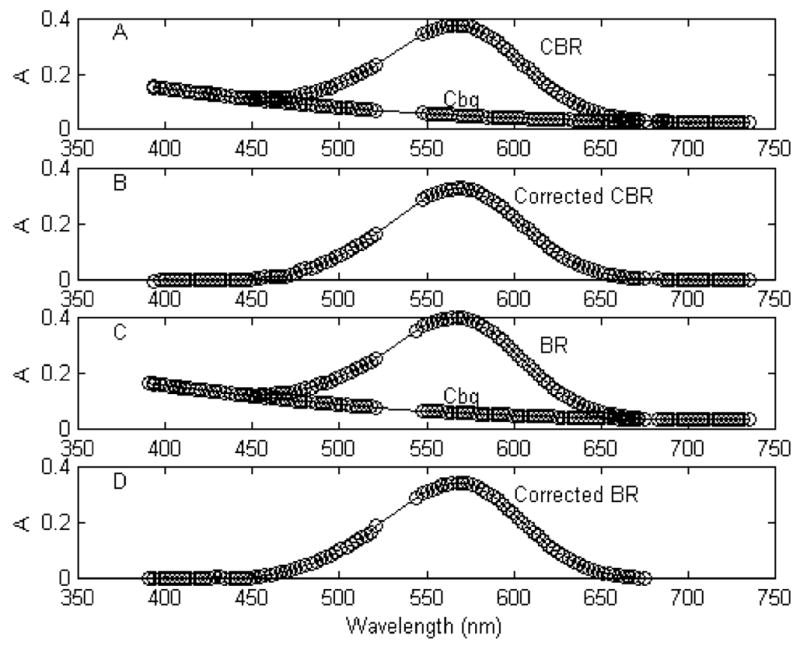
Corrections for light-scattering and offset. The curve labeled CBR in panel A comprises two wavelength anges, one from 391 to 521 nm and the other from 541 to 675 nm. The curve labeled Cbg was constructed, as described in the text, by combining the curve CBR with another spectrum for BR that extended the wavelength to 735 nm and then fitting the low and high wavelength light-scattering regions to a cubic polynomial in order to connect the two light-scattering regions. The corrected curve in panel B was obtained by subtracting Cbg from CBR. The curve labeled BR in panel C is for the BR used in the saturation data displayed in Figure 1. It contains some light-scattering and offset. The corrected curve in panel D was obtained by subtracting Cbg from BR and then for an offset of 0.0096 A. See text for further details.

The absorbance for BR at its peak wavelength before correcting for light-scattering and any offset was 0.3995. In the corrected spectrum, it was 0.3419. The light-scatter-free absorbance changes for amount of BR turnover at the highest level of laser strength were 0.1100 and 0.1143 absorbance units for the duplicate sets of data. Using the average of 0.1121, we find that turnover of BR was 33% when we use the corrected total absorbance for BR and only 28% using the uncorrected value. A turnover of 33% of the total BR corresponds to one monomer per trimer that cycles. From Table 2, we see that at the highest level of laser energy, the average absorbance changes for M_f and M_s, respectively, were 0.02345 and 0.03065 A for a total of 0.05410 A. The fractions of each M_f and M_s, relative to M_tot, were 0.4334 and 0.5665. Since only one monomer per trimer is turning over, we can conclude that an average of 0.4334 monomer of M_f and 0.5665 monomer of M_s cycled per trimer.

4. Theory for Multiple Hits on a Single Target

The equations developed here serve as the basis for evaluating the alternative, homogeneous, branched, photocooperative model presented below.

A. Discrete Projectiles

If n projectiles are fired at a field, what is the probability that a small target within the field will be hit i times? Definitions: A_F = area of the field; A_T = area of the target within the field; p = probability of a hit when n = 1; p_h = probability of one or more hits (fraction cycling); p₀ = probability of no hits; p_i = probability of exactly i hits; x = a measure of flash intensity. Assuming that any spot in the field is equally likely to be hit, a single projectile will yield

$$p=A_{\text{T}}/A_{\text{F}}\text{and}{p}_0=1-p$$

For the n-projectile case, the formulas are given by the binomial theorem:

$$\begin{array}{l}{p}_0={(1-p)}^n\text{and}{p}_{\text{h}}=1-p_0\\ p_1=np{(1-p)}^{n-1}\\ p_2=[n(n-1)/2!]p^2{(1-p)}^{n-2}\\ p_3=[n(n-1)(n-2)/3!]p^3{(1-p)}^{n-3}\end{array}$$

and, in general,

$$p_i=\{[n!/(n-i)!]/i!\}{p}^i{(1-p)}^{n-i}$$

To use fraction cycling as the independent variable, the relation for p₀ yields

$$p=1-{(1-p_{\text{h}})}^{1/n}$$

so that all p_i can be expressed and plotted in terms of p_h.

B. Continuously Variable Flash Intensity

We will now eliminate the need to know n. When the various n in our experiments are very large, e.g., the number of photons in a flash, the flash intensity is continuous for all practical purposes. This allows us to write p₀ as a function of x, a continuously adjustable intensity:

$$p_0=1-p_h=exp(-kx)$$

implying

$$kx=-log(p_0)$$

Since all n of interest are very large, we can ignore the integers being subtracted from them in the binomial formulas above, especially as we will be using only the earliest p_i. Nevertheless, let us carry out the continuous formulation for all p_i for completeness. Note that kx is the continuous version of n, and that the natural base e has replaced 1 − p. The negative sign in the exponent appears because the old base 1 − p is less than 1, while the new base e is greater than 1.

$$\begin{array}{l}{p}_0=exp(-kx)\\ p_1=kxexp(-kx)\\ p_2=[{(kx)}^2/2!]exp(-kx)\end{array}$$

and, in general,

$$p_i=[{(kx)}^i/i!]exp(-kx)$$

Note also that the sum of all probabilities is unity as it should be:

$$\sum _{i=0}^{\infty }{p}_i=exp(-kX)\sum _{i=0}^{\infty }{(kX)}^i(i!)$$

The summation on the right is the Taylor’s expansion of exp(kx), so that the right-hand expression is unity.

C. Conversion from x to p_h

From the formula for p₀:

$$1-p_{\text{h}}=exp(-kx)$$

Taking the log of both sides:

$$kx=-log(1-p_{\text{h}})$$

Substitute for kx in p₁:

$$p_1=-(1-p_{\text{h}})log(1-p_{\text{h}})$$

The probability for multiple hits is

$$p_{\text{m}}=1-p_0-p_1$$

The normalized quantities M_f and M_s are now computable: Let F1 be the fraction fast for p₁, and let Fm be the fraction fast for p_m. Then

$${\text{M}}_{\text{f}}=p_1·\text{F1}+p_{\text{m}}·\text{Fm}$$

and

$${\text{M}}_{\text{s}}=p_1·(1-\text{F}1)+p_{\text{m}}·(1-\text{Fm})$$

RESULTS

Saturation Behaviors for Turnover of M-Fast (M_f) and M-Slow (M_s) Intermediates as Functions of Laser Light Intensity

The results and statistics of fitting the optical multichannel data by SVD-based least-squares are shown in Table 1. Using the fitted kinetic constants, one can obtain the difference spectrum for each transition, and from these the amounts of turnover for the intermediates of interest. Table 2 shows the amounts of turnover of M_f and M_s as influenced by actinic laser energy. These same data are graphically shown in Figure 2.

Figure 2.

Experimental laser saturation curves. BR turnover was initiated by laser flashes of increasing intensity as described in Experimental Procedures. The units of the Y-axis scale represent the number of monomers per trimer that cycle during the photo-cycle, as well as the sum of both M_f and M_s per trimer. Also shown are the fractions of each relative to the total M (M_tot).

The two most important features to be noticed about these results shown in Figure 2 are as follows: (1) The total number of monomers that cycle per trimer asymptotically approaches a limit of one. (2) The fraction of M_s/M_tot appears to have a positive Y-intercept. In this paper, we will use the results presented in Figure 2 to evaluate several models for the photocycle that have been proposed.

Some Cooperative Models, Presented in Chronological Order

1. Ohno’s Model (1981) (2)

The first complete model for photocooperativity and the one with the least assumptions is that of Ohno. Given the probability p that a given monomer will be hit by at least one photon, the probabilities for 0, 1, 2, or 3 monomers in a trimer being hit are

$$\begin{array}{l}0\text{monomers}:{(1-p)}^3\\ 1\text{monomer}:3p{(1-p)}^2\\ 2\text{monomers}:3p^2{(1-p)}^2\\ 3\text{monomers}:p^3\end{array}$$

The only assumptions are that if a single monomer is hit, the cycle passes through M_f, and if two or three monomers are hit, the cycle passes through M_s. In the Ohno model, it is obvious that as the highest level of laser strength is reached (i.e., p → 1), all M_f will be transformed to M_s. If all three monomers in a trimer are free to cycle, we will expect the results shown in Figure 3. This model must be rejected on at least three grounds. (1) The model predicts that 3 monomers per trimer can cycle, but as shown in Figure 2, no more than 1 monomer per trimer cycles. (2) The model predicts that the number of cycling M_f monomers diminishes to zero with increasing laser strength, whereas with actual data the number of cycling M_f monomers rises to a plateau (cf. Figure 2). (3) In contrast to the experimental data shown in Figure 2, the turnover of M_s starts at 0 and shows an initial lag. If we address objection 1 by postulating that only one monomer per trimer may cycle, this model is still not acceptable on grounds 2 and 3.

Figure 3.

Ohno’s model, assuming 3 monomers turnover per trimer. Predicted results based on the model of Ohno where p is the probability that a given monomer will be hit by at least one photon. The units of the Y-axis are the same as described in the legend to Figure 1.

2. Tokaji’s Model (1993) (15)

Tokaji noted that a dimer, with a probability p that a given monomer will be hit by a photon, presents the following probabilities for dimers having 0, 1, or 2 photon hits:

$$\begin{array}{l}0\text{hits}:{(1-p)}^2\\ 0\text{hit}:2p(1-p)=2p-2p^2\\ 2\text{hits}:{\text{p}}^2\end{array}$$

The rule for cooperativity is that 1 hit will lead to the monomer decaying through M_f, whereas 2 hits result in two cycles, one decaying through M_f and the other through M_s. M_f is produced both from a single and from a double hit, whereas M_s arises only from a double hit.

$$\begin{array}{l}{\text{M}}_{\text{f}}=2p-p^2\\ {\text{M}}_{\text{s}}=p^2\\ {\text{M}}_{\text{f}}+{\text{M}}_{\text{s}}=2p\\ \text{fraction}{\text{M}}_{\text{s}}/({\text{M}}_{\text{f}}+{\text{M}}_{\text{s}})=p/2\end{array}$$

A plot of the fraction of M_s vs p yields a straight line with a slope of 1/2. Tokaji presented experimental data for the fraction of M_s vs p obtained for BR at pH 8.3 and 31 °C, and within experimental accuracy, the points were in a straight line with a slope of 1/2.

Tokaji noted that in using different rules for cooperativity for trimeric BR, none of which considered the relative position of monomers in the trimer, he was unable to obtain a predicted slope of 1/2 in plots of M_s vs p. By invoking a rule that specified that only a cycling monomer to the right of an already cycling monomer will produce M_s, Tokaji found that a plot of fraction M_s should produce a straight line with a slope of 1/2. The proposed model for the trimer insists on this asymmetric monomer interaction. In the earlier review (1) of cooperative models, it was pointed out one feature of the model which was not in agreement with actual plots of fraction M_s vs p, using our own data and also the data published by Tokaji; namely, that according to the expected slope of 1/2 the Y-intercept should be 0, whereas in reality a positive intercept is always seen. Later, Tokaji introduced a modification to his original proposal which, in principle, could account for this observation (16). After first reviewing the original model in further detail, we will consider the newer model. Tokaji used Ohno’s probabilities (see above) for n hits on a trimer, but with special rules for the generation of M_f and M_s, as shown in the table below.

hits	Mf	Ms
0	0	0
1	1	0
2	1.5	0.5
3	1.5	1.5

This leads to the following relations concerning monomers per trimer:

$$\begin{array}{l}{\text{M}}_{\text{f}}=3p{(1-p)}^2+1.5(3p^2(1-p))+1.5p^3=3p-1.5p^2\\ {\text{M}}_{\text{s}}=0.5(3p^2(1-p))+1.5p^3=1.5p^2\\ {\text{M}}_{\text{f}}+{\text{M}}_{\text{s}}=3p\\ {\text{M}}_{\text{s}}/({\text{M}}_{\text{f}}+{\text{M}}_{\text{s}})=p/2\end{array}$$

Figure 4 shows some of the relationships that are predicted by the equations just presented. There are several major inconsistencies between the predictions of this Tokaji model and actual experimental data (cf. Figure 2).

Figure 4.

Tokaji’s original model (15). The predicted relations as functions of p (probability for a monomer being hit by a photon) are shown for total monomers of BR cycling per trimer, monomers of M_f and M_s cycling per trimer, fraction M_f/M_tot and fraction M_s/M_tot. See text for further details and Figure 2 for definition of Y-axis units.

1. The predicted number of monomers per trimer cycling at full saturation is 3, whereas the actual data approach a saturation level of 1. Reports of turnovers of more than one monomer per trimer are extremely rare. In one such case (17), absorbance was followed at the single wavelength of 610 nm attributed to the K intermediate. The reported value of near 46% turnover indicates a maximum of 1.5 monomers per trimer (18).

2. In the model, except for the values of p = 0 and p = 1, the amount of M_f cycling always exceeds that of M_s, whereas in the experimental data, the two curves cross well below the saturation level of laser intensity.

3. As in Ohno’s model, there is an initial delay in the appearance of M_s that is not present in the data.

It is obvious that this Tokaji model does not provide an adequate explanation for the experimental data.

3. Shrager Model (1995) (1)

In 1995, Shrager presented a model to show that it is possible to fit experimental data and also the positive Y-intercept found for the fraction of M_s/M_tot, using the principle of photocooperativity. This model is based on three assumptions.

1. When one monomer of a trimer is hit (depending perhaps on where it is hit), it will be geared toward M_f with probability q₁, and toward M_s with probability 1 − q₁.

2. When two monomers of a trimer are hit, the probability of each monomer being geared toward M_f changes to q₂, and when three monomers are hit, that probability changes to q₃.

3. If any monomer in a trimer is geared toward M_s, all other cycling monomers in that trimer become M_s, so that all cycling monomers in a trimer decay with the same rate, all fast or all slow.

Shrager’s model was able to account for an experimental data set obtained over a limited range of laser intensities, as well as to account for the base level of fraction M_s with no further assumptions. As in Tokaji’s model, Shrager’s model predicts that at maximum laser intensity, all three monomers in a trimer will cycle. In view of the data presented here, and elsewhere, that the maximum number of monomers in a trimer that can cycle appears to be one, Shrager’s model must also be rejected. However, when the model is altered to yield only one monomer per trimer, it fares better than the Ohno and Tokaji models because it contains adjustable parameters.

4. Model of Varo, Needleman and Lanyi (1996) (18)

This model was designed to explain the ability of laser light intensity to alter both the relative amounts of M-fast and M-slow intermediates and the different apparent decay paths that they follow back to the ground state in a completely homogeneous population of BR. It is based on the idea that actinic light can alter specific kinetic microconstants, namely, those that link M and N intermediates in the photocycle. Experimental data obtained at two different intensities of actinic light were interpreted according to the following kinetic sequence.

$${\text{M}}_1\to {\text{M}}_2\iff {\text{N}}^{(-1)}\iff {\text{N}}^{(0)}\to \text{BR}$$

The main conclusion reached by the authors was that actinic light is able to affect the microconstants for the N⁽⁻¹⁾ → N⁽⁰⁾ and the N⁽⁻¹⁾ → BR reactions.

No formal scheme based on probabilities was presented so that we cannot compare specific observed behavior with predictions of the proposed model as we did in the cases discussed above. However, we can point out certain aspects of the data and analyses which lead us to question the conclusion. (1) Time course data were measured at only two wavelengths, 410 and 570 nm. (2) The data were fit to only two exponentials, and no statistics for the quality of the fits were given. (3) The actinic intensity range was so low that the mole fraction of M_f in the wild type changed only from 0.87 to 0.70. (4) The data were analyzed using the presumed sequence shown above. This sequence is not universally accepted, and one of the authors (J.K.L.) has more recently proposed an altered sequence (19). (5) It was not demonstrated that the changes in microconstants proposed would account for the observations that M_f decays to background through the O intermediate whereas the M_s does not. (6) In contrast to reports from other laboratories, the time constant for M_s was significantly different at the two different laser light intensities.

In addition, the same kinds of change in the relative amounts of M_f and M_s and the different pathways for decay for the two M-intermediates can be obtained by changes in pH or changes in membrane potential (4). That means that the same microconstants that are affected by photocooperativity would have to be similarly affected by proton concentration or local voltage fields. Additional experimental observations that cannot be explained by changes in the specified microconstants are discussed elsewhere (4).

5. Tokaji Model (1998) (15)

In a later paper, Tokaji dealt only with the problem of the positive Y-intercept for the fraction of M_s cycling. He attributed the base level of M_s to heterogeneity in the ground state of BR. The heterogeneity was attributed to monomers “in M, N, O, or other states”. It was further assumed that these monomers decay through a photocycle that produces no connection to the M kinetics determined at 412 nm. The only explanation offered for the existence of these non-ground level monomers was that they may be the result of a preexisting light pulse. It is important to note that the heterogeneity in this case is quite different from the heterogeneity in parallel models. In the cooperative model, there is a single ground state and heterogeneity is imposed as a result of some prior history of the trimer, whereas in the parallel cycles model the heterogeneity is attributed to different chemical states of the trimer resulting from the local membrane lipid environment of the trimer. In our experiments of several hundred repeats per condition, laser flashes are separated by gaps of 5 s. The starting ground level is always fully attained before the next flash arrives. The dark spectra collected before each successive flash present the same clean spectrum for BR with no evidence of either M or O whose absorption maxima are sufficiently far from that of BR to be easily recognized. It does not appear, then, that our experiments were influenced by the effects of previous flashes.

A Noncooperative Model

Heterogeneous Model of Hendler (1995) (1)

In order to explain observations that at pH ≈7 and T ≈20 °C, M_f decays to BR through intermediates N and O whereas M_s decays directly to BR and that the relative amounts of these two different pathways during a photocycle is regulated by the intensity of actinic light, a photocycle consisting of two separate cycles was considered. Considerable evidence in support of this kinetic model has since been amassed (4). The existence of two separate cycles when only a single form of BR is known to exist suggested that the required heterogeneity of the ground state would depend on specific lipid–protein interactions that influenced the nature of the photocycle. Evidence for the ability of lipids to modify the kinetics and relative amounts of both forms of M during the photocycle was obtained (6). The heterogeneous model is based on four postulates:

1. Two different ground states are present.

2. One species decays through the path M_f → N → O → BR.

3. The other decays through the path M_s → BR.

4. The species decaying through M_f has a higher quantum efficiency and is present in a lower amount than the species decaying through M_s.

The system is described by two equations.

$$\begin{array}{l}{A}_{\text{f}}=A_{\text{f}max}[1-exp(-E_{\text{f}}I)]\\ A_{\text{s}}=A_{\text{s}max}[1-exp(-E_{\text{s}}I)]\end{array}$$

where A_{f max}, A_{s max} = maximum possible M_f and M_s amplitudes; I is laser intensity; and E_f and E_s are measures of the efficiency of the absorbed photon to result in turnover for the two species of BR and have dimensions of reciprocal intensity. The exponential terms (−E_fI) and (−E_sI) are dimensionless.

The results expected from this model depend on the values for the four parameters A_{f max}, A_{s max}, E_f, and E_s. Values for the parameters A_{f max} and E_f were obtained by fitting the experimental curve for monomers M_f shown in Figure 2 to the single exponential expression shown above. The values for the parameters A_{s max} and E_s were similarly obtained using the experimental curve for monomers M_s shown in Figure 2. These values are shown in Table 3. Using these parameters in the two equations that describe the heterogeneous model produced the results shown in Figure 5, which compares well with the experimental data in Figure 2.

Table 3.

Fitted Parameters using Experimental data

parameters	values	errors	dependencies
Af max	4.0367e–1	9.9065e–3	1.1752e0
Ef	2.5310e–1	2.6752e–2	1.1752e0
As max	5.5099e1	1.1154e–2	1.4790e0
Es	1.0731e–1	6.8893e–3	1.4790e0

Figure 5.

Hendler’s heterogeneous model (1). Predicted results based on Hendler’s model as described in the text. See legend to Figure 1 for definition of Y-axis units.

A Different Kind of Homogeneous, Cooperative Model

In the initial presentation of the parallel cycles model (3), it was pointed out that branched and parallel linear photocycle models are mathematically indistinguishable at any given laser intensity. Previously published photocooperative models have all been based on a linear photocycle contained in a homogeneous trimer target. Multiple photon hits were based on photon absorption by the separate monomers within the trimer. None of these models has been found to be consistent with experimental data, as illustrated above and in published literature (4). The alternative photocooperative model examined here is based on a homogeneous, branched target. The distinguishing feature is that a single photon will cause the formation of both M_f and M_s arising from the separate branches in a fixed proportion, dependent on the branching ratio. The photocooperative feature is that subsequent photons striking the target within the 5 ns laser pulse duration will alter the branching ratio and the proportion of M_f to M_s. The maximum opportunity for multiple hits to the target within the 5 ns window is at the level of the ground state. This results in a pair of branched cycles as shown below.

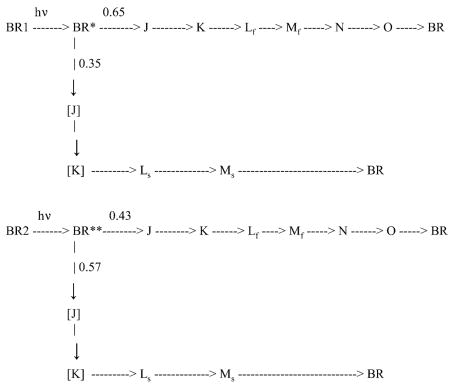
The branching distribution of 0.65 and 0.35 for a single photon hit is consistent with experimental observations obtained at very low laser energy whereas the distribution of 0.43 and 0.57 for multiple hit targets is consistent with experimental data obtained at very high laser intensities. This model has some very obvious advantages over the previously suggested photocooperative models. It is consistent with the different decay paths for M_f to M_s, the fact that M_f reaches and maintains a steady, nonzero plateau, that the ratio of M_s/M_tot has a positive Y-intercept, and that the saturation behaviors of M_f and M_s are different. In order to test this model by comparing its predicted results with experimental data, assumptions must be made as to the nature of the probabilities for single and multiple photon hits and to obtain plots of M_f and M_s as functions of these probabilities.

We considered two different scenarios. One, as was assumed for all the other proposed models, is that each monomer in the trimer is a target for photon absorption. In the other, it is assumed that the entire trimer structure functions as a single target.

The probabilities for the former model are the same as used by Ohno as described above.

$$\begin{array}{l}p=\text{probability}\text{of}\text{a}\text{photon}\text{striking}\text{a}\text{monomer}\\ 0\text{monomers}:p_0={(1-p)}^3\\ 1\text{monomer}:p_1=3p{(1-p)}^2\\ 2\text{monomers}:p_2=3p^2(1-p)\\ 3\text{monomers}:{\text{p}}_3={\text{p}}^3\end{array}$$

It is assumed that p₁ results in the formation of 0.65 M_f and 0.35 M_s, whereas p₂ and p₃ result in the formation of 0.43 M_f and 0.57 M_s.

$$\begin{array}{l}{\text{M}}_{\text{f}}=(p_1·0.65)+(p_2+p_3)·0.43\\ {\text{M}}_{\text{s}}=(p_1·0.35)+(p_2+p_3)·0.57\end{array}$$

To compare the predictions of this model with experimental data, we used the two-exponential fit of M_tot data to laser intensity to convert the model’s predicted M_tot values to the corresponding laser intensities in the experimental situation. The resulting plots M_tot, M_f, M_s, M_f/M_tot, and M_s/M_tot vs laser intensity did not correspond to those from the experimental data (not shown).

In the second model, where the whole trimer is considered as a single target, we must consider the probabilities of any number of multiple photon hits. The mathematical basis for the probability expressions used here is described in Experimental Procedures. As directly above, it is assumed that a single photon hit results in the branching ratio of 0.65 and 0.35, while any number of hits above one results in the branching ratio of 0.43 and 0.57. In this case, only three probabilities are needed, namely, p₀ for 0 photons, p₁ for a single photon and p_m for any number above 1. These expressions can be stated both as functions of the probability of being hit and in terms of laser intensity to which the probability is related.

$$\begin{array}{l}{p}_{\text{h}}=\text{probability}\text{of}\text{one}\text{or}\text{more}\text{hits},\text{which}\text{is}\text{directly}\\ \text{related}\text{to}\text{fraction}\text{of}\text{BR}\text{cycling}\\ p_0=\text{probability}\text{of}\text{no}\text{hits}\\ p_1=\text{probability}\text{of}\text{one}\text{hit}\\ p_{\text{m}}=\text{probability}\text{of}\text{multiple}\text{hits}\end{array}$$

In terms of probability:

$$\begin{array}{l}{p}_0=1-p_{\text{h}}\\ p_1=-(1-p_{\text{h}})·log(1-p_{\text{h}})\\ p_{\text{m}}=1-p_0-p_1\end{array}$$

In terms of laser intensity:

$$\begin{array}{l}{p}_0=exp(-k·I),\text{where}I\text{is}\text{laser}\text{intensity}\text{and}k\text{is}\text{a}\text{constant},\text{or}\\ p_0=exp(-I/\text{tau}),\text{where}\text{tau}\text{is}\text{the}\text{reciprocal}\text{of}k\\ p_1=k·I·exp(-k·I)\\ p_{\text{m}}=1-p_0-p_1\end{array}$$

In either case,

$$\begin{array}{l}{\text{M}}_{\text{f}}=(p_1·0.65)+(p_{\text{m}}·0.43)\\ {\text{M}}_{\text{s}}=(p_1·0.35)+(p_{\text{m}}·0.57)\end{array}$$

To compare the predictions of this model based on probabilities with the experimental data, we use M_tot from the experimental data, which runs from 0 to 1 as p. Figure 6 shows this comparison. We can also directly compare the model predictions based on laser intensity (I) with the experimental data. To do this we used the same laser intensities used experimentally and a value of tau equal to 6.5 mJ, determined by a 1-exponential fit for the experimental M_tot as a function of I (Figure 7). It is immediately obvious that the agreements between the experimental data and the predictions from this model expressed both in terms of probability and laser intensity are far superior to anything obtained from the leading published homogeneous cooperative models studied here. But, in spite of this, the homogeneous, cooperative, branched model cannot be a valid representation of the true kinetic model occurring in nature. It has been shown, both here and previously (1), that the fitting of experimental data for M_tot vs I requires two exponentials. The statistics of a two-exponential fit to the experimental data used here are shown in Table 4. A graphic representation of the fit and residuals is shown in Figure 8A. All homogeneous models, having only a single ground state can have only one source for formation of either M_f or M_s, and consequently for their sum, M_tot. The formation of M_tot, as a function of laser intensity, will display only a single exponential. This may be less apparent in the case of the branched homogeneous model because of its having a second site for photon absorption. If one were to assume that the second site was at the K intermediate and that this target had a different cross section and quantum efficiency, one might expect that a second exponential for M turnover would be involved. But this is not the case. The total amount of BR that cycles is determined solely by absorption of photons at the ground state. Absorption of photons at the second branch site can alter the distribution ratio of how much of the cycle proceeds through M_f and M_s pathways, but not stimulate any new BR molecules to cycle. The requirement of two exponentials for defining the relationship of M_tot to I is fully consistent with a heterogeneous model containing two separate ground states.

Figure 6.

Plots of all functions involving M_f and M_s vs p (probability of photon absorption). Panel A. Experimental data. Panel B. Simulated data based on the homogeneous, photocooperative, branched model.

Figure 7.

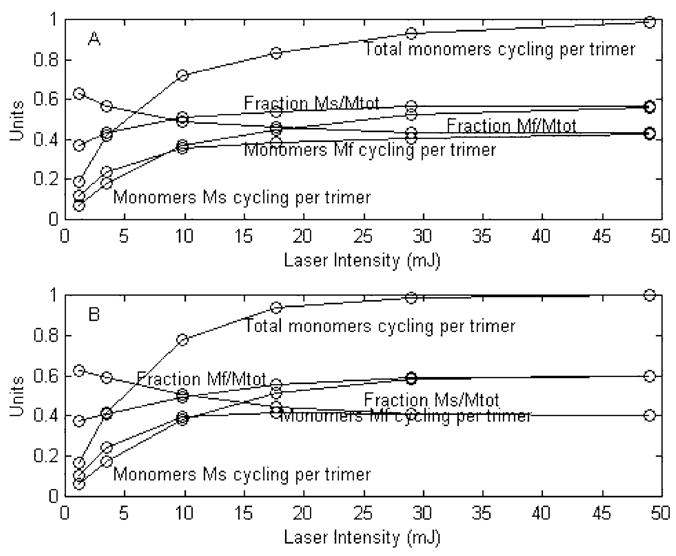
Plots of all functions involving M_fM_s vs laser intensity. Panel A. Experimental data. Panel B. Simulated data based on the homogeneous, photocooperative, branched model.

Table 4.

Fitting of Two Exponentials to Experimental M_tot Data^a

parametersb	values	errors	dependencies
A1 (monomers)	5.5996e–1	2.0042e–1	2.6929e1
tau1 (mJ)	3.6879e0	1.4736e0	6.8792e0
A2 (monomers)	4.5317e–1	1.8313e–1	1.7238e1
tau2 (mJ)	1.8077e1	1.1081e1	1.1381e1

^aThe equation used for the 2-exponential fitting was the same as described herein in the heterogeneous model of Hendler (1995) (1) with an added fitted baseline: M_tot = p(1)*(1 − exp(−I/p(2))) + p(3)*(1 − exp(−I/p(4))) + p(5), where subscripted values of p( ) were the fitted parameters.

^bA1 is the amplitude for tau1 at near 3.7 mJ. A2 is the amplitude for tau2 at near 18 mJ.

Figure 8.

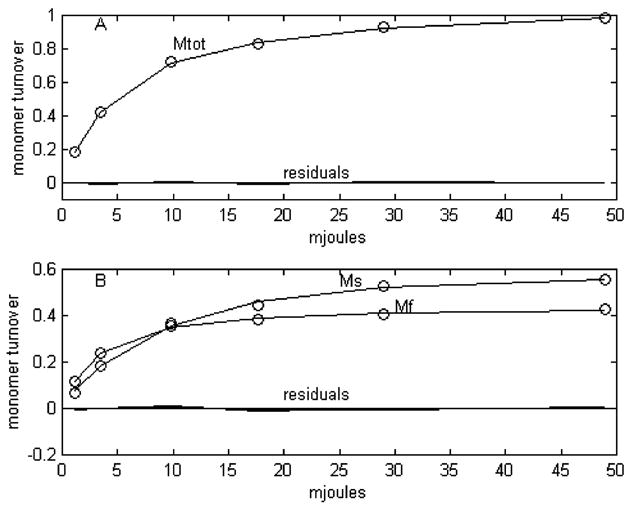
Two exponential fits to experimental data for M_tot (A) and simultaneous fitting to M_f (B) and M_s. The data are represented by points and the two exponential fits by lines. Residuals are shown relative to a zero line.

With the more extensive range of laser intensity used here, we have found that the simultaneous fitting of both M_f and M_s also requires two exponentials. Table 5 shows statistics of the fit, which is graphically represented in Figure 8B. The simultaneous fitting to both M_f and M_s data sets led to significantly decreased error and dependency values compared to the fit to M_tot alone. The low dependency values for tau1 and tau2 show that the second exponential is not superfluous (13). Adding all four amplitudes listed in Table 5 corresponds a total turnover of 1.01 monomers for M_tot. Adding the two amplitudes for M_f leads to an expected maximum turnover of near 0.44 monomer for M_f. Similarly, adding the two amplitudes for M_s leads to an expected maximum turnover of near 0.57 monomer for M_s, which is what is observed. Another interesting observation is that M_f constitutes about 63% of total M turnover at the laser intensity level of tau1, but only about 24% at the level of tau2.

Table 5.

Simultaneous Fitting of Two Exponentials to Experimental M_f and M_s^a

parameterb	value (mJ−1)	errors	dependencies	taus (mJ)	AMF(monomers)	AMS(monomers)
k1	3.4611e–1	9.5782e–2	4.6976e0	2.8892e0	2.7676e–1	1.6203e–1
k2	7.5133e–2	1.3693e–2	5.6437e0	1.3310e1	1.3365e–1	4.3363e–1

^aThe same equation shown in the legend to Table 4 was used for the simultaneous fitting.

^bk1 is the exponential constant whose reciprocal, or tau, is near 3.5 mJ. The fitted amplitude for the M_f data (A_MF) is near 0.28 and for the M_s data (A_MS) is near 0.16 (row 1). k2 is the exponential constant whose reciprocal, or tau, is near 13 mJ. The fitted amplitude for the M_f data (A_MF) is near 0.13 and for the M_s data (A_MS) is near 0.43 (row 2).

An Alternative Heterogeneous, Noncooperative Model

The finding reported here, using a more extensive range of laser intensities, that two exponentials are needed for the fittings of M_f and M_s, as well as M_tot, suggests an alternative heterogeneous model from the one originally introduced. Two exponentials for each M_f and M_s are consistent with the expectations from the branched model as examined above. To illustrate this point, we present a shorter version of the two branched photocycles that is consistent with the 10 μs time resolution of our spectrophotometer, that does not allow the resolution of intermediates J and K.

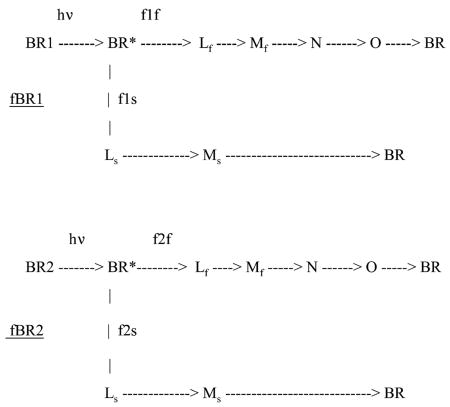
The constants fBR1 and fBR2 represent fractions of the two different ground states for BR as in the original heterogeneous model. As in the original model, the heterogeneity is based on different lipid–protein interactions, and each presents a different target for photon absorption. Hence, the uptake curves of BR1 and BR2 will be single exponentials, while the resulting M_f and M_s will contain contributions from both BR species, thus involving both exponentials. For the target BR1, the fixed branching ratio is f1f leading to the M_f branch and f1s to the M_s branch. For the target BR2, the fixed branching ratio is f2f leading to the M_f branch and f2s to the M_s branch. There are two identical routes for forming M_f and two for forming M_s.

$$\begin{array}{l}\text{BR}1\to \text{BR}\ast \to {\text{L}}_{\text{f}}\to {\text{M}}_{\text{f}}\to \text{N}\to \text{O}\to \text{BR}\\ \text{BR}2\to \text{BR}\ast \to {\text{L}}_{\text{f}}\to {\text{M}}_{\text{f}}\to \text{N}\to \text{O}\to \text{BR}\end{array}$$

and

$$\begin{array}{l}\text{BR}1\to \text{BR}\ast \to {\text{L}}_{\text{s}}\to {\text{M}}_{\text{s}}\to \text{BR}\\ \text{BR}2\to \text{BR}\ast \to {\text{L}}_{\text{s}}\to {\text{M}}_{\text{s}}\to \text{BR}\end{array}$$

The formations of M_f, M_s, and M_tot as functions of I (laser intensity) are expressed as

$$\begin{array}{l}{\text{M}}_{\text{f}}=\text{fBR}1·\text{f}1\text{f}·(1-exp(-I/{\text{tau}}_1))+\text{fBR}2·\text{f}2\text{f}·(1-exp(-I/{\text{tau}}_2))\\ {\text{M}}_{\text{s}}=\text{fBR}1·\text{f}1\text{s}·(1-exp(-I/{\text{tau}}_1))+\text{fBR}2·\text{f}2\text{s}·(1-exp(-I/{\text{tau}}_2))\\ {\text{M}}_{\text{tot}}=(\text{fBR}1·\text{f}1\text{f}+\text{fBR}1·\text{f}1\text{s})·(1-exp(-I/{\text{tau}}_1))+\\ (\text{fBR}2·\text{f}2\text{f}+\text{fBR}2·\text{f}2\text{s})·(1-exp(-I/{\text{tau}}_2))\end{array}$$

This formulation shows two exponentials for both M_f and M_s. In the original presentation of the heterogeneous model, it was stated that a branched model and one consisting of the separate linear sequences contained in the branched model are mathematically equivalent. In both representations, there are the same two linear sequences for M_f and M_s. The amounts of the two separate sequences in both representations are fitted as initial y₀ values in our dy/dt = Jy analysis for finding absolute spectra (3, 4),

DISCUSSION

The reassessment of cooperative models presented here is based both on experimental data obtained with a more extensive range of laser energies than previously used (1) and a variety of newer findings reviewed in ref 4 and briefly summarized in the introductory comments here. None of the predominant cooperative models, based on a homogeneous ground state and linear sequences, that we examined is able to account for the experimental observations. This includes not only the ability of actinic light intensity to change the relative amounts of M_f and M_s but also the fact that each decays through a different pathway and displays different saturation profiles with respect to increasing laser intensity. We also examined a different kind of homogeneous, photocooperative model based on successive photon hits to a single target and a branched photocycle. This model produced results sufficiently similar to the experimental data to merit further consideration. However, in contrast to the experimental data, the simulated data produced a monoexponential relationship for M_tot turnover, as a function of laser intensity. This is because the turnover of each M_f and M_s proceeds from the decay of the same activated source. Therefore, this model as well as all homogeneous models, which are based on a single ground state, must be eliminated.

It was again demonstrated that a heterogeneous, nonphotocooperative model, based on separate ground states and separate decay paths for M_f and M_s, produced results closely resembling experimental data that required two exponentials for fitting. A new finding, resulting from the extended range of laser intensities used here, was that both M_f and M_s also require two exponentials for optimal fitting. We demonstrated that a branched, noncooperative, heterogeneous photocycle leads to two exponential behaviors for both M_f and M_s turnovers.

As previously noted (3) and above, the two forms of heterogeneous model, one consisting of linear chains and the other branched, are functionally and mathematically equivalent, both being based on separate cycles which contain M_f or M_s in different decay pathways. Based on the newly found two exponential behaviors of laser-induced M_f and M_s turnovers, the branched model appears to be more likely.