A Mechanism for the Upper Limit of Vulnerability

Abstract

Introduction

The goal of this study is to examine the mechanism of the upper limit of vulnerability (ULV) in the heart.

Methods

Numerical simulations of cardiac tissue were performed using the bidomain model. An S2 shock was applied during the refractory period of the S1 action potential, and results using a smooth curving fiber geometry were compared to results using a smooth plus random fiber geometry.

Results

When using a smooth fiber geometry only, no ULV was observed. However, when a random fiber geometry was included, the ULV was present. The difference arises from the fate of the shock-induced break wave front when it reaches the edge of the tissue hyperpolarized by the shock (the virtual anode).

Conclusion

Our numerical simulations suggest that local heterogeneities throughout the tissue may be crucial for determining the fate of the shock-induced wave front at the edge of the virtual anode, and therefore play an important role in the mechanism underlying the ULV.

Introduction

A weak shock cannot induce reentry in the heart. However, a stronger shock can, if timed during the “vulnerable period”, causing an arrhythmia that often decays into ventricular fibrillation. Surprisingly, an even stronger shock does not induce reentry (1). The strongest shock that causes reentry is the upper limit of vulnerability (ULV). The ULV is often similar to the defibrillation threshold (2), which has led to the hypothesis that a successful defibrillation shock must not only halt preexisting fibrillation, but also must not re-induce fibrillation by the same mechanism responsible for the ULV (3).

What is the mechanism of the ULV? One suggestion is based on the “virtual electrode-induced phase singularity” model (4). Stimulus-induced hyperpolarization deexcites cardiac tissue, creating an excitable region through which wave fronts can propagate (a “virtual anode”). An electrotonic interaction at the border between depolarized and hyperpolarized tissue triggers a “break” wave front (5,6). This wave front can only propagate in one direction--into the newly created excitable region--resulting in the formation of phase singularities and a reentrant circuit.

How does the virtual electrode-induced phase singularity hypothesis explain the ULV? Several researchers (7–10) proposed a mechanism: a strong shock causes rapid propagation through hyperpolarized tissue, so that when the wave front reaches the edge of the virtual anode the surrounding tissue has not yet recovered excitability and the wave front dies. A weaker shock, however, causes the wave front to propagate through the virtual anode more slowly, providing sufficient time for the surrounding tissue to recover. Cheng et al. (7) observed that the speed of the post-shock wave front depended on the magnitude of the hyperpolarization at the end of the shock, and that reentry occurred only when this speed was slow. Banville et al. (8) observed similar results in their experiments. Rodriguez and Trayanova (10) found analogous behavior in their numerical simulation, and also found that the degree of refractoriness of the surrounding tissue played a role. In all cases, the fate of the shock-induced break wave front when it reached the edge of the virtual anode was found to be the key to understanding the ULV.

In this paper, we examine a similar mechanism for the ULV: the presence of localized virtual electrodes that arise from heterogeneities throughout the tissue. Our numerical simulations suggest that such heterogeneities are crucial for determining the fate of the shock-induced wave front at the edge of the virtual anode, and therefore play an important role in the mechanism underlying the ULV (Fig. 1).

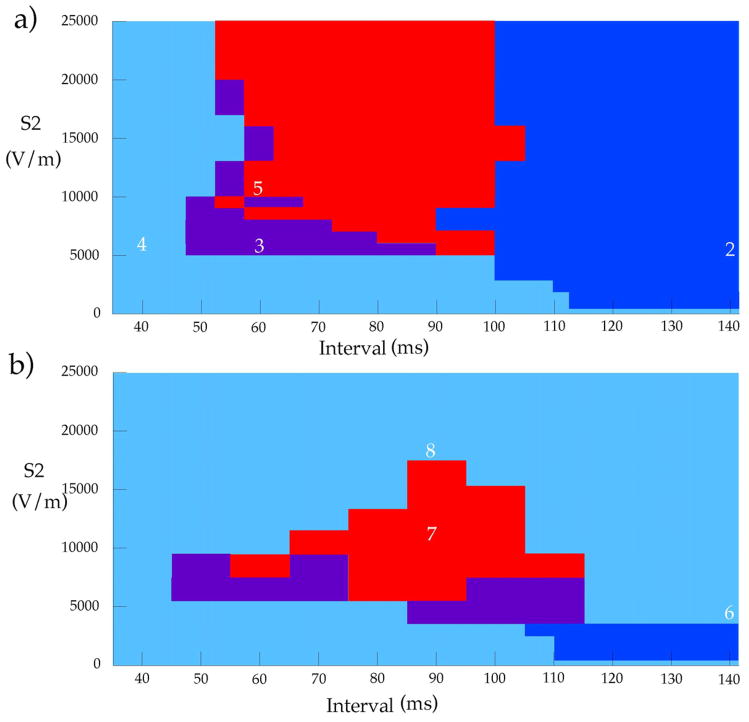
Figure 1.

The response of the tissue to an S2 shock, as a function of S2 strength and the S1-S2 interval. a) With a smooth fiber geometry, and b) with a smooth plus random fiber geometry. Light blue = no excitation, dark blue = make excitation, purple = break excitation, red = reentry. The white digits correspond to figure numbers illustrating that simulation. In b), whole tissue make excitation and no excitation are both shown in light blue. At intermediate S2 strengths there is an obvious difference between no excitation (short intervals) and whole tissue make excitation (long intervals), but at strong S2 strengths whole tissue make excitation and no excitation change continuously into one another.

Methods

We represent the electrical properties of cardiac tissue using the bidomain model (11), and account for the active membrane behavior with the Beeler-Reuter model (12). Details of the calculation have been given previously (13,14). We simulate a 20 × 20 mm sheet of cardiac tissue that is represented by 201 × 201 nodes with a space step of 100 μm. The time step is 5 μs.

Electrical stimulation is performed using an S1-S2 protocol. S1 corresponds to raising the transmembrane potential throughout the entire tissue from rest (−85 mV) to zero at time zero. The S2 stimulus lasts for 5 ms and is applied using an extracellular voltage difference between the top and the bottom edges of the tissue, as shown in Fig. 2. The S2 stimulus strength is specified in terms of the applied electric field. For example, if the upper and lower boundaries, separated by 20 mm, are set to ±10 V, then the electric field strength is 1000 V/m (or 10 V/cm). The interval is defined as the time between S1 and the start of S2.

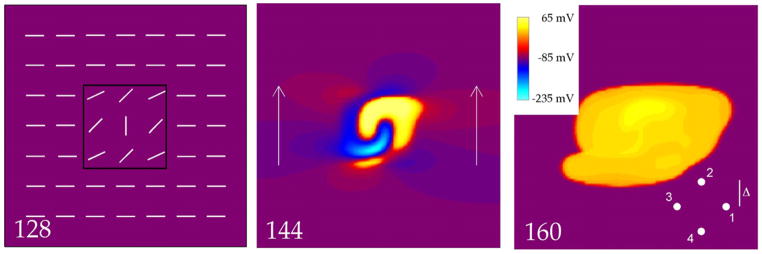
Figure 2.

The transmembrane potential as a function of position in a 20 mm × 20 mm sheet of cardiac tissue. The electric field has a strength of 5500 V/m, and is applied for 5 ms starting at 140 ms (the time of each frame in milliseconds is indicated by the number in the bottom left corner). The 128 ms frame shows the fiber geometry (white line segments), including the middle region (black box) where the fiber angle varies. The 144 ms frame shows the tissue response during the shock. The arrows indicate the direction of the applied electric field. The 160 ms frame indicates that the shock created a closed, outwardly propagating wave front (make excitation). This frame also shows the recording site geometry used to measure conduction velocity (the separation between electrodes, 2Δ, has been exaggerated for better viewing). The inset shows the color scale used in all figures (in some figures, V_m is outside the range of −235 to 65 mV during the S2 shock, and the color scale saturates). The supplemental file Fig2Video.avi contains a video of this simulation.

We use a fiber geometry that is uniform except in a D × D region (D = 6.08 mm), where the angle θ between the fiber direction and the x-axis varies as (13,14)

$$\theta (x,y)=\frac{\pi }{2}{cos}^2(\frac{\pi x}{D}){cos}^2(\frac{\pi y}{D}),$$ (1)

with x and y are measured from the center of the tissue, This geometry results in the fiber angle being π/2 at the tissue center, and decreasing smoothly to zero at x = y = ±D/2 (Fig. 2). In some simulations, throughout the tissue we added a random distribution of fiber angles to the fiber geometry in Eq. 1 (15). The random angles had a normal distribution with a zero mean and a standard deviation of 0.1 radians (5.7°). The transmembrane potential, V_m, obeys the boundary condition ∂V_m/∂n =0 for all boundaries. This condition allows us to ignore any edge effects that would ordinarily be induced near the electrode-tissue interface, thereby focusing on far-field stimulation.

Propagation speed, v, was determined by recording wave front arrival times (t₁, t₂, t₃, and t₄) at four sites forming a square, each a distance Δ from the square center (Fig. 2)

$$v=\frac{2\mathrm{\Delta }}{\sqrt{{(t_4-t_2)}^2+{(t_3-t_1)}^2}}.$$ (2)

This result is exact and independent of propagation direction if the wave front is planar. It is only approximate for curved wave fronts. In our simulations, the center of the square was located at the position indicated by the white dot in Fig. 8, and Δ = 200 μm.

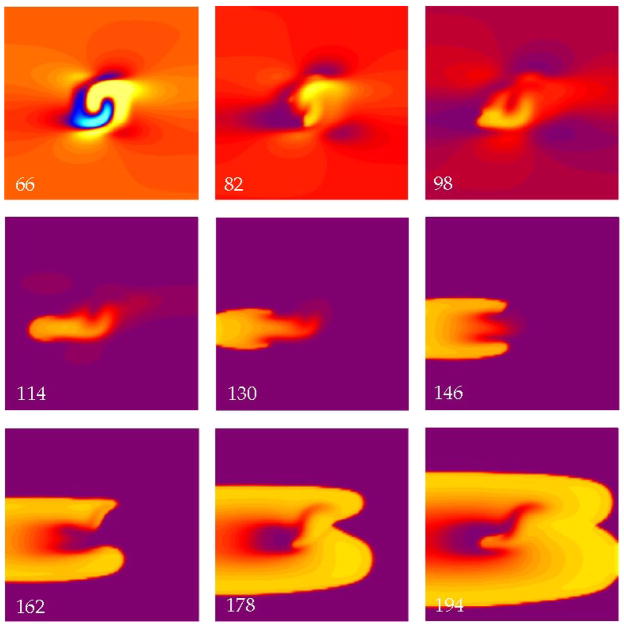
Figure 8.

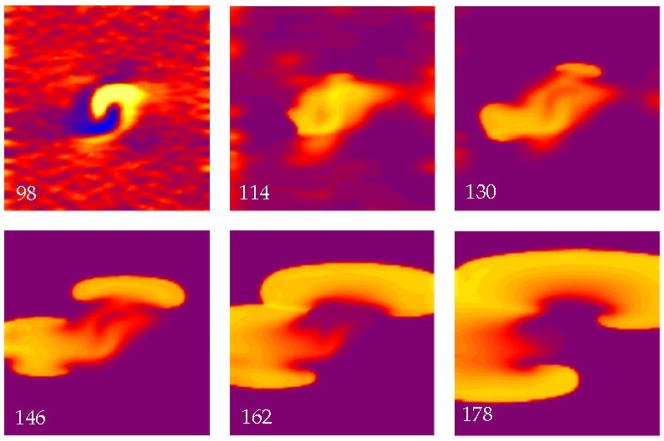
The transmembrane potential as a function of position in a sheet of cardiac tissue. The electric field has a strength of 18,500 V/m and is applied at a time of 90 ms. Throughout the tissue a random distribution of fiber angles was added in addition to the fiber geometry shown in Fig. 2. When the wave front triggered by break excitation reaches the edge of the hyperpolarized region (114 ms), the surrounding tissue is refractory and the wave front dies (130 ms). The propagation speed is measured at the location of the white dot in the 98 ms frame. The color scale is shown in Fig. 2. The supplemental file Fig8Video.avi contains a video of this simulation.

Results

Smooth Fiber Geometry

Figure 1 summarizes the results, in terms of the S2 strength and S1-S2 interval. We first consider a smooth fiber geometry, as shown in Fig. 1a. Four main types of behavior were observed, as indicated in Figs. 2–5.

Figure 5.

The transmembrane potential as a function of position in a sheet of cardiac tissue. The electric field has a strength of 10,500 V/m and is applied at a time of 60 ms. Break excitation leads to figure-of-eight reentry. The color scale and fiber geometry are shown in Fig. 2. The supplemental file Fig5Video.avi contains a video of this simulation.

Figure 2 shows the result of a simulation using an S2 strength of 5500 V/m and an interval of 140 ms. The interval is long enough that by the time of the S2 stimulus the tissue had recovered nearly completely and is at rest (purple in 128 ms frame). During S2 (144 ms), one region of the tissue was depolarized (the virtual cathode, yellow and red) and another was hyperpolarized (the virtual anode, blue), in a pattern similar to that predicted previously (13,15) and qualitatively comparable to virtual electrodes measured experimentally (16,17). A wave front originates from the strongly depolarized region and propagates outward in all directions. This is “make” excitation (5,6), initiated by the turning on of the stimulus pulse, and is typical for an S2 stimulus given so late that the tissue has recovered excitability.

In Fig. 3, the interval is reduced to 60 ms. The tissue is refractory when we apply S2, so make excitation is impossible. Following the S2 stimulus depolarization diffuses from the virtual cathode into the virtual anode, exciting a wave front (96 ms) by the “break” mechanism (5,6). Break excitation is initiated by the turning off of the stimulus pulse. The S2 break wave front propagates to the left until the surrounding tissue recovers excitability, at which point the wave front develops into two spiral waves that propagate to the left, outward, and to the right (144 ms). At 168 ms (not shown) the two wave fronts collide and form a closed wave front propagating outward.

Figure 3.

The transmembrane potential as a function of position in a sheet of cardiac tissue. The electric field has a strength of 5500 V/m and is applied at a time of 60 ms. The hyperpolarized (blue) region in the 64 ms frame creates a excitable path through which a wave front can propagate (96 ms), resulting in break excitation. No reentry occurs. The color scale and fiber geometry are shown in Fig. 2. The supplemental file Fig3Video.avi contains a video of this simulation.

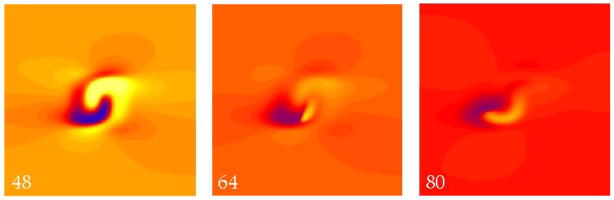
Figure 4 shows a simulation using an S2 strength of 5500 V/m and a very short interval of 40 ms, when the tissue is refractory. The S2 shock produces the usual virtual cathode and anode (48 ms). A break wave front is initiated at the right edge of the virtual anode and is apparent at 64 ms, but when this wave front reaches the left edge of the virtual anode the surrounding tissue has not yet recovered its excitability and the wave front dies. (Defining the “edge of the virtual anode” is somewhat imprecise, since the transmembrane potential distribution varies continuously during the shock and during propagation. However, to a good approximation the break wave front stops propagating when it reaches the left edge of the region that was directly hyperpolarized by the shock.)

Figure 4.

The transmembrane potential as a function of position in a sheet of cardiac tissue. The electric field has a strength of 5500 V/m and is applied at a time of 40 ms. The hyperpolarized (blue) region (48 ms) creates an excitable path through which a break wave front can propagate (64 ms). However, when it reaches the edge of this region, the surrounding tissue remains refractory (red) and the wave front dies (80 ms). The color scale and fiber geometry are shown in Fig. 2. The supplemental file Fig4Video.avi contains a video of this simulation.

Figure 5 shows the tissue response for a stronger shock (10,500 V/m) and an interval of 60 ms.. The immediate response after the S2 stimulus is break excitation like that in Fig. 3. However, when the two arms collide to form a closed wave front (178, 194 ms), a piece of the wave front breaks off and propagates to the left into tissue that has by then recovered from the first break wave front. This forms a figure-of-eight reentrant circuit similar to that predicted by Winfree (18) and observed experimentally by Shibata et al. (19) and others.

Is there some maximum S2 strength--an upper limit of vulnerability--above which we no longer observe reentry? Using our model with a smooth fiber geometry, the answer is no. Stronger stimuli timed during the “vulnerable period” (in our model, about 60–100 ms) always produce reentry. Usually the mechanism is similar to that in Fig. 5: break excitation followed by figure-of-eight reentry. However, for very strong S2 stimuli the reentrant circuits become more complex (14). We have examined stimuli up to a strength of 35,000 V/m and always find reentry during the vulnerable period. Thus, we see no sign of an upper limit of vulnerability when using our smooth fiber geometry.

Smooth plus Random Fiber Geometry

The results of our simulations that included the random fiber distribution are summarized in Fig. 1b. If the shock is weak (less than about 3000 V/m) the random fiber distribution has a negligible influence on the results. For long intervals, the tissue is excited by the make mechanism (not shown, see (14)), with a resulting behavior almost identical to that shown in Fig. 2. However, when the S2 strength increases, a different behavior occurs. Figure 6 shows a simulation for an interval of 140 ms, with a stimulus strength of 4500 V/m. The S2 stimulus shock induces large regions of depolarization and hyperpolarization like those in Fig. 2, but localized virtual electrodes caused by the random fiber distribution are also present (146 ms). For this S2 strength, the small-scale depolarizations are above threshhold, causing all the widely distributed virtual cathodes to excite action potentials (20). These action potential wave fronts begin to propagate, but almost immediately run into adjacent propagating wave fronts. The net result is that by 162 ms the entire tissue has been depolarized. The tissue fires an action potential, but there are no propagating wave fronts (just as there is no S1 wave front) because there is no transmembrane potential gradient. We refere to this phenomena as a “whole tissue make excitation”. In this case, the presence of the random fiber distribution determines the response of the tissue to the shock.

Figure 6.

The transmembrane potential as a function of position in a sheet of cardiac tissue. The electric field has a strength of 4500 V/m and is applied at a time of 140 ms. Throughout the tissue a random distribution of fiber angles was added in addition to the fiber geometry shown in Fig. 2. Small, localized regions of depolarization (146 ms) led to rapid make excitation over the entire tissue (162 ms). The color scale is shown in Fig. 2. The supplemental file Fig6Video.avi contains a video of this simulation.

If the interval is further shortened to 100 ms, S2 triggers a wave front by the break mechanism. In this case (not shown, see (14)), the dynamics following the shock are similar to those in Fig. 3. The virtual cathodes and anodes associated with the random fiber distribution are present, but the virtual cathodes are not strong enough to excite the tissue that is still refractory from the S1 action potential, and the virtual anodes are not strong enough to deexcite the tissue. These localized regions of shock-induced polarization quickly die away, and play little role in the subsequent wave front dynamics. At even shorter intervals (not shown, see (14)), excitation fails by the mechanism shown in Fig. 4, again with the small-scale virtual cathodes and anodes playing little role.

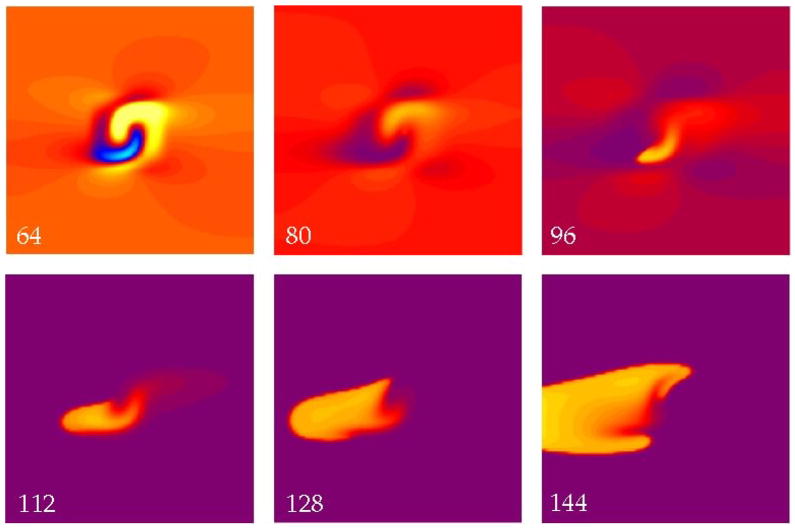
The S2 shock can induce reentry when small-scale virtual electrodes are present throughout the tissue. Figure 7 shows a simulation using an S2 strength of 10,500 V/m and an interval of 90 msec. During the shock, the tissue is refractory and whole tissue make excitation does not occur (98 ms). Instead, the small-scale virtual electrodes die away, so that by 130 ms the surrounding tissue is excitable, and figure-of-eight reentry develops similar to Fig. 5.

Figure 7.

The transmembrane potential as a function of position in a sheet of cardiac tissue. The electric field has a strength of 10,500 V/m and is applied at a time of 90 ms. Throughout the tissue a random distribution of fiber angles was added in addition to the fiber geometry shown in Fig. 2. Break excitation leads to figure-of-eight reentry. The color scale is shown in Fig. 2. The supplemental file Fig7Video.avi contains a video of this simulation.

If we want to search for an upper limit of vulnerability, we should apply an even stronger S2 stimulus and see if reentry disappears. Figure 8 shows a simulation using a S2 stimulus strength of 18,500 V/m and an interval of 90 ms. In this case, the surrounding tissue is influenced by the S2 shock, either exciting a make action potential (as in Fig. 6), or extending the duration of the S1 action potential. Either way, the result is the same. When the break wave front reaches the edge of the virtual anode, it has no excitable path, so it dies. No reentry is induced. Figure 1b shows that there exists a maximum S2 stimulus strength, above which reentry does not occur: the upper limit of vulnerability.

We determined the upper limit of vulnerability to the nearest 100 V/m, and found it to be 17,400 V/m at an interval of 90 ms. Then we varied the seed of our random number generator, so that we used six different random fiber geometries keeping all other parameters fixed, and found that the average ULV at 90 ms was 16,400 ± 800 V/m. Thus, the exact random fiber distribution appears to affect our results quantitatively by about ± 5 %. We also varied the standard deviation of the random fiber geometry while keeping the seed of the random number generator fixed. When the standard deviation was reduced to 0.05 rad, the ULV at 90 ms increased to 36,700 V/m, and when it was increased to 0.2 rad, the ULV at 90 ms decreased to 7300 V/m, indicating that to a good approximation the ULV is inversely proportional to the standard deviation of the fiber geometry.

Discussion

The presence of an upper limit of vulnerability in our model depends crucially on the existence of randomly placed heterogeneities. Krassowska ad Kumar (21) and Fishler (22) proposed the idea of “syncytial heterogeneities” and examined how variations of the bidomain parameters influenced the polarization caused by an applied electric field. We do not believe that our results arise because we add the heterogeneity in the specific form of a fiber angle distribution. Probably had we varied some other parameter randomly, such as surface-to-volume ratio as Fishler did, our results would have been much the same, and possibly the “saw-tooth” effect at the level of individual cells (23,24) would lead to similar behavior (although we have not verified either of these speculations). The key point is the existence of some heterogeneity that will induce small-scale regions of polarization throughout the tissue. These small-scale regions do not exist at the outer edges of the smooth fiber geometry, because in the bidomain model some sort of heterogeneity is required to change the transmembrane potential, and there the fibers are straight and homogeneous. Only when heterogeneity is present, such as that caused by the random fiber geometry, will polarization exist throughout the tissue.

Our model is very similar to the one used by Langrill Beaudoin and Roth (15) for their study of how the spatial frequency of polarization influences the induction of reentry in cardiac tissue. They concluded that “low spatial frequency regions of hyperpolarization carve out excitable pathways, and high spatial frequency regions provide the large gradient of transmembrane potential required to initiate break excitation.” We observe a similar result. The low spatial frequency component of the fiber geometry (that is, the smooth curving fibers) creates an excitable pathway through the virtual anode. If a wavefront is excited by the break mechanism, it can propagate through this excitable pathway. Our analysis extends this idea by examining the fate of the break-excited wavefront once it reaches the far edge of the virtual anode. With no random fiber distribution, this wave front typically propagates into excitable tissue, often resulting in reentry. The addition of the random fiber geometry dramatically affects the fate of the break wave front. If the S2 stimulus is applied late, the surrounding tissue is directly excited by the shock, so it fires an S2 action potential nearly uniformly throughout the tissue (whole tissue make excitation, Fig. 6). The break wavefront, when it reaches the edge of the virtual anode, now encounters inexcitable tissue not because of remaining refractoriness from the S1 action potential, but from the shock-induced S2 action potential. If S2 is applied early, whole tissue make excitation does not occur and the break wave front terminates when it reaches the edge of the virtual anode because of refractoriness from the S1 action potential. Moreover, the S2 shock can extend the refractory period of the S1 action potential, especially for strong shocks (25), making it even more likely that the break wave front will find no excitable tissue to propagate into. Thus, the small-scale, widespread heterogeneities caused by the random fiber geometry are crucial, as they cause the break wave front to be engulfed in depolarized, and therefore refractory, tissue.

The threshold for make excitation is higher for the tissue containing only a random component of the fiber geometry, compared to the tissue with only the smooth fiber curvature. Thus, some intermediate strength S2 shocks are strong enough to trigger wave fronts caused by the smooth fiber curvature, and may even be strong enough to induce reentry, but are not strong enough to excite the surrounding tissue by whole tissue make excitation. In this case, the random fiber geometry does not play a crucial role in the wavefront dynamics. But as soon as the S2 shock is strong enough to excite the surrounding tissue by whole tissue make excitation (or significantly extend the S1 refractoriness), the break wave front is more likely to terminate before it can develop into reentry. Our model suggests that this is one of the key mechanisms underlying the upper limit of vulnerability.

Our results are similar to those reported by Rodriguez and Trayanova (10) in their study of the ULV. However, we did not observe a consistent increase in propagation speed through the virtual anode with increased shock strength, as others have reported (7). When measured at the point in the virtual anode shown in Fig. 8, the conduction velocity actually decreased slightly with increasing S2 strength, from 0.246 m/s for an S2 strength of 139 V/m (0.8×ULV) to 0.243 m/s for a strength of 209 V/m (1.2×ULV). However, the arrival time of the wave front at that point decreased by 1.5 ms as the S2 strength was increased, suggesting that increasing S2 strength reduces the time needed to reach the left edge of the virtual anode primarily by shortening the latency of the break wave front, rather than increasing its speed. We examined other locations, such as those near the peak hyperpolarization, but the wave front dynamics were very complex there, as break excitation occurred along the entire virtual cathode-virtual anode boundary, resulting in a highly curved wave front and wave front collisions. One could argue that the shortened propagation time across the virtual anode, regardless of its cause, could explain the ULV because it would mean the surrounding tissue did not have enough time to recover from refractoriness. However, if changes in arrival time were an important mechanism underlying the ULV, we would expect to observe a ULV even when no random fiber distribution is present, which is not the case (Fig. 1a). This effect may play a minor role in specific cases, such as the elimination of reentry when the S2 shock strength is increased from 12,000 to 14,000 V/m at an interval of 60 ms in Fig. 1a (in a way similar to the “no response phenomenon” observed previously (26)). In general, however, increasing the S2 shock strength cannot eliminate reentry unless the random fiber distribution is present.

Our calculation has several limitations. We use a simplified fiber geometry instead of one taken from experiment, although this geometry results in adjacent regions of depolarization and hyperpolarization during the shock that are similar to those observed experimentally (16,17). Our model is for a two-dimensional sheet, rather than a realistic three-dimensional heart geometry (27). Other models for the membrane kinetics exist (28) that are more up-to-date than the model we use (12). This could influence our results, particularly our observation that the conduction speed does not change much with the degree of hyperpolarization. Our S1 action potential is initiated uniformly throughout the tissue, which is a simplification (although the S1 action potential gradient may not play a significant role in the subsequent dynamics (29,30)). We performed additional simulations in which a weak S1 was delivered through the same electrodes that applied S2. The S1 wave front originated from the virtual cathode near the center of the tissue and propagated outward, but there was no change in the qualitative mechanism of reentry induction or in the presence of a ULV. We used the boundary condition ∂V_m/∂n =0 at all tissue edges to eliminate boundary effects, and thus we focus exclusively on far-field stimulation. We apply a nearly uniform electric field, which implies that our results are more applicable to understanding external defibrillation than internal defibrillation. Electroporation (31) is not included in the model even though V_m could reach hyperpolarizations of several hundred millivolts during the shock. In general, bidomain simulations predict larger polarizations than are observed in experiments, for a variety of reasons (32). The ULV we predict (17,400 V/m, or 174 V/cm) is larger than observed experimentally (17) or predicted in other calculations (27). Fibrillation-induced ischemia (33) is not included in our model, implying that our model is for a shock delivered soon after the onset of fibrillation, and not minutes afterward. All these limitations are restrictive, and represent weaknesses in our study. However, we believe that the simplicity of our model is also a strength, because it allows us to isolate and uncover the essential mechanisms underlying the phenomena, without distracting and confounding details. By comparing the results in Figs. 1a and 1b, the model highlights the role of small-scale heterogeneities in the response of cardiac tissue to strong shocks.

This study elucidates one mechanism for the upper limit of vulnerability in the heart. The ULV is important, both for its own sake and because it often coincides with the defibrillation threshold (2). Thus, these results provide a hypothesis for the mechanism of defibrillation and defibrillation failure. Furthermore, they suggest that situations that increase the widespread heterogeneity throughout the tissue, such as aging, may influence the mechanism of defibrillation. The future verification of this hypothesis may be important for the design of cardiac defibrillators.

Abbreviations

ULV

Upper Limit of Vulnerability

V_m

Transmembrane Potential