Joint modelling of paired sparse functional data using principal components

Summary

We propose a modelling framework to study the relationship between two paired longitudinally observed variables. The data for each variable are viewed as smooth curves measured at discrete time-points plus random errors. While the curves for each variable are summarized using a few important principal components, the association of the two longitudinal variables is modelled through the association of the principal component scores. We use penalized splines to model the mean curves and the principal component curves, and cast the proposed model into a mixed-effects model framework for model fitting, prediction and inference. The proposed method can be applied in the difficult case in which the measurement times are irregular and sparse and may differ widely across individuals. Use of functional principal components enhances model interpretation and improves statistical and numerical stability of the parameter estimates.

1. Introduction

The relationship between two paired longitudinal observed variables has been studied with regression models for longitudinal data (Liang & Zeger, 1986; Fahrmeir & Tutz, 1994; Moyeed & Diggle, 1994; Zeger & Diggle, 1994; Hoover et al., 1998; Wu et al., 1998; Huang et al., 2002). Also, Liang et al. (2003) modelled the paired longitudinal variables using a mixed-effects varying coefficient model with a measurement error in the covariates. Let X_ij and Y_ij denote longitudinal observations of a covariate and response for subject i at time occasion t_ij. The model of Liang et al. (2003) can be written as

$$Y_{ij}={\beta }_0(t_{ij})+{\gamma }_{0i}(t_{ij})+X_{ij}\{{\beta }_1(t_{ij})+{\gamma }_{1i}(t_{ij})\}+e_i(t_{ij})(j=1,\dots ,m_i,i=1,\dots ,n),$$

where β₀(t) and β₁(t) are fixed functions, γ_0i(t) and γ_1i(t) are zero-mean subject-specific random functions and e_i (t) are zero-mean error processes. In contrast to much existing work, the method effectively models the within-subject correlation in a flexible way by considering subject-specific regression coefficient functions.

However, the regression-based methods, including that of Liang et al. (2003), have several limitations. First, one needs to distinguish response and regressor variables, but sometimes such a distinction is not natural. Secondly, as in Liang et al. (2003), the regression-based methods usually focus on the contemporaneous relationship, that is, the relationship at the same time-point, between two variables. One could include lagged variables as regressors, but there are technical difficulties in the implementation of their method when the observation times for different variables differ, as often occurs in practice. Finally, it may be hard to interpret the results from a contemporaneous regression model if we wish to consider all time-points from the past collectively. The usual interpretation of a regression slope as the average change in the response associated with a unit increase in the regressor is hardly satisfactory since the regressors from different time-points are correlated.

To overcome these shortcomings, we propose an alternative approach. The data for each variable are viewed as smooth curves sampled at discrete time-points plus random errors. The curves are decomposed as the sum of a mean curve and subject-specific deviations from the mean curve. The deviations are subsequently summarized by scores on a few important principal component curves extracted from the data. The association of the pair of curves is then modelled through the association of two low-dimensional vectors of principal component scores corresponding to the two underlying variables. By modelling the mean curves and the principal component curves as penalized splines, we cast our approach into a mixed-effects model framework for model fitting, prediction and inference.

Our method views longitudinal data as sparsely observed functional data (Rice, 2004). Ramsay & Silverman (2005) provide a comprehensive treatment of functional data analysis. The approach in this paper is most closely related to that of James et al. (2000) and Rice & Wu (2001). However, those papers considered models only for single curves, instead of paired curves as in this paper. Similarly to James et al. (2000), our approach is model-based, with the principal component curves being directly outputted from the fitted model. Yao et al. (2005a) proposed a different type of principal components analysis for sparse functional data through the eigen-decomposition of the covariance kernel estimated using two-dimensional smoothing. Yao et al. (2005b) dealt with the functional linear model for longitudinal data using regression through principal component scores. Another approach to modelling the association of paired curves is functional canonical correlation (Leurgans et al., 1993; He et al., 2003), but its adaptation to sparse functional data remains an open problem.

2. The mixed-effects model for single curves

2·1. The mixed-effects model

Shi et al. (1996) and Rice & Wu (2001) suggest using a set of smooth basis functions b_l(t) (l = 1, …, q), such as B-splines, to represent the curves, where the spline coefficients are assumed to be random to capture the individual- or curve-specific effects. Let Y_i(t) be the value of the ith curve at time t and write

$$Y_i(t)=\mu (t)+h_i(t)+{\epsilon }_i(t),$$ (1)

where μ(t) is the mean curve, h_i (t) represents the departure from the mean curve for subject i and ε_i (t) is random noise with mean zero and variance σ². Let b(t) = {b₁(t), …, b_q (t)}^T be the vector of basis functions evaluated at time t. Denote by β an unknown but fixed vector of spline coefficients, and let γ_i be a random vector of spline coefficients for each curve with covariance matrix Γ. When μ(t) and h_i (t) are modelled with a linear combination of B-splines, equation (1) has the mixed-effects model form

$$Y_i(t)=b{(t)}^{\text{T}}\beta +b{(t)}^{\text{T}}{\gamma }_i+{\epsilon }_i(t).$$ (2)

In practice, Y_i (t) is observed only at a finite set of time-points. Let Y_i be the vector consisting of the n_i observed values, let B_i be the corresponding n_i × q spline basis matrix evaluated at these time-points and let ε_i be the corresponding random noise vector with covariance matrix σ²I. The mixed-effects model for the observed data is

$$Y_i=B_i\beta +B_i{\gamma }_i+{\epsilon }_i.$$ (3)

The EM algorithm can be used to calculate the maximum likelihood estimates β̂ and Γ̂ (Laird & Ware, 1982). Given these estimates, the best linear unbiased predictors of the random effects γ_i are

$${\widehat{\gamma }}_i={({\widehat{\sigma }}^2{\widehat{\mathrm{\Gamma }}}^{-1}+B_i^{\text{T}}{B}_i)}^{-1}{B}_i^{\text{T}}(Y_i-B_i\widehat{\beta }).$$

The mean curve μ(t) can then be estimated by μ̂ (t) = b(t)^Tβ̂ and the subject-specific curves h_i (t) can be predicted as ĥ_i (t) = b(t)^Tγ̂_i.

2·2. The reduced-rank model

Since Γ involves q(q + 1)/2 different parameters, its estimator based on a sparse dataset can be highly variable, and the large number of parameters may also make the EM algorithm fail to converge to the global maximum. James et al. (2000) pointed out these problems with the mixed-effects model and instead proposed a reduced-rank model, in which the individual departure from the mean is modelled by a small number of principal component curves. The reduced-rank model is

$$Y_i(t)=\mu (t)+\sum _{j=1}^k{f}_j(t){\alpha }_{ij}+{\epsilon }_i(t)=\mu (t)+f{(t)}^{\text{T}}{\alpha }_i+{\epsilon }_i(t),$$ (4)

where μ(t) is the overall mean, f_j is the jth principal component function or curve, f = (f₁, …, f_k)^T and ε_i (t) is the random error. The principal components are subject to the orthogonality constraint ∫f_j f_l = δ_jl, with δ_jl being the δ function. The components of the random vector α_i give the relative weights of the principal component functions for the i th individual and are called principal component scores. The α_is and ε_is are independent and are assumed to have mean zero. The α_is are taken to have a common covariance matrix and the ε_is are assumed temporally uncorrelated with a constant variance of σ².

Similarly to the mixed-effects model (2), we represent μ and f using B-splines. Let b(t) = {b₁(t), …, b_q (t)}^T be a spline basis with dimension q. Let θ_μ and Θ_f be, respectively, a q-dimensional vector and a q × k matrix of spline coefficients. Write μ(t) = b(t)^Tθ_μ and f(t)^T = b(t)^TΘ_f. The reduced-rank model then takes the form

$$Y_i(t)=b{(t)}^{\text{T}}{\theta }_{\mu }+b{(t)}^{\text{T}}{\mathrm{\Theta }}_f{\alpha }_i+{\epsilon }_i(t),{\epsilon }_i(t)\sim (0,{\sigma }_{\epsilon }^2),{\alpha }_i\sim (0,D_{\alpha }),$$ (5)

where D_α is diagonal, subject to

$${\mathrm{\Theta }}_f^{\text{T}}{\mathrm{\Theta }}_f=I,\int b(t)b{(t)}^{\text{T}}dt=I.$$ (6)

The equations in (6) imply that

$$\int f(t)f{(t)}^{\text{T}}dt={\mathrm{\Theta }}_f^{\text{T}}\int b(t)b{(t)}^{\text{T}}dt{\mathrm{\Theta }}_f=I,$$

which are the usual orthogonality constraints on the principal component curves.

The requirement that the covariance matrix D_α of α_i is diagonal is for identifiability purposes. Without imposing (6), neither Θ_f nor D_α can be identified: only the covariance matrix of Θ_f α_i, namely ${\mathrm{\Theta }}_f{D}_{\alpha }{\mathrm{\Theta }}_f^{\text{T}}$, can be identified. To identify Θ_f and D_α, note that Θ_f α_i = Θ̃_f α̃_i, where Θ̃_f = Θ_f C and α̃_i =C⁻¹ α_i for any invertible k × k matrix C. Therefore, by requiring that D_α be diagonal and that the Θ_f have orthonormal columns, we prevent reparameterization by linear transformation. The identifiability condition is more precisely given in the following lemma, which follows from the uniqueness of the eigen-decomposition of a covariance matrix.

Lemma 1

Assume that ${\mathrm{\Theta }}_f^{\text{T}}{\mathrm{\Theta }}_f=I$ and that the first nonzero element of each column of Θ_f is positive. Let α_i be ordered according to their variances in decreasing order. Suppose the elements of α_i have different variances, that is, var(α_i1) > · · · > var(α_ik). Then the model specified by equations (5) and (6) is identifiable.

In Lemma 1, the first nonzero element of each column of Θ_f is used to determine the sign at the population level. With finite samples, it is best to use the element of the largest magnitude in each column of Θ_f to determine the sign, since this choice is least influenced by finite-sample random fluctuation.

The observed data usually consist of Y_i (t) sampled at a finite number of observation times. For each individual i, let t_i1, …, t_ini be the different time-points at which measures are available. Write

$$Y_i={\{Y_i(t_{i1}),\dots ,Y_i(t_{i{n}_i})\}}^{\text{T}},B_i={\{b(t_{i1}),\dots ,b(t_{i{n}_i})\}}^{\text{T}}.$$

The reduced-rank model can then be written as

$$Y_i=B_i{\theta }_{\mu }+B_i{\mathrm{\Theta }}_f{\alpha }_i+{\epsilon }_i,{\mathrm{\Theta }}_f^{\text{T}}{\mathrm{\Theta }}_f=I,{\epsilon }_i\sim (0,{\sigma }^{2}I),{\alpha }_i\sim (0,D_{\alpha }).$$ (7)

The orthogonality constraints imposed on b(t) are achieved approximately by choosing b(t) such that (L/g)B^TB = I, where B = {b(t₁), …, b(t_g)}^T is the basis matrix evaluated on a fine grid of time-points t₁, …, t_g and L is the length of the interval in which we take these grid points; see Appendix 1 for details of implementation. Since (7) is also a mixed-effects model, an EM algorithm can be used to estimate the parameters. By focusing on a small number of leading principal components, the reduced-rank model (7) employs a much smaller set of parameters than the original model (3), and thus more reliable parameter estimates can be obtained.

2·3. The penalized spline reduced-rank model

The reduced-rank model of James et al. (2000) uses fixed-knot splines. For many applications, especially when the sample size is small, only a small number of knots can be used in order to fit the model to the data. An alternative, more flexible approach is to use a moderate number of knots and apply a roughness penalty to regularize the fitted curves (Eilers & Marx, 1996; Ruppert et al., 2003).

For the reduced-rank model (4)–(7), we can use a moderate q, in the range of 10–20, say, and employ the method of penalized likelihood, with roughness penalties that force the fitted functions μ(t) and f₁(t), …, f_k (t) to be smooth. We focus on roughness penalties of the form of integrated squared second derivatives, though other forms are also applicable. One approach is to use the penalty

$${\lambda }_{\mu }\int {\{{\mu }^{″}(t)\}}^{2}dt+{\lambda }_{f1}\int {\{f_1^{″}(t)\}}^{2}dt+\cdots +{\lambda }_{fk}\int {\{f_k^{″}(t)\}}^{2}dt,$$ (8)

where λ_μ, λ_{f 1}, …, λ_fk are tuning parameters. However, for simplicity, we shall take λ_{f 1} = · · · = λ_fk = λ_f. In terms of model (7), this simplified penalty can be written as

$${{\lambda }_{\mu }}^{\text{T}}{\theta }_{\mu }\int b^{″}(t)b^{″}{(t)}^{\text{T}}{\theta }_{\mu }dt+{\lambda }_f\sum _{j=1}^d{\theta }_{fj}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{fj},$$ (9)

where θ_fj is the j th column of Θ_f.

Assume that the α_is and ε_is are normally distributed. Then,

$$Y_i\sim N(B_i{\theta }_{\mu },{\sigma }^{2}I+B_i{\mathrm{\Theta }}_f{D}_{\alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}})(i=1,\dots ,n),$$

and minus twice the loglikelihood based on the Y_is, with an irrelevant constant omitted, is

$$\sum _{i=1}^{n}log\mid {\sigma }^{2}I+B_i{\mathrm{\Theta }}_f{D}_{\alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}}\mid +{(Y_i-B_i{\theta }_{\mu })}^{\text{T}}{({\sigma }^{2}I+B_i{\mathrm{\Theta }}_f{D}_{\alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}})}^{-1}(Y_i-B_i{\theta }_{\mu }).$$

The method of penalized likelihood minimizes the sum of the above expression and the penalty in (9). While direct optimization is complicated, it is easier to treat the α_is as missing data and employ the EM algorithm. A modification of the algorithm by James et al. (2000) that takes into account the roughness penalty can be applied. The details are not presented here. The algorithm can also be obtained easily as a simplification of our algorithm for joint modelling of paired curves to be given in § 3.

3. The mixed-effects model for paired curves

For data consisting of paired curves, an important problem of interest is modelling the association of the two curves. We first model each curve using the reduced-rank principal components model as discussed in § 2·2, and then model the association of curves by jointly modelling the principal component scores. Roughness penalties are introduced as in § 2·3 to obtain smooth fits of the mean curve and principal components.

Let Y_i (t) and Z_i (t) denote the two measurements at time t for the i th individual. The reduced-rank model has the form

$$\begin{array}{l}{Y}_i(t)=\mu (t)+\sum _{j=1}^{k_{\alpha }}{f}_j(t){\alpha }_{ij}+{\epsilon }_i(t)=\mu (t)+f{(t)}^{\text{T}}{\alpha }_i+{\epsilon }_i(t),\\ Z_i(t)=\nu (t)+\sum _{j=1}^{k_{\beta }}{g}_j(t){\beta }_{ij}+{\xi }_i(t)=\nu (t)+g{(t)}^{\text{T}}{\beta }_i+{\xi }_i(t),\end{array}$$

where μ(t) and ν(t) are the mean curves, f = (f₁, …, f_kα)^T and g = (g₁, …, g_kβ)^T are vectors of principal components, ε_i (t) and ξ_i(t) are measurement errors. The α_i s, β_i s, ε_is and ξ_is are assumed to have mean zero. The measurement errors ε_i (t) and ξ_i (t) are assumed to be uncorrelated with constant variances ${\sigma }_{\epsilon }^2$ and ${\sigma }_{\xi }^2$, respectively. It is also assumed that the α_i s, ε_is and ξ_is are mutually independent, as are the β_i s, ε_is and ξ_i s. The principal components are subject to the orthogonality constraints ∫f_j f_l = δ_jl and ∫g_j g_l = δ_jl, with δ_kl being the Kronecker delta.

For identifiability, the principal component scores α_ij (j = 1, …, k_α), are independent with strictly decreasing variances; see Lemma 1. Similarly, the principal component scores β_ij (j = 1, …, k_β), are also independent with strictly decreasing variances. Denote the diagonal covariance matrices of α_i and β_i by D_α and D_β, respectively.

The relationship between Y_i (t) and Z_i (t) is assumed through the correlation between the principal component scores α_i and β_i. To be specific, we assume that cov(α_i, β_i) = C. Then, α_i and β_i are modelled jointly as follows:

$$\left(\begin{array}{c}{\alpha }_i\\ {\beta }_i\end{array}\right)\sim \left\{\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{D}_{\alpha }& C\\ C^{\text{T}}& D_{\beta }\end{array}\right)\right\}.$$

This is equivalent to the regression model

$${\beta }_i=\mathrm{\Lambda }{\alpha }_i+{\eta }_i,$$ (10)

where $\mathrm{\Lambda }=C^{\text{T}}{D}_{\alpha }^{-1}$ or C = D_αΛ^T, from which it follows that the covariance matrix of η_i is Σ_η = D_β − ΛD_αΛ^T. We find this regression formulation to be more convenient when calculating the likelihood function.

The roles of Y (t) and Z(t) and therefore the roles of α_i and β_i are symmetric in our modelling framework. In the regression formulation (10), however, α_i and β_i do not appear to play symmetric roles, and the interpretation of Λ depends on what is used as the regressor and what is used as the response. However, this formulation only serves as a computational device. If we switch the roles of α_i and β_i, we still obtain the same estimates of the original parameters (D_α, D_β, C).

Let $R=D_{\alpha }^{-1/2}C{D}_{\beta }^{-1/2}$ be the matrix of correlation coefficients, which provides a scale-free measure of the association between α_i and β_i. We call diagonal entries of D_α and D_β, together with ${\sigma }_{\epsilon }^2$ and ${\sigma }_{\xi }^2$, the variance parameters and we refer to the off-diagonal entries of R as the correlation parameters.

We represent μ, ν, f and g as a member of the same space of spline functions with dimension q. The basis of the spline space, denoted by b(t), is chosen to be orthonormal, that is, the components of b(t) = {b₁(t), …, b_q (t)}^T satisfy ∫b_j(t)b_l(t) dt = δ_jl. Let θ_μ and θ_ν be q-dimensional vectors of spline coefficients such that

$$\mu (t)=b{(t)}^{\text{T}}{\theta }_{\mu },\nu (t)=b{(t)}^{\text{T}}{\theta }_{\nu }.$$ (11)

Let Θ_f and Θ_g be, respectively, q × k_α and q × k_β matrices of spline coefficients such that

$$f{(t)}^{\text{T}}=b{(t)}^{\text{T}}{\mathrm{\Theta }}_f,g{(t)}^{\text{T}}=b{(t)}^{\text{T}}{\mathrm{\Theta }}_g.$$ (12)

For each individual i, the two variables may have different observation times. However, for simplicity in presentation, we assume that there is a common set of observation times, t_i1, …, t_ini. Write Y_i = {Y_i (t_i1), …, Y_i (t_ini)}^T and similarly for Z_i. Let B_i = {b(t_i1), …, b(t_ini)}^T. The model for the observed data can be written as

$$\begin{array}{l}{Y}_i=B_i{\theta }_{\mu }+B_i{\mathrm{\Theta }}_f{\alpha }_i+{\epsilon }_i,\\ Z_i=B_i{\theta }_{\nu }+B_i{\mathrm{\Theta }}_g{\beta }_i+{\xi }_i,\\ {\beta }_i=\mathrm{\Lambda }{\alpha }_i+{\eta }_i,\\ {\epsilon }_i\sim (0,{\sigma }_{\epsilon }^2{I}_{n_i}),{\xi }_i\sim (0,{\sigma }_{\xi }^2{I}_{n_i}),{\alpha }_i\sim (0,D_{\alpha }),{\beta }_i\sim (0,D_{\beta }).\end{array}$$ (13)

To make this model identifiable, we require that ${\mathrm{\Theta }}_f^{\text{T}}{\mathrm{\Theta }}_f=I$ and ${\mathrm{\Theta }}_g^{\text{T}}{\mathrm{\Theta }}_g=I$, and that the first nonzero element of each column of Θ_f and Θ_g be positive. In addition, the elements of α_i and β_i are ordered according to their variances in decreasing order.

Parameter estimation using the penalized normal likelihood is discussed in detail in § 4. Given the estimated parameters, the mean curves of Y and Z and the principal component curves are estimated by plugging relevant parameter estimates into (11) and (12). Predictions of the principal component scores α_i and β_i are obtained using the best linear unbiased predictors,

$${\widehat{\alpha }}_i=E({\alpha }_i\mid Y_i,Z_i,\mathrm{\Xi }),{\widehat{\beta }}_i=E({\beta }_i\mid Y_i,Z_i,\mathrm{\Xi }),$$

where Ξ denotes collectively all the estimated parameters, and the conditional means can be calculated using the formulae given in Appendix 2. The predictors of the α_is and β_i s, combined with the estimates of μ(t), ν(t), f(t) and g(t), give predictors of the individual curves.

4. Fitting the bivariate reduced-rank model

4·1. Penalized likelihood

If we assume normality, the joint distribution of Y_i and Z_i is determined by the mean vector and variance-covariance matrix, which are given by

$$\begin{array}{c}E(Y_i)=B_i{\theta }_{\mu },E(Z_i)=B_i{\theta }_{\nu },\\ var(Y_i)=B_i{\mathrm{\Theta }}_f{D}_{\alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}}+{\sigma }_{\epsilon }^2{I}_{n_i},var(Z_i)=B_i{\mathrm{\Theta }}_g{D}_{\beta }{\mathrm{\Theta }}_g^{\text{T}}{B}_i^{\text{T}}+{\sigma }_{\xi }^2{I}_{n_i},\\ cov(Y_i,Z_i)=B_i{\mathrm{\Theta }}_f{D}_{\alpha }{\mathrm{\Lambda }}^{\text{T}}{\mathrm{\Theta }}_g^{\text{T}}{B}_i^{\text{T}}.\end{array}$$

Let L(Y_i, Z_i) denote the contribution to the likelihood from subject i. The joint likelihood for the whole dataset is ${\prod }_{i=1}^{n}L(Y_i,Z_i)$. The method of penalized likelihood minimizes the criterion

$$\begin{array}{l}-2\sum _{i=1}^{n}logL(Y_i,Z_i)\\ +{\lambda }_{\mu }{{\theta }_{\mu }}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{\mu }+{\lambda }_f\sum _{j=1}^{k_{\alpha }}{\theta }_{fj}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{fj}\\ +{\lambda }_{\nu }{{\theta }_{\nu }}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{\nu }+{\lambda }_g\sum _{j=1}^{k_{\beta }}{\theta }_{gj}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{gj},\end{array}$$ (14)

where d_αj and d_βj are, respectively, the j th diagonal elements of D_α and D_β, while θ_fj and θ_gj are, respectively, the jth columns of Θ_f and Θ_g. There are four regularization parameters, and this gives the flexibility of allowing different amounts of smoothing for the mean curves and principal components.

Direct minimization of (14) is complicated. If the α_is and β_is were observable, then the joint likelihood for (Y_i, Z_i, α_i, β_i) could be factorized as

$$L(Y_i,Z_i,{\alpha }_i,{\beta }_i)=f(Y_i\mid {\alpha }_i)f(Z_i\mid {\beta }_i)f({\beta }_i\mid {\alpha }_i)f({\alpha }_i).$$

With an irrelevant constant ignored, it follows that

$$\begin{array}{l}-2logL(Y_i,Z_i,{\alpha }_i,{\beta }_i)\\ =n_{i}log({\sigma }_{\epsilon }^2)+\frac{1}{{\sigma }_{\epsilon }^2}{(Y_i-B_i{\theta }_{\mu }-B_i{\mathrm{\Theta }}_f{\alpha }_i)}^{\text{T}}(Y_i-B_i{\theta }_{\mu }-B_i{\mathrm{\Theta }}_f{\alpha }_i)\\ +n_{i}log({\sigma }_{\xi }^2)+\frac{1}{{\sigma }_{\xi }^2}{(Z_i-B_i{\theta }_{\nu }-B_i{\mathrm{\Theta }}_g{\beta }_i)}^{\text{T}}(Z_i-B_i{\theta }_{\nu }-B_i{\mathrm{\Theta }}_g{\beta }_i)\\ +log(\mid {\mathrm{\sum }}_{\eta }\mid )+{({\beta }_i-\mathrm{\Lambda }{\alpha }_i)}^{\text{T}}{\mathrm{\sum }}_{\eta }^{-1}({\beta }_i-\mathrm{\Lambda }{\alpha }_i)+log(\mid D_{\alpha }\mid )+{\alpha }_i^{\text{T}}{D}_{\alpha }^{-1}{\alpha }_i.\end{array}$$ (15)

Clearly, the unknown parameters are separated in the loglikelihood and therefore separate optimization is feasible. We thus treat α_i and β_i as missing values and use the EM algorithm (Dempster et al., 1977) to estimate the parameters.

4·2. Conditional distributions

The E-step of the EM algorithm consists of finding the prediction of the random effects α_i and β_i and their moments based on (Y_i, Z_i) and the current parameter values. In this section, all calculation is done given the current parameter values, although the dependence is suppressed in the notation throughout. The conditional distribution of (α_i, β_i) given (Y_i, Z_i) is normal,

$$\left(\begin{array}{c}{\alpha }_i\\ {\beta }_i\end{array}\right)\sim N\left\{\left(\begin{array}{l}{\mu }_{i,\alpha }\hfill \\ {\mu }_{i,\beta }\hfill \end{array}\right),{\mathrm{\sum }}_i=\left(\begin{array}{ll}{\mathrm{\sum }}_{i,\alpha \alpha },\hfill & {\mathrm{\sum }}_{i,\alpha \beta }\hfill \\ {\mathrm{\sum }}_{i,\beta \alpha },\hfill & {\mathrm{\sum }}_{i,\beta \beta }\hfill \end{array}\right)\right\}.$$ (16)

The predictions required by the EM algorithm are

$$\begin{array}{c}{\widehat{\alpha }}_i=E({\alpha }_i\mid Y_i,Z_i)={\mu }_{i,\alpha },{\widehat{\beta }}_i=E({\beta }_i\mid Y_i,Z_i)={\mu }_{i,\beta },\\ M_{i,\alpha \alpha }=E({\alpha }_i{\alpha }_i^{\text{T}}\mid Y_i,Z_i)={\widehat{\alpha }}_i{\widehat{\alpha }}_i^{\text{T}}+{\mathrm{\sum }}_{i,\alpha \alpha },M_{i,\beta \beta }=E({\beta }_i{\beta }_i^{\text{T}}\mid Y_i,Z_i)={\widehat{\beta }}_i{\widehat{\beta }}_i^{\text{T}}+{\mathrm{\sum }}_{i,\beta \beta },\\ M_{i,\alpha \beta }=E({\alpha }_i{\beta }_i^{\text{T}}\mid Y_i,Z_i)={\widehat{\alpha }}_i{\beta }_i^{\text{T}}+{\mathrm{\sum }}_{i,\alpha \beta }.\end{array}$$ (17)

Calculation of the conditional moments of the multivariate normal distribution (16) is given in Appendix 2.

4·3. Optimization

The M-step of the EM algorithm updates the parameter estimates by minimizing

$$\begin{array}{l}-2E\{logL(Y_i,Z_i,{\alpha }_i,{\beta }_i\mid Y_i,Z_i)\}\\ +{\lambda }_{\mu }{{\theta }_{\mu }}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{\mu }+{\lambda }_f\sum _{j=1}^k{\theta }_{fj}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{fj}\\ +{\lambda }_{\nu }{{\theta }_{\nu }}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{\nu }+{\lambda }_g\sum _{j=1}^k{\theta }_{gj}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{gj},\end{array}$$

or by reducing the value of this objective function as an application of the generalized EM algorithm. Since the parameters are well separated in the expression for the conditional loglikelihood, see (15), we can update the parameter estimates sequentially given their current values. We first update ${\sigma }_{\epsilon }^2$ and ${\sigma }_{\xi }^2$, then θ_μ and θ_ν, and finally D_α, D_β and Λ. Details of the updating formulae are given in Appendix 3. In the last step, some care is needed to enforce the orthonormality constraints on the principal components.

5. Model selection and inference

5·1. Specification of splines and penalty parameters

Given the nature of sparse functional data and the usual low signal-to-noise ratio typical in such datasets, we expect that only the major smooth features in the data can be extracted by statistical methods. Placement of knot positions is therefore not critical for our method, and reasonable ways of doing this include spacing the knots equally over the data range or using sample quantiles of observation times. In our analysis of the AIDS data in § 7, for example, the knots were placed at the common scheduled visit times. Neither is the choice of the number of knots critical, as long as it is moderately large, since the smoothness of the fitted curves is mainly controlled by the roughness penalty. For typical sparse functional datasets, 10–20 knots is often sufficient.

To choose penalty parameters, a subjective choice is often satisfactory. A natural approach for automatic choice of penalty parameters is to maximize the crossvalidated loglikelihood. All examples in this paper use ten-fold crossvalidation. The criterion used for model selection is the sum of the ten calculated testset loglikelihoods.

There are four penalty parameters, so we need to search over a four-dimensional space for a good choice of these parameters. Although the simplex method of Nelder and Mead (1965) could be used, a crude grid search worked well for all examples we considered. With five grid-points on each dimension, there are in total 625 possible combinations for four parameters. Implemented in Fortran, this strategy is computationally feasible and has been used for the data example in § 7. One possible simplification is to let λ_μ = λ_ν and λ_f = λ_g and thus reduce the dimension to two. This simplification, with five grid-points for each of the two dimensions, has been used for our simulation study in § 6.

5·2. Selection of the number of significant principal components

It is important to identify the number of important principal components in functional principal component analysis. For the single-curve model, choosing to fit too many principal components can degrade the fit of them all (James et al., 2000). Fitting too many principal components in the joint modelling is even more harmful, since instability can result if we try to estimate correlation coefficients among a set of latent random variables with big differences in variances.

In our method, we first apply the penalized spline reduced-rank model in § 2·3 to each variable separately and use these single-curve models to select the number of significant principal components for each variable. We then fit the joint model using the chosen numbers of significant principal components from fitting single-curve models; the numbers are refined if necessary. For the single-curve models, we use a stepwise addition approach, starting with one principal component and then adding one principal component at a time to the model. The process stops if the variances of the scores of the principal components already in the model do not change much after the addition of one more principal component, and the variance of the scores of the newly added principal component is much smaller than variances for those already in the model.

A more detailed description of the procedure is as follows. Let k_a and k_b denote the number of important principal components used in a single-curve model for Y and Z, respectively. Let $D_{\alpha ,l}^{(k)}(l=1,\dots ,k)$, denote the variances of the principal component scores for an order-k model for Y. Similarly define $D_{\beta ,l}^{(k)}\text{s}$ for Z. To choose k_a we start with k = 1 and increase k by 1 at a time until we decide to stop according to the criterion described now. For each k, we fit an order-k and an order-(k + 1) single-curve model for Y. If $D_{\alpha ,l}^{(k+1)}\bumpeq D_{\alpha ,l}^{(k)}$ for all l = 1, …, k and $D_{\alpha ,k+1}^{(k+1)}<c{D}_{\alpha ,k}^{(k+1)}$ for some prespecified small constant c, we stop at that k and set k_a = k.

We select k_b similarly. We have used c in the range 1/25 to 1/9 in the above procedure. The joint model is then fitted with the selected k_a and k_b. The variances of the principal component scores from fitting the joint model need not be the same as those from the single-curve models. A refinement using the joint model takes the form of a stepwise deletion procedure. If the variance of the scores of the last principal component is much smaller than the variance of the scores of the previous principal component, delete that principal component from the model. This can be done sequentially if necessary.

We tested this procedure on the simulated datasets from § 6 where, in the true model, the variable Y has one significant principal component and the variable Z has two significant principal components. The results of applying the procedure without the second-stage refinement are as follows. When c = 1/25 was used, among 200 simulation runs, for variable Y, 97% picked one important principal component and 3% picked two important principal components; for variable Z, 98% picked two important principal components and 2% picked three important principal components. When c = 1/9 was used, in all simulations, one principal component was picked for variable Y; for variable Z, in 99% of simulations, two principal components were picked, and in 1% of simulations, one principal component was picked. The first-stage stepwise addition process has thus already provided quite an accurate choice of the number of important principal components, and the second-stage stepwise deletion refinement is not necessary for this example. The use of the second-stage refinement will be illustrated using the data analysis in § 7.

5·3. Confidence intervals

The bootstrap can be applied to produce pointwise confidence intervals of the overall mean functions for both variables and the principal components curves, and of the variance and correlation coefficient parameters. The confidence intervals are based on appropriate sample quantiles of relevant estimates from the bootstrap samples. Here the bootstrap samples are obtained by resampling the subjects, in order to preserve the correlation of observations within subject. When applying the penalized likelihood to the bootstrap samples, the same specification of splines and penalty parameters may be used.

6. Simulation

In this section, we illustrate the performance of penalized likelihood in fitting the bivariate reduced-rank model. In each simulation run, we have n = 50 subjects and each subject has up to four visits between times 0 and 100. We generated the visit times by mimicking a typical clinical setting. The visit times for each subject were generated sequentially with the spacings between the visits normally distributed. In the actual generating procedure, each subject has a baseline visit, so that t_i1 = 0 for i = 1, …, 50. Then, for subject i (i = 1, …, 50), for k = 1, …, 4, we generate t_i,k+1 such that t_i,k+1 − t_i,k ~ N (30, 10²). Let k_i be the first k such that k ≤ 4 and t_i,k+1 > 100. Then, the visit times for subject i are t_i,1, …, t_i,ki.

At visit time t, subject i has two observations (Y_it, Z_it) where Y_it and Z_it are generated according to

$$Y_{it}=\mu (t)+f_y(t){\alpha }_i+{\epsilon }_{it},Z_{it}=\nu (t)+f_{z1}(t){\beta }_{i1}+f_{z2}(t){\beta }_{i2}+{\xi }_{it}.$$

Here, the mean curves have the form μ(t) = 1 + t/100 + exp{−(t − 60)²/500} and ν(t) = 1 −t/100 − exp{−(t − 30)²/500}. The principal component curves are f_y(t) = sin(2πt/100)/√50, f_z1(t) = f_y (t) and f_z2(t) = cos(2πt/100)/√50. The principal component functions are normalized such that ${\int }_0^{100}{f}_y^2(t)dt=1,{\int }_0^{100}{f}_{z1}^2(t)dt=1$ and ${\int }_0^{100}{f}_{z2}^2(t)dt=1$. The variable Z’s two principal component curves are orthogonal: ${\int }_0^{100}{f}_{z1}(t)f_{z2}(t)dt=0$. The principal component scores α_i, β_i1 and β_i2 are independent between subjects, and their distributions are normal with mean 0 and variances D_α = 36, D_β1 = 36 and D_β2 = 16, respectively. The variable Z’s two principal component scores, β_i1 and β_i2, are independent. In addition, the correlation coefficient between α_i and β_i1 is ρ₁ = −0·8 and that between α_i and β_i2 is ρ₂ = −0·45. The measurement errors ε_it and ξ_it are independent and normally distributed with mean 0 and variance 0·5.

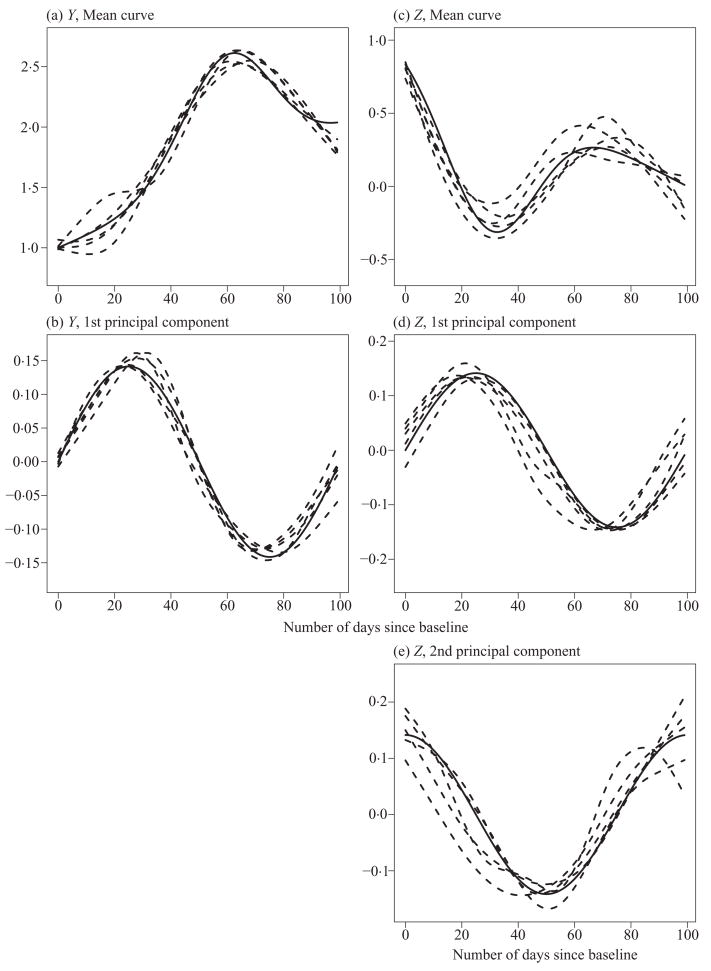
The penalized likelihood method was applied to fit the joint model with k_a = 1 and k_b = 2. Penalty parameters were picked using ten-fold crossvalidation on a grid defined by λ_μ = λ_ν in {k × 10⁴} and λ_f = λ_g in {2k × 10⁵}, for k = 1, …, 5. Figure 1 shows fitted mean curves and the principal component curves for five simulated datasets, along with the true curves used in generating the data. Table 1 presents the sample means and mean squared errors of the variance and correlation parameters, based on 200 simulation runs. Our joint modelling approach was compared with a separate modelling approach that fits Y and Z separately using the single-curve method described in § 2·3. In terms of mean squared error, the single-curve method gives similar, but slightly worse estimates of the variance parameters. However, unlike the joint modelling approach, the single-curve method does not provide estimates of the correlation coefficients of the principal component scores. A naive approach is to use the sample correlation coefficients of the best linear unbiased predictors of the principal component scores from the single-curve model. Since the best linear unbiased predictors are shrinkage estimators, such calculated correlation coefficients can be seriously biased, as shown in Figure 1. Mean integrated squared errors for estimating the mean functions were also computed for the two approaches. The joint modelling approach reduced the mean integrated squared error compared to the separate modelling approach by 23% and 33% for estimating μ(·) and ν(·), respectively. It is not surprising that the joint modelling approach is more efficient than separate modelling, as is well known in seemingly unrelated regressions (Zellner, 1962).

Fig. 1.

Fitted mean curves and principal component curves for five simulated datasets: (a) mean curve of Y, (b) first principal component curve, for Y, (c) mean curve for Z, (d) and (e) first and second principal components for Z.

Solid lines represent true curves and dashed lines represent the fitted curves for the five simulated datasets.

Table 1.

Sample mean and mean squared error (MSE) of variance and correlation parameters in the simulation of § 6. ‘Joint’ and ‘Separate’ refer to, respectively, the joint modelling and separate modelling approach. A number marked with an asterisk equals the actual number multiplied by 100

	Parameter	ρ1	ρ2	Dα	Dβ1	Dβ2	${\sigma }_{\epsilon }^2$	${\sigma }_{\xi }^2$
Joint	True	−0·80	−0·45	36·00	36·00	16·00	0·25	0·25
	Mean	−0·74	−0·49	35·03	35·38	13·08	0·22	0·21
	MSE	2·71*	3·91*	72·11	93·52	25·05	0·15*	0·27*
Separate	Mean	−0·58	−0·37	35·24	36·75	12·88	0·22	0·19
	MSE	6·65*	3·27*	75·07	107·70	30·39	0·19*	0·43*

7. AIDS study example

In this section we illustrate our model and the proposed estimation method using a dataset from a study conducted by the AIDS Clinical Trials Group, ACTG 315 (Lederman et al., 1998; Wu & Ding, 1999). In this study, 46 HIV 1 infected patients were treated with potent antiviral therapy consisting of ritonavir, 3TC and AZT. After initiation of the treatment on day 0, patients were followed for up to 10 visits. Scheduled visit times common for all patients are 7, 14, 21, 28, 35, 42, 56, 70, 84 and 168 days. Since the patients did not follow exactly the scheduled times and/or missed some visits, the actual visit times are irregularly spaced and different for different patients. The visit time varies from day 0 to day 196. The purpose of our statistical analysis is to understand the relationship between virological and immunological surrogate markers such as plasma HIV RNA copies, called the viral load, and CD4+ cell counts during HIV/AIDS treatments.

In the notation of our joint model for paired functional data in § 3, denote by Y the CD4+ cell counts divided by 100 and by Z the base-10 logarithm of plasma HIV RNA copies. As in Liang et al. (2003), the viral load data below the limit of quantification, i.e. 100 copies per ml of plasma, are imputed by the mid-value of the quantification limit, i.e. 50 copies per ml of plasma. To model the curves on the time interval [0, 196], we used cubic B-splines with 10 interior knots placed on scheduled visit days. The penalty parameters were selected by ten-fold crossvalidation. The resampling-subject bootstrap with 1000 repetitions was used to obtain confidence intervals.

Following the method described in § 5·2, we selected the number of important principal components in two stages. In the first stage, the two variables were modelled separately using the single-curve method in § 2·3. A sequence of models with different numbers of principal component functions were considered, and the corresponding variances of principal component scores for these models are given in Table 2. We decided to use two principal components for both Y and Z. In the second step, the model was fitted jointly with k_a = 2 and k_b = 2. The estimates of the variances are D_α1 = 110·1, D_α2 = 1·147, D_β1 = 169·8 and D_β2 = 11·8. Given that the ratio between D_α2 and D_α1 is about 1%, we decided to drop the second principal component for CD4+ counts and to use k_a = 1 and k_b = 2 in our final model. The ratio of D_β2 to D_β1 is about 7%, so that, for the viral load, the second principal component, even though included in the final model, is much less important than the first.

Table 2.

Estimated variances of principal component scores for models with different numbers of principal components in the AIDS example of § 7. The variances are ordered in decreasing order for each model

Number of principal comp.	1	2		3
Principal comp.	1	1	2	1	2	3
Dα	99·6	122·1	7·8	128·7	9·7	(<10−4)
Dβ	93·1	172·9	11·5	174·4	11·5	(<10−4)

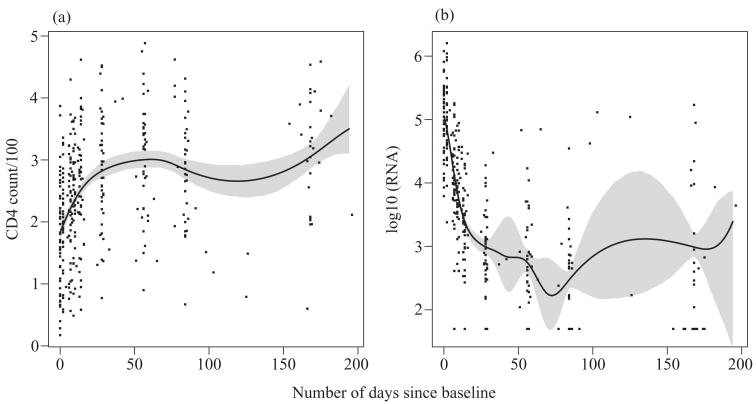
Figure 2 presents CD4+ cell counts and viral load over time, overlaid by their estimated mean curves and 95% bootstrap pointwise confidence intervals for the means. The plots show that on average, CD4+ cell counts increase while viral load decreases dramatically until day 28. After CD4+ counts plateau out at 28 days, but the viral load still drops until about 50 days. The feature after 50 days in the viral-load plot is an artifact of few observations and an outlier affecting crossvalidation; the feature disappears with a larger smoothing parameter.

Fig. 2.

AIDS study. (a) CD4+ cell counts and (b) viral load over time as a function of days, overlaid by estimated mean curves and corresponding 95% bootstrap pointwise confidence intervals.

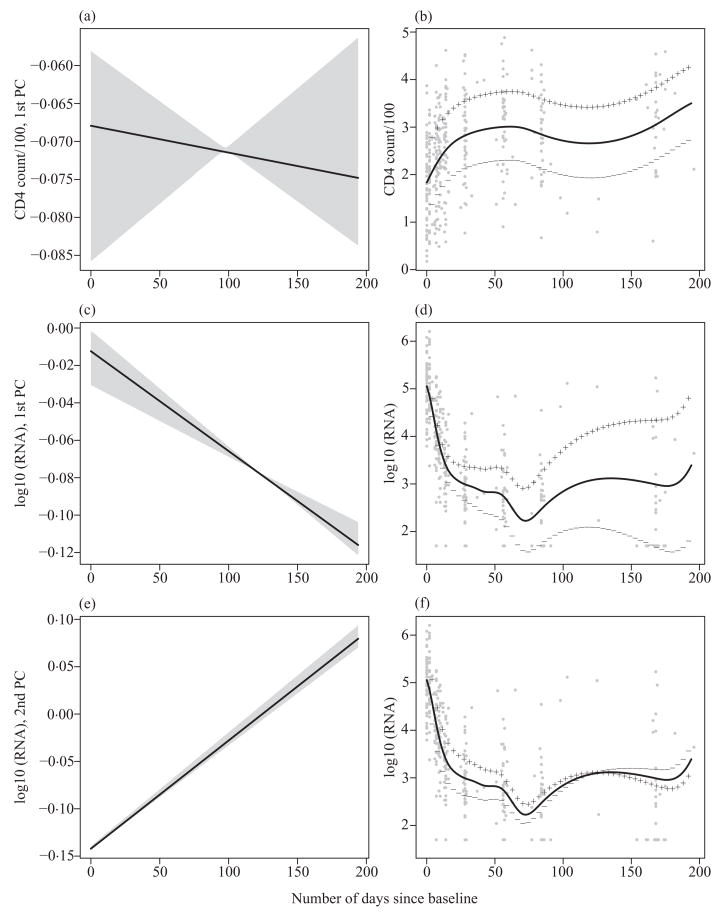
Figure 3 shows the estimated principal component curves of CD4+ counts and the viral load, along with the corresponding 95% bootstrap pointwise confidence intervals. The effect on the mean curves of adding and subtracting a multiple of each of the principal component curves is also given in Fig. 3, in which the standard deviations of the corresponding principal component scores are used as the multiplicative factors. The principal component curve for the CD4+ counts is almost constant over the time range and corresponds to an effect of a level shift from the overall mean curve. The first principal component curve for the viral load corresponds to a level shift from the overall mean with the magnitude of the shift increasing with time. The second principal component curve for the viral load changes sign during the time period and corresponds to opposite departures from the mean at the beginning and the end of the time period. Compared with the first principal component, it explains much less variability in the data and can be viewed as a correction factor to the prediction made by the first principal component. We did not know the shape of the principal component curves prior to the analysis, but it turns out that all estimated principal component curves are rather smooth and close to linear. This may be caused by the high level of noise in the data that prevents the identification of more subtle features; the data-driven crossvalidation does not support the use of smaller penalties. Given that the two principal components are obtained from a high-dimensional function space, dimension reduction is quite effective in this example.

Fig. 3.

AIDS study. Estimated principal component curves for (a) CD4+ cell counts and (c) and (e) viral load with corresponding 95% pointwise confidence intervals. (b), (d) and (f) Effect on the mean curves of adding (plus signs) and subtracting (minus signs) a multiple of each of the principal components, shown on the panels (a), (c) and (e).

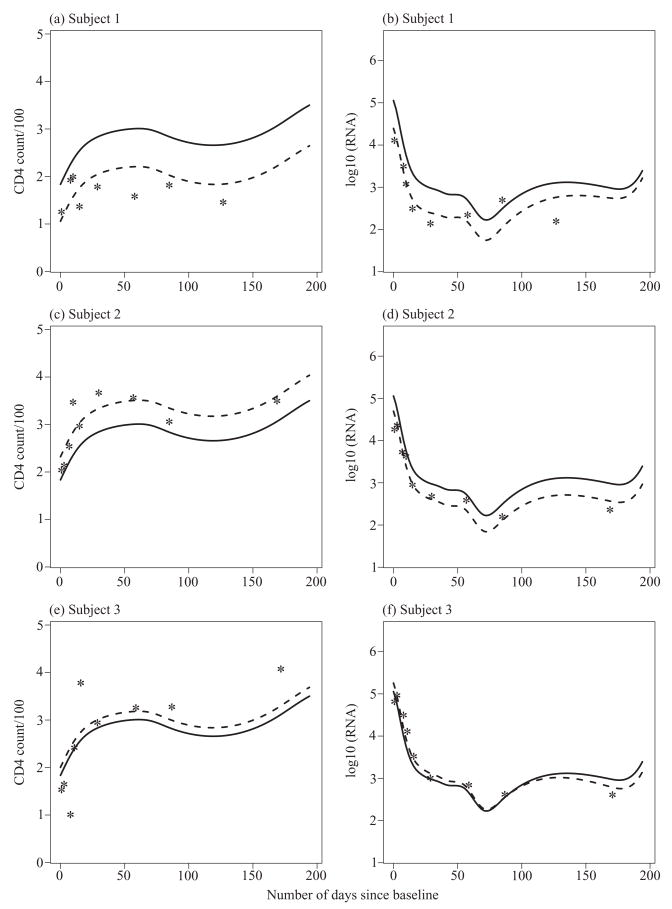
In Fig. 4, we plot observed data for three typical subjects and corresponding mean curves and best linear unbiased predictions of the underlying subject-specific curves. The predicted values of the scores corresponding to the first principal component of CD4+ counts are 11·43, −7·15 and −2·49 for the three subjects, respectively. The predicted values of the scores of the first principal component of viral load are 4·43, 5·11 and 1·05, and those of the second principal component are 4·26, 2·08 and −1·50. These predicted scores and the graphs in Fig. 4 agree with the interpretation of the principal components given in the previous paragraph. For example, the first subject has a positive score while the second and third subjects have negative scores on the first principal component of CD4+ counts, corresponding to a downward and upward shift of the predicted curves from the mean curve, respectively. The crossover effect of the second principal component of viral load is clearly seen in the third subject.

Fig. 4.

Data and predictions for three selected subjects. Asterisks denote observed values of (CD4 + count)/100 and log₁₀(RNA), solid lines denote estimated mean curves and dashed lines denote best linear unbiased predictions of the subject-specific curves.

Estimates of variance and correlation parameters are given in Table 3 together with the corresponding 95% bootstrap confidence intervals. Of particular interest is the parameter ρ₁, the correlation coefficient between α_i1 and β_i1, which are the scores corresponding to the first principal component of CD4+ counts and viral load, respectively. The estimated ρ₁ is statistically significantly negative, which suggests that a positive score on the first principal component of CD4+ counts tends to be associated with a negative score on the first principal component of viral load. In other words, for a subject with CD4+ count lower, respectively higher, than the mean, the viral load tends to be higher, respectively lower, than the mean.

Table 3.

Estimates of variance and correlation parameters and their 95% bootstrap confidence intervals in the AIDS example of § 7. ‘Lower’ and ‘upper’ represent the lower and upper end points of the confidence intervals (CI)

Parameter	ρ1	ρ2	Dα	Dβ1	Dβ2	${\sigma }_{\epsilon }^2$	${\sigma }_{\xi }^2$
Estimate	−0·35	0·04	106·30	170·50	11·66	0·25	0·13
95% CI, lower	−0·92	−0·08	54·68	96·20	5·74	0·20	0·09
95% CI, upper	−0·05	0·08	163·60	302·52	17·43	0·30	0·16

Appendix 1

Creation of a basis b(t) that satisfies the orthonormal constraints

Let b̃(t) = (b̃₁(t), …, b̃_q(t))^T be an initially chosen, not necessarily orthonormal, basis such as the B-spline basis. A transformation matrix T such that b(t) = Tb̃(t) can be constructed as follows. Write B̃ = {b̃(t₁), …, b̃(t_g)}^T. Let B̃ = QR be the QR decomposition of B̃, where Q has orthonormal columns and R is an upper triangular matrix. Then, T = (g/L)^1/2R^−T will be a desirable transformation matrix since

$$\frac{L}{g}{B}^{\text{T}}B=\frac{L}{g}T{\stackrel{\sim }{B}}^{\text{T}}\stackrel{\sim }{B}{T}^{\text{T}}=\frac{L}{g}T{R}^{\text{T}}{Q}^{\text{T}}QR{T}^{\text{T}}=I.$$

Appendix 2

Conditional moments of the multivariate normal distribution (16)

Write ${\mathrm{\sum }}_i^{-1}$ as

$${\mathrm{\sum }}_i^{-1}=\left(\begin{array}{ll}{\mathrm{\sum }}_i^{\alpha \alpha },\hfill & {\mathrm{\sum }}_i^{\alpha \beta }\hfill \\ {\mathrm{\sum }}_i^{\beta \alpha },\hfill & {\mathrm{\sum }}_i^{\beta \beta }\hfill \end{array}\right).$$

Then, the conditional distribution satisfies

$$f({\alpha }_i,{\beta }_i\mid Y_i,Z_i)\propto exp\left[-\frac{1}{2}\{{({\alpha }_i-{\mu }_{i,\alpha })}^{\text{T}},{({\beta }_i-{\mu }_{i,\beta })}^{\text{T}}\}\left(\begin{array}{ll}{\mathrm{\sum }}_i^{\alpha \alpha },\hfill & {\mathrm{\sum }}_i^{\alpha \beta }\hfill \\ {\mathrm{\sum }}_i^{\beta \alpha },\hfill & {\mathrm{\sum }}_i^{\beta \beta }\hfill \end{array}\right)\left(\begin{array}{c}{\alpha }_i-{\mu }_{i,\alpha }\\ {\beta }_i-{\mu }_{i,\beta }\end{array}\right)\right].$$

On the other hand, f(α_i, β_i | Y_i, Z_i) ∝ f(α_i, β_i, Y_i, Z_i)· Comparing the coefficients of the quadratic forms ${\alpha }_i^{\text{T}}{\mathrm{\sum }}_i^{\alpha \alpha }{\alpha }_i,{\alpha }_i^{\text{T}}{\mathrm{\sum }}_i^{\alpha \beta }{\beta }_i$ and ${\beta }_i^{\text{T}}{\mathrm{\sum }}_i^{\beta \beta }{\beta }_i$ in the two expressions of the conditional distribution, we obtain

$$\begin{array}{l}{\mathrm{\sum }}_i^{\alpha \alpha }=D_{\alpha }^{-1}+{\mathrm{\Lambda }}^{\text{T}}{\mathrm{\sum }}_{\eta }^{-1}\mathrm{\Lambda }+{\sigma }_{\epsilon }^{-2}{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}}{B}_i{\mathrm{\Theta }}_f,\\ {\mathrm{\sum }}_i^{\alpha \beta }=-{\mathrm{\Lambda }}^{\text{T}}{\mathrm{\sum }}_{\eta }^{-1},\\ {\mathrm{\sum }}_i^{\beta \beta }={\mathrm{\sum }}_{\eta }^{-1}+{\sigma }_{\xi }^{-2}{\mathrm{\Theta }}_g^{\text{T}}{B}_i^{\text{T}}{B}_i{\mathrm{\Theta }}_g.\end{array}$$

These can be used to calculate Σ_i,αα, Σ_i,αβ and Σ_i,ββ through the formulae

$$\begin{array}{l}{\mathrm{\sum }}_{i,\alpha \alpha }={\{{\mathrm{\sum }}_i^{\alpha \alpha }-{\mathrm{\sum }}_i^{\alpha \beta }{({\mathrm{\sum }}_i^{\beta \beta })}^{-1}{\mathrm{\sum }}_i^{\beta \alpha }\}}^{-1},\\ {\mathrm{\sum }}_{i,\alpha \beta }=-{\mathrm{\sum }}_{i,\alpha \alpha }{\mathrm{\sum }}_i^{\alpha \beta }{({\mathrm{\sum }}_i^{\beta \beta })}^{-1},\\ {\mathrm{\sum }}_{i,\beta \beta }={\{{\mathrm{\sum }}_i^{\beta \beta }-{\mathrm{\sum }}_i^{\beta \alpha }{({\mathrm{\sum }}_i^{\alpha \alpha })}^{-1}{\mathrm{\sum }}_i^{\alpha \beta }\}}^{-1},\end{array}$$

or direct matrix inversion of ${\mathrm{\sum }}_i^{-1}$.

Similarly, comparing the coefficients of the first-order terms, we obtain

$$\begin{array}{l}{\mathrm{\sum }}_i^{\alpha \alpha }{\mu }_{i,\alpha }+{\mathrm{\sum }}_i^{\alpha \beta }{\mu }_{i,\beta }={\sigma }_{\epsilon }^{-2}{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}}(Y_i-B_i{\theta }_{\mu }),\\ {\mathrm{\sum }}_i^{\beta \alpha }{\mu }_{i,\alpha }+{\mathrm{\sum }}_i^{\beta \beta }{\mu }_{i,\beta }={\sigma }_{\xi }^{-2}{\mathrm{\Theta }}_g^{\text{T}}{B}_i^{\text{T}}(Z_i-B_i{\theta }_{\nu }),\end{array}$$

which implies that

$$\begin{array}{l}{\mu }_{i,\alpha }={\sigma }_{\epsilon }^{-2}{\mathrm{\sum }}_{i,\alpha \alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}}(Y_i-B_i{\theta }_{\mu })+{\sigma }_{\xi }^{-2}{\mathrm{\sum }}_{i,\alpha \beta }{\mathrm{\Theta }}_g{B}_i^{\text{T}}(Z_i-B_i{\theta }_{\nu }),\\ {\mu }_{i,\beta }={\sigma }_{\epsilon }^{-2}{\mathrm{\sum }}_{i,\beta \alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}}(Y_i-B_i{\theta }_{\mu })+{\sigma }_{\xi }^{-2}{\mathrm{\sum }}_{i,\beta \beta }{\mathrm{\Theta }}_g^{\text{T}}{B}_i^{\text{T}}(Z_i-B_i{\theta }_{\nu }).\end{array}$$

Appendix 3

Updating formulae for the M-step of the EM algorithm

In the updating formulae given below, the parameters that appear on the right-hand side of equations are all fixed at their current estimates. The involved conditional moments are as defined in (17) of § 4·2.

Step 1

Update the estimates of ${\sigma }_{\epsilon }^2$ and ${\sigma }_{\xi }^2$. We update ${\sigma }_{\epsilon }^2$ using ${\widehat{\sigma }}_{\epsilon }^2={\sum }_{i=1}^{n}E({\epsilon }_i^{\text{T}}{\epsilon }_i\mid Y_i)/{\sum }_{i=1}^n{n}_i$ and ${\sigma }_{\xi }^2$ similarly. The updating formulae are

$$\begin{array}{l}{\widehat{\sigma }}_{\epsilon }^2=\frac{1}{{\sum }_{i=1}^n{n}_i}\sum _{i=1}^n\{{(Y_i-B_i{\theta }_{\mu }-B_i{\mathrm{\Theta }}_f{\widehat{\alpha }}_i)}^{\text{T}}(Y_i-B_i{\theta }_{\mu }-B_i{\mathrm{\Theta }}_f{\widehat{\alpha }}_i)+\text{tr}(B_i{\mathrm{\Theta }}_f{\mathrm{\sum }}_{i,\alpha \alpha }{\mathrm{\Theta }}_f^{\text{T}}{B}_i^{\text{T}})\},\\ {\widehat{\sigma }}_{\xi }^2=\frac{1}{{\sum }_{i=1}^n{n}_i}\sum _{i=1}^n\{{(Z_i-B_i{\theta }_{\nu }-B_i{\mathrm{\Theta }}_g{\widehat{\beta }}_i)}^{\text{T}}(Z_i-B_i{\theta }_{\nu }-B_i{\mathrm{\Theta }}_g{\widehat{\beta }}_i)+\text{tr}(B_i{\mathrm{\Theta }}_g{\mathrm{\sum }}_{i,\beta \beta }{\mathrm{\Theta }}_g^{\text{T}}{B}_i^{\text{T}})\}.\end{array}$$

Step 2

Update the estimates of θ_μ and θ_ν. The updating formulae are

$$\begin{array}{l}{\widehat{\theta }}_{\mu }={\left\{\sum _{i=1}^n{B}_i^{\text{T}}{B}_i+{\sigma }_{\epsilon }^2{\lambda }_{\mu }\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt\right\}}^{-1}\sum _{i=1}^n{B}_i^{\text{T}}(Y_i-B_i{\mathrm{\Theta }}_f{\widehat{\alpha }}_i),\\ {\widehat{\theta }}_{\nu }={\left\{\sum _{i=1}^n{B}_i^{\text{T}}{B}_i+{\sigma }_{\xi }^2{\lambda }_{\nu }\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt\right\}}^{-1}\sum _{i=1}^n{B}_i^{\text{T}}(Z_i-B_i{\mathrm{\Theta }}_g{\widehat{\beta }}_i).\end{array}$$

Step 3

Update the estimates of Θ_f and Θ_g. We update the columns of Θ_f and Θ_g sequentially. Write Θ_f = (θ_α1, θ_α2, …, θ_αkα) and Θ_g = (θ_β1, …, θ_βkβ). For j = 1, …, k_α, we minimize

$$\sum _{i=1}^{n}E\left({\Vert Y_i-B_i{\theta }_{\mu }-\sum _{l\ne j}{B}_i{\theta }_{\alpha l}{\alpha }_{il}-B_i{\theta }_{\alpha j}{\alpha }_{ij}\Vert }^2\mid Y_i,Z_i\right)+{\sigma }_{\epsilon }^2{\lambda }_f{\theta }_{fj}^{\text{T}}\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt{\theta }_{fj}$$

with respect to θ_αj. The solution gives the update for θ_αj,

$${\widehat{\theta }}_{\alpha j}={\left\{\sum _{i=1}^n{\widehat{\alpha }}_{ij}^2{B}_i^{\text{T}}{B}_i+{\sigma }_{\epsilon }^2{\lambda }_f\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt\right\}}^{-1}\sum _{i=1}^n{B}_i^{\text{T}}\left\{(Y_i-B_i{\theta }_{\mu }){\widehat{\alpha }}_{ij}-\sum _{l\ne j}{B}_i{\theta }_{\alpha l}{M}_{i,\alpha \alpha }(l,j)\right\}.$$

Similarly, for j = 1, …, k_β,

$${\widehat{\theta }}_{\beta j}={\left\{\sum _{i=1}^n{\widehat{\beta }}_{ij}^2{B}_i^{\text{T}}{B}_i+{\sigma }_{\xi }^2{\lambda }_g\int b^{″}(t)b^{″}{(t)}^{\text{T}}dt\right\}}^{-1}\sum _{i=1}^n{B}_i^{\text{T}}\left\{(Z_i-B_i{\theta }_{\nu }){\widehat{\beta }}_{ij}-\sum _{l\ne j}{B}_i{\theta }_{\beta l}{M}_{i,\beta \beta }(l,j)\right\}.$$

Step 4

Update the estimate of Λ. The updating formula is

$$\widehat{\mathrm{\Lambda }}=\left(\sum _{i=1}^n{M}_{i,\beta \alpha }\right){\left(\sum _{i=1}^n{M}_{i,\alpha \alpha }\right)}^{-1}.$$

Step 5

Orthogonalization. The matrices Θ_f and Θ_g obtained in Step 3 need not have orthonormal columns. We orthogonalize them in this step and also provide an updated estimate of D_α, D_β and Λ. Compute

$${\widehat{\mathrm{\sum }}}_{\alpha }=\frac{1}{n}\sum _{i=1}^n{M}_{i,\alpha \alpha }\text{and}{\widehat{\mathrm{\sum }}}_{\beta }=\frac{1}{n}\sum _{i=1}^n{M}_{i,\beta \beta }.$$

Let ${\widehat{\mathrm{\Theta }}}_f{\widehat{\mathrm{\sum }}}_{\alpha }{\widehat{\mathrm{\Theta }}}_f^{\text{T}}=Q_f{S}_{\alpha }{Q}_f^{\text{T}}$ be the eigenvalue decomposition in which Q_f has orthogonal columns and S_α is diagonal with diagonal elements arranged in decreasing order. The updated Θ̂_f is Q_f and the updated D̂_α is S_α. Similarly, let ${\widehat{\mathrm{\Theta }}}_g{\widehat{\mathrm{\sum }}}_{\beta }{\widehat{\mathrm{\Theta }}}_g^{\text{T}}=Q_g{S}_{\beta }{Q}_g^{\text{T}}$ be the eigenvalue decomposition in which Q_g has orthogonal columns and S_β is diagonal with diagonal elements arranged in decreasing order. The updated Θ̂_g is Q_g and the updated D̂_β is S_β. The orthogonalization process corresponds to transformations ${\alpha }_i\leftarrow Q_f^{\text{T}}{\widehat{\mathrm{\Theta }}}_f{\alpha }_i$ and ${\beta }_i\leftarrow Q_g^{\text{T}}{\widehat{\mathrm{\Theta }}}_g{\beta }_i$. Thus, the corresponding transformation for Λ̂ obtained from Step 4 is $\widehat{\mathrm{\Lambda }}\leftarrow (Q_g^{\text{T}}{\mathrm{\Theta }}_g)\widehat{\mathrm{\Lambda }}{(Q_f^{\text{T}}{\widehat{\mathrm{\Theta }}}_f)}^{-1}$.