Pendular proteins in gases and new avenues for characterization of macromolecules by ion mobility spectrometry

Abstract

Polar molecules align in electric fields when the dipole energy (proportional to field intensity E × dipole moment p) exceeds the thermal rotational energy. Small molecules have low p and align only at inordinately high E or upon extreme cooling. Many biomacromolecules and ions are strong permanent dipoles that align at E achievable in gases and room temperature. The collision cross-sections of aligned ions with gas molecules generally differ from orientationally averaged quantities, affecting ion mobilities measured in ion mobility spectrometry (IMS). Field asymmetric waveform IMS (FAIMS) separates ions by the difference between mobilities at high and low E and hence can resolve and identify macroion conformers based on the mobility difference between pendular and free rotor states. The exceptional sensitivity of that difference to ion geometry and charge distribution holds the potential for a powerful method for separation and characterization of macromolecular species. Theory predicts that the pendular alignment of ions in gases at any E requires a minimum p that depends on the ion mobility, gas pressure, and temperature. At ambient conditions used in current FAIMS systems, p for realistic ions must exceed ≈300–400 Debye. The dipole moments of proteins statistically increase with increasing mass, and such values are typical above ≈30 kDa. As expected for the dipole-aligned regime, FAIMS analyses of protein ions and complexes of ≈30–130 kDa show an order-of-magnitude expansion of separation space compared with smaller proteins and other ions.

Separation and characterization of ions by using their drift in gases forced by electric field, called ion mobility spectrometry (IMS), is becoming common in analytical and structural chemistry (1–6). As with mass spectrometry (MS), initial applications were to small molecules (1, 5, 7) that could be readily ionized. Coupling to MS and to electrospray (ESI) and matrix-assisted laser desorption ionization (MALDI) ion sources in the 1990s (8, 9) brought IMS to biological analyses (2, 4, 6). In particular, peptide and protein folding (2, 4, 9–14) and amyloidogenic misfolding (15) were explored. Application of IMS and IMS/MS is expanding to ever-larger macromolecules, including noncovalent assemblies with mass (m) > 1 MDa (16–18). Such studies have used both drift tube (DT) IMS (1–5, 7–15) and differential mobility analyzers (DMA) (17, 18) to separate ions by absolute mobility (K). In DT IMS, ions are separated while being pulled through still gas by an electric field. In DMA (17–19) ions traverse a space between 2 electrodes while being displaced laterally by gas flow. Only ions of specific K (determined by the voltage across the gap and flow speed) exit the gap, and mobility spectra are obtained by scanning the voltage.

Recently, field asymmetric waveform ion mobility spectrometry (FAIMS) or differential mobility spectrometry has emerged as a major analytical tool (6, 20–28). FAIMS filters ions based on the difference between K at low and high electric field intensity (E). For any ion, K depends on E, usually via E/N where N is the gas number density (29):

Because the leading term is quadratic in E/N, changing K enough for practical analyses requires high E/N. In FAIMS, ions are entrained in a gas flow (6) through a gap between 2 electrodes carrying a periodic asymmetric waveform U(t). The resulting field E(t) drives ion oscillations across the gap. Because K depends on E, the displacements during E(t) segments of opposite polarity generally do not cancel: ions would drift toward one of the electrodes and be neutralized (6). This drift can be offset for a given species by a constant field, E_C, superposed on E(t) by adding a compensation voltage to U(t). The E_C for an ion depends on K(E/N): a species can be balanced in the gap whereas others drift toward an electrode. Scanning E_C provides a spectrum of species present (6).

The coefficients in Eq. 1 are properties of the ion/gas pair controlled by the characteristics of interaction potential Φ known as collision integrals, Ω. Most DT IMS analyses (1) are performed at low E where K ≅ K(0). In that limit, K is inversely proportional to the first-order collision integral (cross-section) Ω_avg^(1,1):

where q is the ion charge, T is the temperature, μ is the reduced mass of ion–molecule pair, and k is the Boltzmann constant (29). The subscript “avg” denotes averaging over all ion orientations: (30)

where Ω_dir^(1,1) is Ω in the direction set by angles φ and γ with respect to a fixed axis (30). Above some threshold, K(E/N) deviates from K(0) in a way that depends on Φ. Ordinary K(E/N) profiles display a continuous increase (“type A” behavior), a decrease (“type C”), or an increase followed by a decrease (“type B”) (6). At very high E/N, energetic collisions sample the repulsive part of Φ and K(E/N) always decreases because of increasing effective temperature in Eq. 2, whereas Ω remains constant (29). Hence, type A behavior reflects a limited E/N range. More complex K(E/N) forms are possible, such as type B with a dip at low E/N for some metal ion/inert gas pairs with strong dispersion forces relative to polarization interactions (31). All K(E/N) trends are controlled by the interplay of various collision integrals defined in gas-phase transport theory (29). Of importance here is that all those were orientationally averaged by using Eq. 3 or equivalent.

In general, K is a function of E for several reasons, although not all matter in every case. The always present factor is the deviation of ion–molecule relative velocities (v_rel) from the thermal distribution (29) at T when the drift velocity v is not a negligible fraction of v_rel. Because the scattering that determines Ω is sensitive to v_rel, the values of Ω, and thus K, depend on v and hence on E/N, with K increasing or decreasing compared with K(0) depending on the depth of the ion–molecule attractive potential relative to kT and other factors (29). For polyatomic ions, heating by above-thermal collisions also affects the time-averaged geometry because of vibrational anharmonicity (32), increasing Ω_avg^(1,1) at higher E/N. At E/N values used in FAIMS, the difference is minimal for small covalently bound species (32) but may be large for flexible macromolecules (e.g., proteins) and noncovalent complexes (14, 33). The K(E/N) profile (and hence the ion type) are dictated by a combination of these and perhaps other effects.

The result is significantly correlated with ion mass (34): ions shift from type B to C with increasing m. The boundary between the types depends on the gas, with that in N₂ or air at room T located at ≈200–400 Da (34). Hence, all peptide, protein, and other macromolecular ions were believed (6, 22–28) to belong to type C, meaning E_C < 0 for negative E(t) polarity. These studies involved small proteins with m <16 kDa, such as ubiquitin (8.6 kDa) and cytochrome c (cyt c; 12.2 kDa). Protein ions have many structural conformers for a particular charge state (z), and several are often resolved (6, 23–28). However, all had E_C < 0 within a limited range of ≈5 V/mm, limiting the peak capacity to ≈10 with the then-best-achievable FAIMS resolution (r) of ≈0.5 V/mm. Although no information about ion geometry has been extracted from E_C values as yet, FAIMS can preseparate ions for established structural probes such as DT IMS (14).

Recently, FAIMS spectra were measured for ESI-generated ions of 10 proteins ranging in mass from ubiquitin to BSA (66.4 kDa) (34). Although proteins with m < 29 kDa behaved as described above, the 3 with larger m, carbonic anhydrase II (CA; 29.0 kDa), alcohol dehydrogenase (ADH; 39.9 kDa), and BSA, exhibited extremely broad E_C ranges (≈50 V/mm) extending to high positive values (34). Such expansion of FAIMS separation space potentially permits resolving ≈100 conformers at r = 0.5 V/mm and yet more by using new planar FAIMS units (27) with better r. This number would far exceed that of macromolecular geometries distinguished by other techniques in solution or gas phase, including liquid chromatography, capillary electrophoresis, DT IMS, DMA, or H/D exchange. Such capability would be of obvious utility for analysis of 3D protein structure (e.g., in the context of postranslational modifications).

We had rationalized those striking observations in terms of the dipole alignment of ions by electric field in FAIMS. Electric dipoles (p) are usually thought of with regard to neutrals. However, polyatomic ions normally have p ≠ 0: the distribution of net charges (q_i) over atoms may be expressed as a dipole (plus possibly higher multipoles) superposed on q = Σ_iq_i in the center of mass. Even a hypothetical ion with all q on 1 atom (not in the center of mass) is in effect a dipole. Hence, virtually any ion could, in principle, be aligned by electric field. This does not affect the Coulomb force on an ion in a homogeneous field and, hence, the m/q ratio measured in MS. However, the Ω _dir^(1,1) values for nonspherical geometries may substantially differ from Ω_avg^(1,1), with a corresponding impact on the ion mobility.

An electric field seeks to orient dipoles along E. For an angle θ between E and p, the torque τ and dipole energy ε_p are:

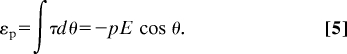Hence, rotating a dipole requires the work of

that has to come from its rotational energy ε_R. Hence dynamics depends on the magnitude of A vs. ε_R. For ε_R ≫ A, the rotation is free and mobility is set by orientationally averaged quantities. As ε_R/A decreases, the rotation becomes hindered, decelerating while the dipole climbs the energy surface and accelerating in the other half-turn. When ε_R drops below A, the barrier to rotation is not surmountable, and the ions librate like a pendulum around the minimal energy position (35, 36). Further decrease of ε_R/A reduces the oscillation amplitude, eventually to an arbitrarily low value—the dipole is “locked” along E.

A pendular state for a species with rotational temperature T_R requires A > ε_R or

meaning p > ≈250 D for T_R = 300 K and typical E = 25 kV/cm in FAIMS. Larger ions and molecules statistically have greater p. For most small molecules, p < 10 D and locking at T_R = 300 K requires an inordinate E > 1 MV/cm (36). Those molecules could, however, be aligned at practical E ≈ 10 kV/cm if cooled in supersonic beams to T ≈ 1 K (35–37). The value of p for proteins is also correlated with size and p > ≈300 D is usually found for larger proteins with m > ≈30 kDa (34). Hence, the emergence of abnormal FAIMS properties for proteins in that mass range supports the pendular ion hypothesis.

Here, we further establish the significance of an ≈30-kDa boundary by FAIMS analyses for additional proteins and first measurements for a noncovalent protein complex, including species with m above the previous maximum of 66 kDa. We introduce the theory for dipole alignment of ions in gases, which, unlike in a vacuum, requires a minimum p regardless of E. This conclusion is consistent with available observations.

Experimental Approach

We have measured E_C spectra for 4 proteins not examined by FAIMS previously. Three (bovine calmodulin, m = 16.8 kDa; bovine pancreatic trypsin, 23.3 kDa; α-chymotrypsinogen, 25.7 kDa) were chosen for their mass somewhat <29 kDa for CA, the lightest protein with “abnormal” behavior in initial experiments (34). The fourth is bovine transferrin (78 kDa), extending the exploration of FAIMS properties to larger proteins. Because protein complexes were not heretofore probed by FAIMS, we have investigated the BSA dimer (132.9 kDa).

The proteins (Sigma) were dissolved in a 1:1 water/methanol mixture to 2–4 μM, except for BSA (15 μM) and transferrin (50 μM). The conformations of proteins in solution are controlled by solution conditions: heating and/or acidification induce denaturation. Some proteins have disulfide (SS) bonds that constrain conformational freedom and are reduced to allow denaturation. Although the geometries of protein ions generated by ESI differ from those of solution precursors, the dependence of DT IMS, FAIMS, and H/D data on solution history evidences a strong correlation (2, 23, 34). To maximize the structural diversity of 3 smaller proteins, we prepared 2 solutions for each. One, minimizing the native conformer disruption, was as close to neutral as possible (“pseudonative” media), although up to 0.1% CH₃COOH was added for reasonable ESI operation. The other, maximizing denaturation, was acidified by 5% CH₃COOH and annealed at 80 °C for 1 h. As shown for CA, intermediate conditions seem to provide intermediate conformers (34). In the denatured samples, the 6 SS bonds of trypsin and 5 of a-chymotrypsinogen were reduced by adding DTT to 0.1 mM final concentration before heating (calmodulin has no SS links). For transferrin and BSA, to maximize the retention of native folds and produce dimers, we prepared only pseudonative solutions containing 0.25–1% CH₃COOH. The data for protein ions with selected z were measured by using the FAIMS/MS system comprising a Selectra FAIMS and the LCQ Deca XP Max ion trap MS stages (Thermo Fisher). The instrument, operating conditions, and experimental procedure were described in ref. 34. The FAIMS waveform had peak E = 25 kV/cm.

Results of FAIMS Measurements

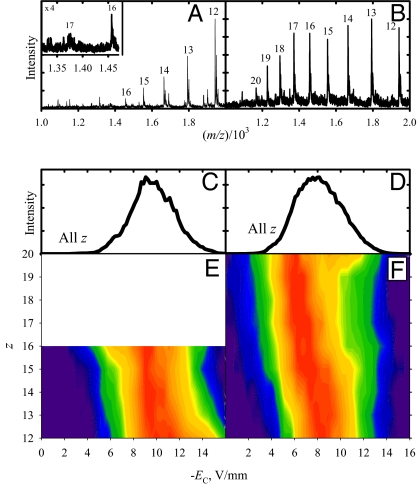
The data for 3 smaller proteins are shown in Fig. 1 and Figs. S1 and S2. Each presents the typical charge state envelope that shifts to higher z upon denaturation (2, 23). The observation and FAIMS analyses for lower z of each protein were precluded, particularly for pseudonative samples, by the MS hardware limitation of m/z < 2,000. The total E_C spectra for all 3 proteins exhibit like featureless distributions between −4 and −14 V/mm. The spectra for denatured species resemble those for pseudonative forms, but slightly displaced to lower absolute E_C with the distribution maxima moved from ≈ −(9–10) to ≈ −(7–8) V/mm. The FAIMS/MS data show that this largely reflects a shift to higher z with somewhat lower ∣E_C∣ values rather than different conformers for specific z. These observations follow those for other proteins with m < 29 kDa (34).

Fig. 1.

Measurements for protonated trypsin ions: MS spectra with charge states labeled (A and B), total FAIMS spectra (C and D), and 2D FAIMS/MS data in false color with intensity on the log scale (E and F). Shown are pseudonative (Left) and denatured (Right) samples.

Transferrin ions behave strikingly differently (Fig. 2). The FAIMS spectrum comprises both E_C > 0 and E_C < 0, extending over ≈50 V/mm (vs. ≤10 V/mm for the 3 smaller proteins). The E_C distribution maximizes at ≈0 with a shoulder at ≈ −5 V/mm. The FAIMS/MS spectra reveal a small peak at ≈23 V/mm for lower z ≈40–45, but otherwise the data for all z are similar. To compare, the spectra for CA, ADH, or BSA cover a similar E_C range (from ≈ −30 to ≈20 V/mm) but are bimodal with maxima at negative E_C of ≈ −(5–10) and positive E_C of ≈ 10–20 V/mm (34). However, they become less bimodal with m increasing from CA to ADH to BSA, and the results for transferrin follow that trend. This may reflect a greater number and diversity of possible folds for larger protein ions. The weakening of the dependence of FAIMS spectra on z in the {CA; ADH; BSA} series (34) also continues for transferrin, although it may be an artifact of our sampling a smaller fraction of the z distribution because of present m/z constraints.

Fig. 2.

Same as Fig. 1 but for transferrin (pseudonative solution).

The MS spectrum obtained for BSA contains intense features between charge states of monomeric BSA [i.e., (H⁺)_zBSA ions] due to BSA dimers (Fig. 3). Stronger Coulomb repulsion between the BSA units with increasing z should make gas-phase dimers progressively unstable. The dimer peaks indeed are less abundant relative to the monomers at higher z, but we could discern them up to (H⁺)₉₃(BSA)₂ by varying the solution conditions. The FAIMS spectra are similar to those for probed proteins with m > 29 kDa in terms of the E_C range. The data are virtually independent of z, continuing the trend of weaker charge dependence for larger proteins noted above. However, the spectra for all z observed (and thus their aggregate) are substantially bimodal, resembling the findings for BSA monomer or ADH more than those for transferrin.

Fig. 3.

Same as Fig. 2 but for BSA dimers with odd z; total FAIMS spectrum is not shown. The dimers are almost certainly present for even z as well, but the mass resolution is far too low to distinguish them from monomers.

Summarizing, all conformers for every measured z of the 3 newly probed proteins with m ≈17–26 kDa belong to type C with negative E_C within a narrow range, as is the case for all proteins with m < 29 kDa reported to date (34). In contrast, conformers of transferrin and BSA dimer ions for every studied z are dispersed over a broad E_C range spanning positive and negative values, as previously observed for m = 29- to 66-kDa proteins. These findings support the concept of a systematic new FAIMS behavior for large macromolecules, ascribed to their dipole alignment in electric field (34). To understand this effect, we developed a model for the pendular alignment of ions in gases.

Model for Pendular Alignment of Ions in Gases

The dipole alignment of molecules or ions in gases differs from that in vacuum where the rotational momentum J must be conserved, and pendular states are field-dependent linear combinations of rotor states created by their adiabatic transformation (35–37). Quantification of that process for quantum states is not trivial (37). Collisions with gas molecules constantly change J and ε_R, and alignment is governed by current conditions regardless of past J or ε_R. For macroions of concern here, ε_R levels are dense and rotation at ≈300 K is classical: ε_R has a continuous distribution subject to thermal statistics. These features greatly simplify the physics of alignment.

The mobilities of aligned ions are still controlled by orientationally averaged cross-sections, but Ω_dir for different orientations are averaged (34) with their weights W:

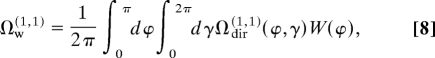where φ = θ. Eq. 8 also works for pendular states, where W(φ) = 0 for some φ. For thermal ions:

The tails of thermal distributions extend to infinity and any ε_p (and thus φ) is found at any T_R, albeit possibly for few ions. Unlike for ions in vacuum with fixed ε_R, the boundary between hindered rotation and pendular motion diffuses: as kT_R/A decreases, the fraction of pendular ions grows, although some continue rotating. So calculating the mobility of dipole-aligned ions reduces to the evaluation of W(φ).

The value of Ω_w will notably differ from Ω_avg when (i) the alignment is strong, i.e., W(φ) is substantially nonuniform and (ii) the ion is aspherical, i.e., Ω_dir significantly depends on φ. The criterion (i) is roughly equivalent to Eq. 7. In the simplest approximation of T_R = T, the value of p needed for material alignment (p_crit) is proportional to 1/E, and any dipole could be locked at E exceeding some E_min. Then Ω depends not on E/N as is usual in ion transport (29) but on E only. This is because the effect is governed by the interaction of ions directly with electric field and not mediated by ion–molecule collisions.

However, ions at high E/N are heated by above-thermal collisions until their internal temperature T_I equals the effective translational temperature:

where M is the gas molecule mass. This “field heating” is mostly known for vibrational excitation that often induces isomerization or dissociation of ions (28) at high E/N. However, the same applies to rotations and the rotational temperature T_R approximately equals T_I by Eq. 10. For example (38), the T_R values for N₂⁺ drifting in He (determined from the rotational state populations measured by laser-induced fluorescence spectroscopy) agree with Eq. 10.

Substituting Eq. 10 into Eq. 7, we obtain a quadratic in E:

that has real solutions only when

As Ω_w, and thus K, of aligned ions depend on p by Eqs. 8 and 10, solving Eq. 11 involves iteration. The convergence depends on the form of Ω_w(p) and remains to be studied, but the initial guess of K at E defined by Eq. 7 might work. Of key importance, a minimum p is needed for alignment regardless of E. For ions with p > p_crit, there arises a finite maximum E allowing alignment, E_max, in addition to E_min. These extremes are the roots of Eq. 11:

For stationary ions (K ⇒ 0), Eq. 12 properly yields p_crit = 0, and Eq. 13 reduces to Eq. 7 for E_min and E_max ⇒ ∞. Alignment requires a minimum p at any E and maximum E for any p because the electric field seeking to lock ions in gases also heats them, pumping energy into rotation and obstructing alignment. The latter effect eventually prevails (unless the electrical breakdown of gas occurs first) because heating scales as E² by Eq. 10, whereas the aligning force scales as E by Eq. 4. For low p and/or high T that require large E for dipole locking, the rotational heating always prevails, and no alignment occurs.

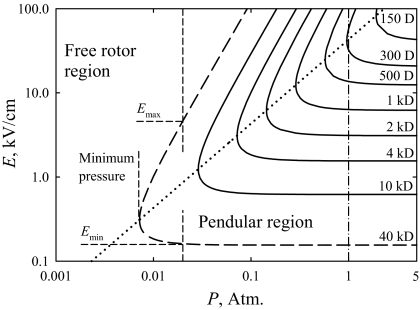
The pendular ion domains defined by Eq. 13 are plotted in Fig. 4. Although electrical breakdown (39) precludes a large region in the upper left-hand corner, this is a useful summary map. Because Eqs. 12 and 13 feature K at experimental conditions, increasing N (i.e., the gas pressure, P) reduces p_crit in proportion to 1/N and expands the range of E for alignment, in theory until the limit of K ⇒ 0 at P ⇒ ∞, where E_max for any ion scales as P². The outcome of reducing P would be opposite, with the range of E allowing alignment for a particular p narrowing and alignment ceasing at the pressure determined from Eq. 12. In the end, the alignment for all ions disappears at low P. At the minimum P allowing alignment for a particular p, the alignment is possible at a single E. Combining Eqs. 12 and 13, we find that value as

or twice E_min by Eq. 7. Hence, if at some pressure no alignment is seen at twice the value of E needed to align a stationary ion, the ion could only be aligned at higher P (Fig. 4). As we discussed, this formalism delineates the approximate boundary of alignment that actually phases in within a margin around that boundary.

Fig. 4.

Pendular region boundaries for species with various dipole moments, calculated for T = 300 K and K₀ = 1.2 cm²/(Vs) in N₂, with relevant quantities shown for p = 40 kD (dashed line). The dotted line connects the minimal pressures for alignment at each p and the dash-dot line marks P = 1 atm.

Rotational ion heating is controlled by molecular collisions and thus by E/N, which inserts N into the problem via K(E/N). This renders the mobility of pendular ions a function of E and N, but not of E/N as for free rotor species.

Comparison of Theory and Experiment

As described, pendular states under present FAIMS conditions require p greater than ≈250 D by Eq. 7. How much is that threshold raised by rotational ion heating? The K values for protein ions studied here are unknown, but can be estimated by scaling mobility as a function of size. The values of Ω for macroions are mainly controlled by their dimensions and not the details of Φ, hence Ω for compact globular proteins is approximately proportional to (volume)^2/3 or m^2/3. The maximum z of those ions produced by ESI scales (40) as m^1/2, thus z/Ω that defines K(0) by Eq. 2 scales as m^−1/6. This dependence is weak, and K(0) for the proteins studied here would be lower than those for ubiquitin or cyt c ions by ≈5–30% only. The actual difference is smaller yet because the finite size of N₂ also contributes to Ω, and thus Ω scales somewhat slower than m^2/3. Indeed, K(0) for ESI-generated ions of ubiquitin, cyt c, and myoglobin (m = 17.0 kDa) are close (41–43). The K(0) of compact ubiquitin and cyt c ion conformers (14, 28) in N₂ are ≈1.0–1.3 cm²/(Vs) at T = 273 K and P = 760 Torr, or ≈1.1–1.4 cm²/(Vs) at T = 300 K. For unfolded proteins, the maximum z scales faster (40) than m^1/2, but their Ω also scales faster than m^2/3.

Substituting K = 1.1–1.4 cm²/(Vs) into Eq. 12, we find p_crit ≈ 260–340 D. By Eqs. 13 and 14, ions with those p could be aligned at E > 37–47 kV/cm, and the alignment at E = 25 kV/cm requires p greater than ≈330–390 D. That would produce alignment in just 1 point of the E(t) cycle, whereas a real effect on FAIMS properties requires that over a significant fraction of time (34), e.g., 20%. In that case, the needed p increases to ≈440–480 D. This is ≈15–20% above p ≈390 D estimated (34) from Eq. 7, indicating a moderate impact of rotational heating on the dipole alignment under present conditions. The effect would be less if the ions studied here have K < 1.1 cm²/(Vs), as suggested by the m^−1/6 scaling, and grow for K > 1.4 cm²/(Vs) at P = 760 Torr or at somewhat lower P that is commonplace because FAIMS is operated at ambient pressure.

The geometries of highly charged protein ions differ from native conformers and likely are substantially unfolded. A priori optimization of proteins with m > 30 kDa is beyond current simulation capabilities, which has prevented modeling of the relevant structures for comparison with FAIMS data via Eq. 8. However, larger molecules or ions (including larger proteins) tend to have higher p regardless of specific geometry, because of both greater dimensions and higher average charge. Therefore, the magnitude of p for free protein ions should broadly track that for native folds. To demonstrate that, we examined ubiquitin ions with characteristic charge states generated by ESI: z = 7 for compact native-like structures, 12 for unfolded geometries, and 10 for a mixture of both (14, 28, 41).

The simulation used a known replica exchange molecular dynamics (REMD) algorithm (44, 45). For adequate sampling, we constructed 22 replicas ranging from 300 to 400 K for each charge state, selecting the temperatures to ensure the exchange acceptance ratio of ≈50% between replicas. Simulations used a modified CHARMM c34b2 software (46) with Langevin integrator, a collision frequency of 2.5 ps⁻¹, and full electrostatics and van der Waals interactions for the entire protein ion. For each replica, the simulation lasted 300 ns, with configuration exchanges allowed every 20 ps. Upon each exchange, the particle velocities were reset (with new values extracted from the Maxwell–Boltzmann distribution at corresponding replica temperature) (45), and frames from REMD trajectories were rotated to align the longest and second-longest principal axes of the protein with the X and Y coordinate vectors, respectively. The net electric moments for proteins were computed by using the established definition (47). The resulting distributions of dipole moments for thus optimized geometries are broad (Fig. 5), and the average p grows at higher z, as may be expected from the increase of both the maximum protein dimensions and total charge. For comparison, one can find near-native protein structures in the Protein Data Bank (PDB) and calculate their dipole moments by using the dedicated web server (48). The result for ubiquitin is 189 D, which is comparable with the typical values for ion geometries with higher z (Fig. 5).

Fig. 5.

Dipole moments computed for ensembles of simulated ubiquitin ions with 20,000 geometries per charge state, versus the radius of gyration. The distributions of dipole moments are plotted on vertical axes.

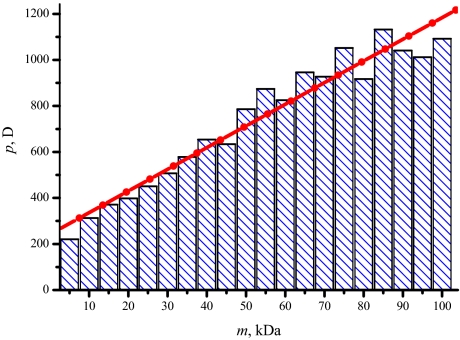
The dipole moments for near-native conformations of larger proteins should be similarly relevant to estimating p for gas-phase ions. Assuming the geometries in PDB, those dipole moments are 427 D for calmodulin, 327 D for trypsin, 376 D for a-chymotrypsinogen, and 1,098 D for (human) transferrin. The value for BSA dimer is likely higher, considering p ≈ 1,100 D for the monomer (34). Overall, these results are consistent with the predicted emergence of pendular states at p > ≈450 D. The correlation of the dipole moments for near-native proteins with size was asserted here and previously (34) based on a limited sample of ≈15 proteins total. This correlation is supported by the statistics for all PDB entries up to 100 kDa (Fig. 6), with p ≈450 D reached at ≈25 - 30 kDa. This threshold is in agreement with all FAIMS measurements for protein ions to date.

Fig. 6.

Histogram of dipole moments calculated for all 3,401 single-strand proteins up to 100 kDa found in the Protein Data Bank (www.rcsb.org).

Conclusions

Studies using differential mobility spectrometry/mass spectrometry have revealed ion mobility properties of gas-phase proteins and protein complexes with masses >30 kDa. The most important finding is an order-of-magnitude expansion of FAIMS separation space to comprise ≈10² distinct conformers at the resolution of existing instruments. That behavior is interpreted as a manifestation of the reversible locking of ion macrodipoles by peak electric fields of FAIMS waveform. The mobilities of pendular ions depend on directional cross-sections that often greatly differ from orientationally averaged quantities controlling the dynamics of free rotors. Because the extent of alignment strongly depends on field intensity, that directional dependence can produce a large difference between mobilities during the high- and low-field segments of FAIMS waveform and a concomitant increase of the separation parameter—the compensation field offsetting that difference. The model for pendular alignment of ions in gases including rotational ion heating predicts a minimum dipole moment for alignment at any field intensity. In N₂ or air at ambient conditions, the value for typical protein ions produced by ESI is ≈450 D.

Simulations for ubiquitin suggest that the dipole moments of highly charged protein ions compare to the values for native geometries such as found in the PDB database. The PDB entries up to 100 kDa exhibit a near-linear statistical correlation between the dipole moment and protein mass, with ≈450 D reached at ≈30 kDa. Hence, the dipole alignment of protein ions in FAIMS should phase in at ≈30 kDa, in consistency with the observed onset of “abnormal” behavior for proteins above that threshold.

The mobility of pendular macroions as a function of electric field intensity is quite sensitive to their geometries that determine the magnitude and direction of ion dipole. Hence, FAIMS may be a powerful tool for detection and analysis of fine variations in the tertiary and quaternary structure of biological molecules.