Universal constant for heat production in protists

Abstract

Using a high sensitivity differential scanning calorimeter in isothermal mode, we directly measured heat production in eukaryotic protists from 5 phyla spanning over 5 orders of magnitude in carbon biomass and 8 orders of magnitude in cell volume. Our results reveal that metabolic heat production normalized to cell mass is virtually constant in these organisms, with a median of 0.037 pW pg C⁻¹ (95% confidence interval = 0.022–0.061 pW pg C⁻¹) at 5 °C. Contrary to allometric models, the relationship between heat production and cell carbon content or surface area is isometric (scaling exponents, 1.056 and 1.057, respectively). That heat production per unit cell surface area is constant suggests that heat flux through the cell surface is effectively instantaneous, and hence that cells are isothermal with their environment. The results further suggest that allometric models of metabolism based on metazoans are not applicable to protists, and that the underlying metabolic processes in the latter polyphyletic group are highly constrained by evolutionary selection. We propose that the evolutionary constraint leading to a universally constant heat production in single-celled eukaryotes is related to cytoplasmic packaging of organelles and surface area to volume relationships controlling diffusion of resources to these organelles.

In the 20^th century, size-dependent scaling (allometry) became a major unifying principle in ecology (1–3). However, to be successful, size-dependent scaling models must explain the enormous variability in metabolism in both single-celled organisms and metazoans. Early research by Rubner (4) revealed that in metazoans metabolism scales with surface area to volume quotients (SA/V), and that metabolic rates are proportional to mass of the animal raised to the power of 2/3. Later work by Kleiber (5) and others defined the relationship of body mass and metabolic rate as the power function aM^b, where a corresponds to a scaling constant (Y intercept), M is body mass, and b is the scaling exponent. Current allometric paradigms suggest a metabolic scaling function of 3/4 for diverse lineages of metazoans (1, 2).

Despite the widespread acceptance of an allometric scaling paradigm (1), numerous studies have questioned the notion of a universal logarithmic relationship between metabolism and mass (6, 7). For example, the relationship between plant biomass and respiration in early developmental stages of trees is isometric, suggesting there may be fundamental differences in scaling functions between plants and animals (7). Differences also exist in metabolic scaling between ontogenetic stages of certain animals (8, 9). A review of benthic and pelagic aquatic organisms revealed that the relationship between respiration and body mass in pelagic animals conforms to an isometric scaling function, whereas benthic animals are best described by allometric scaling exponents (9). In diverse lineages of photosynthetic protists, the scaling exponent of respiration with cell carbon biomass (10) or production with biovolume (11) has been reported to be significantly higher than ¾ in several major protist groups.

Metabolic rates of metazoans vary widely between basal metabolism and maximum oxidative respiration (12). In protists, respiration rates are also highly variable, and depend largely upon resource availability and growth rate (13, 14). The concept of a basal metabolism is rarely applied to unicellular organisms, as available cellular energy is primarily used for anabolic processes or growth (15). Efforts to universally scale metabolism with mass and temperature across all life (1, 2) overlook such fundamental differences (e.g., endothermy vs. ectothermy), and generally overestimate metabolism of unicellular organisms (6). Furthermore, such studies tend to ignore the inherent variability of metabolic rates within species which, after accounting for carbon biomass, appear to vary within universal upper and lower limits, independent of size (6).

In this paper we report on the relationships between biomass, surface area, and heat production in single-celled eukaryotes using high-precision scanning calorimetry in an isothermal mode. Although the use of calorimetry to measure heat production from living organisms has a long tradition dating back to the pioneering experiments of Lavoisier and Laplace (16), there are few studies for either eukaryotic or prokaryotic microbes that have systematically compared heat production between species.

Results and Discussion

Using high-precision microcalorimetry in a differential scanning mode, we measured direct heat production at a constant temperature, against a background signal of culture medium, from five phyla (three kingdoms) of eukaryotic protists spanning more than 5 orders of magnitude in carbon biomass, and representing a large range of cell densities, sizes, and total cell carbon (Table 1). The instrument allows detection of a power compensation signal on the order of 1 microwatt or less, thereby allowing extraordinary precision in estimates of heat production from living cells. Indeed, this is the first study to use calorimetrically measured metabolic heat to address allometric scaling in protists.

Table 1.

Cellular attributes and heat production for eight marine phototrophic protists

Organism	Cells	Mass	Volume	Surface area	Heat	Heat	SA/vol	C/vol	C:SA	Heat flux
		pg C	μm3	μm2	pW cell−1	pW pgC−1	μm2/μm3	pg C/μm3	pg C/μm2	pW/μm2
Micromonas pusilla (2)*	2.23 × 106	2.36	0.904	4.5	0.081 ± 0.057	0.033 ± 0.024	5.0000	2.63	0.524	0.018 ± 0.012
Thalassiosira pseudonana (1)	6.18 × 10 5	9.17	31.4	56.5	0.66	0.069	0.8003	0.292	0.365	0.026
Geminigera cryophila (2)*	8.25 × 104	147.9	9.01 × 102	5.33 × 102	4.85 ± 0.69	0.032 ± 0.005	0.6111	0.164	0.269	0.009 ± 0.001
Myrionecta rubra (3)*	1.41 × 104	1711	8.19 × 103	1.65 × 103	70.67 ± 9.89	0.041 ± 0.013	0.2270	0.209	0.920	0.038 ± 0.010
Coscinodiscus sp. (2)	3.37 × 104	913	1.26 × 104	3.04 × 103	16.67 ± 1.66	0.018 ± 0.002	0.2403	0.072	0.301	0.006 ± 0.001
Akashiwo sanguinea (2)*	1.43 × 103	3763	5.32 × 104	1.42 × 104	203 ± 37.3	0.054 ± 0.010	0.266	0.071	0.266	0.014 ± 0.003
Coscinodiscus wailesii (2)	420	78000	2.66 × 106	1.08 × 105	1980 ± 347	0.025 ± 0.004	0.0406	0.029	0.722	0.018 ± 0.003
Pyrocystis noctiluca (2)*	37	22817	4.11 × 106	1.26 × 105	5004 ± 1260	0.182 ± 0.046	0.0300	0.005	0.181	0.039 ± 0.011

Number of replicates in parentheses.

*, Capacity for motility

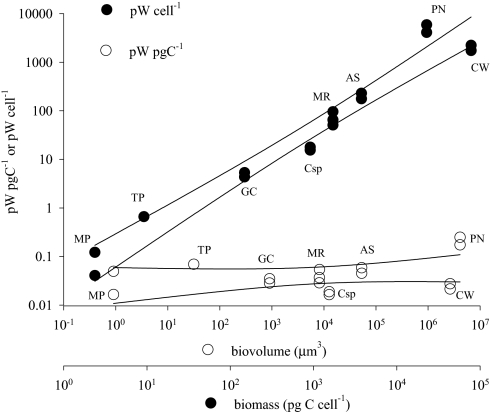
When heat production (pW cell⁻¹) is plotted against total cell mass on a log-log scale, the slope of the relationship is 1.056 with a 95% confidence interval (CI) from 0.93 to 1.19 (Fig. 1). The results are therefore consistent with the assumption that heat production is directly proportional to carbon biomass and inconsistent with the assumption that heat production scales as carbon biomass to a power less than 0.93. In the ciliate, Myrionecta rubra, metabolic heat production was reduced by ≈40% with 50 μM rotenone, an inhibitor for mitochondrial electron transport, whereas simultaneous measurements revealed that oxygen consumption was reduced on average by ≈90% at the same concentration of the inhibitor [supporting information (SI) Fig. S1]. These observations are consistent with those of Loike et al. (17), who found that an inhibitor of glycolysis (NaF) reduced heat production by 68% in murine macrophages. Our results strongly suggest that metabolic pathways other than aerobic respiration provide significant sources of heat in protists. When heat production is normalized to biomass (pW pgC⁻¹), a nearly constant heat production is obtained for all cells (Kruskal-Wallis test, P = 0.09), with a median of 0.037 pW pgC⁻¹ and a 95% confidence interval (CI) of 0.022–0.061 pW pgC⁻¹. Plotting log cellular heat production versus log cell volume, however, produced a nearly allometric slope of 0.72 with a 95% CI of 0.65–0.79 (Fig. S2). Although cell volume is sometimes used as a metric for metabolic scaling, we suggest that cell carbon is a more appropriate parameter for single cells, as carbon content does not always vary directly with cell volume (18) but should be directly proportional to cell metabolism in growing cells (i.e., in cells not storing large amounts of carbon as lipids or polysaccharides). The slope of log carbon versus log volume for the protists we studied is low (0.67, with a 95% CI of 0.60–0.73) compared with the corresponding slopes for diverse phytoplankton, which range between 0.71 (19) and 0.991 (20). However, carbon-to-volume relationships also have been shown to vary systematically between taxonomic groups (18, 19). The difference in our data are due to the extremely large range of cell sizes, with the largest cell, the dinoflagellate, Pyrocystis, having significantly lower carbon values per unit volume than predicted based on allometric relationships, because of the presence of a large intracellular vacuole (21). Excluding this value yields a slope of 0.71 (95% CI = 0.65–0.77), which is consistent with previously published carbon:volume relationships (18, 19). Regardless, the results obtained for heat production per unit cell biomass are inconsistent with general allometric models of metabolism (1, 2), and strongly suggest an isometric scaling function to be appropriate for metabolism in protists. Furthermore, as some of these organisms are motile while others are not (Table 1), clearly suggests that motility, per se, has little metabolic costs (22). Together, a constant value for mass-specific metabolism in protists and a similar isometric relationship for respiration and biomass in protists (10), plants (7), and certain ectothermic metazoans (9) provide strong evidence for a conservation of basic metabolic activity per unit mass in diverse eukaryotic lineages.

Fig. 1.

Heat production of eight protist species measured by microcalorimetry. Heat production measured by microcalorimetry and normalized to cell number or biomass (pg C) and plotted against biomass or cell volume, respectively, for the marine phototrophic protists (from left to right) Micromonas pusilla (chlorophyta) (n = 2), Thalassiosira pseudonana (diatom) (n = 1), Geminigera cryophila (cryptomonad) (n = 2), Myrionecta rubra (ciliate) (n = 3), Coscinodiscus sp. (diatom) (n = 2), Akashiwo sanguinea (dinoflagellate) (n = 2), Coscinodiscus wailesii (diatom) (n = 2), and Pyrocystis noctiluca (dinoflagellate) (n = 2). A linear regression was performed for both rates, yielding a slope of 1.056 for heat production per cell (r² 0.9556) and 0.0532 for heat per unit mass (r² 0.1125).

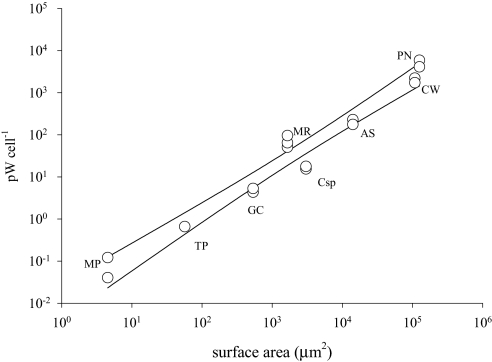
The surface area to volume quotient (SA/V) in protists is often used to explain the ability of a cell to exploit extracellular chemical resources by diffusion or active processes across its cell membrane (23). Less well understood is the role of heat diffusion across cell membranes. The SA/V of the smallest cell studied here is 166 times that of the largest, the C/V of the smallest cells is 482 that of the largest, while the C/SA varied by only a factor of ≈3 from the smallest to largest cell studied (Table 1). When heat is normalized to cell SA (Table 1), the values are remarkably similar across all cell sizes (Kruskal-Wallis test, P = 0.07). Likewise, the slope of log cellular heat production versus log SA is approximately isometric (Fig. 2), with a value of 1.057 ± 0.12 (95% CI). Together, these observations suggest conservation in the relationship of metabolic processes to SA in single-celled eukaryotic organisms.

Fig. 2.

Heat production compared to surface area of eight protist species measured by microcalorimetry. Heat production measured by microcalorimetry, normalized to cell number, and plotted against surface area (μm²), for the marine phototrophic protists (from left to right) Micromonas pusilla (chlorophyte) (n = 2), Thalassiosira pseudonana (diatom) (n = 1), Geminigera cryophila (cryptomonad) (n = 2), Myrionecta rubra (ciliate) (n = 3), Coscinodiscus sp. (diatom) (n = 2), Akashiwo sanguinea (dinoflagellate) (n = 2), Coscinodiscus wailesii (diatom) (n = 2), and Pyrocystis noctiluca (dinoflagellate) (n = 2). A linear regression was performed, yielding a slope of 1.057 (r² 0.9594).

Independent estimates of metabolic heat generated from respiration data of flagellates, ciliates, and sarcodines (24) also revealed no relationship between SA-specific respiration and cell volume, consistent with Rubner's Law (4). Our directly measured cellular heat production rates ranged between 30 and 180 W kg⁻¹, which fall between the optimum and maximum rates of mass-specific metabolism calculated from respiration rates in a wide range of eukaryotes and prokaryotes (6). The conservation of SA-specific heat flux in all cell types examined underscores the evolutionary constraints relating cell metabolism to diffusion processes. Furthermore, the absence of greater SA heat production in cells with high quantities of mitochondria (e.g., Myrionecta rubra) clearly shows that multicellularity is a prerequisite of endothermy; i.e., the diffusion of metabolically derived heat to the environment is, effectively, instantaneous, and thus the heat gradient is infinitely small.

A uniform heat constant for eukaryotic biomass suggests a fundamentally conserved metabolic signature for cellular processes. Our results are consistent with cytological packaging (i.e., organelle density) being critical for maximizing heat or metabolic rate per unit area, and that cellular metabolism, or C per unit volume, ultimately is limited by the SA/V. Micromonas pusilla is one of the smallest eukaryotic cells known (Table 1), packing all of its organelles (including a chloroplast) into a cell roughly the size of a bacterium (25). Conversely, Pyrocystis noctiluca possesses a retractable protoplast largely comprised of a buoyant vacuole, together housed within a cell wall otherwise filled with seawater (21). Differences in C/V between these cell types can thus be explained by cellular architecture and cytoplasmic density of organelles (i.e., mitochondria). Together, our results suggest that internal packaging (i.e., C/V and C/SA), and thus metabolic heat, is evolutionarily constrained by cell SA/V, as carbon density per unit volume inevitably decreases in larger cells. Collectively, our observations reveal a size-independent relationship for mass-specific metabolic rates, consistent with a biochemical conservation of cellular metabolism in protists. The results presented here suggest that allometric scaling models of metabolic processes across many orders of magnitude in size may be “macroscopically” correct but overlook evolutionary constraints on fundamental biological processes.

Materials and Methods

Experimental Preparation.

Cultures were obtained from the Provasoli-Guillard Center for Culture of Marine Phytoplankton (CCMP) and from private collections: M. pusilla (Prasinophyceae, Chlorophyta; CCMP 485), T. pseudonana (Bacillariophyceae, Heterokontophyta; CCMP 1335), G. cryophilia (Cryptophyceae, Cryptophyta; CCMP 2564), M. rubra (Litostomatea, Ciliophora; CCMP 2563), Coscinodiscus sp. (Bacillariophyceae, Heterokontophyta; “Oregon” strain), Akashiwo sanguinea (Pyrocystaceae, Dinoflagellata; SERC 01), Coscinodiscus wailesii (Bacillariophyceae, Heterokontophyta; CCMP 2513), and P. noctiluca (Pyrocystaceae, Dinoflagellata; CCMP 732). Cells, grown in f/2 media using techniques described elsewhere (26), were taken during exponential growth and acclimated to 5 °C for at least 48 hours under constant light before experimental measurements.

Cellular Attributes.

Cell volumes were calculated by microscopic analyses of size using a calibrated reticle. At least 50 individuals of each species were analyzed, and volumes were calculated using standard geometric models (27). Cell concentrations were determined by preserving cells in 1% gluteraldehyde and preparing slides for microscopy as described elsewhere (28). Cellular carbon was measured using an NA 1500 Series Z nitrogen/carbon/sulfur analyzer (Carlo Erba Instruments) and methods described elsewhere (18).

Microcalorimetry and Respiration.

Heat measurements were conducted using a NanoDSC II differential scanning calorimeter (Calorimetry Science Corporation, Provo, Utah) (29). The instrument was set to 5 °C and used in an isothermal mode using specialized software. Samples and buffers were kept on ice before loading, and the instrument was allowed to equilibrate for 30 minutes after loading. The instrument was pressurized to 0.2 atm to prevent outgassing. After equilibration, the power required to maintain sample and reference compartments at the same temperature was recorded for 1 hour. The raw power data (in μW) was corrected for instrument baseline, converted to heat in units of μJ, and normalized for cell densities. Buffer versus buffer baselines were found to be reproducible to better than 0.1 μW, allowing reliable measurements of heat signals as small as 0.3 μW. The differential nature of the DSC instrument allowed us to directly measure inhibition of metabolic heat due to rotenone by placing equal amounts of cells with and without rotenone into sample and reference compartment of the instrument. Rotenone, dissolved in dimethylsulfoxide (DMSO), was added to a concentration of 50 μM immediately before cells were placed in the microcalorimeter. Measurements of oxygen consumption in the dark (i.e., aerobic respiration) were obtained with a calibrated, fluorescence-based Fibox 2 fiber-optic oxygen meter (PreSens).