Haplotype-Based Regression Analysis and Inference of Case–Control Studies with Unphased Genotypes and Measurement Errors in Environmental Exposures

Abstract

Summary. It is widely believed that risks of many complex diseases are determined by genetic susceptibilities, environmental exposures, and their interaction. Chatterjee and Carroll (2005, Biometrika 92, 399–418) developed an efficient retrospective maximum-likelihood method for analysis of case–control studies that exploits an assumption of gene–environment independence and leaves the distribution of the environmental covariates to be completely nonparametric. Spinka, Carroll, and Chatterjee (2005, Genetic Epidemiology 29, 108–127) extended this approach to studies where certain types of genetic information, such as haplotype phases, may be missing on some subjects. We further extend this approach to situations when some of the environmental exposures are measured with error. Using a polychotomous logistic regression model, we allow disease status to have K + 1 levels. We propose use of a pseudolikelihood and a related EM algorithm for parameter estimation. We prove consistency and derive the resulting asymptotic covariance matrix of parameter estimates when the variance of the measurement error is known and when it is estimated using replications. Inferences with measurement error corrections are complicated by the fact that the Wald test often behaves poorly in the presence of large amounts of measurement error. The likelihood-ratio (LR) techniques are known to be a good alternative. However, the LR tests are not technically correct in this setting because the likelihood function is based on an incorrect model, i.e., a prospective model in a retrospective sampling scheme. We corrected standard asymptotic results to account for the fact that the LR test is based on a likelihood-type function. The performance of the proposed method is illustrated using simulation studies emphasizing the case when genetic information is in the form of haplotypes and missing data arises from haplotype-phase ambiguity. An application of our method is illustrated using a population-based case–control study of the association between calcium intake and the risk of colorectal adenoma.

1. Introduction

With the advent of modern genotyping technologies, epidemiologists have been increasingly interested in identifying genetically defined subgroups within a population with unusual resistance or susceptibility to environmental exposures, both because such interactions may yield insight into mechanisms of action of exposures and because they may suggest disease prevention strategies. Case–control studies are often used to detect such gene–environment interactions. Traditionally, case–control data are analyzed using prospective logistic regression ignoring the fact that under this design subjects are sampled retrospectively conditional on their disease status. The validity of this approach relies on the classic results by Cornfield (1956) who showed the equivalence of prospective and retrospective odds ratios. The efficiency of the approach was established in two other classic papers by Andersen (1970) and Prentice and Pyke (1979) who showed that standard prospective analysis of case–control data yields the proper maximum-likelihood estimates of the odds-ratio parameters under the retrospective design as long as the distribution of the underlying covariates are allowed to remain completely unrestricted (nonparametric).

A number of researchers have noted that in studies of genetic epidemiology, the efficiency of the standard analysis for case–control data can be improved by exploiting certain natural model assumptions for the underlying genetic and the environmental covariates. In the context of haplotype-based analysis of case–control studies, Epstein and Satten (2003) and Satten and Epstein (2004) noted that retrospective maximum-likelihood methods can be more efficient than analogous prospective methods by taking full advantage of an assumption of Hardy–Weinberg equilibrium (HWE) for the underlying population. Chatterjee and Carroll (2005) exploited an assumption of gene–environment independence to yield more precise maximum-likelihood estimates of the odds-ratio parameters than those obtained from standard logistic regression analysis. Spinka, Carroll, and Chatterjee (2005) extended the results of Chatterjee and Carroll to allow for missing genetic information and haplotype-phase ambiguity.

In this article, we propose to extend earlier methods for analysis of case–control data under gene–environment independence and possibly HWE to account for measurement error in environmental exposures. Our work was motivated by a case–control study of colorectal adenoma (Peters et al., 2004) designed to investigate the interactions of dietary calcium intake and genetic variants in the calcium-sensing receptor (CASR) region. In this study, a total of 772 cases and 778 controls were sampled from the screening arm of the prostate, lung, colorectal, and ovarian (PLCO) cancer screening trial. Information on dietary food intake of the participants were available from a baseline food-frequency questionnaire (FFQ). Genotype data were available on three nonsynonymous single nucleotide polymorphisms (SNP) in the CASR region. One of the major goals of the study was to investigate the interaction of dietary calcium and the CASR gene based on “haplotypes,” which is a combinations of alleles at three different CASR loci along individual chromosomes. Two technical problems arose. First, as is typical, only locus-specific genotype data are available to provide information on two alleles that a subject carries on the pair of homologous chromosome, at each locus separately. Such genotype data lack the phase information, i.e., which combinations of allele arise together on the individual chromosomes, thus giving rise to an interesting missing data problem. Second, it is well known that FFQ as an instrument for measuring dietary intake is prone to both bias and random error, as illustrated in the OPEN study (Subar et al., 2003). We will use data from an external study (Potischman et al., 2002) to form estimates of the bias and variance of the measurement error for calcium intake. The availability of such external data gives rise to the opportunity for studying the calcium–CASR interaction after correcting for measurement error due to use of FFQ. Development of new methods, however, were needed to allow for such adjustment, which is the main contribution of this article.

Further, in our setting it is undesirable to conduct inferences using the Wald-type procedure. Schafer and Purdy (1996) advocated likelihood analysis for regression models with errors in explanatory variables, for data problems in which the relevant distributions can be adequately modeled. They point out that the likelihood ratio (LR) tests and confidence intervals can be substantially better than tests and confidence intervals based on estimates and standard errors, because the sampling distribution of measurement-error-corrected estimators are very often skewed, especially if the measurement errors are large. The fact that the data are collected using a case–control sampling scheme and are analyzed as if they were a random sample means that LR tests are not technically correct. We correct standard asymptotic results and propose a LR procedure that can be used successfully in this setting, and demonstrate its power in simulations.

An outline of this article is as follows. In Section 2, we give the technical formulation of the problem, describe our methodology, and state the main distributional results. Section 3 gives the results of simulation studies, where we show that our methodology overcomes the bias caused by measurement error. Section 4 analyzes the example discussed above. Section 5 gives concluding remarks. All technical derivations are given in the Web Appendix, along with many more simulation results.

2. Methodology and Main Theoretical Results

2.1 Model and Notation

Let D be the categorical indicator of disease status. We allow D to have K + 1 levels with the possibility of K ≥ 1 to accommodate different subtypes of a disease. Let D = 0 denote the disease-free (control) subjects and D = k, k ≥ 1 denote the diseased (case) subjects of the kth subtype. Suppose there are M loci of interest within a genomic region. Let H^dip = (H₁, H₂) denote the corresponding diplotype status for an individual, i.e., the two haplotypes that the individual carries in his/her pair of homologous chromosomes. Let (X, Z) denote all of the environmental (nongenetic) covariates of interest with X denoting the factors susceptible to measurement error. Given the environmental covariates X and Z and diplotype data H^dip, the risk of the disease in the underlying population is given by the polytomous logistic regression model

$$\begin{array}{l}\text{pr}(D=d\ge 1\mid H^{\text{dip}},X,Z)\\ =\frac{exp\left\{{\beta }_{0d}+m(H^{\text{dip}},X,Z,\beta )\right\}}{1+{\displaystyle \sum _{j=1}^K}exp\left\{{\beta }_{0j}+m(H^{\text{dip}},X,Z,\beta )\right\}}.\end{array}$$ (1)

Here m(·) is a known function parameterizing the joint risk of the disease from H^dip, X, and Z in terms of the odds-ratio parameters β.

The model (1) cannot be used directly for analysis due to two reasons. First, the diplotype information H^dip is not measurable using standard genotyping technology. Typically, multilocus genotype information, denoted by G = (G₁, G₂, …, G_M), is available. Due to lack of haplotype-phase information, the same genotype data can be consistent with multiple configuration of haplotypes for a given subject. For example, if A/a and B/b denote the major/minor alleles in two bi-allelic loci, then subjects with genotypes (Aa) and (Bb) at the first and the second locus, respectively, are considered “phase ambiguous”: their genotypes could arise from either the haplotype-pair (A-B, a-b) or the haplotype-pair (A-B, ab). Let ℋ^dip denote the set of all possible diplotypes in the underlying population. Analogously, let ${\mathcal{H}}_{\mathbf{G}}^{\text{dip}}$ denote the set of all possible diplotypes that are consistent with a particular genotype vector G. We assume independence of H^dip and (X, Z) in the underlying population. Moreover, we assume a parametric model of the form pr(H^dip) = Q(H^dip, θ). Note, however, that our method can be readily extended to a general parametric model for H^dip given (X, Z) that could account for gene–environment association (Chatterjee et al., 2006). For our numerical examples, we assume HWE so that the distribution of the diplotypes can be specified in terms of the frequency of the haplotypes. Our general framework, however, allows use of more flexible models than HWE (see, e.g., Satten and Epstein, 2004; Lin and Zeng, 2006).

A second problem is that in our motivating example, the covariate X is measured with error. Let W denote the error-prone version of X. We assume a parametric model of the form f_mem(w|X, H^dip, Z, D; ξ) for the conditional distribution of W given the true exposure X, additional environmental factors Z, and disease-status D. Measurement error can be modeled both as differential and nondifferential. If measurement error can be assumed to be nondifferential by disease status, then one can simplify the model as f_mem(w|X, H^dip, Z, D; ξ) = f_mem(w|X, H^dip, Z; ξ). We assume that the joint distribution of the environmental factors in the underlying population can be specified according to a semiparametric model of the form f_X,Z(x, z) = f_X(x|z; η)f_Z(z), where f_Z (z) is left completely unspecified.

2.2 Semiparametric Inference Based on a Pseudolikelihood

For d ≥ 1, define n_d to be the number of subjects in the sample with disease at stage d, π_d = pr(D = d), κ_d = β_0d + log(n_d/n₀) − log(π_d/π₀), and κ̃ = (κ₁, …, κ_K)^T. Define κ₀ = β₀₀. Let β̃₀ = (β₀₁, …, β_0K)^T. Let $\mathrm{\Omega }={({\stackrel{\sim }{\beta }}_0^{\text{T}},{\beta }^{\text{T}},{\mathrm{\Theta }}^{\text{T}},{\stackrel{\sim }{\kappa }}^{\text{T}})}^{\text{T}}$, ℬ =(Ω^T, η^T)^T and υ = (η^T, ξ^T)^T. Make the definition

$$\begin{array}{l}S(d,h^{\text{dip}},x,z,\mathrm{\Omega })\\ =\frac{exp\left[I_{(d\ge 1)}(d)\left\{{\kappa }_d+m(h^{\text{dip}},x,z,\beta )\right\}\right]}{1+{\displaystyle \sum _{j=1}^K}exp\left\{{\beta }_{0j}+m(h^{\text{dip}},x,z,\beta )\right\}}Q(h^{\text{dip}},\mathrm{\Theta }).\end{array}$$ (2)

Consider a sampling scenario where each subject from the underlying population is selected into the case–control study using a Bernoulli sampling scheme, where the selection probability for a subject given his/her disease status D = d is proportional to μ_d = n_d/pr(D = d). Let R = 1 denote the indicator of whether a subject is selected in the case–control sample under the above Bernoulli sampling scheme. We propose parameter estimation using a pseudolikelihood of the form

$$L^{\ast }=\prod _{i=1}^N\text{pr}(D_i,W_i,{\mathbf{G}}_i\mid Z_i,R=1).$$

Calculations given in the Appendix show that

$$\begin{array}{l}L(d,g,w,z,\mathrm{\Omega },\eta ,\xi )\\ \equiv \text{pr}(D=d,W=w,\mathbf{G}=g\mid Z=z,R=1)\\ =\frac{\int {\displaystyle \sum _{h^{\text{dip}}\in {\mathcal{H}}_G^{\text{dip}}}}S(d,h^{\text{dip}},x,z,\mathrm{\Omega })f_{\text{mem}}(w\mid d,h^{\text{dip}},x,z,\xi )f_X(x\mid z,\eta )dx}{\int {\displaystyle \sum _{d_{\ast }=0}^{K+1}}{\displaystyle \sum _{h_{\ast }^{\text{dip}}\in {\mathcal{H}}^{\text{dip}}}}S(d_{\ast },h_{\ast }^{\text{dip}},x,z,\mathrm{\Omega })f_X(x\mid z,\eta )dx}.\end{array}$$ (3)

Observe that conditioning on Z in L^* allows it to be free of the nonparametric density function f_Z (z), thus avoiding the need of estimating potentially high-dimensional nuisance parameters. In the absence of measurement error in environmental exposures, Chatterjee and Carroll (2005) and Spinka et al. (2005) used a profile-likelihood technique to show the equivalence of pseudolikelihood of the form L^* with the proper retrospective likelihood of case–control data given by $L^R={\prod }_{i=1}^N\text{pr}(E_i,{\mathbf{G}}_i\mid D_i)$. In the presence of measurement error, although we do not have such a general theorem, a simulation study in a simple scenario shows that L^* has a similar efficiency as the corresponding retrospective likelihood, see Section 3.1.

2.2.1 Rare disease approximation

In the case of rare disease, the denominator of (2) is approximately = 1, in which case

$$\begin{array}{l}S(d,h^{\text{dip}},x,z,\mathrm{\Omega })\\ \approx exp\left[I_{(d\ge 1)}(d)\left\{{\kappa }_d+m(h^{\text{dip}},x,z,\beta )\right\}\right]Q(h^{\text{dip}},\mathrm{\Theta }),\end{array}$$

does not depend on β₀.

2.3 Estimation with Known Measurement Error Distribution

In this section, we assume that the parameter ξ controlling the distribution of the measurement error is known. We show that maximization of L^*, although it is not the actual retrospective likelihood for case–control data, leads to consistent and asymptotically normal parameter estimates. Recall that ℬ = (Ω^T, η^T)^T. Let Ψ(d, g, w, z, Ω, η, ξ) be the derivative of log{L(d, g, w, z, Ω, η, ξ)} with respect to ℬ. Then define

$$\begin{array}{l}{\mathcal{L}}_n(\mathrm{\Omega },\eta ,\xi )={\displaystyle \sum _{i=1}^n}\mathrm{\Psi }(D_i,G_i,W_i,Z_i,\mathrm{\Omega },\eta ,\xi ),\\ \mathcal{I}=-n^{-1}E\left[\partial \{{\mathcal{L}}_n(\mathrm{\Omega },\eta ,\xi )\}/\partial {\mathcal{B}}^{\text{T}}\right],\\ \mathrm{\Lambda }=\sum _d\frac{n_d}{n}E\{\mathrm{\Psi }(D,G,W,Z,\mathrm{\Omega },\eta ,\xi )\mid D=d\}\\ \times E{\{\mathrm{\Psi }(D,G,W,Z,\mathrm{\Omega },\eta ,\xi )\mid D=d\}}^{\text{T}},\end{array}$$

where all expectations are taken with respect to the case–control sampling design. We propose to estimate ℬ as the solution to

$$0={\mathcal{L}}_n(\mathrm{\Omega },\eta ,\xi )={\mathcal{L}}_n(\mathcal{B},\xi ),$$ (4)

calling the solution ℬ̂ = (Ω̂^T, η̂^T)^T. Our main technical result, the proof of which is given in the Web Appendix H, concerns the limiting properties of ℬ̂.

Theorem 1

The estimating function ℒ_n(Ω, η, ξ) is unbiased, i.e., has mean zero when evaluated at the true parameter values. In addition, under suitable regulatory conditions, there is a consistent sequence of solutions to (4), with the property that

$$n^{1/2}(\widehat{\mathcal{B}}-\mathcal{B})\Rightarrow \text{Normal}\{0,{\mathcal{I}}^{-1}(\mathcal{I}-\mathrm{\Lambda }){\mathcal{I}}^{-1}\}.$$ (5)

Remark 1

It is easy to obtain consistent estimates of both ℐ and Λ. For example, to get an estimate Λ̂, in the definition of Λ, we can estimate E{Ψ(D, G, W, Z, Ω, η, ξ)|D = d} by $n_d^{-1}{\sum }_{i=1}^{n}I(D_i=d)\mathrm{\Psi }(d,G_i,W_i,Z_i,\widehat{\mathcal{B}},\xi )$. Similarly, n⁻¹∂{ℒ_n(ℬ̂, ξ)}/∂ℬ^T is a consistent estimate of ℐ. Alternatively, if Σ̂ is the sample covariance matrix of the terms Ψ(D_i, G_i, W_i, Z_i, ℬ̂, ξ), then Σ̂ + Λ̂ consistently estimates ℐ.

Remark 2

An EM-algorithm for computation, based along the lines of Spinka et al. (2005) is given in the Appendix.

Remark 3

Similar to the settings of Chatterjee and Carroll (2005) and Spinka et al. (2005), here, the intercept parameters (β_0d, d ≥ 1) of the polytomous logistic regression model are theoretically identifiable from the pseudolikelihood L^*, even though the sampling is retrospective. For rare diseases, however, $1+{\sum }_{j=1}^{K}exp\{{\beta }_{0j}+m(H^{\text{dip}},X,Z,\beta )\}\approx 1$ in formula (2) and so L^* is expected to contain very little information about β_d. If information on Pr (D = d) is available externally, as could be the situation for population-based case–control studies, then π_d, d ≥ 1 could be treated as fixed known parameters in the definition of κ_d allowing estimation of β_0d to be much more tractable. If Pr (D = d) is not known, one could employ the rare disease assumption under which β_0d’s disappear from the likelihood. Alternatively, one can estimate parameters (Ω, η, ξ) by maximizing the likelihood function for the values of π_d fixed on a grid and then performing a grid-search method to identify the value of π_d that maximizes the profile likelihood ℒ_n{Ω(π_d), η (π_d), ξ}.

Remark 4

Rarely the practical identifiability of intercept parameters β_0d and κ_d, or equivalently, π_d may be a problem. But as illustrated in our example where the practical identifiability is a problem, the other parameter estimates are not much affected. Hence a practical method is to constrain the probability of disease to a wide range and perform a grid-search method to find an estimate.

2.4 Estimated Measurement Error Distribution

In practice, the parameter ξ controlling the measurement error distribution will be unknown, and typically additional data are necessary to estimate it. Here we consider the case of additive mean-zero measurement error with replications of W.

Our convention is that there are at most M replications of the W for any individual. Let W_i denote this ensemble of the M replicates, and let m_i be the number of replicates we actually observe. Let f_mem(w | d, h^dip, x, z, m, ξ) be the joint density of the first m replicates for m = 1, …, M; Ψ(D, G, W, Z, Ω, η, ξ, j),ℐ_j, and Λ_j be matrices defined in the Section 2.3 for the case with exactly m = j replicates for each individual. Assume that m_i is independent of (D_i, W _i, Z_i, G_i, X_i, $H_i^{\text{dip}}$) and that pr(m_i = j) = p(j). Further, define $\mathcal{I}={\sum }_{j=1}^{M}p(j){\mathcal{I}}_j$. It is shown in the Appendix that the estimating function for ℬ = (Ω ^T, η^T, ξ^T)^T can be written in the form

$$0=\sum _{i=1}^n\sum _{j=1}^M{I}_{(m_i=j)}(m_i)\mathrm{\Psi }(D_i,G_i,W_i,Z_i,\mathrm{\Omega },\eta ,\xi ,j).$$ (6)

Theorem 2

The estimating function (6) is unbiased, i.e., has mean zero when evaluated at the true parameter values. In addition, under suitable regulatory conditions, there is a consistent sequence of solutions to (6), with the property that

$$n^{1/2}(\widehat{\mathcal{B}}-{\mathcal{B}}_0)\Rightarrow \text{Normal}\left[o,{\mathcal{I}}^{-1}\left\{\mathcal{I}-\sum _{j=1}^{M}p(j){\mathrm{\Lambda }}_j\right\}{\mathcal{I}}^{-1}\right].$$ (7)

Remark 5

Consistent estimates of ℐ and Λ_j can be obtained by applying formulas that are analogous to those outlined in the Remark 1. Web Appendix H contains the proof of Theorem 2.

2.5 Covariates Z Measured Exactly, Full Retrospective Likelihood

Let f_Z (z) be the marginal density of Z. Abusing notation slightly and using a generic h, define ℋ(d, h, x, z, β_0d, β) = [H{β_0d + m(h, x, z, β)}]^d[1 − H{β_0d + m(h, x, z, β)}]^1−d.

Then the retrospective likelihood is

$$\begin{array}{l}\text{pr}(W=w,H=h,Z=z\mid D=d)\\ =\frac{Q(h,\mathrm{\Theta })f_Z(z)\int \mathcal{H}(d,h,x,z,{\beta }_{0d},\beta )f_U(w\mid d,h,x,\xi )f_X(x\mid z,\eta )dx}{\int {\displaystyle \sum _{h_{\ast }}}\mathcal{H}(d,h_{\ast },x,z,{\beta }_0,\beta )Q(h_{\ast },\mathrm{\Theta })f_X(x\mid z,\eta )f_Z(z)dxdz}.\end{array}$$ (8)

It is clear then that if we want to compute the full retrospective likelihood, we need a parametric model for the marginal distribution of Z.

However, instead of (8), suppose that we construct another retrospective likelihood:

$$\begin{array}{l}\text{pr}(W=w,H=h,\mid D=d,Z=z)\\ =\frac{Q(h,\mathrm{\Theta })\int \mathcal{H}(d,h,x,z,{\beta }_{0d},\beta )f_U(w\mid d,h,x,\xi )f_X(x\mid z,\eta )dx}{\int {\displaystyle \sum _{h_{\ast }}}\mathcal{H}(d,h_{\ast },x,z,{\beta }_{0d},\beta )Q(h_{\ast },\mathrm{\Theta })f_X(x\mid z,\eta )dx}.\end{array}$$ (9)

Note how (9) is a legitimate conditional likelihood function, and it does not involve the marginal distribution of Z.

We are thus led to think about the comparison of (3) and (9). Both make the same assumptions, and both are explicit. The obvious question is: why would we bother with (3) when we already have (9) available?

The key here is that

$$\begin{array}{l}\text{pr}(D=1)=\int \sum _{h_{\ast }}H\{{\beta }_{0d}+m(h_{\ast },x,z,\beta )\}\\ \times Q(h_{\ast },\mathrm{\Theta })f_X(x\mid \eta )f_Z(z)dxdz,\end{array}$$ (10)

cannot be identified merely from (β₀, β₁, θ, η), as it could when there was no Z. On the other hand, pr(D = 1) is identifiable when we use our likelihood (3). Thus, (3) and (9) cannot be made to be the same thing.

The advantage of our method (3) lies in the very identifiability of pr(D = 1).

1. If pr(D = 1) is known in the population, then our method automatically uses this information, whereas (9) does not. Thus, one assumes that when pr(D = 1), the semi-parametric likelihood formulation will be more efficient than attempting to implement (9).

2. Probably even more crucially, we know that pr(D = 1) and β₀ are probably not very precisely estimated. However, in our semiparametric formulation, we can easily place quite realistic bounds on pr(D = 1), and we know from the no-measurement error case that this can improve performance. Thus, the conjecture is that the semi-parametric method will also be more efficient than (9) as long as reasonable bounds are placed on pr(D = 1).

2.6 Construction of Test Statistic for Case–Control Data

The fact that the data are collected using a case–control sampling scheme and are analyzed as if they were a random sample means that LR tests are not technically correct. The main objective of this section is hence to propose a LR procedure that can be used in this setting.

Recall that the standard LR procedure for testing

$$\begin{array}{l}{H}_0:\mathcal{B}\in {\mathcal{B}}_0,\\ H_1:\mathcal{B}\in {\mathcal{B}}_1,\end{array}$$ (11)

is based on the following statistic

$${\lambda }_n=\underset{\mathcal{B}\in {\mathcal{B}}_0}{sup}{\mathcal{L}}_n(\mathcal{B},\xi )/\underset{\mathcal{B}\in {\mathcal{B}}_1}{sup}{\mathcal{L}}_n(\mathcal{B},\xi ).$$ (12)

Under the assumption of a correct model, Wilks (1938) and Roy (1957) derived the limiting chi-square distribution of −2log(λ_n) using consistency and asymptotic normality of the maximum-likelihood estimates. Kent (1982) examined the distribution of the LR statistic when the data do not come from the specified parametric model, but when the “nearest” member of the parametric family still satisfies the null hypothesis. Foutz and Srivastava (1977) studied the asymptotic performance of the LR test when the probability distribution of the data is not a member of the model from which the LR test is constructed.

In this section, we describe a LR test procedure for testing simple and composite hypotheses based on the likelihood function (3). The critical technical part is that the asymptotic distribution of the LR test statistic needs to be adjusted to take the retrospective sampling plan into account. Web Appendix H gives the proofs of our results.

2.6.1 Simple hypothesis

First consider the null hypothesis of the form H₀: ℬ = ℬ₀. If the second derivative of ℒ_n(•) is given as ℒ_ℬℬ(•), then the estimate ℬ̂ satisfies

$$\begin{array}{l}\mathcal{I}+o_p(1)=n^{-1}{\mathcal{L}}_{\mathcal{B}\mathcal{B}}({\mathcal{B}}_0),\\ n^{1/2}(\widehat{\mathcal{B}}-{\mathcal{B}}_0)\Rightarrow \text{Normal}\{0,{\mathcal{I}}^{-1}(\mathcal{I}-\mathrm{\Lambda }){\mathcal{I}}^{-1}\}.\end{array}$$

Our main technical result, the proof of which is given in Web Appendix H, is a limiting property of the test (11) based on a likelihood-type function (3).

Theorem 3

Define 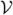= Normal{0, ℐ⁻¹(ℐ − Λ)ℐ⁻¹}. Using Cholesky decomposition the covariance matrix can be factored as ℐ⁻¹(ℐ − Λ)ℐ⁻¹ = LL^T, where L is a lower-triangular matrix. Let λ_i, i = 1, …, k be eigenvalues of the matrix LℐL^T. Let ${\mathcal{Z}}_1^2,{\mathcal{Z}}_2^2,\dots ,{\mathcal{Z}}_k^2$ denote independent ${\chi }_1^2$ random variables. Then when H₀ is true, the adjusted retrospective likelihood ratio (ARLR) test statistic based on the pseudolikelihood (3) has the limiting distribution that is the same as

$${\mathcal{V}}^{\text{T}}\mathcal{I}\mathcal{V}\sim \sum _{i=1}^k{\lambda }_i{\mathcal{Z}}_i^2.$$ (13)

Remark 6

To estimate the λ_i’s, apply Cholesky decomposition to ℐ̂⁻¹(ℐ − Λ̂) ℐ̂⁻¹ = L̂L̂^T and obtain the λ̂’s as the eigenvalues of L̂ℐ̂L̂^T. Percentiles of this weighted sum of chi-squared random variables are easily computed via simulation. Interestingly, in our numerical work we found that ℐ̂⁻¹ Λ̂ℐ̂⁻¹ was very close to zero, and ordinary LR tests also had good coverage.

2.6.2 Composite hypothesis

Let ℬ = (δ, γ), where δ is an r-dimensional vector of interest and γ is (k − r)-dimensional nuisance vector. Let the null hypothesis be H₀: δ= δ₀ whatever γ may be. Here we investigate the LR test for (11) based on a likelihood (3).

Define S₁₁ and S₂₂ to be diagonal blocks of the matrix 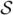= ℐ (ℐ − Λ)⁻¹ℐ that correspond to parameters of interest and nuisance parameters, respectively. Similarly, the corresponding blocks of ℐ are ℐ₁₁ and ℐ₂₂. Let $\mathcal{C}={\mathcal{S}}_{11}-{\mathcal{S}}_{12}{\mathcal{S}}_{22}^{-1}{\mathcal{S}}_{21},\mathcal{J}={\mathcal{I}}_{11}-{\mathcal{I}}_{12}{\mathcal{I}}_{22}^{-1}{\mathcal{I}}_{21}$ and using Frobenius formula it can be easily seen that

$$n^{1/2}(\widehat{\delta }-{\delta }_0)\Rightarrow \text{Normal}(0,{\mathcal{C}}^{-1}).$$

The following theorem is an analog of Theorem 3 for the case of a composite hypothesis.

Theorem 4

Define 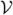₁ = Normal(0, 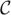−1). Using Cholesky decomposition the covariance matrix can be factored as 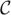⁻¹ = LL^T, where L is a lower-triangular matrix. Let λ_i, i = 1, …, r be eigenvalues of the matrix L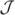L^T. Let ${\mathcal{Z}}_1^2,{\mathcal{Z}}_2^2,\dots ,{\mathcal{Z}}_r^2$ denote independent ${\chi }_1^2$ random variables. Then under H₀ the ARLR test statistic based on the pseudolikelihood (3) has the limiting distribution that is the same as

$${{\mathcal{V}}_{\text{1}}}^{\text{T}}\mathcal{J}{\mathcal{V}}_1\sim \sum _{i=1}^r{\lambda }_i{\mathcal{Z}}_i^2.$$ (14)

Remark 7

To estimate the λ_i’s, apply a procedure analogous to the one described in Remark 6.

3. Simulations

3.1 The Binary Case

When all variables are binary, it is possible to compute the retrospective likelihood of case–control data. In this section, we compare of our pseudolikelihood method with those based on the full retrospective likelihood, in the case that the genetic factor of interest is a directly observable binary variable, such as the carrier status for a variant allele in a specific genetic locus.

In this case, there are no covariates Z; the retrospective likelihood is given as follows. Define H{β₀ + m(h^dip, x, β)} = pr(D = 1|X, H^dip) and ℋ(d, h^dip, x, β₀, β) = [H{β₀ + m(h^dip, x, β)}]^d[1 − H{β₀ + m(h^dip, x, β)}]^1−d. Then

$$\begin{array}{l}\text{pr}(W=w,H^{\text{dip}}=h^{\text{dip}}\mid D=d)\\ =\frac{\int \mathcal{H}\left(d,h^{\text{dip}},x,{\beta }_0,\beta \right)Q(h^{\text{dip}},\mathrm{\Theta })f_{\text{mem}}(w\mid d,h^{\text{dip}},x,\xi )f_X(x\mid \eta )dx}{\int {\displaystyle \sum _{h_{\ast }^{\text{dip}}}}\mathcal{H}\left(d,h_{\ast }^{\text{dip}},x,{\beta }_0,\beta \right)Q\left(h_{\ast }^{\text{dip}},\mathrm{\Theta }\right)f_X(x\mid \eta )dx}.\end{array}$$

Because we have specified a distribution for X, all variables are binary, and there is no Z, the parameters (β₀, β, θ, η) are sufficient to identify pr(D = 1), i.e.,

$$\begin{array}{l}\text{pr}(D=1)\\ =\int \sum _{h_{\ast }^{\text{dip}}}H\left\{{\beta }_0+m\left(h_{\ast }^{\text{dip}},x,\beta \right)\right\}Q\left(h_{\ast }^{\text{dip}},\mathrm{\Theta }\right)f_X(x\mid \eta )dx.\end{array}$$ (15)

Because of this, κ is identified from (β₀, β, θ, η) as well. Hence, simply using (3) as a likelihood function directly will be unstable because of overparametrization. To overcome this issue, we parameterized in terms of pr(D = 1), and let κ and β₀, the latter through (15), be functions of it. The obvious solution is to replace both β₀ and κ in (3) by the appropriate functions of pr(D = 1) as given in (15) and the definition of κ, which is what we did.

We did a small simulation experiment in order to illustrate our approach in this simple case. We assumed that environmental variables (X, W), genetic variant (G), and disease status (D) are binary. Given the values of (G, X) we generated a binary disease outcome D from the logistic model logit {pr(D | G, X)} = β₀ + β_x X + β_g G + β_xg X *G, with parameters (β_x, β_g, β_xh) = (1.099, 0.693, 0.693). The misclassification probabilities were pr(W = 0 | X = 1) = 0.20 and pr(W = 1 | X = 0) = 0.10. Here we assume that the misclassification model and relevant parameters are known.

We estimated parameters using the foregoing algorithm and investigated the effect of knowing the probability of disease. We found that our proposed method yielded estimates that were numerically identical to those based on the full retrospective likelihood: we believe but have not been able to show that this is true in general. Our method showed no noticeable bias in the parameter estimates, either in the risk parameters or in the genotype probabilities, whereas the naive analysis that ignores measurement error resulted in large biases (Table 1).

Table 1.

Biases and root mean squared errors (RMSEs) for ordinary logistic regression, retrospective maximum likelihood, and our approach, where disease status (D), the genetic variant (G), and the environmental covariate (X) are binary. The environmental variable is measured with error, with misclassification probabilities being 0.20 for exposed and 0.10 for nonexposed subjects. The results are based on a simulation study with 500 replications for 1000 cases and 1000 controls. Results are given when pr(D = 1) is known and when it is unknown.

			Logistic		Retrospective		Pseudo-likelihood
pr(D = 1)	Parameter	True value	Bias	RMSE	Bias	RMSE	Bias	RMSE
Known	β0	−5.000	4.294	4.295	−0.006	0.108	−0.006	0.108
	βg	0.693	0.239	0.323	−0.005	0.305	−0.004	0.305
	βx	1.099	−0.327	0.344	0.005	0.155	0.005	0.155
	βxg	0.693	−0.284	0.395	0.001	0.327	0.001	0.327
	pr(X = 1)	0.100			0.002	0.021	0.002	0.022
	pr(G = 1)	0.100			0.000	0.009	0.000	0.008
Unknown	β0	−5.000	4.294	4.295	−1.016	2.042	−1.016	2.042
	βg	0.693	0.239	0.323	−0.009	0.306	−0.009	0.306
	βx	1.099	−0.327	0.344	0.004	0.155	0.004	0.155
	βxg	0.693	−0.284	0.395	0.013	0.333	0.013	0.333
	pr(X = 1)	0.100			0.023	0.022	0.002	0.022
	pr(G = 1)	0.100			0.000	0.009	0.000	0.009
	pr(D = 1)	0.016			0.002	0.019	0.002	0.019

Further, we performed inferences based on the ARLR test and Wald procedures for small (n = 400) and moderate (n = 2000) sample sizes. The results are presented in the Web Table 13. We found that the proposed method closely achieves the nominal coverage, while Wald test resulted in rather elevated error rates, thus causing undercoverage. The sampling distribution of the parameter estimates is slightly skewed, and skewness is more pronounced for small sample sizes. Hence the variance estimate is larger than the mean variance estimate and it is undesirable to use Wald-type confidence intervals, because they are based on asymptotic normality.

3.2 Continuous Simulations

In this simulation, we considered continuous environmental variables and assumed that the genetic risk depends on the number of copies of a putative haplotype. We simulated the true environmental covariate (X) from a Normal distribution with zero mean and variance 0.1. To simulate observed environmental variables we used additive model of the form W = X + U, where U is generated from the normal distribution with zero mean and variance ξ = 0.25. Note that we are simulating a case of large measurement error, such as would occur for dietary measurements. This gives a stern test for our methodology.

Following the simulation setup of Spinka et al. (2005), given the following haplotype frequencies (h₁, h₂, h₃, h₄, h₅, h₆) = (0.25, 0.15, 0.25, 0.1, 0.1, 0.15) we directly generated diplotypes for each subject under the assumption of HWE. Then we coded haplotype h₃ as 1 and all the rest as 0. Given the diplotype information H^dip and environmental covariate X we generated binary disease status according to the following model

$$\begin{array}{l}\text{pr}(D=d\mid H^{\text{dip}},X)\\ =\frac{exp\left[d\left\{{\beta }_0+{\beta }_{x}X+{\beta }_g{N}_3(H^{\text{dip}})+{\beta }_{xg}X{N}_3(H^{\text{dip}})\right\}\right]}{1+exp\left\{{\beta }_0+{\beta }_{x}X+{\beta }_g{N}_3(H^{\text{dip}})+{\beta }_{xg}X{N}_3(H^{\text{dip}})\right\}},\end{array}$$

where N₃(H^dip) is the number of copies of h₃ in H^dip. In this setting we are interested in estimating the relative risk parameters and the frequency of haplotype h₃. To estimate the probability of disease we used a grid-search method on the interval (0.001, 0.051) with step 0.005 by maximizing the pseudolikelihood function for values of probability of disease fixed on a grid and then performing a grid search to identify the value of probability of disease that maximized the likelihood.

3.2.1 Measurement error distribution is known

Within this simulation setup we suppose that the measurement error distribution is known. Moreover, we assessed the effect of missing data by assuming that 50% of subjects were not genotyped and for those who were genotyped linkage phase is unknown.

We found that for our method there is no noticeable bias in parameter estimates, whereas the naive approach that ignores existence of the measurement error results in substantial bias, as illustrated in the Table 2. It is somewhat remarkable that even with 50% of the genotypes being missing, and with such large measurement error, our method still remains largely unbiased.

Table 2.

Biases and (RMSEs) for the naive approach that ignores existence of measurement error and our proposed method. The results are based on a simulation study with 500 replications for 1000 cases and 1000 controls, where disease status (D) is binary, environmental variables (X, W) are continuous, and the genetic variant h₃ is in the form of diplotype with a multiplicative interaction. The environmental variable is measured with error and the error variance is 0.25. Two cases are considered: (a) genotype known for all subjects and (b) genotype missing for 50% of the subjects.

			Naive approach		Proposed method
	Parameter	True value	Bias	RMSE	Bias	RMSE
Complete data	β0	−5.000	1.207	1.459	0.230	0.086
	βg	0.693	0.080	0.011	−0.001	0.007
	βx	1.099	−0.797	0.645	0.001	0.137
	βxg	0.693	−0.478	0.235	0.006	0.088
	pr(h3)	0.250	0.005	0.000	0.000	0.000
	pr(D = 1)	0.046	−0.032	0.001	0.008	0.000
	η1	0.000			0.003	0.001
	η2	0.100			−0.001	0.000
50% of genetic information is missing	β0	−5.000	1.206	1.460	0.228	0.084
	βg	0.693	0.082	0.015	−0.002	0.007
	βx	1.099	−0.794	0.647	0.013	0.161
	βxg	0.693	−0.477	0.243	0.011	0.102
	pr(h3)	0.250	0.004	0.000	0.000	0.000
	pr(D = 1)	0.046	−0.032	0.001	0.008	0.000
	η1	0.000			0.003	0.001
	η2	0.100			−0.002	0.000

Additionally, we constructed Wald and ARLR confidence intervals. The results of this simulation study are presented in Table 3. We found that the ARLR confidence interval achieved coverage close to nominal. The Wald confidence interval performed poorly in this situation, despite the fact that there is essentially no bias in the parameter estimates.

Table 3.

Coverage probabilities of Wald and ARLR confidence intervals. The results are based on a simulation study with 750 replications for 1000 cases and 1000 controls, where disease status (D) is binary, environmental variables (X, W) are continuous, and the genetic variant h₃ is in the form of diplotype with a multiplicative interaction. The environmental variable is measured with error. The probability of disease is known in the population, and the genotype is missing for 50% of the subjects.

Measurement error variance ξ	0.10	0.15	0.20	0.25
True value of βxg	0.693	0.693	0.693	0.693
Mean of β̂xg	0.704	0.708	0.700	0.678
Median of β̂xg	0.694	0.691	0.683	0.700
Coverage of the Wald test	0.793	0.727	0.707	0.697
Coverage of the LR test	0.957	0.947	0.952	0.941

We advocate the use of the ARLR procedure as opposed to Wald-type inferences in situations when large amounts of measurement error are present in environmental covariates.

3.2.2 Distribution of the environmental covariates is mis-specified

The aim of this simulation is to investigate robustness of our procedure to mild misspecification of the environmental covariate distribution. Here we calculated our method under the assumption that the environmental covariate had a normal distribution, while we simulated the environmental covariate from a t-distribution with 10 degrees of freedom.

The results presented in Web Table 1 illustrate that the proposed procedure results in parameter estimates that are nearly unbiased, which illustrates robustness of our methodology to mild misspecification of the environmental covariate distribution.

3.2.3 Measurement error distribution is estimated using replications

In Section 2.4 we developed a method for the case when measurement error distribution is estimated using repeated measurements. The goal of this simulation study is to investigate the performance of the proposed method in the case when measurement error distribution is estimated by replicating 50 randomly selected individuals in order to estimate the measurement error variance. Define ${\chi }_{\text{df}}^2$ to be a random variable distributed as chi square with df degrees of freedom. We generated the estimated measurement error variance ξ̂ as $\xi {\chi }_{50}^2/50$, where ξ = 0.25 is the true measurement error variance.

Simulation results presented in Web Table 2 illustrate that in this setting the proposed methodology resulted in parameter estimates that are nearly unbiased.

3.2.4 With environmental covariates measured exactly

For the setting described above we simulated the error-prone covariate X from the normal distribution with mean a₁Z with a₁ = 0.25 and variance ${\sigma }_x^2=0.10$. The environmental covariate Z measured exactly is simulated from a Normal distribution with mean zero and variance 0.10. Further, we introduced a main effect of Z in the risk model with risk coefficient β_z = log(2.5). The probability of disease is assumed to be known in the population.

The results of this simulation are presented in Web Table 3. The naive approach that ignores existence of the measurement error resulted in estimates of environment and interaction risk parameters that are largely biased. The proposed analysis produced estimates that are nearly unbiased and less variable.

4. Colorectal Adenoma Study Data Analysis

4.1 Modeling

Here we analyze the colorectal adenoma study data described in the introduction. To recap, there were 772 cases and 778 controls, the response D was colorectal adenoma status, the genetic data observed were three SNPs in the calcium receptor gene CaSR, the environmental variable X measured with error was log(1+calcium intake), which was measured by W, the result of a FFQ. The variables Z measured without error were age, sex, and race. The possible haplotypes in the data were ACG, ACT, AGG, GCG, AGT, GGG, and GCT. Because haplotypes AGT, GGG, GCT are rare, we pooled them with the next most common haplotype AGG. A few subjects do not have measurements of calcium intake and we eliminated them from the analysis.

Given calcium intake (X) and diplotype information (H^dip) we considered the following risk model

$$\begin{array}{l}\text{logit}\{\text{pr}(D=1\mid H^{\text{dip}},X)\}\\ ={\beta }_0+{\beta }_x\ast X+{\beta }_{h2}\ast N_2(H^{\text{dip}})+{\beta }_{h4}\ast N_4(H^{\text{dip}})\\ +{\beta }_{h5}\ast N_5(H^{\text{dip}})+{\beta }_{xh2}\ast X\ast N_2(H^{\text{dip}})\\ +{\beta }_{xh4}\ast X\ast N_4(H^{\text{dip}})+{\beta }_{xh5}\ast X\ast N_5(H^{\text{dip}}),\end{array}$$

where N₂(H^dip) is the number of haplotypes ACT observed in a diplotype, N₄(H^dip) is the number of haplotypes GCG observed in a diplotype and N₅(H^dip) is number of haplotypes AGG, AGT, GGG, or GCT observed in a diplotype.

Unfortunately, there is no direct information in the study to assess the measurement error properties of calcium intake W. We used a combination of outside data and sensitivity analysis instead. The outside data come from The Women’s Interview Study of Health (WISH; Potischman et al., 2002). There were ≈400 women in this study, which used the same FFQ as in the colorectal adenoma study and also included the results of six 24-hour recall measurements, which we denote by T_ij for the ith individual and jth replicate. The models for these data are that

$$\begin{array}{l}{W}_i={\alpha }_0+{\alpha }_1{X}_i+U_i,\\ T_{ij}=X_i+V_{ij},\end{array}$$

where U_i = normal (0, ${\sigma }_u^2$) and V_ij = normal (0, ${\sigma }_v^2$). Using variance components analysis, we estimated (α₀, α₁, ${\sigma }_u^2$), and took these as fixed and known in the colorectal adenoma study, although we also varied ${\sigma }_u^2$. The distribution of X was taken to be Gaussian with mean linear in Z and variance ξ. We used the method of Fuller (1987, Chapters 2, 5) and found estimates α̂₀ = 0.22, α̂₁ = 0.75, ${\widehat{\sigma }}_u^2=\widehat{\xi }=0.65$. To assess sensitivity to the measurement error model specification we considered several scenarios by imposing measurement error structure estimated using WISH data and varying it through ${\sigma }_u^2$.

4.2 Results

The probability of disease was constrained to be on the interval (0.001, 0.5), but the likelihood function was flat either as a function of the probability of disease, or, equivalently, as a function of the intercept parameter β₀. However, estimates of the risk parameters are unchanged for different values of probability of disease. This result is illustrated in Web Appendix D.

The four sets of parameter estimates presented in Table 4 correspond to different values of the measurement error variance. These results illustrate sensitivity of parameter estimates to the measurement error variance specification and the importance of assessing the measurement error process, as its incorrect specification results in substantial biases.

Table 4.

Estimates of risk parameters for the colorectal adenoma study assuming different variances (ξ) of the measurement error. The estimated measurement error variance is ξ = 0.65.

Parameter	Naive	ξ = 0.10	ξ = 0.60	ξ = 0.65	ξ = 0.70
βh2	−0.2087	−0.1866	−0.1606	−0.1770	−0.1365
βh4	−0.1663	−0.1908	−0.3710	−0.4289	−0.5377
βh5	−0.2770	−0.3670	−0.6609	−0.7584	−0.9379
βx	−0.0852	−0.0683	−0.1402	−0.1507	−0.1850
βxh2	0.0398	0.0394	0.1296	0.1044	0.2224
βxh4	−0.1886	−0.1749	−0.5192	−0.5817	−0.8124
βxh5	−0.2804	−0.2361	−0.7136	−0.8885	−1.1234

Additionally, the Wald and Bootstrap standard error estimates are presented in Web Tables 9 and 10. Also, 95% model-based and bootstrap confidence intervals are reported in Web Tables 11 and 12. Inspection of these results reveals that for large measurement error the model-based confidence intervals are narrower than those computed using the bootstrap. This phenomena is due to the fact that when large amounts of error in measurement is present in the data, the sampling distribution of parameter estimates can be skewed and thus model-based confidence intervals that are built using the asymptotic normality assumptions inherent in the Wald method have elevated error rates resulting in undercoverage.

Recall that the estimated error variance is ξ = 0.65. Inspection of the interaction parameter estimates β̂_xh4 = −0.58 and β̂_xh5 = −0.89 and corresponding 95% confidence intervals based on the estimated standard errors β_xh4: (−0.98, −0.18) and β_xh5: (−1.31, −0.47) suggests that at significance level 0.05 there is sufficient evidence to indicate that among carriers of h₄ and h₅ haplotypes, increased calcium intake is associated with decrease in risk of colorectal tumor development. Additionally, we computed bootstrap; standard errors and confidence intervals based on 300 samples. 95% bootstrap confidence interval for β_xh4 is (−1.22, −0.02) and for β_xh5 is (−2.11, −0.18). Note that the bootstrap method produced confidence intervals that are wider than those based on the Normality assumption. This effect is due to the fact that sampling distribution of parameter estimates is oftentimes skewed when measurement error is present and skewness is more pronounced for large measurement errors, which is the case in our situation.

Further, we performed inference based on the ARLR and Wald procedures. For the majority of cases λ was very close to 1 and there was no noticeable difference between the ARLR confidence interval and the one based on the standard asymptotics. Both ARLR and Wald procedures announced β_xh2 to be not significant, for all measurement error models we considered, so we based our analysis on a reduced model by setting β_xh2 to be 0. Analysis of the reduced model showed that β_xh5 is significantly different from 0 for all measurement error model specifications we considered. The Wald test announced β_xh4 as significant for measurement error variance 0.5 and greater, while the LR test showed it is significantly different from 0 for measurement error variance of 0.4 and larger.

Because the measurement error distribution was estimated using the WISH study that included female subjects only, we performed the analysis on 451 female cases and 459 female controls. The pattern shown in Table 5 reveals that the ARLR CIs are substantially wider than Wald CI and the difference is more pronounced for large measurement errors. A similar effect is present in the simulation study, namely the coverage probability of the Wald CI is considerably less than nominal. It appears that a symmetric CI centered at the estimate tends to perform poorly, because even for fairly large samples, with large error in measurement and missing data the sampling distribution of parameters can be substantially skewed.

Table 5.

Wald and ARLR confidence intervals for β_xh4 for the Colorectal Adenoma Study assuming various measurement error variances. The estimated measurement error variance is 0.65. The analysis is performed for female subjects.

	Wald CI	LR-type CI
ξ = 0.10	(−0.416, −0.090)	(−0.460, 0.119)
ξ = 0.60	(−0.972, 0.175)	(−1.220, 0.388)
ξ = 0.65	(−1.143, 0.198)	(−1.462, 0.420)
ξ = 0.70	(−1.394, 0.230)	(−1.912, 0.583)

5. Discussion

We have considered the problem of relating risk of a complex disease to genetic susceptibilities, environmental exposures, and their interaction when the environmental covariates are measured with error and some of the genetic information is missing. Utilizing a polychotomous logistic regression model, pseudolikelihood and a model for the distribution of underlying gene information, we constructed a relatively simple yet efficient semiparametric algorithm for parameter estimation. We have shown that the resulting estimates are consistent and derived their asymptotic variance when the distribution of measurement error is known, and when it is estimated from replications.

Our simulation results illustrate that for large studies there is no noticeable bias in our parameter estimates, whereas the naive approach that ignores the existence of the measurement error results in substantial bias.

We also developed an adjusted LR test statistic, the ARLR method, that is appropriate for the sampling design and performs much better in terms of test level than Wald-type inferences.

In our development, we have used a parametric model for the distribution of the environmental covariate measured with error. Our simulations and the example were based upon normal distributions, which seem reasonable in this context, but clearly more general models are possible, e.g., the semi-nonparametric family of Zhang and Davidian (2001). While such parametric assumptions can be wrong, often the resulting inferences are not badly affected by mild misspecification as illustrated in our numerical example, especially for logistic regression. For example, in the running Framingham data example in Carroll et al. (2006), the underlying variable X (transformed systolic blood pressure) appears to be more accurately modeled by a t-distribution with 5 degrees of freedom, but the differences in inference compared to a normal distribution assumption are hardly noticeable.

Issues of testing per se have a different focus than estimation of parameters. As described by Carroll et al. (2006, Chapter 10), generally if one is interested in the global null hypothesis of a null effect for a variable X measured with error, then tests that ignore measurement error are generally valid and often efficient in local power. The reason for this is that under the global null hypothesis, the observed data will also show no effect due to the observed W. If one has a complex model for X, e.g., a quadratic model, or if X is multivariate, then tests for subcomponents of the model associated with X are generally invalid. Tests for factors measured exactly, such as covariates Z or for phase-known haplotypes, are generally invalid, except when X is independent of the relevant covariates.

In models such as that described in Section 4.1, hypothesis testing for interactions or main effects while ignoring measurement error and replacing X by W can have real subtleties. It is clear theoretically that such tests cannot, in general, have nominal test level. Suppose, for example, that one is interested in testing whether there is an interaction between X measured with error and (Z₁, Z₂) measured without error, where (Z₁, Z₂) are independent of X but correlated with each other. Suppose the full model is a linear regression with mean β₀ + β₁X + β₂Z₁ + β₃Z₂ + β₄XZ ₁ + β₅XZ ₂, and the interest is in testing whether β₅ = 0. The observed data model has mean β₀ + β₁E(X | W) + β₂Z₁ + β₃Z₂ + β₄E(X | W) Z₁ + β₅E(X | W) Z₂. Thus, if E(X | W) is linear in W, the naive test for interaction that ignores measurement error will be approximately valid, approximately because the observed data model has some heteroscedasticity due to the interaction between X and Z₁. However, if E(X | W) = W 2, for example, then in ignoring measurement error and replacing X by W, one is fitting a misspecified model, and it is easy to construct situations where the naive test level is far from nominal. For example, take n = 200, β₁ = ··· = β₄ = 1, let (W, Z₁, Z₂) have mean zero and variance one, let the correlation between (Z₁, Z₂) be 0.6, let var (Y | X, Z₁, Z₂) = 0.25², let E(X | W) = W² and var (X | W) = 0.25. Then the naive test for the hypothesis that β₅ = 0 has test level exceeding 0.30, not even close to the nominal 0.05. However, what happens in logistic regression is more difficult to ascertain, and replacing linear regression by logistic regression in the example above does not reveal any major problems with test level.

For logistic regression when W is unbiased for X and with normally distributed measurement error, there are possible methods that can in principle avoid the use of distributional assumptions. The most widely used approach aimed at achieving this nonparametric feature is that of Stefanski and Carroll (1987), who use conditioning on sufficient statistics. Unfortunately, this approach will not work in our context, because in gene–environment interaction studies the sufficient statistic includes the underlying genetic variable, and hence cannot be allowed to be missing. Other methods that might be employed are SIMEX (Cook and Stefanski, 1995; Carroll et al., 2006) and Monte Carlo corrected scores (MCCS; Stefanski Novick, and Devanarayan, 2005; Carroll et al., 2006). Neither method results in actual consistent estimation of the parameters, although the latter is generally close to unbiased. However, MCCS requires the use of complex variable calculations, which users may find to be a practical hindrance.

Finally, we have assumed that H and (X, Z) are independently distributed in the underlying population, and we have assumed a parametric model for the distribution of H. Only changes in notation are required if there is a small number of strata, so that H and (X, Z) are independent within strata. More generally, all that we really require is a parametric model for H given (X, Z).

Appendix

An EM Algorithm

In this section, we describe an EM algorithm for solving the score-equations associated with the pseudolikelihood L^*. All technical arguments are given in A.2. To facilitate the calculations, make the following definitions:

$$\begin{array}{l}T(d,h^{\text{dip}},x,z,\mathrm{\Omega })\\ =\frac{exp\left[I_{(d\ge 1)}(d)\left\{{\kappa }_d+m(h^{\text{dip}},x,z,\beta )\right\}\right]}{1+{\displaystyle \sum _{j=1}^K}exp\left\{{\beta }_{0j}+m(h^{\text{dip}},x,z,\beta )\right\}},\\ \alpha (h^{\text{dip}},d,z,w,\mathcal{B},\xi )\\ \int T(d,h^{\text{dip}},x,z,\mathrm{\Omega })f_{\text{mem}}(w\mid d,h^{\text{dip}},x,z,\xi )f_X(x\mid z,\eta )dx,\\ \gamma (h^{\text{dip}},z,\mathcal{B})\\ =\int \sum _{d_{\ast }}T(d_{\ast },h^{\text{dip}},x,z,\mathrm{\Omega })f_X(x\mid z,\eta )dx,\\ V_{\beta }(d,h^{\text{dip}},x,z,\mathrm{\Omega })\\ \frac{\partial m(h^{\text{dip}},x,z,\beta )}{\partial \beta }\left[\frac{1}{1+{\displaystyle \sum _{j=1}^K}exp\left\{{\beta }_{0j}+m(h^{\text{dip}},x,z,\beta )\right\}}-I(d=0)\right].\end{array}$$

Note that neither α(•) nor γ(•) depend on Θ.

We split up the EM calculations into a series of steps.

EM Algorithm for Θ

Under HWE, if θ_i is the frequency of haplotype h_i, $\text{pr}\{H^{\text{dip}}=(h_i,h_j)\mid \mathrm{\Theta }\}={\theta }_i^2$ if h_i = h_j and = 2θ_iθ_j if h_i ≠ h_j. Let N_k (H^dip) be the number of copies of h_k in H^dip, and note that as in Spinka et al. (2005), N_k(H^dip)/θ_k = ∂log {pr(H^dip)}/∂θ_k. Define

$$\begin{array}{l}{\mathcal{N}}_k(\mathcal{B})=\sum _{i=1}^n{E}_{\mathcal{B}}\left\{N_k(H^{\text{dip}})\mid G_i,D_i,W_i,Z_i,R_i=1\right\},\\ V_k(\mathcal{B})=2\sum _{i=1}^n\frac{{\displaystyle \sum _{h_s}}Q\{(h_k,h_s),\mathrm{\Theta }\}\gamma \{(h_k,h_s),Z_i,\mathcal{B}\}}{{\displaystyle \sum _{h^{\text{dip}}}}Q(h^{\text{dip}},\mathrm{\Theta })\gamma \left(h^{\text{dip}},Z_i,\mathcal{B}\right)}.\end{array}$$

Then if ℬ^(s) is the current value of ℬ, we update θ_k to ${\theta }_k^{(s+1)}$ as

$${\theta }_k^{(s+1)}={\mathcal{N}}_k({\mathcal{B}}^{(s)}){\left\{{\mathcal{V}}_k({\mathcal{B}}^{(s)})\right\}}^{-1}.$$ (A.1)

Further, in each iteration we normalize ${\theta }_k^{(t+1)}={\theta }_k^{(t+1)}/{\sum }_{k^{\prime }=1}^{K_{\mathrm{\Theta }}}{\theta }_{k^{\prime }}^{(t+1)}$.

EM Algorithm for κ_d and β

For j = 1, …, K, we update κ_j by solving the following equation for κ_j:

$$n_j=\sum _{i=1}^n\frac{\int {\displaystyle \sum _{h_{\ast }^{\text{dip}}}}{\displaystyle \sum _{d_{\ast }}}{I}_{(d_{\ast }=j)}(d_{\ast })S\left(d_{\ast },h_{\ast }^{\text{dip}},x,Z_i,\mathrm{\Omega }\right)f_X(x\mid Z_i,\eta )dx}{\int {\displaystyle \sum _{h_{\ast }^{\text{dip}}}}{\displaystyle \sum _{d_{\ast }}}S\left(d_{\ast },h_{\ast }^{\text{dip}},x,Z_i,\mathrm{\Omega }\right)f_X(x\mid Z_i,\eta )dx}.$$ (A.2)

To update β, we solve

$$\begin{array}{l}0=\sum _{i=1}^n\frac{\int {\displaystyle \sum _{h^{\text{dip}}\in {\mathcal{H}}_G^{\text{dip}}}}{V}_{\beta }\left(d,h^{\text{dip}},x,z_i,\mathrm{\Omega }\right)S\left(d_i,h^{\text{dip}},x,z_i,\mathrm{\Omega }\right)f_{\text{mem}}\left(w_i\mid d_i,h^{\text{dip}},x,z_i,\xi \right)f_X(x\mid z_i,\eta )dx}{\int {\displaystyle \sum _{h^{\text{dip}}\in {\mathcal{H}}_G^{\text{dip}}}}S\left(d_i,h^{\text{dip}},x,z_i,\mathrm{\Omega }\right)f_{\text{mem}}\left(w\mid d_i,h^{\text{dip}},x,z_i,\xi \right)f_X(x\mid z_i,\eta )dx}\\ -{\displaystyle \sum _{j=1}^n}\frac{\int {\displaystyle \sum _{d_{\ast }}}{\displaystyle \sum _{h_{\ast }^{\text{dip}}}}{V}_{\beta }\left(d,h_{\ast }^{\text{dip}},x,z_i,\mathrm{\Omega }\right)S\left(d_{\ast },h_{\ast }^{\text{dip}},x,z_i,\mathrm{\Omega }\right)f_X(x\mid z_i,\eta )dxdz}{\int {\displaystyle \sum _{d_{\ast }}}{\displaystyle \sum _{h_{\ast }^{\text{dip}}}}S\left(d_{\ast },h_{\ast }^{\text{dip}},x,z_i,\mathrm{\Omega }\right)f_X(x\mid z_i,\eta )dx}.\end{array}$$ (A.3)

EM Algorithm for β_0d and η

The updating schemes for β_0d and η are of the form (A.3) with V_β(•) replaced by V_β0d(d, h^dip, x, z, Ω) = −pr(D = d ≥ 1|h^dip, x, z) and V_η (x, z, η) = ∂log{f_X(x | z, η)}/∂η for β_0d and η, respectively.

EM Calculations

Here we justify the EM algorithm previously described. In what follows, we will need the following identities:

$$\text{pr}(H^{\text{dip}}=h^{\text{dip}}\mid Z=z,R=1)=\frac{Q(h^{\text{dip}},\mathrm{\Theta })\gamma (h^{\text{dip}},z,\mathcal{B})}{{\displaystyle \sum _{h_{\ast }^{\text{dip}}}}Q(h_{\ast }^{\text{dip}},\mathrm{\Theta })\gamma (h_{\ast }^{\text{dip}},z,\mathcal{B})},$$ (A.4)

$$\begin{array}{l}\text{pr}(H^{\text{dip}}=h^{\text{dip}}\mid G,D=d,W=w,Z=z,R=1)\\ =\frac{Q(h^{\text{dip}},\mathrm{\Theta })\alpha (h^{\text{dip}},d,z,w,\mathcal{B},\xi )}{{\displaystyle \sum _{h^{\text{dip}}\in {\mathcal{H}}_G^{\text{dip}}}}Q(h^{\text{dip}},\mathrm{\Theta })\alpha (h^{\text{dip}},d,z,w,\mathcal{B},\xi )},\end{array}$$ (A.5)

$$\begin{array}{l}\text{pr}(X=x,H^{\text{dip}}=h^{\text{dip}}\mid D,G,W,Z,R=1)\\ =\frac{S(D,h^{\text{dip}},x,Z,\mathrm{\Omega })f_{\text{mem}}(W\mid D,h^{\text{dip}},x,Z,\xi )f_X(x\mid Z,\eta )}{\int {\displaystyle \sum _{d_{\ast }}}{\displaystyle \sum _{h^{\text{dip}}\in {\mathcal{H}}_G^{\text{dip}}}}S(d_{\ast },h^{\text{dip}},x,z,\mathrm{\Omega })f_{\text{mem}}(w\mid d_{\ast },h^{\text{dip}},x,z,\xi )f_X(x\mid z,\eta )dx},\end{array}$$ (A.6)

$$\begin{array}{l}\text{pr}(D=d,H^{\text{dip}}=h^{\text{dip}},X=x\mid Z,R=1)\\ =\frac{S(d,h^{\text{dip}},x,Z,\mathrm{\Omega })f_X(x\mid Z,\eta )}{\int {\displaystyle \sum _{d_{\ast }}}{\displaystyle \sum _{h_{\ast }^{\text{dip}}}}S(d_{\ast },h_{\ast }^{\text{dip}},x,Z,\mathrm{\Omega })f_X(x\mid Z,\eta )dx}.\end{array}$$ (A.7)

Argument for (A.1)

As in Spinka et al. (2005) the estimating equation for θ_k is

$$\begin{array}{l}0=\sum _{i=1}^n{\text{E}}_{(\mathrm{\Omega },\eta )}\left[\frac{\partial log\{Q(H^{\text{dip}},\theta )\}}{\partial {\theta }_k}\mid G,D_i,W_i,Z_i,R_i=1\right]\\ -\sum _{i=1}^n{\text{E}}_{\mathcal{B}}\left[\frac{\partial log\{Q(H^{\text{dip}},\theta )\}}{\partial {\theta }_k}\mid Z_i,R_i=1\right]+\lambda .\end{array}$$

Note that

$$\begin{array}{l}\frac{\partial log\left[\text{pr}\left\{H^{\text{dip}}=(h_i,h_j)\mid \theta \right\}\right]}{\partial {\theta }_k}\\ =2/{\theta }_k,\text{if}{h}_i=h_j=h_k,\\ =1/{\theta }_k,\text{if}{h}_i=h_k\text{and}{h}_j\ne h_k,\text{or}{h}_j=h_k\text{and}{h}_i\ne h_k,\\ =0,\text{if}{h}_i\ne h_k\text{and}{h}_j\ne h_k.\end{array}$$

and

$$\begin{array}{l}\text{E}\left[\frac{\partial logQ\{H^{\text{dip}}\mid \theta \}}{\partial {\theta }_k}\right]=(2/{\theta }_k)\text{pr}\left\{H^{\text{dip}}=(h_k,h_k)\right\}\\ +(1/{\theta }_k)\sum _{h\ne h_k}\text{pr}\left\{H^{\text{dip}}=(h_k,h)\right\}+(1/{\theta }_k)\\ \times \sum _{h\ne h_k}\text{pr}\left\{H^{\text{dip}}=(h,h_k)\right\}\\ =2{\theta }_k+2(1-{\theta }_k).\end{array}$$

Since ${\sum }_{k=1}^{K_{\mathrm{\Theta }}}\{2{\theta }_k+2(1-{\theta }_k)\}=2K_{\mathrm{\Theta }}$, therefore λ = 0. Using (A.4) and (A.5), we arrive at (A.1).

Argument for (A.2)

It is readily seen that the estimating function for κ_j is

$$\begin{array}{l}0=\sum _{i=1}^n{\text{E}}_{(\mathrm{\Omega },v)}\left[\frac{\partial log\{T(D,H^{\text{dip}},X,Z,\mathrm{\Omega })\}}{\partial {\kappa }_j}\mid G_i,D_i,W_i,Z_i,R_i=1\right]\\ -\sum _{i=1}^n{\text{E}}_{\mathcal{B}}\left[\frac{\partial log\{T(D,H^{\text{dip}},X,Z,\mathrm{\Omega })\}}{\partial {\kappa }_j}\mid Z_i,R_i=1\right].\end{array}$$

Since ∂log {T(D, H^dip, X, Z, Ω)}/∂ κ_j = I_(D=j)(D), using (A.7), estimation can be performed by iteratively solving (A.2).

Argument for (A.3)

The estimating function for β is

$$\begin{array}{l}0=\sum _{i=1}^n{\text{E}}_{(\mathrm{\Omega },v)}\left[\frac{\partial log\{T(D,H^{\text{dip}},X,Z,\mathrm{\Omega })\}}{\partial \beta }\mid G_i,D_i,W_i,Z_i,R_i=1\right]\\ -\sum _{i=1}^n{\text{E}}_{\mathcal{B}}\left[\frac{\partial log\{T(D,H^{\text{dip}},X,Z,\mathrm{\Omega })\}}{\partial \beta }\mid Z_i,R_i=1\right].\end{array}$$

Using (A.6) and (A.7), we arrive at (A.3). The arguments for updating the β_0d and η are similar.