The lifetime risk of maternal mortality: concept and measurement

Abstract

Objective

The lifetime risk of maternal mortality, which describes the cumulative loss of life due to maternal deaths over the female life course, is an important summary measure of population health. However, despite its interpretive appeal, the lifetime risk of dying from maternal causes can be defined and calculated in various ways. A clear and concise discussion of both its underlying concept and methods of measurement is badly needed.

Methods

I define and compare a variety of procedures for calculating the lifetime risk of maternal mortality. I use detailed survey data from Bangladesh in 2001 to illustrate these calculations and compare the properties of the various risk measures. Using official UN estimates of maternal mortality for 2005, I document the differences in lifetime risk derived with the various measures.

Findings

Taking sub-Saharan Africa as an example, the range of estimates for the 2005 lifetime risk extends from 3.41% to 5.76%, or from 1 in 29 to 1 in 17. The highest value resulted from the method used for producing official UN estimates for the year 2000. The measure recommended here has an intermediate value of 4.47%, or 1 in 22.

Conclusion

There are strong reasons to consider the calculation method proposed here more accurate and appropriate than earlier procedures. Accordingly, it was adopted for use in producing the 2005 UN estimates of the lifetime risk of maternal mortality. By comparison, the method used for the 2000 UN estimates appears to overestimate this important measure of population health by around 20%.

Introduction

The importance of quantifying the loss of life caused by maternal mortality in a population is widely recognized. In 2000, the UN Millennium Declaration identified the improvement of maternal health as one of eight fundamental goals for furthering human development. As part of Millennium Development Goal 5, the UN established the target of reducing the maternal mortality ratio by three-quarters between 1990 and 2015 for all national and regional populations.¹

The maternal mortality ratio (MMRatio) is obtained by dividing the number of maternal deaths in a population during some time interval by the number of live births occurring in the same period. Thus, the MMRatio depicts the risk of maternal death relative to the frequency of childbearing. A related measure, the maternal mortality rate (MMRate), is found by dividing the average annual number of maternal deaths in a population by the average number of women of reproductive age (typically those aged 15 to 49 years) who are alive during the observation period. Thus, the MMRate reflects not only the risk of maternal death per pregnancy or per birth, but also the level of fertility in a population.

In addition to the MMRatio and the MMRate, the lifetime risk, or probability, of maternal death in a population is another possible measure. Whereas the MMRatio and the MMRate are measures of the frequency of maternal death in relation to the number of live births or to the female population of reproductive age, the lifetime risk of maternal mortality describes the cumulative loss of human life due to maternal death over the female life course. Because it is expressed in terms of the female life course, the lifetime risk is often preferred to the MMRatio or MMRate as a summary measure of the impact of maternal mortality.

However, despite its interpretive appeal, the lifetime risk of maternal mortality can be defined and calculated in more than one way. A clear and concise discussion of both its underlying concept and measurement methods is badly needed. This article addresses these issues and is intended to serve as a basis for official estimates of this important indicator of population health and well-being. In fact, the measure recommended here was adopted for use with the 2005 maternal mortality estimates published by the UN.²

Basic concepts

The lifetime risk, or probability, of maternal mortality could reflect at least three different underlying concepts, which can be summarized briefly as follows:

1. The fraction of infant females who would die eventually from maternal causes in the absence of competing causes of death from birth until menopause.

2. The fraction of infant females who would die eventually from maternal causes when competing causes of death are taken into account.

3. The fraction of adolescent females who would die eventually from maternal causes when competing causes of death are taken into account.

In formulae, these three concepts of lifetime risk can be defined as follows:

(1)

(2)

(3)

where each summation is over an age range, with x = 15 to 49 years. Each formula yields a probability of maternal death over some portion of the female life course, given a particular set of assumptions about other causes of death.

In these three equations, MMRatio_x is the maternal mortality ratio at age x, MMRate_x is the maternal mortality rate at age x, f_x is the fertility rate at age x, ℓ_x is the number of survivors at age x in a female life table, and L_x is the number of woman-years of exposure to the risk of dying from maternal or other causes between ages x and x + 1 for the hypothetical cohort of women whose lifetime experience is depicted in the same life table. The equivalence between the two expressions in each equation follows from observing that 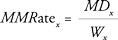, 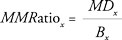and 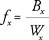, where, for a given time period, MD_x is the number of maternal deaths occurring among women aged x, W_x is the number of woman-years of exposure at age x in the observed population (in contrast to L_x , which refers to the hypothetical population of a female life table), and B_x is the number of live births in women aged x. Therefore, MMRate_x = MMRatio_x × f_x.

Note that LR₂ and LR₃ are related as follows:

(4)

where ℓ₁₅/ℓ₀ is the probability that a woman will survive from birth (i.e. 0 years) to age 15 years, as derived from a female life table. Equation 4 can be used for computing LR₂ from LR₃, or vice versa.

To understand Equation 2 better, observe that each element of the sum can be represented verbally as follows:

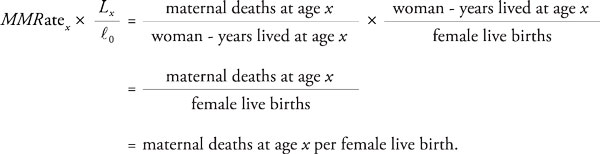Note that “woman-years lived at age x” refers in one case to the observed population and in the other to the hypothetical population of a female life table. Thus, the observed age-specific maternal mortality rates are applied to the fictitious life-table population as a means of constructing a synthetic measure of lifetime risk for a given time period.

Summing Equation 2 across age (i.e. x = 15 to 49 years) yields the number of maternal deaths over the life course per female live birth, or in other words, the full lifetime probability of maternal mortality, with other causes of death taken into account. A similar analysis of Equation 3 illustrates that it represents the adult lifetime probability of maternal mortality per 15-year-old female.

By contrast, Equation 1 contains the implicit assumption that the number of woman-years lived between ages x and x + 1 per female live birth (L_x/ℓ₀) is one for all ages, so in effect it ignores all forms of mortality, including that from maternal causes. Thus, it is theoretically possible within this model for a woman to die more than once from a maternal cause over her lifetime (similar to having more than one birth). This imprecision is unimportant, however, since MMRate_x is typically quite small at all ages, usually less than 1 per 1000, and thus higher-order terms are negligible.

Since 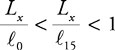in all human life tables, it follows that:

(5)

Therefore, of the three concepts of lifetime risk, the first one, LR₁, yields the largest probability of maternal death over a lifetime. However, this value is inflated because deaths due to other causes are ignored. If such deaths are factored into the calculation, the resulting lifetime risk of maternal death is reduced. A variant of LR₁ was used for computing the lifetime risk of maternal mortality in UN estimates for the year 2000.³

The second concept, LR₂, yields the smallest probability of maternal death over a lifetime, while the third concept, LR₃, yields a value that lies between the other two. Both LR₂ and LR₃ take account of competing risks due to other causes of mortality. However, many deaths from other causes occur in childhood, before the risk of maternal death becomes relevant. If childhood deaths are eliminated from the calculation, LR₃ reflects the adult lifetime risk of maternal death.

The size of the differences between the three measures in Equation 5 depends strongly on the level of overall mortality in a population. In populations with a high probability of survival to adulthood, there is very little difference between them; the three measures differ most in populations with relatively high levels of mortality from all causes, including maternal causes.

For all three concepts, the measures of lifetime risk are hypothetical in the sense that they rely on the demographic patterns observed in a population during a single period of time. Thus, they represent the lifetime risk of maternal mortality for a cohort of females who, hypothetically, are subject throughout their lives to prevailing demographic conditions, as reflected by age-specific rates of fertility and mortality, including maternal mortality. Like life expectancy at birth, they are examples of “period” measures of population characteristics as used in standard demographic analysis.^4–6

Age-specific maternal mortality data

The Bangladesh Maternal Health Services and Maternal Mortality Survey of 2001 was a nationally representative survey that collected information about mortality in general and about maternal deaths in particular.⁷ The data presented here are based on births and deaths that occurred within interviewed households during a period of 3 years before the survey. For each reported death, information was gathered on the age and sex of the deceased. In addition, if the deceased was a woman aged 13–49 years, follow-up questions were asked to determine whether the death was due to a maternal cause.

Using such information, it was possible to compute various age-specific measures of fertility and mortality, including maternal mortality. Table 1 illustrates the results obtained when all three measures of lifetime risk were calculated for Bangladesh during 1998–2001 using data derived from the 2001 survey and Equation 1, Equation 2 and Equation 3. In these calculations, when age-specific information about maternal deaths was used to compute the lifetime risk, the value of each measure was the same whether based on MMRatio_x or MMRate_x.

Table 1. Illustrative calculation of three measures of the lifetime risk of maternal mortality, LR₁, LR₂ and LR₃, based on age-specific maternal mortality data from Bangladesh for 1998–2001.

Age range (years)	Exposure timea		Maternal deathsb		MMRatec (per 1000)	Live births		Fertility rated	MMRatioe (per 100 000)		Life-table exposure timef			LRMM
														Other causes of death ignoredg	Other causes of death considered
															From birthh	From age 15 yearsi
														LR1	LR2	LR3
15–19	90 099		20.501		0.228	12 068		0.134	169.9		4.545			0.0011	0.0010	0.0011
20–24	67 389		29.559		0.439	12 494		0.185	236.6		4.518			0.0022	0.0020	0.0022
25–29	57 605		30.820		0.535	8 600		0.149	358.4		4.485			0.0027	0.0024	0.0026
30–34	48 931		24.399		0.499	4 727		0.097	516.2		4.443			0.0025	0.0022	0.0024
35–39	40 110		10.490		0.262	2 130		0.053	492.5		4.393			0.0013	0.0011	0.0013
40–44	31 989		12.367		0.387	636		0.020	1945.9		4.337			0.0019	0.0017	0.0019
45–49	21 880		3.256		0.149	134		0.006	2435.4		4.252			0.0007	0.0006	0.0007
Totalj	358 007		131.392		0.367	40 788		3.222	322.2		30.972			0.0125	0.0111	0.0122

LRMM, lifetime risk of maternal mortality; MMRate, maternal mortality rate; MMRatio, maternal mortality ratio.
^a Exposure time is the total number of woman-years lived by the survey population during the observation period.
^b The numbers of maternal deaths are fractional because they were estimated from survey data using sample weights.
^c MMRate = maternal deaths ÷ exposure time.
^d Except for the total row, fertility rate = live births ÷ exposure time.
^e MMRatio = maternal deaths ÷ live births.
^f The life-table exposure time is the number of woman-years lived per female live birth derived from a life table constructed using survey data.
^g Except for the total row, elements of the column labelled LR₁ = 5 × MMRate = 5 × fertility rate × MMRatio, showing that equivalent measures of lifetime risk can be derived using age-specific values of either the MMRate or the MMRatio.
^h Except for the total row, elements of the column labelled LR₂ = MMRate × life-table exposure time = fertility rate × MMRatio × life-table exposure time.
ⁱ All elements of the column labelled LR₃ equal the corresponding element of the column labelled LR₂ divided by 0.9115, where 0.9115 is the probability that a female will survive from birth to age 15 years.
^j Values in the total row are the sums of their respective column values except for the MMRate, fertility rate and MMRatio. The MMRate for ages 15–49 years combined equals total maternal deaths divided by total exposure time; similarly, the MMRatio for ages 15–49 years combined equals total maternal deaths divided by total live births. Finally, the sum of fertility rates by 5-year age groups is multiplied by 5 to represent the total fertility rate (TFR) or the hypothetical average number of births per woman according to the age-specific birth rates observed in the survey population, under the assumption that death does not occur before menopause.
All data are from the Bangladesh Maternal Health Services and Maternal Mortality Survey of 2001.7 Data in the columns labelled Exposure time to MMRatio were taken or derived from table 3.2 of that report. The life-table exposure time and the probability that a female will survive to age 15 years (see note i) were derived by computing a female life-table using all-cause death rates as shown in table 3.8 of that report.

Summary maternal mortality data for ages 15–49 years

In most situations, the age distribution of maternal deaths is not known and information is limited to summary measures, such as the MMRatio or the MMRate, which are computed using data on maternal deaths, live births and woman-years of exposure for ages 15–49 years combined. To obtain the formulae for lifetime risk that are used in practice from Equation 1, Equation 2 and Equation 3, one must assume that either the MMRatio or the MMRate is constant across all ages.

For example, if one assumes the MMRatio is constant across all ages, Equation 1, Equation 2 and Equation 3 can be simplified as follows:

(1a)

(2a)

(3a)

Here, TFR is the total fertility rate, or the number of children per woman implied by age-specific fertility rates, f_x , if we assume death does not occur until at least the age when menopause is reached, and NRR is the net reproduction rate, or the expected number of female children per newborn girl given current age-specific fertility and mortality rates. The factor of 2.05 in Equation 2a and Equation 3a comes from assuming a typical sex ratio at birth (i.e. 105 boys per 100 girls) and is needed here because the NRR is expressed in terms of female births only.

Alternatively, if we assume the MMRate is constant across age, the three equations become the following:

(1b)

(2b)

(3b)

Here, T₁₅ – T₅₀ is a life-table quantity representing the number of woman-years lived between ages 15 and 50 years, and the factor of 35 in Equation 1b corresponds to the reproductive interval from age 15 to 50 years. If a different reproductive interval were used for computing the MMRate, these equations would need to be modified accordingly.

These two sets of formulae can be considered as alternative approximations for Equation 1, Equation 2 and Equation 3. Their accuracy depends on the validity of the underlying assumptions: that either MMRatio_x or MMRate_x has a constant value across the age range. In this regard, it is clear which of the two sets of approximations is preferable: MMRate_x tends to be more stable over age than MMRatio_x, as illustrated in Table 1, for the population of Bangladesh between 1998 and 2001. This pattern is expected to be observed in general and follows from the relationship linking these two measures at a given age x. Recall that MMRatio_x × f_x = MMRate_x. Thus, the relative stability of MMRate_x over age occurs because the sharp age-related increase in the risk of maternal death per live birth, MMRatio_x, is balanced by a sharp decline in the fertility rate, f_x, at older ages.

The greater accuracy of approximations based on the MMRate is confirmed in Table 2, which shows all three measures of lifetime risk computed for Bangladesh from 1998 to 2001 using three types of information about maternal mortality: age-specific data, the MMRatio and the MMRate. The differences between rows in the table are consistent with the inequality in Equation 5. The differences between columns confirm that estimates of lifetime risk derived using age-specific data are closer to approximations derived using the MMRate than to those derived using the MMRatio. Observe that, in this example, estimates based on the MMRate have a small but consistent upward bias of around 2–3% in relative terms. However, estimates based on the MMRatio have a much larger downward bias, about 16–17%.

Table 2. Lifetime risk of maternal mortality according to three measures, LR₁, LR₂ and LR₃, calculated using three types of information, based on maternal mortality data from Bangladesh for 1998–2001.

Measure of LRMM	Information about maternal mortality
	Age-specifica (%)	MMRatiob (%)	MMRatec (%)
LR1 (ignoring other causes of death)	1.25	1.04	1.28
LR2 (from birth, taking into account other causes of death)	1.11	0.93	1.14
LR3 (from age 15 years, taking into account other causes of death)	1.22	1.02	1.25

LRMM, lifetime risk of maternal mortality; MMRate, maternal mortality rate; MMRatio, maternal mortality ratio.
^a Estimates are based on age-specific data and are listed as decimal fractions in the bottom row of Table 1.
^b Estimates were derived from Table 1 by assuming that the MMRatio did not vary with age, according to the following formulae: LR₁ = TFR × MMRatio; LR₂ = 2.05 × NRR × MMRatio, and LR₃ = LR₂ ÷ 0.9115, where TFR and MMRatio are the total fertility rate and the MMRatio for ages 15–49 years combined from Table 1, respectively, the NRR (i.e. net reproduction rate) equals the sum over age of the age-specific fertility rates and life-table exposure times from Table 1, and 0.9115 is the probability that a female will survive from birth to age 15 years.
^c Estimates were derived from Table 1 by assuming that the MMRate did not vary with age, according to the following formulae: LR₁ = 35 × MMRate, LR₂ = (T₁₅–T₅₀) × MMRate, and LR₃ = LR₂ ÷ 0.9115, where MMRate and T₁₅–T₅₀ are the MMRate for ages 15–49 years combined and the total life-table exposure time from Table 1, respectively.

Finally, it is important to note that none of the lifetime risk measures in Table 2 is identical to the one used in the published report of UN maternal mortality estimates for the year 2000.³ That measure, here called LR₀, equals 1.2 × LR₁, as computed using Equation 1a. The factor of 1.2 was intended to serve as a means of incorporating maternal deaths associated with pregnancies that did not result in a live birth. However, this adjustment is inappropriate, since the MMRatio depicts the frequency of maternal deaths in relation to the number of live births, not the number of pregnancies.

Discussion

In summary, the choice between possible measures of the lifetime risk of maternal death has two dimensions: the desired concept of lifetime risk and the accuracy of the calculation method. Of the three concepts of lifetime risk considered here, the first should be rejected as inappropriate because it ignores other forms of mortality (i.e. competing risks) and consequently exaggerates the lifetime risk of maternal mortality. The other two concepts both take competing risks into account and differ only in terms of their starting point: either birth or age 15 years, with the latter representing an approximate minimum age of reproduction.

There seem to be few precedents to guide the choice between the second and third concepts of lifetime risk. One source defined the “lifetime risk of maternal death” as the “probability of maternal death during a woman’s reproductive lifetime”.⁸ This definition seems to imply a conditional probability in which the pool of women at risk should include only those who survived to the age when reproduction starts. Members of the working group that produced the UN estimates of maternal mortality for 2005 came to the same conclusion; namely, that the concept of “lifetime risk of maternal mortality” should refer to the probability of maternal death conditional on survival to age 15 years, with other forms of mortality taken into account (i.e. LR₃).

Ideally, measures of lifetime risk should be computed using age-specific data. In most situations, however, one does not possess age-specific information about maternal mortality. For international comparisons, therefore, one needs a method that produces reliable results using either the MMRatio or the MMRate computed for ages 15–49 years. I have demonstrated here that MMRate_x tends to be more stable as a function of age than MMRatio_x and, therefore, that the MMRate yields more accurate estimates of the lifetime risk of maternal death.

Based on these two conclusions about concept and accuracy, I recommend that LR₃ computed using the MMRate be used for international comparisons of the lifetime risk of maternal mortality. As noted already, this approach was used to derive the 2005 UN estimates.²

Table 3 compares estimates, for the world as a whole and for various regional groupings, of the lifetime risk of maternal mortality in 2005 derived using all the calculation methods discussed here, except those that rely on age-specific data. Taking sub-Saharan Africa as an example, the range of estimates extends from 3.41% to 5.76%, or from 1 in 29 to 1 in 17. Note that the measure of lifetime risk used for the 2000 UN estimates, LR₀, gives the highest value of the lot, whereas the measure recommended here and used for the 2005 estimates (i.e. LR₃ based on the MMRate) gives an intermediate value of 4.47%, or 1 in 22.

Table 3. Estimates of the lifetime risk of maternal death in 2005 for the world as a whole and for various regional and developmental groupings calculated using four risk measures, LR₀, LR₁, LR₂ and LR₃, derived using either the maternal mortality ratio (MMRatio) or the maternal mortality rate (MMRate).

Region or development groupa	Maternal deathsb,c		Live birthsb (in thousands)		Women aged 15–49 yearsb (in thousands)		MMRatioc (per 100 000)		MMRatec (per million)		TFR	NRR	T15–T50	ℓ15/ℓ0	LRMMc (%) based on MMRatiod					LRMMc (%) based on MMRatee
															LR0	LR1	LR2	LR3		LR1	LR2	LR3
World	535 898		133 321		1 665 534		402		322		2.60	1.11	30.4	0.904	1.25	1.04	0.91	1.01		1.13	0.98	1.08
More-developed regions	1 482		13 319		299 715		11		5		1.57	0.75	34.2	0.990	0.02	0.02	0.02	0.02		0.02	0.02	0.02
Less-developed regions	534 416		120 002		1 365 819		445		391		2.82	1.19	29.9	0.894	1.51	1.26	1.08	1.21		1.37	1.17	1.31
Least developed countries	246 575		28 239		180 863		873		1363		4.86	1.79	25.3	0.816	5.10	4.25	3.20	3.92		4.77	3.46	4.23
Other less-developed countries	287 841		91 764		1 184 956		314		243		2.51	1.10	31.1	0.918	0.95	0.79	0.70	0.77		0.85	0.75	0.82
Less-developed regions (excluding China)	526 627		102 692		1 004 246		513		524		3.23	1.34	29.2	0.884	1.99	1.65	1.41	1.59		1.84	1.53	1.73
Sub-Saharan Africa	270 474		29 900		174 797		905		1547		5.31	1.84	23.0	0.795	5.76	4.80	3.41	4.29		5.42	3.56	4.47
Africa	276 135		33 511		216 429		824		1 276		4.83	1.74	24.3	0.813	4.77	3.98	2.93	3.61		4.47	3.10	3.81
Eastern Africa	87 105		11 570		66 680		753		1 306		5.41	1.90	23.1	0.812	4.89	4.07	2.93	3.61		4.57	3.02	3.72
Middle Africa	58 834		5 063		24 688		1 162		2 383		6.18	2.07	22.1	0.760	8.61	7.18	4.92	6.48		8.34	5.28	6.94
Northern Africa	10 952		4 777		50 501		229		217		3.04	1.36	31.9	0.939	0.84	0.70	0.64	0.68		0.76	0.69	0.74
Southern Africa	5 199		1 263		14 396		412		361		2.81	1.02	22.8	0.902	1.39	1.16	0.86	0.96		1.26	0.82	0.91
Western Africa	114 045		10 838		60 164		1 052		1 896		5.59	1.90	23.1	0.772	7.05	5.88	4.10	5.31		6.63	4.37	5.66
Asia	242 002		75 751		1 024 809		319		236		2.41	1.06	31.4	0.919	0.92	0.77	0.70	0.76		0.83	0.74	0.81
Eastern Asia	9 229		19 329		409 909		48		23		1.68	0.76	33.1	0.956	0.10	0.08	0.07	0.08		0.08	0.07	0.08
South-central Asia	189 569		39 686		408 753		478		464		3.04	1.30	30.2	0.890	1.74	1.45	1.27	1.43		1.62	1.40	1.57
South-eastern Asia	34 761		11 422		152 378		304		228		2.42	1.10	32.3	0.949	0.88	0.73	0.69	0.72		0.80	0.74	0.78
Western Asia	8 443		5 314		53 770		159		157		3.23	1.45	32.2	0.941	0.62	0.51	0.47	0.50		0.55	0.51	0.54
Europe	931		7 359		183 222		13		5		1.42	0.68	34.1	0.988	0.02	0.02	0.02	0.02		0.02	0.02	0.02
Eastern Europe	621		2 944		79 697		21		8		1.29	0.61	33.5	0.981	0.03	0.03	0.03	0.03		0.03	0.03	0.03
Northern Europe	74		1 060		22 905		7		3		1.66	0.80	34.5	0.993	0.01	0.01	0.01	0.01		0.01	0.01	0.01
Southern Europe	122		1 490		36 697		8		3		1.37	0.65	34.5	0.991	0.01	0.01	0.01	0.01		0.01	0.01	0.01
Western Europe	115		1 865		43 923		6		3		1.56	0.75	34.5	0.994	0.01	0.01	0.01	0.01		0.01	0.01	0.01
Latin America and the Caribbean	15 459		11 694		150 995		132		102		2.47	1.15	33.1	0.966	0.39	0.33	0.31	0.32		0.36	0.34	0.35
Caribbean	2  174		735		9 914		296		219		2.42	1.06	31.2	0.940	0.86	0.71	0.64	0.69		0.77	0.68	0.73
Central America	3  812		3 292		40 020		116		95		2.55	1.19	33.4	0.971	0.35	0.30	0.28	0.29		0.33	0.32	0.33
South America	9  474		7 666		101 061		124		94		2.44	1.14	33.2	0.967	0.36	0.30	0.29	0.30		0.33	0.31	0.32
Northern America	464		4 493		82 190		10		6		1.98	0.95	34.3	0.990	0.02	0.02	0.02	0.02		0.02	0.02	0.02
Oceania	907		513		7 889		177		115		2.27	1.04	32.7	0.955	0.48	0.40	0.38	0.39		0.40	0.38	0.39

LRMM, lifetime risk of maternal mortality; MMRatio, maternal mortality ratio; MMRate, maternal mortality rate; TFR, total fertility rate; NRR, net reproduction rate; T₁₅–T₅₀, woman-years lived between the ages of 15 and 50 years, as derived from a female life-table; ℓ₁₅/ℓ₀, probability that a female will survive from birth to age 15 years.
^a The regional and other groupings correspond to those used by the UN Population Division.^9
b The aggregate numbers of maternal deaths, live births or women aged 15–49 years reported here may be lower than their true values as the figures shown here exclude some small populations for which no maternal mortality estimates were available.
^c Since the purpose here is to illustrate alternative methods of computing the LRMM, values of maternal deaths, MMRatio and MMRate, in this table are not rounded according to standard practice and there is no indication of the uncertainty associated with these estimates. For more information on such topics, please refer to the official report of the 2005 UN estimates.^2
d With the assumption that the MMRatio is constant across age, the different formulae for the LRMM are as follows: LR₀ = 1.2 × LR₁, LR₁ = TFR × MMRatio, LR₂ = 2.05 × NRR × MMRatio, and LR₃ = LR₂ ÷ ℓ₁₅/ℓ₀.
^e With the assumption that the MMRate is constant across age, the different formulae for the LRMM are as follows: LR₁ = 35 × MMRate, LR₂ = (T₁₅–T₅₀) × MMRate, and LR₃ = LR₂ ÷ ℓ₁₅/ℓ₀.
Data on maternal deaths are from the 2005 UN estimates of maternal mortality.² Data on live births, women aged 15–49 years, TFR, NRR, T₁₅–T₅₀ and ℓ₁₅/ℓ₀ were taken or derived from other UN data.⁹

For the population groupings shown in Table 3, the measure of lifetime risk used for the 2000 UN estimates exaggerates the lifetime risk relative to the measure used for the 2005 estimates by an average of around 20%.

Thus, the two sets of estimates are not directly comparable: a trend analysis based on the 2000 and 2005 estimates of lifetime risk would exaggerate the pace of decline in some cases, while it would understate the speed of increase or reverse the direction of change in others. For this reason, and because of other changes in the methods used between the 2000 and 2005 UN studies of maternal mortality, the two sets of estimates should not be used for trend analysis. Any such analysis should focus on the 1990 and 2005 regional estimates of the MMRatio.² ■