Bayesian Analysis of Multivariate Nominal Measures Using Multivariate Multinomial Probit Models

Abstract

The multinomial probit model has emerged as a useful framework for modeling nominal categorical data, but extending such models to multivariate measures presents computational challenges. Following a Bayesian paradigm, we use a Markov chain Monte Carlo (MCMC) method to analyze multivariate nominal measures through multivariate multinomial probit models. As with a univariate version of the model, identification of model parameters requires restrictions on the covariance matrix of the latent variables that are introduced to define the probit specification. To sample the covariance matrix with restrictions within the MCMC procedure, we use a parameter-extended Metropolis-Hastings algorithm that incorporates artificial variance parameters to transform the problem into a set of simpler tasks including sampling an unrestricted covariance matrix. The parameter-extended algorithm also allows for flexible prior distributions on covariance matrices. The prior specification in the method described here generalizes earlier approaches to analyzing univariate nominal data, and the multivariate correlation structure in the method described here generalizes the autoregressive structure proposed in previous multiperiod multinomial probit models. Our methodology is illustrated through a simulated example and an application to a cancer-control study aiming to achieve early detection of breast cancer.

1 Introduction

The past three decades have seen a great deal of research into discrete choice models, especially in the econometrics and transportation systems literature (Hausman & Wise, 1978; Daganzo, 1980; Bierlaire, 1998). The multinomial logit (MNL) model and the multinomial probit (MNP) model are among the most popular discrete choice models. The MNL model assumes independence of irrelevant alternatives (IIA), which limits its use for data with correlated categorical levels. In contrast, the MNP model provides a framework for representing association between levels of a multinomial outcome. However, MNP models are challenging to analyze due to the computational complexity of algorithms to fit them.

Non-Bayesian methods for analyzing MNP models have focused on using simulated maximum likelihood estimation and the method of simulated moments to avoid direct numerical evaluation of the multidimensional probability integrals involved in maximum likelihood estimation (McFadden, 1989; Geweke, Keane, & Runkle, 1994a; McFadden & Ruud, 1994; Börsch-Supan & Hajivassiliou, 1993). These approaches have been seen to be sensitive to the method of estimating the choice probabilities (McCulloch & Rossi, 1994).

Statistical computing innovations including Markov chain Monte Carlo (MCMC) estimation (Tanner & Wong, 1987; Gelfand & Smith, 1990; Gilks et al., 1996; Gamerman, 1998; Carlin & Louis, 2000; M.-H. Chen et al., 2000; Liu, 2001; Congdon, 2001; Gelman et al., 2003; Robert & Casella, 2004) have allowed for the development of Bayesian methods for complex models. Bayesian approaches for fitting MNP models have included Albert and Chib (1993), McCulloch and Rossi (1994), Nobile (1998), Chib, Greenberg, and Chen (1998), Nobile (2000), McCulloch, Polson, and Rossi (2000), Z. Chen and Kuo (2002), and Imai and van Dyk (2005a).

Multivariate discrete choice models generalize these models to permit analysis of multivariate categorical data. Kim, Allenby, and Rossi (2002) proposed an additive random utility model for modeling consumer demand for more than one variety (alternative). Bhat (2005, 2006) developed a new random utility model. These authors employed simulated maximum likelihood estimation. Specialized multivariate discrete choice models have also been considered. The mixed multinomial logit (MMNL) model (Hensher & Greene, 2003) extends the MNL model to relax the IIA assumption and to allow analysis of multivariate nominal correlated measures. Maximum simulated likelihood estimation, the method of simulated moments, and Bayesian methods have been used for inference in the MMNL model (McFadden & Train, 2000; Train, 2001; Sivakumar, Bhat, & Ökten, 2005; Train & Sonnier, 2005).

Extensions of MNP models to nominal data at multiple time points have also been proposed (McCulloch & Rossi, 1994; Geweke, Keane, & Runkle, 1994b, 1997; Z. Chen & Kuo, 2002; Ziegler, 2002; Rendtel & Kaltenborn, 2004). Computational issues in these multiperiod multinomial probit models have confined the covariance matrix of the latent variables to have either a low-order factor structure (Ziegler, 2002), a first-order autoregressive structure (McCulloch & Rossi, 1994; Geweke et al., 1994b, 1997; Rendtel & Kaltenborn, 2004), or a covariance matrix with a random scale (Z. Chen & Kuo, 2002).

In the case where no covariates are used in the model, the data can be represented as a multiway contingency table. A traditional approach to analyzing such data is log-linear modeling (Bishop, Fienberg, & Holland, 1975). For multi-way contingency table data, the model we propose here has some similarities to certain types of log-linear models; distinctions relate to relaxation of assumptions similar to IIA in MNL models.

An alternative approach for analyzing non-normal repeated measures, such as repeated categorical data and repeated ordinal data, is to use the generalized estimating equation (GEE) method (Liang & Zeger, 1986; Zeger & Liang, 1986; Zeger, 1987; Liang, Zeger, & Qaqish, 1992). However, the GEE method is not indicated when inference about the correlation parameters, in addition to inference for regression parameters, is of interest.

Golob and Regan (2002) extend the MNP model for univariate nominal measure to the multivariate MNP (MVMNP) model to analyze multivariate nominal data, using the generalized least-squares approach proposed by Muthen (1983) for structural equation models. To solve the parameter identification, they standardized the covariance matrix, i.e., used a correlation matrix instead of a covariance matrix. However, this technique forces the magnitudes of each latent variables to be equal and this may not be appropriate without any knowledge of the latent variables.

In this paper, we consider the MVMNP model from a Bayesian perspective. We develop an MCMC algorithm allowing general specification for covariance matrices of the latent variables (i.e., the utilities in choice models). Our key statistical computing innovation is to use the parameter-extended Metropolis-Hastings (PX-MH) algorithm to sample the covariance matrix with restrictions on the diagonal elements. The PX-MH algorithm was proposed by Zhang, Boscardin, and Belin (2006) to sample a correlation matrix in the setting of the multivariate probit model. It was used by Boscardin and Zhang (2004) in a mixture of continuous and ordinal repeated measures. The Bayesian methods we propose both avoid parameter identification problems and allow flexible prior distributions on the covariance matrix of the latent variables.

Our paper proceeds as follows. Section 2 describes the MNP and MVMNP models, including some discussion about the model identification problem. Section 3 presents the MCMC sampling algorithm for the MVMNP model and describes the PX-MH algorithm for sampling the restricted covariance matrix. To illustrate our method, we use a simulated example in Section 4 and an example involving incomplete contingency table data from a cancer-control study in Section 5. Finally, we draw some conclusions and discuss other issues relative to MVMNP models in Section 6.

2 Multivariate multinomial probit (MVMNP) models

To describe the MVMNP model, we start with a description and a review of estimation methods for the MNP model.

2.1 MNP models for univariate nominal measures

Letting i = 1, 2, …, n index subjects and j = 1, 2, …, p index levels of a multinomial outcome having p levels, we let y_ij = 1 if subject i has outcome j and y_ij = 0 otherwise, with y_i = (y_i1, …, y_ip) representing a multinomial 1 × p vector. More compactly, we define d = (d₁,…, d_n)^T, where d_i contains the index of the chosen alternative, i.e., d_i = j if y_ij = 1. Following the notation in economics settings where utilities underlie choices, the MNP model assumes that there is a latent 1 × p vector u_i = (u_i1, …, u_ip) underlying each multinomial vector y_i, such that the multinomial outcome is determined by the maximum u_ij, as would happen if the subject chooses the alternative with maximum utility score. That is

$$d_i=j\iff u_{ij}\ge \underset{1\le l\le p}{\max }{u}_{il}$$ (1)

Although a simpler description of the latent-variable mean structure is possible, we proceed with a formulation that allows for covariates. In this framework, the MNP model further assumes that the vector u_i follows a multivariate normal distribution with mean equal to A_iβ and covariance matrix equal to V, where A_i is a p × k covariate matrix for subject i and β is a k × 1 regression parameter vector. With this notation,

$$u_i=A_i\beta +{\delta }_i$$ (2)

where δ_i ∼ N(0, V). The elements of A_i might reflect subject-specific covariates, in which case all of the elements in a row of A_i would be the same, or outcome-level-specific covariates (the classic case being the cost associated with each of the choices), in which case row elements would differ in general.

There are two identification problems in the above MNP model specification. Based on equation (1), we can see that the model will not be changed if a constant is added to both sides of equation (2). This first identification problem is known as additive redundance. This problem is usually solved by subtracting the p-th row of equation (2) from the first (p — 1) rows. The model becomes

$$z_i=X_i\beta +{∊}_i$$ (3)

where ∊_i ∼ N(0,Σ) independently, z_ij = u_ij — u_ip,X_ij = A_ij — A_ip, ∊_ij = μ_ij — μ_ip and Σ = [I_p—1,—1_p—1]V[I_p—1,—1_p—1]^T, with I_s denoting the s × s identity matrix and 1_s a vector of length s comprised of 1′s. Then the model can be described as:

$$d_i=\{\begin{array}{cc}0\hfill & \text{if}{\max }_{1\le l\le p-1}{z}_{il}<0\hfill \\ j\hfill & \text{if}{\max }_{1\le l\le p-1}{z}_{il}=z_{ij}>0\hfill \end{array}\phantom{\}}$$ (4)

We notice that the model defined by equations (3) and (4) is not substantively changed if both sides of equation (3) are multiplied by a non-zero constant. This second identification problem is known as multiplicative redundance. We solve this problem by restricting the first element of Σ, σ₁₁, to be equal 1. This strategy is also used by McCulloch et al. (2000). Thus, accommodating both additive and multiplying redundance, we describe the fully identifiable MNP model as follows:

$$d_i=\{\begin{array}{cc}0\hfill & \text{if}{\max }_{1\le l\le p-1}{z}_{il}<0\hfill \\ j\hfill & \text{if}{\max }_{1\le l\le p-1}{z}_{il}=z_{ij}>0\hfill \end{array}\phantom{\}}$$ (5)

where z_i ∼ N(X_iβ, Σ) and σ₁₁ = 1.

2.2 MVMNP models for repeated nominal measures

Buliding on the notation of Section 2.1, we now extend the MNP model to multivariate nominal measures.

Suppose for each subject i, there are g nominal measures, the first with p₁ levels, the next with p₂ levels, and so on up to the last with p_g levels. Let d_i = (d_i1, …, d_ig) denote the index vector of the alternatives the i-th subject chooses for the g measures. Assume each of these g nominal measures follows an MNP model. Therefore, for the q-th measure, q = 1, …, g, there is a (p_q—1)-dimensional underlying utility vector z_iq satisfying equation (5) with mean equal to X_iqβ and covariance matrix equal to Σ_q with the upper left element {Σ_q}₁₁ = 1.

We describe the MVMNP model for the g measures as follows:

$$z_i=X_i\beta +{∊}_i$$

where z_i^T = (z_i1, …, z_ig) with z_iq = (z_iq1, …, z_iq(pq—1)), $X_i=(X_{i1}^T,\cdots ,X_{ig}^T{)}^T$ and ∊_i ∼ N(0,Σ) with σ_qq = 1, where q = 1, (p₁ + p₂ - 1), (p₁ + p₂ + p₃ - 2), …, (p₁ + p₂ + ⋯ + p_g-1-g-1). We then specify

$$d_{iq}=\{\begin{array}{cc}0\hfill & \text{if}{\max }_{1\le l\le p_q-1}{z}_{iql}<0\hfill \\ j\hfill & \text{if}{\max }_{1\le l\le p_q-1}{z}_{iql}=z_{iqj}>0\hfill \end{array}\phantom{\}}$$

for i = 1, …, n and q = 1, …, g.

Contingency table data can be accommodated as a special case of this model by setting each of the X_i matrices to an identity matrix of dimension g. The correlation structure of the MVMNP model allows associations between pairs of frequencies, much as would occur with a log-linear model with all two-way interactions. We explore this idea further in section 5.

The following section presents a Bayesian sampling algorithm for MVMNP models.

3 Bayesian sampling algorithm for MVMNP models

3.1 MCMC framework

The joint posterior density of β, Σ, and Z = (z₁, …, z_n) given d = (d₁, …, d_n) is characterized as

$$p(\beta ,\Sigma ,Z\mid d)\propto p\left(\beta \right)\times p\left(\Sigma \right)\times \prod _{i=1}^n[I_i\times \varphi (z_i;X_i\beta ,\Sigma \left)\right].$$ (6)

where φ is the standard normal density function and $I_i={\prod }_{q=1}^g{I}_{iq}$

$$\begin{array}{cc}\hfill I_{iq}=& 1_{(d_{iq}=0,z_{iqj}<0,j=1,\dots ,p_q-1)}\hfill \\ \hfill & +\sum _{k=1}^{p_q-1}{1}_{(d_{iq}=k,z_{iqk}={\max }_{1\le l\le p_q-1}(z_{iql},0\left)\right)}.\hfill \end{array}$$

where 1_E is a indicator function equal to 1 when expression E is true and 0 when E is false. Each I_i is thus an indicator function evaluating to 1 if the choice vector d_i is compatible with the latent vector z_i.

To implement our MCMC algorithms, we build on the following:

• Assuming β ∼ N(b, C) as a prior distribution for β and using standard Bayesian linear model results, β|Σ, z, d has a multivariate normal distribution:

  $$\beta \mid \Sigma ,z,d\sim N(\widehat{\beta },V_{\beta }),$$

  where $V_{\beta }={\left({\sum }_{i=1}^N{X_i}^T{\Sigma }^{-1}{X}_i+C^{-1}\right)}^{-1}$ and $\widehat{\beta }=V_{\beta }\left({\sum }_{i=1}^N{X_i}^T{\Sigma }^{-1}{Z}_i+C^{-1}b\right)$.
• The latent variable z_iqj|β, Σ, d_i, z_iq(-j), z_i(-q) has a truncated normal distribution that can be represented:

  $$\begin{array}{cc}\hfill p& (z_{iqj}\mid \beta ,\Sigma ,d_i,{z_{iq}}_{(-j)},z_{i(-q)})\hfill \\ \hfill & \propto I_i\times p(z_{iqj}\mid \beta ,\Sigma ,z_{iq(-j)},z_{i(-q)})\hfill \\ \hfill & =(1_{(d_{iq}=j)}{1}_{(z_{iqj}\ge {\max }_{1\le 1\le p_q-1}(z_{i,q,l},0\left)\right)}\hfill \\ \hfill & +1_{d_{iq}\ne j}{1}_{(z_{iqj}\le {\max }_{1\le l\le p_q-1}(z_{i,q,l},0\left)\right)})\times \varphi (z_{iqj};{\mu }_{iqj},{\Sigma }_{iqj})\hfill \end{array}$$

  where μ_iqj and Σ_iqj are the conditional mean and variance of z_iqj given z_iq(-j), z_i(-q). With missing d_ij, z_iqj|β, Σ, d_iq, z_iq(-j), z_i(-q) has a univariate normal distribution with mean μ_iqj and variance Σ_iqj as before, but without truncation.

• Assuming Σ has prior density p(Σ), we have p(Σ|β, Z, d) is proportional to $p\left(\Sigma \right)\times {\prod }_{i=1}^n\varphi (z_i;X_i\beta ,\Sigma )$. It is not easy to directly draw simulations from the posterior distribution of the covariance matrix Σ with g diagonal elements equal to 1. In the next section, we elaborate in detail the steps involved in drawing p(Σ|β, Z, d) using the PX-MH algorithm.

3.2 Parameter-extended Metropolis-Hastings (PX-MH) step

We first give a brief review of the PX-MH algorithm proposed by Zhang et al. (2006). To sample a correlation matrix, R, in a multivariate probit model, Zhang et al. sample a covariance matrix, W, using the decomposition W = D^1/2RD^1/2 where D is a diagonal matrix of artificial variance components governed by a joint prior distribution, p(R, D), for the correlation matrix R and D. We present the PX-MH algorithm as follows.

Set initial value of (R⁽⁰⁾, D⁽⁰⁾) through setting $W^{\left(0\right)}=D^{\left(0\right)\frac{1}{2}}{R}^{\left(0\right)}{D}^{\left(0\right)\frac{1}{2}}$ to an initial covariance matrix.

Then, at iteration (t + 1)

1. Generate (R*, D*) by generating $W^{\ast }=D^{\ast \frac{1}{2}}{R}^{\ast }{D}^{\ast \frac{1}{2}}$ from Wishart (m, W^(t)).

2. Take

   $$(R^{(t+1)},D^{(t+1)})=\{\begin{array}{cc}(R^{\ast },D^{\ast })\hfill & \text{with probability}\alpha \hfill \\ (R^{\left(t\right)},D^{\left(t\right)})\hfill & \text{otherwise.}\hfill \end{array}\phantom{\}}$$

   where $\alpha =\min \left\{\frac{p(R^{\ast },D^{\ast }\mid \beta ,Z,Y)}{p(R^{\left(t\right)},D^{\left(t\right)}\mid \beta ,Z,Y)}\frac{q(W^{\left(t\right)}\mid W^{\ast })}{q(W^{\ast }\mid W^{\left(t\right)})},1\right\}$. Here, p(R, D|β, Z, Y) is the joint posterior density of (R, D) and q(.|W^(t)), the proposal density, is equal to the product of the Jacobian term for the transformation (W → R, D) and the Wishart density with m degrees of freedom and scale matrix equal to W^(t).

In the MVMNP model, the covariance matrix Σ has g diagonal elements equal to 1. We decompose Σ = D⁰RD⁰ where R is the correlation matrix of Σ and D⁰ is the diagonal standard deviation matrix with elements $(D_1^0,D_{p_1}^0,D_{p_1+p_2-1}^0,\dots ,D_{p_1+\cdots +p_{g-1}-g-1}^0)$ equal to 1. Then we consider a diagonal matrix D replacing those elements of D⁰ equal to 1 with unknown parameters (v₁, v_p1,v_p1+p₂-1, …, v_p1+⋯+p_g-1-g-1). Therefore, the matrix W = DRD is a covariance matrix without restrictions on the diagonal elements. We use the above PX-MH algorithm to sample W, thereby obtaining a draw of Σ. A slight distinction between sampling Σin the MVMNP model and sampling R in the multivariate probit model is that some of the diagonal elements of D are identified parameters in the MVMNP model, while for the multivariate probit model, all the diagonal elements of D are artificial; this distinction does not alter the character of the algorithm, however.

For the prior distribution of Σ, we use a PXW prior proposed by Zhang et al. (2006), with density given by the product of the Jacobian term for the transformation (W → R, D) and the Wishart density with m₀ degrees of freedom and scale matrix equal to Λ. The scale matrix Λ reflects the prior guess for the covariance matrix Σ with higher values of m₀ representing greater prior precision.

Including the g artificial parameters, the joint posterior density of β, R, D, Z given d is

$$p(\beta ,R,D,z\mid d)\propto p\left(\beta \right)\times p(R,D)\times \prod _{i=1}^N[I_i\times \varphi (z_i;X_i\beta ,\Sigma \left)\right].$$

The conditional distributions for β and z_i given other parameters are the same as described in Section 3.1. Through this joint posterior density, we have p(R, D|β, Z, d) is proportional to $p(R,D)\times {\prod }_{i=1}^N\varphi (z_i;X_i\beta ,\Sigma )$. As suggested above, the prior density p(R, D) can be specified by letting the joint prior distribution of (R, D) be from the PXW (m₀, Λ) family of distributions. Therefore, one cycle of the algorithm consists of Gibbs steps to sample β and each component of the latent variable z_i, and a Metropolis-Hastings step for sampling (R, D), with Σ generated as a byproduct of the PX-MH step.

3.3 Software implementation

We implemented our algorithm in C using the GNU scientific library (Galassi et al., 2006). For the univariate MNP model, we compared our algorithm to algorithms proposed by McCulloch and Rossi (1994) (MR) and Imai and van Dyk (2005a) (IvD). We implemented the MR algorithm using the rmnpGibbs function in the bayesm package for R (Rossi, Allenby, & McCulloch, 2006) and the IvD algorithm using the MNP R package (Imai & van Dyk, 2005b). Using a variety of data sets, including simulated examples from McCulloch and Rossi (1994) and the detergent brand choice example included in the MNP package, we obtained similar results to both MR and IvD. Our convergence performance was comparable to MR, which is shown by Imai and van Dyk (2005b) to be slower than the IvD algorithm. Because our primary interest is to provide greater modeling flexibility, based on a Bayesian framework for multivariate nominal measures that allows prior information to be incorporated in a flexible and intuitive manner, we do not view the slower convergence of our method relative to IvD as a fatal flaw, but it does suggest that it is important to be careful in assessing convergence in multivariate applications. In the following sections, we illustrate the use of our algorithm through simulated data on multivariate nominal measures, followed by an analysis of data from a cancer-control study.

4 Illustration using simulated data

To illustrate our MCMC algorithm for the MVMNP model, we use the following simulated example to investigate posterior inference for unknown parameters.

We generated a data set with sample size equal to 2,000. Each subject i was assumed to have two nominal measures for each person, y_i1 and y_i2, with y_i1 having three categorical levels and y_i2 having four categorical levels. We use z_i1 to denote the two-dimensional latent variable corresponding to y_i1 and z_i2 to denote the three-dimensional latent variable corresponding to y_i2. The covariance matrix for z_i1 was a 2 by 2 matrix with the correlation equal to 0.4 and variances equal to 1 and 0.81, respectively, and the covariance matrix for z_i2 was taken to be an AR(1) correlation matrix with first-order correlations equal to 0.5 and variance vector equal to (1, 0.81, 0.90). The correlations between elements of z_i1 and z_i2 were all set to 0.2. The 2 by 1 covariate matrix X_i was generated from iid uniform (-0.5,0.5), and the regression parameter β was set to 2.0.

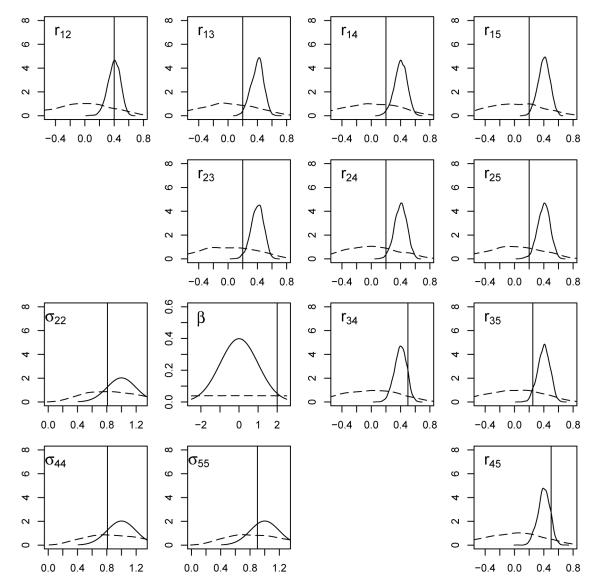
To perform inference using the MVMNP model, we consider two alternative prior formulations for β and Σ. First, we take the prior distribution for β to be N(0, 100), which is very weakly informative, and we assume Σ has a PXW (m₀ = 8, I) distribution, i.e. a prior guess that the covariance matrix is equal to the identity matrix with eight degrees of freedom. A proper prior distribution for the five by five covariance matrix Σ requires m₀ to be greater than or equal to 6, and thus the prior distribution reflects a weakly informative belief in a scenario where the levels of the nominal variable have no association with one another. We also examined examined a strongly informative prior scenario with a N(0, 1) prior distribution for β and a PXW (m₀ = 100, CS(0.4)) prior distribution for Σ, where CS(0.4) indicates a compound symmetry structure with equal correlation 0.4. The degrees-of-freedom parameter m₀ in this case reflects a strong prior belief that the covariance matrix has a CS(0.4) structure. We label the first approach PXW_ID_Weak and the second approach PXW_CS_Strong. The implications of these scenarios for the regression parameter β, the three variance parameters (σ₂₂, σ₄₄ and σ₅₅), and the correlations r_ij are displayed in Figure 1, showing that the PXW_CS_Strong scenario gives much tighter information for all of the parameters than the PXW_ID_Weak scenario does.

Figure 1.

Prior density plots for the regression parameter (β), variance parameters (σ₂₂, σ₄₄, σ₅₅), and correlations (r_ij). The dotted lines are for the PXW_ID_Weak scenario, the solid lines are for the PXW_CS_Strong scenario, and vertical lines have been drawn at the true value for each parameter.

We ran the MCMC algorithm for 101,000 iterations, discarding the first 1,000 iterations as a burn-in period for each of these two prior distribution scenarios. The posterior mean and standard deviation for each parameter are presented in Table 1, and the marginal posterior densities are shown in Figure 2. We see that the correlation parameters and the covariance parameters appear to depend somewhat on the specification of prior distributions. Not surprisingly, the posterior means of the correlations under the PXW_CS_Strong scenario are pulled toward the assumed value of 0.4. Also, the posterior standard deviations under the PXW_CS_Strong scenario are uniformly smaller than those under the PXW_ID_Weak scenario. The coverage of true values appears satisfactory in both scenarios, partly because substantial posterior uncertainty remains. It stands to reason that better prior specification may give better estimated values, but, in general, inference appears to be fairly robust to the choice between these two groups of priors, presumably because the sample size of 2,000 is sufficient to dominate either prior scenario.

Table 1.

Posterior means (posterior standard deviations) for the regression parameter (β), estimable variance parameters (σ₂₂, σ₄₄ and σ₅₅) and correlation parameters (r_ij) under PXW_ID_Weak and PXW_CS_Strong scenarios. This table shows that the posterior means for all parameters, except r₃₅, are similar under these two groups of priors and the posterior standard deviations under the PXW_CS_Strong prior are uniformly smaller than those under the PXW_ID_Weak prior.

Parameters	True	PXW_I_weak	PXW_CS_strong
β	2.00	2.04 (0.08)	2.07 (0.07)
σ22	0.81	0.72 (0.08)	0.78 (0.08)
σ44	0.90	1.08 (0.14)	0.93 (0.09)
σ55	0.81	0.85 (0.13)	0.89 (0.09)
r12	0.40	0.39 (0.23)	0.37 (0.21)
r13	0.20	0.22 (0.23)	0.27 (0.21)
r14	0.20	0.23 (0.23)	0.30 (0.21)
r15	0.20	0.26 (0.23)	0.30 (0.21)
r23	0.20	0.20 (0.23)	0.26 (0.22)
r24	0.20	0.26 (0.23)	0.31 (0.22)
r25	0.20	0.23 (0.24)	0.27 (0.22)
r34	0.50	0.48 (0.25)	0.42 (0.22)
r35	0.25	0.12 (0.28)	0.25 (0.24)
r45	0.50	0.56 (0.23)	0.48 (0.22)

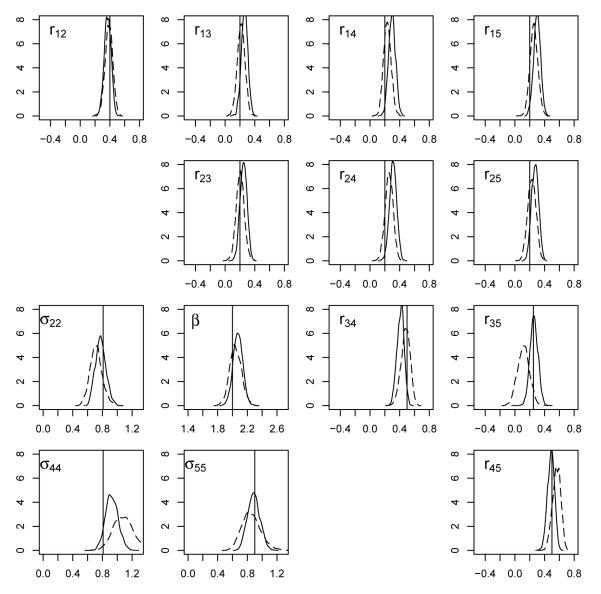
Figure 2.

Posterior density plots for the regression parameter (β), variance parameters (σ₂₂, σ₄₄, σ₅₅), and correlations (r_ij). Dotted lines correspond to the PXW_ID_Weak scenario, and solid lines correspond to the PXW_CS_Strong scenario. Vertical lines have been drawn at the true values for each parameter. The plots show some sensitivity to prior specification for variance parameters, somewhat less sensitivity in correlation parameters (with r₃₅ a possible exception), and little sensitivity for the regression parameter.

The convergence of the MCMC algorithm was assessed by several procedures recommended by Cowles and Carlin (1996). We calculated Gelman and Rubin’s potential scale reduction factor, $\sqrt{\widehat{R}}$ for five dispersed chains with the first 1,000 iterations discarded as burn-in (Gelman & Rubin, 1992). A jumping distribution degrees-of-freedom parameter of m = 2200 gave an acceptance rate of about 10% for the PX-MH step of the algorithm. Although this is below the value of 23% recommended by Gelman, Roberts, and Gilks (1996), we find in practice that higher values for m substantially increased autocorrelations. For the single regression parameter β, ten correlation parameters r_ij and three variance parameters (σ₂₂, σ₄₄ and σ₅₅), the values of $\sqrt{\widehat{R}}$ were all below 1.1 after 40,000 iterations and declined consistently through a further 60,000 iterations. The multivariate potential scale reduction factor for these 14 parameters was 1.04 after 40,000 iterations, improving to 1.02 at 100,000 iterations.

5 Application to a cancer-control study

We illustrate our method for MVMNP models using incomplete contingency table data from a study on adherence to clinical recommendations among women diagnosed with breast abnormalities (Mojica, Bastani, Boscardin, & Ponce, 2006). The study aimed to test the e ect of a telephone counseling intervention to encourage clinical follow-up for diagnosis of breast abnormalities, with telephone counselling or usual care subject to random assignment. The data were collected on a sample of 1,671 women who presented with a breast abnormality at two Los Angeles county hospitals (Hospitals A and B). Six months after enrollment, outcome data were collected via medical chart reviews and a computer-assisted telephone interview.

Here we investigate the between-measure and within-measure associations across the levels of six nominal variables: Final Diagnosis (Yes/No), Patient Language (Spanish/Other), Ethnicity (Hispanic/Non-Hispanic), Age at Referral (3 Categories), Type of Referring Clinic (grouped into 3 categories) and Work Situation (grouped into 4 categories). Descriptive information about these nominal variables is presented in Table 2, showing that there are substantial rates of missingness for several of the measures. Of the n = 1671 subjects, only 314 had complete data on all six measures.

Table 2.

Description of variables used in cancer-control data analysis.

Variable	Categories	Percentage	Missing %	Latent Variables
Final Diagnosis	Yes No	55.1 44.9	0.0	zi;1 (reference)
Patient Language	Spanish Other	61.0 39.0	63.3	zi;2 (reference)
Ethnicity	Hispanic Non-Hispanic	85.0 15.0	36.2	zi;3 (reference)
Age at Referral	< 40 40–49 ≥ 50	26.3 31.5 42.2	2.8	(reference) zi;4 zi;5
Type of Referring Clinic	Breast and Tumor Clinic Emergency and Medical Walk-in Other	35.4 22.4 42.2	18.5	zi;6 zi;7 (reference)
Working Situation	Full-time Part-time Unemployed Homemaker	18.4 20.0 23.6 38.1	36.0	zi;8 zi;9 zi;10 (reference)

We used the proposed MCMC algorithm for MVMNP models including missing values and obtained posterior means and standard deviations for the 10 × 10 correlation matrix of the nominal variables. As discussed at the end of section 2.2, we set X_i = I₁₀ for each subject. We chose an independent N(0,100) prior for each regression parameter and a PXW (m₀ = 18, I) prior for the covariance matrix for the latent vector z_i. We ran 401,000 iterations with 1,000 burn-in iterations, yielding a roughly 15% acceptance rate for the proposed draws in the PX-MH step. Values of univariate potential scale reduction factors (PSRF) for all 10 regression, 45 correlation and 4 variance parameters were well below 1.10 at 200,000 iterations with the exception of three correlation parameters (r₄₅, r₆₇, and r₈₉) for which the PSRF’s were near 1.3 and a single variance parameter (σ_10,10) for which the PSRF was 1.5. The multivariate scale reduction factor for these 59 parameters was 1.3. A further 200,000 iterations reduced all scale reduction factors below 1.1.

In Table 3, we present the posterior mean correlation matrix and variances for the latent vector z_i = (z_i1, …, z_i10) with corresponding posterior standard deviations. The estimated correlations are not typically large in absolute values, with the correlation between the latent variables for Spanish language and Hispanic ethnicity an unsurprising exception that emerges as highly significant despite a large proportion of missing values in the patient language variables. This finding reinforces the ability of the proposed MCMC algorithm in Section 3 to handle data with many missing values. The negative correlations in the third row with the non-reference Working Situation levels suggest a slight tendency for Hispanic subjects to be homemakers. Obtaining final diagnosis is slightly more likely for older women, Working women are less likely than unemployed women to be referred from an Emergency or Medical Walk-in clinic. The four variance components for z_i5, z_i7, z_i9 and z_i10, had 95% credible intervals that include 1, suggesting that the latent variables underlying the multivariate nominal measures are roughly on the same scale.

Table 3.

Posterior means (posterior standard deviations) for the variances and correlations of the latent vector z_i = (z_i1, ⋯, z_i,10).

Diagnosis		Language	Ethnicity	Age		Referring Clinic		Working Situation
	zi1	zi2	zi3	zi4	zi5	zi6	zi7	zi8	zi9	zi,10
zi1	1.00 (0.00)	0.05 (0.25)	0.05 (0.25)	0.19 (0.23)	-0.07 (0.21)	0.00 (0.21)	- 0.01 (0.21)	0.03 (0.24)	0.00 (0.24)	0.03 (0.24)
zi2	0.05 (0.25)	1.00 (0.00)	0.85 (0.20)	-0.12 (0.24)	0.06 (0.27)	0.08 (0.26)	-0.03 (0.26)	-0.17 (0.28)	0.04 (0.31)	-0.39 (0.27)
zi3	0.05 (0.25)	0.85 ( 0.20)	1.00 (0.00)	-0.12 (0.26)	-0.01 (0.25)	0.05 (0.25)	-0.17 (0.25)	-0.23 (0.26)	-0.10 (0.27)	-0.39 (0.24)
zi4	0.19 (0.23)	-0.12 ( 0.24)	-0.12 (0.26)	1.00 (0.00)	-0.25 (0.41)	-0.21 (0.25)	-0.48 (0.23)	0.17 (0.26)	0.04 (0.27)	0.00 (0.27)
zi5	-0.07 (0.21)	0.06 (0.27)	-0.01 (0.25)	-0.25 (0.41)	0.90 (0.24)	0.06 (0.23)	-0.02 (0.24)	0.00 (.25)	-0.01 (0.26)	-0.01 (0.25)
zi6	0.00 (0.21)	0.08 (0.26)	0.05 (0.25)	-0.21 (0.25)	0.06 (0.23)	1.00 (0.00)	-0.03 (0.47)	0.10 (0.26)	-0.14 (0.26)	0.08 (0.26)
zi7	-0.01 (0.21)	-0.03 (0.26)	-0.17 (0.25)	-0.48 (0.23)	-0.02 (0.24)	-0.03 (0.47)	0.83 (0.38)	-0.23 (0.26)	-0.12 (0.26)	0.21 (0.26)
zi8	0.03 (0.24)	-0.17 (0.28)	-0.23 (0.26)	0.17 (0.26)	0.00 (0.25)	0.10 (0.26)	-0.23 (0.26)	1.00 (0.00)	0.00 (0.45)	0.07 (0.45)
zi9	0.00 (0.24)	0.04 (0.31)	-0.10 (0.27)	0.04 (0.27)	-0.01 (0.26)	-0.14 (0.26)	-0.12 (0.26)	0.00 (0.45)	0.93 (0.31)	0.02 (0.44)
zi,10	0.03 (0.23)	-0.31 (0.27)	-0.39 (0.24)	0.00 (0.27)	-0.01 (0.25)	0.08 (0.26)	0.21 (0.26)	0.07 (0.45)	0.02 (0.44)	1.18 (0.28)

Since the data can be represented in a multi-way table, we now compare our approach to a simple log-linear model with all main effects and two-way interactions. The log-linear modeling was performed using the SAS Catmod procedure which only makes use of complete cases. To contrast the two approaches, we used a reduced set of variables: Final Diagnosis with 2 levels, Age at Referral with 3 levels, and Type of Referring Clinic with 3 levels. The data for this 2 × 3 × 3 table have n = 1327 complete cases. For the MVMNP model, we calculated posterior mean fitted probabilities for the 18 cells in the contingency table; the correlation of these 18 values with the corresponding fitted probabilities from the two-way log-linear model was 0.99. Thus, as expected, our method coincides very closely to the standard log-linear model predictions in the situation of a large sample size and a simple model. We note for this reduced set of variables that the MVMNP model has 17 parameters (10 correlation parameters, 2 variance parameters, and 5 mean parameters) and the two-way log-linear model has 13 parameters (5 main effects and 8 two-way interactions). Thus the latent variable structure in the MVMNP model gives it somewhat more flexibility in this complete case setting. More importantly, the MVMNP model is able to directly accommodate incomplete data. In the original setting of six variables, the MVMNP model uses incomplete data on n = 1671 subjects to fit a model with 59 parameters (45 correlation parameters, 4 variance parameters, and 10 mean parameters). In contrast, a two-way log-linear model has 50 parameters (10 main effects and 40 two-way interactions); these 50 parameters would be poorly estimated using the n = 314 complete cases.

6 Conclusions

In this manuscript, we proposed MVMNP models for analyzing multivariate nominal data using the PX-MH algorithm in a Bayesian framework. We illustrated our methodology through a simulated example and an application to incomplete contingency table data from a cancer control study.

The MVMNP model is a general model to handle multivariate nominal data that has several advantages over MNP models and multinomial multiperiod probit models. First, the MNP model is a special case for univariate nominal data using the MVMNP model, whereas the multiperiod multinomial probit model does not have this property. Second, the MVMNP model allows general covariance structures for the latent variables, compared with the multiperiod multinomial probit model which only allows special covariance structures, such as those with AR(1) structures. Third, the prior distribution we used for the MVMNP models allows useful prior information to be incorporated into the model in a flexible manner that is naturally embedded into the sampling algorithm.

In the special case of contingency table data, the MVMNP model provides additional flexibility over a two-way log-linear model, but is more parsimonious than a saturated model. The MVMNP model can also directly accommodate incomplete data as well as covariates.

An inherent concern in the PX-MH algorithm for the MVMNP model is that with high-dimensional repeated nominal measures, the PX-MH algorithm may have high autocorrelations among the posterior draws and therefore result in slow convergence. The identified MVMNP model necessitates a complex Metropolis-Hastings step for sampling the restricted covariance matrix instead of a Gibbs sampler step for the unidentified version. Imai and van Dyk (2005a) have given a similar discussion for the slow convergence induced by solving the identification problem for the MNP model. Statistical computing strategies that offer the prospect of more rapid convergence would be a worthy area for future research.