Abstract
Many common chemical potential equalization (μEq) methods are known to suffer from a superlinear scaling of the polarizability with increasing molecular size that interferes with model transferability and prevents the straightforward application of these methods to large, biochemically relevant molecules. In the present work, we systematically investigate the origins of this scaling and the mechanisms whereby some existing methods successfully temper the scaling. We demonstrate several types of topological charge constraints distinct from the usual single molecular charge constraint that can successfully achieve linear polarizability scaling in atomic charge based equilibration models. We find the use of recently employed charge conservation constraints tied to small molecular units to be an effective and practical approach for modulating the polarizability scaling in atomic μEq schemes. We also analyze the scaling behavior of several μEq schemes in the bond representation and derive closed-form expressions for the polarizability scaling in a linear atomic chain model; for a single molecular charge constraint these expressions demonstrate a cubic dependence of the polarizability on molecular size compared with linear scaling obtainable in the case of the atom-atom charge transfer (AACT) and split-charge equilibration (SQE) schemes. Application of our results to the trans N-alkane series reveals that in certain situations, the AACT and SQE schemes can become unstable due to an indefinite Hessian matrix. Consequently, we discuss sufficient criteria for ensuring stability within these schemes.
INTRODUCTION
For atomistic molecular dynamic (MD) simulations that seek to model biochemical systems to the level of “chemical” accuracy, nonadditive polarizable force fields offer significant advantages over additive fixed-charge potentials. Chemical potential equalization (μEq) methods represent one promising approach for the efficient inclusion of explicit molecular polarizability in these simulations. Such methods typically redistribute charge (possibly in addition to higher order multipole moments) within a molecule in an effort to realistically model the polarization response to conformational and environmental changes. These methods may also be flexibly incorporated into existing MD algorithms at modest computational cost using an extended Lagrangian framework or as a set of simultaneous equations in matrix form. Another attractive (though frequently underexploited) feature of μEq methods is their intrinsic ability to model intermolecular charge transfer without any additional modifications. Thus, accurately parametrized force fields based on such methods are expected to become increasingly desirable for improved accuracy in chemical simulations.
It is equally important that such force fields be straightforward to parametrize and easily transferable to new systems. Concerning the former, a number of excellent parametrization approaches for μEq models have been described in the literature;1, 2, 3, 4 however, achieving broad transferability to new or larger systems remains a considerable challenge for μEq models. Recently, Chelli et al.5, 6, 7 have demonstrated that parameters accurately tuned to small hydrocarbon molecules can egregiously overestimate the linear polarization response in larger molecules depending on the specific μEq method8, 9, 10, 11, 12 employed. While ab initio calculations7, 13 and experimental results14 for the N-alkanes demonstrate a linear increase in molecular polarizability with molecular size, Chelli et al.5, 6, 7 have observed superlinear scaling for some μEq methods. This behavior also poses serious problems regarding the development of polarizable μEq potentials for large biomolecules since the atomic parameters are not transferable among molecules of different sizes.
These issues have led Chelli et al. to propose an alternate μEq scheme, the atom-atom charge transfer (AACT) model,5 in an effort to eliminate this superlinear scaling of the polarizability in the N-alkane series through topological control of charge transfer. Given the ongoing refinement and development of μEq methods, such as those incorporating distance-dependent charge transfer,15 it is timely to precisely characterize the specific origins of this scaling problem so that it may be systematically controlled in all future models.
Our interest in the present work lies in clearly elucidating the source of the superlinear polarizability scaling by an analysis of simple model systems and in assessing the mechanisms by which existing methods moderate this scaling in nonconducting molecules. In Sec. 2, we first review pertinent details of μEq methods expressed in one- and two-body charge variable representations. A systematic examination of the scaling behaviors of four μEq schemes in the context of a linear atomic chain system is pursued in Sec. 3. In the process, we derive closed-form expressions for the polarizability scaling in a few simple cases and suggest some additional approaches for controlling the scaling. Section 4 extends the discussion to more realistic examples including the fully interacting linear atomic chain and the N-alkane series which incorporates additional components of the polarizability tensor. We also discuss conditions under which certain μEq schemes exhibit instabilities arising from an indefinite Hessian matrix. We conclude in Sec. 4 with a summary of our findings and some recommendations regarding the practical control of the polarizability scaling in current μEq methods and in the development of future μEq models.
THEORY AND METHODS
Atomic representations
The charge equilibration (QEq) or electronegativity equalization approach, first described in seminal work by Mortier et al.8 and later by Rappé and Goddard9 as a way of predicting charge distributions within molecules from atomic ionization potentials, electron affinities, and atomic radii, is based on the electrostatic energy of a molecule expanded to second order in atomic charge variables as
| (1) |
Here, the singly indexed uppercase charge variable Qi represents an atomic charge, and the parameters and may be identified as an atomic electronegativity and atomic hardness, respectively. In the above expression, the terms Jij represent screened Coulomb interactions between atoms i and j that are often taken to be the molecular Coulomb integral over atomic Slater or Gaussian orbitals located on the respective nuclei. In the QEq formulation, the diagonal atomic hardness terms represent the self-Coulomb repulsion or idempotential Jii evaluated at zero internuclear separation; however, these terms along with the corresponding atomic electronegativities may also be treated as adjustable model parameters. Differentiation of the energy expression [Eq. 1] with respect to each atomic charge yields a set of N simultaneous equations
| (2) |
which, when set to zero, may be solved for a set of charges which minimize the energy subject to the condition that the second derivative Hessian matrix defined by the elements
| (3) |
and
| (4) |
be positive definite. Cast in matrix form, these equations may be written as
| (5) |
where and Q=(Q1,Q2,…,QN) are vectors formed from the atomic electronegativities and atomic charges, respectively, and the symmetric matrix J (which we also refer to as the atomic hardness matrix) is assembled from the Hessian elements described above. In practice, the above set of equations must be augmented by an additional charge conservation constraint such as
| (6) |
to guarantee molecular charge neutrality. One way in which this constraint may be enforced is through the use of the modified system of equations2, 5, 16
| (7) |
in which J′ is the charge-constrained atomic hardness matrix having elements and for all i≠1. Here, we have chosen to take differences with respect to the first atom for convenience, but this choice is not unique and suggests numerous alternate definitions of the charge-constrained hardness matrix J′. The vector Δχ′ is composed of differences of atomic electronegativities relative to the first atom so that . Components of the polarizability tensor α are computed as
| (8) |
where Rβ denotes the β Cartesian components of the atomic position vector. is formed from the corresponding γ components but relative to an origin placed on the first atom according to . Polarizabilities computed using the above expression are origin independent since the vector Rβ may be defined with respect to any origin.
In keeping with the origins of the QEq scheme, many implementations retain the original formulation in terms of atomic charge variables, electronegativities, and hardnesses. This one-body representation, which we will refer to as the atomic representation (AR), is frequently employed because of intrinsic compatibility with existing fixed-charge MD machinery and the relatively small number of parameters required.
Bond representations
To better describe the perturbative effects of the local chemical environment within the context of a distance-dependent framework and to overcome some methodological shortcomings of AR schemes, recent investigations have found it advantageous to work in a bond representation (BR) built on two-body parameters corresponding to pairs of atoms (bonds). In contrast to the AR which employs atomic charges as the independent variables, the BR charge variables are written with two indices and represent the amount of charge transferred between a given pair of atoms. Thus, a “bond” in this formalism does not necessarily represent a literal chemical bond, but rather the capacity for two atoms to engage in charge transfer; however, in many instances there exists a one-to-one correspondence between BR bonds and actual chemical bonds. A wide variety of nomenclatures for these BR variables exist including bond charge increments,2, 3 atom-atom charges,5 charge transfer variables,15 and split charges.17 For the sake of consistency and clarity throughout, we will refer to the variables in AR schemes as atomic charge variables and those corresponding to BR schemes as bond charge variables (BCVs) where the labels “atomic” and “bond” signify one-body (singly indexed) and two-body (doubly indexed) charge variables, respectively.
The AR and BR representations may be connected by the use of the projection
| (9) |
where the sum runs over all atoms j for which charge transfer to atom i is allowed given that the BCVs (denoted by the lowercase variables qji) satisfy the antisymmetry relation qij=−qji and that qii=0 so that charge transfer from an atom to itself is disallowed. Thus, different projection operators are required depending on the specific charge transfer topology employed. Consequently, the number of BCVs may vary from N−1 to N(N−1)∕2. For BRs isomorphic with the atomic QEq representation [all BRs related to the AR by the simple change of variables of Eq. 9], the BR will be rank deficient for all but the minimum number of BCVs and will contain zero eigenvalues.15 This problem may be avoided by performing a singular value decomposition2, 15 or by restricting the charge transfer topology a priori which is the approach used in the present work.
The BR of the atomic QEq method, which we will refer to as the QE scheme, may be constructed from Eqs. 1, 9 to yield the general energy expression
| (10) |
By exploiting the antisymmetry of the BCVs (qij=−qji) and letting , this expression may be recast2, 15 in the form
| (11) |
for which pairs of indices are subject to the summation conventions j>i and ℓ>k. Differentiating the above energy expression with respect to each BCV in the active topology, we obtain a set of N−1 independent, simultaneous equations
| (12) |
which may be set to zero for the condition of a stationary point in the energy. A minimum in the energy is guaranteed by a positive-definite Hessian matrix which has elements given by
| (13) |
and
| (14) |
We may now write this system of N−1 linear equations in matrix form as Gq=−ΔX where elements of the square, symmetric bond hardness matrix G (counterpart to the atomic hardness matrix J) are given by the corresponding elements of the Hessian matrix2, 15, 17 described above in Eqs. 13, 14. The vector q is formed from the N−1 BCVs while components of the vector ΔX are assembled from differences in the corresponding atomic electronegativities for each pair of atoms i and j associated with a particular BCV.
In this representation, components of the molecular polarizability tensor α are computed from G−1 as
| (15) |
in which components of the vectors and Δrγ represent the projection of each bond vector along the Cartesian directions β and γ. The resulting polarizabilities are origin independent for neutral molecules and identical to polarizabilities obtained in the atomic QEq representation [Eq. 8]. Since the above expression differs from that previously employed by Chelli et al.5 [Eq. (2.13)], we have included a derivation of Eq. 15 which may be found in the Appendix.
Using a split-charge formulation (described below), Nistor et al.17 have demonstrated that to obtain the QE scheme as a limiting case of the general split-charge scheme, all doubly indexed BR parameters ηij and χij must be written in terms of linear combinations of the singly indexed, one-body AR parameters and . Thus, there are no contributions in the QE scheme originating from intrinsic or irreducible two-body parameters ( and ) as is clear from Eq. 10. The introduction of specific two-body parameters and∕or the neglect of certain atomic contributions in the QE scheme leads to two other distinct approaches: The split-charge equilibration (SQE) and AACT schemes.
The AACT scheme5 is specifically designed to alleviate the superlinear scaling of the polarizability as a function of molecular size. To accomplish this, contributions to G arising from the diagonal elements of J [the second set of terms in Eq. 10] are removed and are replaced with terms involving two-body bond hardness parameters . This procedure yields a corresponding AACT energy expression of
| (16) |
where (for correspondence with the QE scheme) we may choose so that . The off-diagonalelements of J (the third set of terms in the above equation) are not modified and are identical to those used in the QE scheme [Eq. 10]. The two-body bond hardness terms [the second set of terms in Eq. 16] are important for describing the diagonal BCV restoring forces that cannot be expressed within the corresponding AR.17 These terms permit more effective localization of molecular charge and are similar in spirit to constraining the overall molecular dipole moment as in more recent μEq models proposed by Chelli et al.18, 19 and Kaminski and co-workers.3, 4 The direct modification of the structure of the G matrix in the AACT approach appears sufficient to convert the superlinear scaling of the polarizability into linear scaling. However, we remark that by the explicit introduction of two-body hardness terms, the AACT scheme is no longer isomorphic with the atomic QEq scheme; this implies an implicit dependence of the AACT energy on the choice of bonding or charge transfer topology. Thus, to eliminate these additional topological considerations we employ the same chemical bonding topology as was used for the QE scheme.
The split-charge or SQE scheme17 has been developed as a generalization (or linear combination) of the QE and AACT methods. The SQE energy expression is given by
| (17) |
where by comparing the QE and AACT energy expressions [Eqs. 10, 16], we see that the parameters κ and λ control the relative magnitudes of AACT and QE character. In the limit λ=0 and κ=1, SQE behavior resembles that of AACT. Similarly, setting λ=1 and κ=0 recovers the QE energy expression with the assumption that the terms are defined in terms of the atomic electronegativities as . As with the AACT and QE schemes, we again employ the same chemical bonding charge transfer topology so that appropriate correspondence is maintained in the SQE energy expression as we tune from QE to AACT behavior. Since no analysis of the polarizability scaling has been reported for the SQE method, it is a priori unclear whether the scaling of this hybrid method should be superlinear (QE-like) or linear (AACT-like) for the general SQE case intermediate between these limiting behaviors.
SCALING IN A LINEAR ATOMIC CHAIN
QEq scheme
In an effort to better elucidate the mechanism governing the superlinear polarizability scaling, we first consider a simple model system that consists of a linear chain of N atoms aligned in the z direction (all colinear) having unit (Å) spacing. Such a geometry is advantageous for two reasons. First, alignment of the system along the z direction conveniently eliminates all but the αzz component of the molecular polarizability tensor. Second, this geometry conceptually simplifies the relationship between the scaling of the molecular polarizability and the number of atoms in the molecule. Since the interatomic spacing is uniform, the vector [from Eq. 8] that describes the z components of the atomic positions relative to the first atom equals (0,1,…,N−1), leading to a simplification of the polarizability calculation.
For the moment, let us restrict the structure of J to be an order N diagonal matrix having no off-diagonal entries (only self-Coulomb terms). Such a matrix having negligible off-diagonal terms could practically arise from a distance-dependent electrostatic cutoff shorter than a bond length; this leads to the isolated-atom case in which the molecular polarizability should nominally scale as the sum of atomic polarizabilities. If we arbitrarily choose the diagonal terms to all be the same (equivalent atom types) and equal to 1 , then J corresponds to the identity matrix.
With J defined as above, we may now compute the polarizability of our linear chain system using Eq. 8. The results are plotted in panel A of Fig. 1 (filled circles) as a function of the number of atoms N and clearly demonstrate superlinear scaling of the polarizability with increasing molecular size despite the isolated-atom structure of the underlying J matrix. Similar scaling of the polarizability is obtained for a fully interacting linear chain system incorporating all off-diagonal elements of J. Consistent with common practice5, 9, 15, 16 we evaluate the matrix elements Jij as molecular Coulomb integrals over Slater-type atomic orbitals.20, 21 At large internuclear separations, the repulsion of the atom-centered electron densities rapidly approaches the standard 1∕R form characteristic of classical Coulomb repulsion. However, at short distances where the electron densities overlap, charge screening allows these integrals to take on finite values as R→0. For our model linear atomic chain, we use the same geometry described above and model the atomic charge densities using only 1s Slater functions having unit exponents. Diagonal hardness terms are determined from the Jii elements in the limit R→0. The resulting polarizabilities are plotted in panel B of Fig. 1 (filled circles) as a function of molecular size and demonstrate a scaling trend similar to that observed for the isolated-atom case above. Thus, the presence of off-diagonal Coulomb terms does not significantly alter the observed scaling behavior with respect to the case where J is strictly diagonal. Consequently, we will make considerable use of the diagonal J case throughout our investigation for reasons of simplicity.
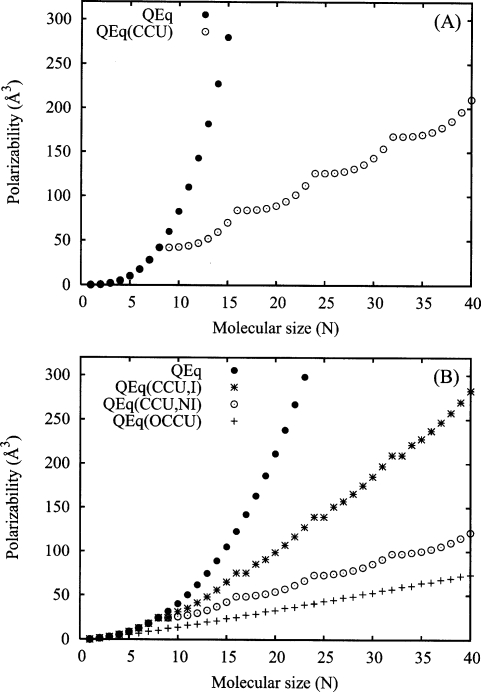
Figure 1.
Scaling of αzz as a function of the number of atoms N for the QEq method in a linear atomic chain. Panel A shows the isolated-atom (unit diagonal J) case for a single molecular charge constraint (filled circles) and for charge constrained units consisting of eight atoms (open circles). Panel B shows the fully interacting (Slater J) case for a single molecular charge constraint (filled circles), for CCUs consisting of eight atoms (stars), for noninteracting CCUs of length NU=8 defined by a block diagonal Slater J matrix (open circles), and for OCCUs in which charge transfer is restricted to pairs of atoms (plus symbols).
It has been observed5 that the overestimation of the polarizability in the QEq approach results from the fact that QEq globally treats a molecule as a conductor rather than as an insulator; charge may move unhindered across the entire molecule in response to an external perturbation. This understanding has prompted some studies7, 12, 22 to adopt additional charge constraints in an attempt to localize the charge redistribution. The constrained charge approximation of Shimizu et al.12 places charge conservation constraints on chemically dissimilar motifs such as side chains and head groups of amino acid residues. For small chemical units consisting of a few atoms, this approach is successful in moderating the scaling. However, as pointed out by Chelli and Procacci,7 as the length of the side chains grows, the scaling problem returns. Thus, even large chemically similar units must be broken down into smaller units optimally consisting of perhaps five to seven atoms. This has been the approach of Patel and Brooks,22 and, as we demonstrate below, is sufficient for modulating the scaling behavior with molecular size.
Returning to the isolated-atom case described above in which J is by construction diagonal and equal to the identity matrix, the charge-constrained hardness matrix J′ of Eq. 7 (which we have arbitrarily referenced with respect to the first atom) has the structure
| (18) |
Thus, the isolated-atom structure of J is not preserved in J′ due to explicit introduction of the charge constraint which introduces off-diagonal matrix elements into J′. In fact, we comment that the structure of J′ appears to model a starlike charge transfer topology in which the first atom functions as a locus through which nonlocal charge transfer may occur. Since all atoms in this topology are treated as “nearest neighbors” to the first atom, the distance dependence of the charge transfer effect is ignored and nonlocal charge transfer occurs with no penalty. In the linear chain geometry, this permits direct charge transfer between the first and last atoms in the chain despite the large physical separation. Such issues have prompted Martinez and co-workers15, 23, 24 to propose a distance-dependent charge transfer attenuation function to penalize charge transfer over large interatomic distances such as those occurring in the context of molecular dissociation.
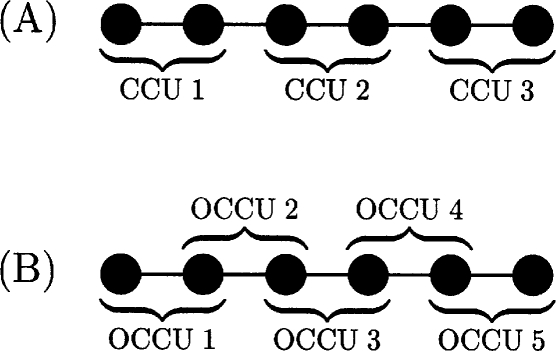
The nonlocal charge transfer effect may be practically controlled by partitioning the molecule into smaller disjoint subunits of length NU and applying charge conservation constraints to each unit rather than to the full system. This is illustrated in Fig. 2 for charge-constrained units (CCUs) containing two atoms. This approach inhibits interunit charge transfer while simultaneously allowing intraunit charge transfer and is an effective means for localizing charge within a molecule. This leads to the full system matrix
| (19) |
where the off-diagonal matrices Jmn of dimension NU describe the electrostatic coupling between the individualmoleculelike subunits themselves characterized by the diagonal submatrix elements Jmm. For the isolated-atom chain, there is no coupling between units so Jsys becomes block diagonal where each diagonal submatrix element Jmm has the same structure as J′ in Eq. 18. The polarizability for the full system may be computed using Eq. 8 by applying the appropriate set of M auxiliary charge constraints which requires modifying to be relative to the position of the first atom of each corresponding unit so that . The corresponding atomic position vector Rβ is not modified. Doing this, we obtain polarizabilities as a function of N for units of length NU=8 which are plotted in panel A of Fig. 1 (open circles). We observe that while the scaling within each unit is superlinear, the overall polarizability scales linearly with the number of CCUs validating current QEq implementations that employ local charge constraints over small chemical units. Extension of this approach to a fully interacting chain having off-diagonal Coulomb elements leads to qualitatively similar linear scaling of the polarizability (Fig. 1, panel B, stars) demonstrating that the additional Coulombic interactions do not qualitatively affect the scaling behavior with respect to the noninteracting case. For comparison, we also consider the block diagonal (isolated-molecule) case for the fully interacting atomic chain in which all off-diagonal elements connecting pairs of CCUs are zeroed (Fig. 1, panel B, open circles). Since in this isolated-molecule case the CCUs are noninteracting, the polarizability of the system must scale linearly with the number of CCUs according to a sum of individual molecular polarizabilities.
Figure 2.
Panel A: A linear atomic chain comprised of three disjoint CCUs. Panel B: A linear atomic chain partitioned into five OCCUs.
However, despite the success of these constrained charge approaches in controlling the overall scaling of the polarizability, the arbitrary partitioning of a molecule into such subunits offers no specific guidance into how these units should be constructed, particularly if one is concerned about preserving transferability. Ambiguities arise when the unit size is varied to accommodate specific chemical moieties or when the chosen unit size does not evenly divide the molecular size. (This may be seen in Fig. 1, panels A and B for which the addition of a new CCU containing a single atom does not lead to an increase in polarizability.) Moreover, even well chosen partitioning schemes are ultimately unphysical (and more so the smaller the unit size) since charge transfer is ultimately present in all real chemical bonds (albeit negligible in some cases). For units that are not too small, this problem may be practically overcome with well chosen model parameters that compensate for the errors introduced by the partitioning scheme.
Therefore, it seems reasonable to consider other generalizations of these constrained-charge approaches designed to alleviate some of the above concerns. We note that all the constrained-charge approaches discussed above employ disjoint partitions which inhibit charge transfer at the unit boundaries. An alternate possibility is to consider overlapping constrained-charge units (OCCUs) in which interior CCUs share constraints with neighboring CCUs. In the simplest case, we might choose to constrain the charge across all nearest neighbor pairs (Fig. 2) so that each constrained pair could polarize along the bond vector connecting both atoms in a manner analogous to induced dipole models but having limited orientational freedom. In the case of chains with odd numbers of atoms, we may relax one pair constraint and include the odd atom in a single constraint containing three atoms instead of two. Applying these bond constraints and solving for the polarizabilities as a function of N, we obtain linear scaling of the polarizability as indicated by the plus symbols in panel B of Fig. 1. Thus, a true topological change in the nature of the charge constraints is sufficient to alter the scaling behavior. This is a strong indication that the usual single-molecule charge conservation constraint explicit or implicit in a given set of atomic QEq equations is ultimately the source of the superlinear polarizability scaling problem.
While the above bond constraints confine charge flow to within each bond, the approach may be further generalized to permit charge redistribution over larger overlapping units. This introduces an effective means to control the size extent of the conductivity within a molecule; the single-molecule constraint defines the fully conducting limit while the individual bond constraints represent the fully insulating limit. In addition to linear scaling behavior, OCCUs also provide a reasonable solution to the problem of partitioning of units since the effects of charge transfer are continuous across the CCU boundaries. In the case of overlapping two-atom charge transfer constraints (which can be chosen to mimic a chemical bonding topology), all units are of the same size and each atom belongs to at least one unit. Unit assignment is then determined by the topology rather than arbitrarily. Thus, the OCCU approach appears to offer several advantages over currently employed CCU approaches and is similar to methods employed by certain BR schemes (which we discuss next) for manipulating charge locality in large molecules.
QE scheme
Since the QE scheme is simply the atomic QEq scheme mapped into a BR, the scaling properties are expected to be identical. However, the structure of the QE hardness matrix yields some unique insights not easily elucidated in the corresponding AR. To perform the mapping, it is necessary toa priori restrict the charge transfer topology to include exactly B=N−1 bonds so that the QE system is nonsingular. [Corresponding AACT and SQE schemes do not share this limitation and may include additional bonds up to a maximum of B=N(N−1)∕2.] The minimal (N−1) number of QE bonds reflects the fact that with a molecular charge constraint, there are only N−1 independent charge variables in the AR. For convenience, we select a charge transfer topology which consists of physically realistic nearest neighbor bonds, mimicking a reasonable chemical bonding topology. Surprisingly, we note that for the QE scheme with a single molecular charge constraint, the choice of topology will not affect any of the computed physical or scaling properties as long as the topology contains exactly the minimum number of bonds (N−1). However, the choice of topology will affect the AACT and SQE results. Starlike topologies (analogous to that of the charge-constrained QEq approach) appear to always yield a conductinglike molecular response regardless of the method (QE, AACT, or SQE) since charge transfer is restricted to be nonlocal. Therefore, to limit the effects of topology, we will consistently employ the same chemical bonding topology for all BR schemes (QE, AACT, and SQE) that is appropriate for describing nonconducting molecules.
In analyzing the polarizability scaling of the QE scheme, we again invoke the isolated-atom linear chain geometry described above in which all atoms are uniformly spaced on the z axis and J is diagonal and equal to the identity matrix. Since all bonds are of the same length and have identical z projections, the vector Δrz in Eq. 15 that describes the z components of all B bond vectors equals (1,1,…,1), again leading to a simplification of the polarizability calculation.
If we now transform the resulting set of atomic QEq equations into the QE BR, we find that the bond hardness matrix G assumes a tridiagonal form having entries {−1,2,−1}. Thus in the BR, we note that there are off-diagonal elements connecting adjacent bonds that originate solely from the diagonal elements of J so that charge transfer is permitted between adjacent bonds in the corresponding BR despite the apparent isolated-atom structure of the underlying atomic J matrix. This illustrates that the molecular charge conservation constraint is also built into the corresponding BR approach since the BR is expressed in terms of N−1 (rather than N) independent variables.
In seeking a closed-form dependence of the polarizability on N or B, the presence of the matrix inverse in Eq. 15 presents a formidable roadblock. However, from the Appendix, the polarizability may be conveniently rewritten as
| (20) |
where sz is a solution of the system Gsz=Δrz. Progress may now be made in the specific case where G is tridiagonal by exploiting the isomorphism between the system of equations Gsz=Δrz and the finite difference method for the solution of second order differential equations having the form . Thus, we may reinterpret G as the discretization of this specific differential equation over a grid consisting of B points. In keeping with the isomorphism, we restrict the continuous bond index variable b∊[1,B], interpret the grid spacing as the bond length, and invoke the Dirichlet boundary conditions sz(0)=sz(N)=0. These particular boundary conditions are justified by the physical interpretation of sz(b) which, as will be demonstrated, is related to the differential change in polarizability with respect to molecular size. Thus, these boundary conditions reflect the physical restriction that there can be no change in molecular polarizability when there are zero atoms and no further contributions once we have accounted for all the atoms in the molecule.
Identification of the matrix system with an explicit differential equation in the continuous variable b now permits us to extract a closed-form solution for sz(b) by solving the corresponding differential equation. Doing so, we obtain
| (21) |
which indicates that sz(b) is quadratic in the bond index variable b and linear in N. The validity of Eq. 21 is explicitly verified by numerical experiments for N=10 and 50 and is plotted in panels A and B of Fig. 3 along with the numerical results (solid circles). The N dependence of sz(b) is a direct consequence of the associated boundary condition sz(N)=0 and implies that we should expect a larger contribution to the molecular polarizability for a given bond in a larger molecule than for the same bond in a smaller molecule. Based on ab initio results and experimental evidence for the N-alkanes, this is clearly unphysical since each interior bond should contribute a roughly constant amount to the polarizability so that the total polarizability increases linearly with molecular size. Likewise, the quadratic scaling of sz(b) with b is also counterintuitive by physical reasoning since it indicates that specific bonds near the center of the molecule will disproportionately contribute to the polarizability in a nonlocal way that depends sensitively on the total number of bonds.
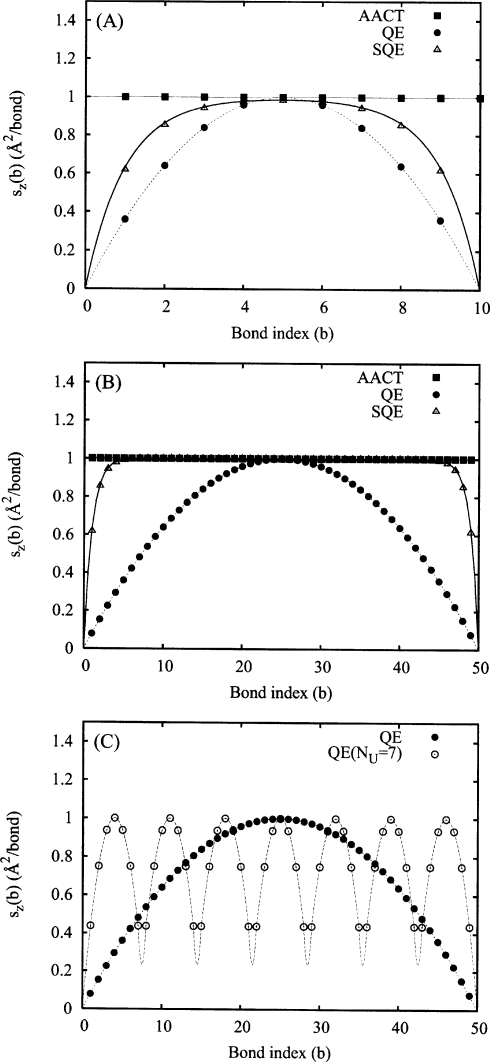
Figure 3.
A plot of the function sz(b) for the AACT, SQE, and QE methods for a linear chain of isolated atoms. Points are taken from numerical experiments while the lines correspond to the corresponding theoretical predictions of Eqs. 21, 30 for the QE and SQE methods. Panels A and B correspond to chain lengths of N=10 and N=50, respectively. All SQE values were obtained using parameters of λ=1 and κ=1. Panel C demonstrates the effect of eliminating bond-bond charge transfer between specific pairs of bonds. The dashed curve represents the weighted average of neighboring units each individually defined by the QE NU=7 case. For convenient comparison, all QE results have been rescaled to have a maximum value of 1 at b=N∕2. A bond length (β) of 1 Å has been employed in all cases.
The structure of sz(b) further aids in understanding how the CCA of Shimizu et al.12 and related methods22 help to alleviate the polarizability scaling problem. In treating macromolecules as collections of smaller units that do not engage in interunit charge transfer, these methods effectively “cut” interior bonds, eliminating corresponding charge transfer through those bonds. While we cannot sever a bond in the BR without altering the dimensionality of G, we may achieve a similar result by selectively disallowing bond-bond charge transfer by zeroing specific off-diagonal elements of G. In terms of sz(b), this is equivalent to imposing auxiliary boundary conditions that fix the value of sz(b) at specific values of the bond index variable b. This is illustrated in panel C of Fig. 3 (open circles) where we have partitioned a molecule of length B=49 into seven subunits by restricting bond-bond charge transfer. We see that over each unit, sz(b) is quadratic as expected and that each unit contributes identically to the overall molecular polarizability. At the edges of each unit, the polarizability contributions do not decay to zero as we might expect for a cut bond, but instead decrease to some finite value dictated by the diagonal bond hardness terms of G which we have not modified. This approach is most effective when bond-bond charge transfer near the center of the molecule is disrupted since these bonds disproportionately contribute to the overall molecular polarizability.
To determine the polarizability scaling of this model system, we consider the dot product between Δrz and sz [Eq. 20] which may be represented in integral form as
| (22) |
where the Dirac delta functions pick out the values of sz(b) and rz(b) at integer values of b. In the above form, this integral may be viewed as a left Riemann sum which, for large N (fine discretization), may be approximated by the integral
| (23) |
This relationship allows us to make a connection between the product sz(b)rz(b) and the derivative of the polarizability with respect to the bond index variable, indicating that sz(b) has units of Å2 (polarizability area) per bond. Similarly, rz(b) may be viewed as a weighting function which in the present case weights all bonds uniformly.
Now, taking rz(b)=1 for all b and performing the integration, we obtain a polarizability scaling of
| (24) |
which may be compared with a result of
| (25) |
derived from a fit to explicit numerical experiments. The difference corresponds to the error of the integral approximation to the discrete sum which is equal to (N−1)∕6 in this case. Due to the symmetry of sz(b), the same error results when approximating the right Riemann sum by integration from 1 to N. To minimize the error of the approximation, we may instead integrate from 1∕2 to N−1∕2 according to a central Riemann sum which is known to have an error bound of
| (26) |
Performing the integration, we find that the central Riemann integral approximation leads to an approximate polarizability scaling of
| (27) |
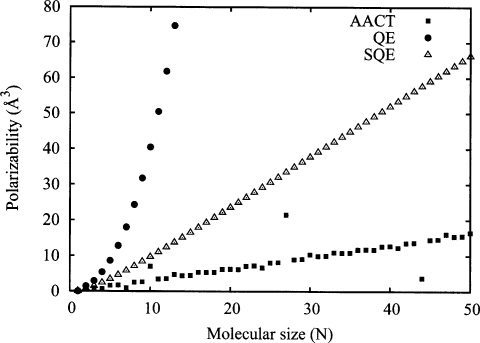
which has an error of exactly (N−1)∕24 relative to the exact result, consistent with the prediction of Eq. 26. This error is a factor of 4 smaller than that obtained from either the left or right Riemann sum approximations. Yet, irrespective of the particular integral approximation employed, we obtain a molecular polarizability for this model system that scales cubically with the number of bonds (or atoms) in the molecule. This is shown in Fig. 4 (panel A) along with the corresponding numerical results (filled circles) as a function of molecular size; from Fig. 4 it is clear that the current theoretical prediction accurately describes the data points. We point out that this cubic scaling is formally worse than the supposed6 quadraticlike scaling obtained from standard QEq methods. It is also clear from Figs. 14 that the polarizabilities computed in the QE scheme are identical to those obtained from the corresponding atomic QEq scheme as expected.
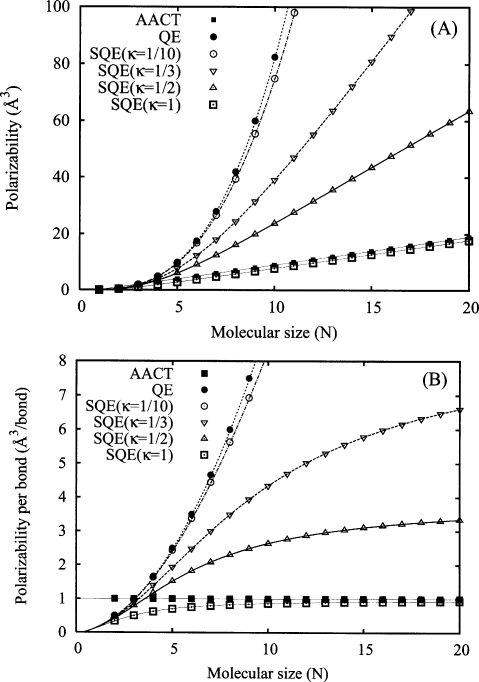
Figure 4.
Scaling of αzz (panel A) and αzz∕(N−1) (panel B) as a function of the number of atoms N for the AACT (solid squares), QE (solid circles), and SQE (open symbols) methods for a linear chain of isolated atoms. Points correspond to the results of numerical experiments while the lines are theoretical predictions of Eqs. 28, 29, 31. QE, AACT, and SQE polarizabilities are evaluated using scaling parameter values of , , and λ=1, respectively. A bond length (β) of 1 Å is employed in all cases.
Having now demonstrated an analytical formulation for accurately estimating the polarizability of a linear chain as a function of the number of bonds, we may now generalize to arbitrary bond lengths β and to scaled terms by solving the modified differential equation . Here, we have introduced the scaling parameter which performs a similar function as λ in Eq. 17 and may be used to control the magnitude of the diagonal hardness terms. By including these scaling factors and employing the central Riemann integral approximation [Eq. 27], we obtain a polarizability scaling of
| (28) |
From this model, we may predict that the introduction of an explicit N dependence into the parametrized values proportional to N2 should be sufficient to guarantee linear scaling of the polarizability with chain length in this system. To within the previously discussed approximation error, this is exactly what is observed in numerical experiments (data not shown) where λ=N and illustrates that size dependent hardness terms may provide a possible alternative route for manipulating the molecular size scaling of the polarizability at large Ni; however, the unphysical quadratic behavior of sz(b) is not altered by this approach and indicates that the molecular physics is still not correctly modeled despite the correct molecular size dependence exhibited by the polarizability.
AACT scheme
Extension of this analysis to the AACT scheme is possible by considering how the AACT formalism modifies the G matrix relative to the pure QE scheme. The matrix G is first built from a modified J matrix in which the diagonal has been zeroed. Second, some diagonal matrix G0 containing the desired two-body bond hardness parameters is added to G. Since all bonds are identical in our model linear chain system, we let all bonds have a scaled hardness of so that the matrix G0 is equivalent to , where I is the order N−1 identity matrix. The scaling parameter is analogous to the parameter κ in Eq. 17. A finite difference interpretation of the modified G matrix yields the linear (nondifferential) equation . Solving, we obtain the function sz(b) for the AACT model which is plotted in Fig. 3 for chains of length N=10 and 50 (solid squares). Integrating, we find a corresponding polarizability scaling of
| (29) |
that is linear in the number of bonds, quadratic in bond length, and inversely proportional to the magnitude of the scaled bond hardness . We plot this function in Fig. 4 (panel A) along with corresponding numerical observations (solid squares); the theoretical prediction exactly matches the observed polarizabilities since, by Eq. 26, is zero for all b and leads to an error of zero. Thus we observe that the AACT scheme yields the physically correct linear scaling of the polarizability that we would expect from a collection of isolated bonds and is similar in mechanism to the OCCU approach discussed above.
SQE scheme
Again relating the structure of G to a differential equation, we may also extend our analysis to the generalized SQE method which introduces an additional term, linear in sz(b) (corresponding to the AACT case above), to yield the second order differential equation . The scaling parameters λ and κ used here correspond to those of the underlying energy SQE energy expression [Eq. 17]. By invoking the usual boundary conditions sz(0)=sz(N)=0 on the interval b∊[1,B] and solving, we find
| (30) |
This function is plotted in panels A and B of Fig. 3 for N=10 and 50, respectively, along with corresponding numerical results (open triangles). Interestingly, we see that moderate scaling of the diagonal relative to the pure QE scheme (by a factor of approximately 1.5 for κ=1) significantly alters the behavior of sz(b), most noticeably at larger N. More specifically, sz(b) transitions from a quadraticlike function into one that is constant for most intermediate values of b. This behavior is qualitatively distinct from that of the pure QE method which (from Fig. 3) remains exactly quadratic for all N. The behavior of sz(b) in the SQE scheme has profound implications for the scaling of the polarizability which will smoothly transition from cubic to linear behavior as N increases. In Fig. 3 we also observe the presence of edge effects which decrease systematically as the ratio of AACT to QE character is increased. Extension to longer chains (not shown) reveals that the shape of sz(b) near the ends of the molecule is independent of N. Thus, once the chain becomes long enough, the two ends become fully decoupled from each other and the overall polarizability is dominated by local rather than nonlocal contributions.
The polarizability scaling of the SQE method is computed from sz(b) [Eq. 30] by the integral approximation of the central Riemann sum and yields
| (31) |
This function is plotted in Fig. 4 (panel A) for the values κ=1∕10, 1∕3, 1∕2, and 1 at λ=1 relative to the QE and AACT predictions and the results of explicit numerical simulations (open symbols). In the limit of large N, the second term in Eq. 31, which describes the nonlinear scaling of the polarizability, approaches a constant and yields a linear polarizability scaling due to the first term. At small N, the polarizability is dominated by the second term and approaches cubic scaling. At no point is the scaling predicted to be quadratic in N. We also observe that the QE result is indeed recovered in the limits κ→0 and λ→1 and that the AACT result is obtained when κ→1 and λ→0. In fact, we observe that the first term in Eq. 31 is identical to that obtained for the AACT scheme [Eq. 29]. In the mixed limit κ→1 and λ→1, the slope of the SQE polarizability increase approaches that of the AACT model though the curve has been shifted vertically by a small amount.
Thus, for a model one dimensional case, we have demonstrated that the polarizability scaling versus chain length may be continuously tuned in the SQE formalism from cubic to linear behavior, reproducing the correct QE and AACT scaling in the respective limits. This indicates that the cubic scaling does not arise from specific J terms which are absent in AACT but present in the QE and SQE forms since SQE (like AACT) is predominantly linear for all but small N. Nor in this case may the polarizability scaling be directly ascribed to any particular N dependence of the bond vector Δrz in the polarizability formula [Eq. 15] as has been previously suggested5, 6 since the same formula and corresponding bond vectors are shared between all BR schemes. Rather, we find that the polarizability scaling of BR schemes (in conjunction with a chemical bonding topology) is controlled by the structure of G; specifically, the degree of diagonal dominance in G (adjustable through the ratio of κ to λ) appears to tune the insulator or conductorlike response of the molecular model. In the limiting case where G is strictly diagonal, we find the total polarizability to be described as a sum of individual bond polarizabilities that increases linearly with the number of bonds as in the AACT scheme and in the bond constrained OCCU QEq approach. The transition from cubic to linear scaling in the general SQE scheme intermediate between the AACT and QE limits indicates that the SQE scheme preferentially models smaller molecules as conductors and larger molecules as insulators. Thus the SQE approach has introduced the physically appealing notion of a length scale dependent conductivity in which the intrinsic length scale may be tuned by the relative diagonal and off-diagonal contributions of G. In the specific QE and AACT limiting cases of SQE, fully conducting or insulating molecular responses may also be modeled. In this way the SQE approach appears to provide similar control of the polarizability scaling as in the general OCCU QEq approach, but in a more continuously tunable fashion.
One important implication concerning the introduction of a length scale modulated conductivity in the SQE approach is that even highly conjugated polymeric systems such as polyacetylene will be modeled as insulators at larger length scales. This behavior is illustrated in panel B of Fig. 4 where we have plotted the polarizability per bond as a function of increasing molecular size. As N→∞, the conductorlike response saturates and levels off demonstrating that all additional monomers contribute equally to the total polarizability. This behavior is not observed with the AACT method, for which each monomer always contributes a constant amount even at small N. Similarly, the per bond polarizability of the QE model increases quadratically with increasing molecular size and continues to increase without bound as N→∞. We comment that the response of the SQE model (relative to the AACT and QE models) appears to more closely follow that of real conjugated polymers and molecular chains for which ab initio results25, 26, 27, 28 indicate a similar asymptotic saturation of the per monomer polarizability. Thus we expect well parametrized SQE models to exhibit improved quality (and perhaps better transferability) over existing AACT and QE models.
ADDITIONAL APPLICATIONS
Fully interacting linear chain in the BR schemes
Having thoroughly investigated the polarization response of a simplified linear atomic chain model in the BR containing only diagonal atomic hardness matrix elements, we now extend our analysis to include the case of the full bond hardness matrix. As before, we evaluate the matrix elements Jij as molecular Coulomb integrals over atomic 1s Slater orbitals having unit exponents. While the presence of a dense G matrix does not invalidate the previously discussed isomorphism between the matrix system and a corresponding differential equation, the added complexity precludes us from easily determining closed-form solutions a priori as in the previous sections. Thus, we will rely on numerical evidence to demonstrate that the observed scaling behavior of the polarizability with chain length is qualitatively unchanged from the trends described above.
In Fig. 5 we plot numerically computed polarizabilities as a function of chain length for the AACT, SQE, and QE schemes. In the case of the AACT and SQE schemes, the diagonal elements of G are scaled to be twice the value of the corresponding elements of G in the QE scheme. From Fig. 5, it is clear that the resulting scaling behavior qualitatively resembles that derived from the isolated-atom linear chain system, again indicating that the presence of the off-diagonal Coulomb terms does not significantly alter the intrinsic scaling behaviors of the respective μEq schemes. For small to intermediate N, the QE results are again well fitted by a cubic polynomial. Similarly, the results for the AACT and SQE schemes are linear at intermediate and large N as expected.
Figure 5.
Scaling of αzz as a function of the number of atoms N for the AACT, QE, and SQE methods for a linear chain of interacting atoms using the full hardness matrix J computed from Slater Coulomb integrals. For the AACT and SQE cases, bond hardness parameters are applied so that the diagonal of the resulting G matrix is equal to twice the diagonal that would be obtained from the pure QE method.
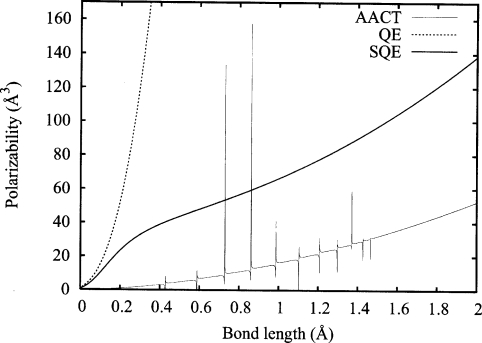
To more fully characterize the conductivity length scale imposed by the SQE method, we have investigated polarizabilities as a function of bond length by compressing and expanding the linear chain with respect to the reference bond length of 1 Å. For comparison, the results of all three BR methods are presented in Fig. 6. Overall, the QE and AACT schemes behave as expected from the theoretical predictions of Eqs. 28, 29, yielding a quadratic dependence on bond length. The SQE method also yields quadratic dependence, but only at very short (β<0.25 Å) or large (β>0.5 Å) bond lengths. The unique behavior at moderately short bond lengths (0.25<β<0.5 Å) results from the concomitant change in the prefactor of the polarizability which transitions from cubic (QE) to linear (AACT) scaling in N over this region. This region signifies the transition from insulatorlike to conductorlike character as we compress the bonds. At short bond lengths, the conductivity length scale is large enough to encompass several adjacent bonds. In the limit that the conductivity length scale is large compared to the length scale of the whole chain, the fully conducting response is achieved.
Figure 6.
Polarizability αzz as a function of bond length for various μEq methods in the N=50 interacting linear chain system. For the AACT and SQE cases, bond hardness parameters are applied so that the diagonal of the resulting G matrix is equal to twice the diagonal that would be obtained from the pure QE method. A value of λ=1 is employed in the SQE case. The vertical asymptotes appearing in the AACT curve are a result of ill-conditioned systems at these bond lengths.
For the AACT results, we observe dramatic instabilities in the computed polarizabilities as we compress the chain. To a minor degree, these instabilities are also noticeable in Fig. 5 for a few specific values of N. These instabilities do not appear in the QE or SQE results or in the AACT results for the isolated-atom case. Closer investigation reveals that under these particular conditions, the AACT G matrix is singular (or near singular) and in some cases contains negative eigenvalues. This indicates that in throwing away select contributions from the diagonal elements of J, the AACT scheme has inadvertently destroyed the positive-definite character of G. To see how this problem arises, we investigate specific elements of the Hessian matrix which must lead to a positive-definite Hessian for the condition of a minimum in the energy to be satisfied. For the QE scheme, both Chelli et al.5 and Nistor et al.17 have derived expressions relating the BR and AR gradient operators:
| (32) |
Elements of the Hessian are constructed by twice applying the BR gradient operator to the energy. In the case of the diagonal Hessian elements, we find
| (33) |
From Eqs. 3, 4, the first two terms may be associated with and while the third term is equal to −2Jij, consistent with Eq. 13. In the AACT scheme, the corresponding Hessian elements are
| (34) |
The first term, , is given by the second derivative of the second term of Eq. 16 after applying the antisymmetry relation qij=−qji for the two cases i>j and i<j. The second term in the above equation, −2Jij, may be obtained from the third term (quadruple summation) of Eq. 16 by explicitly considering cases where k=j and ℓ=i for both i>j and i<j. Since the origin of this contribution is identical for both the QE and AACT cases, it may also be obtained from diagonal elements of the QE Hessian matrix by explicitly removing all QE contributions Jii arising from diagonal elements of J, e.g., by throwing out the first two terms of Eqs. 13, 33 and retaining only the last term.
Thus, unless the two-body bond hardness terms are greater than Jij so that the diagonal Hessian elements are at least positive, the Hessian cannot be positive definite. However, positive diagonal elements which satisfy this criterion are not a sufficient condition to guarantee that the Hessian will be positive definite. This is particularly important since the mixed second derivative terms Hij,iℓ which share an index will also be modified by the AACT scheme (again through removal of all Jii contributions). Yet, it is clear that large enough bond hardness parameters can ultimately restore the positive definiteness of the Hessian. Unfortunately, it is not obvious a priori how large these elements must be without explicitly examining the corresponding AACT matrices for each application. Perhaps most troubling is that for the current choice of Slater orbital exponent (ζ=1.0 a.u.) the observed instabilities cover a wide range of chemically relevant bond lengths. Given these considerations, which could adversely affect the parametrization, usage, and transferability of AACT models, it seems preferable to employ the more general SQE approach. However, we also comment that since the SQE scheme contains the AACT scheme as a limiting case we should expect the SQE scheme to suffer from this problem as well. This may be seen from the diagonal terms of the SQE Hessian:
| (35) |
Therefore, it is necessary in the SQE scheme to restrict λ so that λ⩾1. This restriction forces the SQE scheme to retain all QE terms which are guaranteed to yield a positive-definite Hessian so long as the underlying QE Hessian is positive definite. Since for positive κ we introduce only positive diagonal terms, the positive-definite character of the SQE Hessian can only be further strengthened. We also note that a similar problem may arise in the QE and QEq cases if the diagonal terms are treated as free parameters and are chosen too small (such as zero). In such a case, the QEq Hessian will not be positive definite. However, it appears that a positive-definite QEq or QE Hessian matrix may be obtained by always choosing to be greater than or equal to the corresponding self-Coulomb integral consistent with the definition of the remaining off-diagonal elements Jij. In this way, a well conditioned SQE polarizability response may also be guaranteed.
The trans N-alkane series
To verify that our observations are consistent with more general systems involving all components of the polarizability tensor α, we have investigated the polarization response of the trans N-alkanes as a function of the number of carbon atoms (NC). Geometries for arbitrary length trans alkanes are extrapolated from the bond lengths and angles of an energy minimized CHARMM structure for hexane. In all cases, we employ the exponents of 0.70 and 0.78 a.u. for C and H used by Chelli et al.5 Atomic hardness parameters are taken to be the screened Coulomb idempotential Jii values rather than the optimized hardness parameters of Chelli et al.5 For the AACT and SQE cases, bond hardness parameters are applied so that the diagonal of the resulting G matrix is equal to twice the diagonal that would be obtained from the pure QE method. Since our purpose is to illustrate the scaling behavior only, we have made no attempts to further optimize the model parameters or scaling parameter κ (which will affect the curvature of the polarizability scaling at small NC). For the SQE case, λ has been set to 1.0 to guarantee stability.
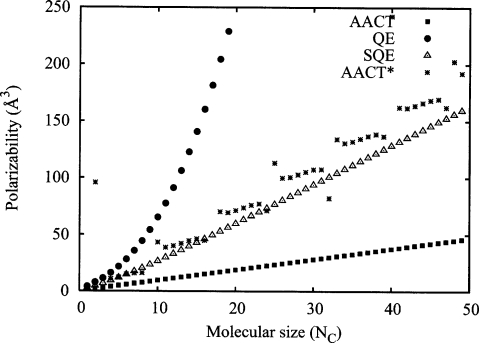
Plotting the resulting isotropic polarizabilities derived from the trace of α (Fig. 7), we see that the QE scaling remains superlinear and is reasonably well fitted by a cubic polynomial. For the current choice of parameters reflecting a strengthened diagonal in G, the SQE and AACT schemes deliver the expected linear scaling. To test for AACT instability in this system, we systematically reduce the bond hardness parameters until problematic behavior is observed. We find the onset of instability to occur near values of that have been reduced by 50% relative to the corresponding diagonal QE values. However, the onset of instability is expected to be sensitive to changes in the other parameters (such as exponents) and the specific molecular conformation. In contrast, the λ-restricted SQE approach remains stable.
Figure 7.
Scaling of as a function of the number of carbon atoms NC for the QE, AACT, and SQE methods for the trans N-alkane series. In all cases, we have used (without optimization) the exponents of 0.70 and 0.78 a.u. for C and H taken from Chelli et al. (Ref. 5) and the full Coulomb J matrix with diagonal hardness elements given by the idempotential Jii values. For the AACT and SQE cases, bond hardness parameters are applied so that the diagonal of the resulting G matrix is equal to twice the diagonal that would be obtained from the pure QE method. A value of λ=1 is employed in the SQE case. For the AACT* case (stars), we have artificially reduced the diagonal bond hardness terms by a factor of 4 to illustrate the AACT instability problem when these terms become too small.
CONCLUSIONS
In this work, we have explored the origins of the superlinear polarizability scaling as a function of molecular size that arises in certain μEq methods. We find that this undesirable scaling ultimately originates from the specific topological charge transfer constraints applied to a given μEq scheme and is not an inherent feature of the representation (atom or bond) on which the scheme is built. We demonstrate this by obtaining superlinear and linear scaling in both the atom and BRs through manipulation of charge transfer constraints in a variety of ways, some explicit, some methodological.
Second, in order to provide guidance when constructing future μEq schemes, we have analyzed the mechanisms whereby various μEq schemes temper the polarization response. In the case of the atomic μEq scheme, we find that constraining charge over small molecular subunits is a practical approach for localizing charge transfer and, upon application, yields overall linear scaling of the polarizability with molecular size. This validates the current use of CCUs in some recent μEq methods. To overcome certain deficiencies associated with constructing and parametrizing CCU-based schemes, we propose the use of OCCUs that localize charge transfer in a more continuous fashion than is possible when using disjoint CCUs.
We also derive closed-form expressions for the polarizability scaling in a linear atomic chain system for three BR schemes (QE, AACT, and SQE) and demonstrate that the superlinear scaling in the QE case varies cubically with molecular size. This is formally worse than previously suspected quadratic scaling and further bolsters the need for utilizing scaling-tempered μEq methods in large molecule applications. We also demonstrate linear scaling of the AACT and SQE schemes for our model system and how the SQE scheme may be tuned to permit either a superlinear (conducting) or a linear (insulating) polarizability response. Similarities between the SQE and atomic CCU and OCCU approaches to controlling the polarizability scaling are evidenced by the natural emergence of a tunable length-scale-dependent conductivity response.
Finally, in applying our analysis to a fully interacting atomic chain system and the trans N-alkane series, we demonstrate that the AACT and SQE methods can become unstable under certain conditions. These instabilities arise when the positive-definite character of the underlying Hessian matrix is destroyed by eliminating or scaling out specific QE contributions. Such instabilities may be avoided in the SQE scheme by retaining all QE contributions (corresponding to no AACT character) before introducing additional diagonal bond hardness terms.
Based on our observations, we recommend the use of CCUs or possibly OCCUs as a practical means for modulating the scaling in atomic QEq descriptions of large molecular systems. In the BR, the SQE approach appears to offer several advantages over the AACT scheme including a tunable scaling response that is useful for describing both insulating and conducting molecules. Given the instabilities we observe in the AACT scheme as well as the AACT limiting case of the SQE scheme, we recommend the SQE scheme be used in place of the AACT, subject to a simple criterion to guarantee stability. Future work will focus on the specific role of the charge transfer topology in moderating the polarizability scaling of large molecules within the context of the BR.
ACKNOWLEDGMENTS
The authors gratefully acknowledge support from the National Institutes of Health sponsored Center of Biomedical Research (COBRE) Grant No. P20-RR017716 at the University of Delaware (Department of Chemistry and Biochemistry).
APPENDIX: BR DIPOLE MOMENT AND POLARIZABILITY EXPRESSION
The dipole moment of the system in the BR (along the β Cartesian direction) may be straightforwardly computed as a vector dot product between a vector Δrβ comprised of the β projection of the individual bond vectors and a second vector q formed from the corresponding BCVs. The dot product may be expanded as a summation over all B bonds in the topology as
| (A1) |
This relation is easily derived beginning from the standard definition of the dipole moment in the atomic charge representation
| (A2) |
Here, the summation is taken over all N atomic sites rβ,i and charges Qi. We may use Eq. 9 which describes the mapping from atomic charges to a set of BCVs to rewrite μβ in terms of the BCVs as
| (A3) |
where the double summation twice includes all pairs of interacting atomic sites (the variables qii are always zero and are therefore excluded). This double summation may be split into two disjoint sums (corresponding to the upper and lower triangular contributions) which, by the additional use of the antisymmetry relationship qji=−qij, may be rearranged to give
| (A4) |
which may now be recombined to give the desired expression for the dipole moment in the BR:
| (A5) |
From Eq. (2.12) of Chelli et al.,5 a similar expression may be derived for the polarizability by using the induced BCV vector Δq and the inverse of the matrix G in the presence of an external, uniform electric field Eγ in the γ direction:
| (A6) |
The induced dipole moment is given by substitution of the above expression into Eq. A5. Taking a derivative of the induced dipole moment with respect to the electric field, we obtain a result for the γβ component of the polarizability tensor
| (A7) |
We also note that for practical calculations of the polarizability tensor, explicit computation of G−1 is unnecessary. By defining an auxiliary vector sγ which is a solution of the system Gsγ=Δrγ, we may simply rewrite Eq. A7 as
| (A8) |
and conveniently avoid a potentially ill conditioned and costly O(B3) construction of the inverse by replacing it with several O(B2) matrix-vector solve operations.
References
- Liu Y.-P., Kim K., Berne B. J., Friesner R. A., and Rick S. W., J. Chem. Phys. 10.1063/1.475886 108, 4739 (1998). [DOI] [Google Scholar]
- Banks J. L., Kaminski G. A., Zhou R., Mainz D. T., Berne B. J., and Friesner R. A., J. Chem. Phys. 10.1063/1.478043 110, 741 (1999). [DOI] [Google Scholar]
- Kaminski G. A., Stern H. A., Berne B. J., Friesner R. A., Cao Y. X., Murphy R. B., Zhou R., and Halgren T. A., J. Comput. Chem. 10.1002/jcc.10125 23, 1515 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern H. A., Kaminski G. A., Banks J. L., Zhou R., Berne B. J., and Friesner R. A., J. Phys. Chem. B 10.1021/jp984498r 103, 4730 (1999). [DOI] [Google Scholar]
- Chelli R., Procacci P., Righini R., and Califano S., J. Chem. Phys. 10.1063/1.480198 111, 8569 (1999). [DOI] [Google Scholar]
- Chelli R. and Procacci P., J. Chem. Phys. 10.1063/1.1530164 118, 1571 (2003). [DOI] [Google Scholar]
- Chelli R. and Procacci P., J. Phys. Chem. B 108, 16995 (2004). [Google Scholar]
- Mortier W. J., Ghosh S. K., and Shankar S., J. Am. Chem. Soc. 10.1021/ja00275a013 108, 4315 (1986). [DOI] [Google Scholar]
- Rappé A. K. and W. A.GoddardIII, J. Phys. Chem. 10.1021/j100161a070 95, 3358 (1991). [DOI] [Google Scholar]
- York D. M. and Yang W., J. Chem. Phys. 10.1063/1.470886 104, 159 (1996). [DOI] [Google Scholar]
- Tabacchi G., Mundy C. J., Hutter J., and Parrinello M., J. Chem. Phys. 10.1063/1.1487822 117, 1416 (2002). [DOI] [Google Scholar]
- Shimizu K., Chaimovich H., Farah J. P. S., Dias L. G., and Bostick D. L., J. Phys. Chem. B 10.1021/jp037315w 108, 4171 (2004). [DOI] [Google Scholar]
- Stone A. J., Hättig C., Jansen G., and Ángyán J. G., Mol. Phys. 10.1080/002689796173930 89, 595 (1996). [DOI] [Google Scholar]
- Miller K. J., J. Am. Chem. Soc. 10.1021/ja00179a044 112, 8533 (1990). [DOI] [Google Scholar]
- Chen J. and Martínez T. J., Chem. Phys. Lett. 438, 315 (2007). [Google Scholar]
- Rick S. W., Stuart S. J., and Berne B. J., J. Chem. Phys. 10.1063/1.468398 101, 6141 (1994). [DOI] [Google Scholar]
- Nistor R. A., Polihronov J. G., Müser M. H., and Mosey N. J., J. Chem. Phys. 10.1063/1.2346671 125, 094108 (2006). [DOI] [PubMed] [Google Scholar]
- Chelli R. and Procacci P., J. Chem. Phys. 10.1063/1.1515773 117, 9175 (2002). [DOI] [Google Scholar]
- Chelli R., Pagliai M., Procacci P., Cardini G., and Schettino V., J. Chem. Phys. 10.1063/1.1851504 122, 074504 (2005). [DOI] [PubMed] [Google Scholar]
- Roothaan C. C. J., J. Chem. Phys. 10.1063/1.1748100 19, 1445 (1951). [DOI] [Google Scholar]
- Roothaan C. C. J. and Ruedenberg K., J. Chem. Phys. 10.1063/1.1740187 22, 765 (1954). [DOI] [Google Scholar]
- Patel S. and C. L.BrooksIII, J. Comput. Chem. 10.1002/jcc.10355 25, 1 (2004). [DOI] [PubMed] [Google Scholar]
- Morales J. and Martínez T. J., J. Phys. Chem. A 10.1021/jp003823j 105, 2842 (2001). [DOI] [Google Scholar]
- Morales J. and Martínez T. J., J. Phys. Chem. A 10.1021/jp0369342 108, 3076 (2004). [DOI] [Google Scholar]
- Mori-Sánchez P., Wu Q., and Yang W., J. Chem. Phys. 10.1063/1.1630011 119, 11001 (2003). [DOI] [Google Scholar]
- van Faassen M., de Boeij P. L., van Leeuwen R., Berger J. A., and Snijders J. G., Phys. Rev. Lett. 10.1103/PhysRevLett.88.186401 88, 186401 (2002). [DOI] [PubMed] [Google Scholar]
- Giese T. J. and York D. M., J. Chem. Phys. 10.1063/1.1756583 120, 9903 (2004). [DOI] [PubMed] [Google Scholar]
- Kirtman B., Toto J. L., Robins K. A., and Hasan M., J. Chem. Phys. 10.1063/1.469262 102, 5350 (1995). [DOI] [Google Scholar]