Abstract
A form of two-dimensional (2D) vibrational spectroscopy, which uses two ultrafast IR laser pulses, is used to examine the structure of a cyclic penta-peptide in solution. Spectrally resolved cross peaks occur in the off-diagonal region of the 2D IR spectrum of the amide I region, analogous to those in 2D NMR spectroscopy. These cross peaks measure the coupling between the different amide groups in the structure. Their intensities and polarizations relate directly to the three-dimensional structure of the peptide. With the help of a model coupling Hamiltonian, supplemented by density functional calculations, the spectra of this penta-peptide can be regenerated from the known solution phase structure. This 2D-IR measurement, with an intrinsic time resolution of less than 1 ps, could be used in all time regimes of interest in biology.
The three-dimensional (3D) structure of peptides and proteins and their fluctuations are essential properties responsible for the extremely high specificity of biological reactions. Progress in understanding biological processes such as enzyme reactions originates from the detailed knowledge of the secondary, tertiary, and quarternary structures of the participating bio-molecules. Two major spectroscopic techniques are responsible for this development: x-ray scattering, which maps out the electron density of the molecule, and two-dimensional (2D)-NMR spectroscopy (1–3), which can measure the distances between pairs of protons. The next step must be the determination of structures in motion over a wide range of time scales. We believe that multidimensional IR spectroscopy can address this new challenge.
The IR spectra of the amide transitions provide information about secondary structural motifs of proteins and peptides. The so-called amide I band, which consists of mostly the stretching motion of the peptide backbone C=O groups, is a strong IR absorber, which is spectrally isolated from other vibrational modes such as those from amino acid side groups. The amide I states can be viewed as vibrational excitons (4, 5) with the individual peptide groups considered as separated but coupled units. The coupling could be either through-space, such as multipole or even dipole-dipole interaction as proposed by Krimm and Bandekar (4), or through-bond, involving charge shifts and kinematic coupling via the Cα atoms of the backbone. The states, which have one excitation present in the whole assembly, can be interrogated by conventional (linear) IR absorption spectroscopy, but the information obtained is insufficient to determine the coupling Hamiltonian, from which a structure might be deduced. More information is available from nonlinear third-order spectroscopic techniques (6) such as the 2D experiment presented here. In a separated system picture both the one-exciton and two-exciton states contribute to the nonlinear IR signal in such a way that all couplings between the separate amide units are available, and in principle a 3D structure of the peptide can be deduced.
The success of NMR spectroscopy as a structural tool in biology was advanced by improvements (1–3) in resolution achieved by spreading out congested spectra into a second dimension where connected groups are represented by cross peaks and can be characterized by excitation transfer. A few examples of applying similar principles to electronic and vibrational transitions have been proposed (7, 8) and realized experimentally (6, 9, 10) lately. Optical and vibrational transitions in solution dephase very rapidly compared with spin transitions so these nonlinear spectroscopies have become possible only as a result of significant recent improvements in ultrafast laser technology. The objective of such developments would be to provide alternative methods of secondary structure determination. IR spectra also can be spread into two dimensions by the variation of external conditions such as temperature or pressure (11), but these approaches differ in principle from the nonlinear spectroscopies that involve perturbations of a quasi-equilibrium distribution by an electromagnetic field.
In a first attempt at nonlinear 2D IR spectroscopy two small globular peptides, scyllatoxin and apamin, (6) were examined. The results clearly manifested the coupling of the amide I states. However, even when spread into two dimensions many positive and negative bands overlapped in the 2D spectra, making it difficult to explore with confidence the coupling mechanisms. Nevertheless these experiments revealed the parameters essential for 2D spectroscopy of amide I bands, namely, the time scales of population relaxation (1.2 ps) and energy transfer between individual amide I states (>2.5 ps); the homogeneous width (10 cm−1), inhomogeneous disorder (25 cm−1), and the degree of delocalization of the amide I states (8 Å).
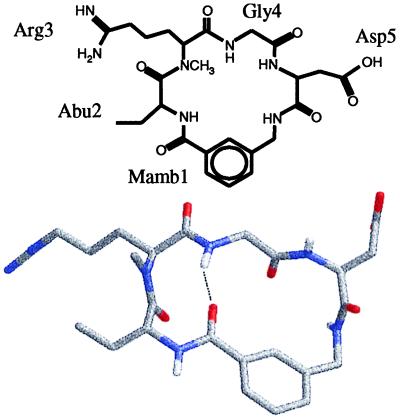
Here, we present results on a peptide that is small enough that all amide I transitions are spectrally resolved, allowing the properties of the nonlinear 2D-IR spectra and the validity of coupling models to be examined critically. The sample chosen is a cyclic penta-peptide (cyclo-Mamb-Abu-Arg-Gly-Asp), for which both the NMR and the x-ray structures are known (12). The chemical formula and the 3D structure are shown in Fig. 1. The structure of the peptide, which is stabilized by a hydrogen bond between the Mamb-1–Abu-2 peptide bond and the Arg-3–Gly-4 peptide bond, was specifically designed (12) to form a single, well-defined conformation in solution with an almost ideal type II′ β-turn centered at the Abu-Arg residues.
Figure 1.
The chemical structure and 3D x-ray structure of the investigated penta-peptide (cyclo-Mamb-Abu-Arg-Gly-Asp) obtained from ref. 10.
MATERIALS AND METHODS
IR Laser System.
For the generation of intense IR pulses at 1,650 cm−1 [bandwidth 130 cm−1 full width at half maximum (FWHM); pulse duration, 150 fs, energy ca. 1 μJ], a white light seeded, two-stage B-barium borate-optical parametric amplifier was used to split the output pulses of a Ti:S-amplifier (800 nm, 500 μJ, ca. 80 fs) into a signal and an idler pulse, which subsequently were difference frequency-mixed in an AgGaS2 crystal. Narrow-band pump pulses were generated by filtering these pulses with an adjustable IR-Fabry-Perot filter, which was constructed from two partial reflectors (r = 90%), one of which mounted on a stepping motor-controlled translation stage. The pump wavelength was tuned by fine adjustment of the distance between both mirrors in steps of 100 nm. In addition, by choosing the order of interference, the spectral width could be adjusted. In these experiments, 13th-order interference was used, yielding pulses with approximately Lorentzian line shape with 12 cm−1 bandwidth. The free spectral range and the peak transmission of the Fabry-Perot were 120 cm−1 and 30%, respectively. The transmitted pulses had an asymmetric pulse shape with a fast rising edge limited by the pulse duration of the original pulse and a falling slope that decayed exponentially with a time constant of 1 ps. Two subsequent wire-grid polarizers controlled the polarization of the probe pulses. Both beams were focused onto the sample with a f = 10 cm off axis parabolic mirror, yielding a spot size of ca. 100 μm for the probe and 150 μm for the pump. A variable delay line was used to control the time delay between pump and probe pulse. Transient spectra were recorded by a 32-channel HgCdTe-detector-array mounted to a spectrograph (f = 270 mm, grating 120 lines/mm) covering 120 cm−1 with a spectral resolution of ca. 4 cm−1.
Sample.
The peptide, cyclo(Mamb-Abu-Arg-Gly-Asp) (see Fig. 1) (12) was dissolved in D2O (as methylsulfonate salt) at a concentration of ca. 50 mM and buffered at pH 3.5. At this pH both Asp-5 and Arg-3 are protonated, leaving one net positive charge on Arg-3. The samples were held in a CaF2 cell (spacing: 25 μm), which was rotated during the experiment to prevent local heating.
Computational Methods.
The coupling between a pair of peptide groups was assumed to be dominated by electrostatics. However, in contrast to our previous work where a dipole approximation was used (6), a set of transition charges was obtained from a density functional theory calculation (B3LYP level, 6–31+G* basis set, gaussian94, ref. 13). These calculations were performed on model compounds chosen to mimic the local electronic structure of the individual peptide bonds: deuterated N-methylbenzamide (C6H5-COND-CH3) for the Mamb-1–Abu-2 peptide bond, N,N-dimethylacetamide (CH3-CON-CH3CH3) for Abu-2–Arg-3, and deuterated N-methylacetamide (NMA, CH3-COND-CH3) for the remaining bonds. Diffuse functions were used in the basis set to ensure the planarity of the peptide bond (14). After geometry optimization, vibrational eigenmodes and a set of Mulliken charges and their first derivatives with respect to the amide I normal mode were calculated. To ensure that the total Mulliken charge derivatives of the peptide group (-CO-NH-) are zero, any charge derivatives from other atoms were added to the C or N atom of the peptide group. The interaction Hamiltonian was calculated by using these transition charges and the x-ray structure of the peptide (structure 1d of ref. 12). The dipole strength (0.37 Debye for NMA) and orientation (25° to the C=O bond) of the individual transition dipoles obtained from these calculations reproduced experimental values very well (4).
EXPERIMENT
The Linear Absorption Spectrum.
The IR spectrum of the peptide in a region between 1,570 cm−1 and 1,680 cm−1 exhibits five partially resolved bands (see Fig. 2a). A multiline Lorentzian fit (Gaussians did not fit so well) yields 1,673 cm−1 (bandwidth Δω1 = 23 cm−1 FWHM), 1,648 cm−1 (Δω2 = 35 cm−1), 1,620 cm−1 (Δω3 = 19 cm−1), 1,610 cm−1 (Δω4 = 19 cm−1), and 1,584 cm−1 (Δω5 = 17 cm−1) for the peak positions and bandwidths, respectively. An additional weaker peak is seen at 1,720 cm−1 (data not shown), which safely could be assigned to the carboxyl group of Asp-5, because it down-shifts on deprotonation. There are no other strong IR bands between 1,500 cm−1 and 2,000 cm−1.
Figure 2.
(a) Absorption spectrum of the penta-petide in D2O. The dashed line shows a representative spectrum of the pump pulses used to collect the 2D pump-probe spectra. (b and c) 2D pump-probe spectra of the peptide measured with the polarization of the probe pulse perpendicular and parallel to the polarization of the pump pulse, respectively. (d–f) A least-squares fit of the experimental data, which reveals the coupling Hamiltonian given in Eq. 3 (see text for details).
We associate the five bands shown in Fig. 2a to the amide I modes of the five peptide groups of the molecule. Only the absorption line at 1,584 cm−1 falls outside the typical range of amide I modes (1,600–1,700 cm−1). However, there are two amino acid derivatives in the molecule for which an abnormally low frequency is expected. The Abu-2–Arg-3 peptide bond, with a methyl group bound to the nitrogen atom instead of a proton, has its C=O double bond character decreased and the reduced mass of the amide I normal mode increased. The amide I frequency of N,N-dimethylacetamide in D2O, used as a model compound for this peptide bond, is 1,608 cm−1, which is 15 cm−1 lower than that of NMA in D2O. Therefore, the lowest frequency absorption line at 1,584 cm−1 is very likely associated with Abu-2. The C=O bond order also is expected to be reduced in the Mamb-1–Abu-2 unit, which is directly bonded to an aromatic ring. Therefore it is expected that one of the other low-frequency lines (1,610 cm−1 or 1,620 cm−1) can be attributed to Mamb-1–Abu-2. Excitonic coupling, the positive charge of the Arg-3 side chain, and the strength of intra- and intermolecular hydrogen bonds all can further influence the amide I vibrational frequencies. These effects readily can explain the range of amide I frequencies found in this peptide.
2D-IR Spectroscopy.
Nonlinear 2D-IR spectra of the peptide are shown in Fig. 2 b and c. These 2D-IR spectra were assembled by measuring the transient difference spectra as a function of the peak frequency of the pulse traversing the interferometer. A representative spectrum of the pump pulses also is shown in Fig. 2a. The time delay between pump and probe pulses was set such that the broad frequency bandwidth probe pulse followed ca. 800 fs after the fast-rising edge of the pump pulse. Fig. 2b shows the spectrum for perpendicular pump and probe polarizations and Fig. 2c the result for parallel polarized beams.
Diagonal Contribution.
In the 2D spectra of Fig. 2, the dominating signals are found along the diagonal. For each absorption line in the linear absorption spectrum, a pair of a negative (red) and a positive (blue) peak appears in the 2D spectrum. The positive peaks are separated from the corresponding negative peaks by ca. 16–20 cm−1 in the direction of lower probe frequency. The spectra are significantly better resolved along the diagonal than in the linear IR spectrum. Important information also can be deduced from the shapes of the individual peaks. For example, whereas the negative peak at 1,648 cm−1 is elongated along the diagonal direction, the negative peak at 1,584 cm−1 is elongated along the pump axis. However, the width of the individual holes and the corresponding positive bands, measured along the direction of the probe axis, is approximately the same for all lines (16 cm−1 FWHM, see also Fig. 3).
Figure 3.
Cuts through the 2D-IR pump probe spectra shown in Fig. 2 b and c along the direction of the probe axes for selected pump frequencies that were chosen to match the peaks in the linear absorption spectrum (□, 1,648 cm−1; ○, 1,620 cm−1; ▵, 1,610 cm−1; ◊, 1,584 cm−1). The frequency positions of the pump pulses are marked by the vertical dotted lines. The spectral width of the burned hole and the corresponding excited state absorption is 16 cm−1 (FWHM). The amplitude of the cross peaks was evaluated by measuring the displacement of the peaks from a linear background as indicated (see arrows).
Off-Diagonal Contribution.
The main focus of this paper, however, is the off-diagonal region, where cross peaks appear. The strongest cross peak is observed for the 1,610–1,584 cm−1 level pair. When pumping the absorption line at 1,610 cm−1, both that absorption line itself and the one at 1,584 cm−1 respond with a pair of a positive and negative bands. The intensity of the cross peak, relative to the intensity of the diagonal contribution, is larger when the spectrum is measured with the polarization of the pumped and probed beams perpendicular (Fig. 2b).
The properties of the other cross peaks are verified in cuts through the 2D spectra along the probe axis for certain pump frequencies. The pump frequencies were selected in Fig. 3 such that they match the individual peaks in the linear absorption spectrum. For most all level pairs, cross peaks can be identified by their dispersive shapes (marked, for example, by the arrows in Fig. 3). In general, the cross peak intensity decreases with increasing frequency separation between pump and probe, and its contrast is larger in the perpendicular spectrum.
Each cross peak signal was evaluated by measuring its peak variation from a background (as indicated in Fig. 3, see arrows). The peak excursions for parallel (I||) and perpendicular (I⊥) polarization, the magic-angle cross peak intensities Ikl = 1/3(I|| + 2I⊥) and the anisotropies rkl = (I| − I⊥ )/(I || + 2I⊥) are listed in Table 1. The anisotropy of the diagonal signals is close to 0.4, which is expected when pumped and probed transition dipoles are parallel. The off-diagonal anisotropies are symmetric, rkl = rlk, so that the same anisotropy is obtained when the pump and probe frequencies are interchanged. The magic angle intensities are only approximately symmetric and the correlation is not as good as in the case of the anisotropies.
Table 1.
Anisotropy and magic angle intensity (measured from the top to the bottom) of all identified cross peaks and diagonal peaks in the 2D-IR spectrum of the peptide
| Pump | Probe
|
||||
|---|---|---|---|---|---|
| 1,673 cm−1 | 1,648 cm−1 | 1,620 cm−1 | 1,610 cm− | 1,584 cm−1 | |
| 1,648 cm−1 | 0.05 ± 0.5 | 0.35 ± 0.05 | 0.2 ± 0.3† | 0.09 ± 0.05 | |
| 0.04 mOD | 0.52 mOD | 0.06 mOD | 0.03 mOD | ||
| 1,620 cm−1 | – | 0.15 ± 0.05 | 0.36 ± 0.05 | – | 0.05 ± 0.02 |
| – | 0.03 mOD | 0.54 mOD | – | 0.15 mOD | |
| 1,610 cm−1 | – | 0.25 ± 0.05 | –† | 0.38 ± 0.05 | 0.11 ± 0.02 |
| – | 0.03 mOD | – | 0.52 mOD | 0.16 mOD | |
| 1,584 cm−1 | – | – | 0.06 ± 0.05* | 0.11 ± 0.02 | 0.36 ± 0.05 |
| – | 0.03 mOD | 0.07 mOD | 0.11 mOD | 0.39 mOD | |
The experimental errors in the magic angle intensities is ca. ± 0.01 milli optical density units (mOD).
Only the negative signal of this band was used, because the positive part overlaps with the stronger contribution from the 1,610 cm−1 transition.
Because of the small frequency separation, no clear distinction between the two bands could be made.
DISCUSSION
The Coupling Hamiltonian.
It is useful to first consider the peptide as a set of five independent amide vibrators mixed by a coupling that is bilinear in the mode displacements. Then, if the individual amide modes were harmonic, the exciton-like, coupled states of the polypeptide also would be a set of five independent harmonic normal modes having frequencies determined both by the coupling and the intrinsic energy shifts of each of the amide units (see Fig. 4). The goal of the experiments is to find the coupling matrix, which then should yield a unique molecular structure. However, in this harmonic picture there would be no third-order IR signal, because there would be no transitions from one independent oscillator to another, and each oscillator could respond only with its harmonic frequency. For example, if the v = 1 transition of one oscillator were pumped by an IR pulse, there would be no net change in absorption because the v = 1→v = 2 loss of probe intensity would precisely cancel its v = 1→v = 0 gain. It is quite general that the third-order response of a harmonic system is zero (15).
Figure 4.
Energy level scheme for a system of two coupled oscillators. The isolated peptide states (Left) are coupled by some weak interaction, which mix them to generate the excitonic states (Right). Anharmonicity, which is crucial for understanding the 2D pump-probe spectra, is introduced into this model by lowering the energies of the double-excited monomeric site states |i〉|i〉 by Δ from their harmonic energies 2ɛii. This anharmonicity mixes into all coupled states, giving rise to diagonal anharmonicity (Δɛkk) and off-diagonal anharmonicity (mixed-mode anharmonicity, Δɛkl) in the basis of the normal modes discussed in the text.
In reality these normal modes are anharmonic so that successive transitions within one manifold are not, in fact, degenerate and transitions can occur between manifolds. The anharmonicity of the independent amide I oscillators can be introduced as a perturbation in the basis of the harmonic excitonically coupled states. This perturbation reduces the zero-order energies of the doubly excited (first overtone) monomeric states by Δ from their harmonic values 2ɛi (see dotted lines in Fig. 4) and mixes the excitonic states. The normal modes now are associated with diagonal, Δɛkk = ɛkk − 2ɛk, and off-diagonal, or mixed-mode, anharmonicity, Δɛkl = ɛkl − ɛk − ɛl (see Fig. 4).
In the 2D experiment, the narrower frequency pump pulse populates a
one-exciton state, which is probed by transitions down to the ground
state and up to the two-exciton states. Along the diagonal of the 2D
spectra, one observes the bleach and stimulated emission signal at
frequency ɛk of the pumped state
|vk〉 and an
excited state absorption to the double excited state
|vk〉|vk〉,
which is down-shifted by diagonal anharmonicity
Δɛkk. In the off-diagonal (cross peak)
region, one sees the bleach of the probed transition
ɛl (because the common ground state is
depopulated) and an excited state absorption to the mixed state
1/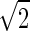 (|vk|vl〉+|vl〉|vk〉),
which is down-shifted by off-diagonal anharmonicity
Δɛkl.
(|vk|vl〉+|vl〉|vk〉),
which is down-shifted by off-diagonal anharmonicity
Δɛkl.
In relating the experimental data with this model we neither consider coherent effects nor relaxation between the excitonic states. We know from previous experiments (6) that the inter-exciton coherence decays very rapidly. Furthermore, in the present example the frequency bandwidth of the pump pulses is too narrow to excite coherent superposition states between the excitonic states. The earlier experiments also showed that the approach to an equilibrium population distribution is much slower than the time scale of these measurements, which therefore can be interpreted as incoherent excitations of quasi-stationary eigenstates, as typified by those in Fig. 4 for a pair of oscillators.
Although in general a numerical matrix diagonalization is needed to find the diagonal and off-diagonal anharmonicities (6), the intensities, and the polarizations of the transitions, the picture simplifies when the frequency separations between the uncoupled modes i,j,… are large compared with Δ and large compared with the individual coupling terms, |βij/(ɛi − ɛj)| < 1. In this case, the coupled states are predominantly localized on single peptide units (see Fig. 4). Coupling terms in the order of |βij| ≲ 10 cm−1 are predicted for nearest neighbors (see below), whereas the basis states are spread over a range of almost 100 cm−1. Therefore, the localization limit should describe the present example reasonably well. In this limit, the diagonal anharmonicities are simply given to first order by Δɛkk = −Δ, and the off-diagonal anharmonicities are easily calculated from perturbation theory. They are in first order of Δ and lowest order in βkl given by:
 |
1 |
The observed shifts of the negative and positive bands along the diagonal are consistently in the range of 16–20 cm−1, which is in perfect agreement with this discussion and the known anharmonicity of 16 cm−1 for isolated NMA (6). The anharmonicities Δɛkl, on the other hand, are smaller than the bandwidths of the probed transitions Δωl, so that the overlapping negative and positive contributions sum up to a signal, which has the shape of the first derivative of the absorption line. The off-diagonal anharmonicity is approximately proportional to the cross peak intensity Ikl:
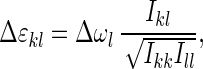 |
2 |
where the Ikk and Ill are the intensities of the corresponding diagonal peaks. The cross peak intensity is not necessarily strictly symmetric because it depends only on the bandwidth of the probed transition Δωl even though the off-diagonal anharmonicities are symmetric, Δɛkl = Δɛlk.
The anisotropy of the cross peaks, rkl, provides additional useful information to reconstruct the coupling Hamiltonian. It measures the angle ϕkl between the pumped and the probed transition dipoles through rkl = 1/5(3cos2ϕkl −1), which in the localization limit is directly given by the orientation of the transition dipoles of the isolated peptide groups. Along the diagonal of the 2D spectra values close to 0.4 are observed as expected, because here the same transition is pumped as is probed. Anisotropies smaller than 0.4 are observed in the off-diagonal region, indicating that pumped and probed transitions are in general not parallel. This finding explains the higher contrast of the cross peaks in the perpendicular spectrum. As expected from this interpretation, the anisotropy is symmetric rkl = rlk.
An assignment of the five bands in the IR spectrum to specific peptide groups is not known a priori. There are 5!=120 possibilities to distribute these frequencies. However, with the information obtained from the cross peak anisotropies and intensities, the number of possibilities can be reduced significantly by examining the correlation coefficients between experimental and calculated Hamiltonian matrices. For each permutation, two correlation coefficients were calculated for those level pairs where experimental data were available: (i) the correlation coefficient between the experimentally obtained anisotropy and the anisotropy of the individual states, which in the weak coupling limit is given by the orientations of the peptide bonds, and (ii) the correlation coefficient between the experimental off-diagonal anharmonicity evaluated according to Eq. 2 and the off-diagonal anharmonicities calculated from Eq. 1. The latter were obtained by using an approximate coupling Hamiltonian Hkl, (in cm−1, see Eq. 3) computed from the x-ray structure of the peptide and a calculated set of transition charges of the individual peptide groups.
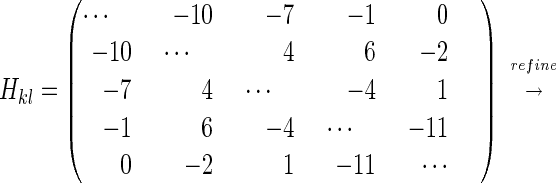 |
3 |
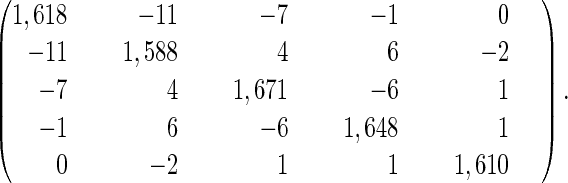 |
Only four of the 120 permutations give a significant positive correlation (>0.5) simultaneously for both observables. The permutation with the highest correlation coefficient (ca. 0.62 in both cases) assigns 1,620 cm−1 to Mamb-1–Abu-2, 1,584 cm−1 to Abu-2–Arg-3, 1,673 cm−1 to Arg-3–Gly-4, 1,648 cm−1 to Gly-4–Asp-5, and 1,610 cm−1 to Asp-5–Mamb-1, respectively. This assignment thoroughly agrees with other findings. For example, it attributes the 1,584 cm−1 transition to the Abu-2–Arg-3 bond, which has a methyl group bound to the nitrogen atom instead of a proton so that one does indeed expect it to have the lowest frequency in the absorption spectrum, as discussed in Experiment. Also, Mamb-1–Arg-2 is attributed to one of the lower transition frequencies, again as predicted in Experiment. Arg-3–Gly-4 is assigned to the highest frequency, which likely is a consequence of its vicinity to the positively charged Arg-3 side chain. In addition, the flexibility of the peptide backbone around Gly-4 (12) is consistent with the large inhomogeneous width of the 1,648 cm−1 absorption line (see also below).
The coupling Hamiltonian subsequently was refined (see Eq. 3) by least-square-fitting the perpendicular and parallel 2D spectra, treating off-diagonal elements for which cross peaks have been identified (see Table 1) and the inhomogeneous width of the individual lines as free parameters. Homogeneous and inhomogeneous broadening were introduced as described (6). During the fitting procedure, the diagonal elements were constantly adjusted such that the eigenvalues of Hkl equate the transition frequencies of the linear absorption spectrum for a given set of off-diagonal elements. The result of the fit (Fig. 2 d-f) agrees almost perfectly with the experimental data. Only the coupling between Gly-4–Asp-5 and Asp-5–Mamb-1, needed to be refined significantly to obtain this correspondence.
Broadening Mechanisms.
The widths of the bleach and excited state absorption bands along the diagonal are all similar (16 cm−1, FWHM), despite significant differences seen for the individual lines in the linear spectrum. The widths of the diagonal peaks represent the homogeneous width of the individual transitions, which according to the results of ref. 6 is ca. 10 cm−1. The fact that some of the diagonal bands are elongated along the diagonal shows that there is a significant inhomogeneous broadening for those transitions. This elongation is particularly evident in the case for the 1,648 cm−1 absorption line, which consistently appears in the linear absorption spectrum as the broadest band. The 1,584 cm−1 absorption line, on the other hand, is predominantly homogeneously broadened. Thus, the differences in bandwidths obtained from the multiple line fit of the linear absorption spectrum are caused by variations in the inhomogeneous width. The inhomogeneous distribution of vibrational frequencies for a given band implies a distribution of environments and structures for the peptide unit. For example, the NMR data indicate that the side groups of the polar Asp-5 and the positively charged Arg-3 are highly flexible in solution (12). This heterogeneity will affect the vibrational frequencies of nearby C=O groups, but other groups should be less sensitive to these fluctuations. Also, the peptide backbone around Gly-4 is more flexible than the portion closer to the aromatic linker (12), which likely is another source of inhomogeneity. These types of structural fluctuations presumably can have components that are slow compared with the measurement process and therefore cause inhomogeneous broadening. These inhomogeneous properties can be used as additional information to assign the range of amide structures (see previous section). The uniformity of homogeneous broadening indicates that all peptide groups have similar exposure to faster fluctuations, such as from the solvent.
CONCLUSIONS
We presented a detailed example of 2D-IR spectroscopy on a small peptide. A variety of individual cross peaks were detected whose intensities and anisotropies could be related to the known 3D structure of the peptide. Simple expressions for this relationship have been derived for the localization limit, where the peptide amide I band is a set of weakly coupled harmonic oscillators perturbed by local anharmonicity. With the help of the cross peaks and an approximate model for the coupling Hamiltonian, an attribution of all diagonal peaks could be given that is consistent with other empirical assignments.
The original Hamiltonian was calculated assuming that the interactions derive from through-space electrostatic interactions. Ab initio calculations on model compounds such as NMA showed that the amide I normal motions involve a flow of charge to the methyl groups and also a bending of the methyl C-H bonds. Both effects will couple neighboring groups by through-bond interactions involving the Cα atom. Therefore, the amide I mode should not be viewed as strictly localized, and any coupling Hamiltonian based on this assumption would necessarily be inadequate. This result is consistent with a nearest neighbor interaction being the main difference between the refined and original coupling Hamiltonians.
It has been shown that the 2D method presented yields more complete and direct information on the structure of the peptide than conventional (one-dimensional) spectroscopy. In the present example we made use of the known structure to relate specific peptide units to the various transition frequencies. In general, the objective will be to invert the 2D-IR spectrum and deduce the structure by using only a basis of experimental data and modeling. Extra information needed for this inversion could be obtained from isotopic labeling and solvent shift experiments. In addition, theoretical information about peptide structure, such as constraints for chemical bond and nonbonded distances and angles, could be introduced into the refinement procedure. Although the signs of the coupling terms and angular parameters were not obtained from the data by using the localization limit formulas, the situation would be different when the excitations are more delocalized, such as in an α-helix or β-sheet. In that case the integrated intensities of the individual excitonic transitions depend on the mixing of states, which, in principle, enables even the signs of the coupling terms to be recovered. For example, for two coupled units, the relative intensities, which depend on the orientation of the two transition dipoles, determine the ordering of the symmetric and asymmetric states and hence sign of the coupling. Armed with this additional information the problem of inverting the 2D data into unique 3D maps of the amide groups in small peptides would appear to be quite feasible.
The type of information available from 2D-IR spectroscopy is analogous to that obtained from 2D NMR correlation spectroscopy. In both cases, a weak interaction mechanism connects the states, so that cross peaks occur in the off-diagonal region of the 2D spectra. It is the additional information on the connectivity of states that allows geometric relationships to be determined. We have demonstrated in this paper exactly the same principle for vibrational transitions. The 2D-IR method has the characteristic of high intrinsic time resolution and rapid data acquisition speed. It could resolve structural motions over essentially all time scales of interest in biology, for example during all stages of protein folding. Multidimensional IR spectra could be obtained by many other experimental arrangements such as transient gratings or photon echoes (16). These approaches, if confined to third-order nonlinearities, would explore the same set of one-excitonic and two-excitonic states as in the present experiment, so the results should be comparable.
Acknowledgments
The research was supported by the National Institutes of Health and the National Science Foundation with instrumentation developed under National Institutes of Health Grant RR13456. P.H. is grateful to the Deutsche Forschungsgemeinschaft for a postdoctoral fellowship.
ABBREVIATIONS
- 2D
two-dimensional
- 3D
three-dimensional
- FWHM
full width at half maximum
- NMA
N-methylacetamide
References
- 1.Ernst R R, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Oxford: Oxford Univ. Press; 1987. [Google Scholar]
- 2.Wuthrich K. NMR of Proteins and Nucleic Acids. New York: Wiley; 1986. [Google Scholar]
- 3.Bax A, Grzesiak S. Acc Chem Res. 1993;26:131–138. [Google Scholar]
- 4.Krimm S, Bandekar J. Adv Protein Chem. 1986;38:181–364. doi: 10.1016/s0065-3233(08)60528-8. [DOI] [PubMed] [Google Scholar]
- 5.Torii H, Tasumi M. J Chem Phys. 1992;96:3379–3387. [Google Scholar]
- 6.Hamm P, Lim M, Hochstrasser R M. J Phys Chem B. 1998;102:6123–6138. [Google Scholar]
- 7.Tanimura Y, Mukamel S. J Chem Phys. 1993;99:9496–9511. [Google Scholar]
- 8.Okumura K, Tanimura Y. Chem Phys Lett. 1998;295:298–304. [Google Scholar]
- 9.Tokmakoff A, Lang M J, Larsen D S, Fleming G R, Chernyak V, Mukamel S. Phys Rev Lett. 1997;79:2702–2705. [Google Scholar]
- 10.Hybl J D, Albrecht A W, Sarah M, Gallagher F, Jonas D M. Chem Phys Lett. 1998;297:307–313. [Google Scholar]
- 11.Noda I. J Am Chem Soc. 1989;111:8116–8118. [Google Scholar]
- 12.Bach A C, Eyermann C J, Gross J D, Bower M J, Harlow R L, Weber P C, DeGrado W F. J Am Chem Soc. 1994;116:3207–3219. [Google Scholar]
- 13.Frisch M J, Trucks G W, Schlegel H B, Gill P M W, Johnson B G, Robb M A, Cheeseman J R, Keith T, Petersson G A, Montgomery J A, et al. gaussian 94. Inc., Pittsburgh, PA: Gaussian; 1995. [Google Scholar]
- 14.Mirkin N G, Krimm S. J Mol Struct. 1996;337:219–234. [Google Scholar]
- 15.Mukamel S. Principles of Nonlinear Optical Spectroscopy. New York: Oxford Univ. Press; 1995. [Google Scholar]
- 16.Zhang W M, Chernyak V, Mukamel S. In: Ultrafast XI. Elsaesser T, Wiersma D, Zinth W, Fujimoto J G, editors. Berlin: Springer; 1999. pp. 663–665. [Google Scholar]