Abstract
This paper presents an algorithm to resolve superimposed action potentials encountered during the decomposition of electromyographic signals. The algorithm uses particle swarm optimization with a variety of features including randomization, cross-over, and multiple swarms. In a simulation study involving realistic superpositions of 2-5 motor-unit action potentials, the algorithm had an accuracy of 98%.
Keywords: Alignment, decomposition, electromyography, particle swarm optimization, superposition
I. INTRODUCTION
The electromyographic (EMG) signal is made up of discharges called motor-unit action potentials (MUAPs). Whenever two or more MUAPs occur within a sufficiently short time interval, their waveforms overlap and superimpose. The problem of identifying the MUAPs involved in a superimposition and finding their precise timing is known as resolving the superimposition [1], [2], [3], [4], [5], [6]. This problem can be formulated as an optimization problem, namely, that of finding the set of MUAPs templates and alignment that gives the best match to the superimposition. Finding the solution is challenging because of the large number of possible combinations and alignments and because there are often many local extrema of the objective function.
A simple approach for resolving superimpositions is the peel-off method, in which the MUAPs are successively aligned and subtracted from the superimposition [7]. Unfortunately, the peel-off method often fails to find the optimal solution, especially when the superimposition involves destructive interference. McGill [8] presented an algorithm that finds the optimal solution by discretizing the search space, using a branch-and-bound approach to efficiently find the global discrete-time optimum solution, and then using interpolation to find the nearest continuous-time optimum. Florestal et al. [9] presented a probabilistic method that uses a genetic algorithm to explore the search space. In this paper we present a different probabilistic approach based on particle swarm optimization (PSO). Part of this work has been presented in abstract form [10] .
II. THE ALGORITHM
A. The Resolution Problem
The resolution problem can be stated as follows. Given a continuous-time waveform w(t) and n continuous template Si(t), i = 1,…, n, find the offsets X = (x1, …, xn) to minimize the squared error of the residual between the given and reconstructed waveforms:
| (1) |
Note that the xi can take on non-integer values. This function can be approximated using trigonometric polynomials as follows [7]:
| (2) |
where is the discrete Fourier transform of the sampled signal , is the discrete Fourier transform of the ith sampled template , and all signals are assumed to be sufficiently zero-padded to avoid wrap-around difficulties associated with circular time shifts. This is called the “known constituent” problem since it is assumed that all n templates are involved in the superimposition. In the “unknown constituent” problem, it is assumed that some subset of the n templates are involved, and the objective is to determine the subset as well as the offsets.
B. Particle Swarm Optimization
PSO is a population-based stochastic optimization algorithm, originally proposed to simulate the social behavior of a flock of birds [11]. PSO is easy to implement and has been successfully applied to a wide range of optimization problems [12]. In this method, each “particle” is a candidate solution that “flies” through the search space. The path of each particle is influenced by its own experience and that of its neighbors. In this paper, the neighborhood of each particle is the entire swarm (star topology) [13].
Each particle i is characterized by these features:
xi : its current position
vi : its current velocity
yi : the personal best position it has found ŷi : the best position discovered by any of the particles so far At each iteration, these features are updated as follows:
| (3) |
| (4) |
| (5) |
| (6) |
where f(X)is the objective function, k is the iteration number, np is the number of particles in the swarm, and ● denotes element-by-element multiplication. The new velocity depends on the previous velocity and on the distances of the particle from the personal and neighborhood best positions [11], with the coefficient ω being the inertia weight, c1 the cognitive acceleration coefficient, c2 the social acceleration coefficient, and r1 and r2 random vectors whose elements are uniformly distributed in U(0,1) . A large value of inertia weight favors global search (“exploration”), while a small value favors local search (“exploitation”). A suitable strategy is to set the value high initially to encourage exploration, and then reduce it towards a low value to fine tune the final solution. To prevent oscillations the velocity components are limited to[-vmax ,vmax] , where vmax is set appropriately [11].
Several extensions and modifications to the standard method have been proposed to speed convergence and discourage premature convergence to a non-global minimum [12], [13], [14]. These include using more than one swarm, running the algorithm multiple times, modifying the velocity update equation to guarantee convergence, and occasionally changing some particle locations either randomly or according to the genetic algorithm.
C. The Known-Constituent Case
The known-constituent problem can be solved by the PSO algorithm by letting the ith element of the particle vector x correspond to the offset of the ith MU, as in (2). Our implementation starts with two swarms of particles each, where n is the number of templates involved in the superposition. We have found that this number gives a good balance between accuracy and computation time. One swarm is initialized randomly in the interval [-N /2,N /2], where N is the template length. Sixty percent of the particles are filled with uniform random values, while the remaining 40% are filled with Sobol's quasirandom sequence [15], which covers the search space regularly. The other swarm is initialized similarly, except that one particle is set to the result of the peel-off method. The maximum number of iterations is max_iter = 500 × n + 200. The acceleration coefficients c1 and c2 are set to 2.0 and 0.5, respectively. The inertia coefficient is set to 1.2 at the first iteration and is linearly decreased to 0.1 at max_iter. Velocities are clamped to Vmax = 4. Positions are not clamped since the time shifts in (2) wrap around.
Randomization, cross-over, and swarm regeneration are used to ensure wide exploration. Every 40 iterations, the positions of 40% of the particles are re-initialized using the next generation of Sobol's sequence. Moreover, every iteration there is a 20% chance that two offspring particles are generated using the arithmetic mean of two randomly chosen (from the non-Sobolian partition) parent particles [16]. If a swarm's best solution does not change for 200 iterations, then a new, randomly initialized swarm is created. If the radius of a swarm becomes less than 1e-5 times the peak-to-peak amplitude of the smallest MUAP, the swarm is deleted. The total number of swarms is limited to n +1. Iteration continues until any of the swarms reaches the maximum number of iterations, or all of them have been deleted, or the overall global best does not change for 1500 iterations.
The PSO algorithm is run twice, and the best solution is selected. Increasing the number of runs increases the chances of finding the global minimum, but at the cost of increased computation time.
We implemented this method both in Matlab and in Microsoft Visual C++. In the C++ version, each swarm was implemented as a separate thread, and a vectorization package [17] was used for vector and matrix operations.
D.The Unknown-Constituent Case
For the unknown constituent problem it is necessary to identify which MUs are involved in the superposition, as well as their offsets. Our approach was to use the continuous-time algorithm described above for the known-constituent problem with the following differences:
(1) The particle vector is augmented with n additional variables to represent the involvement or non-involvement of the n MUs. These continuous variables are mapped to the binary involvement status in the following way: if 1/2 < mod2 xn+i < 3/2 , the ith MU is involved, otherwise it is not involved.
(2) At the start of the algorithm, the peel-off solution is determined for each possible combination of templates, and thenp best solutions are used as starting points for the first swarm on the first run.
III. SIMULATIONS
S imulations were performed to evaluate the performance of the algorithms. Superpositions of 2-5 MUAPs were simulated from two sets of MUAPs. The templates were derived from needle signals from the public domain database at www.emglab.net. Set 1 contained 10 MUAPs with a wide range of energies (differing by a factor of 25), while set 2 contained 6 MUAPs with a high degree of similarity (correlation coefficients ranging from 0.60 to 0.94). The MUAPs were sampled at 10 kHz and high-pass filtered at 1 kHz to emphasize their spikes.
For each simulation, a set of 5 MUAPs was selected at random from the larger data set. The first 2-5 of these MUAPs were shifted randomly by an amount within ±1 ms and then added together with random noise to form a superposition. This range of shifts produced complicated superpositions since the MUAPs overlapped constructively or destructively over most of their lengths. The noise process was white Gaussian noise with a standard deviation equal to 0.05 times the mean peak-to-peak template amplitude. The superposition was resolved using the known-constituent algorithm (given the involved MUAPs) and the unknown-constituent algorithm (given all 5 MUAPs). The accuracy of the resolution was calculated by nc /(nt + n f) , where nc is the number of MUAPs whose identities and offsets were correctly determined to within ±0.1 ms, nt is the total number of MUAPs involved in the superimposition, and nf is the number of MUAPs that were incorrect or off by more than ± 0.5 ms. For each condition, the accuracy was averaged over 1000 simulations. The simulations were performed on an Intel dual-core 1.83 GHz CPU with 2 GB of RAM.
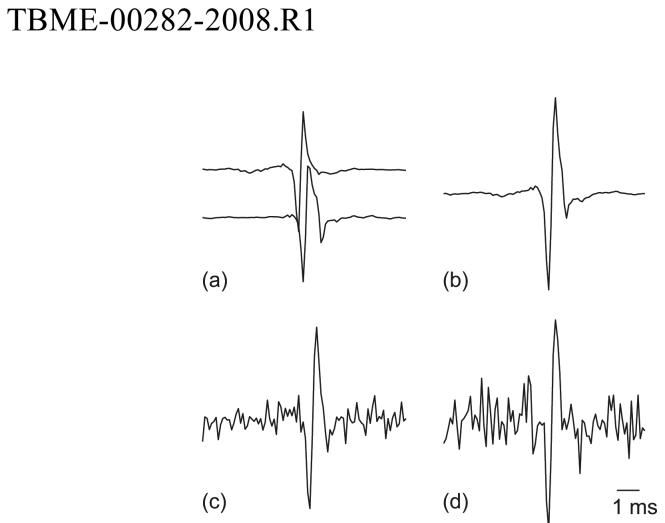
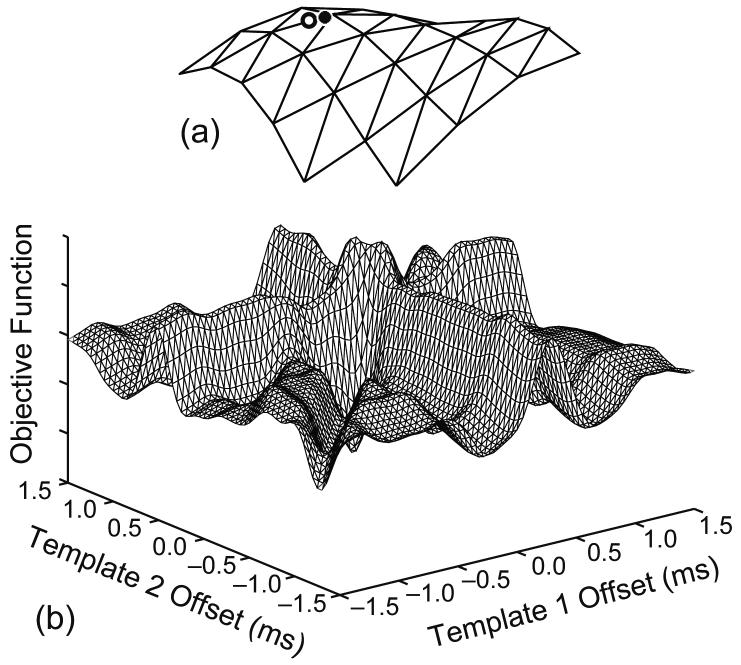
An example simulation is shown in Fig. 1. Two templates from data set 2 were shifted and added with noise to produce the superimposition shown in Fig. 1d. This is a constructive superposition for which the peel-off method was unable to estimate either shift correctly. The central part of the objective function is plotted as a function of template shifts in Fig. 2a. For clarity, it is plotted upside down, so that the peaks correspond to good alignments. The known-constituent PSO algorithm successfully located the global minimum of the objective function (Circle). The true alignment is indicated by (Star). Because of the added noise, the two points do not coincide exactly.
Fig. 1.
Two MUAP templates (a), the resulting constructive superposition (b), and the noisy waveform used in the analysis: SNR = 25 db (c) and SNR = 15 db (d). The vertical scale is the same in all plots.
Fig. 2.
Objective function for the superposition in Fig. 1. For clarity, it is plotted upside down, so that the peaks correspond to good alignments. (a) The central peak. The known-constituent PSO algorithm successfully located the global minimum (circle), which was very close to the true alignment (star). (b) A wider region. In both plots the grid interval is 0.1 ms.
The simulation results are shown in Table I. According to the results, PSO is very accurate. For comparison, the accuracy of the peel-off method is also shown. The superimpositions that were not correctly solved by the peel-off method were hard cases involving constructive or destructive interference, but PSO was able to solve most of them correctly. The PSO algorithm was less accurate for the unknown-constituent case because the search space was much wider and the algorithm sometimes found combinations of templates that fit better than the correct combination. The number of function evaluations grew polynomially as a function of n for both the known and unknown constituent algorithms. The C++ version was much faster than the Matlab version.
TABLE I.
Simulation Results
| n = | Data Set 1 | Data Set 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 | ||
| PO = peel-off method, Acc = accuracy, n = number of involved MUAPs, Evals = number of evaluations of the objective function (x106), Time1: mean execution time per superposition for Matlab implementation (in sec), Time2: mean execution time per superposition for C++ implementation (in sec). Note that no interpolation was used for peel-off methods. | |||||||||
| Known Constituents | |||||||||
| PO |
Acc |
98 |
93 |
83 |
71 |
97 |
85 |
70 |
59 |
| PSO | Acc | 100 | 100 | 100 | 99 | 100 | 100 | 100 | 99 |
| Evals | 0.30 | 0.39 | 0.47 | 0.58 | 0.30 | 0.40 | 0.48 | 0.60 | |
| Time1 | 18 | 36 | 51 | 75 | 19 | 36 | 53 | 80 | |
| Time2 |
1 |
2 |
8 |
- |
1 |
2 |
8 |
- |
|
| Unknown Constituents | |||||||||
| PO |
Acc |
59 |
70 |
66 |
54 |
51 |
58 |
57 |
48 |
| PSO | Acc | 100 | 100 | 99 | 97 | 100 | 99 | 95 | 90 |
| Evals | 0.55 | 0.64 | 0.69 | 0.78 | 0.54 | 0.62 | 0.74 | 0.86 | |
| Time1 | 84 | 94 | 101 | 116 | 88 | 93 | 110 | 133 | |
A sensitivity analysis was performed for the number of particles in each swarm (np), the maximum iteration allowed for each swarm (max_iter), the threshold for swarm re-generation and termination, and the SNR (Table II). The analysis used superpositions of 5 known MUAPs from set 2. Similar results were obtained for set 1. The analysis shows that increasing np, the swarm threshold, and the SNR all increase algorithm accuracy. Increasing np decreases the efficiency. Increasing max_iter, because it affects the inertia, causes the algorithm to terminate without sufficient tuning. On the other hand, decreasing max_iter does not allow sufficient exploration. Both decrease accuracy. The standard values used for the simulations represent a reasonable trade-off between accuracy and efficiency.
TABLE II.
Simulation Results
| The known-constituent case with 5 MUAPs from data set 2 was used. np = number of particles in each swarm; max_iter = maximum number of iterations; thresh. = threshold for swarm re-generation and termination. The standard parameter values used in Table I are shown in parentheses. | |||||||
| np (27) | max_iter (2700) | ||||||
| Parameter | 10 | 40 | 80 | 1e3 | 4e3 | 5e3 | 1e4 |
| ID (%) | 91 | 99 | 100 | 94 | 96 | 93 | 83 |
| Evals | 0.3 | 1.07 | 2.05 | 0.34 | 0.74 | 0.75 | 0.72 |
| thresh. (1e-5) | SNR (dB)(35) | ||||||
| Parameter | 1e-6 | 1e-4 | 20 | 25 | 30 | 40 | 45 |
| ID (%) | 99 | 100 | 57 | 92 | 98 | 99 | 100 |
| Evals | 0.68 | 0.70 | 0.68 | 0.69 | 0.69 | 0.67 | 0.68 |
IV. DISCUSSION
The PSO algorithm is quite versatile and can be used to solve problems with continuous, discrete, or a mixture of continuous and discrete variables. Some of the interesting features of PSO include the ease of implementation and the fact that no gradient information is required [12]. In many optimization problems, gradient information is either unavailable or computationally expensive to calculate. Although a relatively new paradigm, PSO has been applied to a variety of tasks, e.g., training artificial neural networks [21], function minimization [22], and EEG dipole source localization [23].
The main challenge in resolving superimpositions is the complicated topology of the objective function, as shown in Fig. 2b. The number of distinct local minima increases exponentially with the number of MUs involved in the superposition. Also, some of the local minima can be fairly narrow. These factors make it challenging for an optimization method to adequately explore the search space while avoiding getting stuck in local minima.
The organization of the presented algorithm represents a trade-off between exploring the entire search space and fine-tuning the solutions in the regions of the promise. Several techniques including the swarm randomization strategy with quasi-random Sobol's sequence, arithmetic cross-over, and the multi-swarm strategy with re-generation and randomization were used to ensure wide exploration. The termination criteria were chosen to ensure adequate accuracy within a reasonable number of iterations.
The algorithm is most efficient for waveforms sampled at the Nyquist rate, since this minimizes the number of computations involved in each function call. The presented parameter values related to particle velocities and the termination criteria assume Nyquist-rate sampling, and would have to be scaled appropriately to use the algorithm efficiently with oversampled signals.
The complexity of the resolution problem can be understood by considering an exhaustive search over a discrete grid. Such a search is guaranteed to find the global discrete-time optimum solution. For the known constituent problem, an exhaustive search would require (αN)n function evaluations, where α is the interpolation factor. Since this number increases exponentially with n, this is called a “hard” problem in complexity theory. Resolution by exhaustive search is impractical for n above 2 or 3.
The PSO method attempts to explore the search space more efficiently. The algorithm presented here requires at most function evaluations. Since this number grows only polynomially with n, this approach is more suitable for practical use. The independent nature of the multiple swarms also lends itself to an efficient multi-threaded implementation, with minimum critical sections.
Although the PSO algorithm is not guaranteed to find the globally best solution, in our simulation study it was able to find an accurate solution in 98.2% of the records analyzed. Performance on real superimpositions could be lower that this due to MUAP variability and interference from small background MUAPs, which were not modeled in the current simulations. In real EMG signals, firing time information can also be used to help determine which MUAPs are involved in particular superpositions [1], [4], [5]. It should also be pointed out that the residual squared error is not the only possible criterion for determining a match. Florestal et al. [8] accept matches over only portions of the signals, and adjust the acceptance criterion for each MUAP depending on its size.
ACKNOWLEDGMENT
We are grateful to Roberto Merletti for reviewing a draft of this paper.
This work was supported by the Rehabilitation R&D Service of the US Department of Veterans Affairs and the US National Institute of Neurological Disorders and Stroke under grant 5-R01-NS051507.
Footnotes
Personal use of this material is permitted. However, permission to use this material for any other purposes must be obtained from the IEEE by sending an email to pubs-permissions@ieee.org.
REFERENCES
- [1].Lefever RS, De Luca CJ. “A procedure for decomposing the myoelectric signal into its constituent action potentials. Part I: Technique, theory, and implementation,”. IEEE Trans. Biomed. Eng. 1982;BME-29:149–157. doi: 10.1109/tbme.1982.324881. [DOI] [PubMed] [Google Scholar]
- [2].De Figueiredo RJP, Gerber A. “Separation of superimposed signals by a cross-correlation method,”. IEEE Trans. Acoustics, Speech, and Signal Processing. 1983;31:1084–1089. [Google Scholar]
- [3].Bonato P, Erim Z, Gonzalez-Cueto JA. “Decomposition of superimposed waveforms using the cross time frequency transform,”; Proc. 23rd Ann. Intl. Conf. IEEE Eng. Med. Biol. Soc; 2001.pp. 1066–1069. [Google Scholar]
- [4].Etawil H, Stashuk D. “Resolving superimposed motor unit action potentials,”. Med. Biol. Eng. Comput. 1996;34:33–40. doi: 10.1007/BF02637020. [DOI] [PubMed] [Google Scholar]
- [5].Nawab SH, Wotiz R, De Luca CJ. “Improved resolution of pulse superpositions in a knowledge-based system EMG decomposition,”; Proc. 26th Ann. Intl. Conf. IEEE Eng. Med. Biol. Soc; 2004; pp. 69–71. [DOI] [PubMed] [Google Scholar]
- [6].Hass WF, Meyer M. “An automatic EMG decomposition system for routine clinical examinations and clinical research,”. In: Desmedt JE, editor. Computer-Aided Electromyography and Expert Systems. Elsevier; Amsterdam: 1989. pp. 67–81. [Google Scholar]
- [7].Stashuk D. “EMG Signal Decomposition : How can it be accomplished and used?”. J. Electromyogr. Kinesiol. 2001;11:151–173. doi: 10.1016/s1050-6411(00)00050-x. [DOI] [PubMed] [Google Scholar]
- [8].McGill KC. “Optimal resolution of superimposed action potentials,”. IEEE Trans. Biomed. Eng. 2002;49:640–650. doi: 10.1109/TBME.2002.1010847. [DOI] [PubMed] [Google Scholar]
- [9].Florestal JR, Mathieu PA, Plamondon R. “A genetic algorithm for the resolution of superimposed motor unit action potentials,”. IEEE Trans. Biomed. Eng. 2007;54:2163–2171. doi: 10.1109/tbme.2007.894977. [DOI] [PubMed] [Google Scholar]
- [10].Marateb HR, McGill KC. Proc. 17th Congr. Int. Soc. Electrophysiology and Kinesiology. Niagara Falls; Canada: 2008. “Resolving superimposed MUAPs by particle swarm optimization,”. [Google Scholar]
- [11].Kennedy J, Eberhart RC, Shi Y. Swarm Intelligence. Morgan Kaufman Publishers; 2001. [Google Scholar]
- [12].Omran MGH. “Particle swarm optimization methods for pattern recognition and image processing,”. University of Pretoria; 2004. PhD thesis. [Google Scholar]
- [13].Van den Bergh F, Engelbrecht AP. “A study of particle swarm optimization particle trajectories,”. Information Sciences. 2006;176:937–971. [Google Scholar]
- [14].Van Den Bergh F. “An analysis of particle swarm optimizers,”. University of Pretoria; 2001. PhD thesis. [Google Scholar]
- [15].Settles M, Soule T. “Breeding swarms: a GA/PSO hybrid,”; Proc. 2005 Conf. Genetic and Evolutionary Computation; 2005. [Google Scholar]
- [16].Parsopoulos KE, Vrahatis MN. “Modification of the particle swarm optimizer for locating all the global minima,”. In: Kurkova V, Steele N, Neruda R, Karny M, editors. Artificial Neural Networks and Genetic Algorithms. Springer; 2001. pp. 324–327. [Google Scholar]
- [17].Fox B. “Algorithm 647: Implementation and relative efficiency of quasi-random sequence generators,”. ACM Trans. Math. Software. 1986;12:362–376. [Google Scholar]
- [18].Krink T, Lovbjerg M. Lecture Notes in Computer Science: Proceedings of Parallel Problem Solving from Nature VII. vol. 2439. Springer; 2002. “The LifeCycle model: Combining particle swarm optimization , genetic algorithms and hill climbers,”; pp. 621–630. [Google Scholar]
- [19].Sander M. “OptiVec vectorized programming package”. http://www.optivec.com.
- [20].Salerno J. “Using the particle swarm optimization technique to train a recurrent neural model”; Proc. 9th IEEE Intl. Conf. Tools with Artificial Intelligence; 1997.pp. 45–49. [Google Scholar]
- [21].Shi Y, Eberhart RC. “A modified particle swarm optimizer,”. IEEE Intl. Conf. Evolutionary Computation. 1998 [Google Scholar]
- [22].Qiu L, Li Y, Yao D. “A feasibility study of EEG dipole source localization using particle swarm optimization,”. IEEE Congr. Evolutionary Computation. 2005;1:720–726. [Google Scholar]