Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2009 Mar 5;37(7):2405–2410. doi: 10.1093/nar/gkp016

A nonlinear dynamic model of DNA with a sequence-dependent stacking term

Boian S Alexandrov 1, Vladimir Gelev 2, Yevgeniya Monisova 2, Ludmil B Alexandrov 2, Alan R Bishop 1, Kim Ø Rasmussen 1,*, Anny Usheva 2,*
PMCID: PMC2673413  PMID: 19264801

Abstract

No simple model exists that accurately describes the melting behavior and breathing dynamics of double-stranded DNA as a function of nucleotide sequence. This is especially true for homogenous and periodic DNA sequences, which exhibit large deviations in melting temperature from predictions made by additive thermodynamic contributions. Currently, no method exists for analysis of the DNA breathing dynamics of repeats and of highly G/C- or A/T-rich regions, even though such sequences are widespread in vertebrate genomes. Here, we extend the nonlinear Peyrard–Bishop–Dauxois (PBD) model of DNA to include a sequence-dependent stacking term, resulting in a model that can accurately describe the melting behavior of homogenous and periodic sequences. We collect melting data for several DNA oligos, and apply Monte Carlo simulations to establish force constants for the 10 dinucleotide steps (CG, CA, GC, AT, AG, AA, AC, TA, GG, TC). The experiments and numerical simulations confirm that the GG/CC dinucleotide stacking is remarkably unstable, compared with the stacking in GC/CG and CG/GC dinucleotide steps. The extended PBD model will facilitate thermodynamic and dynamic simulations of important genomic regions such as CpG islands and disease-related repeats.

INTRODUCTION

The stability of the DNA double helical structure is determined by the interplay of a host of interactions, including hydrogen bonding, aromatic base stacking, backbone conformational constraints and electrostatic interactions, and the coordination of water molecules and metal ions. These interactions depend on DNA structure in a strongly nonlinear fashion. Not surprisingly, no simple model exists that accurately describes the melting behavior of double stranded (ds) DNA as a function of nucleotide sequence. A relatively successful strain of models for dsDNA denaturation originated from McClare's (1) ideas about the importance of nonlinear dynamics of vibrational excited states in macromolecules, followed by Davydov's prediction that vibrational excitations can be localized and trapped in a long lived state now known as the Davydov soliton (2). Inspired by these ideas Englander et al. (3) proposed that nonlinearity-induced localization of vibrational energy in dsDNA may lead to local DNA melting (DNA bubbles). This work in turn lead to, the Peyrard–Bishop–Dauxois (PBD) model of DNA (4,5), which uses a simple sequence-dependent nonlinear Hamiltonian to represent the separation of the dsDNA strands during a melting transition. The PBD model is unique among DNA models in that it combines elements from efficient ad hoc models of DNA melting and physically meaningful fully atomistic molecular dynamic simulations. Calculations based on the PBD model have successfully reproduced DNA melting and unzipping data for a variety of DNA sequences (6–12) but the model has also been used to calculate the probability for transient melting of the adenovirus genome (13) and to simulate the breathing dynamics of 100 bp long eukaryotic promoter regions (B. S. Alexandrov et al., submitted for publication). The sequence-dependence of the PBD Hamiltonian is encoded by an anharmonic term, which represents the H-bonding of a G–C or an A–T base pair. A nonlinear term representing the stacking energy of the consecutive base pairs mimics long-range effects along the DNA helix, but uses a sequence-independent average stacking force constant. The sequence-independence of the stacking term reflects the observation that the ratio of G–C to A–T hydrogen bonded base pairs is the strongest predictor of dsDNA stability. However, it is well known that relatively subtle differences in the stacking energies of the 10 dinucleotides steps can amount to very significant deviations in the melting temperature expected from a given G/C content (14–17). The best known examples of this phenomenon are the large differences in the melting temperatures of poly(dA).(dT) versus poly(dAdT), and poly(dG).(dC) versus poly(dGdC) (18).

Existing thermodynamic models of DNA melting that incorporate a nearest neighbor (NN) stacking energy term (16,19,20) perform significantly better than simple regression fit empirical formulas for DNA melting temperature. However, homogenous and periodic DNA sequences exhibit cumulative deviations from the ideal B-helix dsDNA structure, which result in further deviations in melting behavior that are difficult to account for by additive thermodynamic contibutions. Dynamic models of DNA, which represent long-range effects offer an advantage in this respect. In addition, such models offer certain mechanistic insight into the initial dynamically governed stages of DNA melting (DNA breathing), that have been implicated as relevant to protein binding and transcription initiation (B. S. Alexandrov et al., submitted for publication; 7,13,21,22). The large deviations in the melting behavior of repeats and homopolymers was first reported in 1970 (18) and has since been discussed at length in the literature due to the abundance of such sequences in vertebrate genomes (23). However, potentially baring computationally intensive fully atomistic simulations, no method exists for analysis of the DNA breathing dynamics of repeats and highly G/C- or A/T-rich regions. Here we extend the original PBD model to include a sequence-dependent stacking term, in order to study such sequences. We collect melting data for several homogenous and periodic DNA oligos, and apply Monte Carlo (MC) simulations to derive 10 (24) distinct stacking force constants for the PBD Hamiltonian. The resulting PBD model has the potential to be applied at the genomic scale to conduct thermodynamic and dynamic simulations of important genomic regions such as CpG islands and disease related repeats.

MATERIALS AND METHODS

DNA oligonucleotides

The sequences of the 36 bp oligonucleotides used in the melting studies are listed in Table 1. The sequence of the L60B36 used in the MC simulations is 5′-CCGCCAGCGGCGTTATTACATTTAATTCTTAAGTATTATAAGTAATATGGCCGCTGCGCC-3′. The sequence of the P5 promoter used in the Langevin simulations is 5′-ACGCTGGGTATTTAAGCCCGAGTGAGCACGCAGGGTC TCCATTTTGAAGCGGGAGGTTTGAACGCGCAGCC-3′. The underlined AT residues at the transcriptional start site are replaced with GC in the transcriptionally silent P5 mutant promoter (7).

Table 1.

Experimentally determined melting temperatures of dsDNA oligos that are used in the simulations

dsDNA Melting Temperature, Tm (°C) Stacking constant
(G)36.(C)36 74 kGG
(GC)18.(GC)18 96 kGC, kCG
(AC)18.(GT)18 67 kAC, kCA
(AG)18.(CT)18 59 kAG, kGA
(A)36.(T)36 45 kAA
(AGC)12.(GCT)12 75 kAG, kGC, kCA
poly(AT).poly(AT)a 38a kAT, kTA
Open in a new tab

aTm taken from Ref. (18).

DNA melting curves

All DNA oligos were synthesized and gel- and HPLC-purified at the Keck DNA Synthesis Facility at Yale University. The DNA was dissolved to 200 mM in 30 mM Na phosphate buffer pH 7.5, 100 mM NaCl, 1 mM EDTA. The complementary oligos were annealed by heating to 100°C and stepwise cooling to room temperature in a PCR cycler. The dsDNA oligos were HPLC purifed on a DEAE-Superose column with a LiCl gradient. The absence of hairpin and G-quartet structures in the dsDNA oligos was verified by native 10% PAGE performed at various temperatures. dsDNA melting curves were collected for 20°C–105°C at 250–280 nm on a Varian Cary 50 Bio UV/Vis spectrometer equipped with a Peltier probe. The temperature was varied by 0.5°C/min. The melting curves were obtained for the maximum absorbance wavelength for each oligo and normalized following the procedure of Breslauer (25). Data were collected from five independent experiments.

PBD simulations

The MC protocol used in this work is similar to what has previously been used (9) to interrogate the melting behavior of the PBD model. Steps were performed using a cutoff value of 10 Å and a strand separation threshold of yn ≥ 1 Å, above which the DNA was considered melted. At least 1000 simulations with different initial conditions were conducted. MC simulations (9,12) of the L60B36 sequence and Langevin dynamic simulations (27) of the P5 promoter were conducted as previously described, using the determined here new sequence-dependent stacking term.

RESULTS AND DISCUSSION

The PBD model

The potential energy of the PBD model is

graphic file with name gkp016m1.jpg 1

where the sum extends over all N base pairs of the DNA molecule and yn denotes the relative displacement from equilibrium of the n-th base-pair. The first term in Equation (1) is the Morse potential, which represents the hydrogen bonding of a Watson–Crick complementary base pair. The parameters Dn and an in this term denote the nature of the n-th base pair, i.e. A–T or G–C. The second term is an anharmonic potential representing the aromatic stacking interaction between the n- and (n-1)-th consecutive base pairs, augmented by a coupling constant that depends on the relative displacement of these two bases in a nonlinear fashion. This term is essential for simulating the local constraints of nucleotide motion, which result in long-range cooperative effects (5). The values of the relevant model parameters were initially chosen to reproduce the melting transitions of long homogeneous sequences. Subsequently, the values β = 0.35 Å−1, DAT = 0.05 eV, DGC = 0.05 eV, aAT = 4.2 Å−1 and aGC = 6.9 Å−1, ρ = 2 and k = 0.025 eV/Å2 were optimized by fitting UV melting curves of three short heterogeneous DNA sequences (6). The stacking constant k is sequence-independent and represents an average value of the stacking energy of the different dinucleotides. Here we used DNA melting measurements and published data (18) to derive 10 k-parameter values, corresponding to the 10 dsDNA dinucleotide steps.

DNA melting studies

A pioneering experimental study of homogeneous and periodic DNA oligomers (18), which reported large differences in the melting temperatures of poly(dAdT) versus poly(dA).poly(dT) and poly(dGdC) versus poly(dG).poly(dC) formed the basic inspiration for the present work. To obtain precise measurements suited to our needs, we performed UV absorbance melting measurements of six synthetic DNA oligonucleotides designed to contain simple repeating combinations of different dinucleotide steps (Table 1). The absence of hairpin, G-quartet or other secondary structures in the DNA samples was verified by native polyacrylamide electrophoresis (PAGE) on the samples at various concentration and temperatures. A poly(dAdT) oligo consistently formed hairpin structures even when annealed at high concentrations and at different salt concentrations, and was discarded from the study. For the simulations, we used the poly(dAdT) melting data presented by Wells et al. (18). As expected, the poly(dG) DNA displayed unusual bands in the presence of K+ ions, but was of homogenous composition with the same gel mobility as control dsDNA in the sodium phosphate/EDTA buffer used for the melting studies (data not shown). None of the remaining oligos used for the melting simulations (Table 1) displayed any non-dsDNA structures as judged by the PAGE assay (data not shown). The melting temperatures obtained from UV absorbance measurements are shown in Table 1. Our data are consistent with those reported by others (18) in terms of the order of melting temperatures, with quantitative differences due to the different experimental conditions, including buffer composition and the defined length of the oligos.

Melting temperature simulations

To establish a protocol for simulating the experimental DNA melting data (see Materials and Methods section), we used a recently developed MC method (9,12) with the original PBD average stacking constant, and reproduced the melting temperature of a known heterogeneous DNA sequence (6). Previously, we showed that the melting temperature of a given DNA sequence predicted by PBD MC simulations varies almost linearly with the value of a chosen average stacking constant, while the shape of the melting curve does not significantly depend on this constant (12). These results were used to obtain the stacking constants kGG and kAA for the poly(dG).poly(dC) and poly(dA).poly(dT) oligos. Next, we obtained the average stacking constants for the poly(dAdT), poly(dAdC).poly(dGdT), poly(dAdG).poly(dCdT) and poly(dGdC) oligos by fitting to the experimentally obtained melting temperatures. To extract the individual stacking constants from these average values we relied on the following observation: it can be easily shown for widely separated DNA strands that in the harmonic stacking limit the partition function for any given sequence can be expressed exactly in terms of an average stacking constant

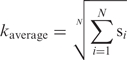graphic file with name gkp016um1.jpg

where ki are the individual stacking constants of the dinucleotides present in the sequence. This relationship yields one equation connecting each pair of stacking constants participating in the oligos poly(dAdT), poly(dAdC).poly(dGdT), poly(dAdG).poly(dCdT) and poly(dGdC).

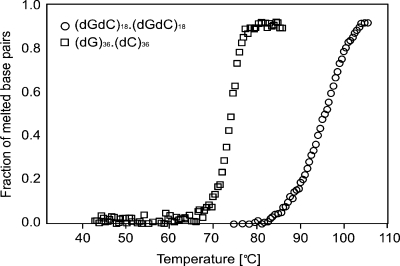
A second equation is derived from of the ratios kGA/kAG, kCA/kAC, kAT/kTA, whose values were obtained from the literature. The proper choice of base stacking constants for a given DNA model is hampered by the complexity of the stacking interaction, and the difficulty of separating the individual contributions to dsDNA stability (28). It should be noted that the choice of constants also depends on the model, as evidenced by a number of seemingly conflicting sets of base stacking energies reported in the literature (28). Given the identical hydrogen bonding patterns, reproducing the large difference in the melting temperatures of the polyGG and polyGC oligos, shown in Figure 1, requires a very weak GG/CC stacking term. As thoroughly described previously (28), there is ample evidence that a GG/CC stack dinucleotide is indeed remarkably unstable compared with GC/CG. To be consistent with this observation, we obtained the necessary stacking force constant ratios from a well-established set of intrinsic stacking energies calculated by Sponer et al. (29) from force-field calculations with the empirical AMBER force field (30).

Figure 1.

Figure 1.

Open in a new tab

Normalized UV absorption melting curves for the (dG)36.(dC)36 (squares) and (dGdC)18.(dGdC)18 (circles) oligos.

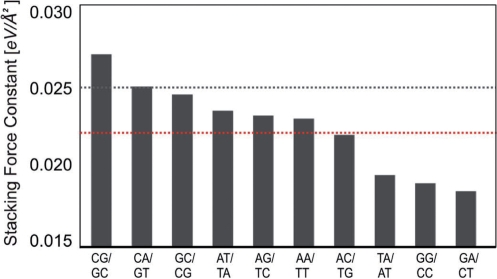
The initial values for the individual PBD stacking constants were calculated using the above two independent relations. These values were further adjusted to fit the experimental melting data using the previously established MC protocol (Materials and Methods section). The final 10 stacking constants are shown in Figure 2.

Figure 2.

Figure 2.

Open in a new tab

Values of the obtained PBD base stacking force constants in eV/Å2. The identity of the 10 dinucleotide steps is shown below the bars. The stacking force constants are shown as vertical bars. The dashed lines indicate the stacking constant of the average stacking PBD model (black) and the average of the 10 stacking constants of the sequence-dependent PBD model (red).

The uniform stacking PBD was conceived largely as a qualitative model aimed at reproducing the basic characteristics of DNA melting transitions. Here, we introduce a more quanitative model that is capable of predicting melting temperatures for the given, physiologically relevant buffer conditions. The sequence-dependent PBD model has an average stacking constant that is 10% lower (Figure 2) than in the homogenous stacking PBD.

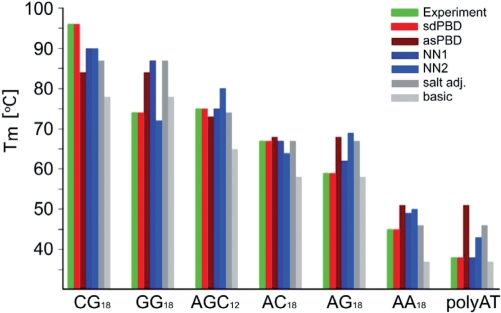
The sequence-dependent stacking force constants were tested on, and accurately reproduced the melting temperature of poly(dAdGdC).poly(dGdCdT) (Figure 3). A comparison of the experimentally determined DNA melting temperatures, and the predictions of various DNA models is shown Figure 3. As can be seen from the figure, the previous PBD model, like most other DNA models performs well for mixed sequences of intermediate G/C content. However, these models fail for sequences of 100% G/C or A/T content. The new sequence-dependent PBD was derived from the shown experimental data (Table 1, Figure 1) and strictly for the given experimental conditions (buffer, salt, DNA concentration). Nevertheless, the advantages of DNA sequence-dependent stacking PBD potential over the previous average stacking potential for thermodynamic and dynamic simulations of genomic sequences are obvious.

Figure 3.

Figure 3.

Open in a new tab

Experimentally determined and calculated melting temperatures of periodic and homogeneous dsDNA sequences. The calculated melting temperatures [Tm (°C), on the vertical axis] are identified as follows: experimentally determined, green bar; sequence-dependent PBD (sdPBD), red; average stacking PBD (asPBD), brown; NN thermodynamic model (NN1, http://www.promega.com/biomath/calc11.htm (16), dark blue; NN thermodynamic model (NN2, http://www.basic.northwestern.edu/biotools/oligocalc.html) (14,31), light blue; salt adjusted model calculated with a regression (http://www.promega.com/biomath/calc11.htm) (32), dark grey; basic regression model (http://www.promega.com/biomath/calc11.htm) (33), light grey. The identity of the sequences is shown bellow the bars.

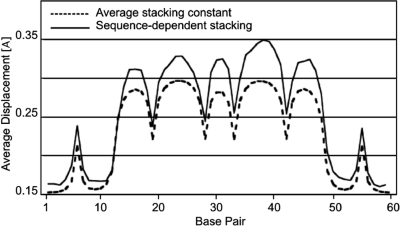
To further evaluate the performance of our extended PBD model, we repeated simulations previously reported by others. Zeng et al. (26) experimentally determined the length and statistical weight of local DNA denaturation bubbles at various temperatures. The PBD model was quite successful at reproducing the nucleation size of internal denaturation bubbles observed in these experiments (9), in contrast to thermodynamic models of DNA melting (26). We repeated the PBD MC simulations (9) with the new sequence-specific stacking constants and found that the two models perform equally well at reproducing the experimental data (data not shown). A more detailed comparison of the two PBD simulations (Figure 4) reveals that the predicted bubble locations are nearly identical. However, the bubble amplitudes predicted by the sequence-dependent model are more pronounced, to various degrees, than the amplitudes predicted by the homogenous stacking model. This effect is independent of the overall baseline shift due to the slightly lower average stacking potential in the new PBD. In this case, the main effect of the intricate cooperativity introduced by the sequence-dependent stacking is larger amplitudes in the bubble-forming region of the DNA sequence.

Figure 4.

Figure 4.

Open in a new tab

Average strand displacements for the sequence L60B36, calculated by MC PBD simulations with an average (dashed line) and a sequence-dependent (solid line) stacking term. Strand displacements are presented on the vertical axis in Å. The base pare position is shown on the horizontal where base pair 1 is the first base at the 5′ end of the sequence.

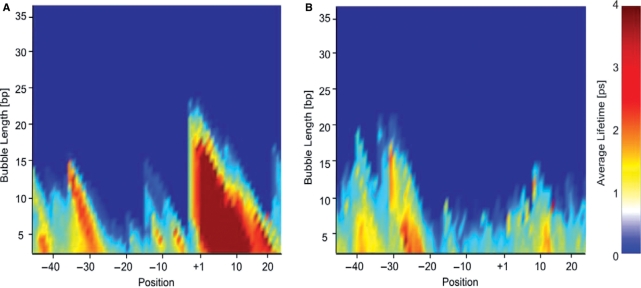
In addition to the bubble probabilities and amplitudes that can be calculated using PBD MC and thermodynamic methods, Langevin dynamics simulations yield the lifetimes of transient DNA bubbles (B. S. Alexandrov et al., submitted for publication; 27). Here, we repeated previous simulations of the DNA bubble dynamics of the P5 adenoassociated virus core promoter (100 bp) and a transcriptionally silent P5 mutant variant (27). In vitro transcription, single strand nuclease data and PBD thermodynamic calculations for this promoter (7,21) have shown strong correlation between transcriptional activity and the presence of a transient bubble at the transcriptional start site. PBD Langevin simulations suggested that bubbles occurring at the start site are more stable than equally likely but shorter lived bubbles forming at the TATA-box of this promoter (B. S. Alexandrov et al., submitted for publication; 27). A propensity of the P5 start site to open transiently was also suggested by in vitro transcription experiments, in which negative supercoiling of a circular DNA template was equivalent to introduction of a 5 bp mismatch at the start site of a linearized template (21). Figure 5 shows bubble lifetimes calculated from PBD Langevin dynamic trajectories of the P5 promoter with the sequence-dependent stacking potential. The simulations predict a stable bubble at the P5 start site, and a lack of dynamic activity at the same location in the transcriptionally silent mutant. The recalculated, with the new stacking, bubble life times, for the P5—wild-type and P5 mutant promoters, showed more delineated differences than previously reported (27).

Figure 5.

Figure 5.

Open in a new tab

Average bubble times (color scales) for (A) P5-wild type and (B) P5-mutant promoters. The bubble times are given in picoseconds on the color scale. The bubble length is shown on the vertical axis in units of base pairs. The positions of the base pairs are shown relative to the transcription start site (+1) on the horizontal axis.

CONCLUSION

We have obtained 10 base stacking force constants that systematically improve the performance of the PBD model for homogenous and periodic DNA sequences. The new stacking constants are all within 20% of the previously used average stacking constant, suggesting that previous PBD calculations on mixed DNA sequences are reasonable. The experiments and numerical simulations reported here show that the GG/CC dinucleotide stacking is remarkably unstable, compared with the GC/CG and CG/GC dinucleotide steps. Similar experimental results (18) and ab initio and force field calculations (28,29) have been reported, but have been frequently overlooked due to the strength of the G–C hydrogen bond, which dominates as a determinant of dsDNA stability. However, such differences in the base stacking interactions must contribute to the dynamic behavior of G/C-rich genomic sites, with likely relevance to genomic function.

The modified PBD model demonstrates significantly improved performance in predicting melting temperatures for all tested homogeneous and periodic DNA sequences, regardless of G/C content.

As we previously reported, PBD dynamic and thermodynamic calculations predict the existence of transient thermally induced bubbles at the transcriptional start sites of many eukaryotic promoters. Langevin dynamic simulations with the new PBD model on the A/T-rich viral P5 promoter strongly support these predictions.

FUNDING

National Institutes of Health (GM073911 to A.U.); National Nuclear Security Administration of the US Department of Energy at Los Alamos National Laboratory (Contract DE-AC52-06NA25396). Funding for open access charge: DE-AC52-06NA25396 and GM073911.

Conflict of interest statement. None declared.

REFERENCES

  • 1.McClare CW. A quantum mechanical muscle model. Nature. 1972;240:88–90. doi: 10.1038/240088a0. [DOI] [PubMed] [Google Scholar]
  • 2.Davydov AS. The theory of contraction of proteins under their excitation. J. Theor. Biol. 1973;38:559–569. doi: 10.1016/0022-5193(73)90256-7. [DOI] [PubMed] [Google Scholar]
  • 3.Englander SW, Kallenbach NR, Heeger AJ, Krumhansl JA, Litwin A. Nature of the open state in long polynucleotide double helices: possibility of soliton excitations. Proc. Natl Acad. Sci. USA. 1980;77:7222–7226. doi: 10.1073/pnas.77.12.7222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Peyrard M, Bishop AR. Statistical mechanics of a nonlinear model for DNA denaturation. Phys. Rev. Lett. 1989;62:2755–2758. doi: 10.1103/PhysRevLett.62.2755. [DOI] [PubMed] [Google Scholar]
  • 5.Dauxois T, Peyrard M, Bishop AR. Entropy-driven DNA denaturation. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1993;47:R44–R47. doi: 10.1103/physreve.47.r44. [DOI] [PubMed] [Google Scholar]
  • 6.Campa A, Giansanti A. Experimental tests of the Peyrard-Bishop model applied to the melting of very short DNA chains. Phys. Rev. E. 1998;58:3585. [Google Scholar]
  • 7.Choi CH, Kalosakas G, Rasmussen KO, Hiromura M, Bishop AR, Usheva A. DNA dynamically directs its own transcription initiation. Nucleic Acids Res. 2004;32:1584–1590. doi: 10.1093/nar/gkh335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Kalosakas G, Rasmussen K, Bishop AR, Choi CH, Usheva A. Sequence-specific thermal fluctuations identify start sites for DNA transcription. Eur. Phys. Lett. 2004;68:127. [Google Scholar]
  • 9.Ares S, Voulgarakis NK, Rasmussen KØ, Bishop AR. Bubble nucleation and cooperativity in DNA melting. Phys. Rev. Lett. 2005;94:035504. doi: 10.1103/PhysRevLett.94.035504. [DOI] [PubMed] [Google Scholar]
  • 10.Voulgarakis NK, Redondo A, Bishop AR, Rasmussen KØ. Probing the mechanical unzipping of DNA. Phys. Rev. Lett. 2006;96:248101. doi: 10.1103/PhysRevLett.96.248101. [DOI] [PubMed] [Google Scholar]
  • 11.Voulgarakis NK, Kalosakas G, Rasmussen K, Bishop AR. Temperature-dependent signatures of coherent vibrational openings in DNA. Nano Lett. 2004;4:629. [Google Scholar]
  • 12.Alexandrov BS, Voulgarakis N, Rasmussen KØ, Usheva A, Bishop AR. Pre-melting dynamics of DNA and its relation to specific functions. In Special issues: DNA melting. J. Phys. Condens. Matter. 2009 doi: 10.1088/0953-8984/21/3/034107. (in press). [DOI] [PubMed] [Google Scholar]
  • 13.Choi CH, Rapti Z, Gelev V, Hacker MR, Alexandrov B, Park EJ, Park JS, Horikoshi N, Smerzi A, Rasmussen KØ, et al. Profiling the thermodynamic softness of adenoviral promoters. Biophys. J. 2008;95:597–608. doi: 10.1529/biophysj.107.123471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Breslauer KJ, Frank V, Blöcker H, Marky LA. Predicting DNA duplex stability from the base sequence. Proc. Natl Acad. Sci. USA. 1986;83:3746–3750. doi: 10.1073/pnas.83.11.3746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.SantaLucia J, Allawi HT, Seneviratne PA. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry. 1996;35:3555–3562. doi: 10.1021/bi951907q. [DOI] [PubMed] [Google Scholar]
  • 16.SantaLucia J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Blake RD, Bizzaro JW, Blake JD, Day GR, Delcourt SG, Knowles J, Marx KA, SantaLucia J., Jr Statistical mechanical simulation of polymeric DNA melting with MELTSIM. Bioinformatics. 1999;15:370–375. doi: 10.1093/bioinformatics/15.5.370. [DOI] [PubMed] [Google Scholar]
  • 18.Wells RD, Larson JE, Grant RC, Shortle BE, Cantor CR. Physicochemical studies on polydeoxyribonucleotides containing defined repeating nucleotide sequences. J. Mol. Biol. 1970;54:465–497. doi: 10.1016/0022-2836(70)90121-x. [DOI] [PubMed] [Google Scholar]
  • 19.Poland D, Sheraga HA. Phase transitions in one-dimension and the helix-coil transition in polyamino acids. J. Chem. Physics. 1966;45:1456–1463. doi: 10.1063/1.1727785. [DOI] [PubMed] [Google Scholar]
  • 20.Yakovchuk P, Protozanova E, Frank-Kamenetskii MD. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006;34:564–574. doi: 10.1093/nar/gkj454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Usheva A, Shenk T. YY1 transcriptional initiator: protein interactions and association with a DNA site containing unpaired strands. Proc. Natl Acad. Sci. USA. 1996;93:13571–13576. doi: 10.1073/pnas.93.24.13571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Leblanc BP, Benham CJ, Clark DJ. An initiation element in the yeast CUP1 promoter is recognized by RNA polymerase II in the absence of TATA box-binding protein if the DNA is negatively supercoiled. Proc. Natl Acad. Sci. USA. 2000;97:10745–10750. doi: 10.1073/pnas.200365097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Venter JC, Adams MD, Myers EW, Li PW, Mural RJ, Sutton GG, Smith HO, Yandell M, Evans CA, Holt RA, et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
  • 24.Goldstein RF, Benight AS. How many numbers are required to specify sequence-dependent properties of polynucleotides? Biopolymers. 1992;32:1679–1693. doi: 10.1002/bip.360321210. [DOI] [PubMed] [Google Scholar]
  • 25.Breslauer KJ. Extracting thermodynamic data from equilibrium melting curves for oligonucleotide order-disorder transitions. Meth. Enzymol. 1995;259:221–242. doi: 10.1016/0076-6879(95)59046-3. [DOI] [PubMed] [Google Scholar]
  • 26.Zeng Y, Montrichok A, Zocchi G. Bubble nucleation and cooperativity in DNA melting. J. Mol. Biol. 2004;339:67–75. doi: 10.1016/j.jmb.2004.02.072. [DOI] [PubMed] [Google Scholar]
  • 27.Alexandrov BS, Wille LT, Rasmussen KØ, Bishop AR, Blagoev KB. Bubble statistics and dynamics in double-stranded DNA. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2006;74:050901. doi: 10.1103/PhysRevE.74.050901. [DOI] [PubMed] [Google Scholar]
  • 28.Sponer J, Riley KE, Hobza P. Nature and magnitude of aromatic stacking of nucleic acid bases. Phys. Chem. Chem. Phys. 2008;10:2595–2610. doi: 10.1039/b719370j. [DOI] [PubMed] [Google Scholar]
  • 29.Sponer J, Jurecka P, Marchan I, Luque FJ, Orozco M, Hobza P. Nature of base stacking: reference quantum-chemical stacking energies in ten unique B-DNA base-pair steps. Chem. Eur. J. 2006;12:2854–2865. doi: 10.1002/chem.200501239. [DOI] [PubMed] [Google Scholar]
  • 30.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
  • 31.Kibbe WA. OligoCalc: an online oligonucleotide properties calculator. Nucleic Acids Res. 2007;35:W43–W46. doi: 10.1093/nar/gkm234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Sambrook J, Fritsch EF, Maniatis T. Molecular Cloning: A Laboratory Manual. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 1989. [Google Scholar]
  • 33.Rychlik W, Rhoads RE. A computer program for choosing optimal oligonudeotides for filter hybridization, sequencing and in vitro amplification of DNA. Nucleic Acids Res. 1989;17:8543. doi: 10.1093/nar/17.21.8543. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES