On the Delayed Ross–Macdonald Model for Malaria Transmission

Abstract

The feedback dynamics from mosquito to human and back to mosquito involve considerable time delays due to the incubation periods of the parasites. In this paper, taking explicit account of the incubation periods of parasites within the human and the mosquito, we first propose a delayed Ross–Macdonald model. Then we calculate the basic reproduction number R₀ and carry out some sensitivity analysis of R₀ on the incubation periods, that is, to study the effect of time delays on the basic reproduction number. It is shown that the basic reproduction number is a decreasing function of both time delays. Thus, prolonging the incubation periods in either humans or mosquitos (via medicine or control measures) could reduce the prevalence of infection.

1. Introduction

Malaria is found throughout the tropical and subtropical regions of the world and causes more than 300 million acute illnesses and at least one million deaths annually (World Health Organization, 2005), especially in Africa. Globally, it is one of the three most dangerous infectious diseases (the others are HIV/AIDS and tuberculosis).

Human malaria is caused by one or a combination of four species of plasmodia: Plasmodium falciparum, P. vivax, P. malariae, and P. ovale. The disease caused by each species is different in terms of the way the species responds to drugs, behaves in the mosquito phase and behaves once inside the human (Kreier, 1980). P. falciparum causes malignant tertian malaria, which causes death more often than the other species. However, P. vivax remains in the body longer than P. falciparum, causing a more gradual health deterioration. P. malariae causes the third most common type of malaria in the world, although it grows slower than the other three species. P. ovale causes the least common and least pathogenic malaria of the four human malaria species (Kreier, 1980).

The parasites are transmitted through the bite of infected female mosquitoes of the genus Anopheles. Mosquitoes can become infected by feeding on the blood of infected people, and the parasites then undergo another phase of reproduction in the infected mosquitoes. Infection of a human host begins with the bite of a female anopheline mosquito and the injection of sporozoite stages into the bloodstream. Once injected into the human host, these parasite stages are carried to the liver where they develop in the parenchymal cells. After an incubation period of several days (see Macdonald, 1957) or even months (see reports Bray and Granham (1982), Lysenko et al. (1977) for P. vivax), these exoerythrocytic stages grow, divide, and release merozoites back into the bloodstream. The merozoites penetrate red cells, where they grow and subdivide to produce more merozoites that rupture the host cells and invade other red cells. At some point of this process, a proportion of the merozoites develop into sexual stages, the gametocytes. Only gametocytes are infective to the mosquito. When a vector mosquito bites a human and ingests male and female gametocytes, these are free from the blood cell, the female gamete is fertilized. Once fertilized, ookinetes are formed in the gut; these cross the wall of the midgut and become oocysts which take 10 days or so to mature (Aron and May, 1982), releasing sporozoites, which circulate through the mosquito, eventually arriving at the salivary glands where they can then be injected into a host when the mosquito next feeds (Oaks et al., 1991).

The earliest attempt to provide a quantitative understanding of the dynamics of malaria transmission was that of Ross (1911). Ross' models consisted of a few differential equations to describe changes in densities of susceptible and infected people, and susceptible and infected mosquitoes. Based on his modeling, Ross (1911) introduced the concept of a threshold density and concluded that “… in order to counteract malaria anywhere we need not banish Anopheles there entirely—we need only to reduce their numbers below a certain figure.” The analyses of Ross were extended by Lotka (1923). Macdonald (1952, 1956, 1957) extended Ross' basic model, analyzed several factors contributing to malaria transmission, and concluded that “the least influence is the size of the mosquito population, upon which the traditional attack has always been made” (Macdonald, 1956).

Assume that r is the per capita rate of recovery in humans such that 1/r is the duration of the disease in humans, μ is the per capita rate of mortality in mosquitos such that 1/μ is the life expectancy of mosquitos, m is the number of mosquitoes per human host, a is the rate of biting on human by a single mosquito (number of bites per unit time), b is the proportion of infected bites on human that produce an infection, c is the transmission efficiency from human to mosquito. The basic reproduction number $R_0=\frac{a^2\mathit{bcm}}{r\mu }$ was first introduced by Macdonald (1957) as the average number of secondary cases produced by an index case during its infectiousness period. In a disease which involves only one host and one vector, the basic reproduction number coincides with the threshold that breaks the stability of the trivial (disease free) steady state (Anderson and May, 1991). Recently, Smith and McKenzie (2004) refined the classical Ross–Macdonald model, in particular, they rederived the related entomological parameters to malaria transmission.

The Ross–Macdonald model has some interesting features. First, the threshold result states that malaria can persist in a population only if the number of mosquitoes is greater than a given threshold. Secondly, the prevalence of infection in the human and the mosquito hosts depends directly on the basic reproduction number and the relationship is non-linear. Thirdly, the model has a stable positive equilibrium when the basic reproduction number is greater than 1. This means that temporary intervention can lead to a temporary reduction of prevalence, when the intervention is relaxed prevalence again increased to the original values (Koella, 1991; Smith and McKenzie, 2004).

Macdonald (1957) performed a sensitivity analysis of the basic reproduction number on the parameters. He found that halving the mosquito population (e.g., by larvicides) reduces R₀ by a factor of two whilst halving biting rate (e.g., with bed nets) reduces R₀ by a factor of four. The largest reduction of R₀ is expected for increase in adult mosquito mortality (e.g., by imagicides) because of their exponential relationship. An important conclusion is thus that imagicides are more effective for controlling malaria than larvicides. The work of Macdonald (1957) had a very beneficial impact on the collection, analysis, and interpretation of epidemic data on malaria infection (Molineaux and Gramiccia, 1980) and guided the enormous global malaria-eradication campaign of his era.

The classical Ross–Macdonald model is highly simplified. Subsequent contributions have been made to extend the Ross–Macdonald malaria models considering age structure in the human population (Aron and May, 1982; Dietz, 1988; Anderson and May, 1991), acquired immunity (Aron and May, 1982; Aron, 1988), latency (Koella, 1991; Lopez et al., 2002; Koella and Antia, 2003; Koella and Boëte, 2003), spatial heterogeneity (Dye and Hasibeder, 1986; Hasibeder and Dye, 1988; Gupta and Hill, 1995; Gupta et al., 1994; Torres-Sorando and Rodriguez, 1997; Rodriguez and Torres-Sorando, 2001), individual-based models (Gu et al., 2003a), habitat-based models (Gu and Novak, 2005), integrated models (McKenzie and Bossert, 2005), among other aspects (Bailey, 1982; Chitnis et al., 2006; Gu et al., 2003b; Killeen et al., 2000; McKenzie, 2000; Ngwa, 2006; Smith et al., 2004, 2005).

Another omission in the classical Ross–Macdonald model is the incubation periods of the parasite in mosquitos (during which period there are no sporozoites in the salivary glands of the “infected” mosquitoes or this incubation period is comparable to the mean life span of the mosquito) and in humans (during which period infections are lost by infective people returning to the uninfected class at a characteristic recovery rate). The feedback dynamics from mosquito to human and back to mosquito involve considerable time delay due to the incubation periods of the several forms of the parasites. Long incubation periods of P. vivax greater than 6 months increase the risk of importing malaria to the United States via the overseas military personnel, with potential for establishing autochthonous transmission (Claborn et al., 2002). Such an increased risk is due to the delayed onset of symptoms, which may not occur until the individual has returned to the US or even left the US Army (Walter Reed Army Institute of Research, 1998). Analysis of Gu et al. (2003b) also shows that prevalence of P. falciparum is significantly correlated with infectious exposures occurring 10–11 months previously. The goal of this article is to model the incubation periods in both human and mosquito and to study the effect of the incubation periods on the basic reproduction number and the dynamics of the transmission models.

In this paper, taking explicit account of the incubation periods of parasites within both the human and the mosquito, we propose a delayed Ross–Macdonald model. We calculate the basic reproduction number R₀ and carry out some sensitivity analysis of R₀ on the incubation periods (as Macdonald, 1957 did for other parameters), that is, to study the effect of time delays on the basic reproduction number. In the case when there is an endemic steady state, we determine the effect of the time delay on its stability. Numerical simulations are carried out to illustrate the obtained results.

2. The delayed Ross–Macdonald model

Consider the human-mosquito interaction for malaria transmission without immunity in which the current density of infectious mosquitos is related to the density of infectious humans at earlier times. The human population is divided into two classes, susceptible and infectious, whereas the mosquito population is divided into three classes, susceptible, exposed, and infectious. Suppose that the infection in the human confers negligible immunity and does not result death or isolation. All new-born are susceptible. For the transmission of the pathogen, it is assumed that a susceptible human can receive the infection only by contacting with infective mosquitos, and a susceptible mosquito can receive the infection only from the infectious human. Also, a susceptible mosquito becomes exposed when it receives the infection from an infective human. It remains exposed for some time and then becomes infectious.

For simplicity, assume the total populations of both humans and mosquitoes are constants and denoted by H and M, respectively. Let X(t) and Y(t) denote the numbers of infected humans and mosquitoes at time t, respectively. Let a be the rate of biting on humans by a single mosquito (number of bites per unit time). Then the number of bites on humans per unit time per human is a/H. If b is the proportion of infected bites on humans that produce an infection, the interaction between the infected mosquitoes Y(t) and the uninfected humans H − X(t) will produce new infected humans of (a/H)b[H − X(t)]Y(t). The incubation period in a human has duration τ₁; it is possible that some individuals recovered from parasitemia during this incubation period (Smith and McKenzie, 2004). Thus, of those individuals infected τ₁ unit times ago, only a proportion (a/H)b[H − X(t − τ₁)]Y(t − τ₁)e^−rτ₁ is infectious at the present time t, where r is the per capita rate of recovery in humans so that 1/r is the duration of the disease in humans. Therefore, the equation for the rate of change in the number of infected humans is

$$\frac{\mathit{dX}}{\mathit{dt}}=-\mathit{rX}\left(t\right)+\left(\frac{a}{H}\right)b\left[H-X(t-{\tau }_1)\right]Y(t-{\tau }_1)e^{-r{\tau }_1}.$$

Similarly, if μ is the per capita rate of mortality in vectors so that 1/μ is the life expectancy of mosquitoes, the incubation interval in the mosquito has duration τ₂, and c is the transmission efficiency from human to mosquito, then we have the equation for the rate of change in the number of infected mosquitoes:

$$\frac{\mathit{dY}}{\mathit{dt}}=-\mu Y\left(t\right)+\left(\frac{a}{H}\right)\mathit{cX}(t-{\tau }_2)\left[M-Y(t-{\tau }_2)\right]e^{-\mu {\tau }_2}.$$

Now define

$$x\left(t\right)=\frac{X\left(t\right)}{H},y\left(t\right)=\frac{Y\left(t\right)}{M},m=\frac{M}{H}.$$

Then x(t) and y(t) are the proportion of infected humans and mosquitoes at time t, respectively, m is the number of mosquitoes per human host, and we obtain the following delayed Ross–Macdonald model (variables and parameter values are listed in Table 1):

$$\begin{array}{cc}\hfill \frac{\mathit{dx}}{\mathit{dt}}& =\mathit{rx}\left(t\right)+\mathit{abm}\left(1-x(t-{\tau }_1)\right)y(t-{\tau }_1)e^{-r{\tau }_1},\hfill \\ \hfill \frac{\mathit{dy}}{\mathit{dt}}& =\mu y\left(t\right)+\mathit{acx}(t-{\tau }_2)\left(1-y(t-{\tau }_2)\right)e^{-\mu {\tau }_2}.\hfill \end{array}$$ (1)

Table 1.

Variables and parameters

Parameters and Variables		Values	References
	Dependent Variables
x(t)	proportion of infected humans
y(t)	proportion of infected mosquitoes
	Parameters and Constants
m	ratio of mosquitos to humans	2	[1, 2]
a	biting rate on a human per mosquito	0.2–0.5/day	[3, 4, 10]
b	infected mosquito to human transmission efficiency	0.5	[5, 6, 10]
c	infected human to mosquito transmission efficiency	0.5	[5, 6, 10]
r	per capita human recovery rate	0.01–0.05/day	[3, 6, 7, 10]
μ	per capita mortality rate of mosquitos	0.05–0.5/day	[3, 6, 7]
τ1	incubation period for P. vivax in humans	10–100 days	[8, 9, 10]
τ2	incubation period in mosquitos	5–15 days	[3, 9]

References: [1] = Harada et al. (1998), [2] = Ishikawa et al. (2003), [3] = Macdonald (1957), [4] = Dietz et al. (1974), [5] = Gu et al. (2003a), [6] = Le Menach et al. (2005), [7] = Aron and May (1982), [8] = Bray and Granham (1982), [9] = Beier (1998), [10] = Smith et al. (2004)

To deduce the threshold for the disease to establish in the human population, we have to analyze the existence of equilibria and their stability for model (1). Define the basic reproduction number by

$$R_0=\frac{a^2{\mathit{bcme}}^{r{\tau }_1}{e}^{-\mu {\tau }_2}}{r\mu }.$$ (2)

An heuristic derivation is as follows. Take a primary case with a recovery rate of r, the average time spend in an infectious state is 1/r. During this time, since the incubation period in humans has duration τ₁, the average number of mosquito bites received from m susceptible mosquitoes each with a biting rate a gives a total of acme^−rτ₁/r mosquitoes infected by the primary human case. Each of these mosquitoes survives for an average time 1/μ and with another incubation period τ₂ in mosquitoes, makes a total of abe^−μτ₂/μ infectious bites. The total number of secondary cases is thus a²bcme^{−rτ₂−μτ₂}/(rμ), which is (2). Notice that a appears twice in the expression since the mosquito biting rate controls transmission from humans to mosquitoes and from mosquitoes to humans. Then we have the following results on the existence of equilibria.

Lemma 2.1. In the first quadrant, system (1) has at most two equilibria. More precisely,

(i) IfR₀ ≤ 1, then system (1) has a unique trivial equilibrium (0, 0);

(ii) IfR₀ > 1, then system (1) has two equilibria, the trivial equilibrium (0, 0) and the positive equilibrium (x*, y*), where

$$\begin{array}{cc}\hfill x^{\ast }& =\frac{a^2{\mathit{bcme}}^{-r{\tau }_1}{e}^{-\mu {\tau }_2}-r\mu }{{\mathit{ace}}^{-\mu {\tau }_2}({\mathit{abme}}^{-r{\tau }_1}+r)}=\frac{R_0-1}{R_0+\frac{{\mathit{ace}}^{-\mu {\tau }_2}}{\mu }},\hfill \\ \hfill y^{\ast }& =\frac{a^2{\mathit{bcme}}^{-r{\tau }_1}{e}^{-\mu {\tau }_2}-r\mu }{{\mathit{abme}}^{-r{\tau }_1}({\mathit{ace}}^{-\mu {\tau }_2}+\mu )}=\frac{R_0-1}{R_0+\frac{{\mathit{abme}}^{-r{\tau }_1}}{r}}.\hfill \end{array}$$ (3)

Next we discuss the stability of (0, 0) and (x*, y*). First we consider the linearized system of (1) at (0, 0)

$$\begin{array}{cc}\hfill \frac{\mathit{dx}}{\mathit{dt}}& =-\mathit{rx}\left(t\right)+\mathit{abmy}(t-{\tau }_1)e^{-r{\tau }_1},\hfill \\ \hfill \frac{\mathit{dy}}{\mathit{dt}}& =-\mu y\left(t\right)+\mathit{acx}(t-{\tau }_2)e^{-\mu {\tau }_2}.\hfill \end{array}$$ (4)

The characteristic equation associated with system (4) takes the form

$$(\lambda +r)(\lambda +\mu )-a^2{\mathit{bcme}}^{-r{\tau }_1-\mu {\tau }_2}{e}^{-({\tau }_1+{\tau }_2)\lambda }=0.$$ (5)

Let

$$F(\lambda ,{\tau }_1,{\tau }_2)=(\lambda +r)(\lambda +\mu )-a^2{\mathit{bcme}}^{-r{\tau }_2-\mu {\tau }_2}{e}^{-({\tau }_1+{\tau }_2)\lambda }.$$

It is clear that F(λ, τ₁, τ₂) is an analytic function. F(0, τ₁, τ₂) = rμ(1 − R₀), and F(λ, 0, 0) = λ² + (r + μ)λ + rμ − a²bcm. To discuss the distribution of the roots of the transcendental Eq. (5), we consider three cases.

(i) If R₀ < 1, then F(0, τ₁, τ₂) > 0 and $F_{\lambda }^{\prime }(\lambda ,{\tau }_1,{\tau }_2)>0$ for all positive λ, τ₁ and τ₂. Hence, Eq. (5) has no zero root and positive roots for all positive τ₁ and τ₂. Now we claim that Eq. (5) does not have any purely imaginary roots. Suppose that Eq. (5) has a pair of purely imaginary roots ±ωi, ω > 0 for some τ₁ and τ₂. Then ω must be a positive root of

$${\omega }^4+({\mu }^2+r^2){\omega }^2+r^2{\mu }^2-{\left(a^2{\mathit{bcme}}^{-r{\tau }_1-\mu {\tau }_2}\right)}^2=0.$$ (6)

However, Eq. (6) does not have nonnegative real roots since R₀ < 1. Hence, Eq. (5) does not have any purely imaginary roots.

On the other hand, F(λ, 0, 0) = 0 has two negative real roots λ_± since R₀ < 1, where

$${\lambda }_{\pm }=\frac{-(r+\mu )\pm \sqrt{{(r+\mu )}^2-4(a^2\mathit{bcm}-r\mu )}}{2}.$$

Also $F_{\lambda }^{\prime }({\lambda }_{\pm },0,0)\ne 0$. By the implicit function theorem and the continuity of F(λ, τ₁, τ₂), we know that all roots of (5) have negative real parts for positive τ₁ and τ₂, which implies that (0, 0) is stable.

(ii) If R₀ = 1, then F(0, τ₁, τ₂) = 0 and $F_{\lambda }^{\prime }(\lambda ,{\tau }_1,{\tau }_2)>0$ for λ ≥ 0, τ₁ > 0 and τ₂ > 0. Hence, Eq. (5) has a simple zero root and no positive root for all positive τ₁ and τ₂. Using a similar argument as in (i), we can obtain that except a zero root, all roots of (5) have negative real parts for positive τ₁ and τ₂. Thus, (0, 0) is a degenerate equilibrium of codimension one and is stable except in one direction.

(iii) If R₀ > 1, then F(0, τ₁, τ₂) < 0 and $F_{\lambda }^{\prime }(\lambda ,{\tau }_1,{\tau }_2)>0$ for λ ≥ 0, τ₁ > 0 and τ₂ > 0. Hence, Eq. (5) has a unique positive real root for all positive τ₁ and τ₂.

On the other hand, F(λ, 0, 0) = 0 has at least one negative real root λ₋. From the implicit function theorem, (5) has a root with negative real part for small τ₁ and τ₂. Therefore, (0, 0) has both stable and unstable manifolds for some τ₁ and τ₂. To determine the unstable manifold of (0, 0) when R₀ > 1, we discuss the stability of the other equilibrium (x*, y*) when R₀ > 1.

Remark 2.2. We would like to point out, as suggested by one of the referees, that the stability of the trivial equilibrium (0, 0) can also be analyzed via the real eigenvalues of its Jacobian matrix by using a theorem on page 92 in Smith (1995).

Consider the linearized system of (1) at (x*, y*)

$$\begin{array}{cc}\hfill \frac{\mathit{dx}}{\mathit{dt}}& =-\mathit{rx}\left(t\right)-{\mathit{abmy}}^{\ast }{e}^{-r{\tau }_1}x(t-{\tau }_1)+\mathit{abm}(1-x^{\ast })e^{-r{\tau }_1}(t-{\tau }_1),\hfill \\ \hfill \frac{\mathit{dy}}{\mathit{dt}}& =-\mu y\left(t\right)+\mathit{ac}(1-y^{\ast })e^{-\mu {\tau }_2}x(t-{\tau }_2)-{\mathit{acx}}^{\ast }{e}^{-\mu {\tau }_2}y(t-{\tau }_2).\hfill \end{array}$$ (7)

The characteristic equation associated with system (7) takes the form

$$\begin{array}{cc}\hfill & (\lambda +r)(\lambda +\mu )+{\mathit{abmy}}^{\ast }{e}^{-r{\tau }_1}(\lambda +\mu )e^{-\lambda {\tau }_1}+{\mathit{acx}}^{\ast }{e}^{-\mu {\tau }_2}(\lambda +r)e^{-\lambda {\tau }_2}\hfill \\ \hfill & -a^2\mathit{bcm}(1-x^{\ast }-y^{\ast })e^{-r{\tau }_1-\mu {\tau }_2}{e}^{-({\tau }_1+{\tau }_2)\lambda }=0.\hfill \end{array}$$ (8)

Let G(λ, τ₁, τ₂) denote the function on the left-hand side of the last equation. Note that

$$G(0,{\tau }_1,{\tau }_2)=r\mu (R_0-1)>0.$$

Case (i). When τ₁ = τ₂ = 0, the equilibrium (x*, y*) becomes

$$(x^{\ast },y^{\ast })=\left(\frac{R_0-1}{R_0+\frac{\mathit{ac}}{\mu }},\frac{R_0-1}{R_0+\frac{\mathit{abm}}{r}}\right)\text{with}{R}_0=\frac{a^2\mathit{bcm}}{r\mu }.$$ (9)

The characteristic Eq. (8) becomes

$${\lambda }^2+\beta \lambda +\gamma =0,$$

where

$$\beta =\frac{\mathit{abm}{(\mathit{ac}+\mu )}^2+\mathit{ac}{(\mathit{abm}+r)}^2}{(\mathit{ac}+\mu )(\mathit{abm}+r)}>0,\gamma =r\mu (R_0-1)>0.$$

The above equation has two negative real roots

$${\lambda }_{\pm }=\frac{-\beta \pm \sqrt{{\beta }^2-4\gamma }}{2},$$

i.e. λ₋ < λ₊ < 0.

Case (ii). When τ₁ > 0, τ₂ = 0, the equilibrium (x*, y*) becomes

$$(x^{\ast },y^{\ast })=\left(\frac{R_0-1}{R_0+\frac{\mathit{ac}}{\mu }},\frac{R_0-1}{R_0+\frac{{\mathit{abme}}^{-r{\tau }_1}}{r}}\right)\text{with}{R}_0=\frac{a^2{\mathit{bcme}}^{-r{\tau }_1}}{r\mu }.$$ (10)

Notice that the equilibrium (x*, y*) exists under the assumption R₀ > 1, that is,

$${\tau }_1<{\tau }_1^{\ast }=\frac{1}{r}\ln \frac{a^2\mathit{bcm}}{r\mu }.$$ (11)

The characteristic Eq. (8) becomes

$${\lambda }^2+a_1\lambda +a_0+\left[b_1\left({\tau }_1\right)\lambda +b_0\left({\tau }_1\right)\right]e^{-\lambda {\tau }_1}=0,$$ (12)

where

$$\begin{array}{cc}\hfill & a_1=r+\mu +{\mathit{acx}}^{\ast },a_0=r\mu +{\mathit{acrx}}^{\ast },\hfill \\ \hfill & b_1\left({\tau }_1\right)={\mathit{abmy}}^{\ast }{e}^{-r{\tau }_1},b_0=\left({\tau }_1\right)=\mathit{abm}\mu y^{\ast }{e}^{-r{\tau }_1}-a^2\mathit{bcm}(1-x^{\ast }-y^{\ast })e^{-r{\tau }_1}.\hfill \end{array}$$

By the implicit function theorem and the continuity of the right-hand side function, Eq. (12) has negative real roots for small τ₁. Now we want to show that Eq. (12) has negative real roots for all ${\tau }_1\in [0,{\tau }_1^{\ast })$. To do so we show that Eq. (12) does not have any purely imaginary roots for all ${\tau }_1\in [0,{\tau }_1^{\ast })$.

Suppose Eq. (12) has a pair of purely imaginary roots ±ωi, ω > 0, for some ${\tau }_1\in [0,{\tau }_1^{\ast })$. Then ω must satisfy the following system

$$\begin{array}{cc}\hfill & {\omega }^2-a_0=b_1\left({\tau }_1\right)\omega \sin \omega {\tau }_1+b_0\left({\tau }_1\right)\cos \omega {\tau }_1,\hfill \\ \hfill & a_1\omega =-b_1\left({\tau }_1\right)\omega \cos \omega {\tau }_1+b_0\left({\tau }_1\right)\sin \omega {\tau }_1.\hfill \end{array}$$

Thus, ω must be a positive root of

$${\omega }^4+B_1{\omega }^2+C_1=0,$$ (13)

where

$$B_1=a_1^2-2a_0-b_1^2\left({\tau }_1\right)C_1=a_0^2-b_0^2\left({\tau }_1\right).$$

Clearly, Eq. (13) has no positive roots ω² if and only if either (i) C₁ ≥ 0 and B₁ ≥ 0 or (ii) $B_1^2-4C_1<0$. We have

$$C_1=r^2{\mu }^2(R_0-1)(1+R_0(1-2x^{\ast })).$$

Similarly, after some tedious computations, we have

$$B_1={\mu }^2+2\mathit{ac}\mu x^{\ast }+a^2{c}^2{x}^{\ast 2}+\frac{r^2(1-2x^{\ast })}{{(1-x^{\ast })}^2}.$$

Note that B₁ > 0 and C₁ > 0 if acr + 2rμ ≥ a²bcm. Therefore, Eq. (13) has no positive roots ω² if 1 < R₀ and a²bcm ≤ acr + 2rμ. Consequently, Eq. (12) does not have any purely imaginary roots for all ${\tau }_1\in [0,{\tau }_1^{\ast })$ so that Eq. (12) only has negative real roots for all ${\tau }_1\in [0,{\tau }_1^{\ast })$.

Case (iii). For ${\tau }_1\in [0,{\tau }_1^{\ast })$, consider τ₂ > 0 so that 1 < R₀ and a²bcm ≤ acr + 2rμ such that the equilibrium (x*, y*) given by (3) exists; that is,

$${\tau }_2\le {\tau }_2^{\ast }\left({\tau }_1\right)=\frac{1}{\mu }\ln \frac{a^2{\mathit{bcme}}^{-r{\tau }_1}}{r\mu }.$$ (14)

Clearly, the left-hand side of the characteristic Eq. (8) is analytic in λ and τ₁, τ₂. As τ₂ varies, by Theorem 2.1 of Ruan and Wei (2003), the sum of the multiplicity of zeros of the left hand side of (8) on the open right half-plane can change only if a zero appears on crosses the imaginary axis.

By Case (ii), Eq. (8) only has negative real roots for τ₂ = 0 and ${\tau }_1\in [0,{\tau }_1^{\ast })$. It follows that there is a τ̄₂(τ₁), $0<{\stackrel{-}{\tau }}_2\left({\tau }_1\right)\le {\tau }_2^{\ast }\left({\tau }_1\right)$, such that Eq. (8) only has [negative real roots for τ₂ < τ̄₂(τ₁).

We show that ${\stackrel{-}{\tau }}_2\left({\tau }_1\right)={\tau }_2^{\ast }\left({\tau }_1\right)$. If ${\stackrel{-}{\tau }}_2\left({\tau }_1\right)<{\tau }_2^{\ast }\left({\tau }_1\right)$ for ${\tau }_1\in [0,{\tau }_1^{\ast })$, there must be a τ̃₂(τ₁), ${\stackrel{-}{\tau }}_2\left({\tau }_1\right)<{\tilde{\tau }}_2\left({\tau }_1\right)<{\tau }_2^{\ast }\left({\tau }_1\right)$, such that the Eq. (8) has nonnegative real roots for τ₂ = τ̃₂(τ₁). By the continuity of τ₂ in τ₁, we have ${\tilde{\tau }}_2\left(0\right)<{\tau }_2^{\ast }\left(0\right)=\frac{1}{\mu }\ln \frac{a^2\mathit{bcm}}{r\mu }$ with τ₁ = 0. However, using a similar argument as in Case (ii), we know that the Eq. (8) only has negative real roots for τ₁ = 0 and ${\tau }_2\in [0,{\tau }_2^{\ast }\left(0\right))$. Thus, ${\stackrel{-}{\tau }}_2\left({\tau }_1\right)={\tau }_2^{\ast }\left({\tau }_1\right)$.

This implies that the positive equilibrium (x*, y*) is stable for ${\tau }_1\in [0,{\tau }_1^{\ast })$ and ${\tau }_2\in [0,{\tau }_2^{\ast }\left({\tau }_1\right))$.

Summarizing the above analysis, we have the following results on the stability of the equilibria.

Theorem 2.3. IfR₀ < 1, system (1) has a unique trivial equilibrium (0, 0) which is stable. If 1 < R₀ anda²bcm ≤ acr + 2rμ, system (1) has two equilibria, the trivial equilibrium (0, 0) which is a saddle, and a positive equilibrium (x*, y*) which is stable.

Remark 2.4. Notice that the condition R₀ > 1 can be rewritten as

$$r{\tau }_1+\mu {\tau }_2<\ln \frac{a^2\mathit{bcm}}{r\mu }.$$ (15)

Thus, the existence and stability of the positive equilibrium depend on the delays. However, Hopf bifurcation does not occur at (x*, y*) since it will vanish once the delays are increased so that the Condition (15) does not hold (see the numerical simulations in Section 3).

Notice that when τ₁ = τ₂ = 0, system (1) becomes the well-known Ross–Macdonald model of two ordinary differential equations (Anderson and May, 1991)

$$\begin{array}{cc}\hfill \frac{\mathit{dx}}{\mathit{dt}}& =-\mathit{rx}\left(t\right)+\mathit{abm}\left[1-x\left(t\right)\right]y\left(t\right),\hfill \\ \hfill \frac{\mathit{dy}}{\mathit{dt}}& =-\mu y\left(t\right)+\mathit{acx}\left(t\right)\left[1-y\left(t\right)\right].\hfill \end{array}$$ (16)

Therefore, by Theorem 2.3, we have the following results on the dynamics of the Ross–Macdonald model (16) (see Aron and May, 1982; Anderson and May, 1991).

Corollary 2.5. Define

$$R_0=\frac{a^2\mathit{bcm}}{r\mu }.$$ (17)

IfR₀ < 1, then the Ross–Macdonald model (16) has a unique equilibrium, the trivial equilibrium (0, 0), which is stable. IfR₀ > 1, then the Ross–Macdonald model (16) has two equilibria, the trivial equilibrium (0, 0) which is unstable, and the positive equilibrium

$$(x^{\ast },y^{\ast })=\left(\frac{a^2\mathit{bcm}-r\mu }{\mathit{ac}(\mathit{abm}+r)},\frac{a^2\mathit{bcm}-r\mu }{\mathit{abm}(\mathit{ac}+\mu )}\right)=\left(\frac{R_0-1}{R_0+\frac{\mathit{ac}}{\mu }},\frac{R_0-1}{R_0+\frac{\mathit{abm}}{r}}\right),$$ (18)

which is stable.

Notice that the steady state values x* and y* given by (18) are positive only if R₀ > 1. The above conclusions give the basis for Ross' threshold theorem of malaria (Ross, 1911): the amount of malaria in a locality tends towards a fixed limit determined by the number of malaria-bearing mosquitoes and by other factors; if the number of malaria-bearing Anophelines is below a certain figure, that limit will be zero. A similar threshold theorem of malaria holds for the delayed Ross-Macdonald model (1).

3. Numerical simulations

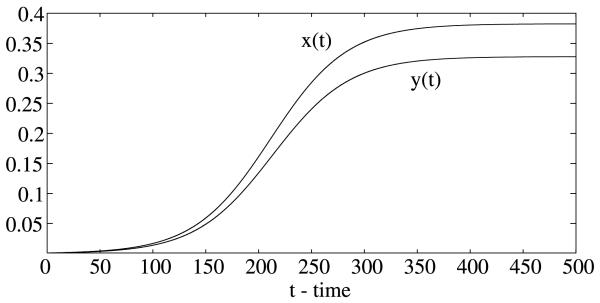
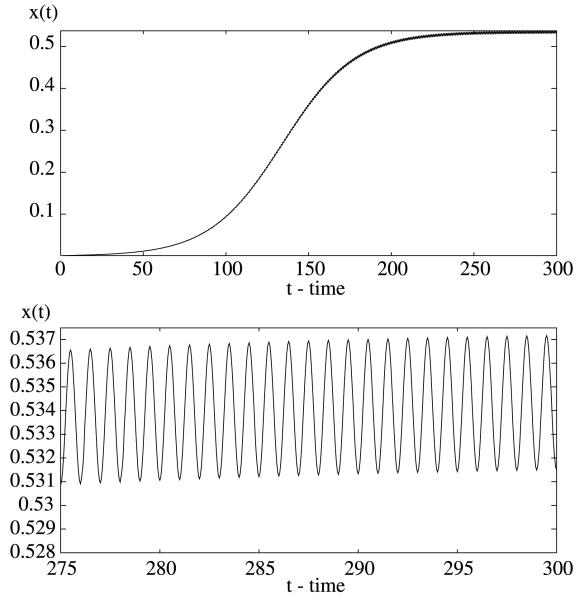
To numerically illustrate the results, we need to choose some parameter values (see Table 1). The per capita human recovery rate R varies from 0.01 to 0.05 per day (Macdonald, 1957; Aron and May, 1982; Smith et al., 2004; Le Menach et al., 2005), we take r 0.05. The biting rate on man by a single mosquito is about 0.2 to 0.5 per day (Macdonald, 1957; Dietz et al., 1974; Smith et al., 2004), here we take a = 0.2 per day. The proportion of infected bites on both human and mosquito that produces an infection is b = c = 0.5 (Gu et al., 2003a; Smith et al., 2004; Le Menach et al., 2005). The number of mosquitoes per human host could be various, we take m = 2 (Harada et al., 1998; Ishikawa et al., 2003). The per capita mortality rate of mosquitoes μ varies from 0.05 to 0.5 per day (Macdonald, 1957; Aron and May, 1982; Le Menach et al., 2005), here we take μ = 0.05 per day. The incubation period for P. vivax in human varies from 10 to 100 days (Bray and Granham, 1982; Beier, 1998; Smith et al., 2004), here it is taken to be τ₁ = 15 days. The incubation period in the mosquitoes is temperature-dependent and varies for different species (Beier, 1998). The period for P. vivax is estimated to be about τ₂ = 9 days under ideal condition (Macdonald, 1952; Beier, 1998). We can see that the basic reproduction number R₀ = 2.4096 > 1 and the positive equilibrium (0.3825, 0.3279) is asymptotically stable (see Fig. 1).

Fig. 1.

The positive steady state of the delayed Ross–Macdonald model (1) is asymptotically stable and the disease is endemic. Here, r = 0.05 per day, a = 0.2 per day, b = c = 0.5, m 2, μ = 0.05 per day, τ₁ = 15 days, and τ₂ = 9 days.

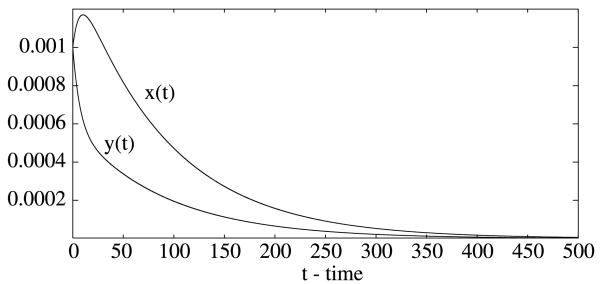
If the per capita mortality rate of mosquitoes is increased to μ 0.105 per day, then the basic reproduction number is reduced so that R₀ = 0.5376 < 1. Prevalence levels in both human host and mosquito decrease and the solutions are approaching the trivial equilibrium (0, 0) (see Fig. 2).

Fig. 2.

The prevalence levels decrease as the per capita mortality rate of mosquitoes is increased. Here μ = 0.105 per day, all other parameter values are as in Fig. 1.

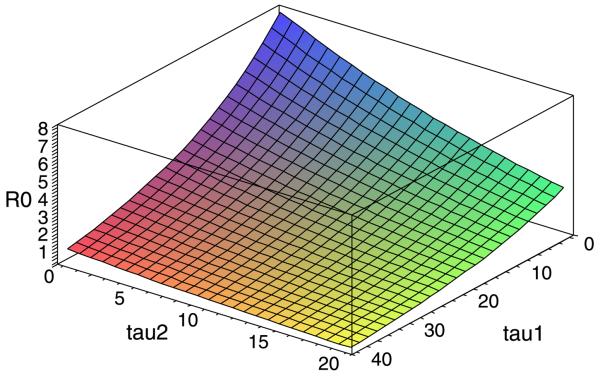
The basic reproduction number R₀ depends on the delays and is a decreasing function of the delays.

$$R_0=\frac{a^2{\mathit{bcme}}^{-r{\tau }_1-\mu {\tau }_2}}{r\mu }$$

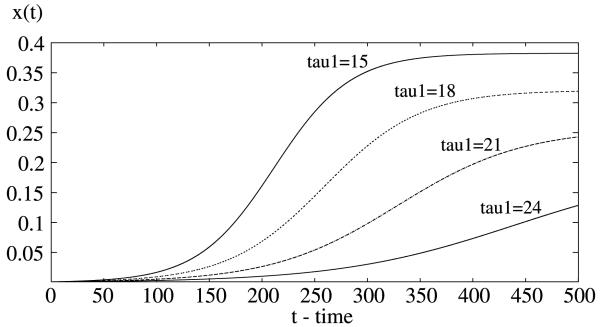
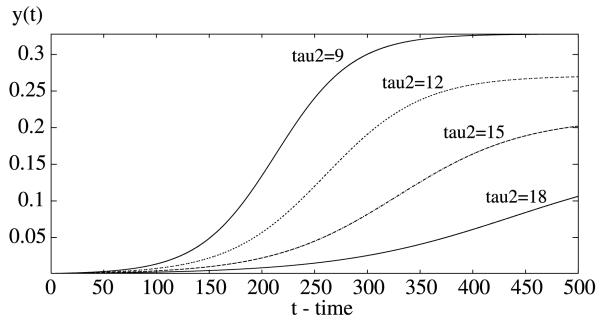
is a decreasing function of both delays τ₁ and τ₂. Numerically, with r 0.05, a 0.2, b = 0.5. c = 0.5, m = 2, μ = 0.05, τ₁ = 15, τ₂ = 9, we have R₀ = 2.4096 > 1. Thus, the positive equilibrium (0.3825, 0.3279) is asymptotically stable (see Fig. 1). Now increasing τ₁, the incubation period in the human, will decrease R₀ so that R₀ passes through 1 and eventually becomes less than 1. Correspondingly, via backward bifurcation, the steady state value of proportion of the infectious human density decreases and eventually approaches to zero as time tends to infinity (see Fig. 3). The delay τ₂ (the incubation period in the mosquito) plays a similar role (see Fig. 4). The simulations in Figs. 3 and 4 indicate that the steady state values are more sensitive in the incubation period τ₂ in the mosquito population than in the incubation period τ₁ in the human population, since small changes in τ₂ induce fast increases in the steady state values while lager changes are required in τ₁ in order to have similar increases in the steady states values. As a function of the incubation periods in both humans and mosquitoes, the basic reproduction number R₀ is plotted against the two delays τ₁ and τ₂ (see Fig. 5).

Fig. 3.

In the delayed Ross–Macdonald model (1), increasing in the incubation period in the human will decrease the proportion of infective human population. Here τ₁ increases from 15 days to 24 days.

Fig. 4.

In the delayed Ross–Macdonald model (1), increasing the incubation period in the mosquito can also decrease the proportion of infected mosquito population. Here τ₂ is increased from 9 days to 18 days.

Fig. 5.

In the delayed Ross–Macdonald model (1), the plot of the basic reproduction number R₀ as a function of the incubation periods in human τ₁ and in the mosquito τ₂.

Our results also show that local threshold densities of mosquitoes with respect to malaria extinction exist, as Ross (1911) suggested. For example, it can be expressed as

$$m=\frac{r\mu e^{r{\tau }_1}{e}^{\mu {\tau }_2}{R}_0}{a^2\mathit{bc}}.$$

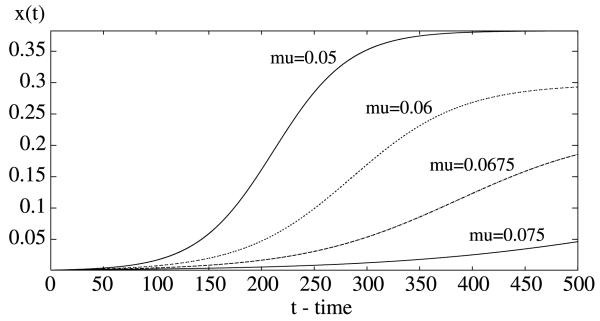
Threshold prevalence exists within a transmission system, akin to Macdonald's “basic reproduction rate” (Macdonald, 1957), but it is likely to be dependent of vector mortality, host infectivity, and other factors within the transmission system. For example, increases in the per capita mortality rate of the mosquito can decrease the basic reproduction number and reduce the human infection level (see Fig. 6).

Fig. 6.

The plots of the proportion of infective humans in the delayed Ross–Macdonald model (1) when the per capita mortality rate of the mosquito increases from μ = 0.05 per day to μ = 0.075 per day.

4. Discussion

Successful interventions in malaria require a better understanding of the relative influence of each of the biological and ecological factors. These factors and their interactions can be represented by measurable parameters in the models. In this paper, we have modified the classical Ross–Macdonald model to include time delays that describe the incubation periods of parasites within both the human and the mosquito. We evaluated the basic reproduction number R₀ and studied the existence of the disease-free equilibrium and the endemic equilibrium. In both models, we found that if R₀ < 1, then the disease-free equilibrium is the unique equilibrium and is stable. If R₀ > 1, then the endemic equilibrium exists and is stable when the delays are small.

It should be mentioned that for the delayed Ross–Macdonald model (1) we only proved the asymptotic stability of the positive steady state for small delay values. However, our numerical simulations (see Figs. 1, 3 and 4) demonstrate that the positive steady state of the delayed Ross–Macdonald model (1) is asymptotically stable for all delay values as long as the reproduction number is greater than one. Since R₀ defined by (2) and the steady state values given in (3) are all delayed dependent, increasing the delay values will decrease R₀ to make it equal to 1 and will make the positive steady state to coincide with the trivial equilibrium. Thus, Hopf bifurcation does not occur when the delay increases and there are no bifurcating periodic solutions due to the increase of the delay values.

Global warming affects disease vectors, which in turn may alter the current patterns of vector-borne diseases (Rogers et al., 2002). Malaria is among the many vector-borne diseases that have been affected by climate (Hay et al., 2000) since warm and moist climates are most conductive to mosquito propagation and survival. Recently, various models of malaria transmission have been developed to improve our understanding of the likely impact of climate change on malaria transmission (Craig et al., 1999; Martens et al., 1995; Rogers and Randolph, 2000; Hoshen and Morse, 2004). The sporogonic incubation of the parasite can strongly influence transmission intensity and can vary seasonally (Burkot et al., 1990; McKenzie et al., 2001) or with longer term climate cycles (Craig et al., 1999). Warming temperatures tend to decrease the duration of the extrinsic incubation period, which will increase the basic reproduction number R₀. Thus, climate changing can induce fluctuations of the basic reproduction number R₀ and possible oscillations in the malaria cases (Teklehaimanot et al., 2004). For example, as in Aron and May (1982), assume m = m(t) = p + q sin(2πt) is periodic with p = 1.5and q = 1, then the proportion of infected human population approaches a periodic value as time involves (see Fig. 7).

Fig. 7.

The plots of the proportion of infective humans in the delayed Ross–Macdonald model (1) when the number of mosquitoes per human host is a periodic function, m(t) = p + q sin(2πt) with p = 1.5 and q = 1.

The analyses and numerical simulations indicate that prolong (via medical drugs or control measures) either of the incubation periods could reduce the proportions of the infected human and mosquito populations and thus could control the disease locally. However, long incubation periods may have a significant role in the “nonlocal” transmission of the disease if we take the migration of both humans and mosquitoes into consideration, since exposed humans and mosquitoes can certainly spread the parasites to different locations, as the exposed US military personals brought the parasites from the South Korea to the US; see Claborn et al. (2002). In modern time, humans travel more frequently on scales from local to global. One million people are reported to travel internationally each day, and one million people travel from developed to developing countries (and vice versa) each week (Garrett, 1996). Almost all existing malaria transmission models assume enclosed systems of people, parasites, and vectors in which neither emigration nor immigration is considered. Travel or migration of exposed individuals can spatially spread infectious diseases (Hasibeder and Dye, 1988; Gupta and Hill, 1995; Gupta et al., 1994). Also, approximately 60% of the 1,500 malaria cases occur each year in the United States are among US travelers (Newman et al., 2004). Therefore, it is more reasonable to consider the combined effect of incubation periods and spatial structure in modeling vector-host interactions (see Ruan, 2006; Ruan and Xiao, 2004 and the references cited therein) in order to understand the spatial spread of malaria.