Fuzzy c-means clustering with prior biological knowledge

Abstract

We propose a novel semi-supervised clustering method called GO Fuzzy c-means, which enables the simultaneous use of biological knowledge and gene expression data in a probabilistic clustering algorithm. Our method is based on the fuzzy c-means clustering algorithm and utilizes the Gene Ontology annotations as prior knowledge to guide the process of grouping functionally related genes. Unlike traditional clustering methods, our method is capable of assigning genes to multiple clusters, which is a more appropriate representation of the behavior of genes. Two datasets of yeast (Saccharomyces cerevisiae) expression profiles were applied to compare our method with other state-of-the-art clustering methods. Our experiments show that our method can produce far better biologically meaningful clusters even with the use of a small percentage of Gene Ontology annotations. In addition, our experiments further indicate that the utilization of prior knowledge in our method can predict gene functions effectively. The source code is freely available at http://sysbio.fulton.asu.edu/gofuzzy/.

Introduction

A clustering algorithm is often applied on microarray data to group genes whose similar expression patterns suggest that they may be co-regulated. Genes that are co-regulated may possibly be involved in a similar biological function. Among the clustering algorithms, hierarchical clustering and k-means clustering are most frequently used for microarray data. Both hierarchical and k-means clustering algorithms can be seen as traditional clustering approaches that generate partitions [1], in which each gene can be assigned to only one cluster.

However, it is commonly the case that the protein products of genes are involved in multiple biological processes and thus the genes producing these proteins can be co-regulated in different ways under different conditions. When a gene experiences differential co-regulation in different samples of the same dataset as a result of being involved in differing functional relationships, traditional clustering approaches are inadequately flexible to represent this behavior. Therefore, several papers [2-4] have proposed the use of fuzzy c-means clustering algorithm on gene expression data. Fuzzy c-means clustering [5] associates each variable with every cluster using a membership function that expresses the variable strength of the association. This produces sets of non-exclusive clusters that allow genes to have memberships in multiple clusters, rather than only in exclusive partitions. Using a fuzzy c-means algorithm to cluster microarray data has the advantage of being able to group genes exhibiting more than one type of co-regulation to multiple clusters. Variations of fuzzy c-means clustering have been proposed over the years, and among them are Fuzzy J-means [6] and FuzzySOM [7]. Fuzzy J-means addresses the issue of having the local minima as the final clustering results, while FuzzySOM extends the fuzzy c-means algorithm by incorporating the idea of self-organizing maps (SOM) [8] for the assignment of centroids.

While fuzzy clustering can increase the accuracy of the cluster representations, there remain several more fundamental sources of ambiguity in clustering. One of these problems is deciding what initial seeds to use to form clusters. Clustering techniques such as fuzzy c-means and k-means clustering algorithms require initial memberships of data points in the process of clustering. Both clustering algorithms rely on the random assignment of memberships of genes to the clusters as the initialization process. As a result, clustering results generated by traditional fuzzy c-means and k-means clustering algorithms suffer the drawback of producing inconsistent clustering results. In multiple runs of the same data, different initial cluster seedings do not converge to the same final set of clusters. To mitigate this problem, Gasch and Eisen [4] modified the initialization method of fuzzy c-means by performing PCA on eigenvectors that describe variation in thgene-expression data to seed centroids. Another source of ambiguity is the requirement of both fuzzy c-mean and k-means clustering algorithms is to specify k (or c in the case of fuzzy c-means), the number of clusters expected.

Once clusters are found, biological knowledge is employed to search for evidence of process-based association within the clusters. Gene Ontology (GO) annotations [9] are quite often used to associate each cluster with appropriate biological processes. Various computational tools and statistical methods have been proposed to detect such associations in the data resulting from expression profiling experiments [10-13].

In this study, we propose an enhanced version of the distance-based fuzzy c-means algorithm, named as GO Fuzzy c-means, that incorporates existing biological knowledge to initially assign and update memberships of genes to clusters. Particularly, we introduce the application of the prior knowledge available in GO annotations as a part of the process of clustering for our modified fuzzy c-means algorithm. The choice of GO annotation as a knowledge set for the method rather than protein-protein interaction data or pathway data is reasonable since it is the most widely applicable, best developed and well structured form of biological prior knowledge. However, the methodology proposed is not limited to the use of GO annotation as prior knowledge.

In related work, Cheng et al. [14] developed an algorithm that utilizes the similarity of genes based on the GO hierarchy to find gene clusters. The similarity of genes was further used to form a similarity matrix for the use of hierarchical clustering on gene expression data. Liu et al. [15] incorporates the GO hierarchy as prior knowledge into the subspace clustering algorithm. Fang et al. [16] utilized the GO hierarchy to determine clusters of genes but genes can only be assigned to already known functions. Huang and Pan [17] proposed an extension of a k-medoids algorithm by incorporating GO annotations. While genes of unknown functions can be assigned to clusters with genes of known functions, their method does not allow genes with known functions to be assigned to other clusters. This can potentially limit the ability to find new functions of already annotated genes by association with other known functions. Brameier and Wiuf [18] proposed a co-clustering algorithm using both expression profiles and GO annotations based on self-organizing maps (SOM) [8]. The method assigns cluster membership of genes initially by random so that the generated clusters can be inconsistent in different runs. On the other hand, the initialization step of our GO Fuzzy c-means algorithm allows the generation of repeatable clustering results and alleviates the need to predefine the number of clusters to be formed. The use of GO annotations as prior knowledge is not restricted to distance-based clustering algorithms. Pan [19] and Huang et al. [20] applied GO annotations to model-based clustering algorithms, which assumes the underlying data to follow some probability distributions. Chopra et al. [21] showed that by obtaining genes that are associated with the chosen biological processes in the process of clustering gene expression data, multiple biological contexts of the data can be identified.

The main idea behind our GO Fuzzy c-means algorithm is that by incorporating GO annotations in the cluster seed steps as well as the membership updating steps, genes involved in the same biological process are more likely to be assigned to the same clusters. The clustering results produced by GO Fuzzy c-means are consistent since it does not assign initial clusters randomly. As the algorithm uses existing biological knowledge to make more informed choices in the estimates of the number and membership of seed clusters, the results it produces could accommodate the known multiplicity of protein functions in a more natural manner and therefore more biologically meaningful compared to results produced by clustering algorithms without using prior knowledge. A further benefit of using GO Fuzzy c-means is the elimination of the extra manual effort to identify the functions associated with the clusters.

The use of prior knowledge is common in the area of semi-supervised learning in the machine learning community. The incorporation of even small amounts of labeled data improves the performance of classification and clustering of unlabeled data [22-24]. In the case of semi-supervised clustering techniques, a small amount of labeled data is used to facilitate the clustering results. The labels for the data usually come from domain knowledge, which can be seen as prior knowledge. Several semi-supervised versions of the k-means algorithm, such as seeded k-means [25], constrained k-means [26] and COP k-means [27], have been proposed to utilize partial label information.

Methods

Gene Ontology

The Gene Ontology (GO) [9] is a hierarchy of terms using a controlled vocabulary that includes three independent ontologies for biological process, molecular function and cellular component. Standardized terms known as GO terms describe roles of genes and gene products in any organism. GO terms are related to each other in the form of parent-child relationships. A gene product can have one or more molecular functions, can be used in one or more biological processes, and can be associated with one or more cellular components [9]. As a way to share knowledge about functionalities of genes, GO itself does not contain gene products of any organism. Rather, expert curators specialized in different organisms annotate biological roles of gene products using GO annotations. Each GO annotation is assigned with an evidence code that indicates the type of evidences supporting the annotation.

GO is an organism-independent ontology that covers a wide range of biological terms for the three different ontologies, containing tens of thousands of terms for each ontology. While it is informative for gene products to be annotated as specifically as possible, sometimes such details can complicate the process of analyzing genes, such as identifying the common functions of the genes. To aid the interpretation of GO, a set of general GO terms called GOSlim¹ terms is defined for various organisms as well as generic use. Examples of general GO biological process terms for yeast are “cell cycle” and “protein biosynthesis”.

In this paper, GOSlim biological process terms defined by SGD² were used to interpret the functions of genes at a general level. The use of GOSlim terms can be seen as a way to determine the similarity of genes. Suppose two genes are annotated to two different GO terms and the two GO terms are descendants of a GOSlim term, then we say that the two genes are similar due to the association with the same GOSlim term. Using this notion of similarity of genes, genes annotated to the same GOSlim term are assigned to the same initial cluster. Other common methods of measuring the similarity of genes using GO annotations are distance measures between GO terms based on levels and lowest common ancestors [28]. Using the number of levels that separate two different GO terms to determine similarity can sometimes be misleading, as the levels of details in GO in each sub-hierarchy can be arbitrary. Besides, making these measures is usually computationally expensive when dealing with a large number of genes.

Datasets

We applied our GO Fuzzy c-means algorithm to analyze two well-known yeast microarray datasets compiled from a variety of expression experiments [4, 29] that provide expression profiles for yeast carrying out a variety of cellular programs and responding to a variety of applied stimuli. The diversity of cellular activities represented by these compiled datasets provides a serious test of the ability to recognize multiple functionalities supported by genes. The first data set [29], denoted as dataset A, contains about 6200 genes with 80 samples, while the second data set [4], denoted as dataset B, contains about 6100 genes with 93 samples. There are 3962 genes in Set A and 3957 genes in Set B with GO functional annotations. The following versions of various data files were used in the results presented in this section: the Gene Ontology used in the study was created in September 2005³, the GOSlim terms by Saccharomyces Genome Database (SGD)⁴ were compiled on September 29, 2005 and the yeast GO annotation⁵ used was generated on September 30, 2005. The reason for using outdated GO annotations is to evaluate the ability of predicting new gene functions for our algorithm. However, the latest version of the annotations can be used with the algorithm.

GO Fuzzy c-means Algorithm

The fuzzy c-means clustering algorithm [5] is a variation of the popular k-means clustering algorithm, in which a degree of membership of clusters is incorporated for each data point. The centroids of the clusters are computed based on the degree of memberships as well as data points. The random initialization of memberships of instances used in both traditional fuzzy c-means and k-means algorithms lead to the inability to produce consistent clustering results and often result in undesirable clustering results [3]. We replace the random initialization of memberships with the use of gene annotations, so that clustering results generated by GO Fuzzy c-means are guaranteed to be repeatable. Since we utilize pre-defined classes in GOSlim, unlike the traditional fuzzy c-means and k-means algorithms, the number of clusters does not need to be determined ahead of time in GO Fuzzy c-means clustering.

In this section, we describe our modified fuzzy c-means algorithm called GO Fuzzy c-means by first describing how the initial memberships of clusters are assigned for each gene, which is an essential component that differs from a traditional fuzzy c-means algorithm. We then illustrate how to utilize gene annotations as well as gene expression values to update memberships for our GO Fuzzy c-means algorithm. To generate optimal clusters, a validity measure is used to verify that the clusters generated by GO Fuzzy c-means are compact with clear separation among them.

Initial membership assignment

Given a set of genes G, the corresponding GO annotations with respect to the biological process ontology are then utilized for the initialization of the fuzzy membership for the fuzzy c-means clustering algorithm. We utilize the set of GOSlim biological process terms defined by SGD [30] which have 32 GOSlim biological processes listed in Table 1. Genes are assigned to the GOSlim biological process terms, denoted as GO_BP, as follows. Each distinct GOSlim biological process term is considered as a cluster. Suppose gene g is associated with biological process bp according to the GO annotation, and bp is a descendant of sbp in the GO hierarchy, where sbp ∈ GO_BP. Then g is assigned to the general biological process sbp. The degree of belief for g to be in cluster associated with sbp depends on the evidence code of the GO annotation.

Table 1.

A list of 32 GOSlim biological process terms used in GO Fuzzy c-means

GO id	Description
GO:0007114	cell budding
GO:0016070	RNA metabolism
GO:0006091	generation of precursor metabolites and energy
GO:0030435	sporulation
GO:0005975	carbohydrate metabolism
GO:0006464	protein modification
GO:0016192	vesicle-mediated transport
GO:0000746	conjugation
GO:0007126	meiosis
GO:0007124	pseudohyphal growth
GO:0007049	cell cycle
GO:0006350	transcription
GO:0007047	cell wall organization and biogenesis
GO:0009653	morphogenesis
GO:0000910	cytokinesis
GO:0007010	cytoskeleton organization and biogenesis
GO:0030163	protein catabolism
GO:0006412	protein biosynthesis
GO:0019725	cell homeostasis
GO:0042254	ribosome biogenesis and assembly
GO:0006997	nuclear organization and biogenesis
GO:0006259	DNA metabolism
GO:0007165	signal transduction
GO:0006950	response to stress
GO:0006118	electron transport
GO:0006810	transport
GO:0006766	vitamin metabolism
GO:0006629	lipid metabolism
GO:0016044	membrane organization and biogenesis
GO:0006519	amino acid and derivative metabolism
GO:0006996	organelle organization and biogenesis
GO:0045333	cellular respiration

The idea of initial membership assignment can be illustrated by the following pseudo code:

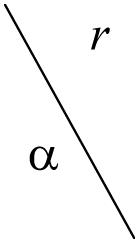
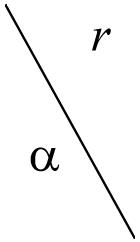
Let u_ij^(k) be the membership of gene g_i in cluster cl_j in the k-th iteration, in which cluster cl_j corresponds to biological process b_j. So u_ij⁽⁰⁾ represents the initial assignment of membership of gene g_i in cluster cl_j. Let p_ij be the degree of belief according to the evidence code that support the annotation g_i being associated with b_j, such that 0 ≤ p_ij ≤ 1. Let α, r be values between 0 and 1 (0 ≤ α, r < 1). Then, for each gene g_i,

1. Initialize u_ij⁽⁰⁾ as α · r.

2. If g_i is involved in biological process b_j, assign u_ij⁽⁰⁾ = p_ij (1 - α) + α · r. The most reliable evidence code is used if there are multiple evidence codes for the annotation.

The role of r is the degree of belief (constant) when g_i is not associated with b_j. While r intuitively should be a small constant, it is necessary to allow genes that are not known to be associated with b_j to be assigned to b_j based on their transcriptional patterns. The role of α in the assignment of u_ij⁽⁰⁾ is to allow variation in the degreeof dependency of the membership u_ij^(k) on gene annotation and gene expression (see the algorithm for details). When α = 0, it implies that the assignment of membership is totally dependent upon gene annotation. On the other hand, the assignment of membership is less dependent on gene annotation when α approaches 1. Assignment of membership is dependent on both gene annotation and gene expression values when 0 < α < 1.

GO Fuzzy c-means algorithm

Once initial membership is assigned to each gene based on GO annotations, we now proceed to update the membership of each gene to clusters based on both data and GO annotations. The algorithm to update the memberships as well as initial membership assignment is illustrated in the following.

Let x_i be a vector of expression values for gene g_i.

1. Initialize membership u_ij of gene g_i of cluster cl_j, as described in the previous subsection, so that U⁽⁰⁾ = [ u_ij ], the validity of cluster measure S* = ∞, fuzzy centroid C* = C⁽¹⁾, fuzzy membership U* = U⁽⁰⁾. U⁽⁰⁾ is obtained from GO annotations.

2. At the k-th step, compute the fuzzy centroid C^(k) = [ c_j ] for j = 1, .., n_c, where n_c is the number of clusters, using

   $${\mathbf{c}}_j=\sum _{i=1}^n(u_{ij}{)}^m{\mathbf{x}}_i/\sum _{i=1}^n(u_{ij}{)}^m,$$

   where m is the fuzzy parameter, x_i is the expression vector for gene g_i, and n is the number of genes.
3. Update the fuzzy membership U^(k) = [ u_ij ], usingwhere

   $$\begin{array}{cc}\hfill u_{ij}={u_{ij}}^{\prime }/\sum _{k=1}^{n_c}{u_{ik}}^{\prime }& ,\hfill \\ \hfill \text{where}{u_{ij}}^{\prime }={\left(\frac{1}{\Vert {\mathbf{x}}_i-{\mathbf{c}}_j\Vert }\right)}^{\frac{1}{(m-1)}}/\sum _{j=1}^{n_c}{\left(\frac{1}{\Vert {\mathbf{x}}_i-{\mathbf{c}}_j\Vert }\right)}^{\frac{1}{(m-1)}}\times {u_{ij}}^{\left(0\right)}& \hfill \end{array}$$
4. Compute validity of cluster measure S using

   $$S=\frac{\sum _{i=1}^n\sum _{j=1}^{n_c}{u_{ij}}^2{\Vert {\mathbf{c}}_j-{\mathbf{x}}_i\Vert }^2}{n\underset{i,j}{\text{min}}{\Vert {\mathbf{c}}_j-{\mathbf{c}}_i\Vert }^2}$$

5. If S < S*, then S* = S, C* = C^(k) and U* = U^(k).

6. Repeat steps 2 to 6 until stopping criteria.

The stopping criterion for GO Fuzzy c-means is when a predetermined number of iterations are reached. When the algorithm reaches the stopping criteria, the optimal cluster C* and memberships U* are the output of the algorithm. A cluster is determined as optimal if S, the validity measure of the cluster, is minimal among the iterations. The fuzzy parameter m in step 2 is set to 2. Notice that steps 3 and 4 are different from the original fuzzy c-means algorithm, in the sense that the initial membership derived from GO annotations is also utilized during the update of membership. Step 4 is a measure of validity of clusters [31], in which the minimal S produces the most compact clusters but with the furthest separation between the clusters. We say that a gene g_i is potentially associated with biological process b_j if u_ij^(*) > δ, where δ was set as 0.05 in our experiments. While GO Fuzzy c-means, as in the original fuzzy c-means algorithm, is able to assign instances to multiple clusters, there is no clear distinction between uncertain cluster membership and membership in multiple clusters. The source code of GO Fuzzy c-means implementation is freely available at http://sysbio.fulton.asu.edu/gofuzzy/.

Results

One of the main differences between fuzzy c-means clustering and other typical clustering algorithms is that fuzzy c-means allows an instance to be assigned to multiple clusters. This key feature allows a more suitable representation of the relationships of genes, as gene products are usually involved in multiple roles in the functioning of the cell. Using datasets A and B (described in Methods section), Table 2 shows that about 50% of the assigned genes (i.e. genes assigned to at least one of the 32 clusters) belong to moren 1 cluster in the clustering results produced by GO Fuzzy c-means. Such multifunctional behavior cannot be represented by traditional clustering algorithms such as hierarchical and k-means. In addition, the proposed method provides another advantage; each cluster generated by our method is automatically annotated with certain biological processes. This alleviates the need for a complete secondary analysis (biological interpretation) of each of the clusters, which can be a time-consuming process.

Table 2.

Assignment of genes to clusters for both datasets A and B with value of membership cutoff = 0.05

	Number of genes assigned	Number of genes assigned to > 1 cluster
Dataset A (α = 0.3, r = 0.2)	4067	1979 (48.66%)
Dataset B (α = 0.1, r = 0.3)	4111	2054 (49.96%)

Another unique feature of our GO Fuzzy c-means algorithm is that the initial assignment of the membership relies on the GO annotation. Every GO annotation comes with an evidence code indicating the type of experiments supporting the annotation. The evidence codes can be used as a measure of reliability of the annotation, and such evidence codes are used as degrees of belief of the annotation for the initial assignment. Table 3 shows the degrees of belief assigned for various evidence code, based on the hierarchy of reliability of GO evidence⁶. When there is no GO support for assigning a gene to a particular cluster, it can be assigned based solely on expression data. In this case, a small degree of belief r is assigned.

Table 3.

Degrees of belief assigned according to the evidence code

Evidence code	Degree of belief
TAS, IDA	0.9
IMP, IGI, IPI	0.8
IC, RCA, ISS, IEP	0.7
NAS	0.6
IEA	0.5

Optimality of clusters

We first analyzed the effect of α and r, the level of dependency on gene annotation and the degree of belief for no annotation support, on the quality of clusters in terms of cluster compactness and separation. Different degrees of α allow varying the influence of the gene annotations and gene expression values in determining the gene memberships in each cluster. The compactness was measured by a well-known validity measure [31, 32], based on a ratio of cluster compactness to separation. The biological significance of the clusters, denoted as the z-scores, was measured as well using ClusterJudge [33]. The higher the value of the z-score, the less chance for the clusters to be produced by random, which indicates the biological significance of the clusters. Tables 4 and 5 show the values of validity (computed as in step 4 of the algorithm Materials and Methods) and z-scores, for the clusters formed using different degrees of α and r. From the values presented in Tables 4 and 5, it can be seen that the clustering results achieve the most compact clusters with furthest separation between the clusters when α = 0.3 and r = 0.2 for dataset A and α = 0.1 and r = 0.3 for dataset B. This suggests that highly compact clusters can be achieved with the use of both gene annotation and gene expression values. The optimal clustering results can be downloaded from http://sysbio.fulton.asu.edu/gofuzzy/ and the results can be visualized using MapleTree⁷.

Table 4.

Validity of clusters depending on different degrees of α for dataset A. Two measures were used: compactness and separation [31] and z-scores [33], shown in parentheses. The z-scores are computed as an average of 10 repetitions for each pair of α and r.

	0.1	0.2	0.3	0.4	0.5
0.00	58.1 (318.5)	58.1 (318.5)	58.1 (318.5)	58.1 (318.5)	58.1 (318.5)
0.10	45.1 (323.1)	35.5 (327.8)	29.4 (315.7)	25.6 (337.1)	23.0 (320.9)
0.20	33.7 (315.4)	24.1 (330.0)	20.3 (330.1)	19.6 (348.0)	24.0 (326.1)
0.30	26.2 (327.3)	19.5 (322.6)	24.9 (335.5)	37.8 (323.7)	58.9 (322.2)
0.50	19.6 (327.0)	50.9 (316.2)	126.5 (331.3)	247.0 (338.8)	432.1 (335.4)
0.70	72.5 (328.2)	363.4 (326.8)	1002.6 (335.6)	2033.6 (307.6)	3480.0 (270.3)

Table 5.

Validity of clusters depending on different degrees of α for dataset B. Two measures were used: compactness and separation [31] and z-scores [33], shown in parentheses. The z-scores are computed as an average of 10 repetitions for each pair of α and r.

	0.1	0.2	0.3	0.4	0.5
0.00	58.8 (317.9)	58.8 (317.9)	58.8 (317.9)	58.8 (317.9)	58.8 (317.9)
0.10	35.9 (316.6)	26.6 (319.6)	23.6 (330.4)	27.4 (336.9)	30.6 (326.4)
0.20	24.8 (322.9)	29.1 (327.2)	31.5 (333.7)	29.6 (332.4)	29.5 (318.7)
0.30	26.9 (329.2)	30.5 (332.5)	30.5 (322.1)	45.4 (338)	60.2 (327.7)
0.50	29.6 (329.1)	53.5 (324.1)	113.0 (323.5)	226.9 (322.6)	325.4 (329.1)
0.70	70.0 (334.8)	289.4 (332.4)	614.1 (320.8)	1090.6 (315.8)	1708.6 (253.9)

It is also important to investigate the effects of the different degrees of α and r on the goodness of the clusters with respect to the biological meaning. The z-scores indicate that quality of the clusters is not significantly different from each other, except in one case when α = 0.5 and r = 0.5. This shows that the quality of the clusters produced are robust, in terms of z-score, despite of the values of α and r.

Influence of the richness of GO annotations

From the previous sub-section, it becomes apparent that optimality of the clusters is reached when α is small, meaning a higher dependence of the use of GO annotations in the process of clustering. We also investigated how the richness of the GO annotations affects the performance of GO Fuzzy c-means. This allows us to gain insights in the performance of GO Fuzzy c-means when it is applied to organisms that do not have annotations as rich as yeast.

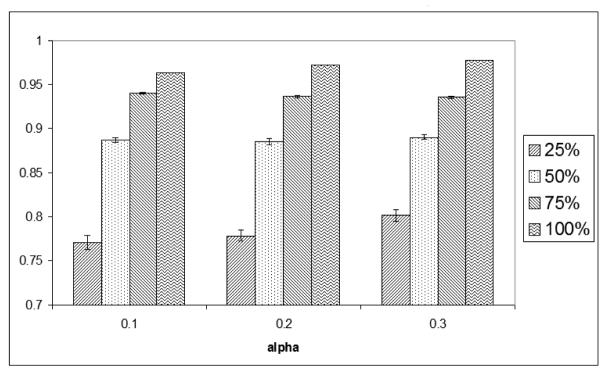
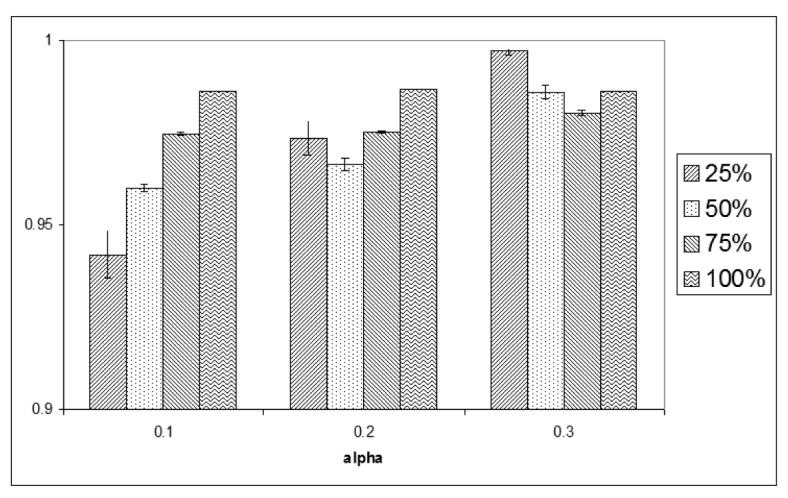
We explored the effects of the richness of the GO annotations on GO Fuzzy c-means by performing experiments using 25%, 50% and 75% of the original GO annotation, and compare the clustering results against the original GO annotation (100%). The evaluation was performed by estimating the accuracy of the assignment of functions of all the genes in the optimal clusters using the original GO annotations as the reference. This acts as a measure of the overall quality of the assignment of gene functions. Tables 6 and 7 show the number of annotations used and the number of genes assigned for different samplings of the original annotation. The overall accuracies of formed clusters are 77% - 99%, as illustrated in Figures 1 and 2. The results showed that despite using various degrees of annotation, high rates of accuracy are achieved in assigning genes to correct GO clusters according to the original full annotation. These results show that GO Fuzzy c-means is suitable to be applied to the analysis of gene expression data that involve organisms whose annotations are not as rich as yeast.

Table 6.

Average number of annotations randomly sampled in 30 repetitions from the original 7483 annotations with respect to the genes in dataset A. Anno_i% indicates the percentage of GO annotation used.

	Anno25%	Anno50%	Anno75%
α = 0.1	1855.23	3735.00	5601.00
α = 0.2	1853.93	3747.77	5610.23
α = 0.3	1881.00	3744.37	5615.93

Table 7.

Average number of annotations randomly sampled in 30 repetitions from the original 7454 annotations with respect to the genes in dataset B. Anno_i% indicates the percentage of GO annotation used.

	Anno25%	Anno50%	Anno75%
α = 0.1	1525.37	2606.73	3371.67
α = 0.2	1528.53	2612.23	3379.13
α = 0.3	1548.20	2611.63	3379.00

Figure 1.

Accuracy of the assignment of gene functions by GO Fuzzy c-means using various degrees of GO annotations for dataset A.

Figure 2.

Accuracy of the assignment of gene functions by GO Fuzzy c-means using various degrees of GO annotations for dataset B.

Performance comparison

We compared the performance of GO Fuzzy c-means with FuzzyK [4], which is a modification of the fuzzy c-means algorithm, using datasets A and B. To achieve a fair comparison, we set the number of clusters k to be 32 for FuzzyK, which is the same number of clusters generated by GO Fuzzy c-means. The membership cutoff value was chosen as 0.08, which is the same value reported in [4]. As shown in Table 8, the z-scores computed by ClusterJudge [33] indicate that GO Fuzzy c-means using 25% of the annotation performs about the same with FuzzyK. However, GO Fuzzy c-means has a better performance over FuzzyK when 50 or higher percentage of annotation was used. We compared our GO Fuzzy c-means algorithm with other fuzzy clustering techniques, such as regular fuzzy c-means and FuzzySOM. Using the implementation in WEKA [34], we configured the algorithms by setting the number of clusters to be 32 with the fuzzy parameter as 1.2, and the maximum iterations as 500. Euclidean distance was used as for the computation of similarity. As indicated in Table 8, we can see that GO Fuzzy c-means performs significantly better. We also performed a similar comparison with FLAME [34], which is a fuzzy clustering algorithm that is capable of handling non-linear relationships and non-globular clusters. Since the number of clusters is automatically determined by FLAME, the default setting (number of k-nearest neighbors = 10 with the maximum number of approximation = 500) was used to perform clustering on datasets A and B. Using Euclidean distance for the computation of similarity, 21 and 28 clusters were generated by FLAME for both datasets A and B. We showed that GO Fuzzy c-means also performs better compared to FLAME as illustrated in Table 8.

Table 8.

Comparison of the clustering performance among GO Fuzzy c-means, FuzzyK, SOM and Gaussian mixture model using datasets A and B. GOFuzzy_x% represents x percentage of GO annotation was used in GO Fuzzy c-means. ClusterJudge [33] was used to compute the z-scores with 10 runs for each of the clustering results. A clustering result with higher z-score indicates that the clusters are more likely to be biologically relevant.

Method	z-scores and standard error for Dataset A	z-scores and standard error for Dataset B
GOFuzzy25%	91.18 ± 3.22	119.10 ± 3.47
GOFuzzy50%	175.90 ± 4.68	181.20 ± 3.36
GOFuzzy75%	248.40 ± 3.81	255.10 ± 4.65
GOFuzzy100%	323.10 ± 7.59	316.60 ± 6.04
FuzzyK	102.33 ± 1.85	108.10 ± 2.32
Fuzzy c-means	68.08 ± 5.52	83.12 ± 4.57
FuzzySOM	68.56 ± 2.66	81.48 ± 5.43
FLAME	66.18 ± 4.83	85.55 ± 5.93
SOM	44.13 ± 0.61	52.62 ± 0.30
Gaussian	0.72 ± 0.030	73.55 ± 0.77

We performed further comparisons of GO Fuzzy c-means with other state-of-the-art clustering methods that do not utilize prior knowledge such as self-organizing maps (SOM) [8] and Gaussian mixture model. The implementations used in our experiments for SOM and Gaussian mixture model were obtained from [35] and [36]. As in the comparison with FuzzyK, we set the number of clusters to be 32 for both SOM and Gaussian mixture model, with the maximum number of iterations of 100,000 and 100 respectively. Since SOM is a non-deterministic algorithm, we performed 5 runs for both datasets. As in Table 8, we can observe that GO Fuzzy c-means outperforms SOM and Gaussian mixture model clustering algorithms for both datasets. While it is more reasonable to compare our GO Fuzzy c-means with other clustering algorithms that utilize prior knowledge, it is unfortunate that the current implementations of these algorithms are not implemented for general use. Thus, it is not feasible to perform such comparison.

Initialization of clusters

We compared the clusters between initialization of cluster memberships of genes based on gene annotations and random initializations. We found that similar clusters were achieved when using random initialization of memberships with update of memberships dependent on both expression values and gene annotations. However, our initialization method ensures that the clustering results for both datasets were deterministic.

Function prediction

Clustering of genes based on expression behavior is a powerful way to uncover unknown functions of genes. By assigning genes with unknown functions to a group of genes whose functions have already been identified, the functions of the unannotated genes can then be inferred based on the similarity of their expression profiles. While the majority of the genes assigned in our clustering results are consistent with the gene annotations, it is important to study the genes that have new assigned functions that were not previously known. Tables 9 and 10 show the number of genes with newly proposed functions for datasets A and B, respectively. These genes have been further investigated. One interesting finding is that the gene YER036C is clustered in the group GO:42254 in our clustering results for both datasets A and B. This suggests that YER036C is involved in ribosome biogenesis and assembly. The GO annotation from SGD which was used to generate the clusters was created in September 2005. From this version of the annotation, YER036C was assigned to biological process unknown (GO:0000004). According to SGD [30], YER036C was assigned a new name ARB1 (ATP-binding cassette protein involved in Ribosome Biogenesis), and was assigned to be involved in ribosome biogenesis on Jan 5, 2006 based on the published article [37]. The correct assignment of the gene function of ARB1 can be explained by the similarity of the expression values of ARB1/YER036C with the values of the genes that are annotated to be involved in ribosome biogenesis. Similarly, the correctness of the gene function assignment based on the latest GO annotation dated in July 2006 is confirmed for 6 other genes. The genes ALB1/YJL122W [38] and RSA4/YCR072C [39] are assigned to the cluster that corresponds to ribosome biogenesis using datasets A and B, in which the genes are associated with ribosomal large subunit biogenesis (GO:0042273) and ribosomal large subunit assembly and maintenance (GO:0000027) respectively according to the latest GO annotation. While not as specific, SAE3/YHR079C-A⁸ [40, 41] is assigned to the cluster that corresponds to meiosis (GO:0007126) using dataset A, and TMA19/YKL056C [42], ASC1/YMR116C [43] and ZUO1/YGR285C [44] are assigned to protein biosynthesis (GO:0006412) using dataset B. These genes are summarized in Table 11.

Table 9.

Number of genes identified to have previously unknown functions for dataset A using all 3962 genes with annotations (α = 0.3, r = 0.2)

Cluster	Number of genes in cluster	Number of genes with new functions
GO:6412	465	9(1.94%)
GO:7049	332	1(0.30%)
GO:30435	160	57 (35.62%)
GO:42254	267	32 (11.99%)
GO:7126	156	29 (18.59%)

Table 10.

Number of genes identified to have previously unknown functions for dataset B using all 3957 genes with annotations (α = 0.1, r = 0.3)

Cluster	Number of genes in cluster	Number of genes with new functions
GO:6091	168	13 (7.74%)
GO:6412	535	73 (13.64%)
GO:16070	463	22 (4.75%)
GO:5975	230	39 (16.96%)
GO:6118	45	18 (40.0%)
GO:45333	89	5 (5.62%)
GO: 6950	385	5 (1.30%)
GO:910	100	5 (5.00%)
GO:42254	314	79 (25.16%)

Table 11.

List of genes with correct assignment of gene functions by GO Fuzzy c-means that are confirmed by the latest GO annotation. The number in the bracket [] (the second column) indicates the level of depth of SGD GO terms under GO terms assigned by GO Fuzzy c-means.

Systematic / Standardized name	Assigned by SGD	Assigned by GO Fuzzy c-means	Reference
YER036C/ARB1	ribosome biogenesis  (GO:0007046) [1]	ribosome biogenesis and  assembly (GO:0042254)	Dong et al., 2005
YJL122W/ALB1	ribosomal large subunit  biogenesis (GO:0042273) [2]	ribosome biogenesis and  assembly (GO:0042254)	Lebreton et al., 2006
YCR072C/ RSA4	ribosomal large subunit assembly and maintenance (GO:0000027) [3]	ribosome biogenesis and  assembly (GO:0042254)	de la Cruz et al., 2005
YHR079C-A/SAE3	meiotic DNA recombinase assembly (GO:0000707) [3]	meiosis (GO:0007126)	Hayase et al., 2004; Tsubouchi and Roeder, 2004
YKL056C/ TMA19	Translation (GO:0043037) [1]	protein biosynthesis  (GO:0006412)	Fleischer et al., 2006
YMR116C/ASC1	negative regulation of  translation (GO: 0016478) [3]	protein biosynthesis  (GO:0006412)	Gerbasi et al., 2004
YGR285C/ZUO1	regulation of translational  fidelity (GO:0006450) [3]	protein biosynthesis  (GO:0006412)	Rakwalska and Rospert, 2004

Further analysis of the cluster GO:16070 for dataset B reveals genes with known interactions being assigned to the same cluster. CNS1, HGH1 and CPR7 are members of this cluster. According to Yeast GRID⁹, CNS1 is known to interact with HGH1 physically [45], while CPR7 has genetic interaction with CNS1 based on various evidence including MIPS [46-48]. The clustering results also suggest some potential interactions within the members of the clusters.

Conclusion

The methodology of utilizing prior knowledge to guide clustering is common among semi-supervised clustering algorithms [25-27]. Our modified version of the fuzzy c-means clustering algorithm is capable of generating consistent clusters by assigning initial clusters using prior knowledge. In this paper, we illustrated the capability of our algorithm by incorporating GO annotations as prior knowledge for clustering gene expression data. This modified form of clustering can be seen as a template for the use of other biological data such as protein-protein interaction and pathway data. By following the approach of using prior biological knowledge for the fuzzy c-means algorithm, other clustering algorithms such as hierarchical and k-means can be adapted to use prior biological knowledge as well. As the clustering results generated by GO Fuzzy c-means are consistent with GO annotations, and this approach can identify previously unknown functions for genes as well, this method has clear biological relevance.

Some of the unique features that distinguish our GO Fuzzy c-means from the one used in the previous study [4] are: (i) the user no longer needs to define the number of clusters, and (ii) the biological annotation of the generated clusters is now automatically assigned. Both are significant advantages, as it is usually non-trivial to define an appropriate number of clusters and time-consuming to analyze the clusters of genes directly from literature. Huang and Pan [17] proposed an extension of a k-medoids algorithm by incorporating GO annotations. While genes of unknown functions can be assigned to clusters with genes of known functions, their method does not allow genes with known functions to be assigned to other clusters. This can potentially limit the ability to find new functions of already annotated genes by association with other known functions.

On the other hand, there are certain limitations of the current GO Fuzzy c-means algorithm. It is important to notice that it is not conclusive if the cluster membership of a gene is assigned by chance, in particular for the membership values that are low. The number of clusters is dependent on the number of GOSlim biological process terms, which can be seen as general GO biological process terms, and only GOSlim biological processes can be identified other than the GOSlim biological processes used in the algorithm. However, one can expand GOSlim terms or use other more extensive prior knowledge without modifying the basic algorithm described in the paper. It is also important to note that the GO Fuzzy c-means algorithm can be applied to organisms other than the budding yeast Saccharomyces cerevisiae. Our method presented in this paper utilizes the GOSlim biological process terms for yeast, but there are other kinds of GOSlim terms defined for various organisms that can be used instead. Given the gene expression data and the prior knowledge, the ability for GO Fuzzy c-means to generate consistent clustering results as a global view of the data is important. However, as demonstrated in work by Chopra [21], different clustering results can be obtained for the same gene expression data by choosing different biological processes to analyze. It is important to investigate how such local context can be incorporated into our algorithm as future work. As in traditional fuzzy c-means clustering algorithm, determining the value of membership cutoff is fairly arbitrary. However, the choice of 0.05 as the membership cutoff value is intuitively reasonable, as it is higher than the uniformly distributed membership (0.03125). The choice of this membership cutoff value is also justified by the observation that about 96% of the genes had membership values of ≤ 0.05, while about 3.6% of the genes had membership values of ≥ 0.1. Another limitation of our algorithm is that the value of α needs to be experimentally determined. It should also be mentioned that since this algorithm is by design strongly biased towards clustering based on the type of prior knowledge used, it is probably not best suited for clustering where associations based on that particular type of prior knowledge are not directly related to the analysis.

While there are certain limitations to GO Fuzzy c-means, the reported results demonstrate that incorporating prior knowledge improves the coherence of the clusters relative to the knowledge domain. Similarly, the ability to assign memberships of genes to multiple clusters improves the biological relevance by allowing the representation of the diverse roles of genes. The experimental results suggest that GO Fuzzy c-means is quite efficient in exploiting even a small percentage of GO annotations in order to assign gene functions. This implies that our GO Fuzzy c-means algorithm will be very useful when applied to gene expression data for organisms in which the annotations are not as rich as in yeast. Our results also show that GO Fuzzy c-means outperforms the state-of-the-art clustering algorithms such as SOM and Gaussian mixture model using a small percentage of GO annotations. This suggests that the use of GO annotations improves the prediction of correct gene functions.