Abstract
Accurate arterial centerline extraction is essential for comprehensive visualization in CT Angiography. Time consuming manual tracking is needed when automated methods fail to track centerlines through severely diseased and occluded vessels. A previously described algorithm, Partial Vector Space Projection (PVSP), which uses vessel shape information from a database to bridge occlusions of the femoropopliteal artery, has a limited accuracy in long (>100 mm) occlusions. In this article we introduce a new algorithm, Intermediate Point Detection (IPD), which uses calcifications in the occluded artery to provide additional information about the location of the centerline to facilitate improvement in PVSP performance. It identifies calcified plaque in image space to find the most useful point within the occlusion to improve the estimate from PVSP. In this algorithm candidates for calcified plaque are automatically identified on axial CT slices in a restricted region around the estimate obtained from PVSP. A modified Canny edge detector identifies the edge of the calcified plaque and a convex polygon fit is used to find the edge of the calcification bordering the wall of the vessel. The Hough transform for circles estimates the center of the vessel on the slice, which serves as a candidate intermediate point. Each candidate is characterized by two scores based on radius and relative position within the occluded segment, and a polynomial function is constructed to define a net score representing the potential benefit of using this candidate for improving the centerline. We tested our approach in 44 femoropopliteal artery occlusions of lengths up to 398 mm in 30 patients with peripheral arterial occlusive disease. Centerlines were tracked manually by four-experts, twice each, with their mean serving as the reference standard. All occlusions were first interpolated with PVSP using a database of femoropopliteal arterial shapes obtained from a total of 60 subjects. Occlusions longer than 80 mm (N=20) were then processed with the IPD algorithm, provided calcifications were found (N=14). We used the maximum point-wise distance of an interpolated curve from the reference standard as our error metric. The IPD algorithm significantly reduced the average error of the initial PVSP from 2.76 to 1.86 mm (p<0.01). The error was less than the clinically desirable 3 mm (smallest radius of the femoropopliteal artery) in 13 of 14 occlusions. The IPD algorithm achieved results within the range of the human readers in 11 of 14 cases. We conclude that the additional use of sparse but specific image space information, such as calcified atherosclerotic plaque, can be used to substantially improve the performance of a previously described knowledge-based method to restore the centerlines of femoropopliteal arterial occlusions.
Keywords: CT angiography, peripheral arterial occlusive disease, vascular centerlines, curved planar reformation, principal component analysis, eigenshape, calcification, circular Hough transform, canny edge detector
INTRODUCTION
The problem of missing data appears frequently in lower extremity CT angiography (CTA) postprocessing—specifically in the form of occluded vessels. In patients with peripheral arterial occlusive disease (PAOD) calcified and noncalcified atherosclerotic plaque accumulates on the luminal surface of the major conducting arteries, resulting in progressive narrowing and∕or occlusion of the arterial flow channels. Complete arterial occlusions occur most commonly in the distal superficial femoral artery and the proximal popliteal artery—or femoropopliteal artery.1
Visual assessment of plaque composition and measurement of occlusion lengths is important for treatment planning and is facilitated by the generation of curved planar reformations (CPRs) through the centerlines of the arterial tree.2 Accurate computation of arterial centerlines is a major problem in occluded vessels, however, because contrast-medium enhanced blood cannot reach the occluded segments of a diseased vessel. Since the CT attenuation value of noncalcified plaque and organized thrombus within an occluded segment is similar to surrounding soft tissues, occluded vessels are inconspicuous and difficult to track automatically. In these cases an expert user has to manually extract the centerlines using his or her anatomic knowledge and, if present, additional visual clues such as the shape and location of calcified atherosclerotic plaque within the occluded artery.
In an attempt to overcome the limitations of density and gradient based approaches to extract the centerlines of occluded arteries we have developed a knowledge-based method that is purely based on shape similarity between femoropopliteal centerlines, called Partial Vector Space Projection (PVSP).3 The PVSP algorithm produced clinically acceptable results for occlusions up to about 100 mm in length, but failed to consistently produce a centerline that stays inside the artery (i.e., with error <3 mm) for longer occlusions. In this article we describe an approach to improve the results of the shape-based centerline extraction, so that it will produce clinically acceptable results in longer occlusions, by automatically finding and selecting a single reliable clue (intermediate point) in image space. We first use the previously described knowledge-based PVSP algorithm to obtain an initial estimate of the centerline. Next, we use a new Intermediate Point Detection (IPD) algorithm to search the image space data for calcified plaque, which may provide additional information regarding the location of the centerline in the occluded region. If the shape of an arterial calcification of appropriate size is crescent- or ring-like, and thus delineates a portion of the vessel wall, this provides a reliable clue to a point through which the centerline must pass. Even smaller blob-shaped calcifications may be useful for reducing the error of PVSP in long occlusions. The new IPD algorithm also includes a prediction model to estimate which of all possible intermediate point candidates is likely to improve the initial shape-based estimate the most.
This paper is organized as follows. Section 2 presents an overview of previous work on centerline estimation and feature detection used in this paper. Section 3 briefly explains the previously described PVSP algorithm followed by a detailed description of the new IPD algorithm. Sections 4, 5 describe the experiments carried out to validate the algorithm and the results. In Secs. 6, 7 we discuss the results and limitations of the method and draw conclusions.
RELATED WORK
When the lumen of a normal arterial segment contains contrast medium, tracking can be accomplished using intensity information from the CT data by cost function minimization,4 by using the connected components with minimal path technique,5 by using flux driven algorithms,6 and by skeletonization.7
As such there is very little literature about tracking centerlines through significantly diseased arteries, where there is no or very little contrast. La Cruz et al. (2004)8 used nonlinear model fitting to improve the centerline estimate of severely diseased but patent arteries in patients with PAOD. Tran et al. (2007)9 showed that it is possible to use the contralateral side to find center-lines through occluded femoropopliteal arterial segments. Such an approach makes use of only one curve as prior knowledge, and its success is limited by the similarity of shapes between the left and the right side. A database of centerlines can also be exploited to bridge occlusions,3 but has limited accuracy for long (>100 mm) occlusions. Since the prevalence of these long occlusions is common, the clinical applicability of PVSP alone is limited.
The new technique we describe in this article uses the Canny edge detector10 and the Hough transform for circles.11 The Canny edge detector is known to be robust in the presence of noise and has been used in medical image processing for applications such as in retinal vessel detection12 and cardiovascular image segmentation,13 among others. The Hough transform for circles is also a popular tool for detecting circles, especially when parts of circular objects are obscured. This technique too has been used in applications such as retinal image processing.14, 15
The contribution of our work is the combination of knowledge-based and image-based techniques to bridge arterial occlusions. Although image space information is sparse and inadequate for automated centerline extraction, particular features in image space can be very specific. One or several points might thus be used to improve an imperfect initial shape-based initial estimate of the entire occlusion length.
METHOD: ALGORITHMS
Two algorithms are discussed in this section, namely, Partial Vector Space Projection (PVSP) and Intermediate Point Detection (IPD). Since PVSP has been previously described,3 it is only discussed briefly in this paper. IPD augments PVSP to improve the results of shape-based centerline extraction, and is presented in detail.
Partial vector space projection (PVSP)
The shapes of femoropopliteal centerlines from different subjects are similar to each other. This similarity can be used to estimate the missing segments of incomplete centerlines. The PVSP algorithm is designed obtain an estimate of the missing segment of a centerline based on the shape of the available segments and a database of centerlines. PVSP computes the basis functions of the centerlines in the database and fits them to incomplete centerlines to obtain estimates of the missing segments.
In this algorithm the end points of the femoropopliteal artery are manually identified. The femoropopliteal artery is to lie between the common femoral artery bifurcation and the popliteal bifurcation. In cases of anatomic variants such as a high (above knee) takeoff of the anterior or posterior tibial arteries, the distal end point of the femoropopliteal artery was defined at the level of the typical takeoff of the anterior tibial artery, at the inferior aspect of the tibio-fibular joint. Then the vessel centerlines are parameterized in oriented frames of reference (OFRs). These frames of references are oriented along the line connecting the two ends of the femoropopliteal artery (common-femoral and popliteal bifurcations). If V is a centerline vector constructed by stacking the X and the Y coordinates of the centerline and B is a matrix of significant principal components of a database of centerlines, then the equation
| (1) |
says that a centerline can be represented as a linear combination of principal components of a database. Since V is not completely known we can write
| (2) |
and
| (3) |
where Vk and Vu correspond to the known and unknown parts of the centerline vector V, respectively. Bk and Bu are constructed by splitting the corresponding rows of matrix B. We estimate Vu in terms of the pseudo-inverse of Bk as
| (4) |
A linear correction term is then added to make the estimate continuous at the end points of the occluded segment. The results in Rakshe et al. (2007)3 show that the estimates were acceptable up to the occlusion length of about 100 mm. The error metric used is called the maximum departure (MD) error. The two centerlines (estimated and reference standard) have an equal number of points, and there is a point-to-point correspondence between them. The MD error is defined as the maximum of the distances between pairs of corresponding points between the two centerlines in the occluded segment and we use this error metric for all of the error measurements in this paper.
Intermediate point detection (IPD)
We based our method for finding an intermediate point on the way it would be done by human readers, i.e., by searching through 2D cross sections for candidates, and using the calcification position and shape to estimate the vessel center on the cross section. In addition we compute features of each calcification and use them to attempt to find the one that will improve the estimate the most. To achieve this we first identify groups of calcified voxels in a restricted region of interest around the initial estimate. Then we detect the edges of these calcifications and fit a circle to the portion of the edge adjacent to the presumed vessel wall. The center of this circle is a candidate intermediate point.
Then we use a linear weighted sum model of characteristic properties of each of these points to predict which of the candidate intermediate points is most useful to reduce the error of the initial estimate. The best candidate is then selected and used as an additional input to the PVSP algorithm, which is then re-run to obtain a more accurate path.
To summarize, the IPD algorithm consists of the following steps: (1) identifying groups of calcified voxels, (2) detecting calcification edge, (3) circle fitting to obtain intermediate point candidates, (4) computing characteristic scores for the candidates, (5) using a weighted sum model to pick the best candidate, and (6) using the intermediate point. These steps are described in detail below.
Identifying groups of calcified voxels
Finding vascular calcification in CT scans is not trivial. Simple thresholding does not work, as partial volume around the edges of bones and calcifications will have artificially depressed intensities, and reducing the threshold to include these edges will result in many soft-tissue voxel inclusions. Also, there are many false candidates from other structures, perhaps even calcification in other blood vessels. In response, we developed our algorithm to search in a restricted space, to find clusters of minimum size, and to replace partial-volume limited calcification edges. The following paragraphs describe these steps.
Let Ep be the initial estimate of the center line in an occlusion, obtained by the PVSP algorithm. Let L(Ep) be the length of the estimate Ep. We define the region of interest (ROI) as a double cone-like zone in three dimensions around the initial estimate Ep. The largest radius of the double cone appears at the midpoint of Ep, where it is set to 4.5% of L(Ep). This comes from the fact that the 90th percentile of the error from the PVSP in simulated occlusions is within 4.5% of the occlusion length.3 Figure 1 illustrates this concept in 2D, with the shaded region representing the ROI around the initial estimate Ep. In this ROI we consider voxels above intensity of 400 Hounsfield Units (HU). On each axial CT slice, any candidate voxel that did not have a connection to another candidate voxel in an eight-voxel neighborhood on that slice is rejected as being “too small.” Also, any similarly connected group of candidate voxels that have farthest voxels more than 20 mm apart were rejected as being “too big,” since calcification is not likely to be spread across such a wide region on a single slice. All the remaining candidate voxels are then labeled as those belonging to calcification. Each of these connected sets of calcined voxels provides a conservative estimate of the complete calcification it belongs to. Each of these sets will be referred to as a “seed” for the next step of the algorithm. Figures 2a, 2b, 2c show an example of an axial CT slice through an occlusion and an identified connected set of calcined voxels or a seed.
Figure 1.
Sketch depicting, in two dimensions, the initial estimate Ep and the double cone-like zone around it as a shaded region. C(i) is the an intermediate point candidate and p(i) is the distance between the midpoint and the point closest to C(i) along Ep.
Figure 2.
Various stages of the process of obtaining the intermediate point candidate: (a) An axial slice image through the CTA data shows one leg. The box encloses the calcification of interest. (b) Magnified view of the calcification in the box in (a). (c) The seed, extracted from (b), used by the modified Canny edge detector. (d) The edge of the calcification detected by the modified Canny edge detector. (e) The outer edge, obtained by finding the smallest convex polygon that encloses the entire edge of the calcification. (f) The circle fit and its center, indicated by the arrow, obtained by the Hough transform for circles. (g) The circle and its center (intermediate point candidate) superimposed on the calcification.
Edge detection with a modified canny edge detector
The conventional Canny edge detector finds edges solely based on the gradient of the image. This results in detecting many other edges in addition to those of the object of interest. We developed a modified version of the Canny edge detector to find the edges of a calcifications, by also accounting for the intensity of the pixels surrounding the edge and the connection of the edge pixels to the seed region. The purpose of a conventional Canny edge detector is to detect edges based on two thresholds for the gradient magnitude.10 The specifications of our implementation of the Canny edge detector are as described below.
We first create a discretized version of the derivative of a Gaussian kernel. With the axial slice image defined to be a function of two orthogonal coordinates as I(i,j), we define a Gaussian kernel as:
| (5) |
where σ=1. The smoothed version of the image is obtained as a discrete 2D convolution,
| (6) |
The partial derivatives of the Gaussian kernel are defined as
| (7) |
and
| (8) |
To obtain the gradient image we first define the directional gradients in the form of discrete 1D convolutions in orthogonal directions as
| (9) |
and
| (10) |
The gradient magnitude image is then defined as
| (11) |
We then find two gradient magnitude values, called the higher and the lower thresholds, such that 70% and 30%, respectively, of the pixels in the image have gradient magnitudes less than these two thresholds. We only consider the pixels that had a gradient higher than the higher threshold and declare them as edge pixels. We then consider the lower threshold and locate all pixels that have a higher gradient value than the lower threshold. These are the potential edge pixels. We then locate all potential edge pixels that are connected to the previously declared edge pixels, through other potential edge pixels (through an 8-pixel neighborhood). These newly located pixels are declared as edge pixels too. To summarize, an edge pixel either has a gradient value greater than the higher threshold or has a gradient value higher than lower threshold along with a connection to a pixel with a gradient greater than the higher threshold.
To complete the modification of the Canny edge detector, we subsequently apply two morphological filtering operations on the edge image. In this step we use the “seed” identified in Sec. 3B1. We only accept edge pixels that are connected to pixels in the seed such that the connecting pixels are in the range [H1low,H1hi]. Moreover we also require that the edge pixels have at least one neighboring pixel in the range [H2low,H2hi]. In our case the two sets of thresholds correspond to [200 HU,1000 HU] and [300 HU,1000 HU], respectively. The first new condition, or filter, makes the edge detector pick edges only in the vicinity of and belonging to the same object as the seed. The second new condition makes the detector less prone to picking edges that belong to bones or other nearby vessels containing the contrast medium. Figure 2d shows an example of an edge obtained in this way.
Circle fitting
Assuming the vessel cross section is approximately circular in the femoropopliteal artery,16 we first identify the edge of a calcification adjacent to the inner vessel wall and then fit a circle to it. To extract this outer edge, we fit the smallest possible convex polygon to the edge of each calcification. Only edge pixels adjacent to the sides of this convex polygon are accepted as the ones of interest. Figure 2e shows an example of an extracted outer boundary of an edge.
We then use the Hough transform for circles11 to fit a circle to these edge pixels. The choice of Hough transform is motivated by the fact it is robust toward partially obscured circular objects and can ignore boundary points that are not on the dominant circle. Figures 2f, 2g show an example of a circle fit to an outer boundary and the circle’s center. Let us denote this center as C(i).
Thus we have n number of C(i)’s as candidates for intermediate point of the centerline of the vessel, where i=1,2,…,n for n calcifications in one occlusion.
Computing characteristic scores for intermediate point candidates
After obtaining all possible candidates for the intermediate point we need to characterize them in a way that allows us to pick the most useful candidate for a given occlusion. Each score defined below represents a property of a given intermediate point candidate. As explained later, we will quantify the usefulness of each candidate to reduce the error of the initial estimate as a function of these scores. For each C(i) we define the following scores.
-
(1)
A score based on radius:
Score Ss(i) is defined as follows:
where r(i) is the radius of the circle, in mm, computed in the previous step, using the Hough transform. The function is constructed to assign the highest score to radii between 3 and 4 mm, the expected size of the femoropopliteal artery. A circular shape in this radius range is more likely to be a calcification formation on the wall of the artery, since the radius of the femoropopliteal artery falls in this range.17, 18 The score tapers off for smaller and larger radii. We assume that an object that has a larger cross-sectional radius than 5 mm is too large to be a calcification inside the femoropopliteal artery and an object with a cross-sectional radius smaller than 1.5 mm radius is too small to be useful for localizing its center.(12) -
(2)
A score based on longitudinal position:
As defined earlier, L(E(p)) is the length of the initial estimate Ep. Let p(i) be the length of Ep between the midpoint of Ep and the point on Ep closest to C(i), as illustrated in Fig. 1. Then the score is
This score essentially represents the proximity of the intermediate point to the plane cutting the initial estimate at its midpoint.(13)
Weighted sum model
The usefulness of an intermediate point candidate is defined as the change in MD error when it is used as additional information by the PVSP algorithm. This change, E(i), caused by the candidate C(i), can be computed exactly if the reference standard is known. However, in a real case, such information is not available and therefore we have to estimate the change in error. We will refer to the estimated value of E(i) as . Since we have two scores characterizing each intermediate point candidate, we model the estimated change in MD error as a function of these scores. We chose to express this function as a weighted sum model, in a polynomial form. We evaluate the intermediate point candidates based on a net score, defined as
| (14) |
In the equation above, a positive indicates reduction in error. The first term in Eq. 14, containing w1, reflects the expectation that the radius of the occluded femoropopliteal artery is likely to be between 3 and 4 mm, In Eq. 12, the score Ss(i) falls off rapidly as the radius increases beyond 4 mm because it is unlikely that the calcifications delineating the inner wall of the artery would have large radii. On the other hand, smaller calcifications are possible and hence we allow the score to fall off less rapidly for radii smaller than 3 mm. The quadratic function terms of Sp(i), containing w2 and w3, represent a dependence more rapid than linear and also account for the possibility that the dependence may have a maximum or a minimum for a certain value of Sp(i). The cross term, containing w4, represents our assumption that Ss(i) and Sp(i) are both indicators of usefulness of the candidate point and we may prefer candidates that have a high radius based score as well as a location close to the middle of the occlusion. The last term, w5, indicates a constant bias.
The condition on the value of Sp(i) in Eq. 14 says that we will consider only for candidates that are not too close to the end points of the occlusion. We do not know the actual value of the change in error, but Eq. 14 attempts to approximate it as a function of computable scores. The scores used in the right hand side of this equation do not depend on knowledge of the true centerline, and hence can be computed for any calcification. To compute the weights w1 through w5, we use a training mechanism as explained later in this article. When these weights are known through a training process, the candidate with the highest is considered to be most useful and is picked as the intermediate point for the next step. It should be noted that since the term w5 is a constant, its value has no impact on the selection process. Its presence, nevertheless, is important as a bias term of the linear regression fit.
Using the intermediate point
The candidate we obtain in the previous step is used for correcting the centerline by running the PVSP algorithm with the additional information about this point.
Knowledge of an intermediate point in the PVSP algorithm (Sec. 3A) means that we have one more “known” point and one less “unknown” point of the centerline. In other words, in Eq. 2 the vector Vk is larger by two elements, since it contains both X and Y coordinates of the centerline points, and in Eq. 3 the vector Vu is smaller by two elements. The matrices Bk and Bu have a correspondingly different number of rows too. So in effect, having one intermediate point for an occlusion is like having two occlusions of smaller lengths. Furthermore, since we can say with great confidence that the centerline passes through this point, we use linear correction to ensure the estimate goes through the point. In the absence of an intermediate point this correction is used only for the end points of the occlusion, where as of now there are two linear corrections terms used. The concept is illustrated in Fig. 3.
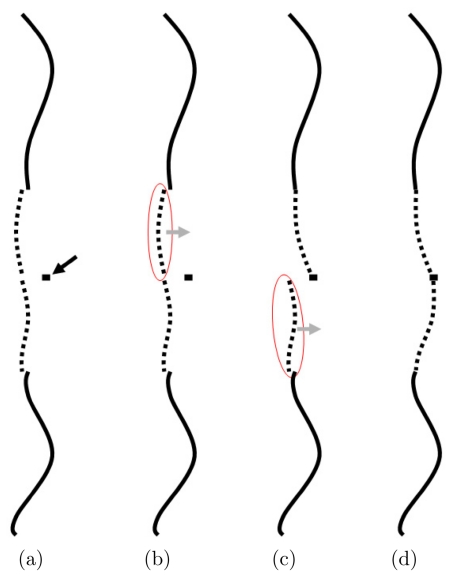
Figure 3.
Schematic shows how an intermediate point effectively turns one long occlusion into two smaller occlusions, and hence reduces the error of the estimate. (a) The PVSP estimate using the additional intermediate point information is shown, prior to the end point correction, as the dotted line and the solid black arrow point to the intermediate point. (b) The estimated segment proximal to the intermediate point is identified and a linear correction is applied to it. (c) The estimated segment distal to the intermediate point is identified and a separate linear correction is applied to it. (d) The final estimate passes through the intermediate point.
EXPERIMENTS
The first step of the experiment involves constructing a database of centerlines, followed by the PVSP algorithm, and then the IPD algorithm for longer occlusions with calcifications.
Database of centerlines
Prior Institutional Review Board approval was obtained for retrospective data collection and all data were anonymized per HIPPA standards. CT data were acquired with an 8- or 16-channel multiple detector-row CT scanner. Transverse CT images (512×512 matrix) were reconstructed at fields of view ranging from 300 to 450 mm with a 1.25 mm nominal section thickness and 0.9 mm section spacing. The database of femoropopliteal centerlines used for the experiments was obtained from two patient populations. We included the left and right femoropopliteal centerlines extracted semiautomatically4 from 30 patients without PAOD. This patient population has previously been described.3 We also included the left and right femoropopliteal centerlines of 30 patients with PAOD and femoropopliteal artery occlusions in our database. Therefore there were a total of 60 subjects in the database. The end points of the femoropopliteal arteries as well as the end points of the occlusions—if present—were identified in consensus by two cardiovascular radiologists. The end points of the femoropopliteal artery were generally the common femoral bifurcation and the popliteal bifurcation. In one case the distal end point of the femoropopliteal artery was selected at the level of the expected rather than the true takeoff of the anterior tibial artery due to the patient’s variant anatomy (high anterior tibial artery takeoff, approximately 8 cm above the tibiofibular joint).
We constructed the database of 60 right and 60 left femoropopliteal arteries as follows. The centerlines through the unobstructed segments of each occluded vessel were tracked using the same semiautomated method.4 The centerlines through the occluded portions were tracked manually by four independent experts (three cardiovascular radiologists, and one radiological technologist), twice each, and the reference standard through the occluded segment was defined as the mean of all eight readings. Since all eight curves have the same number of points, and there is a pointwise correspondence between all of the curves, their mean was found by pointwise averaging.
There were a total of 44 occlusions (24 left, 20 right) in the patients with PAOD. Table 1 shows the distribution of these 44 occlusion lengths.
Table 1.
Occlusion Length (OL) distribution.
| O L(mm) range | No. of occlusions |
|---|---|
| 0–50 | 17 |
| 50–100 | 11 |
| 100–150 | 9 |
| 150–200 | 2 |
| 200–250 | 1 |
| 250–300 | 2 |
| 300–350 | 1 |
| 350–400 | 1 |
Obtaining initial estimate with PVSP
In the first stage of the experiment we applied the PVSP algorithm to get an estimate of the centerline for each of the 44 occlusions. For each occlusion, we used the database such that the patient under consideration was excluded (leave-one-out method). For every occlusion we considered the database only from that particular anatomical side (left-for-left and right-for-right), i.e., for every occlusion we used a total of 59 curves as prior knowledge.
Intermediate point detection
Computing weights
The left hand side of Eq. 14 can be evaluated only if the weights w1 through w5 on the right hand side are known. To obtain these weights, a training process is required. We used a leave-one-out training process, that is to say, for each occlusion that underwent the IPD algorithm the intermediate point candidates from all the remaining occlusions were used as training samples. Since the reference standard, and hence the net score E(i), were known for each intermediate point candidate of the training samples, the weights w1 through w5 were computed using linear regression.
Occlusion length limit
It was shown by Rakshe et al. (2007)3 that the PVSP algorithm gives clinically acceptable results for occlusion lengths up to 100 mm, so we used 80 mm as a conservative limit for accepting the initial PVSP results as final estimates. All the PVSP estimates for occlusions greater than 80 mm were considered for further processing with the intermediate point detection algorithm. If the IPD algorithm did not find any candidate points (C(i)’s) that satisfied all the conditions mentioned earlier, then the initial estimate of the curve from the PVSP algorithm was taken as the final result. If valid candidates were found, we computed the net score for each of these candidates using Eq. 14. For each occlusion, the candidate C(i) with the highest was used as the intermediate point for subsequent reapplication of the PVSP, as described in Sec. 3B6. The MD error (defined in Sec. 3A) relative to the manual reference standard (average of eight readings) served as the error metric for all occlusions. In order to illustrate the performance of the algorithm relative to human reader precision, we also calculated the MD errors for each of the eight manual readings for all occlusions.
RESULTS
Of the 44 occlusions, 20 were estimated by PVSP to have occlusion length more than 80 mm. No valid candidates for intermediate points could be found in 6 of those 20. Thus the IPD algorithm was used for 14 occlusions. The coefficients w1 through w5 were obtained for each occlusion with a regression model from the intermediate point candidates from the remaining 13 occlusions as described in Sec. 4C. The means and standard deviations (in parenthesis) of weights w1 through w5, in mm, were 0.16(0.05), −0.33(0.11), 1.04(0.07), 0.82(0.09), and −1.08(0.09). It can be seen from Fig. 4 that the weights stayed in reasonably tight clusters, even though they were not identical in value.
Figure 4.
The box plot of weights w1 through w5. The box shows the interquartile range with the median, the whiskers show the range of the data, and + marks show outliers. An outlier is defined as a value more than 1.5 times the interquartile range away from the top or the bottom of the box.
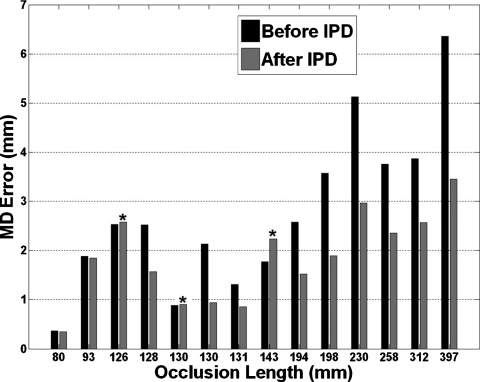
Figure 5 shows the MD error of the 14 occlusions before and after applying the IPD algorithm. The MD error decreased, as shown in Table 2, after IPD was applied with p<0.01 (paired Wilcoxon test). The average error decreased from 2.76 to 1.86 mm. IPD reduced the error in 11 of 14 occlusions. In three occlusions the error increased (Fig. 5). In two of these three the error increased less than 0.05 mm. Even the worst error increase was only 0.47 mm (the 143 mm occlusion in Fig. 5). In the 11 cases where the error was reduced, the average reduction was 1.2 mm or 35%. Overall, 13 of 14 occlusions had errors less than 3 mm. Since the radius of a typical femoropopliteal artery is 3 mm or more,17, 18 the estimates with an MD error less than 3 mm were considered clinically useful. Table 2 shows the summary of results for all 14 occlusions that underwent IPD algorithm.
Figure 5.
MD error before and after the IPD algorithm was applied. The asterisk symbol marks cases where IPD increased the error.
Table 2.
Occlusion Length (OL), MD error using PVSP alone, MD error with IPD, and highest manual error, all in mm (S.D=Standard Deviation, C.I.=Confidence Interval).
| OL | Original error | Post-IPD error | Highest manual error |
|---|---|---|---|
| 80 | 0.37 | 0.35 | 1.18 |
| 93 | 1.89 | 1.85 | 1.70 |
| 126 | 2.53 | 2.57 | 1.50 |
| 128 | 2.52 | 1.56 | 1.14 |
| 130 | 0.88 | 0.90 | 0.80 |
| 130 | 2.13 | 0.94 | 1.37 |
| 131 | 1.31 | 0.85 | 1.11 |
| 143 | 1.77 | 2.24 | 2.31 |
| 194 | 2.57 | 1.52 | 1.29 |
| 198 | 3.57 | 1.89 | 1.25 |
| 230 | 5.13 | 2.97 | 1.16 |
| 258 | 3.76 | 2.35 | 2.09 |
| 312 | 3.87 | 2.57 | 3.08 |
| 397 | 6.36 | 3.45 | 2.23 |
| Average | 2.76 | 1.86 | 1.59 |
| S.D. | 1.64 | 0.89 | 0.62 |
| 95% C.I. | 1.81–3.71 | 1.34–2.37 | 1.23–1.95 |
Figure 6 shows the MD error of the IPD algorithm along with the highest (worst) reader error, with respect to the mean of eight manual readings, for 14 occlusions. Since all of the readers were considered experts with several years of experience in vessel tracking and hence all of the eight readings are considered to be of clinically usable quality, this comparison shows how the IPD performs compared to the manual result spread. The performance would be considered satisfactory if the IPD error was close to or less than the worst reader error. It can be seen in Fig. 6 that the IPD performance is similar to or better than a human reader in all but three cases. The MD errors were not significantly different between IPD and the worst reader (p=0.26; paired Wilcoxon test). The average MD error for IPD and the worst reader were 1.86 and 1.59 mm, respectively (Table 2). Since all of the readers were experienced radiologists or technologists, all of their results were considered acceptable. Thus, we considered it reasonable for the purposes of this study to consider only the manual reading with the highest error for each occlusion, i.e., largest deviation from the average of all eight centerlines.
Figure 6.
MD error for each of the 14 occlusions for the estimates found by the IPD algorithm along with the worst manual reading. In three occlusions (lengths 126, 230, and 397 mm) the IPD error is more than 1 mm higher than the worst manual error.
The performance of the system using the PVSP alone versus the combined PVSP and IPD system can be seen in Fig. 7, where the MD errors of the final estimates are plotted against the occlusion lengths. Estimates for 42 of 44 occlusions had an MD error less than 3 mm when IPD algorithm was used. The slope of the regression line in Fig. 7b was about 40% less than that in Fig. 7a. The occlusion with the worst error of approximately 3.5 mm was also the longest occlusion, 397 mm in length; very long by clinical standards (Fig. 8).
Figure 7.
(a) Performance of only the PVSP method, without using IPD. The dotted line shows linear regression with slope 0.015, y-intercept −0.161, and R2=0.865. (b) Performance of the overall method with the IPD algorithm. The dotted line shows linear regression with slope 0.009, y-intercept 0.138, and R2=0.792.
Figure 8.
Centerline restoration of a long femoropopliteal artery occlusion using Partial Vector Space Projection (PVSP) alone, and augmented by Intermediate Point Detection (IPD) versus the reference standard. (a) Maximum Intensity projection (MIP) shows a long (397 mm) right femoropopliteal artery occlusion (asterisks), and three centerlines obtained with PVSP, IPD, and the reference standard. Arrows in (a) correspond to transverse images shown in (b), (c), and (d): Open arrow level of greatest MD error for IPD; Plain arrow level of arterial calcification detected and selected by IPD; Arrowhead level of greatest MD error for PVSP. Circles in (b–d) indicate area around the occluded artery. Dots correspond to the interpolated (PVSP and IPD) and reference standard centerlines. Panels (e), (f), and (g) are curved planar reformats (CPR) through the centerlines obtained with (e) PVSP, (f) IPD, and (g) the reference standard, generated at a left anterior oblique viewing angles of 73°. Centerlines are shown, and asterisks indicate start and end of the occlusion. Note that the initial centerline estimate obtained with the PVSP algorithm (dots in b–d) is mostly located outside of the occluded artery, which is best seen at the level of the arterial calcification in (c) and at the level of the greatest MD error observed with the PVSP (d). The corresponding CPR image shows the path anteromedially of the occluded artery [plain arrow and arrow head in (e)]. More proximally [open arrow in (e)] the CPR image is constructed anterolaterally of the occluded artery, which is therefore not displayed at this level. After applying the IPD algorithm, a new intermediate point [a dot in (c)] is used at the level of the ring-like calcification shown at this level, resulting in correction of the centerline through most of the occluded artery (f), with the exception of its proximal portion, where the centerline is estimated just at the margin of the femoropopliteal artery [a dot in (b), and open arrow in (f)]. CPR through the reference standard centerline is within the occluded vessel at all levels (g).
DISCUSSION
It is essential to track centerlines accurately for the visualization of contrast enhanced CT angiography data using the curved planar reformation technique. Standard density and gradient based automated and semiautomated algorithms can track centerlines in normal or only mildly diseased vessels, but not in severely diseased or occluded vessels. Today, these occlusions have to be tracked manually, which is a nontrivial and time consuming task, even for an expert.
Experts use their anatomic knowledge of the course of an artery (shape information), along with visual clues on the CT images to track the centerlines of occluded arteries. Vessel wall calcifications are often, but not always, found in occluded arteries. If present, they provide a reliable visual clue.
In this article we proposed a new approach built to augment a previously described knowledge based algorithm with a second, new image based algorithm. The knowledge based PVSP algorithm uses a priori shape information, and is independent of local density and gradient information. The image based algorithm makes use of the high CT attenuation of calcified atherosclerotic plaque and the fact that the shape of the calcification may serve as a reliable indicator of the location of the center of the occluded vessel. We hypothesized that even a single high-yield clue from image space, found at the right location, might improve the results of the shape-based centerline extraction, which is desirable for long (>100 mm) femoropopliteal artery occlusions. We tested our combined approach using both the PVSP and IPD algorithms on 44 occlusions in 30 patients with PAOD. The IPD algorithm was tested on 14 of 44 occlusions, the ones longer than 80 mm and with existing calcification. IPD improved the initial estimates in 11 of those 14 occlusions and achieved results within the range of the human readers in 11 of 14 cases. When the results of the entire method were compared to the reference standard, 43 of 44 had final errors less than 3 mm. Since the maximum departure error is the maximum of point-wise distance between curves, it is ensured that if the MD error is less than 3 mm, then the entire estimate stays within 3 mm vicinity of the reference standard, making the estimate clinically useful.
This work has several limitations. The IPD algorithm works only if there is calcification present in the vessel wall. In this limited study, only 14 of 20 (70%) long occlusions had noticeable calcification present, suggesting that the IPD method will not be applicable to a significant fraction of the patient population. It should be noted that even though there also are published data documenting the frequency of calcifications in femoropopliteal artery, a somewhat relevant study of the lower extremity arterial tree has shown similar (close to 70%) results.2
While it is conceivable that other features—such as vessel portions that are surrounded by low attenuation fat, or certain muscle planes—could also be sought for in image space, we have not attempted to do so in this work. In Sec. 3B5 we model the estimate as a polynomial function of scores. A different choice of function could yield different and possibly better results. An in-depth study of the dependence of the usefulness of one or maybe more intermediate points on various scores and parameters may be helpful to identify a better function. Our method uses a 2D technique to find calcifications and to delineate the wall of the artery, in a manner similar to human readers, who normally scroll through the 2D axial slices to track centerlines. The use of a more involved 3D technique may be able to improve results. Since our study involves a small number of patients, testing on a larger population of patients is warranted to fully evaluate the potential of this approach for automated centerline restoration in patients with PAOD.
CONCLUSIONS
This work shows that it is possible to detect and use image space clues, in the form of calcified atherosclerotic plaque, to substantially improve the performance of a previously described knowledge-based vessel centerline tracking method. The combined approach yields clinically acceptable results in the majority of patients. Further improvements may be achievable by expanding the database of shapes and refining the shape detection and prediction model of the future.
ACKNOWLEDGMENTS
This work was supported in part by Grant No. RO1 HL67194 from the National Institutes of Health (NIH), and in part by Grant No. P-15217 and L291-N04 from the Austrian Science Fund (FWF). J. E. R. was supported by the Swiss National Science Foundation, PBBEB 106796.
References
- Zarins C. K., Xu C., and Glagov S., “Artery wall pathology in atherosclerosis,” in: Vascular Surgery, 6th ed.(Saunders, Philadelphia, 2005), pp. 123–148. [Google Scholar]
- Roos J. E., Köechl A., Rakshe T., Straka M., Napoli A., Kanitsar A., Šrámek M., Gröller E., and Fleischmann D., “Multi-path curved planar reformation (mpCPR) of the peripheral arterial tree in CT angiography (CTA),” Radiology 244, 281–290 (2007). [DOI] [PubMed] [Google Scholar]
- Rakshe T., Fleischmann D., Rosenberg J., Roos J. E., and Napel S., “Knowledge-based interpolation of curves: Application to femoropopliteal arterial centerline restoration,” Med. Image Anal. 11, 157–168 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanitsar A., Wegenkittl R., Felkel P., Fleischmann D., Sandner D., and Gröeller E., “Computed tomography angiography: A case study of peripheral vessel investigation,” Proceedings of IEEE Visualization 2001, San Diego, California, pp. 477–480.
- Cohen L. D. and Deschamps T., “Grouping connected components using minimal path techniques: Application to reconstruction of vessels in 2D and 3D images,” IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’01), 2001, pp. 102–109.
- Bouix S., Siddiqi K., and Tannenbaum A., “Flux driven automatic centerline extraction,” Med. Image Anal. 9, 209–221 (2005). [DOI] [PubMed] [Google Scholar]
- Paik D. S., Beaulieu C. F., R. B.JeffreyJr., Rubin R. B., and Napel S., “Automated flight path planning for virtual endoscopy,” Med. Phys. 10.1118/1.598244 25(5), pp. 629–637 (1998). [DOI] [PubMed] [Google Scholar]
- La Cruz A., Straka M., Köchl A., Šrámek M., Gröller E., and Fleischmann D., “Non-linear model fitting to parameterize diseased blood vessels,” Proceedings of IEEE Visualization 2004, Austin, Texas, pp. 393–400.
- Tran D. N., Fleischmann D., Rakshe T., Roos J. E., Rosenberg J., Straka M., and Napel S., “Femoropopliteal artery centerline interpolation using constralateral shape,” Med. Phys. 10.1118/1.2759603 34, 3428–3435 (2007). [DOI] [PubMed] [Google Scholar]
- Canny J., “A computational approach to edge detection,” IEEE Trans. Pattern Anal. Mach. Intell. 8(6), 679–698 (1986). [PubMed] [Google Scholar]
- Davies E. R., Machine Vision: Theory, Algorithms, Practicalities (Elsevier, Amsterdam, 2005). [Google Scholar]
- Huang K. and Yan M., “A region based algorithm for vessel detection in retinal images,” Medical Image Computing and Computer-Assisted Intervention (MICCAI’06), Copenhagen, Denmark, 2006, pp. 645–653. [DOI] [PubMed]
- Chen Q., Zhou Z. M., Tang M., Heng P. A., and Xia D. S., “Shape statistics variational approach for the outer contour segmentation of left ventrical MR images,” IEEE Trans. Inf. Technol. Biomed. 10(3), 588–597 (2006). [DOI] [PubMed] [Google Scholar]
- Pinz A., Bernögger S., Datlinger P., and Kruger A., “Mapping the human retina,” IEEE Trans. Med. Imaging 10.1109/42.730405 17(4), 606–619 (1998). [DOI] [PubMed] [Google Scholar]
- Park M., Jin J. S., and Luo S., “Locating the optic disc in retinal images,” in Proceedings of the International Conference on Computer Graphics, Imaging and Visualization (CGIV’06), 2006, Sydney, Australia, pp. 141–145.
- Felkel P., Wegenkittl R., and Kanitsar A., “Vessel tracking in peripheral CTA datasets - An overview,” In Proc. SCCG’01, Slovakia, 2001, 269–278.
- Sandgren T., Sonesson B., Ryden-Ahlgren Å, and Länne T., “Factors influencing the diameter of the popliteal artery in healthy humans,” J. Vasc. Surg. 28, 284–289 (1998). [DOI] [PubMed] [Google Scholar]
- Sandgren T., Sonesson B., Ryden-Ahlgren Å, and Länne T., “The diameter of the common femoral artery in healthy humans: Influence of sex, age, and body size,” J. Vasc. Surg. 29, 503–510 (1999). [DOI] [PubMed] [Google Scholar]