Sequential and simultaneous dual-isotope brain SPECT: Comparison with PET for estimation and discrimination tasks in early Parkinson disease

Abstract

Parkinson disease (PD) is the second most frequently occurring cerebral degenerative disease, after Alzheimer disease. Treatments are available, but their efficacy is diminished unless they are administered in the early stages. Therefore, early identification of PD is crucial. In addition to providing perfectly registered studies, simultaneous ^99mTc∕¹²³I imaging makes possible the assessment of pre- and postsynaptic neurotransmission functions under identical physiological conditions, while doubling the number of counts for the same total imaging time. These advantages are limited, however, by cross talk between the two radionuclides due to the close emission energies of ^99mTc (140 keV) and ¹²³I (159 keV). PET, on the other hand, provides good temporal and spatial resolution and sensitivity but usually requires the use of a single radionuclide. In the present work, the authors compared brain PET with sequential and simultaneous dual-isotope SPECT for the task of estimating striatal activity concentration and striatal size for a normal brain and two stages of early PD. Realistic Monte Carlo simulations of a time-of-flight PET scanner and gamma cameras were performed while modeling all interactions in the brain, collimator (gamma camera) and crystal (detector block in PET), as well as population biological variability of pre- and postsynaptic uptake. For SPECT imaging, we considered two values of system energy resolution and scanners with two and three camera heads. The authors used the Cramer–Rao bound, as a surrogate for the best theoretical performance, to optimize the SPECT acquisition energy windows and objectively compare PET and SPECT. The authors determined the discrimination performance between 500 simulated subjects in every disease stage as measured by the area under the ROC curve (AUC). The discrimination accuracy between a normal subject and a subject in the prodromal disease stage was AUC=0.924 with PET, compared to 0.863 and 0.831 with simultaneous and sequential SPECT, respectively. The significant improvement in performance obtained with simultaneous dual-isotope SPECT compared to sequential imaging (p=0.019) was due primarily to the increased number of counts detected and resulted in comparable performance when performing simultaneous SPECT on a two-head camera with 9.2% energy resolution to that obtained with sequential SPECT on a three-head camera with 6.2% energy resolution.

INTRODUCTION

Parkinson disease (PD) is the second most frequently occurring cerebral degenerative disease, after Alzheimer disease. Management of PD is complicated by the fact that clinical symptoms appear only after advanced loss of dopamine sites. Treatments are available, but their efficacy is diminished unless they are administered in the early stages. Therefore, early identification of PD is crucial. Dopamine transporter density is diminished in PD in proportion to disease severity, and the value of PET and SPECT imaging of dopamine transporter function in this and other neurological diseases has been previously established.^{1, 2, 3} Furthermore, it has been suggested that the activity of dopamine receptors is increased in the earliest stages.³ Therefore, simultaneous assessment of pre- and postsynaptic functional status may be an especially promising approach to early identification of PD. Discrimination between normal and early PD brains can be achieved based on striatal size and pre- and postsynaptic dopamine activity concentrations, which are altered during disease progression. However, discrimination is affected by properties of the scanner, such as spatial resolution and sensitivity.

We investigated the performance of dual-isotope SPECT using two- and three-head gamma cameras with an energy resolution at 140 keV of 9.2%, which is that available today with NaI(Tl) crystals from most manufacturers, as well as an energy resolution of 6.2% associated with newer detector materials such as CdZnTe. We compared PET and dual-isotope SPECT (simultaneous and sequential) imaging on the basis of performance when estimating striatal activity concentration and size for dual-isotope SPECT with four different scanner designs. The system performance metric we used was the precision with which activity concentration and size can be estimated, assuming an efficient, unbiased estimator⁴ [computed as the Cramer–Rao bound (CRB)].⁵ We have previously assessed the achievable performance for discriminating between different Parkinsonian syndromes in patients with PD and multiple system atrophy.⁶ In the present work, we calculated the best theoretical performance of different scanners for estimation of parameters that are important for PD diagnosis and staging.

We calculated the CRB on size and activity concentration estimation in the striata for ¹¹C-altropane and sequential and simultaneous ^99mTc-TRODAT∕¹²³I-IBZM studies, for simulated patients in each of three stages—a normal brain and two progressive stages of bilateral early PD (prodromal and early). We used pairwise discriminant analysis, followed by ROC analysis based on likelihood ratios,⁷ to quantify the ability of each imaging system to discriminate between disease stage, with area under the ROC curve as the performance metric.^{8, 9, 10} We chose these radionuclides because they are routinely used in the clinic for diagnostic brain imaging. Although the ¹²³I photopeak is closer in energy to ^99mTc than ¹³¹I (and therefore has a greater cross-talk fraction), ¹³¹I has degraded spatial resolution due to high energy septal penetration. In addition, ¹³¹I produces increased dose and is therefore typically used for therapy. We have assumed perfect radionuclide purity throughout.

MATERIALS AND METHODS

Models

We modeled projections with a combination of realistic Monte Carlo simulated projections of nonspecific binding and realistic analytic projections of specific striatal binding. The analytic striatal projections used PSFs that modeled all physical effects at the location of the striata and were generated by Monte Carlo simulation. Projections were parametrized by the parameters of interest, namely the pre- and postsynaptic activity concentration and the pre- and postsynaptic striatal size.

Six parameters were considered for the SPECT simulations: ^99mTc striatal and background activity concentrations (A₁,A₂), ¹²³I striatal and background activity concentrations (A₃,A₄), and pre- and postsynaptic striatal size, r_pre and r_post, respectively. Three parameters were modeled for the PET system: ¹¹C striatal and background activity concentrations and striatal size. The postsynaptic ¹²³I uptake was assumed not to vary with time, but the time dependence of the ^99mTc and ¹¹C tracers were modeled with gamma variate functions from previously reported patient data.^{3, 11, 12} We modeled the simultaneous SPECT projections, as initially proposed in static mode⁴ by

$$P_{ijkl}=A_1{F}_1\left(t\right)P{\left[\text{str}\left(r_{\text{pre}}\right)\right]}_{ijk}\otimes {\text{PSF}}_{ijkl,\text{Tc}}+A_2{F}_2\left(t\right)P{\left[\text{brain}\right]}_{ijkl,\text{Tc}}+A_{3}P{\left[\text{str}\left(r_{\text{post}}\right)\right]}_{ijk}\otimes {\text{PSF}}_{ijkl,\text{I}}+A_{4}P{\left[\text{brain}\right]}_{ijk\text{l},\text{I}},$$ (1)

where F₁(t) and F₂(t) are the time activity curves of the ^99mTc in the striata and background brain, (i,j) index projection pixels, (k) indexes projection angle, (l) indexes energy bin, and ⊗ denotes convolution with a Monte Carlo simulated point spread function. The projections are denoted by P[brain] (simulated brain projections) and P[str(r)] (analytic striatal projections).

Realistic analytic striatal model

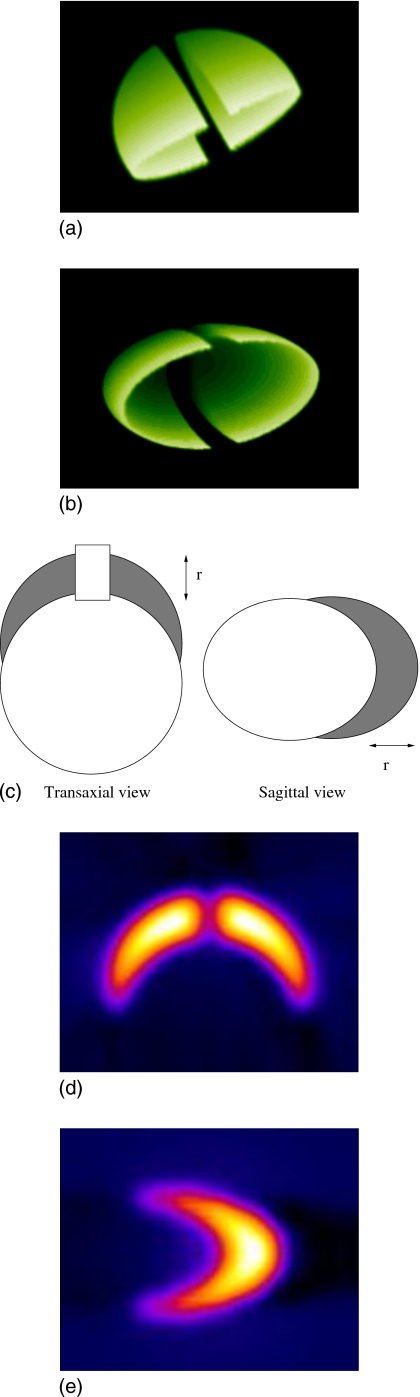
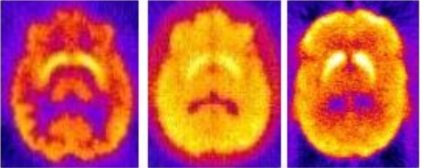
We used a parametrized model for the striata. We chose a model with two offset prolate ellipsoids, where the size parameter is the difference between the upper surfaces of the two ellipsoids (see Fig. 1). A central region was removed to model the separation of hemispheres. The volume between the two ellipsoids represents the striata. For the presynaptic tracers, progression of PD was modeled by increasing the radius of the lower ellipsoid while keeping the radius of the upper ellipsoid, and the separation of the ellipsoid centers constant, thereby reducing the striatal volume. The volumes of the striata were consistent with corresponding MRI measurements.¹³ Typical midstriatal transverse slices, reconstructed with FBP, are displayed in Fig. 2.

Figure 1.

Construction of the striata, parametrized by r. (a,b) Volume-rendered perspectives of the striatal model, displaying the separation of hemispheres. (c) The striatal volume (gray shading) is the difference between two offset prolate ellipsoids with a central region removed to mimic the separation of hemispheres. (d,e) Example striatal slices, convolved with system PSFs.

Figure 2.

Example slices of reconstructed projections for a normal brain containing the striata (FBP, no corrections applied). ^99mTc-TRODAT, ¹²³I-IBZM, ¹¹C-altropane (left to right).

Monte Carlo simulations

We performed Monte Carlo simulations to obtain projection data from the SPECT and PET scanners for nonspecific binding in the brain.

SPECT

Activity distributions in 30 brain structures of a digitized human brain phantom, including the cerebellum, the caudate nucleus, the putamen, the corpus callosum, the hippocampus, and the cortical lobes were modeled¹⁴ based on previously reported clinical studies of ^99mTc-TRODAT [dopamine transporter (DAT)] and ¹²³I-IBZM [dopamine receptor (D2)].^{15, 16} Monte Carlo simulations of ^99mTc and ¹²³I with one billion decays per projection were performed separately to yield sequential dual-isotope studies¹⁷ and then combined according to Eq. 1 to mimic simultaneous dual-isotope studies. Scattered photons were followed for up to nine scattering orders. All decay photons, including low-abundance, high-energy ¹²³I photons above 159 keV, which have increased probability of reaching the crystal due to their greater energy, were explicitly simulated. The simulations included all details of photon transport through the brain, using anthropomorphic attenuation values, and through the LEHR collimator and detector of the e.cam gamma camera (Siemens Medical Systems, Inc.). Compton scatter, coherent scatter, and penetration through the collimator septa, as well as backscatter from camera components behind the NaI(Tl) crystal, were simulated. The simulations therefore represent realistic data. Ninety-six 128×128 projections were simulated separately over 360 deg (2.0 mm×2.0 mm pixels) with 1 keV energy windows in the 90–200 keV range. Next, projections of a point source located at the center of one striatum were simulated, using the same Monte Carlo simulation as above. Simulated PSF projection data were fitted to an analytic model; model parameters were determined for each radionuclide at each projection and within each 1 keV energy window.⁴

PET

We modeled the Philips Gemini-TF PET∕CT¹⁸ in three-dimensional (3D) mode in our Monte Carlo simulations. We used a modified version of the SimSET software¹⁹ Monte Carlo simulation developed and validated in our laboratory to propagate photons in the brain and in the scanner’s flat panel detectors.²⁰ Two billion decays were generated while modeling Compton scatter, photoelectric absorption in the brain and detector, as well as loss of spatial resolution due to light sharing between LYSO crystals. The 3D sinograms were Fourier rebinned into projections yielding 256 260×87 projections with 1.1 mm×2.0 mm pixels in the default 440–665 keV energy bin.

Dopamine transporter and receptor physiological models

During PD, there is a loss of neuron density and dopamine production. TRODAT, a DAT analog, is a transmembrane protein involved in dopamine inhibition. When dopamine is reduced, as in PD, radiolabeled DAT competes with endogenous DAT for dopamine binding, and uptake is reduced. IBZM binds to postsynaptic dopamine D2 receptors. Upregulation of D2 receptors is observed during the early stages of PD, and is thought to represent a partial compensation mechanism.²¹ In the early disease stages, we therefore expect a reduction in active presynaptic size of the striata, presynaptic striatal activity concentration, and an increase in postsynaptic striatal activity concentration. Postsynaptic size is expected to remain the same.

Depletion of dopamine in PD patients was modeled with altered activity concentration and size of the striata. Time dependence was kept the same for all early stages of disease studied here. Table 1 describes the striatal parameters for each simulation, based on previously reported data^{3, 13, 21, 22, 23} for normal and early PD subjects, and the size and activity ratio parameters for each disease stage.^{3, 12, 24, 25} T:B (all) denotes the target-to-background activity concentration ratio for the striata from measured patient data. Also shown are the statistical differences between the groups, using an unpaired two-tailed t test. The ^99mTc-TRODAT time activity curve was modeled to peak at 20 min postinjection (pi). The scan was modeled to begin 60 min pi. For ¹¹C-altropane, presynaptic uptake peaks early (∼15 min pi) and scanning was modeled to begin 10 min pi. SPECT imaging was performed for 30 min (15 min per radionuclide for sequential and 30 min per radionuclide for simultaneous imaging) and PET imaging for 20 min, yielding 7.5 million ^99mTc counts, 5 million ¹²³I counts (simultaneous protocol), and 30 million ¹¹C counts, in their respective photopeaks.

Table 1.

Striatal parameters representing the three disease stages with uncertainties from reported studies and due to biological variability alone. Normal vs prodromal PD (N v P) and prodromal PD vs early PD (P v E) significances of group differences are also shown. Here all and BV denote overall and biological uncertainties, respectively. Measured size uncertainties are assumed to be due to biological variability alone.

		Normal	Prodromal	Early	N v P	P v E
rpre (all, BV)	cm	1.20±0.08	1.18±0.08	1.16±0.07	p=0.6	p=0.5
rpost (all, BV)	cm	1.20±0.08	1.20±0.08	1.20±0.08	—	—
Volume (all, BV)	cm3	15.0±1.5	14.6±1.4	14.1±1.4	p=0.6	p=0.5
T:B (all)	Tc	2.90±0.13	2.82±0.12	2.75±0.12	p=0.05	p=0.07
T:B (all)	I	1.53±0.07	1.56±0.09	1.59±0.09	p=0.1	p=0.2
T:B (all)	C	2.77±0.13	2.70±0.12	2.63±0.11	p=0.4	p=0.4
T:B (BV)	Tc	2.90±0.05	2.82±0.04	2.75±0.05	p<0.001	p<0.001
T:B (BV)	I	1.53±0.03	1.56±0.06	1.59±0.06	p=0.002	p=0.08
T:B (BV)	C	2.77±0.04	2.70±0.02	2.63±0.03	p=0.01	p=0.008

We included a prodromal stage of PD that precedes early PD because neuroprotective treatments are expected to be most effective at the earliest possible stage. This stage was modeled as an intermediate level in terms of striatal DAT loss between the normal stage and the early PD stage based on previous reports of prodromal PD in the literature.^{3, 12, 24, 25}

Analyses

Ideal system performance

The CRB is the theoretical minimum variance of an unbiased parameter estimate.⁵ It is expressed as the diagonal components of the inverse of the Fisher information matrix (FIM), which for an N-length vector, $\vec{\theta }$, of unknown parameters, and Poisson statistics, is given by the matrix

$$J_{mn}=\sum _{ijkl}\frac{1}{P_{ijkl}\left(\vec{\theta }\right)}{\left[\frac{\partial P\left(\vec{\theta }\right)}{\partial {\theta }_m}\right]}_{ijkl}{\left[\frac{\partial P\left(\vec{\theta }\right)}{\partial {\theta }_n}\right]}_{ijkl},$$ (2)

where m,n∊[1,N], (i,j) index projection pixels, (k) indexes projection angle, (l) indexes energy bin, and $P\left(\vec{\theta }\right)$ is the expected projection data set of the system. The simplest example of this is a one parameter model with one energy bin and one projection angle, where the CRB on the variance of the parameter θ is given by 1∕∑_i1∕N_i(dN_i∕dθ)², where N_i is the number of counts in pixel i.

Note that we used projection data rather than reconstructed images because the projection data contain all the acquired information, without being affected by choice of reconstruction algorithm, image processing, or correction procedures. In all cases presented, results are for the simultaneous estimation of both striatal activity concentration and striatal size. For simultaneous imaging there were six unknown parameters (A₁,A₂,A₃,A₄,r_pre,r_post), and for sequential imaging there were three unknown parameters for each of the two FIMs (A₁,A₂,r_pre and A₃,A₄,r_post).

Optimization of spectral acquisition parameters

Single-isotope imaging is typically performed with an energy window that is symmetric about the photopeak and has a width of approximately 20% for a 10% energy resolution at 140 keV. In dual-isotope SPECT, the presence of cross talk between the two radionuclides is substantial for radionuclides with photopeaks that are close in energy to each other (compared with the scanner’s energy resolution) such as ^99mTc and ¹²³I with photopeaks separated by 19 keV. In this case, symmetric energy photopeak windows would lead to substantial cross talk. Therefore, it is crucial to optimize the energy windows used in dual-isotope acquisition (that would be used for any scatter and cross-talk correction afterwards) before assessing the performance of dual-isotope SPECT in order to minimize cross talk while maximizing the useful signal. We optimized the energy windows for pre- and postsynaptic activity concentration estimation by maximizing the CRB-signal-to-noise ratio (SNR), defined as²⁶

$$\text{CRB-SNR}=\frac{A}{\sqrt{\text{CRB}}},$$ (3)

where A is the true value of the parameter being estimated. We calculated the CRB-SNR using the prodromal model described above for a SPECT system with two camera heads and for both values of energy resolution being investigated using the simulated 1 keV energy windows.

We calculated the CRB-SNR for both pre- and postsynaptic activity concentration in two nonoverlapping energy windows that straddle the two photopeaks, for the case of simultaneous estimation of pre- and postsynaptic activity concentration and striatal size. Since other sources of variability (e.g., biological variability) will be the same regardless of the energy windows, we performed this optimization for one patient who represented the mean of all biological distributions (i.e., the mean values from Table 1).

Modeling of biological variability

Our model incorporated biological variability, representing variation in dopamine transporter and receptor levels, as well as striatal size, among subjects. The overall reported uncertainty (denoted “all” in Table 1) is a combination of the contributions from intrinsic biological variability and the uncertainty introduced by the measurement process (which includes the scanner itself and any postprocessing). To disentangle the biological variability from the measurement error in these studies, one can perform a test-retest analysis, where one scans the same patient with the same scanner multiple times over a short time period (i.e., while all biological factors are constant). In this work we used previously reported test-retest values as a surrogate for measurement variability for each radionuclide, to disentangle the biological variability of the population from the errors introduced by the measurement process. These test-retest values were estimated from subjects scanned and processed in the same manner as the subjects we employed for our population values. The biological variability in the size estimates was based on previously reported MRI measurements, which were expected to include minimal uncertainty in measurement of size as compared to dopamine function.

We modeled a test-retest variability of postsynaptic D2 receptors (IBZM) of 4.6±2.7%, based on the work of Catafau et al.²⁷ who reported test-retest results for IBZM binding potential in ten normal patients, scanned twice within 48 h under identical imaging conditions. We used a test-retest variability of 4.6±2.0% based on the work of Huang et al.²⁸ who reported test-retest results for ^99mTc-TRODAT. The altropane parameters employed were based on published work with ¹²³I-altropane, and therefore the SPECT IBZM results were applicable. Since the test-retest analysis does not directly provide a value for the (assumed) Gaussian-distributed measurement variability, we performed an iterative calculation to determine the underlying Gaussian distribution that produced the reported results. We took a distribution with known mean and standard deviation, and randomly sampled two activity concentrations for each of 1000 simulated subjects. We then calculated the average test-retest value and varied the standard deviation until it matched the reported value. By matching the test-retest mean and standard deviation with the results published by Catafau et al.²⁷ and Hwang et al.,²⁸ we determined the width of the underlying Gaussian distributions to be 4.0% (IBZM) and 4.0% (TRODAT) and used them as surrogates of measurement variability. Biological variability is then calculated as the quadrature subtraction of the measurement variability from the overall reported variability in Table 1. The last three lines of Table 1 display the distributions of population parameters used to characterize biological variability.

Pairwise discriminant analysis

We performed pairwise discriminant analyses between two disease stages (normal, prodromal PD, early PD) when modeling systematic measurement variability alone as well as in addition to biological variability.^{8, 9, 10} For the ideal system performance analysis, we assumed all patients in one group had the same biological state, taken as the mean value from Table 1. We computed the CRB on parameter estimation and then sampled the correlated distribution from the inverse of the FIM to obtain a set of measured parameters for 500 subjects in each group.

When including the effects of biological variability, we randomly sampled parameters from normal distributions with means and standard deviations from Table 1 for 500 subjects in each of the three disease stages. For each of these subjects, we computed the CRB on parameter estimation based on their particular set of parameters. We then sampled the correlated distribution from the inverse of each subject’s FIM to obtain a set of measured parameters for each subject. In this manner, both biological and measurement variabilities were modeled.

We performed a binary classification of subjects (i.e., normal versus prodromal PD, or prodromal PD versus early PD) by calculating the likelihood ratio of a subject actually belonging to one group, and then calculating the correlated receiver operator characteristic (ROC) curve for each discrimination task.⁷ The two features used in the discrimination task were the pre- and postsynaptic activity concentration, for both simultaneous and sequential imaging (SPECT) with two- and three-head gamma cameras and with energy resolutions of 6.2% and 9.2%. We used presynaptic activity concentration for PET. We used area under the ROC curve (AUC) as our performance metric. We did not use striatal size as a classifying parameter because the size biological variability was large, and the differences between groups were not significant (see Table 1). Activity concentrations, however, were estimated with size unknown, because this is the clinical situation. In some cases, a priori structural size information may be available from MRI measurements, however, the structural and functional striatal size are not necessarily equal, and uncertainty in the size estimate remains. We have chosen to consider the case where striatal size is unknown.

Comparison of predicted and achieved performance

We compared the ideal estimation performance determined using the CRB when all of the available information is used, to the actual performance achieved with a fast Monte Carlo-based joint iterative reconstruction approach that we have proposed recently, which compensates for scatter, cross talk and attenuation within the forward-projection step of an iterative reconstruction algorithm (MC-JOSEM).²⁹ This algorithm incorporates a fast Monte Carlo estimation of scatter and cross talk in the patient and detector into an iterative OSEM reconstruction and was used to compensate for all physical factors in simultaneous ^99mTc∕¹²³I SPECT where the parameters of interest were the same as those considered here. We calculated the CRB on presynaptic activity estimation with ¹²³I-altropane, using the same experimental conditions as Ouyang et al.²⁹

RESULTS

SPECT optimal energy windows

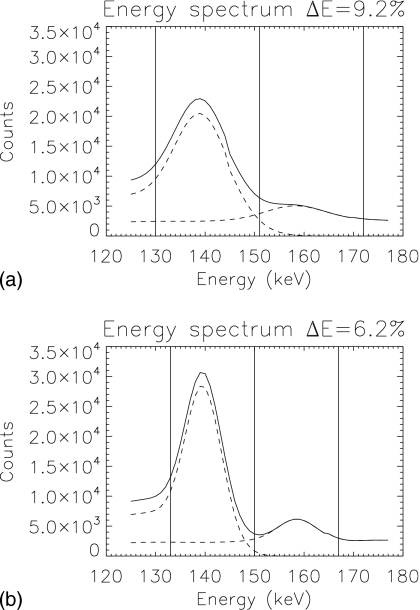
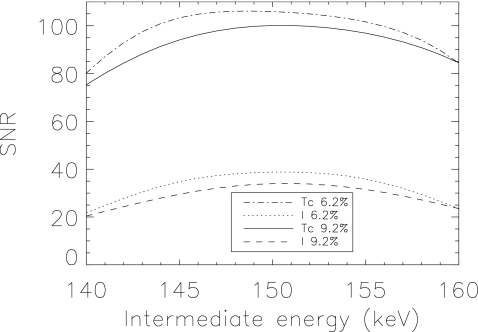
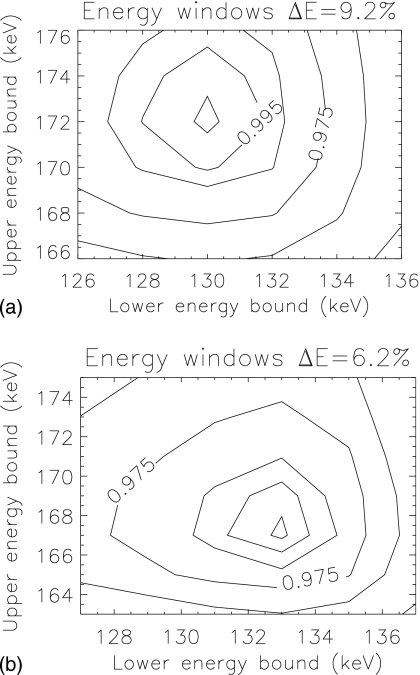
The optimal acquisition windows for pre- and postsynaptic activity concentration estimation for ^99mTc and ¹²³I were (130−151) keV and (151−170) keV, respectively, for ΔE=9.2% (133–150 keV, 150–167 keV for ΔE=6.2%). Performance for both values of energy resolution was maximal for a similar crossover energy between windows—151 keV for ΔE=9.2% and 150 keV for ΔE=6.2%. Figure 3 shows the locations of the optimal windows overlaid on the spectra. The optimal window location and size differed between energy resolutions. Figure 4 displays the CRB-SNR as a function of the intermediate crossover energy for both the pre- and postsynaptic activity concentration, for both values of energy resolution, and for the optimal end point energies. The maximum SNR for each activity occur at different locations. To determine the optimal windows for estimation of both activities, we maximized the product of the two activities’ CRB-SNRs. Figure 5 displays contours of normalized SNR² for the two energy resolutions, as a function of the lower energy of the lower window and upper energy of the upper window, for the optimal crossover energy. Values of SNR² did not change substantially around the optimum. We use (130−151) keV and (151−170) keV for ΔE=9.2%, and (133−150) keV and (150−167) keV for ΔE=6.2% herein.

Figure 3.

Energy spectra for both values of energy resolution investigated (solid) and the contribution from each radionuclide (dashed). Vertical lines indicate edges of the optimal energy windows.

Figure 4.

CRB-SNR for the two energy resolutions investigated, and for pre- and postsynaptic activity concentration estimation, as a function of the intermediate crossover energy between the two radionuclides (and for the optimal end points).

Figure 5.

Contour plots of normalized SNR² as a function of the end points of the two energy windows (lower edge of the lower window and upper edge of the upper window), for the two energy resolutions investigated. The individual SNR results for each activity concentration estimation are multiplied to find the optimal windows. Contours are [0.900,0.950,0.975,0.990,0.995,0.999] of maximum.

Ideal system performance

PET, unlike SPECT, was successful in perfectly discriminating between the disease stages. AUC for discrimination with PET was 1.0 and the maximum value for SPECT was 0.995 (normal versus prodromal PD with a three-head camera, and ΔE=6.2%). This was due primarily to the larger number of detected counts (higher sensitivity) but also to the improved spatial and energy resolution of the PET scanner. Table 2 displays the CRB-SNRs on pre- and postsynaptic activity concentration (A₁,A₃) estimation for simultaneous estimation of activity concentration and size. There is a clear improvement in performance for improved energy resolution and increased number of camera heads, but the largest improvement is observed when comparing sequential with simultaneous imaging. The improvement is $\sim \sqrt{2}$, which is the theoretical improvement expected from increasing counts by a factor of 2, when cross talk is neglected. Bounds were also calculated for fewer counts (one half and one quarter of the total counts used for Table 2) to investigate the impact of counts on these results. SNRs reduced by a factor of 2 when the counts were halved, and a factor of 2 when the counts were quartered. In these cases, the ability to discriminate between disease stages will be reduced. The improvement in SNR of simultaneous imaging compared with sequential imaging remained $\sim \sqrt{2}$ for the reduced counts.

Table 2.

Ideal system performance signal-to-noise ratios on activity concentration estimation, calculated as the ratio of the parameter value to the square-root of the CRB, for presynaptic activity concentration A₁, and postsynaptic activity concentration A₃.

	A1	A1	A3	A3
Normal	Simultaneous	Sequential	Simultaneous	Sequential
PET	—	199.2
SPECT, ΔE=9.2%, two heads	107.0	77.3	33.3	24.7
SPECT, ΔE=6.2%, two heads	113.2	79.7	38.1	26.9
SPECT, ΔE=9.2%, three heads	130.5	94.5	40.8	30.3
SPECT, ΔE=6.2%, three heads	138.1	97.4	46.7	33.0
Prodromal PD
PET	—	186.6
SPECT, ΔE=9.2%, two heads	100.1	72.3	34.0	25.2
SPECT, ΔE=6.2%, two heads	105.9	74.6	38.8	27.4
SPECT, ΔE=9.2%, three heads	122.2	88.4	41.6	30.8
SPECT, ΔE=6.2%, three heads	129.3	91.2	47.5	33.6
Early PD
PET	—	175.7
SPECT, ΔE=9.2%, two heads	95.7	69.1	34.6	25.6
SPECT, ΔE=6.2%, two heads	101.3	71.3	39.5	27.9
SPECT, ΔE=9.2%, three heads	116.9	84.5	42.3	31.4
SPECT, ΔE=6.2%, three heads	123.7	87.2	48.3	34.1

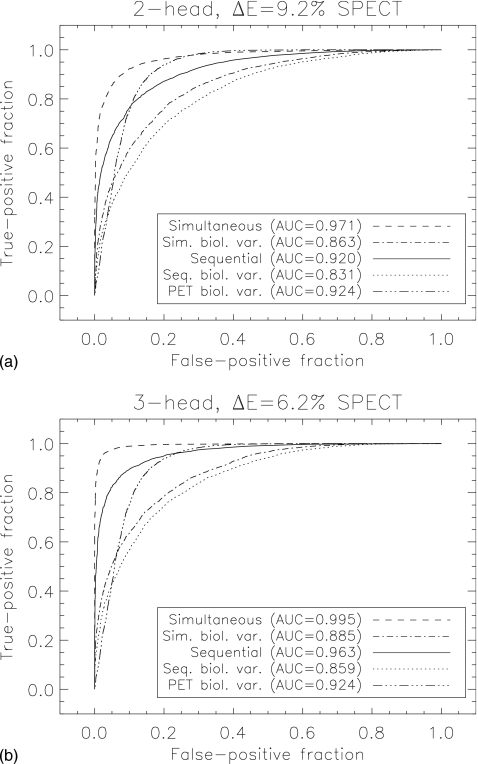
Figure 6 (a) compares ROC curves for two-feature discrimination (pre- and postsynaptic activity concentration) between a normal brain and prodromal PD for ΔE=9.2% and a two-head system, for simultaneous and sequential imaging. Figure 6 (b) displays the same comparison but with ΔE=6.2% and a three-head system. Simultaneous imaging shows improved performance over sequential imaging for both SPECT scanners. Correlated receiver operator areas under the curve for the remaining tasks are displayed in Table 3.

Figure 6.

(a) ROC curves for simultaneous and sequential imaging for a two-head, ΔE=9.2% SPECT system classifying subjects into normal or prodromal PD group. (b) Same, but for a three-head, ΔE=6.2% SPECT system. Both ideal system performance and performance including biological variability are displayed. PET performance with BV is included for comparison.

Table 3.

Two-parameter discrimination analysis with ideal system performance and inclusion of biological variability from binary classification tasks.

Normal vs prodromal, system	Simultaneous	Sequential	Significance p
PET	—	1.000	—
SPECT, ΔE=9.2%, two heads	0.971±0.005	0.920±0.008	<0.001
SPECT, ΔE=6.2%, two heads	0.982±0.003	0.932±0.008	<0.001
SPECT, ΔE=9.2%, three heads	0.990±0.002	0.959±0.006	<0.001
SPECT, ΔE=6.2%, three heads	0.995±0.002	0.963±0.005	<0.001
Normal vs prodromal, BV
PET	—	0.924±0.009
SPECT, ΔE=9.2%, two heads	0.863±0.011	0.831±0.013	0.019
SPECT, ΔE=6.2%, two heads	0.881±0.011	0.845±0.012	0.006
SPECT, ΔE=9.2%, three heads	0.878±0.011	0.851±0.012	0.030
SPECT, ΔE=6.2%, three heads	0.885±0.010	0.859±0.012	0.010
Prodromal vs early, system	Simultaneous	Sequential	Significance p
PET	—	1.000	—
SPECT, ΔE=9.2%, two heads	0.969±0.005	0.919±0.008	<0.001
SPECT, ΔE=6.2%, two heads	0.978±0.004	0.928±0.008	<0.001
SPECT, ΔE=9.2%, three heads	0.987±0.003	0.956±0.006	<0.001
SPECT, ΔE=6.2%, three heads	0.992±0.002	0.959±0.006	<0.001
Prodromal vs early, BV
PET	—	0.962±0.006
SPECT, ΔE=9.2%, two heads	0.864±0.011	0.833±0.013	0.019
SPECT, ΔE=6.2%, two heads	0.864±0.012	0.834±0.013	0.028
SPECT, ΔE=9.2%, three heads	0.883±0.011	0.861±0.011	0.054
SPECT, ΔE=6.2%, three heads	0.887±0.010	0.864±0.011	0.034

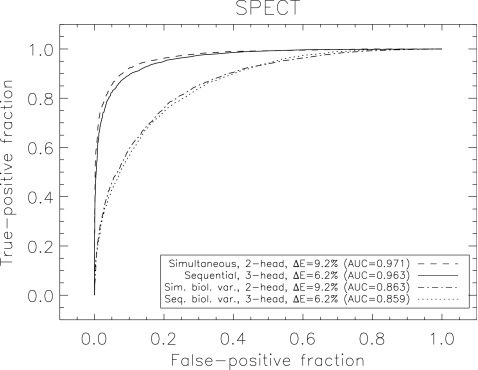
Figure 7 demonstrates that performance with sequential imaging on a ΔE=6.2%, three-head camera (AUC=0.963), was slightly inferior (p<0.001) to that obtained when performing simultaneous imaging on a ΔE=9.2%, two-head system (AUC=0.971).

Figure 7.

Comparison of simultaneous and sequential SPECT imaging with different SPECT system designs for classification of subjects into normal or prodromal disease stages. Simultaneous imaging with a two-head, ΔE=9.2% scanner delivers slightly improved performance over sequential imaging with a three-head, ΔE=6.2% scanner (p<0.001). Both ideal system performance, and performance including biological variability are displayed.

Performance when modeling biological variability

Figure 6 (a) also displays results for a two-head, ΔE=9.2% SPECT system with biological variability included (figure (b) displays results for a three-head, ΔE=6.2% SPECT system). Performance is clearly degraded compared to ideal system performance. We also show PET performance for comparison. Figure 7 also compares ROC curves for sequential imaging performed on a three-head system with ΔE=6.2% with simultaneous imaging performed on a two-head system with ΔE=9.2% with BV included. Similar results were obtained when modeling BV as were obtained without BV (Sec. 3B) showing slightly inferior performance of sequential imaging on a ΔE=6.2%, three-head system (AUC=0.859) compared to simultaneous imaging on a ΔE=9.2%, two-head system (AUC=0.863,p<0.001).

Table 3 displays the remaining discriminant task AUCs and, for SPECT, the significance of discriminating simultaneous from sequential imaging when biological variability is included.

The ideal system performance results of Sec. 3B were reproduced when including biological variability, but with overall reduced performance. The statistical significance of the difference between simultaneous and sequential imaging was also reduced (p=0.01 when including BV, compared to p<0.001 when not including BV, for a three-head, ΔE=6.2% system). This is due to the biological component of variability that was applied equally to both simultaneous and sequential imaging, thereby reducing the difference between them. There was some change in the ordering of best performance for the SPECT studies, but these changes were not significant when considering populations of only 500 patients. A meaningful comparison here is between the sequential and simultaneous imaging protocols, since for each imaging system the ROC curves were generated from the same population of patients, eliminating any additional variability due to different biological population distributions. In this regard, there was a significant improvement in performance of simultaneous imaging over sequential imaging.

Interestingly, although PET yielded a greater ROC AUC, there was a crossover of the PET and SPECT curves at low false-positive fraction (FPF). This demonstrates that for small values of FPF, simultaneous dual-isotope SPECT yielded higher sensitivity values than PET. For clinically relevant false-positive fractions of 0.1 and 0.2 (specificity, SP=90%, SP=80%), the true-positive fractions (sensitivities, SN) were SN=0.738 and 0.929, respectively, for PET and SN=0.638 and 0.806 for simultaneous SPECT with ΔE=6.2% and a three-head system (Table 4). In all cases, simultaneous imaging showed a 5%–7% improvement in sensitivity over sequential imaging (p<0.001). At 80% specificity, PET yielded a >12% improvement in sensitivity over SPECT.

Table 4.

Sensitivity values and one standard deviation uncertainties for two clinically relevant specificity values.

	AUC	SN (SP=0.8)	SN (SP=0.9)
ΔE=9.2%, two heads, simultaneous	0.863±0.011	0.760±0.022	0.607±0.030
ΔE=9.2%, two heads, sequential	0.831±0.013	0.693±0.026	0.516±0.032
ΔE=6.2%, three heads, simultaneous	0.885±0.010	0.806±0.022	0.638±0.033
ΔE=6.2%, three heads, sequential	0.859±0.012	0.752±0.023	0.588±0.031
PET	0.924±0.009	0.929±0.017	0.738±0.042

Comparison of predicted and achieved performance

We compared our predictions of ideal system performance with the results reported by Ouyang et al.²⁹ for the same activity and attenuation distributions. We chose values from the final iteration (No. 15) of the OSEM algorithm that was performed in order to compare with the least biased results (bias <2%). MC-JOSEM (relative standard deviation of 1.93%) yielded results that were close to the ideal performance result (1.59%) ²⁹ and also report signal-to-noise ratio values for presynaptic binding potential. The CRB-SNR for presynaptic binding potential at equilibrium [computed in this work as BP=(A_t−A_b)∕A_b where A_t, A_b denote target and background activity concentration, respectively] was found to be 31.4, compared to MC-JOSEM (24.5).

DISCUSSION

In this work we optimized dual-isotope ^99mTc∕¹²³I acquisition and compared its performance for activity estimation tasks to that of single radionuclide PET, while modeling realistic early PD activity distributions and scanner response. All physical effects were modeled in the projector including contribution from high energy photons for both the PSF and the brain projections. Thus, the CRB yielded the ideal performance for realistic data. We compared optimized sequential and simultaneous dual-isotope SPECT imaging and quantified the improvement in performance that is expected with simultaneous dual-isotope as compared to sequential SPECT. In addition to the identical patient physiological state and the requirement of only one acquisition, simultaneous imaging therefore offers performance benefits for differential diagnosis of early PD from a normal brain. We considered cameras with two energy resolutions to compare performance with currently available systems to future systems with new detector materials such as CdZnTe, and demonstrated that similar performance can be achieved with simultaneous imaging on a two-head, ΔE=9.2% system as compared to sequential imaging on a three-head, ΔE=6.2% system.

We included biological variability of dopamine system parameters to mimic clinical experience. We demonstrated using test-retest analysis that biological variability is a substantial contributor to overall variability, and in this case, contributed a larger uncertainty than the ideal system performance. Biological variability is therefore an important factor that should be considered in clinically relevant simulation studies, the neglect of which leads to significant overestimation of performance.

Rather than use a region-based quantitation of uptake as our performance metric, which may not be related to the clinical task at hand, we performed pairwise discriminant analysis with simulated patient populations, thereby evaluating the power of each imaging system and acquisition protocol to discriminate between the early stages of PD in a clinically meaningful way.

We optimized the spectral acquisitions used in dual-isotope imaging by maximizing CRB-SNR for activity concentration estimation for a range of energy window sizes and positions. This is the first step that is essential to achieve optimal dual-isotope imaging with ^99mTc and ¹²³I. Furthermore, this is essential when assessing performance of compensation methods for cross talk and Compton scatter in dual-isotope SPECT that use only two acquisition windows as in Ref. 29. Our results demonstrate that there is a relatively broad range of energies for which both ^99mTc and ¹²³I CRB-SNR are optimal. This is a favorable situation that enables achievement of optimal image quality for both radionuclides. The size and location of the optimal windows balance the additional information obtained by including photons in a wider window with the degradation of information that results from including scattered photons. The ^99mTc window contains downscatter from iodine photons, and the wider this window, the higher the proportion of scatter. The ¹²³I window, conversely, contains little contamination from the lower window, but is affected by septal penetration of high-energy ¹²³I photons, which broadens the PSF at higher energies.

Discrimination between a normal brain and the prodromal disease stage produced AUC=0.924 with PET imaging as compared to 0.863 with simultaneous dual-isotope SPECT. Our results show that although PET yielded better performance, simultaneous SPECT yielded acceptable results that were significantly better than those obtained with sequential SPECT (p=0.01 for a three-head system with ΔE=6.2%), while acquiring both studies on the same day under identical physiological conditions. Since BV is not dependent on the scanner, we can assume that the order ranking of the three approaches would be maintained in different patient populations. Simultaneous imaging has the advantage of probing the patient’s pre- and postsynaptic uptake while they are in the same physiological state, whereas sequential imaging (that would typically be imaged on different days) does not. We would expect the differences reported here between these protocols to be a lower limit.

For the task studied here, biological variability introduces the largest share of uncertainty into the estimation of parameters for both SPECT and PET. Due to this, differences observed between different types of scanners and scanning protocols were reduced. Nonetheless, simultaneous SPECT imaging yielded similar results (AUC=0.863) to sequential imaging (AUC=0.859) performed on a superior scanner. Although three-head cameras are available, they are not as widespread as two-head systems. Improvement in the acquisition protocol can have a larger impact on performance than using a scanner with improved energy resolution and sensitivity.

For an individual patient, changing energy resolution improved performance (ΔAUC=0.012), however, the shift to a three-head camera (ΔAUC=0.039) or simultaneous acquisition (ΔAUC=0.051) had a greater impact. This statement cannot be made when considering a population of patients. An improvement in energy resolution is most advantageous when one has many finely sampled energy windows (rather than two coarse windows), as demonstrated by Kijewski et al.⁴ In their work, performance was calculated using 1 keV energy windows, thereby improving the contrast between the two radionuclides. In this work, we use only two energy windows, removing much of the spectral information and producing less improvement in performance. Imaging with two energy windows is more practical than several windows: most scanners only allow two energy windows to be defined, unless list-mode data is acquired and rebinned during postprocessing.

The biological variability values employed here were estimates based on the assumption that overall variability is a quadrature sum of biological and measurement uncertainty. Intrapatient variability is an additional source of uncertainty that we have omitted here, but may play a role in test-retest experiments. For some biological functions, one would expect that a patient’s physiological state (such as blood pressure or heart rate for perfusion measurements) would affect the quantities being estimated, and scanning them on different days will produce different results to a simultaneous measurement. We cannot directly probe this because it will be incorporated into the test-retest results, but it is expected to be small for the neuroreceptor imaging considered here, compared to other brain functions such as blood flow.

CONCLUSION

This study considered the performance of simultaneous dual-isotope SPECT imaging for staging of early PD and compared it with both sequential dual-isotope SPECT imaging and presynaptic PET imaging. Single-isotope PET imaging produced an AUC=0.924 when discriminating between a normal brain and prodromal PD, compared to simultaneous dual-isotope SPECT imaging (AUC=0.863), for a clinically relevant acquisition time. Simultaneous imaging produced a statistically significant improvement in AUC of 3% over sequential imaging (p=0.01), for the same total SPECT imaging time. Simultaneous imaging also delivers 5%–7% higher sensitivity for clinically relevant specificity values compared with sequential imaging. A small but significant (p<0.001) improvement in performance was found when using simultaneous SPECT imaging on a two-head camera with 9.2% energy resolution (AUC=0.863) to that obtained with sequential SPECT on a three-head camera with 6.2% energy resolution (AUC=0.859).