Mutual-information-based image to patient re-registration using intraoperative ultrasound in image-guided neurosurgery

Abstract

An image-based re-registration scheme has been developed and evaluated that uses fiducial registration as a starting point to maximize the normalized mutual information (nMI) between intraoperative ultrasound (iUS) and preoperative magnetic resonance images (pMR). We show that this scheme significantly (p⪡0.001) reduces tumor boundary misalignment between iUS pre-durotomy and pMR from an average of 2.5 mm to 1.0 mm in six resection surgeries. The corrected tumor alignment before dural opening provides a more accurate reference for assessing subsequent intraoperative tumor displacement, which is important for brain shift compensation as surgery progresses. In addition, we report the translational and rotational capture ranges necessary for successful convergence of the nMI registration technique (5.9 mm and 5.2 deg, respectively). The proposed scheme is automatic, sufficiently robust, and computationally efficient (<2 min), and holds promise for routine clinical use in the operating room during image-guided neurosurgical procedures.

INTRODUCTION

Modern neuronavigational systems that rely solely on preoperative magnetic resonance images (pMR) are susceptible to inaccuracies that are compounded by brain shift as a result of the complex loading conditions associated with surgical intervention. The magnitude of brain shift can reach more than 20 mm at the cortical surface¹ and often exceeds 3 mm at the tumor margin,² thereby posing a significant challenge to the accuracy of image guidance in neurosurgery. Intraoperative ultrasound (iUS) is an attractive noninvasive technique that images lesions and structures in the deeper brain during neurosurgical procedures. The application of iUS can be traced back to the early 1950s, during which time ultrasound was used to linearly estimate the depth of highly echogenic structures, but without any imaging capabilities.³ With the advent of real-time ultrasound scanning in the late 1970s, it was demonstrated that iUS is able to image a variety of pathologic lesions as well as normal tissues.^{3, 4} Because it offers real time image acquisition that integrates seamlessly with neurosurgical workflow and is low in cost, iUS has emerged as an important and practical navigational tool to account for brain shift during open cranial procedures.^{4, 5, 6, 7} However, its relatively poor soft tissue contrast resolution and overall image noise make parenchymal structures more difficult to delineate with this modality, especially when used alone. Coregistration of iUS with pMR substantially improves the interpretation and understanding of the intracranial features captured with the technique, making the accuracy with which pMR can be aligned with the dominant features in iUS of considerable importance. If iUS is to become a critical component of accurate image-guided neurosurgery, for example, as a method of compensating for intraoperative brain shift, either by itself or as a complement to the overall process, maximizing the registration accuracy with the internal features of surgical interest between iUS and pMR would seem to be essential. Most commonly,⁸ patient head registration is achieved through MR compatible fiducial markers implanted in the skull⁹ or applied externally to the scalp.¹⁰ Fiducial-based schemes establish the required mapping using external markers identified in the two coordinate systems, which does not necessarily optimize the alignment of the internal anatomical structures of interest (e.g., tumor).

In order to achieve a “last-known correct” (i.e., pre-brain-shift) registration between iUS and pMR and to optimize the use of iUS for intraoperative image guidance, an image-based rigid-body re-registration scheme is developed to improve tumor alignment between pMR and iUS pre-durotomy for open cranial resection surgeries. This is achieved by maximizing the mutual information (MI) between the iUS and pMR. Other feature-based methods of registering these two image modalities require segmentation of anatomical structures (e.g., surfaces¹¹ or vessels¹²), which can be difficult to automate and usually requires manual (time consuming) intervention especially in the US images. Application of MI-based registration of US images is relatively unexplored,¹³ and only a limited number of studies have been reported (e.g., between US and MR for brain,^{14, 15} liver,¹⁶ and phantom images;¹⁷ between US and MR angiography of carotid arteries;¹⁸ between US and CT for kidney;¹⁹ between cardiac US and SPECT;²⁰ and between US and US for abdominal and thoracic organs²¹ and breast²²).

In this study, we have adopted the normalized MI (nMI²³) as our image similarity measure because of its accuracy and robustness for aligning intermodality images, as well as its invariance to changes in overlapping regions. Using a fiducial-based registration, the iUS images were first transformed into the stationary pMR imaging space, and then a Powell optimization routine was employed to reregister the two sets of images by maximizing their nMI with respect to the six degrees-of-freedom (DOF; three translations and three rotations) transformational parameters. The corrected tumor alignment (i.e., transformation between the iUS and pMR imaging spaces) provides a more accurate reference for subsequent interpretation and compensation of intraoperative tumor displacement post-durotomy, which is critical for reliable image-guided neuronavigation. We estimate the re-registration performance by analyzing the residual misalignment between tumor boundaries in iUS and pMR using a “closest point projection distance” analysis (similar to that used by Maurer et al.²⁴) applied to six representative resection surgeries where image guidance was deployed. In addition, we investigate the translational and rotational capture ranges that determine an upper bound on the initial misalignment, from which a successful nMI optimization can still be obtained that improves the registration accuracy of internal tumor boundaries. The results show that quantifiable improvements in subsurface feature registration accuracy between pre-durotomy iUS and pMR can be achieved easily and efficiently in the operating room (OR) given an initial registration accuracy that is readily obtained with standard fiducial-based methods.

MATERIALS AND METHODS

To demonstrate the proposed nMI-based re-registration scheme, six patients (N=6) undergoing brain tumor resection at Dartmouth-Hitchcock Medical Center were evaluated retrospectively. The only criterion for patient inclusion was the presence of tumor features in both iUS and pMR that were sufficiently distinct to allow boundary segmentation to be used as a means of assessing registration accuracy (see Sec. 2F). Patient age, gender, type of lesion, location of tumor, approximate tumor volume, and fiducial registration error (FRE⁸) from the fiducial-based registration (mean±std; see Sec. 2A) are given in Table 1.

Table 1.

Summary of patient information and the fiducial-based FRE (in mm).

Patient	Age (gender)	Type of lesion	Location of tumor	Tumor volume (cc)	Fiducial-based FRE
1	62 (M)	Metastasis	Right posterior temporal	10.99	3.9±1.5
2	49 (F)	Ganglioglioma	Right parietal	0.20	2.6±0.98
3	53 (M)	Meningioma	Right parasagittal	53.12	3.0±0.67
4	50 (M)	Metastasis	Left parietal	11.82	3.2±1.2
5	66 (M)	Meningioma	Right frontal	4.97	2.3±0.3
6	61 (F)	Megingioma	Right parietal	0.62	3.1±0.98

Registration in the OR

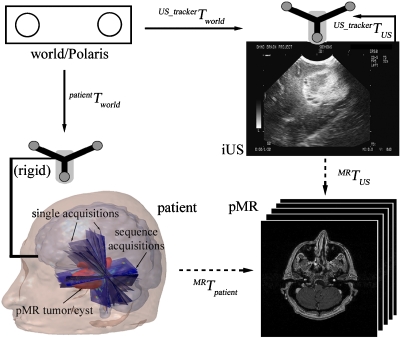
The fiducial-based registration was achieved with a 3D optical tracking system (Polaris; The Northern Digital Inc., Canada), which provides a common “world” coordinate system. Before surgery, an infrared diode tracker (patient tracker) was rigidly fixed to the patient head clamp to establish a reference relative to the world coordinates. A passive digitizing stylus and an active US tracker were used to define the 3D locations of the stylus tip and each US pixel with respect to the world coordinates through calibration procedures using a set of wires arranged in an “N” configuration²⁵ (^US_trackerT_US in Fig. 1). Scalp-affixed fiducial markers (typically N=10–15) were placed symmetrically on both sides of the head and were manually identified in pMR through an interactive software tool. This tool allowed the user to adjust the position of the localized fiducial in three orthogonal views until the identified marker was visually symmetrical in these cross-sectional images. The centers of these fiducial markers were also subsequently identified in the OR using the digitizing stylus. Fiducials in skewed locations were discarded if the stylus was not visible to the tracking system. Typically, 8–10 fiducial markers were successfully identified in the OR. Because the two sets of homologous fiducial points were not paired (no special effort was made to record their acquisition orders with either the digitizing stylus or the software interface to simplify surgical workflow at the start of a case), closed-form solutions (e.g., through singular value decomposition²⁶) that compute the rigid-body spatial transformation directly were not used. Instead, the rigid-body registration was conveniently and efficiently achieved through either an iterative closest point procedure^{25, 27} or a genetic algorithm²⁸ to match the arbitrarily ordered lists of 3D fiducial locations measured in the OR and identified in pMR (computational cost typically of less than 2 min). The resulting registration between the patient tracker and pMR $\left({}^{\mathrm{MR}}T_{\text{patient}}^0\right)$ enabled transformation from iUS to pMR using the following equation (Fig. 1):

$${}^{\mathrm{MR}}T_{\mathrm{US}}^0={}^{\mathrm{MR}}T_{\text{patient}}^0\times {}^{\text{patient}}T_{\text{world}}\times \mathrm{inv}\left({}^{\text{US\_tracker}}T_{\text{world}}\right)\times {}^{\text{US\_tracker}}T_{\mathrm{US}}.$$ (1)

Figure 1.

Coordinate systems used in the image re-registration. Solid arrows indicate transformations determined from calibration, and are fixed. Dashed arrows indicate transformations determined from registration, and are subject to adjustment through the re-registration process. A transformation reversing the arrow direction is obtained by matrix inversion. Intraoperative US images obtained from single and sequence acquisitions before dural opening for a typical patient case are overlaid on the patient head, demonstrating the difference in the two types of acquisitions as well as the incomplete scanning and∕or nonuniform sampling of the tumor volume resulting from free-hand scanning.

However, the resulting transformation is subject to errors from the fiducial-based registration, US scan-head calibration, and possibly brain shift. The nMI-based re-registration scheme was then employed to adjust the transformation accordingly

$${}^{\mathrm{MR}}T_{\mathrm{US}}^{\text{adjusted}}=T^{\text{adjust}}\times {}^{\mathrm{MR}}T_{\mathrm{US}}^0=T^{\text{adjust}}\times {}^{\mathrm{MR}}T_{\text{patient}}^0\times {}^{\text{patient}}T_{\text{world}}^0\times \mathrm{inv}\left({}^{\text{US\_tracker}}T_{\text{world}}\right)\times {}^{\text{US\_tracker}}T_{\mathrm{US}}.$$ (2)

Data acquisition

Prior to surgery, each patient had full volume T1-weighted, gadolinium-enhanced pMR scans of the head from a 1.5 Tesla GE scanner (256×256×124; voxel size (dx×dy×dz): 0.94 mm×0.94 mm×1.5 mm; 16-bit gray scale). After craniotomy but before durotomy, a set of 2D B-mode iUS scans (typically N=20–200; Siemens Sonoline Sienna, C8-5 transducer; image size: 640×480; pixel size: 0.15 mm×0.16 mm; eight-bit gray scale; image acquisition time: 50–60 ms) were digitized through a frame grabber (DT3155; Data Translations Inc., Marlboro, MA). The scan depth was 60 mm during image acquisition for all six surgeries evaluated in this study, although in general it can vary from 30 to 160 mm depending on the optimal imaging window. Through either a single acquisition (N=1) or a sequence of acquisitions (N=20), all six DOF of the transducer were exercised within the confinements of the craniotomy. A single acquisition usually sampled the tumor volume uniquely, while sequence acquisitions were obtained by sweeping the US scan-head across a limited range of translations and∕or rotations.²⁸ A full sampling of the tumor volume was not always achievable even with 3D reconstruction techniques,²⁹ because of the incomplete and∕or nonuniform acquisition sequences resulting from free-hand operation (see Fig. 1 for a typical patient case). The use of these images is described in the next section. The transducer position and orientation were continuously tracked by the Polaris system to tag each iUS image with a transformation relative to the world coordinate system (Fig. 1).

Image preprocessing

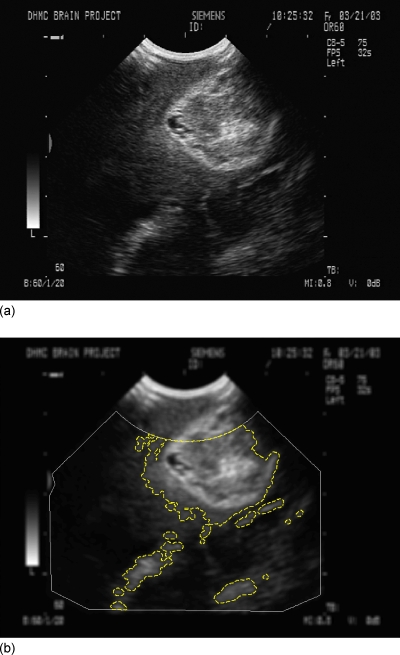
Image preprocessing was necessary for generating a smooth MI hypersurface with respect to the transformational parameters and, hence, a more robust optimization behavior. In this study, patient pMR intensities were quantized into eight-bit gray scale or 256 bins to match that of the iUS. Each pMR image was further median filtered with a 5×5 kernel. By contrast, iUS images were Gaussian blurred by a 5×5 kernel to reduce speckle noise,¹⁶ although other low-pass filters are also available (e.g., median filter,^{20, 21} or “stick” filter).¹⁹ The resulting iUS images were thresholded³⁰ and dilated with a 5×5 kernel to create a binary mask to highlight prominent features (mostly, tumor¹⁴). Nonimaging regions as well as those areas near the transducer probe tip were removed from the resulting mask to reduce artifacts and to minimize the effect of possible compression due to tissue contact during US image acquisitions.¹⁶ They were determined by manually identifying the corners of the actual US image and removing areas within a radius of approximately 2 cm relative to the scan-head probe tip to generate an image mask. The automation of the image preprocessing used in this study was not altered by mask generation because a single image mask was determined during US calibration prior to surgery and applied to all US images acquired intraoperatively. The Gaussian blurred iUS images were then masked, and the resulting pixels were transformed into the pMR space using the fiducial-based transformation. Only pixels residing within the pMR anatomical region (i.e., scalp-air surface, segmented automatically using isosurface extraction) were collected for MI evaluation to avoid large mutual information contributions when iUS pixels matched the pMR background. These simple data preprocessing procedures were automatic and necessary to reduce the influence of areas with low contrast-to-noise ratios and to focus on regions with anatomical features to ensure successful registrations.¹⁸ An illustration of a typical iUS image after preprocessing is shown in Fig. 2.

Figure 2.

A typical iUS image before (a) and after (b) preprocessing. The iUS image was Gaussian blurred, and only pixels within the dashed lines were included for nMI evaluation, while those in regions with few anatomical features or nonimaging regions (exterior to the solid line) were discarded. The outer boundary (i.e., image mask) was determined by manually identifying the corners of the actual US image and removing areas within a radius of approximately 2 cm relative to the scan-head probe tip. This was performed before surgery during US calibration, and, therefore, did not compromise the automation of the image preprocessing in this study.

The time complexity for MI calculation is linearly proportional to the number of iUS pixels involved. To reduce the computational burden, the number of iUS pixels included all iUS single acquisitions but only the 5th and 15th iUS images from each acquisition sequence (provided that the corresponding spatial location from the optical tracking system was available), because single acquisitions usually sampled the target tissue uniquely, while sequence acquisitions tended to cluster with a limited sampling region (e.g., see the collection of iUS images transformed into pMR in Fig. 1). This scheme retained a reasonable sampling of the tumor volume while reducing the total number of iUS pixels used in the computations. Overall, about 10%–60% of the iUS images were utilized for nMI registration (Table 2), depending on the number of iUS sweeps that were acquired during a given case. Typically, the computational cost for the preprocessing of pMR images was 5 sec, and it was 20 sec for 10 iUS images processed collectively. The computational efficiency of the iUS preprocessing can be significantly improved by operating on each image as soon as it becomes available while waiting for the next iUS image to be acquired.

Table 2.

Number of available iUS images, as well as number of single, sequence of, and selected iUS images for each patient. Each single acquisition included one iUS image, while each sequence of acquisitions included 20 iUS images acquired continuously in approximately 2 sec. Two images were selected for each sequence of acquisitions, while all single acquisitions were selected, provided that the corresponding spatial location of the respective US scan-head was available. Numbers in parentheses indicate the iUS images selected from each type of iUS image acquisition, which added to the total number of selected iUS images in the bottom row.

Patient	1	2	3	4	5	6
Available iUS images	69	127	68	151	15	85
Single iUS images	9 (7)	7 (3)	8 (6)	11 (9)	15 (9)	5 (5)
Sequence of iUS images	3 (6)	6 (9)	3 (5)	7 (14)	0 (0)	4 (8)
Selected iUS images	13	12	11	23	9	13

MI and the maximization scheme

An MI-based image similarity measure has been successfully applied to a wide range of intra- and intermodality image registrations since its inception.¹³ In this study, we have chosen the normalized version, due to its accuracy and robustness for aligning intermodality images, and its invariance to changes in overlapping regions.²³ Given two image sets A and B, the nMI [I(A,B)] is defined as the ratio of the sum of marginal entropies [H(A) and H(B)] over the joint entropy [H(A,B)]

$$I(A,B)=\frac{H\left(A\right)+H\left(B\right)}{H(A,B)}.$$ (3)

The marginal and joint entropies were calculated by the histogram method using all iUS pixels selected and the pMR image volume.³¹ To improve the smoothness of nMI and, hence, the robustness of the optimization, a trilinear partial volume distribution interpolation scheme was employed to accumulate the fractional weight of the histogram count into existing intensity pairs, instead of creating new ones.^{13, 31} NMI-based rigid-body registration is essentially a maximization of nMI with respect to the six DOF transformational parameters. MI (including nMI) is generally a nonsmooth function across the transformational parametric space. The optimal transformation derived from the maximization procedure may then correspond to a strong local maximum, but not necessarily the global maximum. Practical issues arise such as the choice of optimization scheme, the initial starting point for parametric optimization, and the capture range. Here, we have adopted the Powell method that minimizes the objective function with respect to each transformational parameter in turn following a line minimization,³² because of its efficient computations, which is critical for application in the OR. It is understood that the negation of nMI [i.e.,−I(A,B)] was used in the Powell minimization routine to generate the maximized nMI.

The extent of the capture range cannot be determineda priori¹³ (see Sec. 2G for its determination in this study). Thus, the initial starting point is important to achieving successful convergence. The fiducial-based registration, although not perfect for tumor alignment between iUS and pMR, serves this purpose very well. To simplify the process, a local coordinate system was established with its origin positioned at the tumor centroid in the pMR space (O_local; also served as the rotational origin) and major axes parallel to the pMR rectilinear grid axes. Convergence was reached when the absolute change in nMI was less than 10⁻³. The nMI code was written in C and compiled in Matlab for computational efficiency. All computations in this study were executed on a Linux computer (2.6 GHz, 8 G RAM), and all data analysis was performed in Matlab (Matlab 7.3; The Mathworks, Natick, MA).

“Ground truth” registration

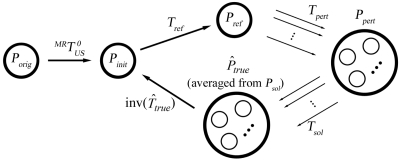
Since the actual ground truth registration between iUS and pMR was unknown in the OR and no definitive artificial landmarks were introduced into both iUS and pMR to compute the ground truth registration, an estimate was used to evaluate the accuracy of the re-registration and determine its capture range (see Sec. 2F). First, the fiducial-based registration was applied to transform the iUS pixels (P_orig; see Sec. 2C) into the pMR space. The resulting set of iUS points (P_init; we term “iUS points” as the transformed spatial locations of iUS pixels throughout this paper) served as a starting reference for parametric optimization and were further transformed using T_ref generated from the nMI maximization process. This transformation (T_ref) was an initial attempt to register iUS and pMR, and was refined to account for possible errors from the use of a finite change in nMI (10⁻³) as the stopping criterion in the optimization process. Based on the transformed points (P_ref), a total of 20 perturbations (T_pert; 10 translational and 10 rotational perturbations) were applied, and 20 sets of new iUS points (P_pert) were obtained. These perturbations were essentially to transform P_ref randomly with the directionality (translational direction and rotational axis passing through O_local) following a uniform distribution.³³ The translational and rotational perturbation magnitudes were randomly generated from an interval of 0 to 2 mm (i.e., the pMR voxel body diagonal [dx²+dy²+dz²]^1∕2) and 0 to 2 deg (0 to 1 deg for patient 5 due to the reduced rotational capture range, see Table 5 in Results), respectively. The average distance between P_ref and P_pert calculated as the mean spatial change in all iUS points as a result of T_pert for all “ground truth” computations was 1.1±0.62 mm. The upper limits of the perturbation magnitudes were kept small enough (less than the expected capture range; see Sec. 2G) to ensure successful registrations (six unsuccessful registrations for patient 5 were discarded; all other registrations involved in computing the “ground truth” transformation were successful in every case). With P_pert, the nMI-maximization scheme was once again invoked to generate 20 sets of optimized iUS points (P_sol) through their respective transformations (T_sol). The estimated “ground truth” transformation $\left({\widehat{T}}_{\text{true}}\right)$ between the spatially averaged P_sol and P_init was finally obtained through a least-squares scheme. All sets of P_sol are expected to be in the vicinity of the actual true location but distributed in a random manner, due to the small and random perturbations that initiated the second maximization process. Thus, we expect ${\widehat{T}}_{\text{true}}$ to be a reasonable estimation of the ground truth for evaluating T^adjust in Eq. 2 (Fig. 3). To ensure that an adequate amount of random sampling was used, we doubled the number of perturbations evaluated, and found that the spatial change in ${\widehat{P}}_{\text{true}}$ was less than 1 mm (i.e., half of the pMR voxel diagonal of 2 mm), indicating that 20 perturbations were sufficient to estimate the ground truth to be within the pMR image resolution.

Table 5.

Translational and rotational capture ranges for each patient. Capture ranges were determined as the largest initial misalignment at or below which the registration success rate was at least 90%. A successful registration was one that had an average distance error of less than the pMR voxel body diagonal ([dx²+dy²+dz²]^1∕2) of 2 mm.

Patient	1	2	3	4	5	6
Translational capture range (mm)	10.5	6.5	12.5	7.6	3.6	4.3
Rotational capture range (deg)	8.7	5.5	5.4	5.4	1.3	8.1

Figure 3.

Schematic for approximating the “ground truth” transformation $\left({\widehat{T}}_{\text{true}}\right)$ between the set of iUS points (P_init) generated from the fiducial-based registration and that $\left({\widehat{P}}_{\text{true}}\right)$ averaged from P_sol. Arrows indicate the ordered steps in the procedure (see text for details).

Quantitative evaluation of the re-registration accuracy

Quantitative evaluation of the nMI-based registration was a practical challenge, because no definitive internal markers were available to assess the registration accuracy. In this study, we utilized a “closest point projection distance” (CPPD) analysis to quantify the residual tumor boundary misalignment in iUS with respect to its pMR counterpart.^{24, 34} Specifically, the segmented tumor boundary from iUS was transformed into the pMR space using the transformation under scrutiny. When a transformed US point was inside∕outside the tumor surface segmented from pMR, a positive∕negative projection distance was obtained between the point and its closest point projection on the triangulated pMR tumor surface.³⁴ Assuming tumor segmentation errors are negligible, the iUS tumor boundary points would exactly coincide with the pMR tumor surface only when the two were perfectly registered. Any residual misalignment, expressed as the average absolute distance from the iUS tumor boundary points relative to their closest point projections on the tumor surface in pMR, is a direct measure of registration accuracy. To evaluate the nMI-based re-registration performance, a paired t-test was used to compare the resulting CPPD with that generated from the fiducial-based registration.

The effectiveness of the CPPD analysis will be influenced by tumor segmentation errors. To minimize any effects, a semiautomatic scheme was used to segment tumor in pMR, in which isosurface extraction (isointensity levels specified by an expert and ranged 4000–6000) was performed and manual adjustments were used to remove regions erroneously included (typically zones isolated from the tumor volume). By contrast, tumor segmentation in iUS was manual. An in-house software program was devised to trace around the tumor, and an interpolation scheme was used to generate equally spaced (0.2 mm, or approximately the iUS pixel size) points to smoothly represent the tumor boundary in each iUS image. To further minimize the sensitivity to segmentation errors, these boundary points were discarded from the CPPD evaluation in regions of poor tumor delineation. While the US segmentation was observer dependent, it is important to note that the US pixel resolution was about one-sixth that of pMR. Although we have not conducted a controlled study, in our experience, expert US segmentations typically vary by only a few pixels (certainly less than five, which is less than the corresponding MR pixel resolution) when the boundaries of interest are well defined. Thus, we do not expect segmentation errors to significantly influence the re-registration accuracy estimates from the CPPD analysis.

Capture range

The optimal registration achieved with the MI-based method generally corresponds to a strong local maximum within the transformation parameter space, whereas attempting to register two grossly misaligned image sets will likely fail. It is, therefore, of practical importance to evaluate the “capture range” that establishes an upper bound on the transformational misalignment, within which nMI optimization is highly likely to succeed. A successful registration was considered to occur when the mean distance from the iUS points (transformed into the pMR space) to their estimated “ground truth” counterparts was less than a specified threshold. Clearly, too small∕large a threshold leads to a too stringent∕lenient criterion.²¹ As a reasonable compromise, we have used the pMR voxel diagonal of 2 mm as the threshold (Ω).

The initial misalignment between iUS and pMR results from a combination of errors that is unlikely to be constrained in a specific way. Therefore, we explored the unconstrained capture range individually for both the translational and rotational (about O_local) parameters. The rotational∕translational parameters were fixed to their estimated “ground truth” values while the translational∕rotational parameters were under evaluation.

Similar to the approach used to estimate the “ground truth” registration, the transformational parameters were randomly perturbed away from the “ground truth” values over a specified range. For each patient, a total of 200 translational and 200 rotational perturbations were evaluated from 0 to 20 mm in translation, and from 0 to 20 deg in rotation about O_local, respectively. Successful registrations were counted, and the capture range was defined as the largest misalignment at or below which the registration success rate was at least 90%. To determine the translational and rotational capture ranges, scatter plots of the average distance error relative to the initial misalignment after perturbation with respect to P_truth were generated for each patient. A total of 2400 registrations were performed to determine the capture ranges for all datasets.

Statistical analysis

In order to investigate the correlation between FRE and tumor boundary misalignment in terms of CPPD and between the nMI-corrected CPPD and number of iUS∕pMR pixels∕voxels used as well as tumor size, Pearson’s correlation test was employed. The same statistical test was also applied to examine relationships with capture ranges.

In addition, we developed a simple measure to quantify tumor feature prominence (Ψ) to investigate the relationship between registration accuracy and the extent of the tumor appearing in iUS. This empirical measure was based on the notion that strong tumor features correspond to well-defined tumor boundaries, which lead to more complete tumor segmentation. Therefore, the number of equally spaced boundary points segmented from iUS, according to Sec. 2F, is an indication of tumor feature prominence. Using dimensional analysis, Ψ is normalized as

$$\Psi =\frac{N}{(n\times V^{2∕3})},$$ (4)

where N is the number of tumor boundary points segmented from iUS, n is the number of iUS images selected, and V is the tumor volume [see Table 1; converted to mm³ in Eq. 4]. Similarly, Pearson’s correlation test was used to evaluate the association between the nMI-corrected CPPD and Ψ. For all statistical tests in this study, the significance level was defined at 95%.

RESULTS

Registration accuracy

The average FRE for the pooled sample was 3.0±0.55 mm, slightly larger than the average initial misalignment of tumor boundary between iUS and pMR (2.5±1.3 mm; see Table 3), even though the latter has additional sources of error (e.g., from US scan-head calibration). This is not necessarily surprising because the FRE is expected to be larger than the true, target registration error (TRE⁸). In addition, the various error contributions do combine differently and the two evaluation measures are not the same (i.e., points versus boundaries). We have found that the correlation between FRE and tumor boundary misalignment in terms of CPPD between iUS pre-durotomy and pMR was only 0.48 in the six patient cases, indicating that accurate patient registration does not necessarily lead to accurate alignment of the tumor. Thus, it is important to improve the registration accuracy of the target tissue (i.e., tumor) at the start of surgery, which is the focus of this study.

Table 3.

Summary of nMI re-registration results. NMI-corrected CPPD (using T_ref) was significantly lower than with fiducial-based registration (p⪡0.001). Shown also are the registration execution time, the number of iUS pixels, and pMR voxels used for nMI evaluation, the number of iUS tumor boundary points segmented from iUS, and the empirical measure of tumor feature prominence Ψ.

Patient	1	2	3	4	5	6
Initial CPPD (mm)	3.0±1.6	1.4±1.0	2.3±1.3	4.9±1.6	1.8±1.2	1.4±0.73
nMI-corrected CPPD (mm)	1.0±0.7	0.90±0.8	1.3±0.95	1.3±1.2	0.85±0.61	0.70±0.65
Execution time (sec)	73	54	45	65	29	91
Number iUS pixels used1	453	344	266	372	165	1133
Number pMR voxels intersected	19 928	20 632	9632	17 744	7368	32 760
Number iUS boundary points segmented	2122	2329	642	650	1535	691
Ψ	0.33	5.72	0.041	0.054	0.88	0.73

^aThe number of iUS pixels in thousands.

^bExceptionally large due to cyst boundaries used.

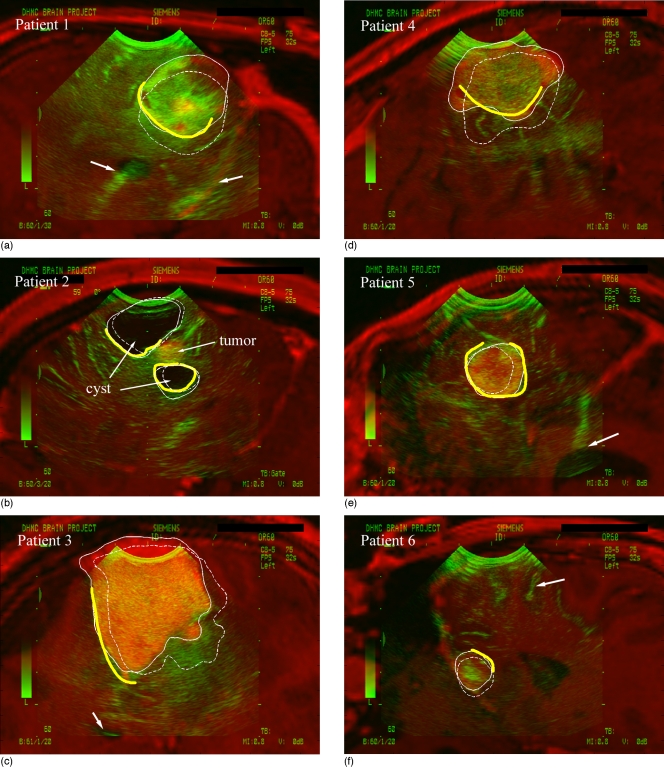
Typical overlays of the iUS images and their corresponding oblique pMR for each patient using the nMI re-registration procedure (T_ref in Fig. 3; see Sec. 2F for detail) are shown in Fig. 4. Shown also are the pMR tumor surface cross sections generated from the nMI (solid thin lines) and fiducial registrations (dashed thin lines). For patient 2, the cyst boundaries were used for analysis due to their very high contrast relative to the involved tumor. The segmented iUS tumor boundaries (thick open lines; cyst boundaries for patient 2) were compared with the pMR tumor surface cross sections. For all patients, visual inspections showed that the nMI re-registration significantly improved the tumor alignment between iUS and pMR (alignment of other internal landmarks are also shown when available). This observation was confirmed with paired t-tests that showed that nMI-corrected CPPDs were significantly lower than those generated from the fiducial-based registrations (p⪡0.001; Table 3).

Figure 4.

Overlay of iUS with corresponding oblique pMR image for each patient using the nMI re-registration procedure (T_ref in Fig. 3). The resulting tumor surface cross sections from pMR (solid thin lines) and those generated by the fiducial-based registration (dashed thin lines) are shown (cross sections of the cyst for patient 2 due to its improved contrast). The alignment between tumor boundary in iUS (thick open lines) and tumor surface in pMR was significantly improved by the nMI re-registration. Shown also are proper alignment of tentorium (patient 1), ventricle (patients 1, 3, and 5) and gyrus (patient 6) in iUS with respect to their pMR counterparts (arrows). Note that segmented tumor boundaries in regions of poor contrast (all patients) or near the transducer probe tip (patients 1 and 2) were discarded.

We used T_ref in Fig. 3 to assess the nMI registration accuracy in terms of tumor boundary alignment because it is the most readily available transformation in the OR that requires only one nMI re-registration effort. As a comparison, the ${\widehat{T}}_{\text{true}}$–corrected CPPD for all patients was 1.0±0.32 mm. Similar magnitudes of CPPDs would be achieved with ${\widehat{T}}_{\text{true}}$ or the transformation between P_init and any P_sol, because they all meet the nMI convergence criterion of the pMR voxel body diagonal of 2 mm and were considered successful registrations. With all patients pooled, the average distance error between P_ref and ${\widehat{P}}_{\text{true}}$ was 1.2±0.13 mm, and it was 1.1±0.25 mm between P_sol and ${\widehat{P}}_{\text{true}}$.

The strong correlation (correlation coefficient of −0.93; Table 4) between the nMI-corrected CPPD and Ψ, an empirical measure of tumor feature prominence, suggests that well-defined tumor boundaries improve tumor alignment between iUS and pMR. Indeed, the CPPD was reduced to an average of 1 mm or less (in patients 1, 2, 5, and 6) when Ψ>0.1, whereas it was greater than 1 mm (patients 3 and 4) when Ψ<0.1. These findings are based on the six patient cases evaluated, which were purposefully selected because distinct tumor features were present, so that readily evident anatomical image features (i.e., tumor boundary) could be segmented (with nominal errors) to assess the accuracy of the re-registration procedure. While one of the attractive aspects of nMI re-registration is the fact that no image segmentation is required, it is important to recognize that the selection of patients with well-defined tumor boundaries may have biased our results. The degree to which this is true awaits further study of clinical cases with less well-defined tumor boundaries, which will present new challenges for accuracy evaluation that we have avoided here in that some other measure (than CPPD) of re-registration performance will be needed (since simple tumor boundary segmentation will no longer be possible).

Table 4.

Correlation coefficients between the nMI-corrected CPPD and the number of iUS pixels, number of pMR voxels, tumor size, and Ψ.

	Number iUS pixels	Number pMR voxels	Tumor size1	Ψ
Correlation coefficient with nMI-corrected CPPD	−0.54	−0.51	0.81	−0.932

^aTumor size calculated as V^1∕3, or the approximate length scale of tumor.

^bPatient 2 excluded from all analyses with respect to Ψ.

Interestingly, larger tumors corresponded to poorer registration performances (Table 4). This was likely due to the reduced tumor feature prominence (patients 3 and 4 in Fig. 4) resulting from the fixed iUS imaging depth used in these cases, as indicated by the correlation between tumor size and Ψ (correlation coefficient of −0.78, not shown). The negative correlation coefficients between CPPD and the number of iUS pixels and pMR voxels used for nMI evaluation (Table 4) suggests a desirability for increased iUS sampling across the tumor volume.

Capture range

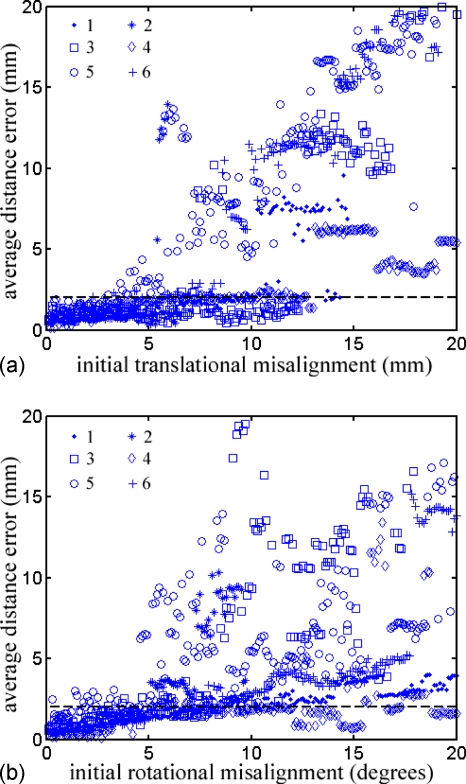
Scatter plots of the average distance error relative to the initial translational and rotational misalignment after perturbation with respect to P_truth are shown in Fig. 5. As expected, small initial misalignments led to small average distance errors (below the dashed horizontal lines that define successful registrations). However, the error growth rate differed for each patient, particularly for patient 5, where the average distance errors were above the threshold, even for some relatively small initial misalignments. The quantitative capture ranges for each patient are reported in Table 5.

Figure 5.

Scatter plot showing the average distance error relative to the initial translational (a) and rotational (b) misalignment for each patient (legend shows patient markers). Each subfigure contains 1200 data points, but average distance errors greater than 20 mm are not shown. NMI-based re-registration was successful when the average distance error was less than the pMR voxel body diagonal (2 mm; dashed horizontal lines).

Strong correlations were found between the translational capture range and tumor size, and between the rotational capture range and the number of iUS pixels and pMR voxels used (Table 6). For the translational capture range, successful convergence of the nMI optimization tended to occur when the tumor in iUS was sufficiently close to that in pMR, such that greater proportions were overlapped. Consequently, larger tumors led to an improved tolerance in the initial misalignment or a larger translational capture range. Practically, when the initial registration is unable to bring the tumor in the two imaging modalities into sufficient proximity, an additional translation may be advisable to match the centroids of tumor segmented from iUS and pMR prior to launching the nMI-based registration scheme.

Table 6.

Correlation coefficients between the translational and rotational capture ranges with the number of iUS pixels, number of pMR voxels, and tumor size.

Correlation coefficient	Number iUS pixels	Number pMR voxels	Tumor size
Translational capture range	−0.31	−0.28	0.79
Rotational capture range	0.66	0.76	−0.073

When the rotational capture range was considered, tumors in the two imaging modalities always overlapped because the rotational origin was set at the tumor centroid. Increased iUS pixels or pMR voxels indicate a higher degree of tumor volume sampling for nMI evaluation, resulting in a smoother nMI function, which allows a larger rotational capture range. Therefore, increasing the iUS sampling over the tumor volume is recommended in practice to improve the tolerance to initial angular misalignment (e.g., patient 5 in this study). In addition, a multistart approach (i.e., initiating the Powell optimization by first spatially transforming the iUS points around the major axes incrementally, e.g., every 1 deg, in a predefined rotational range, e.g., ±5 deg), can be employed to ensure some displaced starting point will lead to a successful registration.

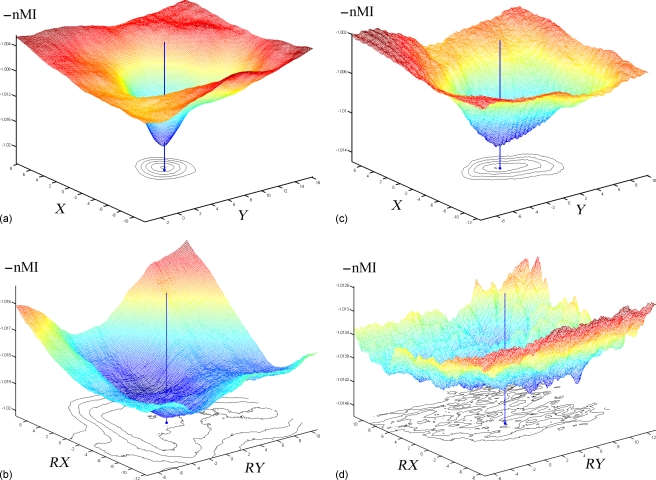
Representative translational and rotational feature spaces were created for two patients with the largest (patient 1) and smallest (patient 5) capture ranges for demonstration purposes (Fig. 6). For both translational and rotational feature spaces, enhanced iUS sampling across the tumor volume (as indicated by the larger numbers of intersected pMR voxels as well as iUS pixels used; Table 3) significantly improved the nMI smoothness, as indicated by the 2D isocontours near the local minimum in the feature space. The difference was more dramatic in the rotational feature spaces [Figs. 6b, 6d], where the decreased sampling across the tumor vol-ume (as indicated by the smaller numbers of intersected pMR voxels as well as iUS pixels used; Table 3) led to a significant deterioration in nMI smoothness [Fig. 6d].

Figure 6.

Feature space of the negation of nMI [−I(A,B)] relative to the translational (ac; in X and Y directions) and rotational (bd; about X and Y axes passing through O_local) misalignment centered at the “ground truth” values for patient 1 (ab) and 5 (cd). With increased number of iUS pixels and pMR voxels (ab) to enhance the sampling across the tumor volume, nMI smoothness is significantly improved [compare (ab) to (cd)], leading to larger capture ranges (Table 5). Shown also are the isocontours at levels near the local minimum to indicate the nMI function smoothness and the distance from the local minimum to the “ground truth” values as indicated by the vertical lines (see Sec. 2E).

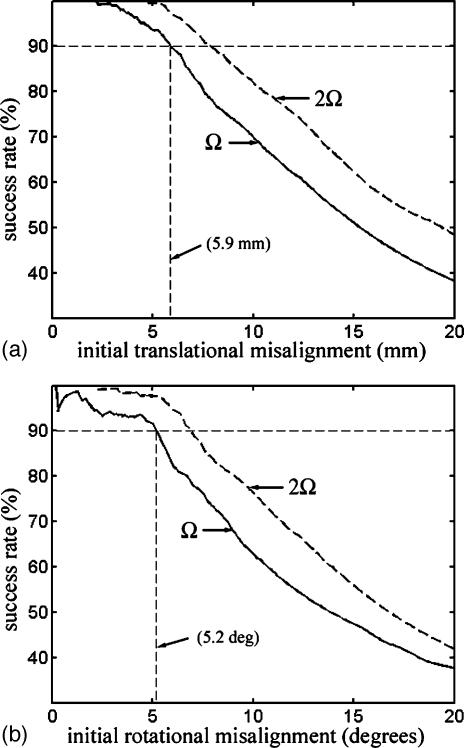
With the results from all six patients pooled, the registration success rate was plotted against the initial translational and rotational misalignment (Fig. 7). The intersection of the success rate curve with the horizontal dashed line at 90% indicates that the overall translational and rotational capture range was 5.9 mm and 5.2 deg, respectively. As a comparison, success rate curves were also plotted for an average distance error threshold of 2Ω or 4 mm (dashed curve). The resulting capture ranges (7.9 mm for translation and 6.9 deg for rotation, respectively) did not vary dramatically.

Figure 7.

Registration success rate relative to the initial translational (a) and rotational (b) misalignment for all six patients. Capture range was determined as the corresponding initial misalignment when the horizontal dashed line at 90% intersected with the success rate curve. As a comparison, success rate curves with the average distance error threshold of 2Ω are shown, where Ω is the pMR voxel body diagonal of 2 mm.

DISCUSSION

In this study, we have evaluated the effectiveness of an nMI-based rigid-body re-registration scheme executed prior to dural opening for this purpose. Results from six surgical resections show that the method is able to improve tumor alignment between iUS and pMR with residual misalignment in the millimeter range. While different sources of error contribute to the initial feature misalignment between iUS and pMR, including those from fiducial registration, US scan-head calibration, accuracy in feature identification in iUS and even possible brain shift at the very beginning of surgery, nMI re-registration collectively corrects these errors (even though it does not differentiate between the different causes) and leads to a “last-known correct” registration between pMR and iUS pre-durotomy that is expected to improve the subsequent use of iUS acquisitions to compensate for intraoperative brain deformation. Importantly, successful nMI-based re-registration has been achieved for different types of tumor (two metastases, one low-grade glioma, and three meningiomas), suggesting the possibility that the technique may be broadly applicable in resection surgeries, although certainly it would have to be evaluated in far more extensive clinical studies to establish the tumor characteristics for which the approach is effective. The automatic and computationally efficient (<2 min) characteristics of the approach are also critical for routine use in the OR.

Accurate patient registration between physical space and pMR image space derived from fiducial-based registration schemes does not necessarily lead to accurate alignment of the internal anatomical structures of interest in iUS, as suggested by the insignificant correlation (0.48) between the two measures. Degradation in registration accuracy stems from a number of sources including fiducial-based registration error (e.g., marker localization error and movement on skin), US feature localization error (e.g., ultrasound image calibration), and even brain shift at this very early stage of surgery. When unaccounted for, these errors may accumulate and compromise the understanding of intraoperative tumor displacement, thereby decreasing the reliability of intraoperative compensation for image guidance. Therefore, it is important to improve tumor boundary alignment at the beginning of surgery as the starting point for incorporating iUS during the procedure for subsequent assessment of brain shift during tumor resection.

The effectiveness of the nMI-based re-registration scheme, however, is reliant on successful convergence. One practical challenge is the fact that the intensity-based image similarity measure does not necessarily correspond to the global maximum upon successful registration. The complexity of the optimization hypersurface is likely greater when registering US with MR, since US images typically highlight tissue boundaries. Incorporating gradient information from MR (e.g., using a polynomial fitting scheme to combine the intensity and gradient information of MR to simulate US images¹¹) may, therefore, hold promise in achieving enhanced robustness in the convergence behavior. However, an iterative solution procedure may be required to account for the angular change that determines the gradient direction, leading to extended computational effort and complexity. Here, we have sought a practical trade off between optimization robustness and computational efficiency so that the procedure can be implemented in the OR.

Without incorporating any MR gradient information, the translational capture range found in this study (5.9 mm) is similar to that reported for registration of cardiac 2D US and SPECT (6.5 mm²⁰), and between reconstructed 3D power Doppler US and MR angiography of carotid arteries (5 mm in transaxial and 10 mm in axial directions¹⁸), but is significantly smaller than that achieved when registering two 3D US volumes (32.5 mm with rigid body transformation, using one times the voxel body diagonal and 90% success rate for capture range determination as in this study²¹). The capture range in Shekhar et al.²¹ may be much larger because the same modality has been registered, although as noted in Walimbe et al.,²⁰ volumetric acquisition (i.e., 3D US) alone increased the capture range by more than three-fold (from 6.5 to 25.5 mm). Results from our study suggest that larger tumors increase the translational capture range, which is not surprising because these tumors are more likely to overlap for a larger translational offset with respect to the true registration, whereas smaller tumors would not (i.e., the translational capture range for a smaller tumor is influenced by other prominent features, e.g., gyrus as in patient 6).

The rotational capture range in our study (5.2 deg) was much smaller than that found in Slomka et al.¹⁸ (40 deg). This may be attributed to the reduced sampling across the tumor volume used here relative to the full volume carotid artery.¹⁸ As suggested by the correlation analysis (Table 6), increasing the number of pMR voxels (i.e., sampling across the tumor volume) increases the rotational capture range. Because the spatial change of an iUS point is proportional to the rotational radius, the tumor centroid in pMR was chosen as the rotational origin so that the overall spatial change was minimized for a given magnitude to avoid rapid changes in nMI that degrade convergence behavior. However, such a strategy may not be optimal when the tumor is not the largest prominent feature in iUS (e.g., small tumors). Assigning a rotational origin to the mean location of all iUS points after the initial transformation may be a better choice in these situations.

Nonetheless, new strategies to enlarge capture ranges, or the likelihood of successful registration are always welcomed. Our results suggest that optimizing the iUS image acquisition window and maximizing iUS tumor volume sampling may significantly improve capture ranges. The latter could be dramatically improved by applying 3D US, as indicated from previous studies.^{18, 20, 21} To avoid the computational costs that result from a substantial increase of iUS pixels that would limit practical use in the OR, it may be necessary to perform multiresolution registration of the two image sets.³⁵ Alternatively, downsampling 3D iUS may prove necessary, although the capture range may be adversely affected because of reduced homologous feature overlap. Further study with volumetric true 3D US generated from a scan-head array that fully samples the region of interest without the need for free-hand sweeps or 3D reconstruction is warranted in the future in order to identify the optimal trade off between computational efficiency, registration robustness, and accuracy.

With enlarged capture ranges that appear possible with true 3D US, one may be able to register US and MR directly without fiducials. For example, we have used the digitizing stylus to draw head contours to match the segmented scalp surface to establish a starting point for the nMI-based method. As long as the initial registration is within the capture range, automatic successful re-registration is expected to be highly effective. Alternatively, incorporating knowledge-based localization of the US scan-head relative to pMR may prove clinically useful. The practical realization of noncontact, image-based (rather than point-based) registration is very attractive in the OR.

We selected nMI as the image similarity measure, instead of the standard MI because we found that the execution time with nMI was lower by a factor of two to five for each registration using Powell optimization, which is critical for OR use. Otherwise, we did not find any significant difference in registration performance between the nMI and MI measures based on the CPPD analysis.

One limitation of the re-registration procedure is its rigid-body underpinnings and once the craniotomy has been performed, nonrigid deformation may have already occurred. However, prior to durotomy (as the case in this study), the magnitude of the motion is typically on the order of the pMR pixel size (e.g., 1.2 mm¹), which is sufficiently small to justify (and even prefer) a rigid registration. Nonrigid registration between iUS postdurotomy and pMR is much more critical because of the larger degree of deformation (3 mm or more²). Alternatively, rigid-body registration could be applied post-durotomy to align tumor boundaries in iUS and pMR to generate local displacement maps that are assimilated by a biomechanical model to estimate whole-brain deformation, which would be nonrigid.

Finally, it is important to recognize that our “ground-truth” registration is only an estimate and that segmentation errors, especially from iUS, have the potential to weaken the CPPD analysis we used for assessing re-registration performance. Phantom studies, which eliminate and∕or reduce these errors by providing more robust knowledge of ground-truth, are certainly possible and may be worth pursuing in the future but the difficulty in representing the MR and US image characteristics and complexity of the human brain is likely to diminish their value as quantitative measures of the re-registration performance that can be achieved in the OR. Studies have shown that tumor segmentation in iUS is more reliable for metastases and some high-grade gliomas, but is poor for low-grade gliomas.^{36, 37} To this end, we included only segmentation of well-defined boundaries to add confidence in the analysis and minimize bias from segmentation uncertainty. Further, in the low-grade glioma case (patient 2), we used the high contrast cyst boundary for the analysis. The degree to which the results presented here suffer from selection bias of cases with well-defined tumor boundaries awaits further study of resection surgeries with more diffusively appearing diseases that will also engender some new challenges in developing appropriate quantitative measures for assessing the nMI re-registration accuracy.

CONCLUSION

We have shown that nMI-based re-registration is feasible and practical and improves tumor alignment between iUS pre-durotomy and pMR, provided that an initial registration within the capture range identified is available. Specifically, in the six patient cases evaluated involving several different tumor types, the average tumor boundary misalignment was reduced from 2.5 to 1.0 mm with the procedure. While the technique is presently reliant on an initial registration estimate, the average capture range required for convergence (found to be 5.9 mm in translation and 5.2 deg in rotation) encompasses the accuracy obtained with point-based fiducial registration as typically practiced in the OR. The automated and computationally efficient (average execution time of 1 min) character of the approach makes it attractive for effective use of coregistered iUS in the OR for brain shift compensation, either as a stand-alone navigational aid^{38, 39, 40} or in concert with other techniques (e.g., brain deformation modeling^{41, 42, 43}) for intraoperative image guidance. This scheme also holds promise for eliminating the reliance on more laborious fiducial-based registration. With enlarged capture ranges likely available from true 3D US that is not dependent on volumetric reconstruction from free-hand sweeps, a fiducial-less approach to patient registration may be possible in the OR. In addition, extending the nMI rigid-body registration to nonrigid registration between iUS post-durotomy and pMR may be attractive for intraoperative brain shift compensation.