4D-CT motion estimation using deformable image registration and 5D respiratory motion modeling

Abstract

Four-dimensional computed tomography (4D-CT) imaging technology has been developed for radiation therapy to provide tumor and organ images at the different breathing phases. In this work, a procedure is proposed for estimating and modeling the respiratory motion field from acquired 4D-CT imaging data and predicting tissue motion at the different breathing phases. The 4D-CT image data consist of series of multislice CT volume segments acquired in ciné mode. A modified optical flow deformable image registration algorithm is used to compute the image motion from the CT segments to a common full volume 3D-CT reference. This reference volume is reconstructed using the acquired 4D-CT data at the end-of-exhalation phase. The segments are optimally aligned to the reference volume according to a proposed a priori alignment procedure. The registration is applied using a multigrid approach and a feature-preserving image downsampling maxfilter to achieve better computational speed and higher registration accuracy. The registration accuracy is about 1.1±0.8 mm for the lung region according to our verification using manually selected landmarks and artificially deformed CT volumes. The estimated motion fields are fitted to two 5D (spatial 3D+tidal volume+airflow rate) motion models: forward model and inverse model. The forward model predicts tissue movements and the inverse model predicts CT density changes as a function of tidal volume and airflow rate. A leave-one-out procedure is used to validate these motion models. The estimated modeling prediction errors are about 0.3 mm for the forward model and 0.4 mm for the inverse model.

INTRODUCTION

Recent developments in computerized cancer treatment planning techniques such as intensity-modulated radiation therapy (IMRT) require precise and efficient calculation of cumulative dose distributions to irradiate the tumor while avoiding surrounding normal structures.¹ It has been long understood that respiratory motion causes significant problems in the treatment planning and irradiation delivery of lung cancer patients. Four-dimensional computed tomography (4D-CT) imaging has been, therefore, proposed to provide valuable information on the shapes and trajectories of tumor and normal structures to guide treatment planning and improve the accuracy of tumor targeting.^{2, 3}

The 4D-CT procedure is usually carried out by acquiring CT data in either ciné or helical modes for multiple times at different couch positions over multiple respiratory cycles, while internal or external respiratory surrogates are measured simultaneously.^{4, 5, 6, 7} The acquired CT data are then mapped to the measured breathing data, and binned into different respiratory phases and reconstructed into 3D-CT volumes. The current protocol used in our institute (Low et al. in 2003) is to scan the patient using a multislice CT scanner in ciné mode and bin the acquired 3D-CT segments into the nearest neighbor phase using amplitude plus breathing direction (inhale or exhale) sorting.^{4, 8} There are several other 4D-CT protocols in the literature (Rietzel et al. in 2005, Keall et al. in 2004, and Vedam et al. in 2003), which acquire CT images or sinogram projection data in either ciné or helical modes.^{2, 6, 7} The acquired 4D-CT data can be sorted by the phase angle or by the respiratory amplitude derived from measured respiratory data, or even by internal organ positions.^{2, 8, 9, 10, 11}

The primary focus of this paper is to use deformable image registration methods to compute the breathing motion from the 4D-CT image data and to construct motion models to approximate the estimated motion field. Our work is related to the following published literature. McClelland et al.¹² reported using a B-spline based deformable image registration method to compute respiratory motion and to build a motion model by approximating the computed motion fields. A breath-holding CT was used as the reference volume for registration. The 4D-CT acquisition protocol used is similar to Low et al.⁴ Sarrut et al.¹³ reported using an optical flow-based deformable registration algorithm to register two breath-holding lung CT volumes acquired at end-of-exhalation and end-of-inhalation phases. An a priori lung density modification (APLDM) algorithm was used to account for changes in lung density due to respiration. Boldea et al.¹⁴ further applied the same method and computed respiratory motion between the 4D-CT images during the entire breathing cycle. This information was used to analyze associated nonlinearities and hysteresis of lung breathing motion. Low et al.¹⁵ in 2005 proposed a 5D (3D+tidal volume+air flow rate) respiratory motion model. The objective of this model was to account for breathing hysteresis effect.^{15, 16}

The following shifts have been made in this work from the current literature: (1) a full volume reference image is reconstructed from the acquired 4D-CT image data and used for deformable image registration; (2) deformable image registration is carried out from each individual multislice CT segment to the reference volume. CT segments of the adjacent couch positions are not involved in the registration computations; therefore, potential artifacts caused by slice misalignments are avoided; (3) the Horn–Schunck optical flow method¹⁷ is used for motion computation. This is because it was more efficient than either the B-spline method or the demons method according to our experiments; (4) a feature preserving maxfilter is applied for image downsampling in the multigrid approach, and the prior knowledge gathered from the acquired 4D-CT data is further used to optimally align the CT segments to the reference volume. The overall registration accuracy is significantly improved by these two procedures; (5) both manually selected landmark points and an artificially deformed CT volume are used to validate the registration accuracy; therefore, the registration accuracy is validated for both selected feature points and the entire lung volume; (6) in addition to the 5D model suggested by Low et al.,¹⁵ an inverse 5D model is proposed to predict the inverse motion fields for different radiation therapy applications.

MATERIALS AND METHODS

4D-CT data acquisition

The 4D-CT data were acquired as 16-slice 3D-CT volume segments using a Philips CT scanner (Brilliance, Philips Medical Systems, Cleveland, OH) operated in the ciné mode. A 3D-CT volume segment, also referred to hereafter as a scan, is 512×512 pixels×16 slices with voxel dimension of 0.9375×0.9375×1.5 mm³. The segments were acquired while the patient breathed freely. Twenty-five segments were acquired at each couch table position and a number of (17 to 19) adjacent couch positions were imaged to contain both lungs and upper abdominal organs. It took the CT scanner 0.42 s to acquire the projection data for a scan (a complete gantry rotation) and 0.25 to 0.3 s idle time between scans. The reconstructed CT volume segments were saved for later offline processing. It took about 18 s to perform 25 scans for one couch table position and about 7 s to transport the couch table to the next couch table position.

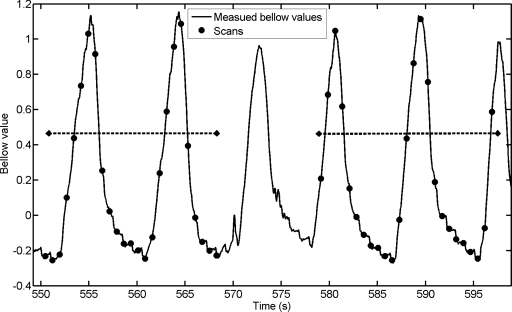
During CT data acquisition, the patient spirometry and abdominal circumference (pneumatic bellows) were continuously measured using an independent data acquisition workstation. The measured spirometry data were processed to correct for drifting. The corrected spirometry data were used to linearly calibrate and convert the measured bellow values to tidal volumes for subsequent sorting.¹⁸ The converted tidal volume values were offset to 0 ml at the fifth percentile tidal volume, which was used as the reference for the end-of-exhalation phase. The workstation also recorded x-ray on∕off signal from the CT scanner to provide synchronization between CT scans and the bellow data. The starting of an x-ray ON signal was synchronized to the starting of a CT scan in time. Because each CT scan took 0.42 s to finish, the bellow values measured at the centers of the 0.42 s periods were used as the bellow values for the CT scans. An example of the measured bellow values and the CT scanning versus time is shown in Fig. 1. Each set of 25 scans typically covered more than two respiratory cycles.

Figure 1.

Plot of measured bellow values vs. time for two couch positions. The small black dots show when CT scans are taken and the corresponding bellow values. There are 25 scans at each couch position. The durations of a couch position are indicated by the big dashed lines.

Reconstructing the reference 3D-CT volume

An amplitude sorting algorithm was used to reconstruct the reference 3D-CT volume from the acquired CT segments at the end-of-exhalation phase. Such a reference volume is used because: (a) the end-of-exhalation phase is typically the most reproducible phase, (b) respiration motion is minimized, and (c) the tissues are at their most superior positions, so that the reference volume would contain all tissues necessary to register CT segments from all couch positions.

Motion estimation

Challenges and solutions for lung CT image registration

There are a few issues that may complicate accurate registration in lung images, especially for the low contrast regions of the lungs. First, motion magnitude of the inferior parts of the lungs can be over 30 mm between the inhaled phases to the exhaled phases.¹⁶ Second, the acquired CT segments have only 16 slices. Third, the lung tissue is sliding along the chest wall during breathing. The motion of the lung tissue and motion of the chest wall are discontinuous. Finally, the lung density changes from the inhaled phases to the exhaled phases.¹³ These density changes are greatest at the inferior parts of the lungs.

Because of these issues and because the end-of-exhalation phase was used as the reference volume, it is generally difficult to register the inhaled inferior lung segments to the reference volume with satisfactory accuracy using most deformable registration algorithms.¹³ A multigrid approach is typically adopted (to sequentially register the two images from the lower resolutions to the higher resolutions) to account for large motions. However, this approach is affected by the limited number of slices per segments and the image smearing problem (e.g., smearing bronchi in the downsampled images). Registration of these smeared images at lower resolution stages may result in larger registration errors, which may not be recovered in subsequent higher image resolution stages. To mitigate these issues, a midrespiration phase might be selected as the reference instead of end of exhalation. However, it is difficult to reconstruct a slice-by-slice aligned 3D-CT volume of the entire lung for the midrespiration phases given the current 4D-CT acquisition protocols.¹⁹ Therefore, the end-of-exhalation reference volume remains the best choice for our purposes.

Our proposed solutions for these issues are the following. The prior knowledge (slice positions of lung apex and diaphragm apex) were derived from the acquired 4D-CT image data and were used to optimally align the CT segments to the reference volume. Thus, the magnitude of the residual misalignment in the superior-inferior (SI) direction is greatly reduced. Nevertheless, the multigrid approach is still needed to account for residual motion in the SI direction and in the axial plane. Therefore, a feature preserving maxfilter was used to replace the commonly used Laplacian pyramid filter²⁰ for image downsampling. The maxfilter (discussed below) preserves small image features, thus, can potentially achieve better registration accuracy across the multiple image resolution stages. The optimal slice alignment procedure and the maxfilter can also help in reducing the problems caused by lung density changes.

The deformable image registration algorithm

Several deformable image registration algorithms have been evaluated in this study. These included the optical flow method by Horn and Schunk,¹⁷ the least mean square (LMS) optical flow method by Lucas and Kanada,²¹ the level set algorithm by Vemuri et al.,²² and the demons algorithm by Thirion.²³ The evaluation results based on 34 manually identified landmarks inside the lungs are summarized in Table 1. This dataset was provided by Princess Margaret Hospital (PMH) and had been previously used in a deformable registration accuracy study as described in Sec. 2D4.²⁴ Accordingly, the Horn and Schunck’s algorithm was chosen due to its computational efficiency and comparable accuracy to other algorithms.

Table 1.

Preliminary comparison of four deformable image registration algorithms using the landmarks. In addition, we show results of Horn–Schunck optical flow algorithm without CT number truncation for comparison with the CT number truncation case.

Algorithms	Registration error (mm)			Computation time (s)
	Mean	Standard deviation	Maximum
Horn–Schunck optical flow	1.57	1.46	7.19	2036
Demons	1.96	1.26	4.77	2906
Lucas–Kanade optical flow	1.55	1.53	8.18	3843
Levelset	3.49	2.06	8.84	3059
Horn–Schunck optical flow (without CT number limiting)	1.88	1.47	6.89	2040

Preprocessing

To improve the computation speed, the patient’s body was segmented using a simple thresholding method and morphological operators. Voxels outside the patient’s body were set to −1000 (CT number of air). All the CT segments were cropped to exclude most of the zero value space.

In order to improve the overall accuracy of image registration, the maximal CT number was limited to 100 (i.e., if a CT number of a voxel was greater than 100, it would be set to 100). The image intensity was then normalized to [0,1] range as required by the Horn–Schunck optical flow algorithm. Truncating larger CT numbers (bony structures) reduces the range of the image intensity before normalization. This resulted in a relative increase of the image gradient values of lower contrast regions (soft tissues) compared to higher contrast regions (bony structures). Consequently, the overall registration accuracy was improved. Table 1 shows preliminary results comparing the registration accuracies achieved with and without such a CT number truncation step.

A priori alignment (APA)

Initially, CT segments were aligned to the reference volume according to their couch table position. A major problem with this simple approach was that the segments of the inferior lung could not be registered accurately because the image motion magnitude (with respect to the reference 3D-CT volume) in these areas was too large, even with a multigrid approach in place. Therefore, slice position parameters derived from the acquired image data were used to achieve an optimal alignment so that the CT segment could be registered more easily and accurately. This procedure is denoted as a priori alignment (APA).

In the APA procedure, the following parameters were derived from the acquired 4D-CT images: the couch table positions of the lung apex and the diaphragm apex for both the end-of-inhalation phase and the end-of-exhalation phase, the tidal volumes of the inhaled phase, the exhaled phase, and every CT segment. The lung was assumed to expand in the SI direction from the exhaled phase to the inhaled phase as a simple linear function of tidal volume. An approximate SI position z where the middle of the CT segment was in the reference volume could then be computed according to simple geometric rules as

$$z=z_{\mathrm{A}}+\frac{(z_{\mathrm{E}}-z_{\mathrm{A}})\times (z_{\mathrm{S}}-z_{\mathrm{A}})}{z_{\mathrm{E}}-z_{\mathrm{A}}+(z_{\mathrm{I}}-z_{\mathrm{E}})V_{\mathrm{S}}-V_{\mathrm{E}}∕V_{\mathrm{I}}-V_{\mathrm{E}}},$$ (1)

where z_A is the lung apex position (same for both the exhaled phase and the inhaled phase), z_E and z_I are the positions of the diaphragm apex in the exhaled phase and the inhaled phase, z_S is the couch position of the middle of the CT segment, V_E, V_I, and V_S are the tidal volumes of the exhaled phase, the inhaled phase, and the CT segment, respectively.

The CT segment was then aligned to the reference volume according to the computed z value. The APA procedure was similar to a SI direction translation-only-rigid-registration procedure. It reduced the SI direction relative motion between the CT segments to the reference volume. Because the lung respiratory motion in the SI motion was usually the largest in magnitude, APA reduced the overall motion magnitude and, thus, made the deformable registration easier. On the other hand, APA also helped to reduce the problems caused by the lung-chest wall sliding issue because the CT segments were aligned optimally, regardless of the position of the chest wall tissues.

Reference volume cropping

After applying the APA procedure, the relative maximal SI motion was reduced from 30 to 9 mm according to our estimation. Therefore, only a subsection of the reference volume extending to a 9 mm range of image motion beyond the target 16-slice segment was needed for the deformable registration computation. To ensure adequate coverage, the reference volume subsection was extended from the target segment by 16 slices, equal to 24 mm, in both superior and inferior directions, resulting in a 48 (3×16) slice volume. Using a subsection of the reference volume instead of the full reference volume for computation helped to improve the overall computational speed.

The multigrid approach and the multiple pass approach

A common limitation of the optical flow methods is that only small motions can be recovered as implied by the Taylor expansion. To allow registration of large motions, the multigrid approach²² was used to perform the optical flow computation sequentially in multiple image resolution stages, from low resolution to high resolution. At each image resolution stage, the multiple pass approach was used²⁵ to perform the computation in multiple passes of a smaller number of iterations. This also allows better and faster computation of the motion fields.

Maxfilter for feature preserving downsampling

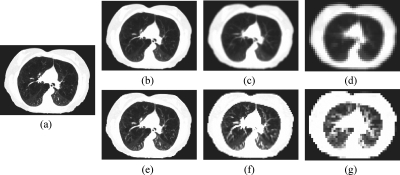
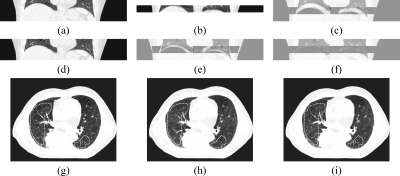
A maxfilter was used in our work for image downsampling operations in the multigrid approach instead of the commonly used Laplacian pyramid filter²³ in order to preserve small image features of the lung (e.g., bronchi and nodes). These features appear brighter than the surrounding air content in the lung. When downsampling the lung CT images with the Laplacian pyramid filter or the Gaussian low-pass filter, smaller bronchi and nodes are often smeared by the darker air content background if the images are half-sampled for two or more times. This problem is illustrated in Figs. 2b, 2c, 2d. Loss of these image features in the downsampled images often causes larger registration errors. A comparison of registration accuracy is shown in Table 2 for using the maxfilter and using the Laplacian pyramid filter.

Figure 2.

Comparison of image downsampling uses the maxfilter and the Laplacian pyramid filter: (a) the original image, (b), (c), and (d) are images sequentially downsampled by 2, 4, and 8 using the Laplacian filter; (e), (f), and (g) are images sequentially downsampled by 2, 4, and 8 using the maxfilter.

Table 2.

Registration error comparison between using the maxfilter and the Laplacian pyramid filter for image downsampling. Reported values are the mean and the standard deviation of the absolute magnitude of registration errors.

Down-sampling filter	Laplacian pyramid filter		Maxfilter
	Inferior	Middle	Inferior	Middle
Registration error (mm)	5.8±3.8	4.5±2.8	2.2±1.8	2.3±2.5

Other considerations

The reference 3D-CT volume is larger than the CT segments and encloses them completely; therefore, the reference volume was chosen as the moving image and the CT segments as the fixed images for deformable registration. One 16-slice motion vector field was computed for every CT segment. The resulting motion fields were defined on the voxels of the CT segments.

Registration accuracy validation

Validation using artificially deformed CT volume

The reference 3D-CT volume of one patient was artificially deformed with the following synthesized motion fields that simulate regular breathing motion:

$$V_{\mathrm{XY}}^{\prime }=G_{\sigma =40}\left[\frac{2X_{\mathrm{XY}}-C_{\mathrm{L}}-C_{\mathrm{R}}}{\mid 2X_{\mathrm{XY}}-C_{\mathrm{L}}-C_{\mathrm{R}}\mid }\right]\min (\mid X_{\mathrm{XY}}-C_{\mathrm{L}}\mid ,\mid X_{\mathrm{XY}}-C_{\mathrm{R}}\mid ),$$ (2)

$$V_{\mathrm{XY}}=5\times V_{\mathrm{XY}}∕\max \left(\mid V_{\mathrm{XY}}^{\prime }\mid \right),$$ (3)

$$V_{\mathrm{Z}}=\frac{z-z_{1∕4}}{\max \left(\mid z-z_{1∕4}\mid \right)}\times 20,$$ (4)

where X_XY is the spatial vector on the X-Y axial plane, C_L and C_R are the manually determined centers of the left lung and the right lung in the X-Y plane, z_1∕4 is the z coordinate of the top 1∕4 lung, G is a 2D Gaussian low-pass filter with sigma=40 pixel, V is the 3D motion vector, V_XY is the projection of V into the X-Y plane, V_Z is the projection of V on the z axis.

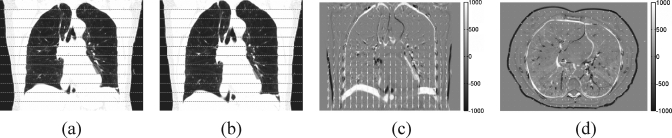
Equation 2 was computed for every pixel on the X-Y plane, excluding the pixels outside the patient’s body. The equation consists of two parts. The first part mainly determines the direction of $V_{\mathrm{XY}}^{\prime }$ with the 2D Gaussian filter to ensure the continuity of the directions. Both parts together determine the magnitude of $V_{\mathrm{XY}}^{\prime }$. Equation 3 was computed for the entire X-Y plane after Eq. 2. It rescales the magnitude of $V_{\mathrm{XY}}^{\prime }$ to a maximum of 5 pixels. The maximal Z motion computed by Eq. 4 is 20 pixels (equal to 30 mm). The values of 5 pixels and 20 pixels were determined empirically. Figure 3 shows a coronal view and a transverse view of the original reference CT volume, the deformed CT volume, and the difference overlaid with the motion field vectors.

Figure 3.

The artificially deformed CT images: (a) the original image; (b) the image deformed with synthesized motion field, the dashed lines mark the 16-slice partitions, (c) the difference image with the motion vectors, (d) the difference image in the axial view.

The dimensions of both the reference volume and the generated new volume were 274×373×192. The generated volume was cut into 12 16-slice segments to emulate the actual 4D-CT data. The segments were registered to the original reference volume individually. The computed motion fields for every segment were then compared to the synthesized motion fields to determine the registration errors for the lung region. The advantage of this validation is the ability to measure registration accuracy for the entire lung and not only for corresponding feature points.

Validation of the maxfilter for image downsampling

The effectiveness of the maxfilter was validated by using the artificially deformed CT volume. Two generated 16-slice segments for the middle lung and the inferior lung were selected. The two segments were registered to the reference volume by using the maxfilter and the Laplacian pyramid filter. The estimated motion fields were compared to the ground truth motion fields.

Validation using patient 4D-CT data

For each patient, validation was carried out by using the reference volume and multiple CT segments randomly selected from multiple and different couch table positions. The CT segments were selected from the middle to the inferior lung of the patients with higher corresponding tidal volumes so that the image motions were at their largest values with respect to the reference volume. Corresponding landmarks were manually selected at visually tractable lung bifurcation points in the reference volume and in the CT segments.

Validation using full volume 4D-CT images

Another 4D-CT lung image dataset was used for independent validations. The image dataset was provided by PMH, Toronto, Canada.²⁴ The dataset contained two 512×512×152 4D-CT volumes from the inhaled and the exhaled phases. Voxel dimension was 0.9766×0.9766×2.5 mm³. There were 38 landmarks defined, 17 for the left lung, 17 for the right lung, two for the aorta, and two for the heart. The same registration parameters and settings were applied in this validation as the parameters and settings used to register the individual CT segment to the reference volume. In this way, the validation results were comparable to the CT segment to reference volume registration validation results.

Inverse motion modeling

The 5D inverse motion field prediction model

The following 5D inverse motion model was proposed to approximate the inverse motion fields that were directly computed by the deformable registration method:

$${\mathbf{M}}_{\mathrm{R}}\left(X\right)=\mathbf{a}\left(X\right)T+\mathbf{b}\left(X\right)F+\mathbf{c}\left(X\right),$$ (5)

where T is the tidal volume (converted from the measured bellow values), F is the flow rate (computed from T by differentiation), X is the imaging space position vector, defined for the imaging device, the parameters a, b, and c are per voxel fitting constant vectors, and M_R is the inverse motion vector similar to the motion fields computed for each CT segment. It is defined on the grid of CT segments and represents how each voxel in a CT segment maps to a position in the reference volume.

This 5D inverse motion model is based on the 5D motion model concept proposed by Low et al.¹⁵ McClelland et al. had also proposed a similar model at the AAPM 2007 conference.²⁶ In this model, the image motion is determined by two variables, the tidal volume and the air flow rate. Time is not a variable, unlike other linear or spline-based temporal fitting models. This 5D model is also able to predict motion hysteresis.^{15, 16} The constant parameters a, b, and c were estimated voxel by voxel using the computed motion fields for the 25 scans of every couch table position by a LMS regression fitting algorithm.

Evaluation of the 5D inverse motion prediction model

To evaluate the accuracy of the 5D model, modelling error (ME), target modeling error (TME), and model prediction error (MPE) were computed.

ME is defined as the error between the predicted motion field and the motion fields used to estimate the fitting parameters. For each CT segment, the predicted motion fields were computed for the same tidal volume and flow rate. ME was then computed between the predicted motion fields and the motion fields computed by deformable image registration.

TME is defined as the error from the transformed reference volume landmark points to the manually identified corresponding landmark points in the CT segments. The reference volume landmark points were transformed using the motion fields predicted for the same tidal volumes and flow rates of the CT segments.

MPE is defined as the error between the predicted motion fields to the known motion field while the known motion field is not used to estimate the modeling parameters. MPE was computed using a leave-one-out procedure. For each of the 25 segments at a couch position, one segment was left out and the modeling parameters were estimated using the motion fields of the other 24 segments. The motion field for the tidal volume and the airflow rate of the left-out segment was predicted using the estimated modeling parameters, and the errors were computed between the predicted motion fields to the motion field of the left-out segment. This procedure was then repeated for all 25 segments for the couch position.

Evaluation of the discontinuity at the segment boundaries

Because image registrations for different CT segments are performed separately, the computed motion fields of CT segments with adjacent couch positions are typically discontinuous at superior and inferior boundaries of these segments. On the other hand, adjacent CT segments are acquired at different time, at different tidal volume, and air flow rate, therefore, the content of the CT segments may partially overlap with each other and motion fields computed of adjacent CT segments need not be continuous. Furthermore, the motion model parameters, which are computed voxel by voxel, are usually continuous within the 16-slice segments because the motion fields are continuous within the 16 slices; however, the model parameters could have discontinuities at the segment boundaries. Please be advised that discontinuities in such cases are not equivalent to having errors because continuous motion fields on discrete voxels also appear discontinuous.

To analyze the boundary discontinuity of the motion field predicted by the model, we computed M_R for inhaled lung using Eq. 5, with T=90th percentile of the measured tidal volume and F=0. The inhaled phase is used because the segments will have the largest motion with respect to the reference volume, and subsequently will have the largest boundary discontinuities. M_R was computed for every pair of adjacent slices (the last slice of a segment, and the first slice of the segment at the next couch position). The absolute magnitude difference of M_R was then computed for each slice pair and its descriptive statistics (mean, standard deviation, and the maximum values) were recorded.

Forward motion modeling

The 5D motion model proposed by Low et al.¹⁵ is

$${\mathbf{M}}_{\mathrm{F}}\left(X_{\mathrm{r}}\right)=\mathbf{\alpha }\left(X_{\mathrm{r}}\right)T+\mathbf{\beta }\left(X_{\mathrm{r}}\right)F+\mathbf{\gamma }\left(X_{\mathrm{r}}\right),$$ (6)

where X_r is the image position vector in the reference volume, M_F is the forward motion vector, α, β, and γ are the per voxel fitting constant vectors.

The forward motion model is similar to the inverse motion model in Eq. 5. The difference is that X_r is defined on the patient position (the reference volume), and M_F indicates where voxels in the reference volume are moving to.

Because the motion fields computed by the optical flow registration algorithm²⁷ are the inverse motion fields, these motion fields have to be inverted to obtain the forward motion fields. A motion field is invertible only if the motion field is well behaved, i.e., smooth with no folding.

The spm_invdef code from Statistical Parametric Mapping²⁸ version 5 package was used for motion field inversion. The method is based on the algorithm by Ashburner et al.²⁹ In this study, the voxels in a 16-slice CT segment were from the voxels in the reference volume outside the 16 slice, especially in the SI direction. In order to accurately invert such a 16-slice motion field, it was extended in both the positive and negative SI directions for the number of slices it reaches. The motion fields of the most superior and inferior boundary slices were used to fill the values for the extended slices. The inversion was then performed on the slice-extended motion field. The resulting forward motion field was considered valid at any voxel if its field vector was pointing into the 16-slice CT segment, otherwise it is invalid. The accuracy of the motion field inversion computation was good. This was verified by computing the inverted motion field for the 16-slice motion fields, then inverting the slice-extended inverted motion fields back, and comparing with the 16-slice motion fields. The estimated error was 0.03±0.05 pixel.

In a similar fashion to the inverse 5D motion model, the computed forward motion fields were used to estimate the modeling parameters α, β, and γ and their accuracy was evaluated by computing ME, TME, MPE and the boundary discontinuities metrics.

Implementation

All the algorithms were implemented in MATLAB (version 7, Mathworks) on a multiprocessor workstation, running a RedHat 4.0 Linux operating system with 8 AMD 1.8 GHz dual core Opteron 865 processors and 16 GB RAM. However, only one thread∕core was used at a time.

To register a CT segment to a reference volume, three multigrid stages were used in the computation. Four, three, and two passes were used for multigrid stage 1, 2, and 3 (stage 3 is the final high resolution stage) with 30, 20, and 10 iterations per pass, respectively. The regularization term in the Horn and Schunck’s algorithm was set to 0.2. After every pass in a stage, and after every stage, a Gaussian low pass filter with sigma of 0.5 pixels was applied to the resulting motion field. A trilinear filter was used for all volumetric interpolations.

RESULTS

The results of the preliminary comparison among four deformable image registration algorithms are listed in Table 1. All registrations were done on the same image data set, with the same or similar parameters and settings. 4D-CT lung images with manually selected landmarks were used for comparison. These preliminary results show that the Horn–Schunck optical flow algorithm is 60 to 90% faster than the other three algorithms and its accuracy is better than or at least similar to the other tested algorithms. Table 1 also shows the comparison of the results with and without using the CT number truncation procedure. One can see that using CT number truncation as a preprocessing step would reduce the overall registration error from 1.88 to 1.57 mm.

Table 2 shows a comparison of the mean and the standard deviation of registration errors between using the maxfilter and the Laplacian pyramid filter. Two CT segments from the artificially deformed CT (Sect. 2D1) were selected for this comparison representing the middle and the inferior lung regions. These results indicate that using the maxfilter for image downsampling in the multigrid approach significantly improves the overall registration accuracy.

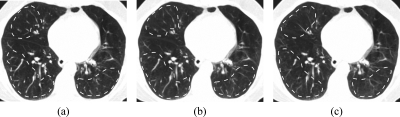
Examples of registration results achieved using the Laplacian pyramid filter and using the maxfilter are shown in Fig. 4. These results suggest that using the maxfilter would lead to better accuracy for lower contrast image regions.

Figure 4.

Comparison of final registration results for using the maxfilter and the Laplacian pyramid filter for image downsampling in the multigrid approach. Dashed lines mark the areas where the most incorrect registration happens in this example: (a) the ground truth target slice, (b) the result by using the maxfilter, (c) the result by using the Laplacian pyramid filter.

Registration accuracy test results using the artificially deformed deformed CT images are summarized in Table 3. The registration errors were 1.55 to 3.23 mm without the APA procedure and were reduced to 0.92 to 1.03 mm using the APA procedure, reflecting significant improvement in registration accuracy. Note that the registration errors in this case were calculated for lung tissues only. Body and chest wall were excluded.

Table 3.

Registration error tested with the artificially deformed CT (Sect. 2D1) with and without using a priori alignment (APA) procedure. The reported registration error values are the mean and the standard deviation of the absolute magnitudes.

Lung position	Maximum axial motion (mm)	Without APA		With APA
		SI motion (mm)	Registration errors (mm)	Maximum SI motion after APA (mm)	Registration errors (mm)
Superior	4.68	−9.2 to 0.4	1.55±1.11	3.14	0.92±0.54
Middle	4.68	0.6 to 13.6	2.48±2.32	2.01	0.77±0.42
Inferior	4.68	13.8 to 30	3.23±3.78	4.97	1.03±1.08
Entire lung	4.68	−9.2 to 30	2.55±2.63	4.97	0.92±0.73

Examples of the APA procedure application are shown in Fig. 5. Significant improvement in registration accuracy is noted, especially in regions bounded by the dashed lines.

Figure 5.

Example of the a priori alignment (APA) procedure: (a) the reference volume section, (b) a CT segment, (c) the difference image that the CT segment is aligned with the reference volume according to the couch table position, (d) the reference volume section shifted by APA, (e) the difference image for the CT segment aligned to the reference volume by APA, (f) the final registration difference image, (g) the target slice in transverse view, (h) the registration result achieved without using APA, (i) the registration result achieved using APA. Regions with most apparent improved results by APA are circled by dashed lines.

The registration accuracy test results on the manually selected landmarks are summarized in Table 4. The test was carried out according to the procedure outlined in Sect. 2D3 for images of three patients. The mean registration error was about 1.2 mm, which is smaller than the 1.5 mm voxel size in the SI direction. We further applied the test to the full 4D-CT images according to the description in Sect. 2D4. The mean registration error in this case was about 1.5 mm. This is again below the 2.5 mm mark corresponding to the voxel size in the SI direction of this dataset.

Table 4.

Validation of registration errors using landmarks. For patients 1 to 3, the landmarks were manually selected in the CT segments and the reference volume. The CT segments used in the validation were randomly selected from the middle to inferior lung and with higher corresponding tidal volumes so that image motions were the largest with respect to the reference volume.

	Landmark pairs	Mean (mm)	Standard deviation (mm)	Maximum (mm)
Patient 1	137	0.98	0.47	2.78
Patient 2	43	1.47	0.95	3.72
Patient 3	43	0.96	0.62	3.08
Full volume 4D-CT	34	1.48	1.34	5.87

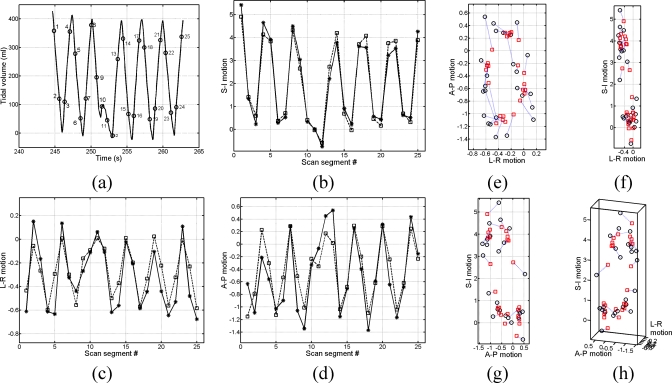
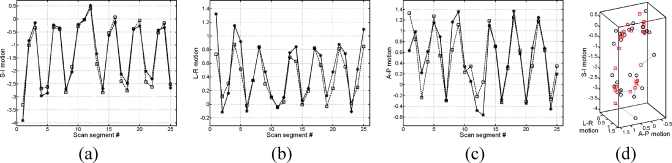
Figure 6 shows LMS parameter fitting examples of the inverse 5D motion model. The fitting was performed for one voxel in the left lung of a selected patient. Figure 7 shows parameter fitting examples of the forward 5D motion model at the same voxel. It is noticed that the parameter fitting process is working well for motions in all directions for both the inverse model and the forward model.

Figure 6.

Example of the inverse motion field fitting for a point selected in the left-inferior lung of a patient. All motion values are in voxels: (a) the tidal volume vs time for the selected point, where the numbered circles mark the time of the CT scan, (b) the SI motion fitting where the circles are the original motion values and the squares are the fitted values, (c) the LR motion fitting, (d) the AP motion fitting, (e) the AP motion vs the LR motion, (f) the SI motion vs the LR motion, (g) the SI motion vs the AP motion, (h) the motion fitting presented in 3D.

Figure 7.

Examples of the forward motion field fitting for the same point as used for Fig. 6. All motion values are in voxels: (a) SI motion fitting, (b) LR motion fitting, (c) AP motion fitting, (d) the motion fitting presented in 3D.

The 5D motion model validation results are listed in Table 5. For the inverse 5D model, the averaged values for TME, ME, and MPE were about 1.2, 0.5, and 0.5 mm. For the forward 5D model, the average values for TME, ME, and MPE were about 0.4, 0.3, and 0.2 mm. It is noticed that the TME values were typically larger than ME values because: (1) there might have been some inconsistencies during the landmark manual selecting procedure, (2) the ME values were averaged for all the CT segments of the patients, including the CT segments without significant motion, whereas the landmarks were always selected at the points that have large motions. The MPE values demonstrate that both 5D models are able to predict motion with averaged errors of about 0.5 and 0.2 mm (magnitude of error in 3D), respectively. For both 5D models, the mean value of boundary discontinuity was in the range of 0.5 to 1.5 mm. This indicates that the predicted motion field was generally continuous at the segment boundaries. By contrasting the validation results of both 5D models, one can notice that the forward 5D model worked generally better than the reverse 5D model. This issue is further discussed in Sect. 4F.

Table 5.

Number of landmark pairs (LPs) used to compute target modeling errors (TME), modeling error (ME), modeling prediction error (MPE), and boundary discontinuity (BD). Values enclosed in braces are the maximum error values.

Patient	Inverse 5D model					Forward 5D model
	LP	TME (mm)	ME (mm)	MPE (mm)	BD (mm)	LP	TME (mm)	ME (mm)	MPE (mm)	BD (mm)
1	131	1.02±0.52 (2.6)	0.40±0.31	0.40±0.37	1.0±0.8 (6.1)	2025	0.52±0.32 (2.8)	0.19±0.36	0.24±0.39	0.9±0.8 (6.7)
2	37	1.71±1.04 (4.4)	0.38±0.29	0.27±0.35	0.7±0.6 (4.5)	929	0.59±0.36 (3.0)	0.25±0.42	0.27±0.48	0.7±0.5 (5.1)
3	42	1.04±0.49 (2.3)	0.77±0.63	0.55±0.82	1.5±0.9 (6.1)	1198	0.67±0.61 (4.9)	0.37±0.62	0.47±0.77	1.4±1.1 (5.2)

In Fig. 8, we show representative examples of the deformed reference volume using the predicted inverse motion fields to generate 3D-CT volumes at selected breathing phases. The generated 3D-CT volumes in row (b) are compared to the reference volume and the differences are shown in row (c). The generated 3D-CT volumes are also compared to the 3D-CT volume reconstructed by the amplitude sorting method as shown in row (a). The differences are presented in row (d). It can be seen that the differences shown in row (d) are small, especially for the lung tissues. This is a qualitative validation of the deformable registration accuracy and the modeling accuracy of the inverse 5D motion model.

Figure 8.

Examples of the reference volume being deformed to generate 3D-CT volumes for different breathing phases. Columns 1, 2, and 3 are for the exhaling phases of tidal volumes equal to 30, 60, and 90% of the 90th percentile tidal volume. Row (a) is the 3D-CT volume reconstructed by using the amplitude sorting method. Row (b) is the 3D-CT volume generated by deforming the reference volume by the motion fields that are predicted by the inverse 5D motion model. Row (c) is the difference between row (b) and the reference volume. Row (d) is the difference between row (a) and row (b).

Examples of the estimated fitting parameters of the 5D forward motion model for a selected patient are shown in Fig. 9. Further information can be quantitatively derived from these parameter maps as follows. Given the tidal volume difference between the exhaled phase to the inhaled phase, the respiratory motion between the two phases can be estimated from the α parameter maps (Fig. 9, column 1). For instance, if the tidal volume difference was 0.5 L, and α in SI direction for inferior lung was about 40 mm∕L (Fig. 9, column 1), then the SI motion of an inferior lung can be estimated to be about 20 mm. Similarly, if the air flow rates were known, the β parameter maps could be used to estimate the motion hysteresis. Please be advised that the γ parameter maps (Fig. 9, column 3) are expected to be 0 only if the reference volume is reconstructed from CT segments with tidal volume=0 and air flow rate=0 for all couch table positions. The γ parameter maps are not 0 in this example because such a condition was not met under the current 4D acquisition protocol.

Figure 9.

Slice views of the estimated fitting parameters of the forward 5D motion model for patient 2. Column (1) is the coronal view of the parameter α [Eq. (9)] vector field, units are in mm∕L. Column (2) is the coronal view of the parameter β, units are in mm∕L∕s. Column (3) is the view of parameter γ, units are in mm. Row (a) is the parameter vector field projection in the AP direction. Row (b) is the LR projection. Row (c) is the SI projection. Row (d) is the magnitude of the vector fields.

The average computation time for the most critical procedures is summarized in Table 6. Computation of the fitting parameters for the forward 5D model takes a longer time than the parameter fitting computation for the inverse 5D model. This is because the forward motion fields from the segments of the adjacent couch positions are required in the forward 5D model parameter fitting procedure.

Table 6.

Average computation time of important tasks.

Task	Average computation time (s)
Deformable registration of a scan to the reference volume	170
Motion estimation for 25 scans	4250=170×25
Invert a 304×448×16-slice motion field	8.2
Compute the fitting parameters for the inverse 5D model for one couch position	140
Compute the fitting parameters for the forward 5D model for one couch position	230

DISCUSSION

Deformable registration accuracy

The deformable image registration accuracy in our implementation is generally good after applying the a priori alignment (APA) procedure for slice alignment and the maxfilter for image downsampling. The absolute registration error is about 1 to 2 mm, less than the voxel vertical size. However, sometimes relatively larger registration errors have been noticed for certain inferior lung CT segments. This is due to the fact that the lung motion in the SI direction is not uniform transversely. Even though the APA procedure can successfully align most parts of the lung vertically for a given CT segment, it may sometimes fail to align other parts. According to our observation, the multigrid approach by itself is not sufficient to capture large motions for unaligned parts of the lung. For these reasons, a better alignment procedure (or rigid registration procedure) should probably be developed in order to achieve better alignment from the CT segments to the reference volume.

Another problem associated with APA is that it might decrease the registration accuracy for the chest wall. Practically, this error could be tolerated if respiratory motion of lung is the purpose of the study.

The problem of lung density changes due to respiration is generally overcome by applying the APA procedure and the maxfilter for image downsampling. There are other alternative solutions that could be incorporated into our framework, such as the a priori lung density modification (APLDM) method reported by Sarrut et al.,¹³ and mass conservation approaches for optical flow algorithms, reported by Wildes et al.,³⁰ and by Bereziat et al..³¹

Slice misalignments in the reference volumes

The segments in the reference volumes are usually aligned fairly well because the reference volume was reconstructed for the end-of-exhalation phase, even though minor slice misalignments may still be present at segment boundaries because of the temporal discontinuities in the 4D acquisition protocol. The minor slice misalignments have not caused major registration errors in this study. McClelland et al. avoided the possible slice misalignment problem by using a separately acquired breath-holding helical CT scan as the reference volume.¹² In our future work, we plan to acquire breath-holding CT and compare against this approach.

Quality of the respiration data

The measured bellows data was used in this study as the respiration surrogate. It was assumed in our method that the respiratory motion could be fully reflected by these measured respiration data. However, the quality of the measured bellows data could be affected by many artifacts, including nonrespiratory patient motion and highly irregular breathing patterns (e.g., coughing). Our method can tolerate minor artifacts in the measured respiration surrogate data. In fact, the deformable image registration step is less affected by such artifacts and the model parameter fitting step can smooth out these minor artifacts through the LMS fitting procedure. The problems with the measured bellows data may be detected by checking the curve shapes and the histories of the bellow values. Moreover, problematic CT segments can be excluded from motion estimation and modeling parameters computation.

Motion computation efficiency

Currently, it takes about 3 min to register one CT segment to the reference volume. The total computation time is still relatively long. There are several possible ways to improve the computation speed: (1) the number of slices for the cropped reference volume could be optimally reduced according to the breathing phase (inhalation versus exhalation) of the segment. Such a step can improve the speed by a factor of 2; (2) the image motion could be computed on the 1∕2 X-Y resolution and full Z resolution, and this step can improve the speed by a factor of 4. We are planning to validate the accuracy of such registration schemes versus the full resolution registration results in our future work, (3) the software can be programmed in C∕C++ instead of MTLAB. Graphic processing unit (GPU) acceleration technology and multiprocessors parallel computation technologies can also be utilized.

Applications of the inverse motion model

At a given tidal volume T and a flow rate F, the model in Eq. 5 could be applied to predict the inverse motion fields. These inverse motion fields can then be used to deform the information defined on the reference volume onto the target CT volume such as image intensity, dose, contour information, etc. Moreover, this model could be applied to generate 4D-CT images for any target breathing phase. To do so, the inverse motion fields for the target breathing phase are computed for every cough position to form a full volume motion field. This full volume motion field could be smoothed by a Gaussian low pass filter in order to reduce discontinuities at the 16-slice segment boundaries. The reference volume is then deformed by the smoothed full volume motion field to generate the target 4D-CT image. Compared to the 4D-CT image reconstructed by the amplitude or phase angle sorting algorithms, the 4D-CT images generated in this way are usually more continuous, with less slice misalignment problems²⁷ as shown in Fig. 8 [(a1) to (a3)].

Another potential application is to deform the structures defined on the treatment planning CT to any breathing phase. If the structures were defined at the end-of-exhalation reference volume, then for every structure, the corresponding binary mask volume could be generated. This binary mask volume is of the same dimensions as the reference volume, and has a value of 1 inside the structure and a value of 0 outside the structure. The binary mask volume is deformed using the predicted motion fields for a selected target breathing phase. The deformed binary mask volume can then be converted into slice by slice contours corresponding to the moved structure of the target breathing phase. If these structures were defined on another treatment planning 3D-CT volume instead of the reference volume, then structures need to be deformed into the reference volume before they can be used.

The model predicts the 4D motion using three parameter vector maps a, b, and c. The parameter maps could be further parametrized. For instance, the parameters can be approximated by certain polynomial equations of X. Thus, the model will be more compact and efficient to use. This will be the subject of future research.

Relation and differences between the two 5D motion models

The forward motion model predicts the tissue and tumor motion. However, it is not suitable to deform the entire reference volume because such deformation procedure requires that the inverse motion fields be defined on the target coordinates. The forward motion fields could be inverted again to get such inverse motion fields, but this requires more computation and may introduce more errors. The inverse 5D model is recommended for such applications that require inverse motion fields.

Our model evaluation results show that the forward 5D model is more accurate than the reverse 5D model in almost every measurement. This is not intuitive because the forward 5D model needs an extra motion field inversion step. An extra step would usually result in more uncertainties rather than less uncertainties. However, we think that this difference of the modeling accuracy could be attributed to the difference in these motion field definitions. In both 5D models, the model parameters are computed voxel-by-voxel by fitting the 25 motion vectors. In the forward 5D model, the 25 motion vectors at any voxel position define how the tissue piece in the reference volume moves. In contrast, in the reverse 5D model, the 25 motion vectors define how the voxels at the position of the 25 CT segments move; however, the 25 voxels at the same spatial position represent different tissue pieces for the 25 CT segments. For example, a piece of tissue in the exhaled inferior lung could move over 30 mm further in the inferior direction, while at the same voxel position a tissue piece of inhaled lung could be 20 to 30 mm away in the superior direction. Because the forward motion vectors at any voxel position describe the motion of the same piece of tissue with respect to different tidal volume T and flow rate F, the motion vectors tend to be more correlated. The 25 backward motion vectors at any voxel position describe the motion of the 25 different pieces of tissue, therefore, the motion vectors are less correlated. Therefore, the forward motion vectors could provide better fit to T and F compared to the backward motion vectors and would result in less ME, TME, and MPE error values.

Different 4D-CT acquisition protocols

The 4D-CT data used in this paper were acquired as multislice volume segments according to the protocol developed by Low et al.⁴ The acquisition of the CT volume segments was discontinuous in time and consequently the computed motion fields for every couch table position were also discontinuous in time. The modeling parameters were computed by LMS fitting over 25 motion fields and temporal discontinuity was smoothed by the LMS fitting process. In general, our motion computation and modeling method could be applied to other 4D-CT acquisition protocols. If the acquired 4D-CT data are in sinogram domain, then they need to be reconstructed into 3D-CT images before deformable image registration is applied.

CONCLUSION

In this paper, a new method based on the optical flow deformable image registration algorithm has been presented to compute image motion from acquired 4D-CT data (ciné mode multislice volume segments). The motion fields were computed for each acquired CT segment with respect to a reference volume, which was reconstructed by an amplitude sorting method at the end-of-exhalation phase. To achieve higher image registration accuracy, a priori alignment (APA) procedure was applied to optimally align the CT segments to the reference volume and a feature preserving maxfilter was used instead of the commonly used Laplacian pyramid filter for image downsampling. Two 5D motion models were proposed to approximate the computed image motion in order to predict the motion at arbitrary breathing phases. The inverse motion prediction model was able to directly predict the inverse motion fields. The forward 5D motion model was able to predict tissue movements of the reference volume. Both motion models are potentially useful in image-guided radiotherapy applications.