Abstract
A proton beam delivery system on a gantry with continuous uniform scanning and dose layer stacking at the Midwest Proton Radiotherapy Institute has been commissioned and accepted for clinical use. This paper was motivated by a lack of guidance on the testing and characterization for clinical uniform scanning systems. As such, it describes how these tasks were performed with a uniform scanning beam delivery system. This paper reports the methods used and important dosimetric characteristics of radiation fields produced by the system. The commissioning data include the transverse and longitudinal dose distributions, penumbra, and absolute dose values. Using a 208 MeV cyclotron’s proton beam, the system provides field sizes up to 20 and 30 cm in diameter for proton ranges in water up to 27 and 20 cm, respectively. The dose layer stacking method allows for the flexible construction of spread-out Bragg peaks with uniform modulation of up to 15 cm in water, at typical dose rates of 1–3 Gy∕min. For measuring relative dose distributions, multielement ion chamber arrays, small-volume ion chambers, and radiographic films were employed. Measurements during the clinical commissioning of the system have shown that the lateral and longitudinal dose uniformity of 2.5% or better can be achieved for all clinically important field sizes and ranges. The measured transverse penumbra widths offer a slight improvement in comparison to those achieved with a double scattering beam spreading technique at the facility. Absolute dose measurements were done using calibrated ion chambers, thermoluminescent and alanine detectors. Dose intercomparisons conducted using various types of detectors traceable to a national standards laboratory indicate that the measured dosimetry data agree with each other within 5%.
Keywords: proton, commissioning, uniform, scanning
INTRODUCTION
With the expansion of proton therapy has come the desire to update the beam delivery technology for the goal of increasing the conformality of the delivered dose while minimizing risks to the patient such as from out of field dose, mainly from neutrons. The efforts stem from the fact that the vast majority of proton therapy centers rely on the historic passive double foil spreading beam production with fixed range modulators.1, 2 Although the passive beam spreading technology is capable of delivering highly conformal fields, improvement can be realized by active beam scanning3, 4, 5, 6, 7, 8, 9 while also reducing out of field dose.10 The maximum field size for passive spreading systems also becomes practically limited due to the increased thickness of scattering material required for larger field sizes. This compromises the maximum attainable range at a given accelerator energy. Compared with a scattering system with an inherent additional energy loss, a uniform scanning system can provide a useful increase in water range of about 2.5 cm or more, depending on the field size and the maximum available energy.
Beam scanning can result in uniform or nonuniform delivery. A form of scanning, continuous uniform scanning, combined with energy layer stacking provides a flexible method of constructing depth dose distributions. Because the range of individual beams is controlled in, or upstream of the nozzle, a desired spread-out Bragg peak (SOBP) distribution can quickly be created or modified. Flexible SOBP generation techniques also exist for fixed range modulators,11, 12 but not without related challenges such as the requirements for high beam intensity stability and fast beam modulation control.13, 14 With regard to the advantages of a uniform scanning system it should be mentioned that these possible advantages may be offset to a certain degree by the potential increase in sensitivity to target motion from a scanning system. However, this has yet to be determined for uniform scanning systems as it is usually a design goal of such systems to minimize this effect by providing a high transverse “repainting rate” and fast range shifting.
This work reports on the development and characterization of the continuous uniform scanning proton therapy delivery system developed at the Indiana University Cyclotron Facility (IUCF) and Midwest Proton Radiotherapy Institute (MPRI).15, 16 This paper was motivated by the lack of guidance on the testing and characterization for uniform scanning systems. This paper describes some of the tasks performed during the commissioning of a uniform scanning beam delivery system. A description of the uniform proton scanning delivery system is given followed by clinical commissioning results and absolute dosimetry findings. The relative dosimetry characterization required the use of new multielement detectors. Some of these detectors were designed, built, and evaluated during the commissioning, and were reported in a separate publication.17 Not reported here is the system dose calibration stability with time, dose rate, and monitor units. Also, mechanical alignment results, snout proton leakage, and out of field dose results are omitted. Most of these are standard practices for commissioning medical accelerators. System sensitivity to target motion and out of field dose performance remain current areas of investigation.
METHODS AND MATERIALS
The MPRI facility uses beam produced by the IUCF split sector cyclotron after acceleration to nominally 208 MeV. The beam is then degraded to the required patient maximum range and transported through beam line magnets into one of three available treatment rooms (TR1–TR3). Figure 1 shows the accelerator and room layouts. TR1 consists of a typical double scattering system with fixed range modulator in a fixed horizontal beamline geometry.18 Because patient treatments have been under way in TR1 since 2003 with over 200 treated, “without adverse dosimetry problems,” that system is used at the facility and in this paper as a reference for relative and absolute dosimetry.
Figure 1.
Scale rendering of the IUCF∕MPRI facility. The split sector cyclotron (a) feeds three treatment rooms: the fixed horizontal beam line (b) and two scanning gantries [(c) and (d)].
The continuous uniform scanning system development is installed onto two commercial isocentric ganties (Ion Beam Applications: Louvain-la-Neuve, Belgium) in the MPRI Treatment Rooms (TR) 2 and 3. Because the two rooms were designed to be “twinned,” this paper describes primarily the results from TR2 with the exception of some absolute dosimetry testing that is also reported for TR3.
The continuous uniform scanning system and the methods used to characterize its performance are described in the following.
Proton uniform scanning system
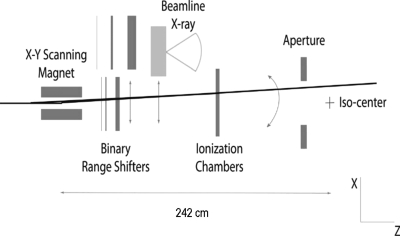
A schematic view of the major continuous uniform scanning system components is presented in Fig. 2. Scattering foils are not used. Instead, an X–Y scanning magnet spreads the beam laterally and can provide beam deflection of up to ±18 cm at the isocenter. The laterally spread-out beam then passes through the range modulator, which pulls back the pristine Bragg peak consecutively to different ranges, resulting in layer-by-layer irradiation of the target volume. The ionization chambers are used to monitor the beam flatness and symmetry as well as to control the dose delivery. Patient-specific apertures and range compensators (boluses) are used for transverse and longitudinal shaping of the dose fields, respectively.
Figure 2.
Schematic (not to scale) of the continuous uniform scanning nozzle.
The beam scanning system can generate uniform transverse dose distributions up to 30×30 cm2 treatment area by continuously scanning the beam according to a predefined scanning pattern. Patient-specific apertures then shape the radiation field appropriate for the treatment. In a typical field delivery scenario, the beam spot travels along the specified scan pattern hundreds of times at the rate of 10–16 Hz, “painting” a transversely flat dose distribution. In depth, however, each layer is only delivered once for each field.
Due to multiple Coulomb scattering from the beam delivery system components and in the patient both the beam spot size and the shape of the pristine Bragg peak vary with the beam energy selected for treatment. The SOBP delivery is therefore split into three regimes, with the dose layer stacking optimized separately for beam penetration ranges in water between 6 and 12 cm, between 12 and 20 cm, and for deep seated targets between 20 and 27 cm. Similarly, scan patterns were optimized to achieve the required dose uniformity for all field sizes and depths. In particular, to take into account changes in beam spot size at different energies, different scan patterns are used for beam penetration ranges below 20 and above 20 cm. The scanning system also uses different scan patterns for different field sizes. The available combinations are shown in Table 1. The proton therapy control system selects from these combinations an appropriate configuration for scanning and for the dose layer stacking based upon the patient-specific field data, which includes proton range in water, SOBP width, and field size.
Table 1.
Proton therapy system delivery regimes. A requested delivery field is categorized in range and field size regimes. Within a regime set the scan pattern and range modulator weights are nominally fixed.
| Maximum field diameter (cm) | Range in water | ||
|---|---|---|---|
| Up to 12 cm | 12–20 cm | 20–27 cm | |
| Up to 12 | X | X | X |
| 12–20 | X | X | X |
| 20–30 | X | X | Not used |
Beam scanner
The scanning magnet consists of a novel dual axis approach in a single enclosure. The vertical (X) scanning is performed with an elephant ear coil and the horizontal (Y) with a saddle coil. They are capable of about 2 kG at 375 A, which provides up to a 30 cm field diameter at the isocenter position 242 cm distal to the magnet center position. Because of the coincident dual scanning magnet design, the distance from the same magnet centers to the isocenter is the same in X and Y. Additional details of the scanning magnet are available elsewhere.19
Range modulators
The system range setting is accomplished by two different devices: a beryllium wedge range degrader proximal to the treatment rooms to set the maximum required field range and a binary range modulator in the therapy nozzle. The binary system is comprised of six plates of proportional thickness. There are two Lucite plates and four graphite plates providing 3, 6, 12, 24, 48, and 96 mm of water equivalent range loss, respectively. After the maximum field range is set the binary system is used to successively pull back the range in appropriately dose weighted increments to generate the specified SOBP. While the range modulator has the maximum Bragg peak pull back in water of only 19 cm, it is sufficient to generate a full modulation at 90% dose level in beams of up to the maximum energy of the IUCF cyclotron.
In practice, the individual Bragg peak weights (Wi) for range modulators are usually determined quasianalytically, validated dosimetrically, and sometimes recalculated in an iterative process until a clinically acceptable modulation is achieved.1 In the case of the uniform scanning system described in this work the binary range modulator provides more flexibility than do fixed devices because the Wi can be adjusted in software. However, the general process remains the same. In order to reduce the total number of fixed range modulators, beam gating has been used in other systems.11, 14 This system, as described earlier in Sec. 2A, uses a series of energy regimes within which the SOBP weights are adjusted to remain within the uniformity requirements due to the variability in the increased straggling of pristine beam ranges across the regime.
A simple algorithm to correct for a SOBP tilt was developed and tested. It is based on a linear model and employs a parameter called tilt (T), which is defined as the percentage of dose variation per centimeter of depth (%∕cm), along the SOBP plateau. The T is minimized from the original Wi giving the set of N Bragg peaks resulting in a uniform SOBP with nominal tilt,
| (1) |
Renormalization of the weights after correction allows are keep to the absolute dose at the center of SOBP unchanged,
| (2) |
The algorithm can be applied to SOBP distributions of any extent, and with upward or downward tilts (positive or negative tilt). An example of this algorithm application is presented in Sec. 3A2.
Field characterization
Relative dosimetry
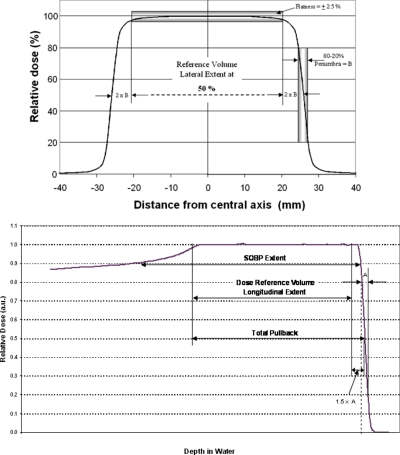
Without recognized standards, especially for longitudinal proton field parameters, it has been common practice to use facility-specific definitions20, 21, 22 of “irradiated volume.” It should be noted that all of these definitions are empirical in nature. For this facility the clinical field validation and commissioning was performed according to an internal standard termed the dose reference volume (DRV). This DRV definition applies to field sizes larger than 2 cm in diameter and with SOBP widths larger than 2 cm. The DRV (Fig. 3 top and bottom) is defined as two penumbra widths (80%–20%) inside the 50% isodose laterally, 1.5 distal fall-off widths (80%–20%) inside the 50% isodose distally and 1 total pullback water-equivalent thickness inside the (distal) 50% isodose proximally. The total pullback is defined as the number of longitudinal steps or layers within the volume multiplied by the water equivalent step widths. The design goal for dose uniformity (flatness and symmetry) within the DRV was specified at 2.5%.
Figure 3.
Dose reference volume definitions. See the text for details.
In order for the system to perform to acceptable clinical performance criteria for field flatness, symmetry, and penumbra, care was required to optimize the system in these respects, which is discussed in more detail in Sec. 3A1. This optimization was performed for all energy regimes and field sizes. During clinical commissioning comparison was also made to a commercial treatment planning system (TPS) (Computerized Medical Systems, Inc., St. Louis, MO; model XiO version 4.2.2 with the proton module installed). For each energy regime and a variety of field sizes, dose distributions produced with continuous uniform scanning and layer stacking were characterized in terms of field size, lateral and longitudinal flatness, and penumbra size. The total number of commissioned field size, range, and SOBP width combinations exceeded 100.
Two types of single element ionization chambers were used, a commercial Markus parallel plate chamber (PTW, Freiburg Germany; model 23343), and a miniature (“mini”) 0.7 cm3 thimble chamber based on a design from the National Accelerator Center (NAC), South Africa.23 The mini chamber used here (NAC-mini) was fabricated at the IUCF from Vespel. The Markus chamber calibration was determined by an accredited laboratory (University of Wisconsin Accredited Dosimetry Calibration Laboratory, Madison, WI). The NAC-mini holds an in-house relative calibration to the calibrated Markus chamber. The Markus chamber was used for longitudinal measurements and delivery system dose calibration. The NAC-mini chamber was used for penumbra measurements or, if indicated, for characterizing fields of less than 5 cm diameter. With the aim of comparing the resultant clinical penumbra between the scanning (TR2) and scattering (TR1) systems all measurements were performed with the NAC-mini in water using a commercial phantom (Wellhofer∕Scanditronix, Schwarzenbruck, Germany; model 3D Blue Phantom).
The uniformly scanned proton beam places special requirements on dose measurement methods. This is because the primary proton beam is not stationary on a singular detector if that detector’s cross section is smaller than the beam profile laterally. This suggests either point by point measurements with a single detector and repeating the entire field for each point, an integrating area detector, or a discrete multielement type. Although point by point measurements were required for the initial system characterization, their relative time inefficiency forced the migration to integrating and multielement types.
The multielement detectors used were all of the ionization chamber type. One commercially available detector was used and two were designed and built at the facility. Both longitudinal and transverse detectors were required. The longitudinal (range) detector is a multilayer ionization chamber (MLIC). The MLIC contains 122 small volume ionization chambers stacked at a 1.82 mm step water equivalent for depth dose profile measurements. The MLIC detector can measure profiles up to 20 cm in depth, and determine the distal dose fall off with about 1 mm precision. Also developed and used at the IUCF and MPRI is a large multipad ionization chamber (MPIC) transverse detector. The MPIC has 128 ionization chambers arranged in one plane and is designed to measure lateral profiles in fields up to 38 cm in diameter. The MPIC pads have a 5 mm pitch for fields up to 20 cm in diameter and a 7 mm pitch for larger fields, providing the accuracy of field size determination about 1 mm. Both the MLIC and MPIC share common instrumentation electronics and a computerized data acquisition system.17 Another transverse detector used is a commercial product providing 1020 vented pixel ionization chambers in a 32×32 grid with 7.6 mm of separation between the centers of the chambers (IBA Dosimetry, Schwarzenbruck, Germany, model I’mRT MatriXX).
The integrating dosimeter used for relative dosimetry characterization was radiographic (Kodak, Rochester, NY; type X-Omat V) film. The film measurements were performed within blocks of polystyrene as well as within the 3D Blue Phantom using an in-house positioning rack. After film development and optical scanning (Vidar Systems Corporation, Herndon, VA; model VXR-16), the relationship between irradiated dose and optical density was determined over the range of relevant physical dose of approximately 1–250 cGy.
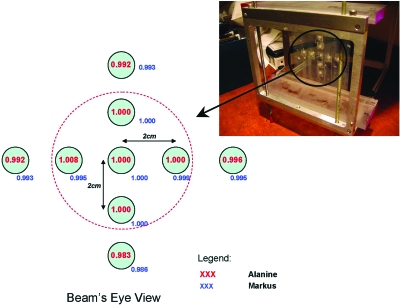
In addition to the absolute dosimetry investigation with alanine dosimeters (Secs. 3A1, 2B2) an independent characterization of field uniformity was also performed with the alanine dosimeters. The experimental setup is presented as part of Fig. 4.
Figure 4.
Alanine dosimeter placement in measurement jig (photo) and reported results with position relative to beam central axis. The jig was placed for irradiation in a water phantom. Directly after the alanine irradiations an ionization chamber was used to measure the relative doses at the alanine measurement locations. The alanine and ionization chamber measurements are normalized here to the central axis values, respectively. The result indicates excellent agreement between the detectors and field uniformity.
Absolute dosimetry
Although not specifically indicated for scanning beam dosimetry, all treatment rooms were calibrated according to International Commission on Radiation Units and Measurements (ICRU) Report 5924 using the calibrated Markus chamber. In Sec. 3B1 the Markus and NAC-mini chambers were used contemporaneously within 20 min on a single day under reference conditions to compare the calibrations between TR1 and TR2. The reference conditions were defined as the field from a 10 cm physical diameter aperture, at the center of a 10 cm SOBP, which was located at a depth of 11 cm in water and coincided with the gantry isocenter. However, the lack of standards guidance and concern over recombination in high fluence rate particle beams prompted additional absolute dosimetry comparisons. Therefore, two additional methods were used for this work: alanine dosimetry pellets25, 26 and thermoluminescent dosimetry.27
Nine alanine dosimetry pellets produced by Far West Technologies and having a NIST-traceable calibration were obtained from Armed Forces Radiobiological Research Institute (AFRRI) and irradiated in the reference field, at the center of SOBP, to a dose of 250 Gy. AFRRI also provided the alanine readout using the electron spin resonance method.
Thermoluminescent dosimeters (TLD) were obtained from and processed by the Radiological Physics Center (RPC) of the University of Texas. The test protocol was derived from their electron beam mailable TLD assay system.28, 29 It uses six TLD capsules, three at each of two depths, measuring two points in the SOBP. The TLDs are placed at the positions within a 9×9×9 cm3 phantom. The phantom was irradiated in air at the gantry isocenter.
RESULTS AND DISCUSSION
Relative dosimetry
Transverse relative dosimetry
Due to the lack of use of physical scatterers or ridge filters in this system, in contrast to a similar heavy-ion irradiation system,30 additional optimization of the system in terms of the scanning patterns was necessary. This was because the beam spot size changes as a result of multiple Coulomb scattering in matter including air, beamline components including varying range shifter thickness, and the target medium, tissue or water. Although the beam optics were optimized to minimize the spot size at the virtual source position in the nozzle all of these effects serve to increase the spot size. Ultimately, for the energy regime corresponding to 20–27 cm of range in water a distance of about 1.5 cm between adjacent scan lines was used. Two other energy regimes, with beam ranges 6–12 and 12–20 cm in water, required 2 cm of line spacing. In order to ensure the 2.5% uniformity over the entire DRV laterally, an overscan distance was required. This was empirically determined to be 3 cm on each side of the field.
Figure 5 demonstrates a typical transverse dose profile measured with the MatriXX and radiographic film. The slight ripple due to the scan pattern observed across the field is within the facility DRV tolerance of ±2.5% and reduces further with increasing depth and∕or modulation. The dose difference result (upper right) in Fig. 5 illustrates the higher resolving power of radiographic film in comparison to the MatriXX detector. In practice, due to their relative ease of use and data analysis, the MatriXX and the MPIC detectors were preferred for measurements over film or point by point ionization chamber measurements if high resolution penumbra information was not required. This was the case for much of the scanning beam pattern and density optimization. Representative results from the MPIC detector are shown in comparison to treatment planing system (TPS) in Fig. 6. As seen in Fig. 6, and across the commissioning of the uniform scanning system, no modification of the TPS dose calculation algorithm was required. This result was expected as effectively, other than penumbra considerations, there should be no difference in the physical dose deposition between uniform scanning and scattering. In this case the TPS (XiO Version 4.2.2) was originally developed for physical scattering proton beam systems. The results of independent field uniformity check using the alanine dosimetry are presented in Fig. 4.
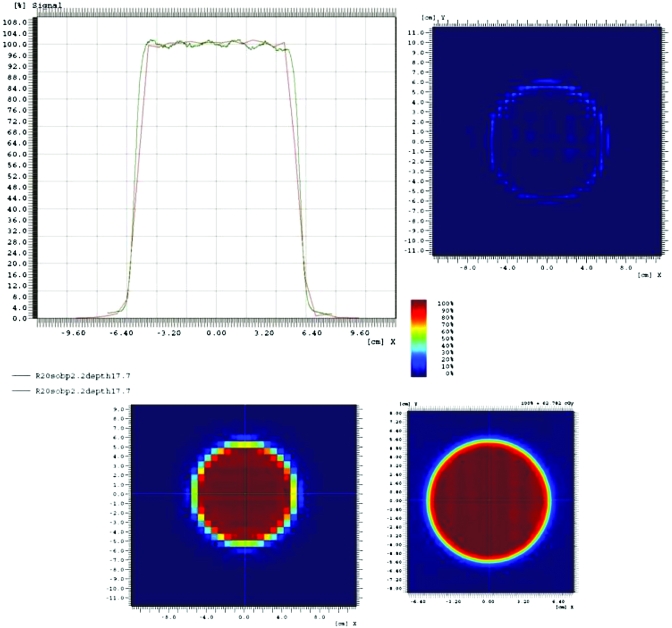
Figure 5.
Measurement of a representative beam profile using the MatriXX device (red line) and film (green line) with the following conditions: measurement at the center of the dose reference volume (depth=17.7 cm) for 20 cm water range and a 2.2 cm SOBP. The MatriXX data are presented in the bottom left, the film scan in the bottom right. The data are compared in the top left and subtracted in the top right.
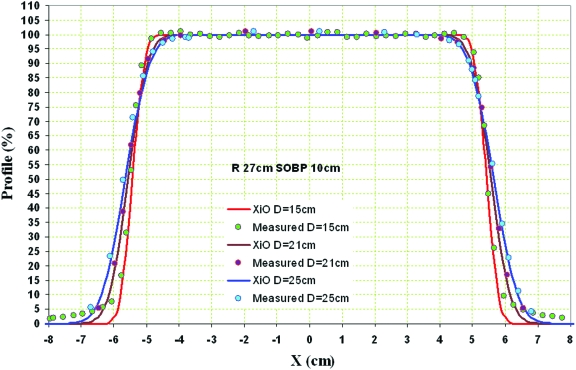
Figure 6.
Transverse beam profiles approximately at the proximal, center, and distal planes of the DRV for a field of 27 cm water range, 10 cm SOBP, and constrained by a 10 cm physical diameter aperture 10 cm from isocenter. The field size projected at isocenter is approximately 10.9 cm in diameter. The measurements were performed in this case with the MPIC and a comparison to dose distribution calculation from the treatment planning system (XiO) is shown.
Another consideration was the dependence of transverse field uniformity on the amount of repainting. Typically, for fields less than 20 cm in diameter, 2–5 nA of beam current is required in the nozzle. The number of times a layer is scanned (“painted”) is inversely proportional in general to the fluence rate and in specific the beam current for a given field size and dose. A design goal was to achieve a minimum of 100 paints per layer. In practice, this sensitivity was tested by increasing the beam current to the maximum permitted just below the hardware induced safety limit level for a given field size. Although this setting was in excess of what would be requested clinically, it served to test the robustness of the transverse delivery uniformity. A test for the common field of 10 cm diameter (usually requiring 2 nA) used 8 nA of proton current, effectively reducing the number of repaintings from 100 to about 25–30. No discernible difference was observed in the transverse field uniformity. However, it is facility policy to validate field uniformity at the time of patient-specific quality assurance for those fields which require higher dose rates or large diameters.
Because lateral field falloff is of importance in proton therapy, usually due to the need to trim the lateral field edge from a critical anatomical structure, penumbra characterization was required. For this analysis it is interesting to compare the physical condition of the TR2 scanning system to the TR1 scattering system. It might be expected that beam delivery without metal scattering foils reduces penumbra due to the reduced multiple Coulomb scattering. Conversely, the source to isocenter distance (SID) in TR1 is 320 cm, whereas the physical SID in TR2 is 242, giving an expected increase in penumbra of the scanning system for the shorter distance. These effects interact in a competing manner to contribute to the overall penumbra distribution between the two systems. The range modulation process increases the penumbra. The range modulator in TR1 is of the rotating type (360 rev∕min) located just proximal to final collimation, whereas the modulator in TR2 is a binary type located further up-beam in the nozzle. The TR1 modulator position is variable but generally about 50 cm from isocenter, whereas the TR2 modulator is fixed at 165 cm.
To consider the situation without the range modulator effect, measurements were initially performed with pristine (unmodulated) beams using radiographic film. Table 2 presents the comparison. The data indicate a slight (few tenths of millimeters) reduction in nominal beam penumbra with the scanning system, even considering the shorter SID. Table 2 also compares TR1 and TR2 26 cm range beams with a 10 cm SOBP modulation. Interestingly, although the range modulator sits further away from the measurement point in TR2 compared to TR1, TR2 still outperforms the TR1 penumbra by an observed difference of about 0.7 mm. This may be because the TR2 beam, due to not using scattering foils, presents a more forwardly focused beam to the modulator than in TR1, masking the distance of travel effect. The amount of air through which the beam travels is also smaller in TR2, and causes less scattering. An equivalent reduction in penumbra with comparison to TR1 was found at the conditions 16 cm water equivalent range with a 10 cm SOBP. The effect of field size on penumbra was studied over the range 3–10 cm but found to affect penumbra only a few tenths of a millimeter, primarily at deeper depths. In summary, the measured penumbra in TR2 outperforms that of TR1 by about 7∕10 mm and is judged to be acceptable for clinical use. The values also compare favorably to reported measurements from other institutions.31, 32, 33
Table 2.
Top: Values of penumbra widths (TR1 penumbra and TR2 penumbra) for pristine (no modulation) full energy beams measured with radiographic film. The maximum range for TR1 is 25.9 cm in water and 27 cm for TR2. The range loss in TR1 is due to the use of scattering foils. The measurement depth in water is reported together if it was the same, or individually if different (TR1, TR2). The deepest TR1 data may have been collected beyond R90 due to uncertainty of polystyrene∕film range loss estimate. The field size was defined by a 10.9-cm-diam aperture placed 10 cm proximal to the isocenter of each system. Bottom: Values of the measured penumbra widths for the conditions 26 cm range in water, 10 cm SOBP, otherwise the same.
| Measurement depth (cm) | TR1 penumbra (mm) | TR2 penumbra (mm) | Difference (mm) |
|---|---|---|---|
| Pristine, maximum range | |||
| 5 | 1.0 | 0.8 | −0.2 |
| 10 | 2.2 | 1.9 | −0.3 |
| 20 | 5.7 | 5.5 | −0.3 |
| 25 | 8.7 | 7.4 | −0.7 |
| 25.8, 26.7 | 9.5 | 8.2 | −0.7 |
| 10 cm modulation, 26 cm water range | |||
| 5 | 1.6 | 0.9 | −0.7 |
| 16 | 4.8 | 4.1 | −0.7 |
| 21 | 6.9 | 6.1 | −0.8 |
| 25 | 8.9 | 8.5 | −0.4 |
Longitudingal relative dosimetry
As described in Sec. 2A2, the tilt of the SOBP is defined as the slope (%∕cm) of the SOBP flattop. As the tilt deviates from 0.0%∕cm, the flatness moves closer to being out of tolerance (maximum ±2.5%). For a given set of Bragg peak weights, this effect depends, among other factors, on the width of the pristine Bragg peak. From 12.0 to 19.5 cm range in water, the Bragg peak width at 50% of its maximum increases in the TR2 system from 1.5 to 2.3 cm. In principle, this difference can cause a significant tilt of the SOBP. The longitudinal flatness can be optimized by increasing the pullback between the individual peaks and by changing their relative weights (Sec. 2A2). It can also be used to closely match the delivered SOBPs to those calculated by the pencil beam model in the TPS. Figure 7 presents an example of a practical tilt adjustment testing result.
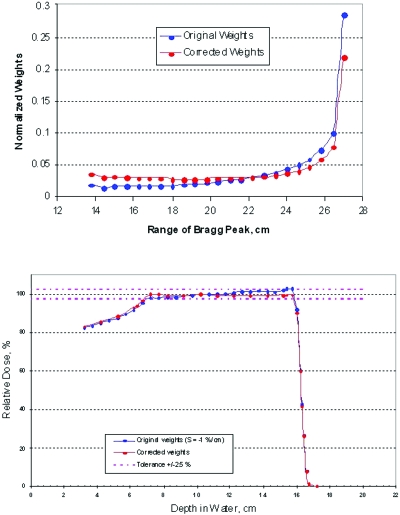
Figure 7.
Distribution of weights before and after applying the correcting algorithm to a 16 cm SOBP (23 pullback layers). The correction has been applied to a SOBP with a negative tilt (tilt=−8.8%).
Within the beam energy regimes (Table 1), a SOBP library data set was constructed using the above described approach. The SOBP extents developed range from 14.5 to 2.2 cm. The layer definition files which define the step size, weighting, and number of layers were designed to deliver a flat SOBP at maximum energy within the regime. All SOBPs constructed achieved acceptable clinical performance. Some typical SOBP profiles commissioned for the high energy regime are shown in Fig. 8 and compared with those calculated by the TPS. Similar to what was found transversely, (Sec. 3A1), the TPS adequately calculated the SOBPs longitudinally for field sizes 5 cm in diameter and larger. SOBP profiles measured for the medium and low energy regimes are very similar and therefore are not presented here. In practice the construction of a range of any desired SOBP extents is possible within ±1 mm. In summary, the longitudinal beam shaping from this binary range modulator has been shown to provide accuracy, precision, ease of use, and flexibility.
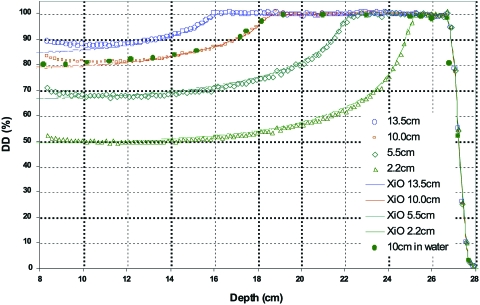
Figure 8.
Representative spread-out Bragg peaks for the high energy regime measured with the MLIC detector. The SOBPs were designed in part by adjusting the individual layer weights to produce the nominally flat longitudinal distributions shown at a chosen energy. In this case the chosen energy was 208 MeV (range of 27 cm in water). A comparison to the longitudinal dose calculation by the treatment planning system (XiO) is also shown.
Absolute dosimetry
Currently the absolute dosimetry for TR1 follows the ICRU 59 protocol. Although ICRU 59 does not provide guidance for scanned beams, because the TR2 is a uniform scanning system the protocol can, in principle, be applied with the following assumption: The action of beam scanning across the ionization chamber does not significantly perturb the measurement.
Several authors have studied the effects of scanned or pulsed proton beams on the response of the ionization chambers used for delivery system calibration.34, 35, 36 These investigations were driven by the observation that neither of the primary proton beam dosimetry protocols, ICRU 59 or the International Atomic Energy Agency (IAEA) TRS-398,37 provide guidance for scanned beams. The previous studies, under the conditions evaluated, and similar to the conditions of this system could not detect this effect below about 2%. It was not the purpose of this study to find possible differences below this level, but rather to validate clinically rational dosimetry practice for the scanning system, that is within the limits of the protocol uncertainties themselves, or about 3%.
Internal facility absolute dose comparison
Using the principles of ICRU 59 with the facility reference conditions, described in Sec. 2B2, an intercomparison was performed between the scattering and uniform scanning systems. The results (Table 3) indicate good agreement between the facility calibration of the two systems, not withstanding induced systematic errors. The results for a 4 month observation period of daily TR2 calibration also indicate excellent precision at the level ±1%.
Table 3.
Simultaneous ionization chamber dosimetry comparison between passive scattering system (TR1) and continuous uniform scanning system (TR2). Under the reference condition, TR1 and TR2 had both been calibrated to deliver the same dose output for the same machine monitor setting. The chambers used were a PTW model 23343 parallel plate type and the NAC-mini (Sec. 2B). For comparison the individual chamber responses are normalized to their respective TR1 values.
| Chamber type | TR1 normalized output | TR2 relative output to TR1 |
|---|---|---|
| Markus | 1.000 | 1.013 |
| NAC-mini | 1.000 | 1.004 |
Absolute dose comparison
Results from the alanine dosimetry and TLD dosimetry are listed in Table 4. These integrating dosimeters have NIST-traceable calibrations and have the advantages of (1) dose rate insensitivity and (2) independent dose validation. These qualities satisfied the concerns of ionization chamber sensitivity to higher instantaneous dose rates provided by the scanning system and the possibility of internal facility systematic dosimetry errors. Repeated machine monitor unit settings were required for the high total dose delivered to the alanine dosimeters, which is a relative weakness of the method. However, the facility reported doses for all three treatment rooms, calculated using both the ICRU 59 and IAEA TRS-398 protocols, agree with the alanine and TLD results within the respective uncertainties of the methods. The approximately 2% difference between ICRU–59 and TRS–398 determined dose is due primarily to different wair values used in the protocols. An updated protocol release from the ICRU has been recently published addressing this difference and providing guidelines for scanned proton beams.38
Table 4.
Independent absolute dosimetry results from the three treatment rooms at MPRI. TR1 is passive scattering; TR2 and TR3, continuous uniform scanning. The dose deliveries followed the ICRU 59 protocol. The RPC results have been converted for comparison from dose in muscle to dose in water (about a 1% difference based on density and stopping power at the relevant average energy). Comparison is also provided to IAEA TRS-398 equivalencies.
| Treatment room | Detector type | ICRU 59 delivered dose (cGy) | Reported dose (cGy) | ICRU 59∕ reported | IAEA TRS-398∕ reported | Reported uncertainty (%) | Confidence interval (%) |
|---|---|---|---|---|---|---|---|
| TR1 | TLD | 299 | 302 | 0.99 | 0.97 | 5 | 90 |
| TR2 | TLD | 298 | 301 | 0.99 | 0.97 | 5 | 90 |
| TR2 | Alanine | 25 000 | 24 100 | 1.02 | 1.04 | 3.5 | 95 |
| TR3 | TLD | 299 | 308 | 0.97 | 0.95 | 5 | 90 |
CONCLUSIONS
The clinical commissioning of a uniform proton beam scanning system has been completed. Regimes of continuous uniform scanning and dose layer stacking to produce required dose distributions have been optimized. All of the facility clinical performance requirements were satisfied. The field commissioning results indicated a reduction in transverse penumbra by about 1 mm compared with passive beam spreading for the therapeutic beams tested having maximum ranges in water between 16 and 26 cm. No modification of the treatment planning system dose calculation algorithm was required from classic double scattering to continuous uniform scanning. The system dosimetry was validated against national standards. Patient beam delivery durations have been found to be efficient matching those of the scattering system also in use at the facility.
The scanning system has received the United States Food and Drug Administration 510(k) clearance. Acceptance testing and commissioning of the system has been completed and patient treatments are now under way in both uniform scanning gantries.
ACKNOWLEDGMENTS
The authors wish to acknowledge the work of the Indiana University Cyclotron Facility staff for the contribution of over 120 man years of work to realize the MPRI project. This work was conducted in a facility constructed with support from Research Facilities Improvement Program Grant No. C06 RR17407-01 from the National Center for Research Resources, National Institutes of Health. Also recognized is the Radiological Physics Center, Houston, TX, and the Armed Forces Radiobiological Research Institute, Bethesda, MD, for providing detectors and performing the absolute dosimetry readouts.
References
- Koehler A. M., Schneider R. J., and Sisterson J. M., “Range modulators for protons and heavy ions,” Nucl. Instrum. Methods 10.1016/0029-554X(75)90430-9 131, 437–440 (1975). [DOI] [Google Scholar]
- Koehler A. M., Schneider R. J., and Sisterson J. M., “Flattening of proton dose distributions for large fields,” Med. Phys. 10.1118/1.594317 4, 297–301 (1977). [DOI] [PubMed] [Google Scholar]
- Lomax A., Bortfeld T., Goitein G., Debus J., Dykstra C., Tercier P., Coucke P., and Mirimanoff R., “A treatment planning inter-comparison of proton and intensity modulated photon radiotherapy,” Radiother. Oncol. 10.1016/S0167-8140(99)00036-5 51, 257–271 (1999). [DOI] [PubMed] [Google Scholar]
- Lomax A. J., Pedroni E., Rutz H., and Gotien G., “The clinical potential of intensity modulated proton therapy,” Med. Phys. 14, 147–152 (2004). [DOI] [PubMed] [Google Scholar]
- Lomax A. J., Böhringer T., Bolsi A., Coray D., Emert F., Goitein G., Jermann M., Lin S., Pedroni E., Rutz H., Stadelmann O., Timmermann B., Verwey J., and Weber D., “Treatment planning and verification of proton therapy using spot scanning: Initial experiences,” Med. Phys. 10.1118/1.1779371 31, 3150–3157 (2004). [DOI] [PubMed] [Google Scholar]
- Kanai T., Kawachi K., Kumamoto Y., Ogawa H., Yamada T., and Matsuzawa H., “Spot scanning system for proton radiotherapy,” Med. Phys. 10.1118/1.594693 7, 365–369 (1980). [DOI] [PubMed] [Google Scholar]
- Oelfke U. and Bortfeld T., “Intensity modulated radiotherapy with charged particle beams: Studies of inverse treatment planning for rotation therapy,” Med. Phys. 10.1118/1.599002 27, 1246–1257 (2000). [DOI] [PubMed] [Google Scholar]
- Flynn R., Barbee D., Mackie T., and Jeraj R., “Comparison of intensity modulated x-ray therapy and intensity modulated proton therapy for selective subvolume boosting: A phantom study,” Phys. Med. Biol. 10.1088/0031-9155/52/20/001 52, 6073–6091 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haisen L., Romeijn H., Fox H., Palta J., and Dempsey J., “A computational implementation and comparison of several intensity modulated proton therapy treatment planning algorithms,” Med. Phys. 10.1118/1.2836954 35, 1103–1112 (2008). [DOI] [PubMed] [Google Scholar]
- Schneider U., Agosteo S., Pedroni E., and Besserer J., “Secondary neutron dose during proton therapy using spot scanning,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(01)02826-7 53, 244–251 (2002). [DOI] [PubMed] [Google Scholar]
- Gardey K. U., Oelfke U., and Lam G. K., “Range modulation in proton therapy—An optimization technique for clinical and experimental applications,” Phys. Med. Biol. 10.1088/0031-9155/44/6/402 44, N81–N88 (1999). [DOI] [PubMed] [Google Scholar]
- Lu H.-M. and Kooy H., “Optimization of current modulation function for proton spread-out Bragg peak fields.” Med. Phys. 10.1118/1.2188072 33, 1281–1287 (2006). [DOI] [PubMed] [Google Scholar]
- Li Y., Zhang X., Lii M., Sahoo N., Zhu R. X., Gillin M., and Mohan R., “Incorporating partial shining effects in proton pencil-beam dose calculation.” Phys. Med. Biol. 10.1088/0031-9155/53/3/007 53, 605–616 (2008). [DOI] [PubMed] [Google Scholar]
- Lu H.-M., Brett R., Engelsman M., Slopsema R., Kooy H., and Flanz J., “Sensitivities in the production of spread-out Bragg peak dose distributions by passive scattering with beam current modulation.” Med. Phys. 10.1118/1.2776255 34, 3844–3853 (2007). [DOI] [PubMed] [Google Scholar]
- Anferov V., Broderick B., Collins J. C., Friesel D. L., Jenner D., Jones W. P., Katuin J., Klein S. B., Starks W., Self J., and Schreuder N., “The Midwest Proton Radiation Institute project at the Indiana University Cyclotron Facility,” in Cyclotrons and their Applications 2001, edited by Marti F. (AIP, New York, 2001), Issue 1, pp. 27–29. [Google Scholar]
- Friesel D. L., Anferov V., Collins J., Katuin J., Klein S., Nichiporov D., and Wedekind M., “The Indiana University proton therapy system,” European Particle Accelerator Conference Edinburgh, UK, 2006, p. 2349.
- Nichiporov D., Solberg K., Hsi W., Wolanski M., Mascia A., Farr J., and Schreuder A., “Multichannel detectors for profile measurements in clinical proton fields.” Med. Phys. 10.1118/1.2746513 34, 2683–2690 (2007). [DOI] [PubMed] [Google Scholar]
- Mesoloras G., Sandison G., Stewart R., Farr J., and Hsi W. C., “Neutron scattered dose equivalent to a fetus from proton radiotherapy of the mother,” Med. Phys. 7, 2479–2490 (2006). [DOI] [PubMed] [Google Scholar]
- Anferov V., “Combined X–Y scanning magnet for conformal proton radiation therapy,” Med. Phys. 3, 815–818 (2005). [DOI] [PubMed] [Google Scholar]
- Arduini G., Cambria R., Canzi C., Gerardi F., Gottschalk B., Leone R., Sangaletti L., and Silari M., “Physical specifications of clinical proton beams from a synchrotron,” Med. Phys. 10.1118/1.597735 23, 939–951 (1996). [DOI] [PubMed] [Google Scholar]
- “Specifications for a proton therapy research and treatment facility,” Massachusetts General Hospital and Lawrence Berkeley Report No. 4, Boston, MA, 1992.
- Chu W., “Performance specifications for a proton medical facility,” Lawrence Berkeley Laboratory, University of California Davis Cancer Center, University of San Francisco Medical School, LBL Report No. 33749, Berkeley, CA, 1993.
- Schreuder A. N., Jones D. T. L., and Kiefer A., “A small ionization chamber for dose distribution measurements in a clinical proton beam,” in Advances in Hadrontherapy, edited by Amaldi U., Larsson B., and Lemoigne Y. (Elsevier, Amsterdam, 1997), pp. 284–289. [Google Scholar]
- “Clinical proton dosimetry. I. Beam production, beam delivery and measurement of absorbed dose,” Report No. 59, International Commission on Radiation Units and Measurements, Bethesda, MD, 1998.
- Onori S., d’Errico F., De Angelis C., Egger E., Fattibene P., and Janovsky I., “Alanine dosimetry of proton therapy beams,” Med. Phys. 10.1118/1.597911 24, 447–453 (1997). [DOI] [PubMed] [Google Scholar]
- Nichiporov D., Kostjuchenko V., Puhl J., Bensen D., DesRosiers M., Dick C., McLaughlin W., Kojima T., Coursy B., and Zink S., “Investigation of applicability of alanine and radiochromic detectors to dosimetry of proton clinical beams,” Appl. Radiat. Isot. 10.1016/0969-8043(95)00213-W 46, 1355–1362 (1995). [DOI] [PubMed] [Google Scholar]
- Ibbott G., “The radiological physics center TLD proton dosimetry credentialling program,” private communication, 2008.
- Kirby T. H., Hanson W. F., Gastorf R. J., Chu C. H., and Shalek R. J., “Mailable TLD system for photon and electron therapy beams,” Int. J. Radiat. Oncol., Biol., Phys. 12, 261–265 (1986). [DOI] [PubMed] [Google Scholar]
- Kirby T. H., Hanson W. F., and Johnston D. A., “Uncertainty analysis of absorbed dose calculations from thermoluminescence dosimeters.” Med. Phys. 10.1118/1.596797 19, 1427–1433 (1992). [DOI] [PubMed] [Google Scholar]
- Kanai T., Kanematsu N., Minohara S., Komori M., Torikoshi M., Asakura H., Ikeda N., Uno T., and Takei Y., “Commissioning of a conformal irradiation system for heavy-ion radiotherapy using a layer-stacking method.” Med. Phys. 10.1118/1.2219771 33, 2989–2997 (2006). [DOI] [PubMed] [Google Scholar]
- Urie M. M., Sisterson J. M., Koehler A. M., Goitein M., and Zoesman J., “Proton beam penumbra: Effects of separation between patient and beam modifying devices,” Med. Phys. 10.1118/1.595974 13, 734–741 (1986). [DOI] [PubMed] [Google Scholar]
- Oozeer R. and Mazal A., “A model for the lateral penumbra in water of a 200-MeV proton beam devoted to clinical applications,” Med. Phys. 10, 1599–1604 (1997). [DOI] [PubMed] [Google Scholar]
- Safai S., Bortfeld T., and Engelsman M., “Comparison between the lateral penumbra of a collimated double-scattered beam and uncollimated scanning beam in proton radiotherapy,” Phys. Med. Biol. 10.1088/0031-9155/53/6/016 53, 1729–1750 (2008). [DOI] [PubMed] [Google Scholar]
- Nohtomi A., Sakae T., Tsunashima Y., and Kohno R., “Dosimetry of pulsed clinical proton beams by a small ionization chamber,” Med. Phys. 10.1118/1.1380435 28, 1431–1435 (2001). [DOI] [PubMed] [Google Scholar]
- Jakel O., Hartmann G., Karger C., Heeg P., and Vatnitsky S., “A calibration procedure for beam monitors in a scanned beam of heavy charged particles,” Med. Phys. 10.1118/1.1689011 31, 1009–1013 (2004). [DOI] [PubMed] [Google Scholar]
- Coray D., Pedroni E., Böhringer T., Lin S., Lomax A., and Goitein G., “Dosimetry with the scanned proton beam on the PSI gantry,” in International Symposium on Standards and Codes of Practice in Medical Radiation Dosimetry, Book of Extended Synopses, IAEA, Vienna, 2000, CN-96, p. 213.
- “Absorbed dose determination in external beam radiotherapy: An international code of practice for dosimetry based on standards of absorbed dose to water,” Report No. TRS-398, IAEA, Vienna, 2000.
- “ICRU Report No. 78: Prescibing, recording, and reporting proton-beam therapy,” Technical Report, International Commission on Radiation Units and Measurements, Inc., Washington, DC, 2007.