Abstract
Breast density has been established as an independent risk factor associated with the development of breast cancer. It is known that an increase of mammographic density is associated with an increased cancer risk. Since a mammogram is a projection image, different body position, level of compression, and the x-ray intensity may lead to a large variability in the density measurement. Breast MRI provides strong soft tissue contrast between fibroglandular and fatty tissues, and three-dimensional coverage of the entire breast, thus making it suitable for density analysis. To develop the MRI-based method, the first task is to achieve consistency in segmentation of the breast region from the body. The method included an initial segmentation based on body landmarks of each individual woman, followed by fuzzy C-mean (FCM) classification to exclude air and lung tissue, B-spline curve fitting to exclude chest wall muscle, and dynamic searching to exclude skin. Then, within the segmented breast, the adaptive FCM was used for simultaneous bias field correction and fibroglandular tissue segmentation. The intraoperator and interoperator reproducibility was evaluated using 11 selected cases covering a broad spectrum of breast densities with different parenchymal patterns. The average standard deviation for breast volume and percent density measurements was in the range of 3%–4% among three trials of one operator or among three different operators. The body position dependence was also investigated by performing scans of two healthy volunteers, each at five different positions, and found the variation in the range of 3%–4%. These initial results suggest that the technique based on three-dimensional MRI can achieve reasonable consistency to be applied in longitudinal follow-up studies to detect small changes. It may also provide a reliable method for evaluating the change of breast density for risk management of women, or for evaluating the benefits∕risks when considering hormonal replacement therapy or chemoprevention.
Keywords: breast density, breast MRI, fibroglandular tissue segmentation, fuzzy c-means clustering segmentation, intra-, inter-operator variation
INTRODUCTION
Mammographic breast density has been shown as a strong risk factor associated with the development of breast cancer.1, 2, 3, 4, 5 The general term of “mammographic density” is widely used in the literature, which reflects that most studies are based on the breast density analyzed on mammograms, qualitatively or semiquantitatively. The BI-RADS category is the only established criteria, with percent density <25% as category 1, 25%–50% as category 2, 50%–75% as category 3, and >75% as category 4. It has been reported that women with a mammographic density percentage greater than 50% have an increased breast cancer risk 1.8 to 6.0 times that of women with very low density.5 Changes of breast density over time have been shown related to changes in cancer risk.3, 6, 7, 8 It has been shown that an increase in BI-RADS density category over 3 years is associated with an increase in breast cancer risk; on the other hand, a decrease in density is associated with a decreased risk.7 Therefore, a reliable method that can be applied to measure small changes of density in individual women will be very helpful for risk management.
Most women fall within BI-RADS density category 2 and 3, and the broad range makes it unsuitable to evaluate small changes.9 Several computer-aided algorithms have been developed for quantitative measurement of breast density on mammograms.10, 11, 12, 13, 14 However, the nature of two-dimensional projection image makes it difficult to assess the true volume of the dense tissue. The degree of compression may also lead to different breast density. Moreover, a small difference in x-ray exposure calibration may result in different density, and all these problems may render evaluation of longitudinal changes unreliable.10 A recent paper by Kopans investigated the possible variation arising from these factors, and the results suggested that studies showing small percentage differences between groups are likely to be inaccurate, and researchers who are interested in exploring tissue density and breast cancer risk need to start fresh and think three-dimensionally.15
Breast MRI provides strong soft tissue contrast between fibroglandular and fatty tissues with a three-dimensional coverage of the entire breast and thus may be used for precise measurements of breast and fibroglandular tissue volumes. With the recommendation of annual breast MRI screening for women with a lifetime risk of greater than 20%–25%, it is expected that many more breast MRI studies will be performed. If a good density analysis method is available, additional information about density can also be obtained during screening MRI.
Two components are required for quantitative analysis of breast density. These are the segmentation of the whole breast from the body, and segmentation of fibroglandular tissue within the breast. Only a few studies have reported breast density measurement using MRI.16, 17, 18, 19, 20, 21 In these studies, the main challenge is on the segmentation of the breast from the body. Since there is no clear boundary, it is more a problem of consistency rather than accuracy, and there is no gold standard. In studies where the algorithm-based method was applied, only limited imaging slices through the midsection of the breast could be analyzed;16, 17, 18 in studies where the whole breast was analyzed, the outer contour of the breast was manually drawn by the operator.19, 20, 21 The analysis based on limited number of slices, or manual segmentation of the whole breast, is not suitable for analysis of changes over time. On the other hand, once the breast is segmented, the segmentation of fibroglandular tissue could reach a high level of reproducibility.21
In this article, we present a method that uses some operator input to allow analysis from the whole breast, and employ computer algorithms to achieve efficiency and reproducibility. The body landmarks of each individual woman were first identified for initial segmentation, and then computer algorithms, including fuzzy C-means (FCM), B-spline fitting, and dynamic searching, were applied to segment out the breast from the body. An adaptive fuzzy C-means algorithm was applied for fibroglandular tissue segmentation within the segmented breast.22 Since there is no accepted gold standard, the consistency, including intraoperator variation, interoperator variation, as well as the variation coming from different positions of women inside the scanner, was evaluated.
The aim of this study was to provide a reliable density analysis method based on three-dimensional MRI, which will allow evaluation of small density changes over time in the same woman. Such a tool may help each individual woman to evaluate her own risk∕benefit ratio when considering hormonal replacement therapy or chemoprevention. It may also be applied for evaluation of density changes in some regions, which may be associated with increased risk and warrant more attention.
MATERIALS AND METHODS
A Subjects and MRI protocol
At our institute we have established a breast MRI research database that contains more than 600 cases. The study enrolled patients who had suspicious findings and were scheduled for additional workup or biopsy to participate in the MRI study. It was approved by the Institutional Review Board, and was HIPAA-compliant. Every patient gave written informed consent.
In the present study we selected 11 cases from this database for development and testing of the density analysis method. These cases were selected to cover a wide spectrum of the densities varying from very fatty to very dense. The age of these 11 patients was from 31 to 76 years old (49±10, median 49). The radiology and pathology reports were reviewed for each patient to identify the concerned breast, and only the normal breast was used for the density analysis. The MRI study was performed on a 1.5 T Eclipse scanner (Philips, Cleveland, OH) using a dedicated four-channel breast coil. The pre-contrast T1-weighted images without fat saturation were acquired using a 3D SPGR (RF-FAST) pulse sequence, with TR=8.1 ms, TE=4.0 ms, flip angle=20°, matrix size=256×128, FOV=38 cm, slice thickness=4 mm. Thirty-two axial slices were used to cover the entire breast.
In addition to these 11 cases, two normal volunteers without any history of breast diseases were scanned at five different body positions for the position dependence study. These two studies were performed on a 3.0 T Achieva scanner (Philips, Cleveland, OH), using the standard six-channel phased array coil that came with the scanner. The bilateral axial view T1-weighted images without fat saturation were acquired using a turbo spin-echo (TSE) sequence. The imaging parameters were as follows: TR=800 ms, TE=9.0 ms, flip angle=90°, acquisition-matrix size=256×203 (reconstructed to 288×288), FOV=38 cm, slice thickness=3 mm. A total of 55 images was acquired to cover the entire breast. After completing one acquisition at the neutral position, the subject was asked to change to four other body positions: twisting to the right, twisting to the left, moving body forward, and moving body backward. One set of images was acquired at each position. These images were used to study the position dependence of our technique for density measurements.
Overall analysis scheme
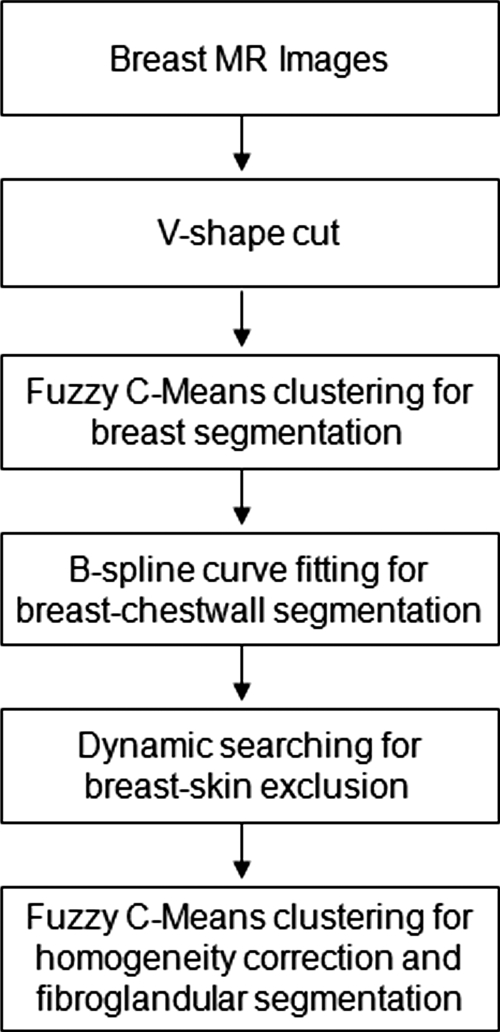
Computer-assisted algorithms were used to segment the breast and the fibroglandular tissue. The breast segmentation procedures consisted of: (1) perform an initial V-shape cutting using three body landmarks to determine the posterior cutoff points of breast in the lateral boundary; (2) apply a fuzzy C-means (FCM) based segmentation algorithm with the B-spline curve fitting to obtain the breast boundary; (3) apply dynamic searching to exclude the skin along the breast boundary. After the breast was segmented out, the total breast volume was calculated. For fibroglandular tissue segmentation, the adaptive FCM was applied for bias field correction to remove image intensity nonuniformities, and for segmentation of the fibroglandular tissue from the surrounding fatty tissue. After completing the segmentation from all two-dimensional imaging slices, the volume of fibroglandular tissue was calculated, and the percent density was obtained by normalizing to the total breast volume. The full analysis flow chart is shown in Fig. 1.
Figure 1.
Overall analysis flow chart for breast segmentation and fibroglandular tissue segmentation.
Breast segmentation
Initial V-shape cut using three body landmarks
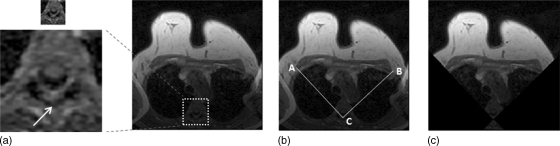
The V-shape cut is used to define the lateral posterior margin of bilateral breasts and to exclude the arm-folding artifact as shown in Fig. 2. The level of the aortic arch is first identified on the axial T1 weighted image, shown in Fig. 2a. Using this image, two lines connecting the spinous process of the thoracic spine and the lateral margin of the bilateral pectoralis muscles can be further defined, as shown in Fig. 2b, resulting in a V-shape cut image in Fig. 2c. The two lines defined on this image are applied to all other slices to perform the initial cut. For every studied case, the operator inspected the results to verify that no breast tissue was excluded on any imaging slice.
Figure 2.
The process for initial V-shape cut. (a) The first slice showing the level of the aortic arch which identifies the thoracic spine is selected. (b) The V-tip of spinous process of the thoracic spine, and the lateral margin of the bilateral pectoralis muscles are defined as landmarks. Two lines along AC and BC are extended for V-shape cut. (c) The segmentation defines the posterior lateral margin at both sides; also, the arm-folding artifacts seen in (a) and (b) are excluded.
Breast area segmentation by FCM
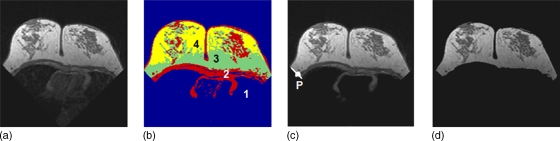
A fuzzy C-means (FCM) algorithm is applied to segment the breast area.22, 23, 24 FCM employs pixel-based segmentation where each cluster (n) is defined by its centroid in the n-dimensional space. The initial centroids are randomly initialized and then their location is interactively optimized, and lastly pixels are classified into different clusters according to their probability to the cluster’s centroid values.23 To perform the analysis, the operator needs to define the number of clusters to be used in the FCM segmentation. Since air has no signal and chest wall has a relatively low gray level, while breast is the brightest among these three regions, typically three clusters are used. The cluster #1 with the lowest signal intensity contains air and lung tissue. The brightest two clusters are then grouped to form the breast area. For a large breast, sometimes the anterior breast may be very close to the wiring of the coil, and shows very bright signal intensity. In such cases a fourth cluster may be needed, and the three brightest clusters, clusters #2–4, are defined as the breast area, as for the case shown in Fig. 3.
Figure 3.
Breast segmentation using fuzzy C-means clustering. (a) original precontrast images after V-shape cut. (b) four-clusters FCM segmentation result. The cluster #1 has the lowest signal intensity, representing air and the lung tissue. (c) cluster #1 is excluded to obtain the breast area that still contains chest wall muscle. The dividing point P between the two clusters representing breast fat and chest wall muscle at the lateral posterior boundary is automatically identified for B-spline fitting. (d) segmented breast after exclusion of chest wall muscle based on the boundary obtained from b-spline fitting.
Chest wall muscle exclusion
The dividing point P between the two clusters representing breast fat and chest wall muscle at the lateral posterior boundary is automatically identified. As shown in Fig. 3c, the muscle has intermediate intensity between breast fat and the lung tissue on the image, so its upper border can be defined based on the intensity gradient. The chest wall boundary is outlined using gradient tracing starting with reference P. The searching process can be written as
| (1) |
where m=−3,−2,−1,0,1,2,3; I(x,y) is the intensity of point (x,y).
All boundary points are then sorted using x-coordinates, and a uniform B-spline model fitting is applied to refine the boundary between the breast and the chest wall muscle.17 The smoothing functions are described as
| (2) |
| (3) |
Where
| (4) |
I=T, 2T, 3T, and 4T, and T is the interval of the control points; t=j∕T, j=0,1,…,T−1.
After excluding the chest wall muscle, the segmented breast outline is then superimposed on the original MR image for visual inspection. The computerized technique could perform the majority of work reasonably well, but in cases where some chest wall muscle is not excluded satisfactorily, a graphic interface is used to allow the operator to manually correct the segmentation result. This problem mainly happens in two situations, as illustrated in Fig. 4. One case has extreme dense breasts where fibroglandular tissue and chest wall muscle is connected without fat in between, so the contrast between the breast and the chest wall muscle is low and cannot be well separated. The other case is an inferior ending slice where the liver has appeared on the image, right beneath the chest wall muscle; again, their similar intensity does not give sufficient contrast to distinguish between them.
Figure 4.
Illustration of cases with incomplete breast segmentation that requires manual correction. The left column shows a dense breast with fibroglandular tissue connected to the chest wall muscle, and the right column shows one inferior slice where the liver tissue appears right underneath the chest wall muscle. In both cases the contrast for chest wall muscle is not sufficient to allow boundary detection by B-spline fitting. (a) original MR image; (b) computerized segmentation result; (c) manual correction result after the operator tracing the boundary between the breast and the chest wall muscle.
Skin exclusion
Dynamic searching is used to exclude skin. As shown in Fig. 5a, the skin shows hypointensity compared to the fat, and it may be mistakenly considered as the fibroglandular tissue; therefore, it needs to be removed from the breast territory. As shown in Fig. 5b, if the skin is not excluded, the FCM analysis will reveal a layer of tissue on the breast boundary, which is categorized into the same cluster as fibroglandular tissue. Therefore, skin exclusion is a necessary step. Since the air signal is dark and the breast fat tissue appears bright, the skin shows intermediate gray level intensity between them. The dynamic searching is based on the change of gray level gradient. After the breast-air boundary is determined, the coordinates of each pixel along the boundary are recorded. The slope of the tangential line [the white arrow as shown in Fig. 5b] at each location is calculated from the nearby 3 pixels along the curve, and the dynamic searching is performed along the perpendicular direction. The upper border of the skin is determined when the negative gradient from skin to air is found; the lower border of the skin is determined when the positive gradient from skin to fatty tissue is found. The pixels between these two borders are defined as skin, as shown in Fig. 5c. If the upper border is found, but the lower border cannot be identified within 3 pixels, then 3 pixels are excluded. This may happen when close to the nipple. Lastly, the left and right breasts are separated using midsternum, performed by the operator. The segmented breast area on every slice in the acquired dataset is measured, and combined together to obtain the total breast volume.
Figure 5.
Skin exclusion result. (a) The segmented breast, same as Fig. 3d. (b) The initial FCM clustering segmentation results performed for breast segmentation, same as Fig. 3b. The skin and some fibroglandular tissues are categorized into the same cluster. The tangential line at each location along the breast-air boundary curve was found (white arrows), and the dynamic searching was performed along the perpendicular direction (black arrows). The upper border is determined when the negative gradient from skin to air is found, and the lower border is determined when the positive gradient from skin to the breast fat is found. (c) The obtained segmentation results of the skin.
Fibroglandular tissue segmentation
The breast coil for the 1.5 T scanner is a four-channel phased array coil that is designed to have a large sensitive region for bilateral imaging. Consequently, the intensity is not homogeneous within the imaging field. Correction based on the known sensitivity profile of the coil is not practical for such a large phased array coil. Nevertheless, background correction can be performed by adopting a fast fuzzy C-means algorithm proposed by Chen et al. that simultaneously estimates the bias field while segmenting the image.22 In each iteration, the bias field is estimated based on the current tissue class centroids and the membership values of pixels, and then smoothed by an iterative low-pass filter. This filtering strategy is based on the fact that the bias field is of low spatial frequency and the assumption that other components in the residual image have higher frequencies.
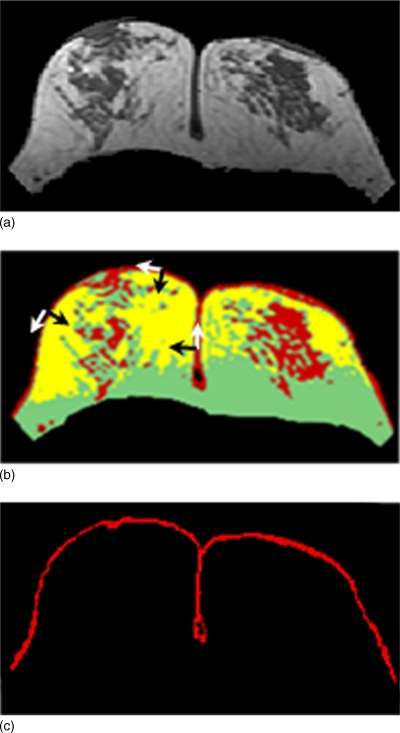
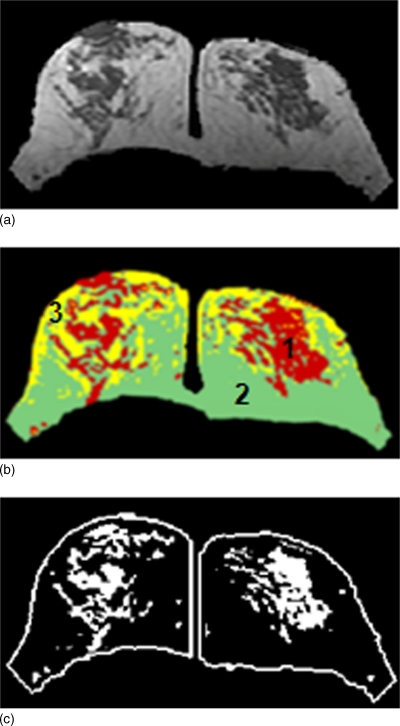
The fibroglandular tissue shows hypointensity compared to fat, and this is used for FCM-based clustering segmentation. Typically three to four clusters are chosen to segment the fibroglandular tissue. For each pixel within the breast, depending on its membership value, the pixel is classified into a cluster, as shown in Fig. 6b. The dense tissue ROI is determined as the cluster with the lowest signal intensity (the darkest in the case of three clusters), as shown in Fig. 6c. When more than three clusters are used, the operator will determine a combination of some clusters as dense tissue. After completing the process, the dense tissue ROI is mapped onto the original MRI to allow the operator to evaluate the segmentation performance. If the selected ROI is too small (i.e., not covering all dense tissues), or too big (i.e., covering some fatty tissues), a change of cluster number is needed. After the segmentation is completed, the total fibroglandular tissue volume is calculated as the total number of pixels multiplied by the pixel size and slice thickness. Finally, the percent breast density is calculated as the fibroglandular tissue volume divided by the total breast volume, converted into percentage.
Figure 6.
Fibroglandular tissue segmentation result. (a) The segmented breast after skin exclusion, by subtracting the skin shown in Fig. 5c from the original image shown in Fig. 5a. (b) The adaptive FCM clustering segmentation results performed for fibroglandular tissue segmentation. The algorithm also performs homogeneity correction. The cluster #1 is selected as the fibroglandular tissue, and cluster #2 and #3 both represent fatty tissues. (c) The breast territory and the outlined fibroglandular tissue, separately for the right and left breasts.
Reproducibility analysis
In order to evaluate the reproducibility of the segmentation technique, the intraoperator and interoperator variations from three operators were investigated. Operator 1 analyzed all studies three times, with at least 2 days between each analysis session. These 11 cases were rearranged in a random order to minimize the chance that the operator recalling the number of clusters used previously. Operator 2 and Operator 3 only analyzed these 11 datasets once, and their performances were compared with that of the first trial done by the Operator 1.
The mean and the standard deviation of the total breast volume, fibroglandular tissue volume, as well as the percent breast density, were calculated for each of these 11 cases. The variation was calculated as the percentage of the standard deviation to the mean. The correlation coefficient was determined among three trials of Operator 1, and among three operators. All statistical analysis was conducted using SPSS for Windows (version 15.0).
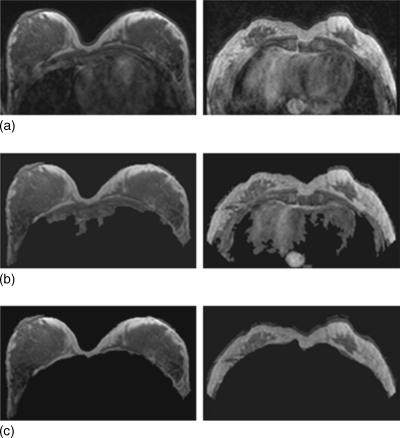
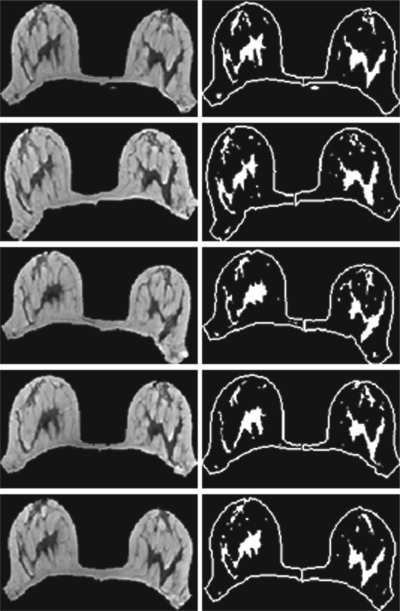
The density from two normal volunteers, each at five different positions, was analyzed to estimate the variation arising from body positioning inside the scanner. The change of position was done by the volunteer according to verbal instruction, not based on specific degree of movements (examples shown in Fig. 7). The left and right breasts were separately analyzed. The standard deviation in the total breast volume, the fibroglandular tissue volume, and the percent breast density were analyzed from five positions, and the variation was calculated as the percentage of the standard deviation to the mean.
Figure 7.
Segmentation results of one subject at five different positions (from top down, neutral, twisting to the right, twisting to the left, moving upper body forward, and moving upper body backward. In each study one image selected from the midsection of the breast at a comparable level is shown.
RESULTS
Operator reproducibility result
The mean and standard deviation of the breast volume and the percent density measured three times by Operator 1 were used to evaluate intraoperator variation. The results for all 11 cases are shown in Table 1. The first trial result of the Operator 1 and the results of the other two operators were used to evaluate the interoperator variation, also shown in Table 1. Repeated measures showed no significant differences in breast volume or the percent density analyzed by three different operators (P<0.001, r=0.97 for breast volume, and P=0.001, r=0.93 for percent density), or among different trials analyzed by Operator 1 (P<0.001, r=0.99 for breast volume and P<0.001, r=0.98 for percent density).
Table 1.
Interobserver and intraobserver variability in breast volume and percent density measurement.
| Subjects | Breast volume (mean±SD) in cm3 | Percent breast density (mean±SD) in % | ||||
|---|---|---|---|---|---|---|
| Cluster #a | Intraobserver | Interobserver | Cluster #b | Intraobserver | Interobserver | |
| Case #1 | (3,3,3,3,3) | 604±10 (1.6%) | 606±32 (5.2%) | (3,3,3,3,3) | 14.7±0.2 (1.4%) | 14.7±0.5 (3.4%) |
| Case #2 | (3,3,3,3,3) | 530±19 (3.0%) | 514±30 (5.8%) | (3,3,3,4,3) | 11.0±0.4 (3.5%) | 12.2±1.2 (9.5%) |
| Case #3 | (3,3,3,3,3) | 509±14 (2.7%) | 516±17 (3.3%) | (3,3,3,3,3) | 15.7±0.6 (3.7%) | 15.4±0.6 (3.9%) |
| Case #4 | (3,3,3,3,3) | 522±20 (3.9%) | 523±21 (4.0%) | (3,3,3,3,3) | 21.3±0.4 (1.7%) | 21.7±0.7 (3.3%) |
| Case #5 | (3,3,3,3,3) | 501±12 (2.3%) | 500±9 (1.8%) | (3,3,3,3,3) | 13.5±0.5 (3.7%) | 13.3±0.5 (3.4%) |
| Case #6 | (3,3,3,3,3) | 597±12 (2.0%) | 601±11 (1.8%) | (3,3,3,3,3) | 15.2±0.2 (1.3%) | 15.2±0.3 (1.9%) |
| Case #7 | (3,3,3,3,3) | 589±16 (2.7%) | 595±20 (3.4%) | (3,3,3,3,3) | 18.3±0.7 (3.6%) | 17.8±0.6 (3.5%) |
| Case #8 | (4,4,4,4,4) | 770±6 (0.8%) | 762±14 (1.9%) | (3,3,3,3,3) | 11.0±0.3 (2.3%) | 10.8±0.5 (4.2%) |
| Case #9 | (4,4,4,4,4) | 860±24 (2.8%) | 843±27 (3.2%) | (3,3,3,3,3) | 17.9±0.4 (2.1%) | 17.8±0.2 (1.3%) |
| Case #10 | (3,3,3,3,3) | 270±12 (4.6%) | 258±13 (5.0%) | (4,4,4,4,4) | 8.2±0.2 (2.2%) | 8.8±0.4 (4.5%) |
| Case #11 | (3,3,3,3,3) | 440±18 (4.2%) | 448±23 (5.1%) | (4,4,4,4,4) | 10.2±0.5 (5.3%) | 9.5±0.3 (3.2%) |
| Averaged STDEV | 2.8% | 3.7% | 2.8% | 3.9% | ||
The total cluster number selected by the operator for the breast segmentation using FCM. The first three were chosen by Operator 1 in three trials. The last two were chosen by Operator 2 and Operator 3, respectively.
The total cluster number selected by the operator for the fibroglandular tissue segmentation using FCM.
The number of clusters selected by three operators for breast and fibroglandular tissue segmentation using FCM (three times for the Operator 1, and one time each for Operator 2 and Operator 3) is also listed in Table 1. Typically three clusters were used for breast segmentation, but four clusters might be needed for very large breast; and typically three or four clusters were chosen for fibroglandular tissue segmentation.
The averaged variation for the breast volume measurements analyzed from all 11 patients was 2.8% (0.8%–4.6%) among three trials of Operator 1, and 3.7% (1.8%–5.8%) among three operators. The averaged variation for the percent density measurements was 2.8% (1.3%–5.3%) among three trials of Operator 1, and 3.9% (1.3%–9.5%) among three operators. In Table 1 it was noted that the interoperator variation for the percent density measurements was the highest for case #2 (9.5%). The number of FCM clusters used in segmentation of fibroglandular tissue was three in all three trials of Operator 1, four for Operator 2, and three for Operator 3. The analyzed percent density was (11.4, 10.5, 11.0) for three trials of Operator 1, 11.7 for Operator 3, but was much higher (13.6) for Operator 2. The results showed that the segmentation results were affected by the choice of the number of FCM clusters.
Position dependence result
Figure 7 shows representative images selected from a corresponding level of the scans acquired at five different body positions of a normal volunteer. It is noted that the imaging planes are different at different body positions, particularly at twisting to left and right positions. The density analysis was performed once by one operator. The breast and fibroglandular tissue segmentation results are also shown in the figure, separately for left and right breasts. The mean and standard derivation of the breast volume, fibroglandular tissue volume, and the percent density analyzed from five positions of two volunteers are summarized in Table 2. In the four analyzed breasts, the variation (percent of standard derivation to the mean) due to different body positions was from 1.8–5.4% for breast volume measurements, and 1.9–4.3% for fibroglandular tissue volume measurements, and 3.2%–6.1% for the percent density. As shown in Fig. 7, the five positions were deliberately set to be very different. In real life, one would never position a woman into the scanner using such awkward positions. Therefore, to give a realistic estimate of the variation coming from the position difference, the highest and the lowest number in the percent density were excluded in the analysis. Then, the variation was 3.6% for subject-1 left breast, 2.6% for subject-1 right breast, 3.0% for subject-2 left breast, and 3.1% for subject-2 right breast.
Table 2.
The total breast volume, fibroglandular tissue volume, and breast density of two subjects at five different positions inside the scanner. All volume measure in units of cm3.
| Position | Subject-1 left | Subject-1 right | Subject-2 left | Subject-2 right | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Breast vol. | Fibro. vol. | Density % | Breast vol. | Fibro. vol. | Density % | Breast vol. | Fibro. vol. | Density % | Breast vol. | Fibro. vol. | Density % | |
| 1 | 811 | 58 | 7.2 | 808 | 63 | 7.8 | 600 | 116 | 19.3 | 610 | 96 | 15.7 |
| 2 | 761 | 54 | 7.1 | 819 | 63 | 7.6 | 632 | 113 | 17.8 | 582 | 102 | 17.5 |
| 3 | 799 | 54 | 6.8 | 788 | 64 | 8.1 | 587 | 120 | 20.5 | 600 | 105 | 17.5 |
| 4 | 753 | 57 | 7.6 | 786 | 64 | 8.2 | 547 | 116 | 21.3 | 575 | 96 | 16.7 |
| 5 | 773 | 60 | 7.8 | 795 | 66 | 8.3 | 616 | 124 | 20.1 | 624 | 103 | 16.5 |
| Mean | 779 | 57 | 7.3 | 799 | 64 | 8.0 | 596 | 118 | 19.8 | 598 | 100 | 16.8 |
| STDEV | 24 | 2.4 | 0.39 | 14 | 1.2 | 0.26 | 32 | 4.4 | 1.2 | 20 | 4.1 | 0.74 |
| (%) | 3.2% | 4.3% | 5.3% | 1.8% | 1.9% | 3.2% | 5.4% | 3.7% | 6.1% | 3.4% | 4.1% | 4.4% |
DISCUSSION
In this study we presented a quantitative method to measure the breast volume and fibroglandular tissue volume based on three-dimensional images acquired by breast MRI. The results suggest that our technique could yield reasonable reproducibility (around 3%–4% variation) in measurements of breast volume and the percent density. With increasing use of breast MRI in screening and management of breast cancer, this analysis tool can be used to provide additional information about breast density, and may contribute in risk management. For example, in annual screening breast MRI for high-risk women, if one area shows increased density, this region may need close follow-up. For women who are considering taking hormonal replacement therapy but worry about the increased breast cancer risk, the change in density measured on MRI may provide a predictor for evaluating the increase of cancer risk. In this article we presented the analysis method, and investigated the variability arising from the operator performance, as well as from body positioning inside the scanner.
In order to determine the percent breast density, the first step is to segment the breast. This is a challenging task, because there is no obvious boundary indicating where the breast ends. Therefore, it is more a problem of consistency rather than accuracy. We proposed a solution using V-shape landmarks of each individual woman to determine the lateral posterior boundary of the breast, to separate the breast from the body fat. This procedure can also exclude the area with an arm-folding artifact (shown in Fig. 2). The three landmarks are chosen from the chest region that has a rigid structure, and it can be reasonably assumed that the location and shape would remain consistent in serial breast MRI scans. If the initial cut is not chosen optimally, it will increase the level of difficulty for the subsequent procedures to exclude the unwanted regions. For identifying the lateral boundary of the breast, apart from the V-shape, we have also tried other anatomic landmarks, including drawing a line parallel to the posterior breast margin at 1 cm dorsal to the sternum, drawing a line connecting the posterior margin of the bilateral pectoris muscles, or drawing a line perpendicular to the segment connecting the sternum and the thoracic vertebral body in the midthoracic cavity. However, these alternative methods all had their own problems. In some cases the tissue area with an arm-folding artifact or lateral thoracic fat not belonging to the breast were included into the breast region; in some cases part of the glandular tissue in the lateral aspect of the breast were excluded. Therefore, the V-shape cut was determined to be the optimal choice.
Breast segmentation is also an important step for the development of a computer-aided detection (CAD) system for diagnosis of lesions. In this area several approaches have been proposed. Some studies used straight lines or curves to estimate the chest wall boundary, which appears to be primitive.19, 25 Arbach et al.26 and Hayton et al.27 suggested using a dynamic searching technique to refine the initial estimation, but dynamic searching does not guarantee smoothness and continuity. Chittineni et al.28 included the chest wall muscle within the breast area, which may be needed for detection of breast cancer which has invaded into chest wall muscle, but not suitable for analysis of breast density.
The measurement of percent breast density requires precise breast segmentation. Manual drawing is very time consuming and not a viable opion.17 Yao et al.16 and Lu et al.29 obtained their first estimation of chest wall muscle using straight lines connecting the left axilla, midsternum, and right axilla on each imaging slice. Then, the dynamic searching based on a user-defined muscle model was applied to refine the chest wall boundary, assuming it is a curved slab with various thicknesses at difference places. However, the method would fail when these landmarks are not visible, especially for large breasts where left and right sides are compressed together. Recently, Ertas et al. proposed using four nets of cellular neural networks (CNN) to classify the pixels near the breast-chest wall boundary.30, 31, 32 Although this method seemed to achieve a beautiful segmentation, it only worked near the midsection of the breast where the contrast of the chest wall muscle is strongest; also, for patients with large size breasts the method might fail. The segmentation in superior and inferior breast areas was not demonstrated in their work, which is much more challenging, but is required for analysis of breast density.
Compared to these methods, our method requires some operator interaction, but it can be applied to almost any woman with any breast size without major limitations. Unsatisfactory segmentation results might occur at the superior and inferior end of images. The problem may also occur when the chest wall muscle is connected to the fibroglandular tissue, or is adjacent to the liver tissue underneath. For these cases some manual modification by the operator is needed. We have investigated whether other images can be used to help improve the segmentation quality, including comparing the density analyzed based on fat-suppressed vs non-fat-suppressed images. In general, the contrast between fat and fibroglandular tissue and the chest wall muscle is strong on the non-fat-suppressed T1-weighted images due to the bright intensity of the fat. The fat-suppressed image decreases the intensity of fat, and as such it also reduces the contrast. The nonuniform fat suppression makes the fat tissue present different intensity depending on the location, and that may lead to a more difficult bias field correction problem. Nevertheless, the fat-suppressed images may be used to suppress the liver signal for cases where the separation of liver from breast is a problem (e.g., Fig. 4), and this needs to be investigated further.
The skin has similar intensity as that of the fibroglandular tissue, and if not excluded, it will be misidentified as part of the fibroglandular tissue, as shown in Fig. 5b. We assumed that skin thickness was within 3 pixels (<5 mm) and searched in this range. The skin is connected to the nipple, and it is not practical to separate the nipple from the skin. In order to achieve consistency, in our method the skin exclusion was searched through the nipple. Since the nipple is thicker than 3 pixels, only a thickness of 3 pixels will be excluded. A more precise skin exclusion method should be investigated further.
The operation time for completing the entire process, from breast segmentation to fibroglandular tissue segmentation, was approximately 10 min on a personal computer with a 3 GHz Intel Pentium 4 CPU with 1 GB RAM processor. If manual correction was needed for some slices, the operator drew the correction curve for each slice, and this could be done in several seconds. Further developments of more sophisticated methods, such as using active model to refine the chest wall boundaries, may reduce the need for manual correction.
For quantitative fibroglandular tissue segmentation, the thresholding18, 20 and clustering-based algorithm such as fuzzy C-means16, 21 or K-means clustering14 have been utilized in the literature. Klifa et al. compared the results using manual, thresholding, and FCM methods to segment the fibroglandular tissue in the breast.21 The interuser variation using the FCM was around 7%, while that using the thresholding method was >15% and that using manual segmentation was >18%. The intrauser variation also showed the same trend, which indicated that the FCM clustering-based algorithm was the optimal method to minimize user variation. Therefore, in this study we adopted the fast fuzzy C-means algorithm for fibroglandular tissue segmentation. It could also be used to perform bias field correction simultaneously to save computation time. The bias field correction is required since the fat tissue signal is not uniform on the image. As shown in Fig. 6b, the brightest two clusters both represent fatty tissues. In extreme fatty breast, since the contrast between fibroglandular and fatty tissues is not strong, more clusters may be needed to increase the possible combinations that the operator can choose to find the optimal segmentation results. Glide et al. applied K-means clustering to analyze breast density quantitatively on mammograms. In each segmentation routine, the operator could evaluate the segmenting performance by varying the number of clusters until a satisfactory result was reached. They also reported that typically three to four clusters would be enough, and more clusters were needed for extremely fatty breasts.14
The operator reproducibility using our technique was investigated using 11 selected studies. The averaged standard deviation for the breast volume analyzed from these 11 cases was 2.8% for intraobserver comparison, and 3.7% for interobserver comparison. The averaged standard deviation for the percent density was 2.8% for intraobserver comparison, and 3.9% for interobserver comparison. The interoperation variation was 9.5% for case #2 because of the use of different FCM cluster number (3 vs 4). The finding was consistent with that of Glide et al. suggesting that this is an intrinsic problem when using the FCM analysis for segmentation.14 The results suggested that if change of density from an individual woman at different times will be evaluated, the same FCM cluster number has to be used.
Since eventually the proposed method will be applied to assess the change of breast density over time, and in each scan the patient will be at slightly different body positions, we also investigated the position dependence. Two normal volunteers each had five scans at different positions performed. Axial images were acquired, and therefore different body positions will lead to different imaging plans, thus different images (Fig. 7). A total of 55 images, each 3 mm thick, was used to cover both breasts; that is, the breast tissues within the 16.5 cm region were imaged. Because it is almost impossible to determine the superior starting slice and the inferior ending slice of the breast, all 55 images were analyzed. Therefore, the measured breast volume would change due to slightly different coverage, and the measured fibroglandular tissue volume would change due to different presentations of the tissues. Voxels at the boundary between fatty and fibroglandular tissues have a partial volume effect (i.e., containing both fatty and fibroglandular tissues). The segmentation result may change slightly depending on whether these boundary voxels are classified as fat or fibroglandular tissue. The change of different body positioning may also lead to slightly different image uniformity, and that can also affect the segmentation result. In this study, the volunteers intentionally exaggerated the body movement, and that probably represented the worst extreme. After taking out the highest and the lowest density measurements from the five measurements, then the variation was around 3%–4%. In an actual MRI scan, the woman is placed into the scanner at a straight neutral position, not only for better quality but also for patient comfort. Therefore, a reasonable variation due to body position difference can be assumed to be within 4%, as estimated in this study. Other than positioning difference, it is possible that the system variation of the MRI scanner may lead to slightly different image quality even when the same sequence with the same parameters is used. However, the contrast between fatty and fibroglandular tissues is strong, and the impact of this possible system variation should be small. As shown in Fig. 7 the tissue contrast is similar in all images, and the most noticeable difference is the different imaging planes from different positions.
Due to the concern of radiation exposure, the repetitive study on mammogram for investigating body position or compression level variation cannot be performed; thus, no such data on mammographic density are available for comparison. As suggested by Kopans, these factors may lead to a large variation on the projection mammogram, and the analysis based on three-dimensional images should be investigated.15
In summary, we presented a semiautomated method for quantitative evaluation of breast density on breast MRI. The operator needs to mark some body landmark points for breast segmentation, and also needs to select the number of clusters in performing the FCM. Unfortunately, a fully automated method for this purpose, even if at all possible, may be inaccurate. We have shown that the process for one study could be done within 10 min, and this could be achieved with a reasonable reproducibility of 3%–4% variation. The MRI-based method may provide a reliable means for evaluating the change of breast density for risk management of women, or for evaluating the benefits∕risks when considering hormonal replacement therapy or chemoprevention.
ACKNOWLEDGMENT
This work was supported in part by NIH∕NCI CA90437, CA121568, and California BCRP # 9WB-0020.
References
- Boyd N. F., Guo H., Martin L. J., Sun L., Stone J., Fishell E., Jong R. A., Hislop G., Chiarelli A., Minkin S., and Yaffe M. J., “Mammographic density and the risk and detection of breast cancer,” N. Engl. J. Med. 10.1056/NEJMoa062790 356, 227–236 (2007). [DOI] [PubMed] [Google Scholar]
- McCormack V. A. and dos Santos Silva I., “Breast density and parenchymal patterns as markers of breast cancer risk: A meta-analysis,” Cancer Epidemiol. Biomarkers Prev. 15 1159–1169 (2006). [DOI] [PubMed] [Google Scholar]
- Vachon C. M., Pankratz V. S., Scott C. G., Maloney S. D., Ghosh K., Brandt K. R., Milanese T., Carston M. J., and Sellers T. A., “Longitudinal trends in mammographic percent density and breast cancer risk,” Cancer Epidemiol. Biomarkers Prev. 16, 921–928 (2007). [DOI] [PubMed] [Google Scholar]
- Yaffe M. J., Boyd N. F., Byng J. W., Jong R. A., Fishell E., Lockwood G. A., Little L. E., and Tritchler D. K., “Breast cancer risk and measured mammographic density,” Eur. J. Cancer Prev. 7 Suppl 1, S47–55 (1998). [DOI] [PubMed] [Google Scholar]
- Boyd N. F., Dite G. S., Stone J., Gunasekara A., English D. R., McCredie M. R., Glies G. G., Tritchler D., Chiarelli A., Yaffe M. J., and Hopper J. L., “Heritability of mammographic density, a risk factor for breast cancer,” N. Engl. J. Med. 10.1056/NEJMoa013390 347, 886–894 (2002). [DOI] [PubMed] [Google Scholar]
- Maskarinec G., Pagano I., Lurie G., and Kolonel L. N., “A longitudinal investigation of mammographic density: The multiethnic cohort,” Cancer Epidemiol. Biomarkers Prev. 15, 732–739 (2006). [DOI] [PubMed] [Google Scholar]
- Kerlikowske K., Ichikawa L., Miglioretti D. L., Buist D. S., Vacek P. M., Bindman R. S., Yankaskas B., Carney P. A., and Ballard-Barbash R., “Longitudinal measurement of clinical mammographic breast density to improve estimation of breast cancer risk,” J. Natl. Cancer Inst. 99, 386–395 (2007). [DOI] [PubMed] [Google Scholar]
- Guthrie J. R., Milne R. L., Hopper J. L., Cawson J., Dennerstein L., and Burger H. G., “Mammographic densities during the menopausal transition: A longitudinal study of Australian-born women,” Menopause 14, 208–215 (2007). [DOI] [PubMed] [Google Scholar]
- Obenauer S., Hermann K. P., and Grabbe E., “Applications and literature review of the BI-RADS classification,” Eur. Radiol. 15, 1027–1036 (2005). [DOI] [PubMed] [Google Scholar]
- Harvey J. A. and Bovbjerg V. E., “Quantitative assessment of mammographic breast density: Relationship with breast cancer risk,” Radiology 10.1148/radiol.2301020870 230, 29–41 (2004). [DOI] [PubMed] [Google Scholar]
- Byng J. W., Boyd N. F., Fishell E., Jong R. A., and Yaffe M. J., “The quantitative analysis of mammographic densities,” Phys. Med. Biol. 10.1088/0031-9155/39/10/008 39, 1629–1638 (1994). [DOI] [PubMed] [Google Scholar]
- Zhou C., Chan H. P., Petrick N., Helvie M. A., Goodsitt M. M., Sahiner B., and Hadjiiski L. M., “Computerized image analysis: Estimation of breast density on mammogram,” Med. Phys. 10.1118/1.1376640 28, 1056–1069 (2001). [DOI] [PubMed] [Google Scholar]
- Martin K. E., Helvie M. A., Zhou C., Roubidoux M. A., Bailey J. E., Paramagul C., Balen C. E., Klein K. A., Sonnad S. S., and Chan H. P., “Mammographic density measured with quantitative computer-aided method: Comparison with radiologists’ estimated and BI-RADS categories,” Radiology 10.1148/radiol.2402041947 240, 656–665 (2006). [DOI] [PubMed] [Google Scholar]
- Glide C., Duric N., and Littrup P., “A new method for quantitative analysis of mammographic density,” Med. Phys. 10.1118/1.2789407 34, 4491–4498 (2007). [DOI] [PubMed] [Google Scholar]
- Kopans D. B., “Basic physics and doubts about relationship between mammographically determined tissue density and breast cancer risk,” Radiology 246, 348–353 (2008). [DOI] [PubMed] [Google Scholar]
- Yao J., Zujewski J. A., Orzano J., Prindiville S., and Chow C., “Classification and calculation of breast fibroglandular tissue volume on SPGR fat suppressed MRI,” in Med. Imag, Proc SPIE, pp. 1942–1949 (2005).
- Lee N. A., Rusinek H., Weinreb J., Chandra R., Toth H., Singer C., and Newstead G., “Fatty and fibroglandular tissue volumes in the breasts of women 20–83 years old: Comparison of X-ray mammography and computer-assisted MR imaging,” AJR, Am. J. Roentgenol. 168, 501–506 (1997). [DOI] [PubMed] [Google Scholar]
- Li H., Chu Y., Salem A. F., and Clark R. A., “Image segmentation and 3D visualization for MR Mammography,” in Med. Imag. Proc. SPIE, pp. 1780–1789 (2002).
- van Engeland S., Timp S., and Karssemeijer N., “Volumetric breast density estimation from full-field digital mammograms,” IEEE Trans. Med. Imaging 10.1109/TMI.2005.862741 25, 273–282 (2006). [DOI] [PubMed] [Google Scholar]
- Wei J., Chan H. P., Helvie M. A., Roubidoux M. A., Sahiner B., Zhou C., Paquerault S., and Goodsitt M. M., “Correlation between mammographic density and volumetric fibroglandular tissue estimated on breast MR images,” Med. Phys. 31, 923–942 (2004). [DOI] [PubMed] [Google Scholar]
- Klifa C., Carballido-Gamio J., Wilmes L., Laprie A., Lobo C., Gibbs J., and Hylton N., “Quantification of breast tissue index from MR data using fuzzy cluster,” Proc. IEEE Eng. Med. Biol. Soc. 3, 1667–1670 (2004). [DOI] [PubMed] [Google Scholar]
- Chen W. and Giger M. L., “A fuzzy c-means (FCM) based algorithm for intensity inhomogeneity correction and segmentation of MR images,” in International Symposium on Biomedical Imaging (ISBI), pp. 1307–1310 (2004).
- Kulkarni A. D., “Fuzzy logic fundamentals,” in Computer Vision and Fuzzy-Neural Systems (Prentice-Hall, Englewood Cliffs, NJ, 2001), pp. 61–101. [Google Scholar]
- Bexek J. C., Pattern Recognition with Fuzzy Objective Function Algorithm (Plenum, New York, 1981). [Google Scholar]
- Koenig M., Kohle S., and Peitgen H. O., “Automatic cropping of breast regions for registration in MR mammography,” in Med. Imag. Proc. SPIE, pp. 1563–1570 (2005).
- Arbach L., Ph.D. thesis, University of Iowa, 2004. [Google Scholar]
- Hayton P., Brady M., Tarassenko L. and Moore N., “Analysis of dynamic MR breast images using a model of contrast enhancement,” Med. Image Anal. 10.1016/S1361-8415(97)85011-6 1, 207–224 (1997). [DOI] [PubMed] [Google Scholar]
- Chittineni R., Su M. Y., and Nalcioglu O., “A fast marching algorithm for breast delineation to facilitate coregistration of serial MRI studies for therapy response evaluation,” Med. Imag. Proc. SPIE, pp. 1890–1896 (2007).
- Lu W., Yao J., Lu C., Prindiville S., and Chow C., “DCE_MRI segmentation and motion correction based on active contour model and forward mapping,” in Proc. SNPD, pp. 208–212 (2006).
- Ertas G., Gulcur H. O., and Tunaci M., “Improved lesion detection in MR mammography: Three-dimensional segmentation, moving voxel sampling, and normalized maximum intensity-time ratio entropy,” Acad. Radiol. 14, 151–161 (2007). [DOI] [PubMed] [Google Scholar]
- Ertas G., Gulcur H. O., Osman O., Ucan O. N., Tunaci M., and Dursun M., “Breast MR segmentation and lesion detection with celluar neural networks and 3D template matching,” Comput. Biol. Med. 10.1016/j.compbiomed.2007.08.001 38, 116–127 (2008). [DOI] [PubMed] [Google Scholar]
- Ertas G., Gulcur H. O., Tunaci M., Osman O., and Ucan O. N., “A preliminary study on computerized lesion localization in MR mammography using 3D nMITR maps, multilayer cellular neural networks, and fuzzy C-partitioning,” Med. Phys. 10.1118/1.2805477 35, 195–205 (2008). [DOI] [PubMed] [Google Scholar]