Abstract
The purpose of this work was to demonstrate, both in phantom and patient, the feasibility of using an average 4DCT image set (AVG-CT) for 4D cumulative dose estimation. A series of 4DCT numerical phantoms and corresponding AVG-CTs were generated. For full 4D dose summation, static dose was calculated on each phase and cumulative dose was determined by combining each phase’s static dose distribution with known tumor displacement. The AVG-CT cumulative dose was calculated similarly, although the same AVG-CT static dose distribution was used for all phases (i.e., tumor displacements). Four lung cancer cases were also evaluated for stereotactic body radiotherapy and conformal treatments; however, deformable image registration of the 4DCTs was used to generate the displacement vector fields (DVFs) describing patient-specific motion. Dose discrepancy between full 4D summation and AVG-CT approach was calculated and compared. For all phantoms, AVG-CT approximation yielded slightly higher cumulative doses compared to full 4D summation, with dose discrepancy increasing with increased tumor excursion. In vivo, using the AVG-CT coupled with deformable registration yielded clinically insignificant differences for all GTV parameters including the minimum, mean, maximum, dose to 99% of target, and dose to 1% of target. Furthermore, analysis of the spinal cord, esophagus, and heart revealed negligible differences in major dosimetric indices and dose coverage between the two dose calculation techniques. Simplifying 4D dose accumulation via the AVG-CT, while fully accounting for tumor deformation due to respiratory motion, has been validated, thereby, introducing the potential to streamline the use of 4D dose calculations in clinical practice, particularly for adaptive planning purposes.
Keywords: dose accumulation, 4DCT, AVG-CT, dose calculation, adaptive radiation therapy
INTRODUCTION
One impediment to the precise delivery of thoracic radiotherapy is the influence of respiratory-induced tumor and organ motion, which limits knowledge of both the anatomical position of objects and the dose received by them. Respiratory correlated CT (or 4DCT) has improved the accuracy of target definition by reducing imaging uncertainty.1, 2, 3 4DCT inherently provides temporal information for both tumor and organ motion during different phases of the breathing cycle. By contrast, conventional helical CTs are acquired under free-breathing (FB) conditions (i.e., at arbitrary states of the breathing cycle) during which patient anatomy and density distribution are not static. Using this FB helical scan as the planning CT could clearly cause differences between the planned and delivered dose distribution.
With the advent of 4DCT, a natural progression has been made toward estimating the dose delivered during respiration through the use of 4D treatment planning.4, 5, 6, 7, 8, 9, 10 Briefly, these methods rely on dose calculation to patient datasets representing multiple instances of the patient anatomy (both intra- and interfraction), and an algorithm to then accumulate these multiple dose instances to a reference geometry of the patient. Both 4DCT and 4D dose accumulation are integral components of image-guided adaptive radiation therapy (IGART), which uses patient-specific dynamic or temporal information for treatment planning and potential modifications during treatment.11, 12 However, due to the extensive amount of information acquired via 4DCT (commonly >1000 CT slices) and time required for physician target delineation, several groups have worked toward developing automated contour delineation7, 13 and deformable image registration techniques.4, 5, 10 Furthermore, recalculation of the dose on daily 4DCT images would result in hundreds of required dose calculations, which is not feasible in the clinic today. Therefore, efforts to simplify 4D dose calculation and planning using 4DCT datasets have been proposed by including fewer breathing phases9 or using the midventilation phase.14, 15 Some groups have also averaged the CT density over the entire breathing cycle to create an average 4DCT (AVG-CT) and utilized that image set for dose calculation.6, 16
Here we present a novel algorithm where the AVG-CT is used to represent the mean voxel density for dose calculation, and a displacement vector field (DVF) from deformable registration of the corresponding 4DCT is used to sample and accumulate dose from the AVG-CT-based dose calculation. Essentially, this method generates a voxel-specific probability density function that provides a voxel-specific convolution for dose accumulation. This work investigates the feasibility of this approach for cumulative dose estimation through comparison to a full 4D dose summation. As a proof of concept, results are demonstrated from a series of numerical phantoms with varied tumor excursion. Our methodology is further validated with four in vivo lung cancer cases planned using both conventional conformal and stereotactic body radiotherapy (SBRT) techniques. By developing a simplified 4D dose accumulation taking into account respiration-induced deformation, adaptive planning strategies may be better streamlined in clinical practice.
METHODS AND MATERIALS
Phantom analysis
The overall purpose of the phantom study was to evaluate the effects of tumor and diaphragm motion on cumulative dose evaluation while holding the beam aperture static. In this study, “cumulative” dose implies the accumulation of dose intrafraction—representing variation in the anatomy due to periodic respiration—and interfraction by representing day-to-day variations in anatomy, position, and respiration pattern. For many lung cancer patients, tumor motion has been reported to be most significant in the superior-inferior (S-I) direction.17, 18 To reflect this motion, a series of computer-generated numerical phantoms simulated 2, 3, and 4 cm of tumor and diaphragm excursion. Each phantom was designed to span a half-cycle of respiration in nine phases, with four phases both superior (i.e., exhale) and inferior (i.e., inhale) to the mean position of the tumor.
Contours for the lung, gross tumor volume (GTV), and diaphragm (density=0.2, 1.0, and 1.0 g∕cc, respectively), were also generated, as shown for the 3 cm phantom at the mean position in Fig. 1a. Note that Fig. 1a represents a stationary phase, and that the corresponding other eight phases have the same image intensity with different tumor and diaphragm locations. The isocenter was set to the GTV center of mass at the mean position, with an isocenter-diaphragm distance of 3.7 cm. An AVG-CT for each phantom was generated by averaging the voxel intensities of all nine phases. Figures 1b, 1c, 1d demonstrate the AVG-CT for 2, 3, and 4 cm motion, respectively, of the tumor and diaphragm. As expected, the density is “smeared” in these averaged images, with a higher density in the central regions of the tumor and diaphragm due to these structures overlapping in different phases. Figures 1e, 1f illustrate the AVG-CT generated when the tumor was shifted 1 cm closer and 1 cm farther from the diaphragm, respectively.
Figure 1.
Sagittal view at mean position for the numerical phantom series. Shown are: (a) static mean position of the 3 cm phantom, and average CTs (AVG-CT) for the following excursions: (b) 2 cm, (c) 3 cm, (d) 4 cm, (e) 3 cm with diaphragm shifted 1 cm superior, and (f) 3 cm with diaphragm shifted 1 cm inferior. The surrounding regions represent the diaphragm and lung (ρ=1.0 and 0.2 g∕cc, respectively), with the isocenter as the GTV center of mass (ρ=1.0 g∕cc).
The phantom with 3 cm S-I motion was used for dose comparison in all studies. All dose calculations in this study (both phantom and patient) were performed using a convolution-superposition algorithm with heterogeneity correction (Pinnacle3, Research Version 8.1t, Philips Radiation Oncology Systems, Milpitas, CA). A four-field box treatment plan with 100 monitor units (MU) prescribed to the GTV isocenter was designed to cover the GTV with 95% of the cumulative dose at the mean position (i.e., reference phase). The four-field box treatment plan for the phantom demonstrated a simple conformal case and more complex beam arrangements were considered for the in vivo examples. An appropriate margin was added after initial dose accumulation to address any detriment in dose coverage. This margin was a block margin, not a clinical target volume to planning target volume (i.e., CTV-to-PTV) margin, designed to compensate for the blurring effect of respiration. The determination of the margin involved an iterative process that could not be applied prior to dose calculation as described previously.14, 19 Margin calculation involved calculating the static dose on each phase utilizing a block margin, accumulating dose, and reevaluating the coverage of the GTV. The prescription isodose coverage to the edge of the GTV was used to determine the dosimetric deficit of the dose accumulation process, and additional margin was added and cumulative dose recalculated. This process was iterated until the GTV was covered by the desired cumulative isodose line.
The same beam aperture required for cumulative dose coverage of the 3 cm motion was then applied to each phase and the AVG-CT for all other phantoms. By using the same beam aperture and treatment plan, the anatomical and density changes between phantoms could be used to simulate patient change in an adaptive radiotherapy context. To create the full 4D dose summation over all phases, the static dose was calculated on each 4DCT phase, and the resulting dose matrix was sampled with the known displacement vector from phantom construction. Finally, in-house software convolved the displacement vector for each phase with its corresponding dose distribution. If we let di represent the static dose corresponding to the ith 4DCT phase, where 1⩽i⩽M, the cumulative dose (D) delivered over M phases was calculated as:
| (1) |
where v represents an image voxel, vi is the position at phase i, and di(vi) is the static dose distribution based on the phase i image. To calculate cumulative dose for the AVG-CT methodology, the static dose distribution d(vi) was calculated on the AVG-CT image, and was assumed to be the same for each phase. The cumulative dose was then computed by using a similar formula to Eq. 1 by replacing di(vi) with d(vi). Deformable image registration was not necessary for phantom evaluation because the phase images were generated by specific rigid body shifts. The dose discrepancy between the two methodologies was calculated by subtracting the full 4D dose summation using all 4DCT phases from the AVG-CT dose. This was then converted to a percentage by dividing by the full 4D dose and multiplying by 100%.
Diaphragm shift
This study was designed to quantify the relative error in the AVG-CT method based on internal anatomy changes and deformation, which may depend on the relative position of objects of different density and their position within the dose distribution. To evaluate this effect, two additional 3 cm S-I motion phantoms were created with a change in diaphragm to tumor distance. Here, one phantom had increased diaphragm to tumor distance (4.7 cm), while the other phantom had decreased distance (2.7 cm) relative to our reference phase (3.7 cm). AVG-CTs of these additional phantoms are shown in Figs. 1e, 1f. The beam aperture designed for the original 3 cm motion reference phantom was then applied to the two additional phantoms to evaluate the effects of diaphragm proximity on the two dose accumulation methods.
Target mispositioning
Another study was designed to simulate a series of setup errors, and to determine their effects on the relative error of the AVG-CT method. In practice, this could be translated to an uncorrected positional error that could be present if the patient were being treated with an (offline) adaptive approach rather than an online correction technique. The implementation of IGART does not necessarily imply a daily target position correction; examples may include a case with offline correction or without the use of online guidance at all. This study was designed to serve as a worst-case scenario to evaluate the differences in the AVG-CT and full 4D summation techniques. For this experiment, three different aperture and isocenter shifts of the 3 cm S-I phantom were made: 1 cm superior to, 1 cm inferior to, and 1 cm left of the original isocenter. To estimate the magnitude of the shift effect, the cumulative dose using the AVG-CT approximation and full 4D dose summation were then compared to that calculated at the isocenter.
Patient analysis
Patient sample
Three patients assessed in this study were recruited from William Beaumont Hospital, with the imaging procedures performed under an Institutional Review Board approved protocol and in compliance with the Health Insurance Portability and Accountability Act. A fourth patient (Patient 3) dataset with very large respiration-induced tumor motion was obtained from the University of Wisconsin under a hospital-approved protocol. Similar to the phantom, dose calculation techniques were applied to four nonsmall cell lung cancer cases with varied tumor location, size, and magnitudes of motion, as determined by the centroid displacement over all 4DCT phases (summarized in Table 1). Free breathing 4DCT acquisition was performed using multislice helical CT (Brilliance Big Bore; Philips Medical Systems) coupled with an abdominal strain gauge for retrospective temporal sorting into 9–10 different phases.1
Table 1.
Patient sample used in dose accumulation study. RUL and RLL stand for right upper and right lower lobe, respectively. The magnitude of tumor motion was determined by the centroid displacement over all 4DCT phases.
| Patient | GTV Location | GTV (cm3) | GTV centroid displacement (cm) | ||
|---|---|---|---|---|---|
| Lateral | A-P | S-I | |||
| 1 | RUL | 33.93 | 0.15 | 0.28 | 0.37 |
| 2 | RLL | 5.23 | 0.12 | 0.08 | 0.80 |
| 3 | RLL | 6.01 | 0.52 | 0.09 | 2.00 |
| 4 | RLL | 31.81 | 0.31 | 0.57 | 1.42 |
The clinical cases were planned with both SBRT and conformal radiation therapy techniques. SBRT cases were copies of the clinical treatment plan, and, thus, were based on an IRB-approved patient protocol with prescription dose of 60 Gy to the 80% isodose line delivered in five fractions. The block margins did differ from the clinical plan; however, due to the use of the GTV (as opposed to the PTV for the clinically treated plan) for planning our approach. Using the GTV for planning allowed an estimation of the worst-case situation where the differences in coverage between the AVG-CT and all phase cumulative dose may be most evident. Here, an iterative margin design was used to take into account the amount of dose detriment caused by dose accumulation and respiration. This iterative technique was similar to that described for the phantom study. Briefly, margin evaluation involved calculating the static dose on each phase utilizing a block margin, accumulating dose, and reevaluating the coverage of the GTV. This block margin was not a clinical target volume to planning target volume (i.e., CTV-to-PTV) margin, but was designed to compensate for the blurring effect of respiration. The prescription isodose coverage to the GTV edge was used to determine the dosimetric deficit of the dose accumulation process, additional margin was added, and cumulative dose was recalculated. This process was iterated until the GTV was covered by the desired cumulative isodose lines: 60 Gy for SBRT and 95% of prescription dose for conformal radiotherapy. For SBRT, three patients were planned using seven beams, while one case had six beams. For conformal radiation therapy, 180 cGy∕fraction was prescribed to the average GTV isocenter for 39 fractions using four beams for all patients.
Deformable image registration
For the rigid-body motion phantom cases, the motion pattern was specifically designed, so it could be used for dose accumulation. However, for the patient, deformable image registration was necessary to obtain the patient-specific displacement field from 4DCT using in-house software previously described.13 Briefly, grayscale-based deformable image registration using trilinear interpolation was applied to minimize the sum of squared differences between the reference image (Phase 1 of 4DCT—end of inspiration) and all other phases. This process generated displacement vector fields (DVFs) for each image voxel that, when used together, represented the voxel-specific probability density function of organ motion. A physician delineated the target and critical structures on the reference image, binary contour masks were created, and ROIs for the remaining 4DCT phases were propagated using the displacement. All contours were visually inspected for agreement to their corresponding image sets. Mean contours for each ROI were created by warping the average DVF with the physician-delineated contours from the reference image. These mean contours were used for subsequent treatment planning.
AVG-CT dose accumulation
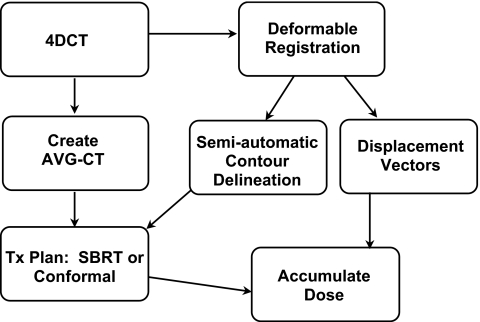
Similar to the phantom simulation, an AVG-CT for each patient was created through the temporal averaging of each voxel intensity over all 4DCT images using commercially available software (AcQSim3, Philips Medical Systems). The overall workflow for treatment planning and dose accumulation in the patient analysis using the AVG-CT approach is best described by Fig. 2. First, for each patient case, the clinical treatment plan was copied to the AVG-CT, although with a block margin, and the static dose was then calculated. The DVFs generated by deformable registration of the 4DCT, as described in the previous section, were then used to sample the static dose on the AVG-CT image. For the AVG-CT approach, the dose was assumed to be the same for all phases when sampling with the DVFs. Similar to the phantom experiment, an appropriate margin was added after initial dose accumulation to address any detriment in dose coverage, and the dose accumulation process was iterated. Finally, the dose distribution and dose to target and critical structures were tabulated and compared to the full 4D dose accumulation results described in the next section.
Figure 2.
Workflow for in vivo dose accumulation incorporating deformable image registration and the AVG-CT to approximate the patient CT density over all 4DCT phases.
Full 4D dose accumulation
Full 4D dose accumulation has been evaluated previously by a number of investigators,4, 8 and as a result, we used this approach to evaluate our AVG-CT method. The same beam arrangement, block margin, and number of MU used for AVG-CT dose calculation was copied to each phase of the clinical 4DCT image set. The static dose was then calculated on each phase. Using the same DVF described for the AVG-CT approach, the dose matrix was sampled and the dose was accumulated over all phases according to Eq. 1. The major difference between the 4D accumulation and the AVG-CT method is that for 4D accumulation, dose was sampled from the phase corresponding to the DVF, whereas, for the AVG-CT method, dose was always sampled from the AVG-CT calculated dose, regardless of respiration phase. The dose discrepancies (in cGy) for the GTV, lung, and other critical structures were calculated by subtracting the full 4D summation from the AVG-CT results. The differences were then converted to percentages by dividing by the full 4D summation results and multiplying by 100.
RESULTS
Phantom analysis
Motion magnitude
Table 2 summarizes the key findings from the dose discrepancy analysis for the numerical phantom study. For all motion patterns, estimations of the GTV parameters (maximum, mean, minimum, D99, and D1) using the AVG-CT approximation were slightly higher than the full 4D dose summation, yielding a positive dose discrepancy. For most cases, the dose to 99% of the GTV and mean lung dose exhibited the highest amount of discrepancy. In general, as the magnitude of motion increased, discrepancies in dose calculation also increased. The largest discrepancy (1.74 cGy, 1.99%) was observed for the 4 cm S-I phantom. However, for all phantom scenarios, the dose discrepancy between the full 4D dose summation and AVG-CT approximation was less than 2%, and for most cases, less than 1%.
Table 2.
Dose discrepancy, calculated by subtracting full 4D summation dose from the AVG-CT dose, in cGy. The percentage was calculated by dividing the dose difference by the 4D summation dose and converting to a percentage for each numerical motion phantom. GTV D99 and D1 represent the dose to 99% and 1% of the GTV, while MLD stands for mean lung dose.
| S-I Amplitude (cm) | Dose discrepancy (cGy) | ||||
|---|---|---|---|---|---|
| GTVMin | GTVMean | GTV D99 | GTV D1 | MLD | |
| 2 | 0.27 | 0.35 | 0.80 | 0.45 | 0.25 |
| (0.30%) | (0.37%) | (0.88%) | (0.47%) | (0.25%) | |
| 3 | 0.56 | 0.55 | 0.70 | 0.70 | 0.39 |
| (0.63%) | (0.58%) | (0.77%) | (0.73%) | (1.01%) | |
| 4 | 1.74 | 0.29 | 1.20 | 0.60 | 0.39 |
| (1.99%) | (0.31%) | (1.34%) | (0.63%) | (1.01%) | |
| 2.7 cm diaphragm-tumor distance | 0.81 | 0.03 | 0.75 | 0.10 | 0.22 |
| (0.89%) | (0.03%) | (0.82%) | (0.10%) | (0.58%) | |
| 4.7 cm diaphragm-tumor distance | 0.19 | 0.21 | 0.40 | 0.45 | 0.63 |
| (0.22%) | (0.23%) | (0.44%) | (0.47%) | (1.61%) | |
Diaphragm shift
To quantify the relative error in the AVG-CT method based on internal anatomy changes, two additional diaphragm-shift phantoms were evaluated. Table 2 summarizes the results obtained for the diaphragm shift phantoms. Using the discrepancies reported for the 3 cm phantom for comparison, the presence of the diaphragm (i.e., diaphragm shifted superior) caused no appreciable change in discrepancy. The largest difference between the 3 cm phantom (3.7 cm diaphragm-tumor distance) and the 2.7 cm diaphragm-tumor distance was observed for the maximum dose to the GTV, although the calculation was less than 1 cGy different. When the diaphragm was shifted 1 cm inferior to the tumor (4.7 cm diaphragm-tumor distance), slight reductions in discrepancy were observed for the GTV and lung parameters studied when compared to the 3 cm phantom.
Target mispositioning
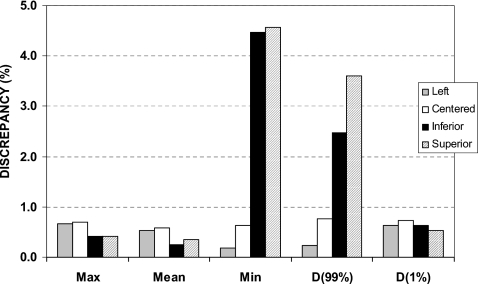
To simulate a series of setup errors (i.e., an uncorrected positional error), a target mispositioning experiment was performed. Figure 3 summarizes the results for the beam aperture mispositioned in the following configurations: centered (i.e., correctly positioned), shifted 1 cm left, shifted 1 cm superior, and shifted 1 cm inferior. For the maximum dose, mean dose, and dose to 1% of the GTV volume, the dose discrepancy was less than 1% (all less than 1 cGy). Furthermore, no appreciable difference was observed when the beam aperture was shifted to the left of the tumor; the dose discrepancy for this case was similar to the correctly positioned aperture. However, when the beam aperture was shifted superior and inferior, the discrepancy in dose calculation minimum dose to the GTV and D99 were substantial. The largest discrepancy (4.57%) was observed for the minimum dose to the GTV when the aperture was shifted superior.
Figure 3.
Discrepancy (%) results for the GTV of the numerical phantom with 3 cm of tumor motion and target mispositions designed to simulate a series of setup errors. The aperture shifts are 1 cm to the left, inferior, and superior of the GTV. D(99%) and D(1%) are the delivered dose to 99% and 1% of the GTV, respectively.
Patient analysis
Building on the phantom results, four lung cancer patient datasets were also analyzed. Table 3 summarizes the discrepancy for the most sensitive parameters evaluated. The top number indicates the dose discrepancy in both cGy (AVG-CT minus the corresponding full 4D for each dose indices) and percent (percent of the full 4D dose index). For most of the dose indices studied, the AVG-CT approach yielded slightly higher results than using the full 4D approach. The largest difference observed in the GTV was for the SBRT plan for Patient 3, where the D1 was −2.44% (−187.50 cGy) discrepancy between techniques. The SBRT plans yielded a larger dose discrepancy than the conformal plans when expressed in cGy, however, when expressed as a percentage, the dose discrepancy was less than 1% for all techniques. The mean lung dose discrepancy was largest for Patient 3, although still under 2% difference.
Table 3.
Dose discrepancy results for four patients planned with both conformal and stereotactic body radiotherapy, with the dose difference expressed in cGy (top) and percentage of full 4D dose (bottom, in %). D99 and D1 are the dose delivered to 99% and 1% of the GTV, respectively. For the lungs excluding the GTV, MLD stands for the mean lung dose and V20 defines the volume receiving 20 Gy.
| Patient | Conformal discrepancy (cGy) | SBRT discrepancy (cGy) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GTV D99 | GTV D1 | Mean | MLD | V20 (%) | GTV D99 | GTV D1 | Mean | MLD | V20 (%) | ||
| 1 | 70.00 | 41.00 | 48.67 | 5.95 | 0.08 | 15.00 | 2.50 | 2.43 | 1.60 | 0.03 | |
| (1.16%) | (0.58%) | (0.72%) | (0.96%) | (0.77%) | (0.24%) | (0.03%) | (0.03%) | (0.29%) | (0.42%) | ||
| 2 | 30.24 | 32.50 | 25.30 | 0.83 | −0.01 | 80.00 | 7.50 | 14.88 | 0.45 | 0.01 | |
| (0.43%) | (0.46%) | (0.37%) | (0.18%) | (−0.13%) | (1.37%) | (0.10%) | (0.21%) | (0.15%) | (0.28%) | ||
| 3 | −40.00 | −144.00 | −51.91 | 3.76 | 0.04 | 40.00 | −187.50 | −87.97 | 2.91 | 0.09 | |
| (−0.65%) | (−2.04%) | (−0.78%) | (1.60%) | (1.09%) | (0.64%) | (−2.44%) | (−0.78%) | (1.60%) | (4.09%) | ||
| 4 | 30.00 | 8.50 | −3.15 | −1.32 | −0.02 | 70.00 | 7.20 | −10.81 | −1.52 | −0.03 | |
| (0.48%) | (0.12%) | (−0.05%) | (−0.28%) | (−0.28%) | (1.18%) | (0.10%) | (−0.15%) | (−0.42%) | (−0.76%) | ||
| Average | 22.56 | −15.50 | 4.73 | 2.31 | 0.02 | 51.25 | −42.58 | −20.37 | 0.86 | 0.03 | |
| (−0.69%) | (−0.39%) | (−0.55%) | (−0.91%) | (−0.93%) | (−0.86%) | (−0.08%) | (−0.12%) | (−0.68%) | (−1.60%) | ||
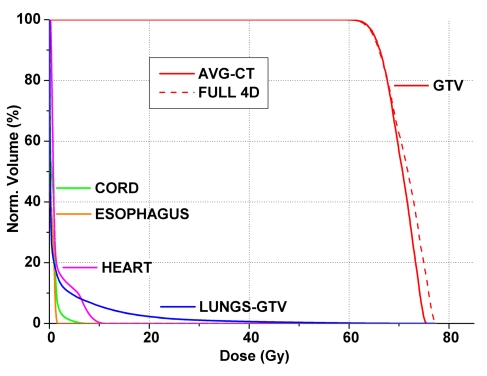
For critical structures (spinal cord, heart, and esophagus), the maximum dose, mean dose, and generalized equivalent uniform dose (gEUD, a=2) were also investigated for both 3DCRT and SBRT (not shown). The greatest dose discrepancy (59.86 cGy, 1.47%) was observed for Patient 3 for the maximum heart dose planned using 3DCRT. When taking into account the percentage of the full 4D dose index, the largest discrepancy was observed in Patient 3 for the esophagus planned with SBRT (−3.25%, −5.74 cGy). Overall, the discrepancies of all critical structures, regardless of the planning technique (i.e., SBRT and conventional fractionation) were at clinically insignificant levels, with an average discrepancy of −0.10 (range: −3.25% to 1.05%) for the former and 0.23% (range: −0.42% to 2.13%) for the latter. This was further demonstrated by Fig. 4 that summarizes the SBRT DVH results obtained for Patient 3 whose tumor exhibited prominent centroid motion in the S-I direction. Visual inspection of the DVHs for all critical structures yielded undetectable differences between the two 4D dose calculation techniques. In this case, the tumor was inferiorly situated near the diaphragm, and the beam was perturbed by the diaphragm in three of the 10 4DCT phases. Here, the solid lines indicate the AVG-CT approximation, while the dashed lines represent the full 4D dose summation. Note the undetectable differences for all critical structures. In the GTV, the coverage was practically identical; however, the full 4D summation exhibited slightly higher maximum dose and dose to 1% of the GTV (D=−2.00 and −2.04%, respectively).
Figure 4.
Dose volume histogram for Patient 3 (superior-inferior displacement ∼2.0 cm) with solid and dashed lines indicating the cumulative dose using the AVG-CT and full 4D summation, respectively, for stereotactic body radiotherapy plans. Note the similar histogram shape for all critical structures and the tumor (GTV), yielding no noticeable differences for the critical structures between techniques. The most sensitive parameters were the maximum dose and dose to 1% of the GTV.
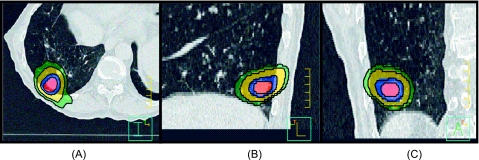
The dose coverage between the plans is also demonstrated by Fig. 5. Here, the cumulative dose distribution for Patient 3 planned with stereotactic body radiotherapy techniques is shown. The isodose washes represent 30 (green), 40 (yellow), 60 (blue), and 70 (red) Gy coverage of the GTV. For the full 4D cumulative dose summation, the corresponding black lines are shown. Negligible differences were observed in dose distribution and target coverage between the two approaches, further validating the use of AVG-CT for 4D dose accumulation. Similar results were observed for the other three patients investigated in this study (not shown).
Figure 5.
Cumulative dose distribution on the reference images for Patient 3 planned with stereotactic body radiotherapy techniques showing the (A) transverse, (B) sagittal, and (C) coronal views at the isocenter level. For the cumulative dose calculated using the AVG-CT approximation, the isodose washes represent 30 (green), 40 (yellow), 60 (blue), and 70 (red) Gy coverage of the GTV. For the full 4D cumulative dose summation, the corresponding black lines are shown. Negligible differences were observed in dose distribution and target coverage between the two approaches.
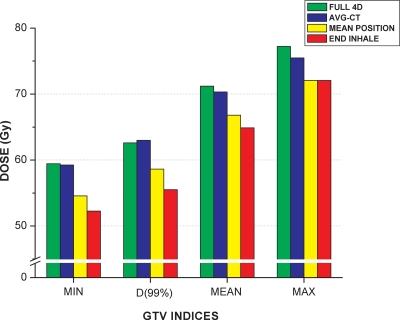
Rosu et al.9 evaluated the number of intermediate 4DCT states required to approximate the cumulative dose. Using our dose accumulation approach, we repeated our calculations for two additional studies by computing dose using the same treatment plans: (1) on the end of inhale phase (i.e., Phase 1) and (2) on the phase in which the tumor centroid was closest to the average centroid position over all 10 phases (i.e., mean position phase). These calculations were performed for the SBRT plan of Patient 3, where the most pronounced dose discrepancies between the AVG-CT and full 4D dose summation were observed. The results are summarized in Fig. 6. The figure demonstrates that the AVG-CT approach yielded closer approximations to the full 4D dose accumulation than using the mean position phase. Using the mean position phase, the dose discrepancies for D99 and D1 to the target were −5.15% (−397.50 cGy) and −6.58% (−508.50 cGy), respectively. Using the end of inhale phase for dose calculation, the dose discrepancies for D99 and D1 to the target were even higher at −9.19% (−710.00 cGy) and −7.08% (−546.50 cGy), respectively. This was expected, however, due to the tumor and diaphragm being at an extreme phase of the breathing cycle. The close agreement between the AVG-CT and full 4D dose summation supports the use of the AVG-CT for 4D dose calculations.
Figure 6.
Comparison of 4D dose accumulation using all 10 phases (full 4D), AVG-CT, mean position phase, and end of inhale phase for the SBRT plan of Patient 3. The mean position phase was defined as the phase in which the tumor centroid was closest to the average centroid position over all 10 phases. The AVG-CT approach yielded closer approximations to the full 4D dose accumulation.
DISCUSSION
This study sought to demonstrate the feasibility of representing temporal patient anatomy via the AVG-CT, and combining that information with deformable registration to calculate cumulative dose. First, several phantom experiments were performed to validate the use of the AVG-CT to estimate the subject density for dose accumulation. In general, as the magnitude of phantom tumor motion increased, the dose discrepancy between the two techniques also increased, particularly for the minimum dose to the GTV. For 4 cm of tumor excursion, the maximum discrepancy (∼2%, 1.74 cGy) was observed for the minimum dose to the GTV. However, this magnitude of motion likely exceeds the deviation that we may clinically observe, as typical tumor motion is less than 1 cm.17, 20
The effects of surrounding structures near the tumor were also evaluated via two diaphragm shift numerical phantoms. The results suggest that the presence of a nearby structure tends to increase the more sensitive dose discrepancy indices including the minimum dose and D99 of the GTV. When the diaphragm was moved out of the field by shifting 1 cm inferior to the tumor, a reduction in discrepancy was observed for all GTV parameters. This can be attributed to the reduced amount of scatter contribution due to the increased distance between the tumor and diaphragm.
In practice, shifting the aperture could simulate a number of different scenarios, including the tumor moving outside of the planned treatment field during delivery, the presence of a baseline shift,14, 21 or in the instance of large tumor deformation due to tumor radiation dose response. The minimum dose to the GTV and D99 were most affected for the superior and inferior aperture shifts, with discrepancies on the order of 3%–5%. These large discrepancies are likely due to the relative change in target and diaphragm position of 1 cm. In practice, 1 cm relative variations between the target and normal tissue would be a rare occurrence,21 therefore, reducing the dose discrepancy expected in this instance.
For the four patients planned with both SBRT and conventional techniques, no clear trend with discrepancy was observed between the two approaches, although for the lung metrics, the parameters studied tended to be larger using the AVG-CT methodology. This was not observed in the analysis of the GTV and other critical structures. The majority of the GTV, lung, and critical structures parameters demonstrated dose discrepancies <2%. The overall dose discrepancies were similar for both SBRT and conformal radiation therapy plans for all patients.
While this work evaluated a new technique of 4D dose accumulation using the AVG-CT in only four patients, one was considered to be a worst-case scenario with the tumor abutting the diaphragm and exhibiting 2 cm of S-I motion. This case likely represents the largest deviation that we may clinically observe, as typical tumor motion is less than 1 cm.17, 20 For this patient in particular, the largest deviation was observed for the maximum dose and dose to 1% of the GTV, although both discrepancies were on the order of 2%. This result is consistent with that observed for the phantom case, where increased tumor excursion led to increased dose discrepancy.
4D dose calculations for lung cancer radiotherapy have been described in the literature, although not in the same context as the method we are presenting. The approach by Admiraal and colleagues was similar to ours; however, they utilized elastic body spline deformable registration within their research version of Pinnacle3 (8.1r), which they suggested was not accurate enough to estimate cumulative doses outside of the CTV.6 Our results were consistent with their key finding: insignificant differences were observed between dose calculation on the AVG-CT and the cumulative dose coverage on all phases. Rosu et al. described 4D dose calculations on the “ave-state” dose; however, they defined this as the time-weighted average phase over the breathing cycle.9 Whereas, the AVG-CT we used was an image with the intensity at each spatial position averaged over time of all 4DCT phases (i.e., phase based).
Several investigators have utilized deformable registration in their 4D dose summation on some or all of the 4DCT phases; however, none of them evaluated the use of the AVG-CT.7, 8, 22 The goal of the current AVG-CT approach is to reduce the required number of dose calculations, while preserving the dose calculation accuracy in relation to these 4D dose accumulation techniques.
Fluence convolution is another method designed to approximate the 4D accumulated dose, which reduces the required number of dose calculations.23, 24 In this method, the fluence is first convolved with a single probability density function to generate the 4D fluence. This 4D fluence is then used to calculate dose in a single instance of the anatomy. Using the AVG-CT for this single instance would be analogous to the current approach. Still, the fluence convolution method relies on the assumption that the probability density function is constant for all voxels in the patient, whereas in the current approach we use a voxel-specific probability distribution derived from the 4DCT scan.
Wolthaus et al. described the “midventilation scan” of the 4DCT dataset, which was defined in one of two ways: (1) calculate the mean tumor position and determine the corresponding respiration phase, or (2) select the CT scan using the diaphragm motion.15 Our AVG-CT approach offers the advantage of not requiring the determination of which 4DCT phase best reflects the mean centroid position. By offering an alternative to a full 4D dose summation, our technique has important implications clinically as it reduces computational and evaluation time required for each patient case. Because an AVG-CT can be generated via conventional simulation packages and handled in standard treatment planning systems, its widespread implementation is possible.
Other research has also evaluated the use of Monte Carlo coupled with deformable registration for 4D dose calculation,10 although this approach currently has limited clinical applicability due to the lack of Monte Carlo treatment planning systems commercially available. As Monte Carlo becomes more available, the use of the AVG-CT to estimate patient density may be particularly beneficial in this context to reduce overall computation and planning time required for 4D dose estimations.
One of the assumptions in the in vivo study included each 4DCT phase being time sorted and equally distributed over the breathing cycle, and this equal weighting was also assumed for the 4D dose accumulation. It may be particularly advantageous to develop a time-weighted sorting scheme to describe the patient’s breathing cycle during simulation and treatment. This may more accurately predict the cumulative dose delivered during more natural respiratory conditions. In this case, the method we have proposed here would still be applicable; however, appropriate weighting factors would be integrated into 4DCT phase sorting and Eq. 1 for the calculation of cumulative dose, which can be addressed in future studies. While the patients used in this study represented a varied subsample (i.e., different tumor sizes, tumor excursion, and proximity to surrounding structures), studies are warranted to further investigate different planning techniques and strategies.
Dosimetric advantages have not been realized in the application of adaptive radiotherapy techniques (ART) for SBRT of nonsmall cell lung cancer.22, 25 However, a significant reduction in tumor size, particularly for large GTVs, has been observed throughout the radiation therapy course for conventional fractionation, suggesting that these patients may benefit most from adaptive planning techniques.20, 26, 27, 28, 29 Consideration must also be given to normal tissue response, respiratory patterns,30 and tumor motion26 changing over treatment course. To account for this large interfraction variability throughout treatment, adaptive planning strategies must be implemented that are both efficient and accurate. Our approach of using the AVG-CT for dose accumulation fulfills both of these needs, thereby supporting the implementation of ART in nonsmall lung cancer radiation therapy.
CONCLUSION
We have demonstrated the feasibility of approximating the subject’s density distribution via an AVG-CT and utilizing deformable registration for cumulative dose calculation. Numerical phantom results demonstrated an initial proof of concept, and this was validated in four lung cancer cases planned with both conventional and SBRT techniques. Using the AVG-CT coupled with deformable registration yielded only modest differences in cumulative dose relative to a full 4D dose summation, at clinically insignificant levels. The AVG-CT method is straightforward, can save time, and eliminates cumbersome dose calculation on each 4DCT phase. By describing the applicability of this technique, simplification in 4D dose calculation is demonstrated, thereby introducing the potential to streamline clinical practice, namely, in the implementation of adaptive radiotherapy.
ACKNOWLEDGMENTS
This work was supported by NIH Grant No. R01 CA 116249. The authors would like to thank Ana Paula Galerani, MD for volume delineation and Tiezhi Zhang, Ph.D. for help with deformable registration. The authors would also like to acknowledge the University of Wisconsin for the 4DCT patient dataset with large motion.
References
- Keall P. J., Starkschall G., Shukla H., Forster K. M., Ortiz V., Stevens C. W., Vedam S. S., George R., Guerrero T., and Mohan R., “Acquiring 4D thoracic CT scans using a multislice helical method,” Phys. Med. Biol. 10.1088/0031-9155/49/10/015 49, 2053–2067 (2004). [DOI] [PubMed] [Google Scholar]
- Vedam S. S., Keall P. J., Kini V. R., Mostafavi H., Shukla H. P., and Mohan R., “Acquiring a four-dimensional computed tomography dataset using an external respiratory signal,” Phys. Med. Biol. 10.1088/0031-9155/48/1/304 48, 45–62 (2003). [DOI] [PubMed] [Google Scholar]
- Ford E. C., Mageras G. S., Yorke E., and Ling C. C., “Respiration-correlated spiral CT: A method of measuring respiratory-induced anatomic motion for radiation treatment planning,” Med. Phys. 10.1118/1.1531177 30, 88–97 (2003). [DOI] [PubMed] [Google Scholar]
- Orban de Xivry J., Janssens G., Bosmans G., De Craene M., Dekker A., Buijsen J., van Baardwijk A., De Ruysscher D., Macq B., and Lambin P., “Tumour delineation and cumulative dose computation in radiotherapy based on deformable registration of respiratory correlated CT images of lung cancer patients,” Radiother. Oncol. 10.1016/j.radonc.2007.08.012 85, 232–238 (2007). [DOI] [PubMed] [Google Scholar]
- Keall P. J., Siebers J. V., Joshi S., and Mohan R., “Monte Carlo as a four-dimensional radiotherapy treatment-planning tool to account for respiratory motion,” Phys. Med. Biol. 10.1088/0031-9155/49/16/011 49, 3639–3648 (2004). [DOI] [PubMed] [Google Scholar]
- Admiraal M. A., Schuring D., and Hurkmans C. W., “Dose calculations accounting for breathing motion in stereotactic lung radiotherapy based on 4D-CT and the internal target volume,” Radiother. Oncol. 10.1016/j.radonc.2007.11.022 86, 55–60 (2008). [DOI] [PubMed] [Google Scholar]
- Rietzel E., Chen G. T., Choi N. C., and Willet C. G., “Four-dimensional image-based treatment planning: Target volume segmentation and dose calculation in the presence of respiratory motion,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2004.11.037 61, 1535–1550 (2005). [DOI] [PubMed] [Google Scholar]
- Guckenberger M., Wilbert J., Krieger T., Richter A., Baier K., Meyer J., and Flentje M., “Four-dimensional treatment planning for stereotactic body radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2007.04.074 69, 276–285 (2007). [DOI] [PubMed] [Google Scholar]
- Rosu M., Balter J. M., Chetty I. J., Kessler M. L., McShan D. L., Balter P., and Ten Haken R. K., “How extensive of a 4D dataset is needed to estimate cumulative dose distribution plan evaluation metrics in conformal lung therapy?,” Med. Phys. 10.1118/1.2400624 34, 233–245 (2007). [DOI] [PubMed] [Google Scholar]
- Flampouri S., Jiang S. B., Sharp G. C., Wolfgang J., Patel A. A., and Choi N. C., “Estimation of the delivered patient dose in lung IMRT treatment based on deformable registration of 4D-CT data and Monte Carlo simulations,” Phys. Med. Biol. 10.1088/0031-9155/51/11/006 51, 2763–2779 (2006). [DOI] [PubMed] [Google Scholar]
- Yan D., Vicini F., Wong J., and Martinez A., “Adaptive radiation therapy,” Phys. Med. Biol. 10.1088/0031-9155/42/1/008 42, 123–132 (1997). [DOI] [PubMed] [Google Scholar]
- Yan D., “Developing quality assurance processes for image-guided adaptive radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 71, S28–S32 (2008). [DOI] [PubMed] [Google Scholar]
- Zhang T., Chi Y., Meldolesi E., and Yan D., “Automatic delineation of on-line head-and-neck computed tomography images: Toward on-line adaptive radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2007.01.038 68, 522–530 (2007). [DOI] [PubMed] [Google Scholar]
- Hugo G. D., Yan D., and Liang J., “Population and patient-specific target margins for 4D adaptive radiotherapy to account for intra- and inter-fraction variation in lung tumour position,” Phys. Med. Biol. 10.1088/0031-9155/52/1/017 52, 257–274 (2007). [DOI] [PubMed] [Google Scholar]
- Wolthaus J. W., Schneider C., Sonke J. J., van Herk M., Belderbos J. S., Rossi M. M., Lebesque J. V., and Damen E. M., “Mid-ventilation CT scan construction from four-dimensional respiration-correlated CT scans for radiotherapy planning of lung cancer patients,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2006.04.031 65, 1560–1571 (2006). [DOI] [PubMed] [Google Scholar]
- Soofi W., Starkschall G., Britton K., and Vedam S., “Determination of an optimal organ set to implement deformations to support four-dimensional dose calculations in radiation therapy planning,” J. Appl. Clin. Med. Phys. 9, 69–82 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seppenwoolde Y., Shirato H., Kitamura K., Shimizu S., van Herk M., Lebesque J. V., and Miyasaka K., “Precise and real-time measurement of 3D tumor motion in lung due to breathing and heartbeat, measured during radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(02)02803-1 53, 822–834 (2002). [DOI] [PubMed] [Google Scholar]
- Mageras G. S., Pevsner A., Yorke E. D., Rosenzweig K. E., Ford E. C., Hertanto A., Larson S. M., Lovelock D. M., Erdi Y. E., Nehmeh S. A., Humm J. L., and Ling C. C., “Measurement of lung tumor motion using respiration-correlated CT,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2004.06.021 60, 933–941 (2004). [DOI] [PubMed] [Google Scholar]
- Balter J. M., Brock K. K., Lam K. L., Tatro D., Dawson L. A., McShan D. L., and Ten Haken R. K., “Evaluating the influence of setup uncertainties on treatment planning for focal liver tumors,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2005.05.014 63, 610–614 (2005). [DOI] [PubMed] [Google Scholar]
- Erridge S. C., Seppenwoolde Y., Muller S. H., van Herk M., De Jaeger K., Belderbos J. S., Boersma L. J., and Lebesque J. V., “Portal imaging to assess set-up errors, tumor motion and tumor shrinkage during conformal radiotherapy of non-small cell lung cancer,” Radiother. Oncol. 10.1016/S0167-8140(02)00287-6 66, 75–85 (2003). [DOI] [PubMed] [Google Scholar]
- Sonke J. J., Lebesque J., and van Herk M., “Variability of four-dimensional computed tomography patient models,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2007.08.067 70, 590–598 (2008). [DOI] [PubMed] [Google Scholar]
- Wu J., Li H., Shekhar R., Suntharalingam M., and D’Souza W., “An evaluation of planning techniques for stereotactic body radiation therapy in lung tumors,” Radiother. Oncol. 87, 35–43 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetty I. J., Rosu M., Tyagi N., Marsh L. H., McShan D. L., Balter J. M., Fraass B. A., and Ten Haken R. K., “A fluence convolution method to account for respiratory motion in three-dimensional dose calculations of the liver: A Monte Carlo study,” Med. Phys. 10.1118/1.1581412 30, 1776–1780 (2003). [DOI] [PubMed] [Google Scholar]
- Beckham W. A., Keall P. J., and Siebers J. V., “A fluence-convolution method to calculate radiation therapy dose distributions that incorporate random set-up error,” Phys. Med. Biol. 10.1088/0031-9155/47/19/302 47, 3465–3473 (2002). [DOI] [PubMed] [Google Scholar]
- Haasbeek C. J., Lagerwaard F. J., Cuijpers J. P., Slotman B. J., and Senan S., “Is adaptive treatment planning required for stereotactic radiotherapy of stage I non-small-cell lung cancer?,” Int. J. Radiat. Oncol., Biol., Phys. 67, 1370–1374 (2007). [DOI] [PubMed] [Google Scholar]
- Britton K. R., Starkschall G., Tucker S. L., Pan T., Nelson C., Chang J. Y., Cox J. D., Mohan R., and Komaki R., “Assessment of gross tumor volume regression and motion changes during radiotherapy for non-small-cell lung cancer as measured by four-dimensional computed tomography,” Int. J. Radiat. Oncol., Biol., Phys. 68, 1036–1046 (2007). [DOI] [PubMed] [Google Scholar]
- Kupelian P. A., Ramsey C., Meeks S. L., Willoughby T. R., Forbes A., Wagner T. H., and Langen K. M., “Serial megavoltage CT imaging during external beam radiotherapy for non-small-cell lung cancer: Observations on tumor regression during treatment,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2005.04.046 63, 1024–1028 (2005). [DOI] [PubMed] [Google Scholar]
- Woodford C., Yartsev S., Dar A. R., Bauman G., and Van Dyk J., “Adaptive radiotherapy planning on decreasing gross tumor volumes as seen on megavoltage computed tomography images,” Int. J. Radiat. Oncol., Biol., Phys. 69, 1316–1322 (2007). [DOI] [PubMed] [Google Scholar]
- Harsolia A., Hugo G. D., Kestin L. L., Grills I. S., and Yan D., “Dosimetric advantages of four-dimensional adaptive image-guided radiotherapy for lung tumors using online cone-beam computed tomography,” Int. J. Radiat. Oncol., Biol., Phys. 70, 582–589 (2008). [DOI] [PubMed] [Google Scholar]
- Hugo G., Vargas C., Liang J., Kestin L., Wong J. W., and Yan D., “Changes in the respiratory pattern during radiotherapy for cancer in the lung,” Radiother. Oncol. 10.1016/j.radonc.2006.02.015 78, 326–331 (2006). [DOI] [PubMed] [Google Scholar]