Objective assessment of deformable image registration in radiotherapy: A multi-institution study

Abstract

The looming potential of deformable alignment tools to play an integral role in adaptive radiotherapy suggests a need for objective assessment of these complex algorithms. Previous studies in this area are based on the ability of alignment to reproduce analytically generated deformations applied to sample image data, or use of contours or bifurcations as ground truth for evaluation of alignment accuracy. In this study, a deformable phantom was embedded with 48 small plastic markers, placed in regions varying from high contrast to roughly uniform regional intensity, and small to large regional discontinuities in movement. CT volumes of this phantom were acquired at different deformation states. After manual localization of marker coordinates, images were edited to remove the markers. The resulting image volumes were sent to five collaborating institutions, each of which has developed previously published deformable alignment tools routinely in use. Alignments were done, and applied to the list of reference coordinates at the inhale state. The transformed coordinates were compared to the actual marker locations at exhale. A total of eight alignment techniques were tested from the six institutions. All algorithms performed generally well, as compared to previous publications. Average errors in predicted location ranged from 1.5 to 3.9 mm, depending on technique. No algorithm was uniformly accurate across all regions of the phantom, with maximum errors ranging from 5.1 to 15.4 mm. Larger errors were seen in regions near significant shape changes, as well as areas with uniform contrast but large local motion discontinuity. Although reasonable accuracy was achieved overall, the variation of error in different regions suggests caution in globally accepting the results from deformable alignment.

INTRODUCTION

Deformable image registration has found many applications in radiation therapy ranging from dose accumulation and contour propagation for adaptive therapy^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} to generation of analytical models of breathing motion based on deformation maps of the thorax.¹⁴ Some of these applications are extremely sensitive to the results of image registration. For example, when deformable alignment is used for dose accumulation in adaptive therapy, small errors in the deformation map can result in significant changes in the dose at points in high dose gradient regions. If deformable alignment is to be used for these sensitive applications, we need to have a quantitative measure of the accuracy of the resulting deformation maps.

Quantitative evaluation of image registration is a very difficult task. Current methods that are used include use of analytically deformed images some of which consider the biomechanical properties of the patient,^{15, 16, 17, 18, 19, 20} and∕or use of contours and bifurcations identified on both image sets for comparison.^{15, 21, 22, 23, 24} A voxel-based evaluation method was proposed by Zhong et al. which automatically detects a region in an image where the registration is not performing well using a finite-element-based elastic framework to calculate the unbalanced energy in each voxel after substitution of the displacement vector field.²⁵ Use of phantoms with known physical deformation or phantoms with easily identifiable markers where motion can be accurately measured is another method investigated by other groups.^{15, 26} Studies describing deformable registration methods, as well as those validating a method for a specific anatomical site, have all used one or more of the methods described here, for validation of their results. Studies where deformable alignment is used as a tool usually test the registration accuracy based on a few manually identified landmarks, however, the problem is that these landmarks may not be sufficient for generalizing the accuracy results to the entire region of interest. Therefore, an objective assessment of image registration is necessary, where the points chosen for validation are not the driving forces in the local deformation parameters, and their scarcity does not mask the difference in global versus local registration accuracy estimates. In this study we use a deformable phantom with a large number of markers, for a blind objective test of various deformable image registration methods. It should be noted that this study will not attempt to compare the different registration techniques directly because we believe that the lack of coarse structure in the lung can bias the performance of certain methods compared to others, as will be discussed later on in the manuscript. The purpose of this study is to investigate potential uncertainties that may be overlooked by the commonly used validation techniques.

METHODS AND MATERIALS

Study design

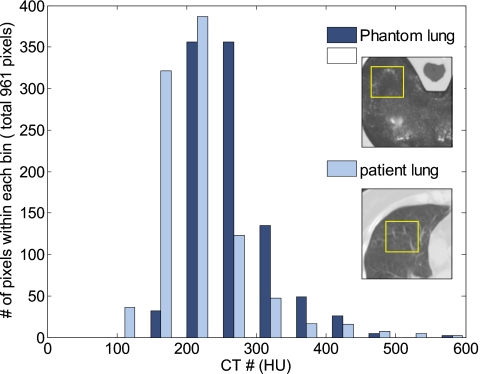
We previously described the design and implementation of a deformable phantom for validation of image registration results.^{27, 28, 29} The phantom consists of an anthropomorphic plastic chest wall, a skeleton, and a compressible section made of high density foam and embedded with four tumor-simulating spheres of different size. The phantom was further impregnated with iodinated contrast which, upon drying, left an intermediate contrast pattern within the foam that provided some differential signal. While not the same as the substructure seen in thoracic images (or lack thereof in scans of the liver), a histogram comparing the intensity distribution between the foam section and a typical lung CT image shows reasonably similar variations in intensity (Fig. 1).

Figure 1.

Histogram of the intensity distribution in a typical section of the foam at the simulated exhale state (dark bars), and the intensity distribution of a sample segment from an image of the left lung at exhale (light bars).

In addition to the larger tumor-simulating objects, the foam was also embedded with 48 small (2.5 mm diameter) markers and then compressed using a one-dimensional drive stage, to simulate various breathing states. As described previously, the markers were manually localized to measure the true motion and deformation inside the foam. These markers were then removed from the image by replacing their voxel values with intensity values from the neighboring voxels, and applying Gaussian smoothing to that region in order to avoid any potential bias caused by using these visible structures as reference points for evaluation of image registration results. As a proof of principle, three simple alignment methods were tested using the phantom.²⁹ This study is designed to test the feasibility of applying the developed methodology to a broader analysis of alignment accuracy. Toward this end, we have designed and implemented a multi-institution blind study of the accuracy of deformable image registration algorithms.

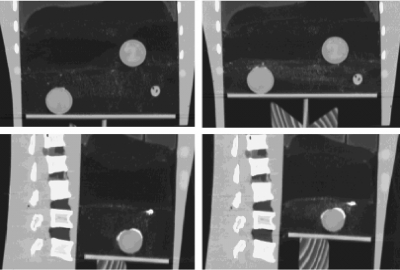
For this study, the phantom was scanned at two different compression states using a single-slice commercial CT scanner (HiSpeed, General Electric, Milwaukee, WI). The “exhale” state involved a higher compression of the foam (30 mm motion of the compression plate) than the “inhale” state. High resolution (0.78×0.78×1 mm) CT images were acquired through the foam-containing region. Figure 2 shows example images of the phantom at two compression states. The positions of the markers embedded at various locations in the foam were manually identified by a single observer. Repeat measurements of the locations of a random set of ten markers showed an average standard deviation of better than 0.2 mm in all dimensions.²⁹ The maximum standard deviation in each direction was 0.3 mm in right–left (RL), 0.4 mm in anterior–posterior (AP), and 0.6 mm in superior–inferior (SI). The uncertainty in manual measurement of the marker motion between the two datasets depends on the accuracy of marker localization on both datasets. Therefore, the overall accuracy in the measurement of the true motion of the reference marks is 0.4, 0.5, and 0.8 mm in the RL, AP, and SI directions as reported previously.²⁹ After localization, the markers were removed from the CT images by replacing the intensity values of the voxels occupied by each marker with a value randomly chosen from the intensities of the surrounding voxels. Once the voxel values were replaced, Gaussian smoothing with a kernel width of 20 voxels was applied to the intensities of the voxels inside the space in which the marker was located. This would result in a nonuniform intensity distribution among the voxels inside each marker that is similar to the surrounding local intensity distribution.²⁹

Figure 2.

Sample images of the deforming phantom (coronal and sagittal views) at inhale (left) and exhale (right) breathing states with a 30 mm differential compression between the two states.

A total of eight alignment methods were tested at six institutions. Each institution was provided with the modified inhale and exhale images from the phantom (in DICOM format) as well as the coordinates of the markers on the inhale dataset. The position of the markers on the exhale dataset was not provided to participants until after completion of the study, but a single, easily identifiable point was chosen and its coordinates on both datasets were sent to all institutions to ensure the consistency of the coordinate systems. At each institution, expert users who were algorithm developers or primary users were asked to align the inhale dataset to the exhale dataset using their technique of choice. There were no restrictions on time or preprocessing (i.e., masking or cropping) of the image sets, but prior assumptions about the nature of motion or deformation inside the foam were not allowed. For example, despite the fact that the foam was compressed in the longitudinal direction only, the registration could not assume that the motion is solely cranial-caudal. Once a satisfactory alignment was achieved, as determined by the user, the resulting deformation map was used to transform the coordinates of the markers on the inhale dataset to estimate their positions on the exhale dataset. Each institution then reported their estimated marker positions for comparison to the manually measured locations.

Registration methods

The following provides a brief overview of each registration method tested in this study, as well as references to publications that describe each technique in more detail. Table 1 summarizes this information.

Table 1.

Summary of registration methods and references.

Method	Model	References	Comments
1	Thin-plate splines	22	Cropped to foam
2	Thin-plate splines	31, 32, 33	No cropping or masking
3	B-splines	34, 35	No cropping—Masked the vertebrae
4	B-splines	36	No cropping—Masked the vertebrae
5	B-splines	30, 37	Cropped to foam
6	Demons algorithm	15, 38	No cropping or masking
7	Fluid flow	1, 39, 41	No cropping or masking
8	Free form with calculus of variations	40	No cropping or masking

1. Thin-plate splines with manual control point selection and mutual information as a similarity measure. This method is an implementation based on thin-plate splines, where control points are chosen manually on both image sets as an initial estimate of the transformation between the two geometries. The positions of the homologous points are iteratively manipulated by a Nelder–Mead simplex algorithm to maximize the mutual information between the two image sets, using thin-plate splines as an interpolant. In this study the reference image set (inhale) was automatically cropped to the lungs (foam) prior to registration, and a total of 29 control points was distributed throughout the foam. This implementation of thin-plate splines has been described and evaluated for alignment of inhale and exhale lungs previously.²²

2. Thin-plate splines with automatic control point selection. In this method, the transformation matrix that relates a point on the moving image to its correspondence in the fixed image is found using a thin-plate spline (TPS) deformable model to model the deformation of the phantom.^{31, 32} Currently, the TPS method still needs manual placement of control points and this work automates the control point selection by using the scale invariant feature transformation (SIFT) tissue feature searching.³³ Roughly 200 control points are selected based on the prominent tissue features as identified by the SIFT.

3. Multiresolution B-splines using correlation ratio as a similarity measure. This method is an original implementation of the nonuniform multilevel free-form deformation framework described by Schnabel et al. with a multiresolution extension.³⁴ For this study, a rigid transformation based on the tumor center displacement was applied as an initial step followed by a B-spline registration, with control point (knot) spacing starting at 80 mm and going down to 20 mm in three steps. The correlation ratio of the image intensities was chosen as the similarity measure.³⁵ The image pair was thresholded below a Hounsfield value of 0 and above 1000 and the vertebrae were masked out to 1000 HU. Calculation of the similarity measure did not include intensities below 0 HU where deformation was also prohibited through B-spline control point adaptation.

4. Single-resolution B-splines using sum of squared differences as a similarity measure. This is an implementation of the B-splines, previously described by Hartkens et al.³⁶ For this study, the registration was initialized by manually applying a translation and scaling in the longitudinal direction as a starting point for the B-spline-based alignment of the two image sets. This method used a multiresolution approach for the image, with voxel dimensions changing from 3 to 1.5 mm in two steps. Control points were spaced evenly at a constant 20 mm interval. The similarity measure used was the sum of squared differences between voxel intensities. This method, similar to method 3, masked the majority of the vertebrae to eliminate their signal from driving the cost function.

5. Multiresolution B-splines using mutual information. This method is another implementation of the B-splines, which has been described previously.^{30, 37} In this study, a single control point was used as a starting point for an automatic rigid registration allowing for translations and rotations only. After convergence, the initial rigid registration was used as a starting point for the multiresolution deformable registration which iteratively changed the weights of the B-splines at each control point (knot), to maximize the mutual information between the reference and the homologous image. A multiresolution approach was used for both the image and the B-spline knot spacing, with the image resolution changing from 4 voxels to 2 (voxel size of 0.78 mm×0.78 mm×1 mm) and the knot resolution starting at 16 voxels and going down to 4 voxels in two steps. The multiresolution approach helps speed up the convergence and avoids local minima. The reference dataset (inhale) was automatically cropped to the lung prior to registration.

6. “Demons” algorithm. This method is a grayscale-based fully automatic deformable image registration known as the demons algorithm and previously described.^{15, 38} This method uses the intensity information of the image sets as well as the gradient information to automatically determine the displacement field from one dataset to the other. A multiresolution approach and a symmetric force are applied to improve algorithm efficiency. In the accelerated demons algorithm an “active force” is used with an adaptively adjusted strength that is modified during the iterative process. No cropping or masking was used to separate the chest wall from the lung tissue in the registration process.

7. Fluid flow. This is an intensity-based technique that makes use of fluid flow models. In this method the transformation is found by minimizing an energy term which is based on the squared difference of the image intensities and a regularization term. The regularization term is derived from compressible fluid flow equations as described previously.^{1, 39} The registration is driven by a force applied to the fluid at each point, the magnitude and direction of which are determined based on the difference in the intensities of the two images.

8. Free-form deformation with calculus of variations. This is a fully automatic intensity-based free-form deformation with a multiresolution approach.⁴⁰ In this method, the similarity and smoothness criteria are combined into one energy function, which is minimized in the registration process. A set of partial differential equations are used to represent the minimization problem, and these equations are iteratively solved using a Gauss–Seidel finite difference scheme.

It should be noted that method 8 was developed and evaluated by a commercial entity. No special treatment was given to this organization for the study, and the results of this specific study should not be interpreted in establishing the superiority or lack thereof for one alignment method over another.

Data analysis

Global evaluation of registration

The error in image registration was defined as the difference between the manually measured exhale marker position and the estimated position based on the deformation map from each registration technique. This difference was measured in three dimensions, right–left (d_RL), anterior–posterior (d_AP), superior–inferior (d_SI), and the 3D vector distance (d) between the true and estimated marker positions was calculated from these components.

The global accuracy of each registration method was evaluated by calculating the mean $\left({\overline{d}}_k\right)$ and standard deviation (σ_k) of the 3D error (d) over all marker positions for each registration technique (k). Although metrics like the mean and the standard deviation of 3D error can provide a basic understanding of the behavior of each image registration technique, they do not provide any insight into the distribution of the error in different regions, since similar mean and standard deviation values can result from significantly different distributions in data. Therefore, in this study the frequency distribution of the 3D error was also evaluated using a differential histogram with 2 mm bins, where the percentage of the marker location errors within each bin was calculated. It should be emphasized that no spatial information about the error distribution can be taken from the histogram, and only information on the magnitude distribution is provided.

Regional evaluation of registration

The behavior of different algorithms in regions with different characteristics was evaluated. The mean and standard deviation of the 3D error for each marker across all registration techniques were calculated. Markers that show small mean and small standard deviation correspond to regions with intensity and deformation characteristics where the majority of registration methods perform well. Markers that show a large mean error and a relatively small standard deviation indicate regions where most techniques cannot predict the deformation well.

Comparison of registration methods

This study was not designed to provide a direct comparison of different image registration techniques. Various alignment methods have been optimized to take advantage of different features and∕or expected resolutions of shape change for real patient data, and employ vastly different goodness-of-fit metrics as well as search schemes and methods of describing local shape change. The intensity distribution and deformation characteristics of the phantom can be biased toward certain types of algorithms compared to others, and a direct comparison between different registration methods is not possible. The reported results were randomized to completely eliminate any potential inferences made regarding the relative or absolute accuracy of different registration techniques.

One subset of methodologies applied, however, is worthy of some intercomparison. In this study, three groups used B-splines to characterize deformation. An evaluation of these methods as a group highlights some of the complexities involved in assessing the performance of an alignment technique simply by the mechanism for describing deformation.

Comparison of registration accuracy in the phantom to a sample lung patient

In order to estimate whether the magnitude of variations seen in the phantom study are on par with those in clinical image alignment scenarios, we evaluated the accuracy of alignment in breath-held CT scans of a patient at inhale and exhale states, using manually identified landmarks at visible bifurcations of vessels and bronchioles as true locations.²² Deformable alignment was performed using our in-house B-spline-based method with the same parameter settings (knot spacing and image resolution) as those used for the phantom alignment.

RESULTS

All deformable registration methods performed generally well, with an average error $\left({\overline{d}}_k\right)$ ranging from 1.5 to 3.9 mm depending on the registration technique. These values are on the same order as accuracies reported in the literature.^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25} The maximum error, however, showed a wider range, from 5.1 to 15.4 mm, indicating nonuniformity in the results of deformable image registration and the potential for large regional inaccuracy in alignment in spite of overall acceptable accuracy. Table 2 summarizes the results of the different methods, showing the maximum component errors in three dimensions ($d_{\mathrm{RL}}^{\max }$, $d_{\mathrm{AP}}^{\max }$, $d_{\mathrm{SI}}^{\max }$) as well as the mean $\left({\overline{d}}_k\right)$, standard deviation (σ_k), and the maximum 3D error $\left(d_k^{\max }\right)$ for each registration technique. The results are randomized and each registration method is identified by a different letter from A to H in the following tables and graphs (Table 2, Figs. 345).

Table 2.

Maximum component errors in RL, AP, and SI directions, as well as the mean, standard deviation, and maximum 3D vector distance for each registration method, shown in random order.

Method (k)	Component errors (mm)			3D vector error (mm)
	$d_{\mathrm{RL}}^{\max }$1	$d_{\mathrm{AP}}^{\max }$2	$d_{\mathrm{SI}}^{\max }$3	${\overline{d}}_k$4	σk5	$d_k^{\max }$6
A	7.7	7.3	9.9	3.6	2.7	10.1
B	1.7	2.7	5.1	1.8	1.1	5.1
C	4.2	1.9	6.7	1.8	1.6	8.1
D	1.5	1.5	6.2	1.5	1.3	6.4
E	1.3	1.0	10.3	2.8	2.3	10.3
F	2.2	3.6	5.1	1.7	1.1	5.5
G	4.5	2.7	4.1	2.3	1.1	6.0
H	4.0	7.3	15.2	3.9	3.0	15.4

^aAbsolute maximum component error in RL direction.

^bAbsolute maximum component error in AP direction.

^cAbsolute maximum component error in SI direction.

^dMean 3D error.

^eStandard deviation 3D error.

^fMaximum 3D error.

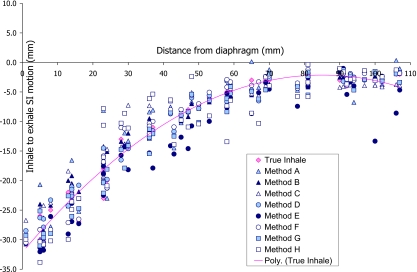
Figure 3.

Inhale to exhale SI motion of markers under 30 mm compression as estimated by various registration methods, shown as a function of the marker’s distance to diaphragm. The true motion of the markers from inhale to exhale is also shown (diamond marks) with a second degree polynomial fitted to the data to help with visualization of the results.

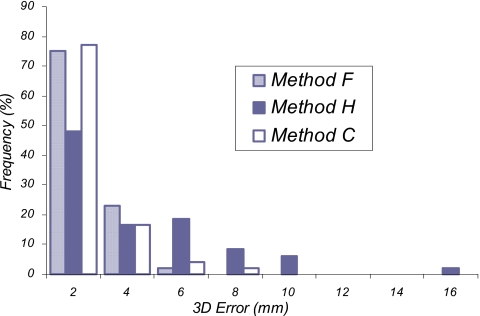
Figure 4.

Frequency distribution of the 3D error for each image registration method is displayed, with the frequency of markers within each bin shown as the percentage of the total markers.

Figure 5.

Comparison of 3D error distribution between different B-spline-based registration methods.

The dominant error was in the SI direction (direction of foam compression) for most markers, as expected. However, errors as large as 8 mm in the RL and 7 mm in the AP directions were observed for some registration techniques. Figure 3 shows the SI motion of each marker from inhale to exhale (i.e., under 30 mm differential compression), plotted against the marker’s distance to the diaphragm. The true motion of the markers is also plotted with a line (second degree polynomial) through the data to help with visualization of the results. It can be seen that, while some methods perform very uniformly throughout the phantom, others do well in some regions while showing large errors in other areas. Therefore, it is clear that the mean and maximum 3D errors shown in Table 2 are useful but not sufficient metrics for comparison or evaluation of registration accuracy alone. To gain a better understanding of the performance of each method, histograms of the frequency distribution of registration error are plotted in Fig. 4. These histograms show the percentage of the markers (total of 48 markers) that have errors within the limits of each bin.

The authors also compared the results from three different implementations of B-splines tested in this study. As seen in Fig. 5, there is a significant difference in the frequency distribution of the 3D error among these three methods. Methods C and F both used a multiresolution approach for the image and knot spacing, while method H used a multiresolution approach for the image but a single-resolution knot spacing. The three methods also used different similarity measures in the optimization process as well as differences in the users and the user specified settings. Although no specific conclusion should be made about which method is better, it would appear from these findings that a multiresolution knot spacing can potentially result in better registration accuracy.

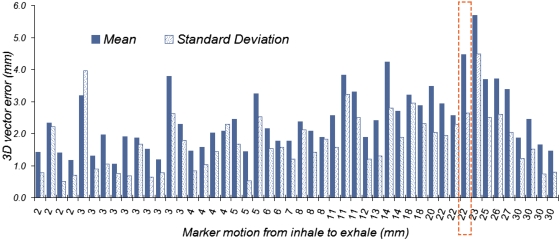
The mean and standard deviation of the error was calculated for each marker over all registration methods, and plotted against the marker’s motion from inhale to exhale in Fig. 6. Markers with small mean and small standard deviation error correspond to regions inside the phantom where most registration methods perform well. On the other hand, a large mean with a relatively small standard deviation indicates a region in the foam where most registration techniques fail. One example is the marker shown with a dashed line around it (Fig. 6), with a large mean and a smaller standard deviation. This marker falls in a region with relatively low intensity distribution, located next to a high intensity region with a large change in intensity between inhale and exhale but without much deformation, as shown in Fig. 7. Figure 6 also shows that a slight increase in the average error is observed as the motion in the markers increases from inhale to exhale, however, there are some markers with very small motion between the two deformation states that show large errors.

Figure 6.

Mean and standard deviation of the 3D error for each marker calculated over all registration methods. The horizontal axis displays each marker’s motion from inhale to exhale in millimeters. The marker for which the results are shown with a dashed line around it corresponds to an example with a large mean and a small standard deviation. The image of this marker is shown in Fig. 7.

Figure 7.

Axial image of the region inside the foam at inhale (left) and exhale (right) where most registration methods performed poorly.

In comparing the sample patient registration accuracy to the phantom results, the authors saw no significant changes between the mean or maximum error in the SI direction, with a mean of 0.2 and 0.5 mm, and maximum of 3.1 and 3.3 mm for the phantom and the sample patient, respectively (Table 3). However, the patient data showed larger registration errors in the AP and RL directions, and therefore the 3D vector error was also larger for the sample patient compared to the phantom. This is expected considering the minimal motion and deformation of the phantom in the AP and RL directions.

Table 3.

Comparison of registration results for the phantom and a sample patient dataset for our in-house B-spline-based method, using the same parameter settings. The results for error in registration of the inhale state to other deformation states of the phantom (1 and 2 cm compressions) are also shown.¹

		RL (mm)	AP (mm)	SI (mm)	3D (mm)
Sample patient	$\overline{d}$	−1.0	−0.8	−0.5	2.2
	σ	1.2	2.1	1.8	2.4
	dmax	−3.3	−5.1	−3.3	6.9
Phantom 3 cm diaphragm compression	$\overline{d}$	0.0	−0.1	−0.2	0.8
	σ	0.4	0.4	0.8	0.6
	dmax	−1.7	−1.3	−3.1	3.1
Phantom 2 cm diaphragm compression	$\overline{d}$	−0.2	−0.2	−0.2	0.7
	σ	0.3	0.4	0.6	0.4
	dmax	−1.5	−1.4	−2.3	2.3
Phantom 1 cm diaphragm compression	$\overline{d}$	−0.3	−0.2	−0.1	0.7
	σ	0.3	0.3	0.7	0.5
	dmax	−1.1	−1.0	−2.8	2.8

^a$\overline{d}$ is mean error; σ is standard deviation of error; and d^max is maximum error in estimation of marker position.

The test was also performed on two additional deformation states of the phantom (1 and 2 cm diaphragm compressions) for the same parameter settings. Similar registration accuracies were obtained for these deformation states of the phantom, indicating that the registration accuracies reported here are not affected by the deformation state of the phantom.

Of note, the phantom study actually identified a small error in postprocessing of deformation results for our in-house alignment method. The multi-institutional analysis reflects the effect of this variation. However, the further analysis of intermediate phantom states as well as on anatomic images is based on the corrected process (Table 3).

DISCUSSION

In this study a blind test of accuracy of different image registration methods was performed using a simple deformable lung phantom. The purpose was to objectively evaluate the accuracy of each registration technique and identify potential errors that may be overlooked by other validation methods. The large number of markers distributed throughout the phantom allowed for a better understanding of the variations in the registration error in all regions compared to other methods that use a few bifurcations. Our results showed mean and standard deviation errors that were on the same order as what has been reported by other validation studies. However, maximum errors as high as 15 mm were observed, suggesting that the subvoxel accuracies reported based on evaluation of a few bifurcations may not be adequate to represent the overall accuracy of an algorithm. Currently, there is no consensus on what to report for the accuracy of the registration. This study suggests that a distribution of residual error could be valuable in evaluating the performance of an algorithm.

Although the phantom was rather simplistic, it had certain properties observed in the lungs such as density change, a nondeforming moving object within a deforming geometry, and some sliding against the chest wall. However, the microstructure represented in the phantom by the differential deposition of iodine should not be considered equivalent to that manifest by the vascular architecture of the lungs. This difference could potentially bias the performance of some registration methods over others. As a result, a direct comparison of registration accuracy of different techniques was not attempted. Some of the participating investigators stated that their registration techniques would have benefited from more substructures that would make the foam more comparable to real lungs. Their main concern was that certain parameter settings that they had optimized for registration of lungs would have to be perturbed to get the best results for the phantom. However, they all felt that the study was fair for the conclusions drawn. One thing that should be considered here is that the coarse structures in the lung (vessels and bifurcations) are not homogeneous, and if the registration technique is dependent on these substructures (i.e., these structures are the driving forces of the registration), then the accuracy that is measured at these points cannot be propagated to other regions inside the lungs (e.g., across a tumor or in regions with other structures at different scales such as the mediastinum and bronchi). Such a dependence could thus be a source of bias, and not be reflected in accuracy reports that similarly depend on high spatial frequency content of image signals.

This also suggests that a difference in the registration accuracy of real lung images and the phantom images is expected and the structural detail in the lung may result in better registration overall, even though the test of the sample clinical data shows errors on the same order as the phantom at least in the SI direction. However, we speculate that the registration error reported for real lungs based on measurement of bifurcations and anatomical landmarks would underestimate the true error in alignment of the majority of other points in the lung. Therefore, evaluation of the error distribution results presented here would be a useful tool in understanding the limits in accuracy of various deformable alignment tools.

One important observation made in this study was that different implementations, different users, or different parameter settings of the same type of registration can result in different accuracies, suggesting a need for careful assessment of each implementation as well as standards on user-defined parameters or automation of the registration process. For example, the possibility exists for the algorithms to select and be sensitive to a specific range of intensities, thus yielding different results as these ranges are varied. Future studies will consider guidelines for modifying these ranges and studying sensitivity, as opposed to the optimal application of algorithms by their developers from the current trial design.

Another significant factor in registration accuracy is time and as a general rule a compromise between time and accuracy has to be made in clinical settings depending on the application. In this study, the reported registration times ranged from 2 min to 37 h, however, no significant correlation between the registration time and accuracy was observed mainly due to variations in computer resources.

CONCLUSION

In this study the accuracy of different registration methods was evaluated for a phantom with characteristics similar to lungs. The results indicated a distribution in the registration error in different regions, which may be overlooked in the standard evaluation techniques that make use of a few anatomical landmarks. Variations in the performance of different implementations, users, and settings of the same type of registration were also observed in this study, all of which suggest the need for careful assessment of potential sources of error in any type of deformable alignment. These results also show that generalization of the reported accuracies should be done very carefully. Further improvements to the design of the phantom would be necessary for a more comprehensive evaluation and comparison of the different registration techniques.