Abstract
The physical factors that govern 2D and 3D imaging performance may be understood from quantitative analysis of the spatial-frequency-dependent signal and noise transfer characteristics [e.g., modulation transfer function (MTF), noise-power spectrum (NPS), detective quantum efficiency (DQE), and noise-equivalent quanta (NEQ)] along with a task-based assessment of performance (e.g., detectability index). This paper advances a theoretical framework based on cascaded systems analysis for calculation of such metrics in cone-beam CT (CBCT). The model considers the 2D projection NPS propagated through a series of reconstruction stages to yield the 3D NPS and allows quantitative investigation of tradeoffs in image quality associated with acquisition and reconstruction techniques. While the mathematical process of 3D image reconstruction is deterministic, it is shown that the process is irreversible, the associated reconstruction parameters significantly affect the 3D DQE and NEQ, and system optimization should consider the full 3D imaging chain. Factors considered in the cascade include: system geometry; number of projection views; logarithmic scaling; ramp, apodization, and interpolation filters; 3D back-projection; and 3D sampling (noise aliasing). The model is validated in comparison to experiment across a broad range of dose, reconstruction filters, and voxel sizes, and the effects of 3D noise correlation on detectability are explored. The work presents a model for the 3D NPS, DQE, and NEQ of CBCT that reduces to conventional descriptions of axial CT as a special case and provides a fairly general framework that can be applied to the design and optimization of CBCT systems for various applications.
Keywords: 3D imaging, noise-power spectrum, NPS, detective quantum efficiency, DQE, noise-equivalent quanta, NEQ, computed tomography, cone-beam CT, flat-panel detector, imaging performance, imaging task
INTRODUCTION
Cone-beam computed tomography (CBCT) with flat-panel detectors (FPDs) is finding use in a broad range of applications, including preclinical imaging (e.g., small animal imaging), screening and diagnosis (e.g., breast imaging), and image-guided procedures (e.g., surgery and radiotherapy). The technology exhibits submillimeter spatial resolution and soft-tissue visibility across a large volume of reconstruction obtained from a single rotation of the source and detector about the subject. While artifacts (e.g., x-ray scatter artifacts, ring artifacts, etc.) remain a significant challenge to image quality, the fundamental limits to CBCT imaging performance lie in the image noise and the correlations therein.
A prevalent approach to describing imaging performance involves Fourier metrics, such as the modulation transfer function (MTF), noise-power spectrum (NPS), noise-equivalent quanta (NEQ), and detective quantum efficiency (DQE). These metrics offer widespread, practical means of system characterization, and the methods of experimental measurement of each are becoming standardized. Moreover, they provide a basis for evaluating performance with respect to an intended task, an essential aspect of image quality as discussed in ICRU Report No. 54.1 Theoretical analysis of these metrics has proven important in understanding and optimizing imaging performance in many areas of 2D digital x-ray imaging,2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 particularly in the early stages of technology development. Such an understanding of the factors governing fundamental imaging performance should prove similarly valuable in the development of CBCT.
One of the earliest treatments of CT noise was given by Barrett et al.,13 yielding now familiar relationships between voxel noise and dose, slice thickness, etc. The spatial frequency characteristics of the noise were addressed by Riederer, Pelc, and Chesler,14 who described the axial CT NPS in terms of the reconstruction filter and a weighting factor (1∕f) associated with back-projection, noting that the NPS for each projection corresponds to a delta function (“spoke”) through the frequency domain at a corresponding angle. Hanson15 further described the effect on detectability and defined a scalar NEQ in terms of the number of photons contributing to the 3D image per unit length along the detector, which could be determined from the low-frequency slope of the axial NPS. In the same year, Wagner16 related these properties to the observer signal-to-noise ratio (SNR) in terms of an optimal matched filter in the presence of colored noise. Faulkner and Moores17 described the effect of discrete detector elements and the reconstruction matrix. Kijewski and Judy18 described the effect of a discrete number of projections and showed that the zero-frequency noise in axial CT is entirely attributable to noise aliasing in the reconstruction domain, demonstrating that the noise characteristics of a CT reconstruction are not trivially related to the projection noise alone. Rather, the entire imaging chain must be considered to understand the noise in CT reconstructions.
With the development of CBCT using FPDs, many of these early findings hold, but some require reexamination in the context of fully 3D imaging. In the sections below, a theoretical model for the 3D NPS of FPD-based filtered back-projection CBCT is presented and validated in comparison to measurements. The results are related to classical results for axial CT where possible (e.g., the voxel noise as described by Barrett et al.13 and aliasing as described by Kijewski and Judy18). The 3D NEQ and DQE are defined in terms that make explicit the effect of various nonideal characteristics of FPDs—e.g., quantum detection efficiency, Swank factor, blur, and electronics noise. A number of nontrivial factors affecting the 3D NPS are exposed—e.g., the effects of 3D noise aliasing, 2D pixel binning, and 3D voxel averaging. Finally, the 3D metrics are applied in evaluation of the detectability index to describe the influence of acquisition and reconstruction parameters on task performance. This work builds on a series of related papers reported in developmental stages and for specific applications in conference proceedings.19, 20, 21, 22, 23 This paper details the mathematical rigor of the model, presents the approach as a general framework, and includes aspects of CBCT imaging not previously considered (such as 2D and 3D binning).
THEORETICAL ANALYSIS
Background: Cascaded linear systems analysis
The basic aspects of cascaded linear systems analysis have been discussed in detail in previous work24, 25, 26 as has its application in a variety of 2D imaging applications.2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 The basic concepts and derivation of the 2D projection NPS are briefly summarized below.
Cascaded systems analysis models the imaging chain as a series of discrete stages (gain, stochastic spreading, deterministic spreading, or sampling) as summarized in Table 1. The mean signal and NPS [Si(u,v)] at stage i are determined from that at stage i−1 by the mean gain , gain variance , and∕or MTF [Ti(u,v)2].
Table 1.
Signal and noise transfer relations for the various types of stages considered in cascaded systems analysis.
| Stage | Signal | Noise |
|---|---|---|
| Gain | ||
| Stochastic spreading | ||
| Deterministic spreading | ||
| Sampling | Si(fu,fv)=Si−1(fu,fv)**auavIII(fuau,fvav) |
Assumptions include linearity, shift invariance, and stationarity of the first-and second-order statistics. The degree to which these assumptions hold have been discussed elsewhere and are subjects of ongoing research.27, 28, 29, 30 For example, Cunningham28 showed that if a system exhibits discrete periodic invariance (cyclostationarity), as with a sampled detector, familiar image quality metrics are applicable. Albert and Maidment29 showed that shift-variant properties at the subpixel scale are small, particularly for systems employing “alias-free” detectors for which presampling blur shares signal between multiple pixels (e.g., as in indirect-detection FPDs). Other issues potentially relevant in CBCT—but neglected in the current analysis—include nonuniformities in detector response, heel effect, oblique x-ray incidence,31 as well as x-ray scatter,32 geometric misalignment,30 and variation in projection ray density across the detector.
Image formation in indirect-detection FPDs has been described as a seven-stage process2, 3 including: (0) incident x-ray photons; (1) interaction of x-rays with the converter; (2) production of secondary quanta; (3) spread of optical quanta within the detector; (4) coupling of optical photons to the photodiode and conversion to electron-hole pairs; (5) integration of optical photons by the pixel aperture; (6) sampling of the image at discrete pixel locations; and (7) readout with additive electronics noise. The resulting 2D projection image NPS is:
| (1) |
where notation is consistent with that of previous work,2, 3 and each term is defined in Table 2. Factors related to K-fluorescence and conversion noise in stage 2 are as described by Yao,26 with PK [equal to in the case of no K-fluorescence] as in Richard et al.33 The term III6 [equal to auIII(aufu)avIII(avfv), in terms of the sampling function III(x)] is a Fourier domain comb function (a sum of equally spaced, unit area delta functions) associated with pixel sampling.
Table 2.
Summary of terms used in theoretical description of NPS. Nominal values correspond to a typical CBCT image acquisition [120 kVp; 2.5 mm Al inherent filtration +5.1 mm Cu added filtration; 2 mAs per projection (14.8 mGy air kerma per projection at the detector); 320 projections; 360° circular orbit with uniform projection weighting; SAD=93.5 cm; SDD=144.4 cm].
| Term | Definition | Nominal value |
|---|---|---|
| Tj | Transfer function for stage j | — |
| Si | Noise-power spectrum at stage j | — |
| Mean fluence incident on the detector for a given projection | 3.24×104 mm−2 | |
| Mean fraction of incident photons interacting with the detector | 0.48 | |
| Mean number of optical photons produced per incident photon, including k-shell interactions | 2850 | |
| Pk | Transfer function associated with k-fluorescence | — |
| T3 | Transfer function due to spread of optical photons | — |
| Coupling efficiency of photodiode | 0.6 | |
| apd | Width of (square) photodiode | 0.32 mm |
| T5 | Transfer function due to photodiode aperture | — |
| ai | Detector sampling interval in direction i | 0.4 mm |
| III | Sampling function (comb, or Shaw function) | — |
| σadd | Additive electronics noise | 3975 e∕pixel |
| Ai | Width of binning aperture (in pixels) in direction i | 1 |
| Bi | Downsampling factor in direction i | 1 |
| T8 | Transfer function due to 2D binning aperture | — |
| T10 | Ramp filter | — |
| T11 | Apodization filter | — |
| hwin | Smoothing parameter | 0.5 |
| T12 | Interpolation filter | — |
| m | Number of projections acquired across circular orbit | 320 |
| M | Magnification factor, SDD∕SAD | 1.54 |
| T13 | Transfer function associated with back-projection | — |
| Θ13 | Transfer function associated with back-projection of noise | — |
| bi | 3D sampling interval in direction i | 0.259 mm |
Cascaded systems model for flat-panel cone-beam CT
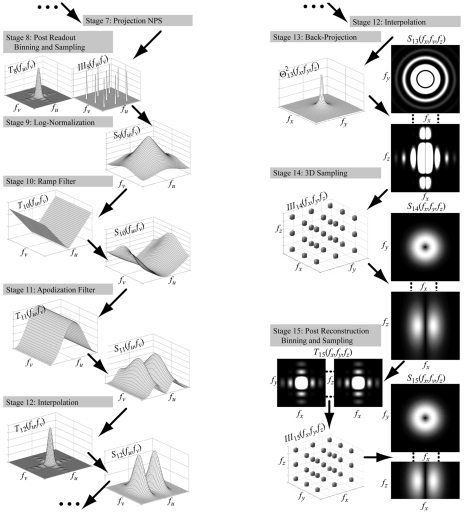
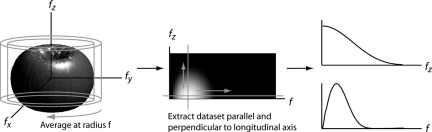
The cascaded systems model is extended to 3D reconstruction through eight additional stages (stages 8-15) illustrated in Fig. 1. Notation for geometry is summarized in Table 3.
Figure 1.
Illustration of the cascaded systems model for CBCT reconstruction. Stage 7 is the output of the basic 2D projection cascade. Stages 8–15 correspond to processes of 3D reconstruction. Transfer functions are illustrated at left, and noise-power spectra at right. Adapted from Ref. 23.
Table 3.
Summary of notation for 2D and 3D geometric coordinates.
| Coordinates | Description |
|---|---|
| (u,v) | Column and row coordinates of 2D projection image |
| (fu,fv) | Spatial frequency coordinates corresponding to (u,v) |
| (x,y,z) | Spatial coordinates of 3D image reconstruction. (Note: u and v axes are parallel to x and z axes, respectively) |
| (fx,fy,fz) | Spatial frequency coordinates (Cartesian) corresponding to (x,y,z) |
| f | Cylindrical spatial frequency coordinate |
| θi | Projection view angle of the ith projection with respect to the x axis |
| (xi,yi,z) | 3D image reconstruction coordinates rotated by θi such that yi is parallel to the ith projection view |
| (fxi,fyi,fz) | Spatial frequency coordinates rotated by θi as above |
Stage 8: Postreadout (2D) binning and sampling
Detector elements may be arbitrarily binned and∕or downsampled according to the desired resolution, noise, and reconstruction time for the 3D image. Binning is described by a 2D rectangular aperture (a sinc function in the Fourier domain) of size Au and Av along rows and columns, respectively (for example Au=Av=2 for 2×2 binning). The image is subsequently sampled at interval Bu and Bv, giving discrete data at the output of stage 8. The process is described as follows:
| (2a) |
| (2b) |
| (2c) |
Note that if Au=Av=Bu=Bv=1, then S8=S7 (no detector binning). The process of binning and up or downsampling can be included between any two stages in the reconstruction, with nontrivial effect on NPS.
Stage 9: Log normalization
Detector signal is converted to attenuation by dividing the image by the mean flood-field signal, followed by the negative logarithm (Beer-Lambert law). Potential nonlinearities associated with dark-flood correction were not considered in this model. Assuming small image fluctuations (i.e., low-contrast or noise-only data) the logarithm imparts a factor of 1∕mean upon the noise. This assumption is valid when the signal (and noise) fall within a linear and symmetric range of the logarithm function and when the mean signal is constant over the field of view (such that 1∕mean is constant). As discussed in an appendix by Barrett et al.,13 this assumption is valid for typical radiological applications. The NPS is, therefore,
| (3a) |
where the mean signal (in air) is:
| (3b) |
The result is simply the normalized NPS that is typically reported for 2D projection applications (inversely proportional to exposure). The application of a logarithm demands that signal and noise be dimensionless at this stage, giving an NPS with units of mm2.
Stage 10: Ramp filter
The ramp filter:
| (4a) |
is the ideal reconstruction filter for a scan with an infinite number of projections. The transfer function associated with this stage carries units of (mm−1) and gives the signal the appropriate units of linear attenuation while making the NPS dimensionless. Typical numerical implementation includes a small nonzero value at zero frequency, which avoids nulling the DC value. The NPS is transferred deterministically:
| (4b) |
Stage 11: Apodization filter
To reduce high-frequency noise amplified by the ramp filter, an apodization (smoothing) filter is often applied. For example, a Hamming window:
| (5a) |
provides adjustable smoothing through variation of the parameter hwin (with 0.5⩽hwin⩽1). Such a digital filter depends on the sampling distance (auBu) but not the binning aperture Au. The NPS is transferred as a deterministic convolution:
| (5b) |
Stage 12: Interpolation of the filtered projection
In voxel-driven reconstruction, the projection signal should be known at arbitrary locations on the detector that may not correspond to the pixel centers. Typically, interpolation is used to approximate a continuous image. Bilinear interpolation is common, with the associated transfer function given by the Fourier transform of a unit area triangle function with width equal to twice the sampling distance:
| (6a) |
Nearest-neighbor interpolation (generally a poorer choice23) is described by the Fourier transform of a rect function with width equal to the sampling distance:
| (6b) |
The NPS at this stage is no longer periodic, attenuated at frequencies beyond the Nyquist region by T12 squared:
| (6c) |
Stage 13: 3D back-projection
Three factors need to be accounted for in modeling 3D back-projection. The first is geometric magnification. Even under the parallel beam approximation (invoked below), magnification must be incorporated to account for the change in scale between detector pixel size and 3D image voxel size. The scaling property of the Fourier transform implies:
| (7) |
The Nyquist frequency, thus, increases by the magnification factor.
The second is the back-projection process itself, which is a linear operation under the assumption of a parallel beam. Fan-to-parallel rebinning and spatially varying weights associated with a divergent beam will be considered in future work. Back-projection, thus, amounts to a smearing of the 2D image along a given angle (and along a given length, denoted d) through the 3D field of view. The length d corresponds to the extent of the 3D reconstruction field of view, which can range from some arbitrarily small length up to the SDD (as shown below, d cancels out of the NPS, and its exact value is unimportant.). The signal and noise transfer can be modeled as a convolution with a rect function of width d. Writing in terms of the 3D reconstruction coordinates, for the ith projection we have:
| (8a) |
The NPS is transferred deterministically and scaled by 1∕d, since it is associated with the Fourier transform of the average autocorrelation function (i.e., the volume averaged over in stage 13 is related to the area in stage 12 by a factor of d):
| (8b) |
While this process does not change the units of the signal or noise, the signal is spread across another dimension and its Fourier descriptions, therefore, gain units of mm (due to the units of the differential in the Fourier integral). Note that for large d,
| (8c) |
and
| (8d) |
such that the projection NPS is simply superimposed along a given angle through the 3D Fourier domain, as implied by the Fourier slice theorem. This behavior has been described as “spokes”14, 18 or “vanes,”21 and has been interpreted to mean that the presampling 3D NPS is continuous in the radial and longitudinal directions, but discrete in the angular coordinate. While this is a useful description, for a finite value of d, the 3D presampling NPS (S13) is continuous and technically not discrete.
The last factor is superposition of the back-projected signal for each projection view, where signal and noise behavior fundamentally diverge. The signal transfer can be written simply as a superposition:
| (9a) |
where m is the number of projections, and M is the magnification factor. As shown in Appendix A, the transfer function is equal to:
| (9b) |
which exactly cancels out (up to the 2D Nyquist frequency) with the ramp filter (T10=∣fu∣=f∕M). This gives a properly behaved MTF that is 1 at zero frequency and smoothly varying at higher frequencies.
Assuming that each projection is statistically independent (see the Discussion section for possible incorporation of image lag effects), the 3D NPS is given by superposition of the individual back-projected NPS:
| (9c) |
As shown in Appendix A, this may be simplified to:
| (9d) |
At this stage, the usual intuitive process of noise simply being blurred by the transfer function (i.e., the NPS attenuated by T2) does not apply. However, it is possible to associate a “transfer function” for noise only at this stage:
| (9e) |
The NPS is cylindrically symmetric, continuous, and not periodic (i.e., extends to infinite spatial frequencies, attenuated primarily by T12). Because digital filters are periodic about the sampling frequency, whereas is not, the 1∕f term resulting from superposition cancels out at frequencies up to the 2D Nyquist frequency, an affect that can be observed experimentally in the “corners” of the NPS (see, for example, Fig. 7).
Figure 7.
Experimental and theoretical 3D NPS evaluated for various reconstruction filters: (a) axial, (b) longitudinal profiles of the 3D NPS.
Stage 14: Sampling of the 3D voxel matrix
Sampling at discrete locations defined by the 3D voxel matrix corresponds to convolution of the NPS with a 3D comb function. Such alters the spatial frequency content of the 3D NPS through aliasing:
| (10a) |
| (10b) |
In particular, noise power from above the Nyquist region is aliased (added) at lower frequencies. As noted by Kijewski and Judy,18 the zero-frequency noise is attributable entirely to aliasing.
Stage 15: Postreconstruction (3D) binning and sampling
Postreconstruction binning and sampling of the 3D image (e.g., slice averaging) can be described in a manner similar to that described for stage 8:
| (11a) |
| (11b) |
| (11c) |
where (Ax,Ay,Az) is the aperture size (in voxels) in the (x,y,z) directions, and (Bx,By,Bz) is the associated resampling. For example, averaging of adjacent slices corresponds to (Ax,Ay,Az)=(Bx,By,Bz)=(1,1,2). Again, if Ax=Ay=Az=Bx=By=Bz=1, then S15=S14, which corresponds to reconstruction at the “natural” voxel size (the detector pixel size divided by the geometric magnification).
Analytic form of the 3D NPS
The resulting 3D image NPS can be written as (dropping the arguments of functions for conciseness):
| (12a) |
where the ∼ over the f indicates periodicity about the 2D Nyquist frequency—i.e., T10 is implemented as a digital filter and is, therefore, periodic, whereas corresponds to a redistribution (smearing) of quanta and is not. Therefore,
| (12b) |
Because the terms f and T10 depend only on the frequencies in the x−y direction, and not the z direction, the 3D NPS is asymmetric. These features impart a bandpass noise characteristic in the axial direction, whereas noise in the longitudinal direction is low pass as governed by the interpolation kernel and detector MTF. This asymmetry is fundamental to filtered back-projection and is unrelated to the cone-beam artifact. The cylindrical symmetry of the presampling NPS (S13) is broken by aliased noise arising from 3D sampling. Furthermore, the process is irreversible, with sampling occurring at up to four points in the imaging chain [sampling on the detector (optional) 2D binning and resampling of detector data, sampling in the reconstruction matrix, and (optional) 3D binning and resampling of the reconstruction]. Each imparts irreversible noise aliasing effects.
The result can be written in a simplified form under some assumptions. For example, without 2D or 3D binning and resampling (S7=S8, S14=S15), and taking noise above the detector Nyquist frequency (noise in the “corners” of the NPS) to be negligible (i.e., ), the 3D NPS reduces to:
| (12c) |
which is simply the normalized projection NPS modulated by the reconstruction filters (T11 and T12) and convolved with the 3D sampling function (III15). The scale factor relates to the radial projection density (m projections over π radians, where density decreases as 1∕f) and transformation to the reconstruction coordinates (1∕M2). While many of the qualitative features of the 3D NPS are evident in this simple product of transfer functions with the projection NPS, the irreversible sampling step (with associated 3D noise aliasing) is intrinsic to the process.
The units of the 3D NPS are signal squared times length cubed, where signal may be measured in terms of linear attenuation coefficient (mm−1 or cm−1) or Hounsfield units (HU). Taking the former, the units are, therefore [(mm−1)2(mm3)], or simply [mm], which we denote as [μ2 mm3] to avoid possible confusion associated with the cancellation of terms.
Variance
The variance in voxel values is given by the integral over the 3D NPS within the Nyquist region. As shown in Appendix B, a result consistent with the well known result of Barrett13 is obtained:
| (13a) |
where the last equation is cast in a familiar form in terms of the natural voxel size. The bandwidth integral, Kxyz is defined (analogous to the “IBWI” of Wagner et al.16) as:
| (13b) |
The key assumptions in obtaining the simple, closed form include no binning or downsampling and a constant detector DQE (an assumption that must be applied carefully, particularly in low-dose applications where electronic noise is not negligible). One can see that variance is inversely proportional to x-ray fluence, number of projections, and detector DQE. In addition, it is proportional to the 3D bandwidth integral (i.e., integrals over the MTF, reconstruction filters, etc.). The inverse dependence of voxel variance on maxyaz is due to the total fluence through a given voxel, and the additional two powers of axy are due to the noise amplifying ramp filter. Finally, while not evident in the form of Eq. 13b shown above, the variance depends on the square of the magnification, an important point for considering system geometry. The familiar rule of thumb (i.e., variance inversely proportional to x−y voxel size cubed and slice thickness) must be interpreted carefully. In fact, the volume can be reconstructed at any voxel size and slice thickness (keeping Ax=Ay=Az=1, but choosing Bi≠1) without changing the variance. Postreadout (2D) binning and downsampling however (i.e., Au=Bu≠1, Av=Bv≠1), follows closely with the rule of thumb, as shown in Sec. 3E.
The 3D DQE and NEQ
In projection radiography, the DQE and NEQ can be interpreted in several equivalent ways (i.e., the conceptual, descriptive, stochastic, and predictive definitions, as posed by Cunningham34). In CBCT, they cannot be interpreted both as a signal to noise ratio, and as a description of the departure from an ideal detector. This is in part due to the logarithm stage, which complicates the definition of SNR, and in part to the back-projection stage where signal and noise propagation are decoupled. An appropriate definition is given by Cunningham’s “stochastic” form, where the NEQ describes the number of photons at each spatial frequency for which an ideal detector would produce the same NPS, and the DQE describes this value as a fraction of incident photons. As such, the NEQ is given by:
| (14a) |
where the denominator is the 3D NPS (either calculated as S15 or measured from 3D images, below). The NEQ is, therefore, proportional to m and (i.e., the total incident fluence). From the ratio of NPS, we see that the NEQ is also proportional to and the Swank factor (i.e., the zero-frequency detector DQE)
| (14b) |
This provides a basic form for the 3D NEQ, with units of [photons∕mm2], which should be contrasted to [photons∕mm], as discussed for a linear detector and 2D axial tomography.15 Note that Eq. 14b implies that the NPS can be written (dropping functional dependence for the moment):
| (15a) |
which has the same form as proposed by Hanson.15 Following Hanson’s reasoning regarding the low-frequency behavior [i.e., in the limits Ti→1 and NEQ→const=NEQ(0)], we obtain the familiar rule that the slope of low-frequency NPS is inversely proportional to the zero-frequency NEQ:
| (15b) |
The DQE can be similarly written as:
| (16) |
which provides a basic form for the 3D DQE. As familiar, DQE is dimensionless, has a maximum of 1, varies with and Swank factor, and depends on exposure only to the (typically small) extent that additive electronics noise contributes in proportion to the total detected fluence.
Task and detectability index
The performance of any imaging system should be considered with respect to the imaging task. The detectability index can be defined based on the 3D MTF and NPS in direct analogue to the familiar form1 by considering d′ as the SNR2 for a matched filter receiver:
| (17a) |
where ΔH is the task function (i.e., the Fourier transform of the difference between binary hypotheses). The task function represents a low-contrast stimulus (i.e., a small signal difference such that the image statistics are unaffected). This can be related to the system NEQ as:
| (17b) |
This definition is consistent with the optimum SNR for a receiver using the matched filter technique, as described by Hanson for 2D images,15 except that the assumptions of radial symmetry of the task and NPS, constant NEQ, and lack of magnification were not required here. The factor of (1∕πf) provides appropriate scaling for radial density of projections that slightly alters the interpretation of the NEQ as a function describing the spatial-frequency-dependent SNR that can be integrated with the task function to yield the detectability index; rather, that function is given by NEQ scaled by (1∕πf).
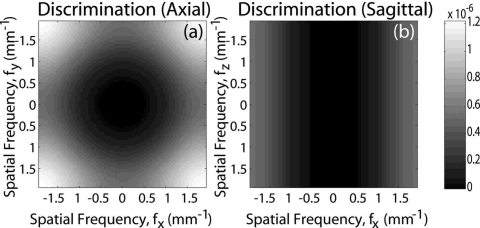
To demonstrate some important features of the 3D NPS, the detectability index was computed for two tasks: (i.) a simple delta function detection task that weighs each spatial frequency equally; and (ii.) a discrimination task between two 3D Gaussians of different widths, which weighs high frequencies very strongly. Slices through the corresponding task functions are shown in Fig. 2. The delta-function detection task is not shown due to its simplicity (a constant), and the discrimination task is shown in both the axial and sagittal domains. The two tasks were normalized to have equal signal power, and the detectability index was computed according to Eq. 17a across the range of exposures and filters discussed above.
Figure 2.
Task functions for calculation of detectability index: (a) axial and (b) sagittal slices of the task function for high-frequency discrimination between two small 3D Gaussians. The Gaussians had the same width in the z direction such that the task function is small near fz=0 where the integrand of Eq. 17a diverges.
Numerical calculations
The NPS, NEQ, and DQE were calculated numerically based on Eqs. 12a, 14b, 16, respectively. Calculations were implemented in Matlab (The Mathworks, Natick MA) using a 127×127 grid (in 2D) or 127×127×127 grid (in 3D) to sample Fourier space up to the Nyquist frequency. Convolutions with comb functions at stages 8, 14, and 15 were implemented by first calculating a presampling NPS to beyond the Nyquist region (as far as memory limitations would allow—up to seven times the sampling frequency in 2D, and two times the sampling frequency in 3D). The contribution from each aliased replicant to the NPS within the Nyquist region was computed by repeatedly shifting the presampling NPS by the sampling frequency and adding the result within the Nyquist region.
EXPERIMENTAL METHODS
Measurements of the 3D NPS, NEQ, and DQE were performed across a broad range of image acquisition and reconstruction techniques as described below, and compared to theoretical predictions.
Experimental platform
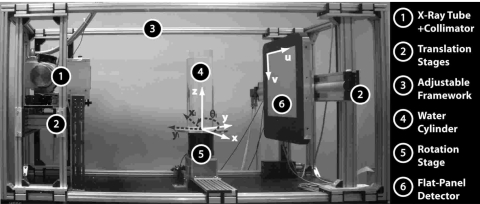
Measurements were performed on the CBCT bench shown in Fig. 3 incorporating the following components: an 80 kW constant potential generator and (CPX-380, EMD Inc., Montreal, QC); an x-ray tube (14° W anode, 0.4 mm focal spot, Varian Medical Systems, Salt Lake City, UT); filtration (2.5 mm Al inherent and 5.1 mm Cu added); and a flat-panel detector (250 mg∕cm2 CsI:Tl converter, 1024×1024 sampling grid, 0.4 mm pixel pitch, 80% fill factor, RID-1640A, PerkinElmer Optoelectronics, Santa Clara, CA). The system geometry provided a source-to-axis distance of 93.5 cm and source to detector distance of 144.4 cm (magnification of 1.54), chosen similar to that of systems for CBCT-guided radiation therapy.
Figure 3.
Illustration of experimental setup.
All projections were acquired at the nominal techniques mentioned in Table 2. Each 3D image was reconstructed from 320 projections across a 360° circular orbit acquired at an angular increment of 1.125° with uniform projection weighting. The exposure at the detector was measured using a Barracuda R100 diode (RTI Electronics, Molndal, Sweden), showing agreement with the exposure predicted by the x-ray spectral model35 used to estimate . Dark-flood processing was based on the mean of 50 dark and flood images obtained immediately prior to the projections, and defect pixels were corrected using a median filter. Neither a bowtie filter nor an antiscatter grid were used.
Images were reconstructed using the Feldkamp algorithm36 for 3D filtered back-projection. Nominal reconstruction parameters (unless otherwise noted) included a von Hann window (hwin=0.5), 1:1 pixel binning (Au=Av=Bu=Bv=1), and isotropic voxel size given by the detector pixel size divided by the magnification (0.259×0.259×0.259 mm3). Reconstructions were obtained of air as well as a 20 cm diameter water phantom. The results shown below pertain to the air scan reconstructions, with potential complications associated with NPS nonstationarity in water reconstructions27 to be investigated in other work.
Measurement of the 3D image NPS
NPS measurement
The NPS were measured from the ensemble average of the FFT (squared) of noise-only images. For the 2D projection NPS:
| (18a) |
where bu=bv=0.4 mm, and Lu=Lv=127 (the width in pixels of each ROI). The term ΔI(u,v) denotes a noise-only realization, obtained from first-order detrending (subtraction of a 2D planar fit) of each ROI. The symbol ⟨ ⟩ denotes the ensemble average over all (n=1600) ROIs. Similarly, the 3D NPS was measured from the FFT of noise-only 3D image reconstructions:
| (18b) |
where, for example in a 1:1 reconstruction, ax=ay=az=0.259 mm and Lx=Ly=Lz=127. The term ΔI(x,y,z) was obtained from first-order detrending (subtraction of 3D hyperplane fit) of each volume of interest (VOI), with a total of 36 VOIs used for the ensemble average. The VOIs were placed along concentric circles at radii of ∼36 mm (12 VOIs) and 73 mm (24 VOIs) about the origin, avoiding both the center (stronger influence of ring artifacts) and edge (circle of reconstruction) of the 3D image. Such provided good sampling of the well-behaved (i.e., uniform, artifact-free) regions of the image. Uncertainty in the NPS estimate behaved as expected:37
| (18c) |
As in the theoretical analysis above, the 3D NPS [Eq. 18b] has units of signal (attenuation coefficient, mm−1) squared times length cubed—e.g., [(mm−1)2(mm3)], which is equivalent to [mm] but is written [μ2 mm3] to avoid possible confusion with cancellation of terms. The units of the 2D NPS [Eq. 18a] vary from stage to stage depending on the units of the signal—in each case, the 2D NPS having units [(signal)2(mm2)].
While methodology for measuring the multidimensional NPS has not yet been standardized (currently the topic of an AAPM task group, TG169), the procedure outlined above is consistent with current literature (for example, Dobbinset al.38 for the 2D NPS and Siewerdsen et al.39 for the 3D spatiotemporal or volumetric NPS). However, it is important to recognize the assumptions associated with this method. Ideally, many volumes would be reconstructed and averaged to obtain a “noise-free image” that accurately describes the mean signal as well as any deterministic trends (e.g., cupping artifacts). The term ΔI in Eqs. 18a, 18b would then be obtained from the raw image minus the noise-free image. For 3D images, this approach requires a large amount of data to estimate the noise-free image. Subtraction of a polynomial fit is a common alternative to yield uniform ΔI. Assuming small ROIs (or VOIs), the noise-free image can be approximated by a first- or second-order fit. Similarly, subtraction of two (independent) volume images could be used to yield uniform ΔI (correcting the resulting NPS by a factor of 2). Throughout this work, ΔI was obtained by subtraction of a planar (hyperplanar) fit from each ROI (VOI) of the raw image, allowing measurement of the NPS due to quantum noise (with minimal influence from deterministic trends, cupping artifacts, etc.) from a limited amount of data.
Experimental parameters
Stage-by-stage analysis of NPS
The NPS of images at each stage in the reconstruction process were analyzed. This helped identify differences between the analytic forms of transfer functions described above and their actual numerical implementation in the reconstruction algorithm. Moreover, it demonstrated that each stage was modeled correctly (i.e., ruled out possible errors that simply cancel out).
Imaging dose
The NPS was investigated as a function of dose. The tube current was modified to 0.4, 1, 2, and 4 mAs per projection, and the measured exposure was converted to air kerma by a factor of 0.00876 mGy∕mR, giving 3.4, 8.0, 14.8, and 30.8 mGy air kerma per projection at the detector. This range extended from the lowest available tube output to a fairly high dose still within the linear response range of the detector (∼20% pixel saturation).
Reconstruction filter
The effect of reconstruction filter was analyzed by reconstructing data across a range of apodization filters described by Eq. 5a, with hwin set to 0.5, 0.65, 0.85, and 1.0. A value of hwin=0.5 corresponds to a smooth von Hann filter, whereas hwin=1.0 corresponds to a sharp Ram-Lak (ramp) filter.
Voxel size
Reconstructions were performed for cases of: (a.) 2D post readout binning, for which 2D projection data were binned on the detector; and (b.) 3D postreconstruction binning, for which 3D image data were binned in the 3D reconstruction. For the 2D binning case, aperture and sampling intervals considered combinations of (Au,Av) and (Bu,Bv) equal to 1, 2, and 4. Similarly for the 3D binning case, combinations of (Ax,Ay,Az) and (Bx,By,Bz) equal to 1, 2, and 4 were considered. In each case, Ai=Bi (no over- or undersampling). A total of 13 cases were examined to elucidate differences in noise associated with the two techniques.
Measurement of voxel noise
For each VOI used in the NPS analysis, the standard deviation in voxel values therein was recorded as an estimate of the voxel noise. The mean and standard deviation across the ensemble was compared to the voxel noise calculated from Eq. 13a and examined across the range of dose, reconstruction filter, and voxel size described above.
Analysis of the 3D NEQ and DQE
The 3D NEQ was measured according to Eq. 14b, taking the denominator as the measured 3D NPS [Eq. 18b]. The 3D MTF was not directly measured in this work and was taken equal to the product of transfer functions, T3, T5, T11, and T12. The DQE was calculated by dividing NEQ by the total fluence according to Eq. 16. While comparison of measured and theoretical 3D NEQ and DQE does not constitute a separate validation of the model beyond the NPS results, it does place the comparison on a more interpretable scale. Moreover, it describes the results in terms of more prevalent, portable metrics of image quality.
Experimental error and display of data
To visualize the resulting 3D NPS, NEQ, and DQE on paper, profiles were extracted from the volumes in a manner that illustrated the frequency dependence therein. Typically, extracting data along the x-y-z axes is a poor choice, as such often exhibits characteristics more associated with artifacts of the analysis (e.g., imperfect detrending) than the more interesting underlying features of the NPS. Additionally, due to the limited amount of data, extraction of a 1D profile from 3D data can yield a fairly noisy plot. To overcome both of these difficulties, after calculating each of the NPS, NEQ, and DQE, the radial average about the fz axis was computed using 64 frequency bins. As such, the 127×127×127 dataset was reduced to a 64×64 dataset (considering the redundant data present in the Fourier transform). The experimental error was thereby reduced as one over the square root of the number of nonredundant samples per bin (nbin), which varied from bin to bin:
| (19a) |
where “X” is understood to be the NPS, NEQ, or DQE, as the error has an equivalent form in each case.
Due to aliasing, the NPS (and to a larger extent, the NEQ) is not actually radially symmetric, so presenting the data in the manner described above somewhat distorts the underlying frequency dependence, although it still provides a fair comparison of theory with measurement (similarly distorted). To convey the magnitude of distortions caused by radially averaging, two sets of error bars were calculated: one presented experimental error as described above, and the second included the additional variability in data over each angular bin (added in quadrature to the basic experimental error):
| (19b) |
If the sample from each bin has the same variance (or equivalently, the same mean value), then the data are radially symmetric, and the two definitions of uncertainty are equal. In all cases, the difference between the two definitions of uncertainty was negligible, indicating that distortions caused by radial averaging were small compared to the basic experimental error. As illustrated in Fig. 4, the results presented are the radial average one voxel above the axial plane (avoiding on-axis peaks) for X(fx,fy) and a radial average over a cylindrical shell parallel to the fz axis located at the peak in the axial NPS for X(fz). The 2D projection NPS were simply displayed along a diagonal in the frequency plane to avoid on-axis peaks.
Figure 4.
Schematic illustration of the radial averaging performed for display of results.
RESULTS
Stage-by-stage analysis of NPS
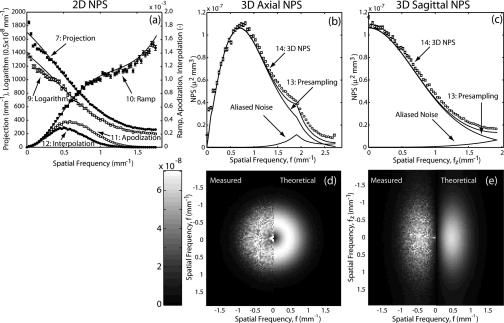
The NPS for stages 7 (projection), 9 (log normalization), 10 (ramp filter), 11 (apodization), and 12 (interpolation) are shown on a common plot in Fig. 5a. Theoretical calculations are shown as solid curves and measurements are shown as circles with error bars. The results show good agreement between theory and measurement at each stage and demonstrate the significant change in the NPS prior to back-projection. For example, one observes from this plot that the projection NPS (stage 7) does not fall off at high frequencies nearly as strongly as the apodized NPS (stage 11). Moreover, the dramatic effect of the ramp and apodization filters, as well as the nontrivial effect of the interpolation process in limiting aliasing of high-frequency noise, can be appreciated.
Figure 5.
Experimental and theoretical NPS evaluated at individual stages in the process of 3D reconstruction: (a) the 2D NPS at stages 7 and 9–12 shown on a common plot. The NPS as stages 7 and 9 are plotted on the left-vertical axis (with units mm-1), and the NPS for stages 10–12 are plotted on the left-vertical axis (dimensionless). (b) and (c) Plots of the 3D NPS at stages 13 and 14 for a sharp reconstruction filter (hwin=1), highlight the effects of noise aliasing. (d) Axial and (e) sagittal slices of the 3D NPS, with the measured NPS shown on the left, and the theoretical NPS shown on the right.
The NPS for stages 13 (back-projection) and 14 (postsampling NPS) are shown on a common axis together with the difference (S14−S13, which is the aliased noise component of the total NPS) for the sharpest filter in Figs. 5b, 5c. Aliased noise, although small, is important to the interpretation of the 3D NPS: it freezes in the effect of the deterministic filters such that they do not cancel out in the NEQ and imparts nontrivial effects on image quality. Aliasing has its most deleterious effect on image quality when it is large relative to the presampling NPS at that frequency. It, therefore, has its largest impact at very low frequencies and near the Nyqust frequency. Overall agreement between measured and theoretical 3D NPS is illustrated in the axial and sagittal slices shown in Figs. 5d, 5e.
Radiation dose
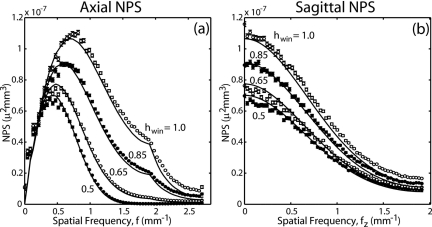
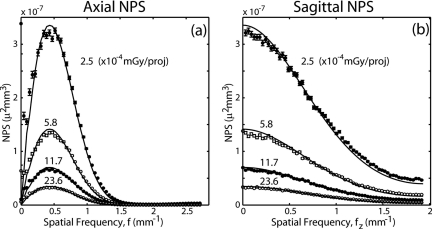
Plots of theoretical and measured 3D NPS for four levels of dose are shown in Fig. 6 in the axial and sagittal domains. These results demonstrate good agreement between experimental and theoretical results and elucidate some important features of the 3D NPS. First is the gross asymmetry between the axial and sagittal domain (bandpass versus low-pass, respectively), which has implications on performance when viewing slice images in one of these domains.22, 40 Second is that the low-pass character of the sagittal domain is more gradual than that in the axial domain. This has implications for the extent of noise aliasing in the longitudinal (z) direction and suggests that additional apodization in the longitudinal direction should be examined in terms of its effect on detectability.
Figure 6.
Experimental and theoretical 3D NPS evaluated at various levels of radiation dose (air kerma per projection): (a) axial, (b) longitudinal profiles of the 3D NPS. Adapted from Ref. 23.
Reconstruction filter
Plots of theoretical and measured 3D NPS for four reconstruction filters are shown in Fig. 7. Since the sagittal NPS is plotted at a location corresponding to the peak in the axial domain (which in turn depends on the filter), the longitudinal (fz) profiles must be interpreted carefully. While they cannot be directly compared in terms of amplitude, it can be seen that their structure is largely unaffected by apodization in the orthogonal direction. The effect of sharper filters on high frequency noise and overall variance is seen to be quite large. As a final note, a kink at the 2D Nyquist frequency (i.e., at ) can be seen for sharper filters. This is caused by the fact that the ramp filter only cancels out with the back-projection transfer function up to the detector Nyquist frequency, as mentioned in Sec. 2B6. One can see that the theory slightly underestimates the NPS at high frequencies, caused primarily by an incomplete calculation of aliased noise [i.e., due to memory limitations, only 3×3×3 nearest-neighbor replicants of the NPS were counted in the convolution of Eq. 10b].
Voxel size
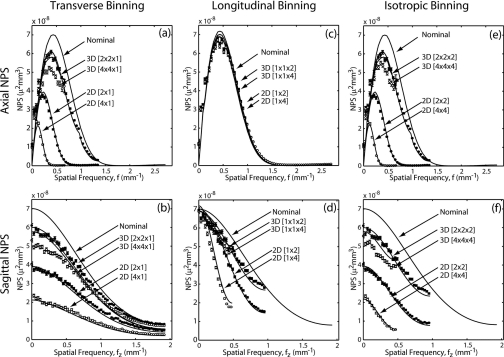
The NPS is shown in Fig. 8 for a variety of 2D and 3D binning methods. In each case, “2D binning” refers to 2D postreadout binning and downsampling of pixels on the detector, and “3D binning” refers to postreconstruction binning and dowsampling of voxels in the 3D reconstruction. Note that the 2D u and v directions correspond, respectively, to the 3D x-y and z directions. For example, 2D binning of detector rows [1×2 in (u,v)] is compared to 3D “slice averaging” [1×1×2 in (x,y,z)]. In each case, the theoretical result for nominal reconstruction (no binning) is shown as a baseline of comparison. Again, the longitudinal profiles must be interpreted carefully as the peak of the NPS depends on the binning method and interval.
Figure 8.
Experimental and theoretical results for the 3D NPS evaluated for various binning methods. (a, b) Axial binning in the u or x-y direction. (c, d) Longitudinal binning in the v or z direction. (e, f) Isotropic binning in the (u,v) or (x,y,z) directions. Axial NPS profiles are across the top (a, c, e), and sagittal NPS profiles are across the bottom (b,d,f). The nominal [1×1] reconstruction is shown as a solid line.
One immediately notes a dramatic difference in the 3D NPS for the two binning methods. 2D binning reduces noise to a much larger extent than 3D binning in all cases, particularly with respect to pixel binning in u versus voxel binning in x-y. The reason is that 2D binning∕downsampling reduces the cutoff frequency of the apodization filter and, therefore, reduces the noise to a greater extent. The case of 3D binning [1×1×2] (i.e., “slice averaging”) is seen to have the smallest effect on the NPS. While slice averaging is common (as it is computationally simple), the analysis demonstrates more effective means of reducing noise for a given voxel size. Note also from Fig. 8c that neither 2D nor 3D binning in the longitudinal direction affect the axial NPS, since such does not affect correlations in the central axial plane (fz=0), although such does reduce the NPS off the axial plane as shown in Fig. 8d. This further motivates description of the fully 3D NPS, as these out-of-plane correlations (not evident in an axial slice of the NPS) do have an impact on noise and image quality. Reasonable agreement between theory and measurement is observed in all cases.
Variance
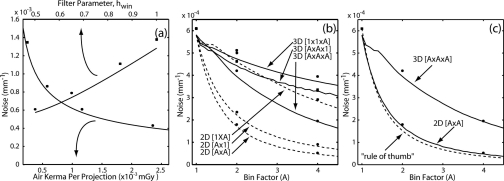
Experimental measurements and theoretical calculations of voxel noise are shown in Fig. 9. Points show the measured standard derivation of voxel values, and curves show the theoretical predictions computed as the square root of volume under the 3D NPS [Eq. 13a]. As shown in Fig. 9a, noise exhibits the expected 1∕sqrt behavior as a function of dose and exhibits a monotonic increase for sharper reconstruction filters. Figure 9b shows the behavior of noise with respect to binning and downsampling methods. Voxel noise is shown for binning in 2D and 3D in the transverse, longitudinal, and isotropic directions. Figure 9c shows noise for the isotropic binning methods and conditions described in Figs. 8e, 8f. Each case is compared to the conventional rule of thumb for voxel noise depending on the inverse cube root of and inverse square root of voxel size in Eq. 13a, which is seen to agree reasonably well with the 2D binning method, but not 3D binning (e.g., slice averaging).
Figure 9.
Experimental and theoretical evaluation of voxel noise. Symbols are experimental measurements (with error bars included, but nearly the same size as the symbol). Solid curves are theoretical expectations based on the integral of the 3D NPS. (a) Voxel noise versus dose (air kerma per projection) to the detector (bottom axis) and reconstruction filter (top axis). (b) Voxel noise versus the binning factor for 3D binning (solid curves) and 2D binning (dotted curves). Results are shown for binning in each of the transverse, longitudinal, or isotropic directions. (c) Voxel noise versus the (isotropic) binning factor, contrasting the case of 2D binning and 3D binning to the basic rule of thumb (noise proportional to and ) shown as a dotted line
The results suggest a slight, systematic underestimation of the noise by theory, which worsens as the binning factor approaches 1. This is likely caused by an incomplete sum over replicants in the 3D aliasing calculations (due to computer memory limitations). As the voxel size gets smaller, replicants become further apart and demand more memory for calculations. The underestimation can be seen most dramatically at low values of A for 3D binning, where aliasing calculations demand the most memory.
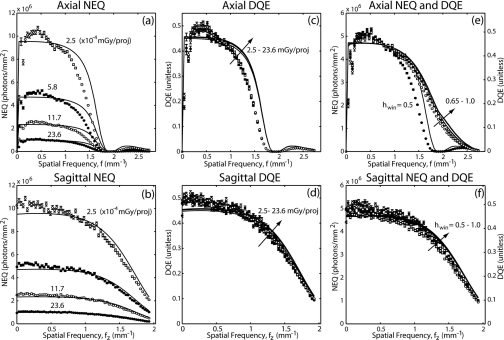
NEQ and DQE
The 3D NEQ and DQE for CBCT reconstructions are shown in Fig. 10 for various levels of dose [(a)–(d)] and reconstruction filters [(e) and (f)]. The linear dependence of NEQ on dose is evident in (a) and (b). The DQE is seen to be fairly independent of dose in (b) and (c), with a very slight dependence owing to additive electronics noise (stage 7). One can see that even across this broad range of exposures considered (down to the lowest deliverable technique of the x-ray generator), the system is effectively input quantum limited.
Figure 10.
Experimental and theoretical 3D NEQ and DQE shown in the axial (a, c, e) and sagittal (b, d, f) domains. Dependence on dose is illustrated in (a–d), and dependence on reconstruction filter is shown in (e–f). Adapted from Ref. 23.
The NEQ and DQE are shown for a variety of reconstruction filters (T11) in Figs. 10e, 10f. The smoothing filter alters both the MTF and NPS, but aliased noise at stage 14 prevents it from canceling completely from the NEQ. With the exception of hwin=0.5, for which a zeroing of the filter at the Nyquist frequency reduces NEQ, there is only a weak dependence on the smoothing filter. The slight reduction in NEQ and DQE for smoother (sharper) filters is attributed to a larger relative contribution of aliased noise at the highest (lowest) frequencies. As discussed in Sec. G, the differences in high-frequency NEQ contribute little to the overall detectability index as compared to those at low frequency, where the smoothest filter exhibits the highest NEQ. For consistency with the results shown above, longitudinal profiles (fz) are again shown at different frequencies corresponding to the peak NPS (which is different for different filters) and should, therefore, be cross-compared carefully.
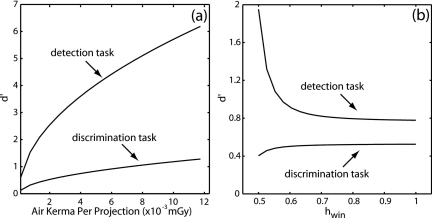
Detectability index
The theoretically calculated detectability index for the tasks described above are plotted in Fig. 11 as a function of (a) radiation dose and (b) reconstruction filter. For both the detection task (which weighs all frequencies equally) and the discrimination task (which weighs high frequencies), detectability is proportional to . Figure 11b illustrates a more complicated, task-dependent behavior with reconstruction filter. For the detection task, detectability index decreases for sharper filters, demonstrating the extent to which the 1∕f term in Eq. 17b emphasizes low frequencies in the detectability index. In this case, the high-frequency NEQ contributes little to the detectability index, whereas noise aliasing, which significantly affects the low-frequency NEQ, contributes more significantly. On the other hand, for the high-frequency discrimination task, sharper filters improve the detectability index, with the improvements in high-frequency NEQ outweighing the impact of noise aliasing.
Figure 11.
Detectability index for a delta-function detection task and a high-frequency discrimination task (Fig. 2) computed as a function of (a) exposure per projection and (b) reconstruction filter parameter (hwin).
DISCUSSION AND CONCLUSIONS
The cascaded systems model of the 3D NPS is seen to agree well with measurements across a fairly broad range of acquisition and reconstruction parameters. The approach provides a quantitative understanding of the 3D NPS, giving a starting point for the evaluation of other image quality metrics (e.g., NEQ, DQE, and detectability index) in a manner that is consistent with prevalent 2D descriptions. The model successfully describes the frequency-dependent signal and noise characteristics of CBCT despite a number of limitations, assumptions, and approximations.
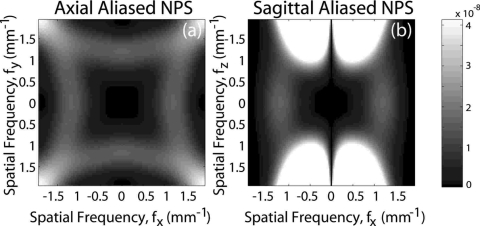
An important indication of the fully 3D model is that 3D aliasing prevents deterministic filters from canceling in the NEQ. Thus, 3D imaging performance is not trivially related to 2D detector performance. This demands an accurate calculation of aliased 3D noise (approximated in the calculations above as addition below the Nyquist frequency from 3×3×3 nearest-neighbor “replicants” of the 3D NPS at multiples of the sampling frequency). Figure 12 illustrates the contribution of 3D aliased noise in axial and sagittal planes computed as the difference of S15(fx,fy,fz) and S14(fx,fy,fz). Note that in the axial plane, the aliased NPS has its largest magnitude near the detector Nyquist frequency where signal power is already low and, thus, significantly degrades the NEQ and detectability. While there is little aliased noise power near zero frequency, its contribution to degrading detectability is amplified by the 1∕f term in Eq. 17b. For these reasons, it can be seen that bilinear interpolation gives superior NEQ compared to nearest neighbor interpolation, due to a reduced contribution of aliased noise. Finally, it is apparent that aliased noise is highest at higher longitudinal frequencies, as there is no apodization filter to remove high frequency noise in this direction. Longitudinal filters analogous to the axial apodization filter should be considered as a means of managing such aliasing effects.
Figure 12.
The 3D aliased NPS in (a) the axial domain and (b) the sagittal domain. Adapted from Ref. 23.
The approach provides definition of the NEQ, DQE, and detectability index for CBCT, which, while fairly straightforward and intuitive, deserves careful consideration. The NEQ is properly interpreted as the effective number of photons per square mm on the detector, over all projections, that contribute to the image at a given spatial frequency. The DQE similarly describes the efficiency with which photons contribute in this manner. The detectability index was defined in relation to a matched filter receiver and task function, but its relation to human observer performance deserves further investigation. For example, the model corresponds to an ideal observer that is able to consider the entire 3D image at once. While this may be a reasonable abstraction for a 2D image (displayed at once on a monitor), 3D data are typically displayed as slices from which it is difficult to obtain a complete sense of a fully 3D stimulus and out-of plane correlations. Forms of the fully 3D NPS, NEQ, etc. that describe single 2D slices may be written according to “extraction” of slices from the 3D data (with an associated convolution with the Fourier transform of the extracted slice aperture required to account for out-of-plane correlation39) but were not shown for the sake of brevity. These considerations suggest that the fully 3D results should be interpreted as an upper bound to human observer performance (2D slice viewing).
Furthermore, it should be reiterated that the model presented describes detectability in quantum noise. Images of real anatomy, of course, present a mixture of quantum noise and background anatomical structure. The frequency content of the latter has been described in terms of a 1∕fβ characteristic—an approach common in 2D mammography 41, 42, 43 and recently extended to 3D imaging. 22, 44, 45, 46 Such anatomical NPS may be added to the quantum NPS in “generalized” forms 47, 48 of the NEQ and detectability index, typically diminishing the importance of the low-frequency NEQ and causing a greater contribution to task performance from the high-frequency image characteristics.
The model was shown to accurately describe the 3D NPS for CBCT images of uniform (air) volumes for which the exposure to the detector is uniform and the resulting 3D reconstructions exhibit fairly stationary statistics (i.e., uniform mean and standard deviation). Extension to other circumstances (e.g., CBCT images of a water cylinder) can be similarly described, although the stationarity assumption can begin to fail and warrant a location-dependent analysis. Considering Eq. 9c, the 2D NPS for each projection can be combined in the 3D NPS if the exposure at each point in the 2D projection is known. The 1∕f term that emerges from the sum is modulated in a 1∕q(θi) fashion. For simple objects (e.g., a circular or elliptical water cylinder), the 2D NPS can be calculated analytically at each point and combined accordingly. Regions for which there is a high degree of exposure modulation from view to view exhibit a corresponding asymmetry in the NPS. For example, Fig. 13a illustrates an axial image of a water cylinder with a region of interest chosen near the edge of the cylinder (where view-to-view modulation in exposure is high). The axial NPS associated with this region exhibits an asymmetric “dumbbell” shape [Fig. 13b], distinct from the symmetric axial “donut” NPS described above—in agreement with theory [Fig. 13c].
Figure 13.
Example measurement and calculation of the NPS for a water cylinder. An axial slice of the 3D NPS for the location shown in (a) is shown in (b—measured) and (c—predicted). The asymmetric “dumbbell” shape of the axial NPS is due to variation in the detector fluence from view to view, and causes correlations to be strongest in the radial direction [as can be appreciated from the inset image in (a)].
Two factors known to degrade CBCT image quality—x-ray scatter and image lag—should be considered in future work. The model neglects x-ray scatter effects, and the measurements were performed under conditions for which x-ray scatter was small. As described above, to the extent that the exposure to the detector can be determined from view to view (even nonuniform fluence patterns as presented by x-ray scatter), such could potentially be included in a refined model. Similarly, the effects of lag could potentially be incorporated by modifying Eq. 9c to reflect that each projection is not statistically independent. Initial studies (computer simulations) suggest azimuthal correlation of the noise and a change in the strict ramp-like nature of the low-frequency NPS—viz., increased low-frequency noise as lag increases.
This work describes several factors that are unique to fully 3D FPD-based CBCT, but axial, helical, and multidetector (MD) CT could be similarly described in terms of a 3D NPS, NEQ, and DQE. For all three, the axial NPS exhibits the bandpass “donut” characteristic of filtered back-projection. In the longitudinal (fz) direction, however, differences in the NPS are to be expected: for axial CT, the model suggests independence between slices and a correspondingly “white” NPS in the fz direction; for helical CT, on the other hand, the longitudinal NPS(fz) would be modulated by z-interpolation; for MDCT, the modeling would be very similar to that described above for FPDs (adapted, of course, to the particular detector characteristics contributing to S7). The differences in longitudinal NPS among these modalities may be of importance considering the ever-increasing extent to which sagittal, coronal, and oblique slices are used in diagnostic CT. For example, Tward et al.40 demonstrated a dependence in human observer performance owing to NPS asymmetry and longitudinal correlation.
This work extends theoretical analysis of 2D imaging performance to 3D CBCT and demonstrates agreement with measurement. The model accounts for a number of nonideal characteristics of FPDs (e.g., a correlated 2D NPS, Swank factor, and electronics noise) and highlights a number of characteristics of 3D reconstruction that can significantly affect the 3D NPS—e.g., choice of reconstruction filter, interpolation method, and 2D versus 3D binning. Assumptions of shift invariance and stationarity deserve further investigation, although the results above suggest that such factors do not prohibit a basic Fourier-based approach to the first- and second-order image statistics. Quantifying the degree of noise stationarity in CBCT—e.g., as described by Pineda et al.27—will help define conditions for which the assumption is reasonable. Refinement and standardization of experimental methods for 3D NPS measurement will similarly help ground such work for the many applications being considered for CBCT. The theoretical methods presented above provide a fairly general framework that can be applied to the design and optimization of CBCT systems for various applications.
ACKNOWLEDGMENTS
The authors acknowledge numerous fruitful discussions with experts in digital x-ray imaging and CBCT over the past decade. Dr. Ian A. Cunningham (University of Western Ontario, London ON), Dr. Norbert Pelc (Stanford University, Palo Alto CA), and Dr. John Boone (University of California-Davis, Davis CA) assisted the development of theoretical and experimental methods for 3D NPS determination. Dr. Angel Pineda (California State University-Fullerton, Fullerton CA) assisted with aspects related to noise stationarity and model observer performance. Collaboration with Dr. David Jaffray (Princess Margaret Hospital, Toronto ON) formed the early foundation for this work. Mr. Samuel Richard (University of Toronto, Toronto ON) assisted with the 2D cascaded systems model forming the basis for 3D modeling. Dr. Doug Moseley, Mr. Graham Wilson, and Mr. Steve Ansell (Princess Margaret Hospital, Toronto ON) assisted with hardware and software aspects of the 3D imaging bench. The work was supported by National Institutes of Health Grant No. R01-CA-127944-02.
APPENDIX A: BACK-PROJECTION
The signal transfer associated with Stage 13 (back-projection) can be written as:
| (A1) |
where m is the number of projections and k is a normalization constant to be determined. This can be rewritten as:
| (A2) |
Multiplying and dividing by Δθ=π∕m (for a 180° scan; the derivation for a 360° scan differs by a factor of 2 in the numerator, but gives the same form for the result), we have:
| (A3) |
For large m, the sum approaches an integral:
| (A4) |
where θ=0 is chosen as the angle of the first projection with respect to the x axis. Introducing a change of variables:
| (A5) |
gives:
| (A6) |
Since the sinc function is even, we can write:
| (A7) |
Since the integral is over one full period of the ∣cos∣ function, the phase is irrelevant, such that:
| (A8) |
Here the radial symmetry of the function is evident (i.e., the transfer function depends only on f, not on φ, or θ). Now let:
| (A9) |
giving:
| (A10) |
Note that as d (or f) approaches infinity, the ratio in the integrand reduces to 1 for any finite ψ, and the integral is equal to unity. The dependence of the integral on d is weak, except for at very low frequencies. Therefore,
| (A11) |
The factor k is chosen such that the transfer function is 1 at zero frequency. Since we have already multiplied by the ramp function at stage 10 (∣fu∣=f∕M), the correct normalization is k=πM∕m. The transfer function is, therefore,
| (A12) |
Since the projections are independent, the noise from each combines in quadrature. We can now write for the noise propagation:
| (A13) |
For large m and d (since the integral over a sinc2 is equal to that over a sinc function), this reduces to:
| (A14) |
APPENDIX B: CLOSED FORM EXPRESSION FOR VOXEL NOISE IN CBCT
The voxel variance is given by the integral of the 3D NPS over the Nyquist region:
| (B1) |
For simplicity, we assume a natural voxel size (i.e., equal to the detector pixel size divided by the magnification, with Ai=Bi=1). The integral of the (sampled) NPS S15 over the Nyquist region is equivalent to the integral of the (presampling) NPS S13 over the entire frequency domain. Therefore,
| (B2) |
Since the presampling 3D NPS is cylindrically symmetric and longitudinally symmetric:
| (B3) |
| (B4) |
where S12M is defined in Eq. 7. The 1∕f term cancels out with the Jacobian (fdf), giving:
| (B5) |
Because the magnification scale factor in S12M(f,fz) does not change the pixel values (nor, therefore, the variance), the integral can be replaced by the (unscaled) form in the 2D projection domain:
| (B6) |
Note that the only term that is bandlimited (i.e., not periodic about multiples of the sampling frequency) is T12. Hence, T12 is the only term that limits very high frequency noise. We can rewrite the bracketed part in terms of the detector MTF and DQE, giving:
| (B7) |
Without further assumptions on the nature of the MTF and DQE, this is as far as we can simplify the 3D voxel noise. In order to relate this to the familiar form as derived for transaxial CT,13 we may assume a constant detector DQE, giving:
| (B8) |
which can be written:
| (B9) |
where Kxyz is dimensionless bandwidth integral analogous to the “IBWI” of Wagner et al.:16
This can be written in a form analogous to the familiar relationship derived by Barrett et al.13
| (B10) |
Specifically, the voxel noise is seen to be inversely proportional to dose , detector efficiency (DQE), axial voxel size cubed , and slice thickness (az). The noise reduces with detector blur (T3 and T5), smoother filters (T11), and interpolation methods (T12) as contained in the bandwidth integral. In the case of nearest neighbor interpolation (T12 given by a sinc), the bandwidth integral can be reduced to an integral over just the Nyquist region, since the other transfer functions are periodic about multiples of the sampling frequency.
References
- ICRU Report 54. Medical Imaging-The Assessment of Image Quality (Bethesda, MD, International Commission on Radiation Units and Measurements) (1996).
- Siewerdsen J. H., Antonuk L. E., El Mohri Y., Yorkston J., Huang W., Boudry J. M., and Cunningham I. A., “Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology,” Med. Phys. 10.1118/1.597919 24(1), 71–89 (1997). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Antonuk L. E., El Mohri Y., Yorkston J., Huang W., and Cunningham I. A., “Signal, noise power spectrum, and detective quantum efficiency of indirect-detection flat-panel imagers for diagnostic radiology,” Med. Phys. 10.1118/1.598243 25(5), 614–628 (1998). [DOI] [PubMed] [Google Scholar]
- Zhao W. and Rowlands J. A., “Digital radiology using active matrix readout of amorphous selenium: Theoretical analysis of detective quantum efficiency,” Med. Phys. 10.1118/1.598097 24(12), 1819–1833 (1997). [DOI] [PubMed] [Google Scholar]
- Zhao W., Ji W. G., and Rowlands J. A., “Effects of characteristic x-rays on the noise power spectra and detective quantum efficiency of photoconductive x-ray detectors,” Med. Phys. 10.1118/1.1405845 28(10), 2039–2049 (2001). [DOI] [PubMed] [Google Scholar]
- Vedantham S., Karellas A., Suryanarayanan S., Albagli D., Han S., Tkaczyk E. J., Landberg C. E., Opsahl-Ong B., Granfors P. R., Levis I., D’Orsi C. J., and Hendrick R. E., “Full breast digital mammography with an amorphous silicon-based flat panel detector: Physical characteristics of a clinical prototype,” Med. Phys. 10.1118/1.598895 27(3), 558–567 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vedantham S., Karellas A., and Suryanarayanan S., “Solid-state fluoroscopic imager for high-resolution angiography: Parallel-cascaded linear systems analysis,” Med. Phys. 10.1118/1.1689014 31(5), 1258–1268 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganguly A., Rudin S., Bednarek D. R., and Hoffmann K. R., “Micro-angiography for neuro-vascular imaging. II. Cascade model analysis,” Med. Phys. 10.1118/1.1617550 30(11), 3029–3039 (2003). [DOI] [PubMed] [Google Scholar]
- Bissonnette J. P., Cunningham I. A., and Munro P., “Optimal phosphor thickness for portal imaging,” Med. Phys. 10.1118/1.598002 24(6), 803–814 (1997). [DOI] [PubMed] [Google Scholar]
- Bissonnette J. P., Cunningham I. A., Jaffray D. A., Fenster A., and Munro P., “A quantum accounting and detective quantum efficiency analysis for video-based portal imaging,” Med. Phys. 10.1118/1.598009 24(6), 815–826 (1997). [DOI] [PubMed] [Google Scholar]
- Drake D. G., Jaffray D. A., and Wong J. W., “Characterization of a fluoroscopic imaging system for kV and MV radiography,” Med. Phys. 10.1118/1.598955 27(5), 898–905 (2000). [DOI] [PubMed] [Google Scholar]
- Lachaine M., “Detective quantum efficiency of a direct-detection active matrix flat panel imager at megavoltage energies,” Med. Phys. 10.1118/1.1380213 28(7), 1364–1372 (2001). [DOI] [PubMed] [Google Scholar]
- Barrett H. H., Gordon S. K., and Hershel R. S., “Statistical limitations in transaxial tomography,” Comput. Biol. Med. 10.1016/0010-4825(76)90068-8 6(4), 307–323 (1976). [DOI] [PubMed] [Google Scholar]
- Riederer S. J., Pelc N. J., and Chesler D. A., “The noise power spectrum in computed X-ray tomography,” Phys. Med. Biol. 10.1088/0031-9155/23/3/008 23(3), 446–454 (1978). [DOI] [PubMed] [Google Scholar]
- Hanson K. M., “Detectability in computed tomographic images,” Med. Phys. 10.1118/1.594534 6(5), 441–451 (1979). [DOI] [PubMed] [Google Scholar]
- Wagner R. F., Brown D. G., and Pastel M. S., “Application of information theory to the assessment of computed tomography,” Med. Phys. 10.1118/1.594559 6(2), 83–94 (1979). [DOI] [PubMed] [Google Scholar]
- Faulkner K. and Moores B. M., “Analysis of x-ray computed tomography images using the noise power spectrum and autocorrelation function,” Phys. Med. Biol. 10.1088/0031-9155/29/11/003 29(11), 1343–1352 (1984). [DOI] [PubMed] [Google Scholar]
- Kijewski M. F. and Judy P. F., “The noise power spectrum of CT images,” Phys. Med. Biol. 10.1088/0031-9155/32/5/003 32(5), 565–575 (1987). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Cone-beam CT with a flat-panel imager: Noise considerations for fully 3D computed tomography,” Proc. SPIE 10.1117/12.384515 3977, 408–416 (2000). [DOI] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Unified iso-SNR approach to task-directed imaging in flat-panel cone-beam CT,” Proc. SPIE 10.1117/12.465565 4682, 245–254 (2002). [DOI] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Three-dimensional NEQ transfer characteristics of volume CT using direct and indirect-detection flat-panel imagers,” Proc. SPIE 29(11), 2655–2671 (2003). [Google Scholar]
- Siewerdsen J. H., Moseley D. J., and Jaffray D. A., “Incorporation of task in 3D imaging performance evaluation: The impact of asymmetric NPS on detectability,” Proc. SPIE 5368, 89–97 (2004). [Google Scholar]
- Tward D. J., Siewerdsen J. H., Fahrig R., and Pineda A. R., “Cascaded systems analysis of the 3D NEQ for cone-beam CT and tomosynthesis,” Proc. SPIE 10.1117/12.772999 6913, 69131S (2008). [DOI] [Google Scholar]
- Rabbani M., Shaw R., and Van Metter R., “Detective quantum efficiency of imaging systems with amplifying and scattering mechanisms,” J. Opt. Soc. Am. A 4(5), 895–901 (1987). [DOI] [PubMed] [Google Scholar]
- Cunningham I. A., Westmore M. S., and Fenster A., “A spatial-frequency dependent quantum accounting diagram and detective quantum efficiency model of signal and noise propagation in cascaded imaging systems,” Med. Phys. 10.1118/1.597401 21(3), 417–427 (1994). [DOI] [PubMed] [Google Scholar]
- Yao J. and Cunningham I. A., “Parallel cascades: New ways to describe noise transfer in medical imaging systems,” Med. Phys. 10.1118/1.1405842 28(10), 2020–2038 (2001). [DOI] [PubMed] [Google Scholar]
- Pineda A. R., Siewerdsen J. H., and Tward D. J., “Analysis of image noise in 3D cone-beam CT: Spatial and Fourier domain approaches under conditions of varying stationarity,” Proc. SPIE 10.1117/12.772966 6913, 69131Q–69131Q-10 (2008). [DOI] [Google Scholar]
- Cunningham I. A., Sattarivand M., Hajdok G., and Yao J., “Can a Fourier-based cascaded-systems analysis describe noise in complex shift-variant spatially sampled detectors?,” Proc. SPIE 10.1117/12.534791 5368, 79–88 (2004). [DOI] [Google Scholar]
- Albert M. and Maidment A. D., “Linear response theory for detectors consisting of discrete arrays,” Med. Phys. 10.1118/1.1286592 27(10), 2417–2434 (2000). [DOI] [PubMed] [Google Scholar]
- Daly M. J., Siewerdsen J. H., Cho Y. B., Jaffray D. A., and Irish J. C., “Geometric calibration of a mobile C-arm for intraoperative cone-beam CT,” Med. Phys. 10.1118/1.2907563 35(5), 2124–2136 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badano A., Kyprianou I., and Sempau J., “Anisotropic imaging performance in indirect x-ray imaging detectors,” Med. Phys. 10.1118/1.2208925 33(8), 2698–2713 (2006). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H. and Jaffray D. A., “Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography),” Med. Phys. 10.1118/1.1286590 27(8), 1903–1914 (2000). [DOI] [PubMed] [Google Scholar]
- Richard S., Siewerdsen J. H., Jaffray D. A., Moseley D. J., and Bakhtiar B., “Generalized DQE analysis of dual-energy imaging using flat-panel detectors,” Proc. SPIE 5745, 519–528 (2005). [DOI] [PubMed] [Google Scholar]
- Cunningham I. A., “Analyzing system performance,” Frey G. D. and Sprawls P., eds., The Expanding Role of Medical Physics in Diagnostic Imaging (Advanced Medical Publishing, Madison, WI, 1997). [Google Scholar]
- Siewerdsen J. H., Waese A. M., Moseley D. J., Richard S., and Jaffray D. A., “Spektr: A computational tool for x-ray spectral analysis and imaging system optimization,” Med. Phys. 10.1118/1.1758350 31(11), 3057–3067 (2004). [DOI] [PubMed] [Google Scholar]
- Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 10.1364/JOSAA.1.000612 1, 612–619 (1984). [DOI] [Google Scholar]
- Dainty J. C. and Shaw R., Image Science: Principles, Analysis and Evaluation of Photographic-Type Imaging Processes (Academic Press, London, 1974). [Google Scholar]
- J. T.DobbinsIII, Ergun D. L., Rutz L., Hinshaw D. A., Blume H., and Clark D. C., “DQE(f) of four generations of computed radiography acquisition devices,” Med. Phys. 10.1118/1.597627 22(10), 1581–1593 (1995). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Cunningham I. A., and Jaffray D. A., “A framework for noise-power spectrum analysis of multidimensional images,” Med. Phys. 10.1118/1.1513158 29(11), 2655–2671 (2002). [DOI] [PubMed] [Google Scholar]
- Tward D. J. and Siewerdsen J. H., “Soft-tissue detectability in cone-beam CT: Evaluation by 2AFC tests in relation to physical performance metrics,” Med. Phys. 10.1118/1.2790586 34(11), 4459–4471 (2007). [DOI] [PubMed] [Google Scholar]
- Burgess A. E., Jacobson F. L., and Judy P. F., “Human observer detection experiments with mammograms and power-law noise,” Med. Phys. 10.1118/1.1355308 28(4), 419–437 (2001). [DOI] [PubMed] [Google Scholar]
- Bochud F. O., Abbey C. K., and Eckstein M. P., “Visual signal detection in structured backgrounds. III. Calculation of figures of merit for model observers in statistically nonstationary backgrounds,” J. Opt. Soc. Am. A Opt. Image Sci. Vis 17(2), 193–205 (2000). [DOI] [PubMed] [Google Scholar]
- Heine J. J., Deans S. R., Velthuizen R. P., and Clarke L. P., “On the statistical nature of mammograms,” Med. Phys. 10.1118/1.598739 26(11), 2254–2265 (1999). [DOI] [PubMed] [Google Scholar]
- Glick S. J., Vedantham S., and Karellas A., “Investigation of optimal KVp setting for CT mammography using a flat-panel imager,” Proc. SPIE 10.1117/12.465581 4682, 392–402 (2002). [DOI] [Google Scholar]
- Metheany K., Boone J. M., Abbey C. K., and Packard N., “A comparison of anotomical noise properties between breast CT and projection breast imaging,” Med. Phys. 34(6), 2563 (2007). [Google Scholar]
- Nishikawa R. M., Engstrom E., and Reiser I., “Comparison of the breast tissue power spectrum for mammograms, tomosynthesis projection images, and tomosynthesis reconstruction images,” Annual Meeting of the Radiological Society of North America (RSNA) (2007).
- Barrett H. H., Rolland J. P., Wagner R. F., and Myers K. J., “Detection and discrimination of known signals in inhomogenous, random backgrounds,” Proc. SPIE 1090, 176–182 (1989). [Google Scholar]
- Barrett H. H., Denny J. L., Wagner R. F., and Myers K. J., “Objective assessment of image quality. II. Fisher information, Fourier crosstalk, and figures of merit for task performance,” J. Opt. Soc. Am. A 12(5), 834–852 (1995). [DOI] [PubMed] [Google Scholar]