Quantitative image quality evaluation of MR images using perceptual difference models

Abstract

The authors are using a perceptual difference model (Case-PDM) to quantitatively evaluate image quality of the thousands of test images which can be created when optimizing fast magnetic resonance (MR) imaging strategies and reconstruction techniques. In this validation study, they compared human evaluation of MR images from multiple organs and from multiple image reconstruction algorithms to Case-PDM and similar models. The authors found that Case-PDM compared very favorably to human observers in double-stimulus continuous-quality scale and functional measurement theory studies over a large range of image quality. The Case-PDM threshold for nonperceptible differences in a 2-alternative forced choice study varied with the type of image under study, but was ≈1.1 for diffuse image effects, providing a rule of thumb. Ordering the image quality evaluation models, we found in overall Case-PDM ≈ IDM (Sarnoff Corporation) ≈ SSIM [Wang et al. IEEE Trans. Image Process. 13, 600–612 (2004)] > mean squared error ≈ NR [Wang et al. (2004) (unpublished)] > DCTune (NASA) > IQM (MITRE Corporation). The authors conclude that Case-PDM is very useful in MR image evaluation but that one should probably restrict studies to similar images and similar processing, normally not a limitation in image reconstruction studies.

INTRODUCTION

There are extraordinary developments in magnetic resonance (MR) imaging to speed acquisition and∕or improve image signal-to-noise ratio (SNR), creating a great need for quantitative image quality evaluation. With regards to hardware, new developments include increased field strength to 7 T; multicoil parallel imaging to 32 channels and beyond to speed MR scanning and∕or increase SNR. There are a large number of MR reconstruction algorithms aimed at utilizing partial k space for image reconstruction including SENSE,¹GRAPPA,²HYPR,³k−tSENSE,⁴TGRAPPA,⁵ and PROPELLER,⁶ where the “t” algorithms correspond to dynamic imaging over time. It is common for a researcher to describe new hardware or image reconstruction algorithms, and assert that it is an improvement based upon SNR or contrast-to-noise ratio (CNR) values, root-mean-squared (RMS) values, Shannon’s information content,⁷ or anecdotal evaluations. There is a substantial need to provide more rigorous image quality evaluations. In addition, particularly with regards to image reconstruction where many parameters can be involved, it is possible to create optimization experiments consisting of thousands of images to be evaluated. In this case, there is a great need for computer evaluation of images.

As compared to x-ray, computed tomography (CT), and radionuclide imaging, relatively little has been done in quantitative image quality evaluation of MR images. With regards to the other imaging modalities, there has been very significant effort to evaluate image quality using task based, detection studies. Receiver operating characteristic (ROC) and alternative forced choice (AFC) are two popular experimental methods in medical imaging.^{8, 9, 10, 11, 12} In a typical ROC experiment, a specified signal may or may not be present and the human observer uses a rating scale to express his confidence in a decision as to signal presence or absence.¹³ In an AFC experiment, the signal is always present, and the observer must choose between multiple alternative images, parts of images, or alternative signals in one image.¹³ Much less has been done with detection in magnetic resonance imaging (MRI). Yoshikawa et al.¹⁴ used ROC experiments to compare the breath hold gradient and spin-echo T2-weighted imaging for the detection and characterization of focal liver lesions. Lee et al.¹⁵ used ROC experiments to compare high-resolution breathing-free imaging techniques to breath-hold imaging techniques for image quality and focal region detection on T2-weighted MR imaging of the liver. Arbab et al.¹⁶ used ROC experiments to detect hypoperfused segments in flow-sensitive alternating inversion recovery images for optimization of inversion time to quantify regional cerebral blood flow. In our laboratory, Huo et al.¹⁷ and Jiang et al.¹⁸ recently used detection experiments to evaluate reconstruction algorithms using a 4-AFC task for detecting a simulated lesion in the liver. Saeed¹⁹ used 2-AFC experiments to measure the detection threshold for an artificially induced lesion in MR thumb images.

We believe that the detection paradigm has several shortcomings with regards to image quality evaluation for many MR images. First, in MR disease diagnosis, the radiologist’s task is much more varied than that of finding a focal lesion in x-ray or radionuclide imaging. For brain imaging, there are over 100 potential findings identified in a common atlas of clinical imaging.²⁰ Some are diffuse dilation of ventricular system; signal intensity changes in necrotic tissues; multiple lesions with irregular confluent margins; multifocal, nonconfluent abnormal regions with distinct margins; diffuse foci patches caused by meningeal enhancement; cluster of serpiginous flow voids; asymmetry or malformation of the brain, etc. In many cases (e.g., multiple sclerosis), multiple findings are required to make a differential diagnosis.²⁰ It would be impractical to create experiments evaluating ones ability to identify such large numbers of findings. Moreover, because of the complexity of the diagnosis and because of the extraordinary variability in acquiring MR data and reconstructing it, there is a chance that if one optimizes an image for detection of a single focal lesion, the image might be rendered unusable for some other aspect. Second, the large variety of anatomical pathologies do not map well to the significant effort in detection modeling for finite lesions in x-ray and radionuclide imaging. (See Barrett, Ref. 21 and Eckstein, Ref. 22, for some representative recent publications.) It is noteworthy that this modeling typically assumes a statistical background, whereas in MRI, there is often a rich anatomical background which is well known to radiologists. From these arguments, it does not appear that we have a useful, generally applicable computational method for detection experiments in MRI. Third, in the case of interventional MRI (iMRI), the task is not detection at all. For example, in iMRI guided radio-frequency ablation of tumor, the task is no longer detection of pathology. The needle, the target tumor, and any critical tissue to avoid, like arteries, must all be well above the detection threshold. Fourth, a significant design issue in MR is the creation of fast imaging techniques, many of which can introduce localized reconstruction artifacts in the image. The artifacts are undesirable and must be minimized. However, the artifacts might not fall on a particular lesion of interest and not interfere with its detection at all. Fifth, sometimes the task is to determine visually if a volume (heart wall, brain ventricular region, tumor, etc.) has changed. Again this does not match well to the detection paradigm, although there has been image quality research expressly on this subject.²³ Last, and most important, the time and effort for human detection studies would preclude performing them over the thousands of reconstruction possibilities for fast MR imaging.

Given the complications associated with the detection paradigm, we have used other approaches to quantitatively assess image quality. A favored experimental method is double-stimulus continuous-quality scale (DSCQS) experiment^{24, 25, 26} where we ask subjects to compare a possibly degraded “fast MR” test image to a full k-space reference and directly rate the image quality of the test image as compared to the high quality reference. DSCQS is considered the most reliable and widely used method for subjective testing proposed by the International Telecommunication Union of the television industry, Rec. ITU-R BT.500–10.²⁷ This method has been shown to have low sensitivity to contextual effects, a feature that is of particular interest considering the aim of our testing.²⁸ DSCQS has also been used to evaluate image compression methods for still images.^{29, 30, 31, 32} More recently, it has been applied to the evaluation of medical images, including MR, CT, ultrasound, and telemedicine images.^{17, 19, 24, 25, 33, 34, 35} This methodology matches well our experiments in fast MR imaging because we can routinely create a “slow” high quality “gold standard” reference.

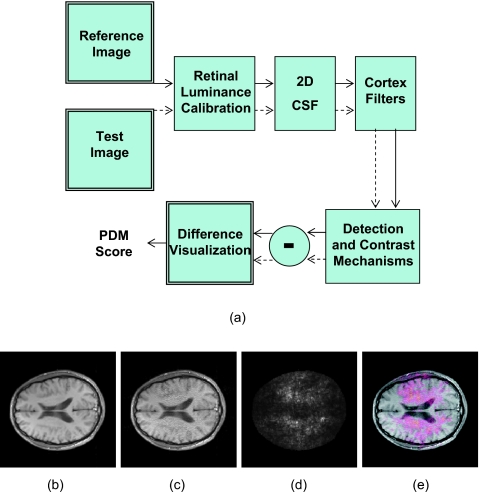
In addition to detection, there are a variety of other approaches for quantitatively assessing image quality. To assess MR image reconstruction algorithms, we have used a perceptual difference model (Case-PDM) which mimics the functional anatomy of the visual pathway and contains components that model the optics and sensitivity of the retina, the spatial contrast sensitivity function, and the channels of spatial frequency found in the visual cortex. Its structure diagram is shown in Fig. 1a and described in detail by Salem et al.²⁴ Inputs are a fast, probably degraded, MR imaging method [Fig. 1c] and a slower high quality reference image [Fig. 1b]. Outputs are a spatial map [Fig. 1d] of the likelihood of a perceptible difference and a scalar image quality metric averaged over the spatial map. Similar perceptual difference methods have been often applied to evaluate image compression. Among them, there are models which incorporate the CSF and luminance adaptations (e.g., Ref. 36), models which incorporate the observer preferences for suprathreshold artifacts (e.g., Ref. 37), and perceptual metrics which attempt to model human visual processing based on psychophysical and physiological evidence (e.g., Refs. ^{38, 39}). Several numerical observer models have been created for such comparisons including Sarnoff’s IDM (or the JNDmetrix-IQ),⁴⁰ DCTune (developed by NASA),⁴¹ and SSIM (structural similarity index).^{42, 43} There are some other subjective image quality metrics applied to image compression which consider only one input image. They include IQM (developed by MITRE)⁴⁴ and NR (no-reference perceptual image quality assessment).⁴⁵ These metrics are based upon the power spectrum estimation and artifact measurements. Finally, in MRI there are particular objective image quality metrics, including signal-to-noise ratio,⁴⁶ peak signal-to-noise ratio,⁴⁷ CNR,⁴⁸ mean-squared error (MSE),²⁴ root-mean-squared error,⁴⁹ and Shannon’s information content.⁷ Another similar objective measurement called artifact power was used in some parallel imaging applications.^{50, 51, 52} These mathematically based objective metrics do not utilize any information about viewing conditions and do not adapt to local image content, while these two issues play a major role in human perception of image quality.⁵³

Figure 1.

Block diagram of the perceptual difference model (Case-PDM) is shown in (a). The inputs of the model are two images, a reference image (b) and a test image (c). The output is a spatial map (d) showing the perceived difference between two images. PDM could be used to tell the visual difference between two input images, as shown in the overlaid display in (e).

In this article, we experimentally measure fast MR image quality and compare results to seven image quality evaluation methods. The seven different image quality evaluations have different features; i.e., some include a contrast sensitivity function and some include cortical filters. To aid the reader, we classify features succinctly below where a (Case-PDM), b (Sarnoff’s IDM), c (SSIM), d (NR), e (DCTune), f (IQM), and g (MSE). Features are: subjective model {abcdef}, objective model∕metric {cg}, color images {bcef}, gray scale images {abcdefg}, viewing condition {abef}, luminance adaptation {abc}, contrast sensitivity function {a}, contrast pyramid {b}, cortical filtering {ab}, masking effects {ab}, Q-norm {ab}, and temporal effect {b}.

Three kinds of experiments were used. They include DSCQS experiments which aim to determine model-subjects correlation; functional measurement theory (FMT) experiments which aim to test the comparability of model evaluation scores across images with different contexts while compared to human subject; and new designed 2-AFC experiments which aim to determine the imperceptible difference threshold for the models as a threshold discrimination method. Numerical observer evaluation is done with Case-PDM (v2, as established by Huo in his Ph.D. thesis,⁵⁴ this version has been used in recent publications,^{17, 25, 55} and it is only slightly different than the original, described in 2002), Sarnoff’s IDM,⁴⁰ DCTune,⁴¹ SSIM,⁴² IQM,⁴⁴ and NR.⁴⁵ MSE is also included as an objective metric because MSE has been used in many MR applications^{43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58} although researchers have reported limitations and poor performance of MSE as the image quality measurement.^{24, 25, 27, 59} And we apply seven image quality evaluation methods to fast MR images; these include Case-PDM by comparing model∕metric results to human evaluation of image quality. We then discuss the applicability of Case-PDM based on these experiment data and make our suggestions.

METHODS

Three different types of experiments will be described in this article. The DSCQS experiment was used for testing the correlation between human subjects and perceptual models when rating identical raw images with similar processing. To minimize context effects, the FMT experiment was used instead of DSCQS when rating different raw images with different processing. To detect the just perceptible difference, the 2-AFC experiment was used. The same parameter set (viewing distance=0.3 m, pixel size=0.3 mm, minimum luminance=0.01 cd∕m², maximum luminance=99.9 cd∕m², and display bits=8) was applied to all models whenever possible (some models∕metrics like MSE do not have parameter value input).

Experimental conditions

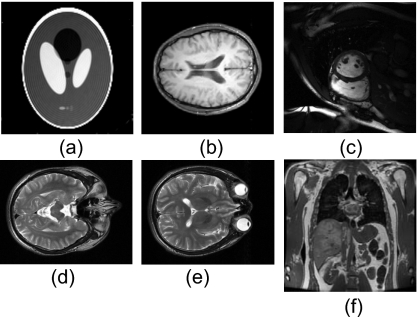
In the DSCQS experiment, we examined three different reconstruction algorithms [SENSE,²⁵SPIRAL,¹⁷ and GRAPPA (Ref. ⁶⁰)] on different images. Details of the reconstruction algorithms are described in the references. Images are: brain MR images (SENSE) in Fig. 2b, cardiac MR images (GRAPPA) in Fig. 2c, and phantom MR images (SPIRAL) in Fig. 2a, with image sizes of 256×256, 209×256, and 128×128 pixels, respectively. For the FMT experiment, two raw brain images [Figs. 2d, 2e] of size 198×256 were used to generate test images as described in Sec. 2C. For the 2-AFC experiments, two different original images [(Figs. 2d, 2f] were used to generate the whole test image data sets, with the same size of 256×256. One is a brain MR image and the other is an abdomen MR image. Each image was processed by adding three types of artifacts: noise artifacts, blur artifacts, and reconstruction artifacts. Gaussian white noise with zero means and different standard deviations (σ=1−30) were added to the original image to create the noisy data sets. Blurred data sets were created by convolving the original image with a circular averaging filter (pillbox) of the radius 0.5–0.7. The reconstruction artifacts were added by modifying the k-space data. The original full-sampled k-space data were decimated by the factor of 2 (i.e., one of every two k-space lines in phase encoding direction is omitted), except for certain number of center k-space lines, and the missing k-space data were estimated with GRAPPA (Ref. ²) or zero-filling method. And all test images in the 2-AFC experiment were carefully adjusted to have subtle difference with the original image. All the experiments’ test data sets are summarized in Table 1.

Figure 2.

Raw images used for human observer experiments. Of them, (a)–(c) are for the DSCQS experiment; (d) and (e) are for the FMT experiment; and (b) and (f) are for the 2-AFC experiment.

Table 1.

Descriptions of protocols, image data sets, and processing algorithms

	Image types	Image processing or reconstruction algorithm
DSCQS	Brain, heart, phantom	SPIRAL,1SENSE,2GRAPPA3
FMT	Brain	GRAPPA,4WGRAPPA5
2-AFC	Brain, abdomen	Adding white noise or Gaussian blur in image,GRAPPA,4 zero-filling

^aReference ¹⁷.

^bReference ²⁵.

^cReference ⁶⁰.

^dReference ².

^eReference ⁶³.

We used a display software running on a conventional Dell Precision 330, 1.8-GHz personal computer (Dell, Inc., Round Rock, TX) with a display adapter of NVIDIA GeForce2 GTS with 32 MB RAM. The display had an 8-bit dynamic range and the luminance response was adjusted using a ColorVision Spider™ monitor calibration unit (Color Vision, Inc., Rochester, NY) and OptiCal™ software (Color Vision, Inc., Rochester, NY). We used a standard SONY Trinitron flat-surface display color monitor (model CPDG520P) with a refresh rate of 85 frames per second and a display resolution of 1280×1024 pixels. The display gamma was set to be 3.0, giving a result which is nearly perceptually linear. The display pixel size on the screen was 0.3 mm. The minimum and maximum luminance was 0.01 Cd∕m² (black) and 99.9 Cd∕m² (white) at gray levels of 0 and 255, respectively. An alternative is to use a perceptually linear display as described in DICOM PS 3.14 2007. All experiments were performed in a dark room. The viewing was binocular and the viewing distance was fixed at 0.3 m. To maintain constant display conditions across observers, subjects were not allowed to adjust window or level settings or to use the zoom function.

Totally eight subjects, aged between 21 and 45 years, participated as observers: two radiologists (named Rad_1 and Rad_2), and six engineers including five experts (Eng_1−5). All observers had normal or corrected-to-normal visions, and their acuities were measured using a Snellen eye chart at a distance of 10 ft (3.05 m) and a reading card at 14 in. (0.356 m). Four subjects, including two radiologists and two engineers (Eng_1 and Eng_2) took the DSCQS experiment with the data set of SENSE reconstruction. Three subjects, including one radiologist (Rad_1) and two engineers (Eng_1 and Eng_2), took the DSCQS experiments with spiral and GRAPPA data sets. Four subjects, all engineers (Eng_1, Eng_4−6), took the FMT experiment. And two subjects, both engineers (Eng_1 and Eng_3), took all the six 2-AFC experiments.

Human subject correlation: DSCQS experiment

DSCQS is a human subject rating method recommended by the International Telecommunication Union,²⁷ and it is similar to that previously reported by Salem et al.²⁴ as applied to MR images and by Martens and Meesters²⁹ in a similar model validation study as applied to other images. We used the method previously reported from our laboratory.²⁵

Experimental setup

To test the full range of image quality in our images, for each experiment, we selected 40 test reconstructed images with Case-PDM scores uniformly spread from best to worst. Each human subject presentation consisted of a two-panel display, with the high-quality reference image and a randomly selected test image on the left and right, respectively. Observers were instructed to score the quality of the test image on a scale of 100–0, with 0 being the best quality and 100 being the worst quality. Observers were aware that we considered the reference image to be “best” and that they should consider it to have a score of 0. A training session consisted of 30 test images was supplied for each subject before the experiment. The training data set was representative of the images found in our test cases. Subjects were asked to compare the test image to its reference and rate its quality on a scale of 100–0, with 0 being best. Subjects were told to assume that the reference image had a score of 0. Aspects of image quality such as artifacts, sharpness, noise, etc. were all considered in the single score. Data were entered using a mouse or keyboard. To account for intraobserver differences, each of the 40 test images was displayed and evaluated twice within the same session. The experiment was carried out in a darkened room and normally took 1 h. There was no time limitation, and subjects were allowed to revise their results, including backtracking, at any time.

Data analysis

DSCQS data were processed to reduce intraobserver variability and interobserver scale differences. First, the two scores for the same test image, from the same subject, were averaged to reduce intraobserver variability, and we use $\overline{u}$ to represent the average. To compensate for interobserver scale effects, a nonlinear scale transformation was used for each subject, as recommended by the International Telecommunication Union in their report on methods for assessing television images.²⁷ The transformation is given below where $\overline{u}$and u_corr are scores before and after transformation, respectively; u_min, u_max, and u_mid are minimum, maximum, and median scores, respectively, for each subject; u_{0 min} and u_{0 max} are the hard boundaries, 0 and 100, respectively,

(1)

The performance of different subjects was compared to investigate the possible difference. The intracorrelation was defined as the linear correlation coefficient of the two measurements from the same subjects. The intercorrelation was defined as the linear correlation coefficient between two different subjects’ averaged measurements. Mean-dif and max-dif were calculated as the average and maximal difference between the two rating scores given to the same image. Subject rating data from each subject were fitted to modely=ax+b separately, the x intercepts of these fitted lines were also calculated, and these intercepts actually corresponded to the data points where Case-PDM found the difference but human subjects did not. Therefore, they could be regarded as a measurement of the “nonperceptible” threshold.

Model data were compared to human evaluation in different ways. For the testing of prediction accuracy, model predictions and corresponding human ratings were fitted to a linear model y=ax+b, and the correlation coefficients and the RMS errors were calculated. To test the prediction monotonicity, rank information was extracted from the data (absolute values were not considered) and compared with the human ranking order information, giving a “Spearman rank-order correlation coefficient,” as calculated in Ref. 61. Outlier ratios were calculated by dividing the number of outliers by the total number to measure the prediction consistency. Outliers were defined as the points who give errors larger than two times of the standard deviation, assuming the linear model fitting. The predictions for the same data set from the other similar models were also calculated and compared to Case-PDM using the above four parameters.

Minimizing context effects: FMT experiment

To validate Case-PDM score for different MR images and reconstruction methods, FMT experiment was used instead of the DSCQS experiment. In image quality research, it is known that if multiple scenes (or one scene, but multiple types of distortions) have to be judged in a session of direct rating experiment like DSCQS, subjects may use a separate internal quality scale for each of those scenes (or distortions). The FMT experiment is adopted from Anderson’s functional measurement theory,^{62, 30} and in this approach image qualities are compared rather than separately evaluated in order to force subjects to link the quality ratings for both images that have different scenes or degradation patterns. This approach has been used efficiently in image quality assessment.³⁰

Experimental setup

Two raw brain images (hereafter called brain 1 and brain 2), taken from the MR scan of a healthy volunteer, and two reconstruction methods (GRAPPA and WGRAPPA)⁶³ were used for generating two data sets by applying different sizes of k-space ACS region. Each data set has 12 images and can be classified into two groups. For data set 1, all 12 images were generated by using GRAPPA reconstruction, with six of brain 1 images and another six of brain 2 images; for data set 2, all 12 images are images of brain 1, with six generated by using GRAPPA reconstruction and another six generated by using WGRAPPA reconstruction. For each data set, each test image was compared to every other test image, including a comparison to itself, giving a total 78 comparisons. Each pair of images was shown randomly twice, giving 144 evaluations. Each image pair was displayed side by side on the screen, and the human subject was asked to rate the quality difference between them (subjects were asked: “how much left image is better than right image”) using a scale from −10 to +10, where +10 means that the left image is maximally better than the right. Subjects were instructed to consider all aspects of image quality including artifacts, sharpness, noise, etc. The plus and the minus signs were used to indicate whether the left or the right image was preferred. And, a training session of 60 randomly selected images pairs, which were not included in the test data sets but similar to them, was presented to each subject before the start of the actual experiment. For each trial there was 18 s time limit.

Data analysis

For each subject, one 12×12-element matrix was obtained (one row and one column per stimulus) for each part of the experiment, with element (i,j) representing the score given by the subject for the difference in quality between the pair of stimuli, stimuli i and j being displayed on the left and the right hand sides of the GUI, respectively. To apply the FMT method, one needs to observe parallelism for the scores within the different rows and columns or to calculate the interaction between rows and columns by means of two-way analysis of variance method.³⁰ If parallelism was observed or no significant interaction was found, according to FMT, a quality score on an interval scale for each stimulus can be determined by averaging (with opposite signs) the row and column means of the matrix that correspond to that stimulus. A general quality score for all subjects can now be obtained by averaging the individual quality scores. Before being averaged over the subjects, the individual scores were normalized using a z-score transform³⁰

$$z_i=\frac{x_i-\overline{x}}{\sigma },$$ (2)

where $\overline{x}$ and σ are mean and standard deviation for score x, to minimize the variation in the individual score, which is caused by the fact that not all subjects used the full range of the numerical scale in comparing image qualities.

Just perceptible difference: 2-AFC experiment

Psychophysical measures such as forced-choice task have commonly been used in determining signal threshold especially in medical images.^{13, 64, 65} We adopted signal detection theory⁸ into our experiment design and data processing. We use the 2-AFC experiment to measure the human perception of the small differences between the reference image and test image. The ability to detect this small difference was represented by the probability of correctness in the 2-AFC experiment. It was then converted to d^′ (detectability index) and compared with the Case-PDM predictions. And this is a different situation with the pervious SKE∕BKE detection experiments.

Experimental setup

For each trial, one reference image is displayed on the top of screen, and two test images are displayed side by side at the bottom of screen. In these two test images, one of them is the same as the original image, and the other one is a slightly degraded image. The locations (left or right) of the test image and reference image were randomly selected, and the subjects were asked to specify the correct location of the reference image by inspecting and comparing any image details. Training sessions were provided before the actual experiment to help the subjects familiar with the image contents. The train data set is independent of the experiment data sets. The experiment was carried out in a darkened room. A perceptually linearized, high quality monitor was used. There was no time limitation in the experiment, but the subjects were not allowed to revise their results. If the subject made a correct choice in one trial, the subject was informed by a beep from the computer.

For each of the six experiment conditions (two original images times three types of processing), 30 test images were generated with different levels of degradation. All degradations were very subtle and not very easy to detect from the original image. Each experiment was divided into six sessions. And in each session, 30 test images were randomly displayed eight times (resulting in 30×6×8=1440 trials∕experiment∕subject). There were no time limitations for the subject in the experiment, but on average, subjects spent about 15–20 min in a session.

Data analysis

For each test image, experiment results of 48 trials directly generate a probability of correct choices. These percentage value were converted to d^′ or detectability index using the detection theory. Before calculating d^′, we averaged z scores of left and right choices to minimize the bias.⁶⁶ The detailed descriptions of this process were discussed in the Appendix of Ref. 13. We fitted these data points into the model of y=ax^b (a, b are constants) to optimize the regression line, in which y represents for d^′ and x represents for the Case-PDM predictions.

After the relationship between the Case-PDM predictions and d^′ was determined, we could determine the threshold value. The threshold is often defined as the stimulus strength that produces a probability correct halfway up the psychometric function. A definition of threshold that is relatively independent of the method used for its measurement is to define threshold as the stimulus strength that gives a fixed value of d^′. The stimulus strength that gives d^′=1 (76% correct for 2-AFC) is a common definition of the threshold.⁸ We use this definition and the Case-PDM value that corresponds to d^′=1, which is determined as the threshold value.

RESULTS

Identical raw images with similar processing (DSCQS)

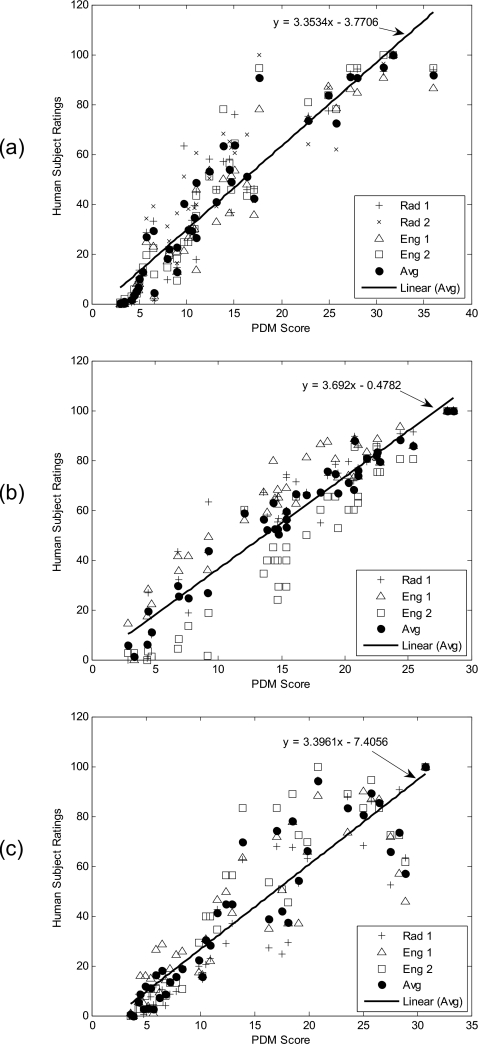
For each of the three DSCQS experiments, the 40 test images of the corresponding data set were evaluated by the subjects, and the human rating results were plotted as the function of Case-PDM scores. Figures 3a, 3b, 3c correspond to results from SENSE, Spiral, and GRAPPA, respectively. Cross points represent responses from radiologists, open square and triangle points represent responses from image engineers, and solid circle points represent average responses. The average human subject data were fitted to a model y=ax+b. High correlations were observed between the human subject ratings and Case-PDM predictions for all three plots.

Figure 3.

Experiment to evaluate correlation to human subject. Data are from SENSE (a), SPIRAL (b), and GRAPPA (c) reconstructions in the DSCQS experiment with correlation coefficients of 0.94, 0.97, and 0.91 correspondingly. Cross points represent responses from radiologists, open square and triangle points represent responses from image engineers, and solid circle points represent average responses. The average human subject data (solid circle) were fitted to y=ax+b, and the functions were represented by the straight lines in the figures.

The human subject ratings were further analyzed and the results are shown in Table 2 for SENSE data set. As described in Sec. 2, intracorrelation, mean-dif, and max-dif were calculated to analyze the consistency between two measurements of the same subject. Correlations with Case-PDM and x intercepts are shown in the bottom two rows. Similarly, human subject data from the SPIRAL and GRAPPA data sets were analyzed (Tables 3, 4, respectively). The intercorrelation between different subjects is shown in Table 5.

Table 2.

Data analysis for SENSE data set.

	Rad 1	Rad 2	Eng 1	Eng 2	Average
Intracorrelation	0.971	0.972	0.962	0.985	N∕A
Mean_dif	5.297	6.152	5.115	3.725	N∕A
Max_dif	21.179	20.742	19.700	10.000	N∕A
Corr_with Case-PDM	0.912	0.895	0.951	0.939	0.944
Intercept	1.09	−0.28	1.98	1.64	1.13

Table 3.

Data analysis for SPIRAL data set.

	Rad 1	Eng 1	Eng 2	Average
Intracorrelation	0.933	0.941	0.951	N∕A
Mean_dif	7.810	9.360	8.600	N∕A
Max_dif	28.820	34.060	30.000	N∕A
Corr_with Case-PDM	0.885	0.842	0.922	0.972
Intercept	−1.28	−3.59	4.40	0.13

Table 4.

Data analysis for GRAPPA data set.

	Rad 1	Eng 1	Eng 2	Average
Intracorrelation	0.916	0.936	0.981	N∕A
Mean_dif	8.586	6.359	3.750	N∕A
Max_dif	38.650	24.670	20.000	N∕A
Corr_with Case-PDM	0.912	0.878	0.899	0.914
Intercept	3.29	0.85	2.25	2.17

Table 5.

Intercorrelation analysis in the DSCQS experiment for four subjects.

	Correlation coefficient			Rank-order correlation coefficient
		SENSE	SPIRAL	GRAPPA	SENSE	SPIRAL	GRAPPA
Rad 1_Rad 2	0.954	N∕A	N∕A	0.955	N∕A	N∕A
Rad 1_Eng 1	0.956	0.926	0.935	0.964	0.854	0.952
Rad 1_Eng 2	0.963	0.882	0.948	0.973	0.920	0.974
Rad 2_Eng 1	0.951	N∕A	N∕A	0.957	N∕A	N∕A
Rad 2_Eng 2	0.953	N∕A	N∕A	0.973	N∕A	N∕A
Eng 1_Eng 2	0.974	0.904	0.949	0.979	0.921	0.970
Average	0.959	0.904	0.944	0.967	0.898	0.965

Case-PDM and other models were compared to averaged human evaluation in Table 6, both with regards to correlation coefficient, rank order, outlier ratio, and RMS. The Spearman rank-order correlation coefficients measure the prediction monotonicity. Outlier ratios measure the prediction consistency. IQM showed an inverse correlation because a low IQM score indicates poor image quality, whereas low scores from other models indicate good image quality. Results were good for the Case-PDM, IDM, and SSIM models. For comparison, we performed a similar analysis comparing one human subject rater with another, and results are given in Table 5. Values in Tables 5, 4 are similar indicating that the best models can be used to rank images almost as well as human raters.

Table 6.

Comparison of Case-PDM with other similar models from averaged human subjects data. (Correlation is between method and subjects.)

	SENSE	SPIRAL	GRAPPA
	Gray 256×256	Gray 128×128	Gray 209×256
Data set	Correlation coefficient (prediction accuracy)
Case-PDM	0.944	0.972	0.914
IDM	0.955	0.971	0.958
SSIM	0.951	0.962	0.941
NR	0.824	0.916	0.930
MSE	0.712	0.825	0.891
DCTune	0.715	0.191	0.319
IQM	−0.600	−0.688	−0.241
	Rank-order correlation coefficient (prediction monotonicity)
Case-PDM	0.971	0.974	0.932
IDM	0.978	0.944	0.963
SSIM	0.974	0.943	0.958
NR	0.705	0.886	0.897
MSE	0.946	0.868	0.955
DCTune	0.815	0.091	0.459
IQM	−0.166	−0.713	−0.074
	Outlier ratio (prediction consistency)
Case-PDM	0.050	0.000	0.025
IDM	0.000	0.000	0.000
SSIM	0.025	0.000	0.000
NR	0.050	0.000	0.000
MSE	0.050	0.000	0.025
DCTune	0.050	0.000	0.000
IQM	0.075	0.026	0.050
	RMS error
Case-PDM	10.643	5.936	12.869
IDM	9.637	6.073	9.081
SSIM	10.002	6.881	10.755
NR	18.364	10.121	11.608
MSE	22.735	14.293	14.410
DCTune	22.638	24.800	30.030
IQM	25.901	18.337	30.759

Different raw images with different processing (FMT)

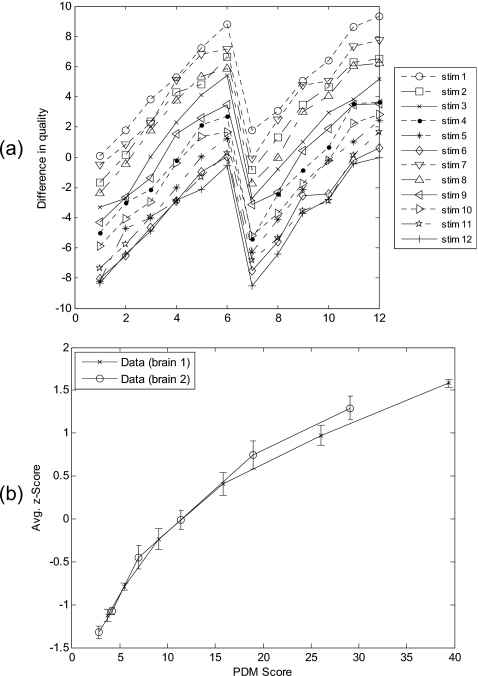
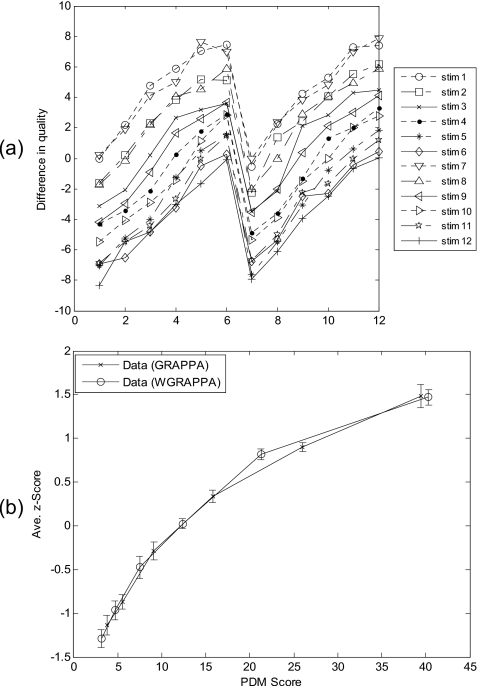
To evaluate different raw images with identical processing, data set 1 (described in Sec. 2C) was used in the experiment. The scores in the 12×12 matrix averaged over all subjects were plotted in Fig. 4a. It shows that the lowest curve corresponds to the stimulus with the highest image quality and the other 11 stimuli are rated as having lower quality in each comparison. At observation, the immediate salient feature is an overall pattern of N-shaped parallelism, arguing for an additive-type integration rule.⁶⁷ After z-score transformed, the averaged human subject data were plotted against PDM scores in Fig. 4b, and data from two different raw brain images were linked by solid line to form two FMT curves, respectively. Each of two FMT quality curves is only slightly different to the other, indicating Case-PDM agreed with human subject nicely.

Figure 4.

Image quality evaluation with different raw brain images (brain slices 1 and 2) identical processing (GRAPPA reconstruction). Difference-in-quality scores, averaged over all subjects were shown in (a). The numbers 1–6 and 7–12 on the x axis correspond to brain slice 1 and brain slice 2, respectively. Each point on the curves indicates the score for the difference-in-quality between the corresponding row and column stimuli in the 12×12 stimulus matrix. Averaged subjective quality curves obtained by using Anderson’s FMT are shown in (b). Error bars represent standard deviations.

To evaluate identical raw image with different processing, data set 2 (described in Sec. 2C) was used in the experiment. The averaged score matrix was plotted in Fig. 5a. Same pattern of parallelism can be observed from this plot. Human subject ratings were transformed into z scores and then averaged over all four subjects. The averaged human subject data were plotted against PDM scores in Fig. 5b, and data from two different reconstruction methods were linked by solid line to form two FMT curves, respectively. Two FMT quality curves almost overlaps, indicating Case-PDM agreed with human subject nicely.

Figure 5.

Image quality evaluation with identical raw brain images (brain slice 1) different processing (GRAPPA and WGRAPPA reconstructions). Difference-in-quality scores, averaged over all subjects were shown in (a). The numbers 1–6 and 7–12 on the x-axis correspond to GRAPPA reconstruction method and WGRAPPA reconstruction method, respectively. Each point on the curves indicates the score for the difference-in-quality between the corresponding row and column stimuli in the 12×12 stimulus matrix. Averaged subjective quality curves obtained by using Anderson’s FMT are shown in (b). Error bars represent standard deviations.

To exam model’s prediction monotonicity for each data set, we calculated the Spearman rank-order correlation coefficient with 1 indicating perfectly correlated. The Spearman rank-order correlation coefficient in Table 7 shows that all three models have similar performance in prediction monotonicity, and Case-PDM was better correlated with subjects than IDM when evaluating images with similar contents and identical processing.

Table 7.

Spearman rank-order correlation coefficients for the models. (Correlation is between method and subjects.)

	Case-PDM	IDM	MSE
Similar raw image Identical processing	1.000	0.980	1.000
Identical raw image Similar processing	0.990	0.990	1.000

Just perceptible difference (2-AFC)

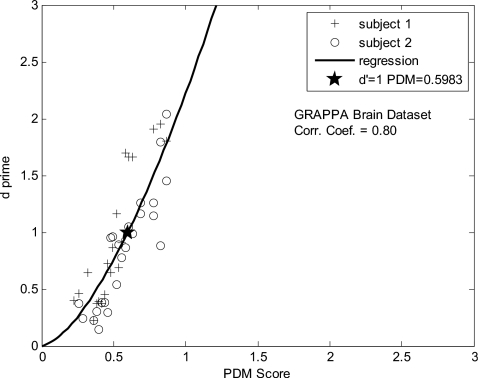
For each of the six experimental conditions (two raw images, three types of processing), a plot of the relationship between d^′ and Case-PDM values was generated. One result from the brain images reconstructed with GRAPPA is shown in Fig. 6. Data points were fit to a model y=ax^b with estimated a and b using a least-squares approach. The fitted line was plotted in the figure, and the threshold (d^′=1) was marked with a star. The fitting accuracy was examined by calculating the correlation coefficient of the model transformation log(y)=log(a)+b log(x). The correlation coefficient, threshold value and fitted a and b value are listed in Table 8.

Figure 6.

One result from the 2-AFC experiment. Reconstruction artifacts were included into a brain MR image, and the relationship between d^′ and Case-PDM predictions is shown. One could observe that Case-PDM scores show good correlation with d^′, but the relationship is not linear. The threshold value was represented with a star in the plot.

Table 8.

Data analysis for the 2-AFC experiment. (Correlation is between method and subjects.)

	Correlation	Fitted “a”	Fitted “b”	Threshold
Brain-noise	0.770	1.394	1.452	0.795
Brain-blur	0.790	1.085	0.802	0.902
Brain-recon	0.800	2.222	1.556	0.598
Abdomen-noise	0.450	0.583	0.936	1.779
Abdomen-blur	0.790	0.692	0.908	1.498
Abdomen-recon	0.730	0.919	0.747	1.118

DISCUSSION

Analysis of experiments

Case-PDM compared very favorably to human observers across similar reconstructions in DSCQS and FMT experiments with identical and similar raw image data, respectively. The DSCQS experiment was designed to test the performance of Case-PDM and other image quality measures as compared to human evaluation. Test images are distributed in a large range of image quality. As we could see in Fig. 3, in all three experiments (SENSE regularization, SPIRAL imaging, and GRAPPA reconstruction), the 40 test images covers the range from high to low quality, corresponding to Case-PDM scores from 0 to about 40. The Case-PDM scores and human subject ratings showed good linear correlation (r>0.9) over this large range of image quality. Despite the large range, our correlation results are nontrivial. That is, rather than creating images having remarkably different image quality, many were rather subtly different. The subject data were further analyzed as shown in the Tables 2, 3, 4, 5. One could see that in general the intracorrelation between the two measurements of the same subject is higher than the correlations between the subjects and Case-PDM. And we observed that radiologists and engineers performed similarly; this is because the experiment was not connected with a particular clinical task. If comparing subject-subject correlation (Table 5) and PDM-subject correlation (Table 6), one can easily find that both have similar correlation coefficients: for three different data sets, the former are 0.96, 0.90, and 0.94; the latter are 0.94, 0.97, and 0.91. Similar rank-order correlation coefficients are also obtained: the former are 0.97, 0.90, and 0.97; the latter are 0.97, 0.97, and 0.93. In all cases, the differences in rank order scores arise from at most one image out of order. This indicates that Case-PDM ranking can be as good as human ranking. A 95% confidence interval (CI) was used to indicate the reliability of all correlation coefficients in this article because 95% CI is recommended and commonly used in clinical trials.^{68, 69}

The x intercepts in Figs. 3a, 3b, 3c provide one method to determine the “nonperceptible difference” threshold. We could observe from Tables 2, 3, 4 that these x intercepts vary from different subjects and from different image reconstruction, and we even find some physically meaningless, negative numbers in our results. Obviously, this is not a very robust method to calculate the threshold because significant extrapolation is required. The 2-AFC experiment is a better method and the results are more consistent and reliable.

In some instances, rather than simply ranking image quality, we would like to determine image reconstructions which are imperceptibly different from the full k-space, reference images. In this case, we wish to use Case-PDM as a threshold discrimination tool. We compared results to human evaluation using the 2-AFC experiments. One could see that for all the three types of artifacts we tested (noise, blur, and GRAPPA reconstruction), the test images are all with only subtle differences with the original image (giving a low Case-PDM score of 0–3). As seen in Fig. 6 and Table 8, for all six experiment conditions (two raw images times three types of processing) Case-PDM correlated well with d^′ measurements in the small range. These proved that Case-PDM could still be used to represent the image quality under low-degradation conditions, although as we observed from Table 6, the relationship between Case-PDM and d^′ was not linear and was different between these six experiment conditions. The mean value of the threshold Case-PDM scores from six experiment conditions is 1.1 and the standard deviation is 0.45 which is about 40% of the mean value.

Comparison of models

One could compare the performance of Case-PDM and other similar models for rating tasks from Table 6. In general, Case-PDM, IDM, and SSIM outperform other models (MSE, NR, DCTune, and IQM); they give better prediction accuracy (higher correlation coefficients and lower RMS), prediction monotonicity (higher Spearman rank-order correlation coefficients), and prediction consistency (lower outlier ratios). With identical raw images and similar processing, we found that three “perceptual difference” models (Case-PDM, IDM, and SSIM) gave virtually identical results, with Sarnoff IDM insignificantly better than the other two. This strengthens our confidence that these models are useful. In fact, if we rank order MR reconstructions according to image quality scores, at most we found one image difference among the three methods. In the 2-AFC experiment, we examined both different images and different processing. A DSCQS experiment did not make sense because moving heart images always are degraded as compared to brain. Instead, we did a test to examine the just perceptible difference threshold with the 2-AFC. We also computed the mean and standard deviation of nonperceptible difference thresholds for different models. For mean value, Case-PDM is 1.1; IDM is 1.7; SSIM is 0.0059; and MSE is 2.9. For standard deviation value, Case-PDM is 0.45; IDM is 0.89; SSIM is 0.0091; and MSE is 3.9, which correspond to standard-to-mean ratios of 0.4, 0.9, 1.5, and 1.3, respectively. Results with the Case-PDM were much tighter than the other methods. Although, the variation for Case-PDM was greater than we had hoped, if we get a score around 1.1, we can be fairly confident that we are down near the threshold for human detection of a difference. If one needs an absolute value for just perceptible difference, a human subject experiment for the particular images and processing is in order. And the result from the FMT experiment also showed that Case-PDM outperformed IDM by showing a higher rank-order correlation coefficient when evaluating similar raw brain images with similar reconstructions. Considering all the tests, Case-PDM scored the best of all seven models.

IDM also performed well in our studies. IDM compared favorably to ROC studies of x-ray mammographic images by Krupinski et al.^{70, 71} In one study, they measured performances of six radiologists for viewing 250 mammographic images with microcalcifications of different contrast levels and compared results to those for IDM. IDM showed a high correlation [r²(quadratic)=0.973] in this study. It is encouraging that IDM has done well with these x-ray medical image data which are very much different than MR images.

Range of applicability of Case-PDM

PDM models are only applicable when there is a gold standard reference. They are not applicable to sequence optimization where one is changing MR contrasts. And one cannot compare PDM scores across different input images. That is, we cannot reconstruct two different input images, evaluate their PDM scores, and rate the quality of the reconstructions. This is seen from results from the DSCQS experiment. However, if images are very similar, then it is possible to compare PDM scores. This can be seen in the result from the FMT experiment in Fig. 4 where two different MR slices from the same brain and acquisition formed two very close curves after the same processing, which means subjects had no preference toward either of the two different images.

Case-PDM is very applicable for ranking results from an experiment to optimize reconstruction∕acquisition parameters. In this case there is a single input image and image data are processed with the same algorithm but different parameters. So in this instance, we have identical raw image, similar processing.^{24, 25} The DSCQS experiment supports its applicability for ranking. The 2-AFC experiment supports this too. And all three models (Case-PDM, IDM, and SSIM) gave similar rankings in our case. So Case-PDM could be used in a multiple data set, too. Although the Case-PDM scores from different data sets may not be directly comparable, one could extract the ranking information from them, and the ranking information is comparable. At least in some cases, we can extend the Case-PDM to evaluate single images with algorithms having a different structure. That is, we found that in the result from the FMT experiment in Fig. 5 where two curves overlapped for both GRAPPA and WGRAPPA.

Another way to apply such models is to determine when there is an imperceptible difference between the reference∕gold standard image and the test image. The threshold values for imperceptible difference were similar and the average value 1.1 can be used, as a rule of thumb. However, it was somewhat disappointing that the threshold did depend upon the image under investigation. If the application requires an absolutely imperceptible difference, then additional forced choice experiments are required for the images and processing under investigation. Alternatively, one is probably quite safe using the lowest threshold value obtained 0.6. This is our conservative recommendation.

The use of similar or identical images is not a limitation, allowing one to evaluate the many algorithmic approaches and the almost infinite number of variables in MR image reconstruction.

CONCLUSIONS

In conclusion, considering all tests, Case-PDM scored the best of the seven models by providing high model-subject correlations and consistent prediction of detection thresholds for just perceptible differences across a variety of images and processing. Two other models (IDM and SSIM) also described results from the DSCQS experiment. In FMT experiments, Case-PDM compares favorably to human evaluation for situations with similar images (e.g., brain images) and similar processing (e.g., GRAPPA and WGRAPPA) over a broad range of image quality, allowing us to rate different image reconstruction algorithms. In addition, if we focus on very high quality images, then we can determine images having no perceptible difference from the reference. The Case-PDM threshold for nonperceptible differences varied with the type of image under study, but was ≈1.1 for diffuse image effects, providing a rule of thumb for evaluations. We conclude that Case-PDM is very useful in MR image evaluation but that one should probably restrict studies to similar images and similar processing, normally not a limitation in image reconstruction studies.