Quantifying the interplay effect in prostate IMRT delivery using a convolution-based method

Abstract

The authors present a segment-based convolution method to account for the interplay effect between intrafraction organ motion and the multileaf collimator position for each particular segment in intensity modulated radiation therapy (IMRT) delivered in a step-and-shoot manner. In this method, the static dose distribution attributed to each segment is convolved with the probability density function (PDF) of motion during delivery of the segment, whereas in the conventional convolution method (“average-based convolution”), the static dose distribution is convolved with the PDF averaged over an entire fraction, an entire treatment course, or even an entire patient population. In the case of IMRT delivered in a step-and-shoot manner, the average-based convolution method assumes that in each segment the target volume experiences the same motion pattern (PDF) as that of population. In the segment-based convolution method, the dose during each segment is calculated by convolving the static dose with the motion PDF specific to that segment, allowing both intrafraction motion and the interplay effect to be accounted for in the dose calculation. Intrafraction prostate motion data from a population of 35 patients tracked using the Calypso system (Calypso Medical Technologies, Inc., Seattle, WA) was used to generate motion PDFs. These were then convolved with dose distributions from clinical prostate IMRT plans. For a single segment with a small number of monitor units, the interplay effect introduced errors of up to 25.9% in the mean CTV dose compared against the planned dose evaluated by using the PDF of the entire fraction. In contrast, the interplay effect reduced the minimum CTV dose by 4.4%, and the CTV generalized equivalent uniform dose by 1.3%, in single fraction plans. For entire treatment courses delivered in either a hypofractionated (five fractions) or conventional (>30 fractions) regimen, the discrepancy in total dose due to interplay effect was negligible.

INTRODUCTION

In intensity modulated radiation therapy (IMRT) treatment planning and dose delivery, it has been shown that the interplay between intrafraction organ motion and the motion of the multileaf collimator (MLC) or the MLC position can lead to a variation in the dose delivered to each voxel.¹ The interplay effect causes hot and cold spots within the target volume,^{1, 2, 3, 4, 5, 6, 7} which can result in discrepancies on the order of 10% (of the isocenter dose) for a single fraction, though for a large number of fractions (>30) the effect is much smaller, generally less than 1%.^{2, 4} The interplay effect is exacerbated in situations (even for a large number of fractions) where small monitor unit (MU) segments, delivering below 10–15 MU, are delivered. Under such circumstances, large daily variations in dose, on the order of 15%−35% have been reported.⁸

The Calypso system (Calypso Medical Technologies, Inc., Seattle, WA) is capable of real-time tracking of the intrafraction prostate motion,⁹ therefore the actual dose delivered in the presence of intrafraction motion can be evaluated by convolving the static dose distribution with the motion probability density function (PDF). Similar approaches have been reported previously^{10, 11, 12, 13, 14, 15, 16, 17, 18} to account for setup errors and organ motion in other tumor sites. The conventional convolution approach uses the PDF generated by population-based motion data,¹⁵ e.g., an entire fraction, an entire treatment course of a patient, or even an entire patient population. This approach assumes that in each segment the prostate experiences the same motion pattern (PDF) as that of the population. If each fraction consists of only one segment and only the motion data through the dose delivery of the segment is used to generate the PDF, there is no problem with the conventional approach. However, if a fraction consists of multiple segments, the segmental PDFs are in general different from the average PDF over the entire fraction, due to the random nature of prostate motion and the short interval of individual segments compared to entire fraction. Seco et al. have pointed out that a convolution of the static dose distribution with the motion PDF (without synchronization between the tumor location at a given time and the MLC segment position at the same time) may result in large differences between the planned and delivered doses, especially in cases where a large number of small MU segments are delivered.⁸ To mitigate this concern, we propose a method to account for the interplay effect by convolving the dose distribution from each segment in the IMRT treatment plan with the PDF of the intrafraction motion synchronized with the time interval over which that particular segment is delivered. In this manner both the intrafraction motion and interplay effect are taken into account during the convolved dose evaluation. For convenience, we call the proposed new method “segment-based convolution” and the conventional approach “average-based convolution.” The input PDFs for the intrafraction prostate motion were generated from real-time tracking data acquired from electromagnetic beacons implanted within the prostate (Calypso Medical Technologies, Inc., Seattle, WA).⁹ The purpose of this article is to introduce the segment-based convolution method and apply this approach to quantify the interplay effect in prostate IMRT delivered in step-and-shoot manner.

METHODS AND MATERIALS

One general approach for accounting for organ motion in treatment planning involves convolving the static dose distribution with the motion PDF averaged over the course of treatment, as follows:

$$D_{\text{ave}\text{conv}}\left(\vec{r}\right)=\int D_{\text{static}}\left(\vec{r}+{\vec{r}}^{\prime }\right)P\left({\vec{r}}^{\prime }\right)d{\vec{r}}^{\prime }=D_{\text{static}}\otimes P_{\text{ave}},$$ (1)

where P_ave is the PDF based on motion data in an average sense, D_static is the static dose distribution for the treatment plan, and D_{ave conv} is the dose distribution incorporating the time-averaged motion over the course of treatment. To account for both the intrafraction organ motion and the synchronization between dose delivery and the motion observed within each segment, consider the motion PDF for single segment i, of beam (i.e., gantry position) j, and during fraction k, denoted as P_ijk, which is generated from the motion data belong to that segment only. If the static dose distribution for that segment is $D_{\text{static}}^{\left(ijk\right)}$, then the segment-based convolved dose over the course of treatment is given by

$$D_{\text{seg}\text{conv}}=\sum _{i,j,k}{D}_{\text{static}}^{\left(ijk\right)}\otimes P_{ijk}.$$ (2)

Similarly, the segment-based convolved dose for one fraction (e.g., fraction k) is

$$D_{\text{seg}\text{conv}}^{\left(k\right)}=\sum _{i,j}{D}_{\text{static}}^{\left(ijk\right)}\otimes P_{ijk}.$$ (3)

In the absence of setup uncertainty, we assume that the static dose distribution is independent of the fraction, k, and that each fraction contributes the same dose to the cumulative dose distribution. By including any offset into the motion PDF, the assumption holds even in the case that setup error exists. Therefore, Eq. 2 can be written as follows:

$$D_{\text{seg}\text{conv}}=\sum _{i,j}\left(D_{\text{static}}^{\left(ijk\right)}\otimes \sum _k{P}_{ijk}\right)=\sum _{i,j}\left[N\times D_{\text{static}}^{\left(ijk\right)}\otimes \left(\frac{1}{N}\sum _{k=1}^N{P}_{ijk}\right)\right],$$ (4)

where N is the total number of fractions. Substituting $N\times D_{\text{static}}^{\left(ijk\right)}$ with $D_{\text{static}}^{\left(ij\right)}$, which represents the static planned dose distribution for segment i of beam j summed over all fractions, Eq. 4 becomes

$$D_{\text{seg}\text{conv}}=\sum _{i,j}\left[D_{\text{static}}^{\left(ij\right)}\otimes \left(\frac{1}{N}\sum _{k=1}^N{P}_{ijk}\right)\right].$$ (5)

The term $1∕N{\Sigma }_{k=1}^N{P}_{ijk}$ represents the PDF for segment i of beam j averaged over all fractions. While D_{seg conv} represents the dose after accounting for both the intrafraction organ motion and interplay effect, D_{ave conv} represents the dose after accounting for intrafraction organ motion only, with no interplay effect. Evaluating the difference between D_{seg conv} and D_{ave conv} provides an estimate of the interplay effect.

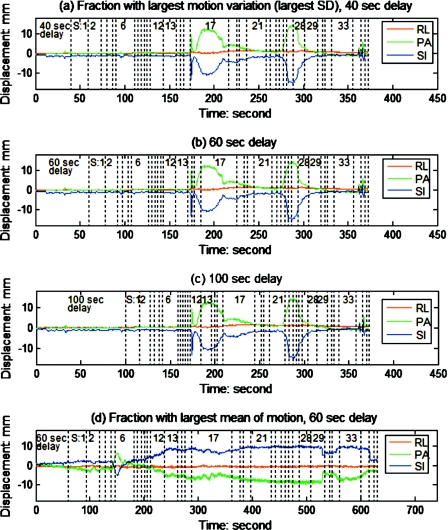
The prostate intrafraction motion data for 35 patients, each with approximately 40 fractions, has been reported previously.¹⁹ From this population, individual patients and fractions exhibiting extreme motion characteristics, i.e., with the largest mean or the largest standard deviation (SD) of motion (variation in magnitude or direction), were selected for study. Figure 1a shows the motion trace of the fraction with largest SD [0.3, 3.8, and 3.3 mm in right-left (RL), posterior-anterior (PA) and superior-inferior (SI) direction, respectively] among the 1267 fractions of the population. Motion traces were subsequently partitioned based on the MU weighting of each segment during IMRT dose delivery; analysis was performed retrospectively. This is illustrated by the vertical dotted lines, with the segment number indicated, in Fig. 1a, for a fraction consisting of 36 segments in which segment 17 has the largest number of monitor units. In the clinical Calypso implementation, there was a delay of approximately 60 s between initiation of tracking and initiation of the first beam. 40, 60, and 100 s delays were incorporated into our analysis to account for this practice, and to vary synchronization of the tracking data with the IMRT segments to evaluate the impact of this factor on the interplay effect. It should also be pointed out that in this study the time necessary for gantry rotation and MLC positioning has not been taken into account when partitioning the tracking data. Figures 1b, 1c show the same tracking data as Fig. 1a, but with different delays between the beginning of tracking and the initiation of delivery. Figure 1d shows the tracking data exhibiting the largest mean amplitude (−0.6, −4.7 and 6.3 mm in the RL, PA, and SI directions, respectively) observed during any single fraction. Following partitioning, the PDF for each segment (i.e., P_ijk) was obtained by binning the tracking data as a function of segment.

Figure 1.

Tracking data were partitioned by the IMRT segment based on monitor unit proportions; numbers indicate the specific IMRT segments. For the fraction with largest variation in motion (largest SD among the 1267 fractions) in (a)–(c), different delays between the starts of dose delivery and motion tracking were simulated.

Two arbitrary prostate cancer cases treated with a step-and-shoot IMRT technique were included in the study. Each plan consisted of seven gantry angles, with a total of approximately 36 segments per fraction. The prostate-to-PTV margin was 2 mm in both cases; this margin was found to be dosimetrically acceptable when accounting for intrafraction prostate motion only, in the absence of setup uncertainty.^{19, 20} Treatment planning was performed using the Pinnacle³ version 8.1s treatment planning system (Philips Radiation Oncology Systems, Madison WI). After obtaining an optimized IMRT plan, the static dose attributed to each segment was computed by setting the monitor units for other segments and beams to zero. The individual dose matrices were exported to a desktop computer for the purpose of performing the convolution. The convolved doses were then imported to the Pinnacle³ system for evaluation.

The interplay effect was analyzed for several scenarios, including: (a) individual segments, specifically segments 13, 15, and 17 in Figs. 1a, 1b, 1c, which have 17, 4, and 52 MU, respectively. By varying the initial delay, the effect of small MU segments with respect to intrafraction motion can also be evaluated; (b) plans for the single fraction in which the largest motion variation (i.e., SD) was observed [tracking data of Figs. 1a, 1b, 1c]; (c) plans for the single fraction in which the largest motion amplitude was observed [tracking data of Fig. 1d]; (d) plans for the patient in which the largest motion variation was observed over the entire course of treatment; (e) hypofractionated plans incorporating tracking data from the five fractions which exhibited the largest motion variation in any single patient; and (f) plans incorporating the average motion over the entire patient population. For scenarios (d)–(f), the average PDFs were obtained by binning the tracking data from all the relevant fractions. To obtain the corresponding segmental PDFs, the tracking data for each fraction were partitioned by segment according to the method described previously, following which the data were binned by segment for all involved fractions. The binning process follows the calculation of $1∕N{\Sigma }_{k=1}^N{P}_{ijk}$ in Eq. 5, where N is the number of fractions applied.

Dosimetric differences based on dose volume histograms (DVHs), generalized equivalent uniform dose (gEUD), and mean and minimum CTV dose were compared among the static, segment- and average-based convolved plans generated in the six scenarios described previously. The gEUD is based on the concept of the EUD, which is defined as the uniform dose distribution that gives an effect equivalent to that of a given heterogeneous dose distribution. The gEUD can be calculated as follows:

$$\text{gEUD}={\left(\frac{1}{N}\sum _{i=1}^N{D}_i^a\right)}^{1∕a},$$ (6)

where D_i is the dose in the ith voxel, N is the number of voxels in the anatomic structure of interest, and a is the dose-volume effect parameter specific to the structure of interest. The gEUD for targets and normal tissues were calculated using a=−10 and a=1, values representative of tumors and healthy tissues, respectively.²¹ When the parameter, a, approaches a large negative value (modeling a highly radio-resistant tumor) the gEUD converges to the minimum dose within the structure of interest.

RESULTS

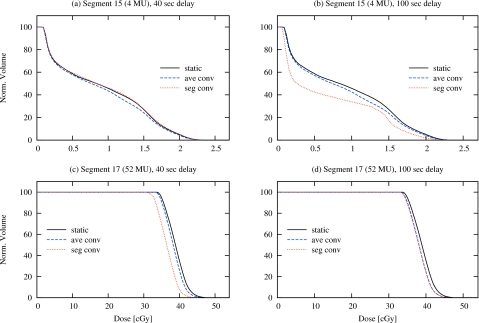
Figure 2 shows prostate DVHs for individual segments from multisegment plans, following the synchronization schemes of Figs. 1a, 1c, comparing the segment-based convolution approach with the average-based convolution (intrafraction motion without interplay effect) and in the absence of intrafraction motion (static). Significant differences can occur, though this is highly dependent on how the intrafraction motion is synchronized with IMRT delivery. Table 1 shows these differences in terms of the mean prostate dose. In the 40 s delay scheme [Fig. 1a], segment 15 experiences very little motion, and despite the small number of monitor units in that segment (4 MU), the differences in mean CTV dose are also small. In the 100 s delay scheme, however, the delivery of segment 15 [Fig. 1c] coincides with a large motion excursion, and the resulting interplay effect produces a significant change in both the DVH [Fig. 2b] and the mean CTV dose (25.9%).

Figure 2.

Comparison of prostate DVHs, in which the dose is contributed only by an individual segment, shown for static, average- and segment-based convolution plans. The segments are from a single-fraction plan consisting of 36 segments; the motion incorporates the tracking data from the fraction with largest SD [see Figs. 1a, 1c]. With a 40 s delay, segment 15 (small number of MU) experiences little motion, while segment 17 (large number of MU) experiences a large excursion. With a 100 s delay, segment 15 occurs within the excursion while segment 17 is relatively unperturbed.

Table 1.

Percentage differences of the mean CTV dose among the static, average- and segment-based convolved plans, for two segments of a single-fraction plan [see Figs. 1a, 1c]. The plan incorporated the intrafraction prostate motion of the fraction with largest SD. Column 4 shows the differences due to interplay effect (i.e., differences between two convolution methods) while column 5 shows the differences due to the combined effect of the intrafraction motion and interplay. Plans were generated for patient case 1.

Segment Index	Number of monitor units	Synchronization scheme	$\%(\mid {\overline{D}}_{\mathrm{seg}\mathrm{conv}}-{\overline{D}}_{\mathrm{ave}\mathrm{conv}}\mid ∕{\overline{D}}_{\mathrm{seg}\mathrm{conv}})$ (interplay effect)	$\%(\mid {\overline{D}}_{\mathrm{seg}\mathrm{conv}}-{\overline{D}}_{\text{static}}\mid ∕{\overline{D}}_{\mathrm{seg}\mathrm{conv}})$ (motion and interplay effect)
15	4	40 s delay [Fig. 1a]	5.3	1.2
	4	100 s delay [Fig. 1c]	25.9	33.5
17	52	40 s delay [Fig. 1a]	5.0	6.8
	52	100 s delay [Fig. 1c]	0.2	2.2

Similarly, when the delivery of a large monitor unit segment (such as segment 17, with 52 MU) coincides with a large excursion of motion [as in Fig. 1a], the interplay effect can result in a segmental PDF that differs considerably from the average PDF. The dosimetric difference is apparent in Fig. 2c; the mean CTV dose is reduced by 5.0% and 6.8% for the average-based convolution and static condition, respectively. Clearly, when there is very little motion during delivery of a large monitor unit segment, [such as segment 17, with 52 MU in Fig. 1c], the difference between the segment-based convolution approach and the average-based convolution are insignificant [Fig. 2d].

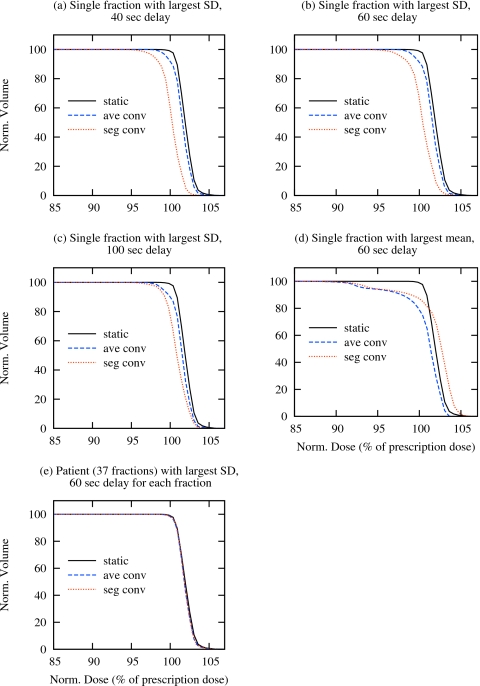
Figures 3a, 3b, 3c show prostate DVHs for single-fraction plans, following the synchronization schemes of Figs. 1a, 1b, 1c, from the tracking fraction which exhibits the largest SD in their intrafraction prostate motion. Differences are apparent when accounting for intrafraction motion alone (ave. conv.) and intrafraction motion with the interplay effect (seg. conv.), though these differences are small (note that the DVHs have been magnified). These effects are further quantified in Tables 2, 3, which show the variation in prostate gEUD and prostate minimum dose, respectively. Under this motion scenario, which again represents the largest variation observed in 1267 fractions, the maximum reduction in prostate gEUD due to interplay is 1.3%, while that due to intrafraction motion and interplay in conjunction is 1.7%. The compromise in terms of minimum prostate dose is, however, more significant. While the average-based convolution provides prostate coverage above 95% of the nominal dose, coverage in the segment-based approach falls short by 4.4%. Figure 3d shows the dose volume histograms for the plan which incorporates tracking data from the fraction exhibiting the largest average motion [Fig. 1d]. In this case, the difference between the static calculation and either of the convolution approaches is equally significant. The impact of interplay on the prostate gEUD is 1.2% in the worst case, increasing to 2.1% when both intrafraction motion and interplay accounted for (Table 2). In both approaches the prostate is significantly underdosed (Table 3).

Figure 3.

Comparison of prostate DVHs for a single patient for static, average- and segment-based convolution plans, which are delivered in single fraction [(a)–(d)] or 37 fractions (e). The single-fraction plan incorporates the tracking data from the fraction with largest SD or mean among all 1267 fractions. The plan delivered in 37 fractions incorporates the tracking data from the patient with largest overall SD among all 35 patients. For the fraction with largest SD, the synchronization between the motion and delivery is varied to evaluate the maximum interplay effect.

Table 2.

Comparison of the CTV gEUD among the static, average- and segment-based convolution plans delivered in a single fraction and in 37 fractions (entire treatment course). The single-fraction plans incorporated the tracking data from the fractions with largest SD and mean; while the plans for the entire treatment incorporated the motion of the patient with largest overall SD. Column 3 shows the differences due to the interplay effect (i.e., differences between the two convolution methods) while column 4 shows the differences due to the combined effect of the intrafraction motion and interplay.

Motion scenario	IMRT plan	%(∣gEUDseg conv−gEUDave conv∣∕gEUGseg conv) (interplay effect)	%(∣gEUDseg conv−gEUDstatic∣∕gEUDseg conv) (motion and interplay effect)
Single fraction with largest motion variation (SD)	1	0.9	1.7
	2	1.3	1.7
Single fraction with largest mean motion	1	1.2	1.0
	2	1.1	2.1
Patient with largest motion variation (SD)	1	0.0	0.1
	2	0.0	0.1

Table 3.

Comparison of the minimum CTV dose (in % of the nominal dose) among the static, average- and segment-based convolution plans in a single fraction and in 37 fractions (entire treatment course). The single-fraction plans incorporated the tracking data from the fractions with largest SD and mean; the plans delivered in 37 fractions incorporated the motion of the patient with largest overall SD

Motion scenario	IMRT plan	Minimum CTV dose (% of nominal dose)
		Static plan	Ave. conv. plan	Seg. conv. plan
Fraction with largest motion variation (SD)	1	98.2	97.2	92.8
	2	98.1	95.8	93.2
Fraction with largest mean motion	1	98.2	86.0	86.0
	2	98.1	83.3	84.8
Patient with largest motion variation (SD)	1	98.2	97.3	97.3
	2	98.1	97.2	97.0

For comparison, DVHs for plans incorporating the tracking data of the single patient with largest variation (SD) in prostate motion over the course of 37 fractions are shown in Fig. 3e. Any difference between intrafraction motion and∕or interplay effect and the static case, in terms of either gEUD (Table 2) and the minimum dose to the prostate (Table 3), are negligible.

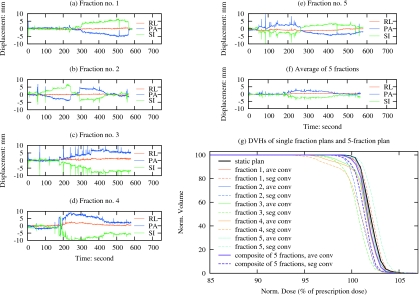
Finally, to evaluate the effect of intrafraction motion and interplay effect on a hypofractionated regimen, plans were created incorporating tracking data from the five fractions exhibiting the largest variation in prostate motion (SD), all from the single patient also exhibiting the largest variation in prostate motion over the entire course of treatment. Figures 4a, 4b, 4c, 4d, 4e show the tracking data for each of the five fractions. While individual fractions exhibit significant variation in motion magnitude and∕or direction, the variation within the average motion [Fig. 4f] is significantly less. For comparison, five single-fraction plans were created, each incorporating a different tracking data set from Figs. 4a, 4b, 4c, 4d, 4e. Figure 4g shows a comparison of DVHs from a static plan, the individual single-fraction plans, and the composite five fraction plan, each accounting intrafraction motion with and without the interplay effect. Tables 4, 5 show the minimum CTV coverage and gEUD, respectively, comparing the segment-based convolution approach with the average-based convolution (intrafraction motion without interplay effect) and in the absence of intrafraction motion (static). The minimum dose to the CTV is reduced in both cases, for the individual fractions specifically, and less so for the five fraction course of treatment. However, the combined effects produce differences in gEUD of 1.7% or less in the single fraction plans while differences for the interplay effect alone are all less than 1.0%. The overall impact on gEUD for the five fraction course treatment is negligible in both cases.

Figure 4.

Comparison of prostate DVHs for the static, average- and segment-based convolution plans, which are delivered in one or in five fractions. Each single-fraction plan incorporates the tracking data from one of the five fractions exhibiting the largest SD, as shown in [(a)–(e)], from the patient who was also observed to exhibit the largest SD over the course of treatment. The five-fraction plan incorporates the tracking data from all five fractions. The average of the five motion traces in (a)–(e) is shown in (f).

Table 4.

Comparison of the minimum CTV dose (in % of the nominal dose) among the static, average- and segment-based convolution plans for five individual fractions and a composite plan consisting of all five fractions. The tracking data for the individual fractions are those with the largest SDs from the patient also with the largest SD among all 35 patients. Calculations are based on IMRT plans constructed for patient 1.

Fraction	Minimum CTV dose (% of nominal dose)
	Static plan	Ave. conv. plan	Seg. conv. plan
1	98.2	96.6	96.5
2	98.2	98.2	96.2
3	98.2	94.6	90.5
4	98.2	93.9	90.7
5	98.2	96.2	96.8
Five-fraction composite	98.2	97.7	96.9

Table 5.

Comparison of the CTV gEUD among the static, average- and segment-based convolved plans for five individual fractions and a composite plan consisting of all five fractions. The tracking data for the individual fractions are those with the largest SDs from the patient also with the largest SD among all 35 patients. Column 2 shows the differences due to interplay effect alone while column 3 shows the differences due to the combined effect of the intrafraction motion and interplay. Calculations are based on IMRT plans constructed for patient 1.

Fraction	%(∣gEUDseg conv−gEUDave conv∣∕gEUGseg conv) (interplay effect)	%(∣gEUDseg conv−gEUDstatic∣∕gEUDseg conv) (motion and interplay effect)
1	0.3	0.1
2	0.9	1.0
3	0.9	1.6
4	0.8	1.7
5	0.6	0.5
Five-fraction composite	0.4	0.7

DISCUSSION

To accurately evaluate the dose delivered by segmental IMRT delivery in the presence of motion, PDFs for individual segments can be derived by binning the motion data from individual fractions according to their monitor unit within each IMRT segment. This assumes that information is available with respect to the synchronization between the tracking data and treatment. Intratreatment interruptions, such as motion of the gantry between beams, were also neglected.

In this study, the interplay effect was quantified retrospectively, using the motion data tracked through dose delivery of each fraction. In the case that the motion trajectory for each segment can be predicted in advance, the approach can also be used prospectively to mitigate the discrepancy between the planned and delivered dose due to interplay and intrafraction motion by incorporating the segment-based convolved dose into IMRT optimization.²²

In the case of respiratory motion, Seco et al.⁸ have reported that in two patients treated with five IMRT beams over 30 fractions, there was a likelihood of up to 7.0% and 33.9% that the dose error due to interplay was greater than 1%. In one patient there was a 12.6% likelihood of a 2% dose error; for segments delivering less than 10–15 MU, errors were considerably larger. Based on these observations, they recommended that small monitor unit segments be avoided in order to reduce the significance of the interplay effect. Though the prostate IMRT plans in this study contained many small segments with small numbers of monitor units, the overall interplay effect was considerably less than that reported by Seco et al.⁸ In one plan containing 36 total segments, 13 segments used 5 MU or less, and 11 more used 10 MU or less. There are several reasons why the interplay effect is less for prostate motion than for respiratory motion. First, intrafraction prostate motion is quite random; in the 1267 fractions evaluated in this study, approximately 75% exhibited very small standard deviations. In contrast, respiratory motion is relatively periodic and therefore systematic; thus each fraction experiences the same extent of variation in magnitude and phase. Second, the amplitude of intrafraction prostate motion is significantly less than that of respiratory motion. In our population of 35 patients, the largest intrafraction motion observed in one fraction was 7.9±2.4 mm (mean±SD); the largest intrafraction motion observed in any one patient (over all fractions) was 2.4±1.8 mm.¹⁹ Seco et al.⁸ employed amplitudes between 2 and 4 cm.

When applying the segment-based convolution to evaluate the dose delivered in the presence of intrafraction motion and MLC interplay, we have assumed that the traditional average-based convolution method is sufficient to account for intrafraction motion in absence of the interplay effect. This also assumes “shift invariance,”¹³ i.e., that the dose distribution does not vary when a patient or organ is shifted by a clinically reasonable distance. Though this assumption may fail in the presence of internal tissue heterogeneities and surface curvature, the investigation by Craig et al.¹³ showed that the resulting errors are very small for patients with deep-seated tumor such as prostate cancer.

CONCLUSION

We have used a segment-based convolution approach to quantify the interplay effect in treatment planning and dose delivery with step-and-shoot IMRT under conditions of intrafraction prostate motion. In this study we observed errors as large as 25.9% in mean CTV dose for single segment delivery; for entire fraction, errors of 1.3% in CTV gEUD and 4.4% in the minimum CTV dose. The interplay effect becomes negligible when treatment is delivered in either a hypofractionation regimen (five fractions) or with conventional fractionation (30−40 fractions). For a hypofractionated and conventionally fractionated treatment course, we observed a maximum error in the resulting gEUD of 0.4% and 0.1%, respectively; the minimum CTV dose variation was also negligible.

For the purpose of evaluating the cumulative physical dose delivered by multiple fractions (≥5) under intrafraction prostate motion, the conventional average-based convolution appears to be sufficiently accurate. While the interplay effect is of little significance in conventional treatment of prostate cancer, the method can easily be extended to other tumor sites in which motion data can be obtained. It should also be pointed out that our application focused only on segmental IMRT delivery; extension of this approach to the case of IMRT delivered by dynamic MLC is not straightforward.