Abstract
Purpose: Finite element method (FEM) models are commonly used to simulate radio frequency (RF) tumor ablation. Prior FEM models of RF ablation have either ignored the temperature dependent effect of microvascular perfusion, or implemented the effect using simplified algorithms to reduce computational complexity. In this FEM modeling study, the authors compared the effect of different microvascular perfusion algorithms on ablation zone dimensions with two commercial RF electrodes in hepatic tissue. They also examine the effect of tissue type and inter-patient variation of perfusion on ablation zone dimensions. Methods and Materials: The authors created FEM models of an internally cooled and multi-tined expandable electrode. RF voltage was applied to both electrodes (for 12 or 15 min, respectively) such that the maximum temperature in the model was 105 °C. Temperature dependent microvascular perfusion was implemented using three previously reported methodologies: cessation above 60 °C, a standard first-order Arrhenius model with decreasing perfusion with increasing degree of vascular stasis, and an Arrhenius model that included the effects of increasing perfusion at the ablation zone boundary due to hyperemia. To examine the effects of interpatient variation, simulations were performed with base line and ±1 standard deviation values of perfusion. The base line perfusion was also varied to simulate the difference between normal and cirrhotic liver tissue. Results: The ablation zone volumes with the cessation above 60 °C perfusion algorithm and with the more complex Arrhenius model were up to 70% and 25% smaller, respectively, compared to the standard Arrhenius model. Ablation zone volumes were up to ∼175% and ∼100% different between the simulations where −1 and +1 standard deviation values of perfusion were used in normal and cirrhotic liver tissue, respectively. Conclusions: The choice of microvascular perfusion algorithm has significant effects on final ablation zone dimensions in FEM models of RF ablation. The authors also found that both interpatient variation in base line tissue perfusion and the reduction in perfusion due to cirrhosis have considerable effect on ablation zone dimensions.
Keywords: thermal ablation, radiofrequency ablation, rf ablation, tumor ablation, bio-heat transfer
INTRODUCTION
Radio frequency (RF) ablation is a local treatment method for inoperable cancer of liver, as well as in other organs such as kidney, lung, bone, and adrenal gland.1, 2, 3, 4 Computational finite element method (FEM) models of tumor ablation have been used in several previous studies to examine the impact of changes in tissue properties on temperature profiles5, 6 and to examine the impact of microvascular7, 8 and macrovascular perfusion.9, 10 Microvascular perfusion occurs at the capillary level and affects the overall ablation zone size and shape,8, 11, 12 while macrovascular perfusion refers to the heat sink effect of large blood vessels that results in local ablation zone deviations.9, 13, 14 Both types of tissue perfusion are of particular importance in tumor ablation procedures, as they significantly influence ablation zone dimensions.
In this study, we examined the significance of microvascular perfusion implementation in FEM modeling of tumor ablation. While all previous studies have utilized the bioheat equation as conceived by Pennes et al. as the principal microvascular perfusion model,15 the implementation of temperature-dependent effects on perfusion has varied. Several models have assumed constant perfusion independent of temperature,9, 10, 16, 17, 18, 19, 20, 21, 22 while other studies have assumed either a threshold temperature above which perfusion is absent due to vascular coagulation,5, 8, 23 or cessation of perfusion according to a first-order kinetic Arrhenius model.7, 24, 25, 26 However, it is well documented that during RF ablation, a hyperemic region exists near the ablation zone in tissue that is at hyperthermic temperatures (below ∼45 °C),27 which results in increased perfusion mediated cooling in the tissue adjacent to the ablation zone.14, 28, 29 A more complex perfusion model that includes the effects of increased perfusion (up to 1.6×) in the hyperemic zone as well as subsequent perfusion cessation according to a first-order kinetic Arrhenius model has been included in a study on thermal injury of porcine kidney by He et al., where perfusion parameters were determined from in vivo measurements.30 While a similar study is not available for liver tissue, it has been shown that perfusion increases by a maximum factor of 1.5 in proximity to the ablation zone in a mouse liver model,28 which is similar to the maximum perfusion increase seen in the He et al. kidney study (1.6x).30
The current study aims to answer the following questions:
-
(1)
How does the inclusion of the hyperemic region in the perfusion model implementation affect tissue temperature profile and ablation zone dimensions?
-
(2)
How do ablation zone dimensions change due to interpatient variation of perfusion rates in both healthy and cirrhotic liver tissue?
MATERIAL AND METHODS
FEM software
We used PATRAN 2005 r2 (The MacNeal–Schwendler Co., Los Angeles, CA) to create model geometries, perform meshing, and assign all temperature and voltage boundary conditions. The software generated data files suitable for use with ABAQUS∕STANDARD 6.5 FEM solver software (Hibbitt, Karlsson, and Sorensen, Inc., Pawtucket, RI). We used the built-in POST module in ABAQUS for postprocessing to create profiles of electric potential, temperature, thermal damage, and survival fraction. All simulations were run on a Dell Optiplex GX620 workstation with 3 GB of RAM.
FEM model geometry
We created models of two different commercial RF electrodes in this study. The first was a three-dimensional (3D) model of a multi-tined expandable electrode (Rita Starburst XL, Angiodynamics, Queensbury, NY) (Fig. 1) which was placed in the center of a cylinder (320 mm high×320 mm diam) of normal liver tissue with the tines fully deployed to a length of 40 mm. Due to the symmetry of the electrode geometry, we only modeled a quarter of the cylinder to reduce computational time.
Figure 1.
Fully deployed Rita Starburst XL electrode used in FEM. The prongs and the distal 5 mm of the shaft are electrically conductive.
The second modeled electrode (Cool-tip, Valleylab, Boulder, CO) was internally cooled with an active length of 30 mm. This electrode was represented in a two-dimensional axisymmetric model (due to its geometry) in which the electrode was placed at the edge of a block of normal liver tissue 170 mm high with a radius of 100 mm.
The mesh parameters for both models are shown in Table 1, and a close-up of the mesh at the tip of both electrode types is shown in Fig. 2. In both models, the distance between adjacent nodes increased with the distance from the RF electrode. We performed convergence tests with varying mesh size to ensure that no errors result due to insufficient element size. However, we did use a finer mesh than suggested by convergence tests in the two-dimensional (2D) model since simulation time was not an issue there.
Table 1.
Mesh parameters for the internally cooled and multi-tined expandable electrode models.
| Electrode type | Model type | Element type | No. of nodes | No. of elements | Node spacing (mm) |
|---|---|---|---|---|---|
| Internally cooled | 2D axisymmetric | Triangular (first order) | 18 000 | 36 000 | 0.1–4 |
| Multi-tined expandable | 3D | Tetrahedral (first order) | 35 000 | 189 000 | 0.1–8 |
Figure 2.
Close-up of mesh around the tip of the internally cooled (a) and multi-tined expandable electrodes (b). The node spacing at the boundary between the tissue (white) and the electrodes (gray) was 0.1 mm.
Electric field equations
During RF ablation, the applied alternating electric field results in tissue heating due to both resistive heating and dielectric losses (caused by the rotation of molecules in an alternating electric field). At radio frequencies, however, resistive heating due to conduction currents is the dominant heating mechanism and dielectric losses are negligible.31 Thus, we can determine the resulting electric field in the tissue from Laplace’s equation
| (1) |
where σ is the electrical tissue conductivity (S∕m) and V represents the electric potential (V). The boundary conditions for the electric field problem are
| (2) |
| (3) |
Equation 2 describes that ground potential (0 V) was applied to the model boundaries for both models. Equation 3 describes that a varying voltage was applied to the active part of the electrodes. The voltage was varied using a proportional-integral controller so that the maximum temperature at the hottest node of both models was 105 °C.
Electric field intensity E (V∕m) and current density J (A∕m2) are calculated from
| (4) |
| (5) |
The power density produced by the electric field is determined by the product of current density J and electric field intensity E [refer to Eq. 6, second term on right side].
Bioheat equation
The coupled thermal-electrical models that we created in this study used the Pennes bioheat equation [Eq. 3] to determine tissue temperature profiles during RF ablation.15 The equation considers the effects of thermal conduction, resistive heating due to RF energy deposition and tissue cooling due to microvascular blood perfusion. In the absence of large blood vessels (i.e., macrovascular perfusion), the Pennes model has been shown to describe the effect of blood perfusion with acceptable accuracy32
| (6) |
where ρ is the density (kg∕m3), c is the specific heat [J∕(kg K)], k is the thermal conductivity [W∕(m K)], J is the current density (A∕m2), E is the electric field intensity (V∕m), Tbl is the temperature of blood (°C), ρbl is the blood density (kg∕m3), Cbl is the specific heat of blood [J∕(kg K)], Wbl is the blood perfusion [m3∕(m3 s)], and Qm is the metabolic heat production (W∕m3).
The metabolic heat production per volume term Qm was ignored due to its relatively small size compared to the other terms.33
Thermal boundary conditions and material properties
The initial temperature for all elements and the boundary temperature were set at 37 °C. To simulate the internal cooling of the Cool-tip electrode, a boundary condition of 10 °C (typically seen during clinical procedures) was applied to the entire electrode shaft. We simulated ablation for 15 min in the multi-tined expandable model and for 12 min in the internally cooled model, which are standard clinical treatment times for both electrode systems. For the internally cooled electrode model, we also simulated (for 1 min) the post-ablation period where the internal cooling flow is deactivated to allow the ablation zone to fill in adjacent to the electrode.
Table 2 shows the material properties from the literature that were used in both models.34 The temperature dependence of the electrical conductivity of liver tissue was implemented as a coefficient of 1.5% °C−1.35 Temperature dependence of the thermal conductivity of liver tissue was implemented according to ex vivo measurements from a prior study.34 The value of latent heat of vaporization for water was used for liver tissue as in previous studies.36, 37 We did not include any changes in electrical tissue conductivity due to tissue vaporization above 100 °C because these data were unavailable.
Table 2.
Model material properties, where ρ is mass density, c is specific heat, k is thermal conductivity, and σ is electrical conductivity. All values represent properties at 37 °C.
| Element | Material | ρ (kg∕m3) | c [J∕(kg K)] | k [W∕(m K)] | σ (S∕m) | Latent heat of vaporization (J∕kg) |
|---|---|---|---|---|---|---|
| Electrode | Stainless steel | 21 500 | 132 | 71 | 4×107 | NA |
| Shaft | Polyurethane | 70 | 1045 | 0.03 | 1×10−5 | NA |
| Tissue | Liver | 1060 | 3500 | 0.51 | 0.36 | 2.25×106 |
Perfusion algorithms and experimental groups
The magnitude of the perfusion term wbl was varied with temperature using three different algorithms that have been previously utilized in thermal ablation models. In the first, the perfusion for each element was constant until the temperature crossed the 60 °C threshold, after which it was set to 0 for the remainder of the simulation (representing complete vascular coagulation).5, 8 The second algorithm employed a first-order kinetic Arrhenius model of vascular coagulation in which perfusion decreased linearly as the degree of vascular stasis increased, as shown in Eqs. 7, 8,30
| (7) |
| (8) |
where DS is degree of vascular stasis (between 0 and 1), T(τ) is the absolute temperature as a function of time, R is the universal gas constant (8.314 J mole−1 K−1), A is the frequency factor (1.98×10106 s−1), ΔE is the activation energy (6.67×105 J mole−1), w(t) represents the time dependent perfusion, and wo is the base line perfusion. The values for ΔE and A were taken from a previous experimental study in muscle tissue.38
The third algorithm also used the first-order kinetic Arrhenius model of vascular stasis with the parameters shown above [Eqs. 7, 8], but also included an increase in relative perfusion when the degree of stasis is low (between 0 and 0.02) (Fig. 3). Since there are no studies showing perfusion versus degree of stasis in liver tissue, we used a curve determined experimentally by He et al. in a previous animal study in renal tissue.30
Figure 3.
Relative perfusion vs degree of stasis (DS) used in algorithm 2 and 3. For algorithm 3 (solid line), the graph depicts the original curve determined experimentally in renal tissue in He et al. (Ref. 30), which was modeled as a series of linear approximations. For algorithm 2 (dotted line), the relative perfusion was inversely proportional to DS.
In our model, the relative perfusion from Fig. 3 was separated into four linear approximations to reduce computational time [Eqs. 9, 10, 11, 12]. The average error for the approximations was ∼5%,
| (9) |
| (10) |
| (11) |
| (12) |
We performed a total of 16 simulations in this study (Table 3). For each electrode type, we ran a simulation using each of the three perfusion algorithms described above with a value for normal liver tissue perfusion according to data from measurements in humans.39 To examine the effect of intrapatient variation of hepatic perfusion, we also ran simulations using algorithm 3 (i.e., first-order kinetic Arrhenius model with increase in perfusion at low degree of vascular stasis) in normal liver tissue with perfusion values ±1 standard deviation from the base line value, based on human data.39 Additionally, we performed simulations with algorithm 3 (Fig. 3) in which we used the average and ±1 standard deviation values of perfusion for cirrhotic human liver tissue.39 We used the reported base line perfusion value for Child–Pugh class B cirrhosis in our models since RF tumor ablation is typically contraindicated for class C cirrhosis cases (i.e., the most severe cases).40, 41, 42
Table 3.
Summary of simulations. We performed eight different simulations with each electrode type. In algorithm 1, perfusion was constant up to 60 °C and zero above it. Algorithm 2 included a linear decrease in relative perfusion based on a first order kinetic model of vascular stasis, while algorithm 3 added the effects of increased perfusion at low degrees of vascular stasis to algorithm 2 (Fig. 3).
| Algorithm | Tissue type | Perfusion | Wbl (mL∕min 100 mL) |
|---|---|---|---|
| 1 | Normal | Average | 108 |
| 2 | Normal | Average | 108 |
| 3 | Normal | Average | 108 |
| 3 | Normal | +1 Stdev | 142 |
| 3 | Normal | −1 Stdev | 74 |
| 3 | Cirrhotic | Average | 69 |
| 3 | Cirrhotic | +1 Stdev | 99 |
| 3 | Cirrhotic | −1 Stdev | 39 |
Ablation zone boundary calculation
To determine the boundaries of each simulated ablation zone, we utilized an Arrhenius damage model as shown in Eq. 13, where thermal damage Ω(t) is related to the expected cellular survival fraction as shown in Eq. 14,
| (13) |
| (14) |
where A is the frequency factor (2.984×1080 s−1), ΔE is the activation energy (5.064×105 J mole−1), T(τ) is the absolute temperature as a function of time, c(t) represents the concentration of living cells as a function of time, and c(0) is the initial concentration of living cells. The values for ΔE and A in Eq. 13 were shown in a previous experimental study to accurately predict the cell death boundary in an animal model when used with a threshold value of 4.6 for Ω(t) (which corresponds to 99.0% cell death).43 Note that while the equations used to calculate thermal damage [Eq. 13] and degree of vascular stasis [Eq. 7] have the same form, the optimal values for A and ΔE (determined in experimental studies) are different in the two equations. For both electrode types, the axial and maximal transverse diameters were determined from the thermal damage profile using this threshold value. To determine ablation zone volume for the multi-tined electrode model, we created a custom program (Microsoft Visual C++, Redmond, WA) that calculated and summed the volumes of all elements that had at least one node above the thermal damage threshold. For the internally cooled electrode model, we manually selected a series of points along the thermal damage threshold; ablation zone volume was then calculated as the sum of the solid of revolution integrals for each set of adjacent points.
Limitations
In this study, we examine the effect of lower hepatic blood flow due to cirrhosis on ablation zone dimensions during RF ablation. However, cirrhotic tissue may have different thermal and electric properties from normal liver tissue; these data are, however, not available in the literature. These differences may lead to inaccurate modeling results.
RESULTS
The final ablation zone dimensions from all 16 simulations are summarized in Table 4. A comparison of the temperature profile to the cell survival fraction for a representative trial with each electrode is shown in Fig. 4. Additionally, a comparison of temperature and relative perfusion using algorithm 3 with the multi-tined electrode is shown in Fig. 5. For clarity, all graphical representations of the multi-tined expandable electrode show a representative two-dimensional plane intersecting three of the tines of the three-dimensional model.
Table 4.
Ablation zone dimensions for all trials. Note: in two trials (marked with *) with the multi-tined expandable electrode, the zones of cell death around each tine were not confluent.
| Probe | Tissue | Relative perfusion | Wbl (mL∕min 100 mL) | Algorithm | Axial diameter (cm) | Maximal transverse diameter (cm) | Volume (cm3) |
|---|---|---|---|---|---|---|---|
| Internally cooled | Normal | Normal | 108 | 1 | 3.87 | 1.90 | 9.07 |
| Internally cooled | Normal | Normal | 108 | 2 | 4.22 | 2.78 | 19.31 |
| Internally cooled | Normal | Normal | 108 | 3 | 4.16 | 2.66 | 17.80 |
| Internally cooled | Normal | +1 sigma | 142 | 3 | 4.05 | 2.42 | 14.58 |
| Internally cooled | Normal | −1 sigma | 74 | 3 | 4.31 | 2.98 | 22.61 |
| Internally cooled | Cirrhotic | Normal | 69 | 3 | 4.33 | 3.02 | 23.50 |
| Internally cooled | Cirrhotic | +1 sigma | 99 | 3 | 4.20 | 2.74 | 18.94 |
| Internally cooled | Cirrhotic | −1 sigma | 39 | 3 | 4.56 | 3.44 | 31.82 |
| Multi-tined expandable* | Normal | Normal | 108 | 1 | 2.29 | 1.86 | 12.15 |
| Multi-tined expandable | Normal | Normal | 108 | 2 | 5.75 | 5.00 | 40.38 |
| Multi-tined expandable | Normal | Normal | 108 | 3 | 5.62 | 4.90 | 32.69 |
| Multi-tined expandable* | Normal | +1 sigma | 142 | 3 | 2.70 | 2.20 | 17.83 |
| Multi-tined expandable | Normal | −1 sigma | 74 | 3 | 5.90 | 5.32 | 49.37 |
| Multi-tined expandable | Cirrhotic | Normal | 69 | 3 | 5.98 | 5.34 | 52.25 |
| Multi-tined expandable | Cirrhotic | +1 sigma | 99 | 3 | 5.68 | 4.98 | 37.32 |
| Multi-tined expandable | Cirrhotic | −1 sigma | 39 | 3 | 6.34 | 5.82 | 73.39 |
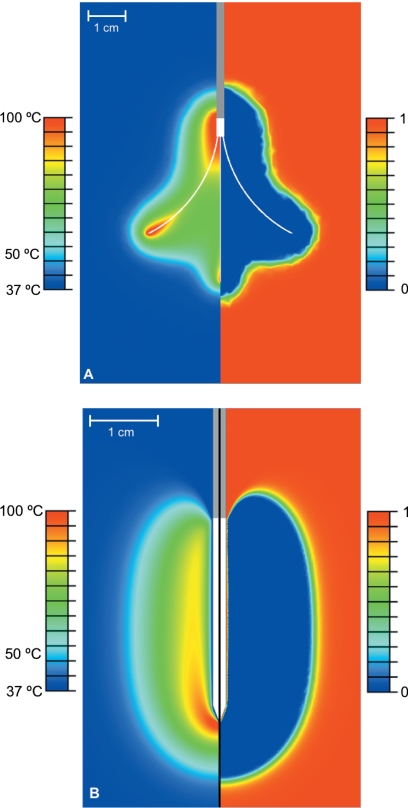
Figure 4.
Comparison of temperature (left side of pictures) and survival fraction (right side of pictures) for (a) the multi-tined expandable electrode and (b) the internally cooled needle electrode (with normal tissue, base line perfusion, and algorithm 3). A survival fraction of 1 indicates no cell death and a survival fraction of 0 indicates 100% cell death. A value of 0.01 for the survival fraction (corresponding to 99.0% cell death) was used to calculate ablation zone dimensions. In picture (a), temperature and cell death profile are shown after 15 min of power application, while in picture (b), the profiles are shown immediately after 12 min (1 min period without power or cooling flow not shown).
Figure 5.
Comparison of temperature (left) and relative perfusion (right) for the multi-tined expandable electrode. The relative perfusion varied from 0 to 1.6 times the base line value for the trial, based on the degree of stasis calculated using Eqs. 7, 8, 9, 10, 11, 12.
The differences in ablation zone dimensions due to the perfusion algorithm implemented, changes in perfusion rate, and in normal versus cirrhotic tissue for both electrodes are shown in Figs. 6789. (Note: the results for both electrode models were mirrored around the central symmetry axis to show the complete plane.)
Figure 6.
Comparison of ablation zone dimensions (based on 99.0% cell death isocontour) using the three different perfusion algorithms in (a) the multi-tined expandable electrode model and (b) the internally cooled needle electrode model. The black line represents algorithm 1 (no perfusion after 60 °C), the light gray line represents algorithm 2 (standard Arrhenius model), and the dark gray line represents algorithm 3 (Arrhenius model with hyperemic region).
Figure 7.
Comparison of ablation zone dimensions (based on 99.0% cell death isocontour) in normal liver tissue using three different perfusion rates with (a) the multi-tined expandable electrode model and (b) the internally cooled needle electrode model. The dark gray line represents base line perfusion, while the light gray and black lines denote +∕− one standard deviation perfusion, respectively.
Figure 8.
Comparison of ablation zone dimensions (based on 99.0% cell death isocontour) in cirrhotic liver tissue using three different perfusion rates with (a) the multi-tined expandable electrode model and (b) the internally cooled needle electrode model. The dark gray line represents base line perfusion, while the light gray and black lines denote +∕− one standard deviation perfusion, respectively.
Figure 9.
Comparison of ablation zone dimensions (based on 99.0% cell death isocontour) for normal and cirrhotic liver tissue with their respective base line perfusion rates in (a) the multi-tined expandable electrode model and (b) the internally cooled needle electrode model. The black line represents normal liver tissue and the gray line represents cirrhotic liver tissue.
DISCUSSION
Computational heat-transfer models have been frequently used to determine tissue temperature profile during ablation therapies7, 8, 9, 16, 17, 18, 19, 20, 21, 22, 24, 26, 30, 44 as well as hyperthermia therapies.45, 46, 47 To date, most of these models have included microvascular tissue perfusion according to Pennes’ bioheat equation,15 since this perfusion model is simple to implement and has been shown to accurately describe blood perfusion in the absence of large vessels.32 However, the modeling of temperature-dependent effects on tissue perfusion has varied between studies. In this study, we compared different implementations of temperature-dependent perfusion that were utilized in prior studies. In particular, one of the temperature-dependent perfusion algorithms that we investigated, which was based on data from a previous in vivo study in renal tissue, included the effect of hyperemia that occurs adjacent to the ablation zone boundary during thermal ablation.30 Although the existence of this hyperemic region has been well documented,14, 28, 29 its effect on the formation of the ablation zone has not been included in any previous computational models of hepatic tumor ablation. For all simulations, we used an Arrhenius type damage model to determine ablation zone boundary as has been used in previous studies.25, 26, 30, 43 The ablation zone boundary correlated with final tissue temperatures in the range of 48–50 °C in our models.
Since hepatic RF ablation protocols generally call for the ablation (i.e., coagulation) of both the tumor and a ∼1 cm margin of surrounding normal liver tissue, in most cases the entire tumor will reach temperatures that will cause coagulation, leaving the tumor devoid of perfusion at some point during the ablation. Therefore, the perfusion of normal liver tissue (i.e., the tissue at the final boundary of the ablation zone) is likely more significant than the tumor perfusion in determining the tissue temperature profile and final ablation zone dimensions. Thus, in this study, we only considered a single tissue type in each model with one base line perfusion rate for all tissue in the model.
Overall, the ablation zone dimensions from our simulations with the internally cooled electrode in normal tissue with algorithm 3 (Table 4) were near the average values reported in previous in vivo experiments in a porcine liver model.48 The ablation zone dimensions from our simulated ablations with the multi-tined expandable electrode in normal tissue with algorithm 3 (Table 4) were slightly larger (18% and 30% for transverse and axial diameters, respectively) than those reported in another in vivo porcine liver experiment.49 The ablation zone sizes are, however, smaller compared to those reported in clinical literature,48 likely due to reduced blood flow in tumors compared to normal liver as suggested by a recent study.50
We found that ablation zone dimensions after 12 min were considerably different between the three perfusion algorithms with both electrode types (Table 4, Fig. 6), with more pronounced differences in the multi-tined expandable electrode trials. The simulations using algorithm 1 in particular produced markedly (as much as 70%) lower ablation zone volumes than the simulations that were based on the Arrhenius model (algorithms 2 and 3). Additionally, the use of the standard Arrhenius perfusion model (algorithm 2) resulted in ablation zone volumes that were as much as 25% larger than the simulations that used the more complex Arrhenius model that included the effect of the hyperemic region (algorithm 3). Due to these large differences, it is evident the choice of perfusion algorithm for RF tumor ablation models is important in generating accurate results.
In addition to comparing different temperature-dependent tissue perfusion implementations, we also investigated how interpatient variation in tissue perfusion affects the ablation zone geometry during hepatic RF ablation (using algorithm 3 as presented in He et al.30). A previous study examined how perfusion affects the 50 °C-isotherm (a commonly used estimate for the ablation zone boundary) over a wide range of perfusion values [0–60 mL∕min∕(100 mL)].8 They found that increased tissue perfusion reduced both the 50 °C-isotherm diameter and time required to reach thermal equilibrium. In the current study we investigated a more narrow range of perfusion values (based on average values measured in human patients) to determine how variation in perfusion between different patients may affect ablation zone dimensions.39 The values shown in Table 4 and depicted graphically in Figs. 78 represent the typical variation in ablation zone dimensions that can be expected due to differences in perfusion between patients. For normal liver tissue, we found that ablation zone volume increased by ∼175% and 55% for the multi-tined and internally cooled electrodes, respectively, as the perfusion rate was decreased from one standard deviation above to one standard deviation below the average rate (an interval which represents ∼70% of the population). This suggests that ablation zones created by the multi-tined electrode are more susceptible to variation in the perfusion rate than those created with the internally cooled electrode.
In addition to changes in perfusion rates among patients, perfusion may be purposely reduced via pharmacologic modulation to obtain large ablation zones.51 Computational models such as the ones presented may be used to estimate the impact of pharmacologic modulation if the magnitude of reduction in perfusion by a specific agent is known.
In the study that provided the base line perfusion values for the current work, patients with Child–Pugh class B cirrhosis had ∼36% lower hepatic perfusion than the control patients (Table 3).39 The lower perfusion rate of cirrhotic tissue is of particular importance for RF tumor ablation because approximately 90% of patients with primary liver cancer (HCC) suffer from cirrhosis.52 Table 4 shows how ablation zone volume and diameters were affected when perfusion was varied by +∕−1 standard deviation around the base line values reported in the previous study in cirrhotic tissue.39 We found that ablation zone volume increased by 97% and 68% for the multi-tined and internally cooled electrodes, respectively, over the perfusion range in this tissue type. Note that for both electrode types and both tissue types, an increase in perfusion had a greater effect on the maximal transverse diameter than it did on the axial diameter (Table 4, Figs. 78).
Due to the lower perfusion rates in cirrhotic patients, larger ablation zones were produced in cirrhotic liver tissue than in normal liver tissue (Table 4, Fig. 9). However, as mentioned in Sec. 2H, it is important to consider that thermal and electrical tissue properties may be different in cirrhotic liver tissue than in normal liver tissue, which may affect tissue temperature profiles and consequently final ablation zone dimensions. Additionally, tissue perfusion varies not only between patients, but also varies between different locations in the liver of each individual patient. A pretreatment protocol utilizing patient- and site-specific measurement of tissue perfusion could allow for more accurate prediction of final ablation zone dimensions using computational models similar to those presented in this study.
CONCLUSION
We compared different perfusion implementations in computational models of RF tumor ablation and found that the inclusion of a hyperemic zone considerably changes tissue temperature profile in computational models of tumor ablation compared to a first order kinetic model only including cessation of perfusion. A model that assumes cessation above a threshold temperature is likely not sufficient as it does not consider the exponential time-temperature relationship of microvascular perfusion cessation. We also found that both interpatient variation in base line tissue perfusion and the reduced perfusion found in cirrhotic liver tissue have considerable effect on ablation zone dimensions. Finally, we found that perfusion affected the maximal transverse diameter more than the axial diameter of the ablation zone for both electrode types, and in general the ablation zones created with the multi-tined electrode were more susceptible to variation in perfusion than the ablation zones created with the internally cooled electrode.
ACKNOWLEDGMENTS
This work was conducted in a facility constructed with support from the National Institute of Health, Grant No. C06 RR018823 from the Extramural Research Facilities Program of the National Center for Research Resources. In addition, this work was supported by National Institute of Health Grant No. R01 CA108869.
References
- Gillams A. R., “The use of radio frequency in cancer,” Br. J. Cancer 92, 1825–1829 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- McTaggart R. A. and Dupuy D. E., “Thermal ablation of lung tumors,” J. Vasc. Interv. Radiol. 10, 102–113 (2007). [DOI] [PubMed] [Google Scholar]
- Schiller J. D., Gervais D. A., and Mueller P. R., “Radio frequency ablation of renal cell carcinoma,” Abdom. Imaging 30, 442–450 (2005). [DOI] [PubMed] [Google Scholar]
- Solbiati L., “Percutaneous ultrasound-guided radio frequency ablation of HCC and liver metastases: Results and long-term 7-year follow-up,” Ultrasound Med. Biol. 29, S48 (2003). [Google Scholar]
- Lobo S. M., Liu Z., Yu N. C., Humphries S., Ahmed M., Cosman E. R., Lenkinski R. E., Goldberg W., and Goldberg S. N., “RF tumour ablation: Computer simulation and mathematical modelling of the effects of electrical and thermal conductivity,” Int. J. Hyperthermia 21, 199–213 (2005). [DOI] [PubMed] [Google Scholar]
- Tungjitkusolmun S., Woo E. J., Cao H., Tsai J. Z., Vorperian V. R., and Webster J. G., “Thermal-electrical finite element modelling for radio frequency cardiac ablation: Effects of changes in myocardial properties,” Med. Biol. Eng. Comput. 10.1007/BF02345754 38, 562–568 (2000). [DOI] [PubMed] [Google Scholar]
- Chang I. A. and Nguyen U. D., “Thermal modeling of lesion growth with radio frequency ablation devices,” Biomed. Eng. Online 3, 27 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z., Ahmed M., Sabir A., Humphries S., and Goldberg S. N., “Computer modeling of the effect of perfusion on heating patterns in radio frequency tumor ablation,” Int. J. Hyperthermia 23, 49–58 (2007). [DOI] [PubMed] [Google Scholar]
- Haemmerich D., Wright A. W., Mahvi D. M., F. T.Lee, Jr., and Webster J. G., “Hepatic bipolar radio frequency ablation creates coagulation zones close to blood vessels: A finite element study,” Med. Biol. Eng. Comput. 41, 317–323 (2003). [DOI] [PubMed] [Google Scholar]
- Tungjitkusolmun S., Staelin S. T., Haemmerich D., Tsai J. Z., Cao H., Webster J. G., Lee F. T., Mahvi D. M., and Vorperian V. R., “Three-dimensional finite-element analyses for radio-frequency hepatic tumor ablation,” IEEE Trans. Biomed. Eng. 10.1109/10.972834 49, 3–9 (2002). [DOI] [PubMed] [Google Scholar]
- Aschoff A. J., Merkle E. M., Wong V., Zhang Q., Mendez M. M., Duerk J. L., and Lewin J. S., “How does alteration of hepatic blood flow affect liver perfusion and radio frequency-induced thermal lesion size in rabbit liver?,” J. Magn. Reson. Imaging 13, 57–63 (2001). [DOI] [PubMed] [Google Scholar]
- Goldberg S. N., Hahn P. F., Tanabe K. K., Mueller P. R., Schima W., Athanasoulis C. A., Compton C. C., Solbiati L., and Gazelle G. S., “Percutaneous radio frequency tissue ablation: Does perfusion-mediated tissue cooling limit coagulation necrosis?,” J. Vasc. Interv. Radiol. 9, 101–111 (1998). [DOI] [PubMed] [Google Scholar]
- Lu D. S., Raman S. S., Vodopich D. J., Wang M., Sayre J., and Lassman C., “Effect of vessel size on creation of hepatic radio frequency lesions in pigs: Assessment of the ‘heat sink’ effect,” AJR Am. J. Roentgenol. 178, 47–51 (2002). [DOI] [PubMed] [Google Scholar]
- Wright A. S., Sampson L. A., Warner T. F., Mahvi D. M., and F. T.Lee, Jr., “Radio frequency versus microwave ablation in a hepatic porcine model,” Radiology 236, 132–139 (2005). [DOI] [PubMed] [Google Scholar]
- Pennes H. H., “Analysis of tissue and arterial blood temperatures in the resting human forearm,” J. Appl. Physiol. 1, 93–122 (1948). [DOI] [PubMed] [Google Scholar]
- Chang I., “Finite element analysis of hepatic radio frequency ablation probes using temperature-dependent electrical conductivity,” Biomed. Eng. Online 2, 12 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haemmerich D., Staelin S. T., Tungjitkusolmun S., F. T.Lee, Jr., Mahvi D. M., and Webster J. G., “Hepatic bipolar radio-frequency ablation between separated multiprong electrodes,” IEEE Trans. Biomed. Eng. 10.1109/10.951517 48, 1145–1152 (2001). [DOI] [PubMed] [Google Scholar]
- Haemmerich D., Tungjitkusolmun S., Staelin S. T., F. T.Lee, Jr., Mahvi D. M., and Webster J. G., “Finite-element analysis of hepatic multiple probe radio-frequency ablation,” IEEE Trans. Biomed. Eng. 10.1109/TBME.2002.800790 49, 836–842 (2002). [DOI] [PubMed] [Google Scholar]
- Kolios M. C., Sherar M. D., and Hunt J. W., “Blood flow cooling and ultrasonic lesion formation,” Med. Phys. 10.1118/1.597694 23, 1287–1298 (1996). [DOI] [PubMed] [Google Scholar]
- Liang P., Dong B., Yu X., Yu D., Cheng Z., Su L., Peng J., Nan Q., and Wang H., “Computer-aided dynamic simulation of microwave-induced thermal distribution in coagulation of liver cancer,” IEEE Trans. Biomed. Eng. 48, 821–829 (2001). [DOI] [PubMed] [Google Scholar]
- Liu Z., Lobo S. M., Humphries S., Horkan C., Solazzo S. A., Hines-Peralta A. U., Lenkinski R. E., and Goldberg S. N., “Radio frequency tumor ablation: insight into improved efficacy using computer modeling,” AJR Am. J. Roentgenol. 184, 1347–1352 (2005). [DOI] [PubMed] [Google Scholar]
- Verhey J. F., Mohammed Y., Ludwig A., and Giese K., “Implementation of a practical model for light and heat distribution using laser-induced thermotherapy near to a large vessel,” Phys. Med. Biol. 10.1088/0031-9155/48/21/010 48, 3595–3610 (2003). [DOI] [PubMed] [Google Scholar]
- Schramm W., Yang D., Wood B. J., Rattay F., and Haemmerich D., “Contribution of direct heating, thermal conduction and perfusion during radio frequency and microwave ablation,” Open Biomed. Eng. J. 1, 47–52 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson P. C. and Saidel G. M., “Thermal model for fast simulation during magnetic resonance imaging guidance of radio frequency tumor ablation,” Ann. Biomed. Eng. 10.1114/1.1519263 30, 1152–1161 (2002). [DOI] [PubMed] [Google Scholar]
- Kim B. M., Jacques S. L., Rastegar S., Thomsen S., and Motamedi M., “Nonlinear finite-element analysis of the role of dynamic changes in blood perfusion and optical properties in laser coagulation of tissue,” IEEE J. Sel. Top. Quantum Electron. 10.1109/2944.577317 2, 922–933 (1996). [DOI] [Google Scholar]
- Schwarzmaier H. J., Yaroslavsky I. V., Yaroslavsky A. N., Fiedler V., Ulrich F., and Kahn T., “Treatment planning for MRI-guided laser-induced interstitial thermotherapy of brain tumors—The role of blood perfusion,” J. Magn. Reson. Imaging 8, 121–127 (1998). [DOI] [PubMed] [Google Scholar]
- Song C. W., Lokshina A., Rhee J. G., Patten M., and Levitt S. H., “Implication of blood flow in hyperthermic treatment of tumors,” IEEE Trans. Biomed. Eng. 10.1109/TBME.1984.325364 31, BME-9–BME-16 (1984). [DOI] [PubMed] [Google Scholar]
- Kruskal J. B., Oliver B., Huertas J. C., and Goldberg S. N., “Dynamic intrahepatic flow and cellular alterations during radio frequency ablation of liver tissue in mice,” J. Vasc. Interv. Radiol. 12, 1193–1201 (2001). [DOI] [PubMed] [Google Scholar]
- McGhana J. P. and Dodd G. D., “Radio frequency ablation of the liver: Current status,” AJR Am. J. Roentgenol. 176, 3–16 (2001). [DOI] [PubMed] [Google Scholar]
- He X., McGee S., Coad J. E., Schmidlin F., Iaizzo P. A., Swanlund D. J., Kluge S., Rudie E., and Bischof J. C., “Investigation of the thermal and tissue injury behaviour in microwave thermal therapy using a porcine kidney model,” Int. J. Hyperthermia 10.1080/0265673042000209770 20, 567–593 (2004). [DOI] [PubMed] [Google Scholar]
- Berjano E. J., “Theoretical modeling for radio frequency ablation: State-of-the-art and challenges for the future,” Biomed. Eng. Online 5, 24 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkin H., Xu L. X., and Holmes K. R., “Recent developments in modeling heat transfer in blood perfused tissues,” IEEE Trans. Biomed. Eng. 10.1109/10.284920 41, 97–107 (1994). [DOI] [PubMed] [Google Scholar]
- Jain M. K. and Wolf P. D., “A three-dimensional finite element model of radio frequency ablation with blood flow and its experimental validation,” Ann. Biomed. Eng. 10.1114/1.1310219 28, 1075–1084 (2000). [DOI] [PubMed] [Google Scholar]
- Valvano J. W., Cochran J. R., and Diller K. R., “Thermal conductivity and diffusivity of biomaterials measured with self-heated thermistors,” Int. J. Thermophys. 10.1007/BF00522151 6, 301–311 (1985). [DOI] [Google Scholar]
- Cameron J., Chapter “Thermal properties of tissue” in “Physical properties of tissue,” edited by Duck F. A., Academic, London, 1990, pp. 167–223. [Google Scholar]
- Haemmerich D., Chachati L., Wright A. S., Mahvi D. M., F. T.Lee, Jr., and Webster J. G., “Hepatic radio frequency ablation with internally cooled probes: Effect of coolant temperature on lesion size,” IEEE Trans. Biomed. Eng. 50, 493–500 (2003). [DOI] [PubMed] [Google Scholar]
- Yang D., Converse M. C., Mahvi D. M., and Webster J. G., “Expanding the bioheat equation to include tissue internal water evaporation during heating,” IEEE Trans. Biomed. Eng. 10.1109/TBME.2007.890740 54, 1382–1388 (2007). [DOI] [PubMed] [Google Scholar]
- Brown S. L., Hunt J. W., and Hill R. P., “Differential thermal sensitivity of tumour and normal tissue microvascular response during hyperthermia,” Int. J. Hyperthermia 8, 501–514 (1992). [DOI] [PubMed] [Google Scholar]
- Van Beers B. E., Leconte I., Materne R., Smith A. M., Jamart J., and Horsmans Y., “Hepatic perfusion parameters in chronic liver disease: Dynamic CT measurements correlated with disease severity,” AJR Am. J. Roentgenol. 176, 667–673 (2001). [DOI] [PubMed] [Google Scholar]
- Chhabra D. G., Shah R. C., Parikh V., and Jagannath P., “Radio frequency ablation of liver tumors: Experience with open and percutaneous approach,” Indian J. Gastroenterol. 25, 66–70 (2006). [PubMed] [Google Scholar]
- Low S. C., Lo R. H., Lau T. N., Ooi L. L., Ho C. K., Tan B. S., Chung A. Y., Koo W. H., and Chow P. K., “Image-guided radio frequency ablation of liver malignancies: Experience at Singapore General Hospital,” Ann. Acad. Med. Singapore 35, 851–857 (2006). [PubMed] [Google Scholar]
- Lu D. S., Yu N. C., Raman S. S., Lassman C., Tong M. J., Britten C., Durazo F., Saab S., Han S., Finn R., Hiatt J. R., and Busuttil R. W., “Percutaneous radio frequency ablation of hepatocellular carcinoma as a bridge to liver transplantation,” Hepatology 41, 1130–1137 (2005). [DOI] [PubMed] [Google Scholar]
- Breen M. S., Breen M., Butts K., Chen L., Saidel G. M., and Wilson D. L., “MRI-guided thermal ablation therapy: Model and parameter estimates to predict cell death from MR thermometry images,” Ann. Biomed. Eng. 10.1007/s10439-007-9300-3 35, 1391–1403 (2007). [DOI] [PubMed] [Google Scholar]
- Hariharan P., Chang I., Myers M. R., and Banerjee R. K., “Radio-frequency ablation in a realistic reconstructed hepatic tissue,” ASME J. Biomech. Eng. 10.1115/1.2720912 129, 354–364 (2007). [DOI] [PubMed] [Google Scholar]
- Kumaradas J. C. and Sherar M. D., “Edge-element based finite element analysis of microwave hyperthermia treatments for superficial tumours on the chest wall,” Int. J. Hyperthermia 19, 414–430 (2003). [DOI] [PubMed] [Google Scholar]
- Zhu L. and Xu L. X., “Evaluation of the effectiveness of transurethral radio frequency hyperthermia in the canine prostate: Temperature distribution analysis,” J. Biomech. Eng. 10.1115/1.2800857 121, 584–590 (1999). [DOI] [PubMed] [Google Scholar]
- Lang J., Erdmann B., and Seebass M., “Impact of nonlinear heat transfer on temperature control in regional hyperthermia,” IEEE Trans. Biomed. Eng. 10.1109/10.784145 46, 1129–1138 (1999). [DOI] [PubMed] [Google Scholar]
- Mulier S., Ni Y., Miao Y., Rosiere A., Khoury A., Marchal G., and Michel L., “Size and geometry of hepatic radio frequency lesions,” Eur. J. Surg. Oncol. 29, 867–878 (2003). [DOI] [PubMed] [Google Scholar]
- Denys A. L., De Baere T., Kuoch V., Dupas B., Chevallier P., Madoff D. C., Schnyder P., and Doenz F., “Radio-frequency tissue ablation of the liver: In vivo and ex vivo experiments with four different systems,” Eur. Radiol. 13, 2346–2352 (2003). [DOI] [PubMed] [Google Scholar]
- Montgomery R. S., Rahal A., G. D.DoddIII, Leyendecker J. R., and Hubbard L. G., “Radio frequency ablation of hepatic tumors: Variability of lesion size using a single ablation device,” AJR Am. J. Roentgenol. 182, 657–661 (2004). [DOI] [PubMed] [Google Scholar]
- Goldberg S. N., Hahn P. F., Halpern E. F., Fogle R. M., and Gazelle G. S., “Radio-frequency tissue ablation: Effect of pharmacologic modulation of blood flow on coagulation diameter,” Radiology 209, 761–767 (1998). [DOI] [PubMed] [Google Scholar]
- Saffroy R., Pham P., Reffas M., Takka M., Lemoine A., and Debuire B., “New perspectives and strategy research biomarkers for hepatocellular carcinoma,” Clin. Chem. Lab. Med. 45, 1169–1179 (2007). [DOI] [PubMed] [Google Scholar]