An automated CT based lung nodule detection scheme using geometric analysis of signed distance field

Abstract

The authors present a new computerized scheme to automatically detect lung nodules depicted on computed tomography (CT) images. The procedure is performed in the signed distance field of the CT images. To obtain an accurate signed distance field, CT images are first interpolated linearly along the axial direction to form an isotropic data set. Then a lung segmentation strategy is applied to smooth the lung border aiming to include as many juxtapleural nodules as possible while minimizing over segmentations of the lung regions. Potential nodule regions are then detected by locating local maximas of signed distances in each subvolume with values and the sizes larger than the smallest nodule of interest in the three-dimensional space. Finally, all detected candidates are scored by computing the similarity distance of their medial axis-like shapes obtained through a progressive clustering strategy combined with a marching cube algorithm from a sphere based shape. A free-response receiver operating characteristics curve is computed to assess the scheme performance. A performance test on 52 low-dose CT screening examinations that depict 184 verified lung nodules showed that during the initial stage the scheme achieved an asymptotic maximum sensitivity of 95.1% (175∕184) with an average of 1200 suspicious voxels per CT examination. The nine missed nodules included two small solid nodules (with a diameter ≤3.1 mm) and seven nonsolid nodules. The final performance level after the similarity scoring stage was an absolute sensitivity level, namely, including the nine missed during the initial stage, of 81.5% (150∕184) with 6.5 false-positive identifications per CT examination. This preliminary study demonstrates the feasibility of applying a simple and robust geometric model using the signed distance field to identify suspicious lung nodules. In the authors’ data set the sensitivity of this scheme is not affected by nodule size. In addition to potentially being a stand alone approach, the signed distance field based method can be easily implemented as an initial filtering step in other computer-aided detection schemes.

INTRODUCTION

Multidetector, thin-section, x-ray computed tomography (CT) has been widely recognized as a sensitive diagnostic imaging modality for the early detection of lung cancer,^{1, 2, 3} the leading cause of cancer-related deaths in the USA.⁴ However, the thin-section lung CT examinations result in a large number of images (e.g., as many as 600). While higher spatial resolution of thin-section CT images should enable earlier detection of smaller nodules,^{5, 6} the task of viewing and interpreting these images on a routine basis is quite laborious resulting in large interobserver variability.^{7, 8} Hence, the development of computer-aided detection (CAD) schemes for the detection and classification of lung nodules has been the focus of a large number of investigations in recent years.

The different approaches to develop CAD schemes for lung nodule detection can be divided into several broad categories. Intensity based schemes^{9, 10, 11, 12} explore the intensity (voxel value) properties of lung nodules as compared with the surrounding background (tissue structure). Using multiple threshold levels combined with feature analyses (e.g., shape, size), Giger et al.¹⁰ computed the likelihood of a suspected region representing an actual nodule. The primary advantage of this approach is its simplicity but it is frequently difficult to determine robust threshold levels for different CT examinations, often resulting in a relatively low sensitivity and a high false positive detection rate. Li et al.¹² used three enhancement filters for different shapes such as blobs, lines, and planes based on an eigenvalues analysis of the Hessian matrix, which is relatively sensitive to noise due to the need for computing second derivatives of voxels’ intensity values. Image transformation based approaches^{13, 14, 15} transform CT images into an intuitive form by emphasizing specific features depicted on the original CT images (e.g., intensity gradient,¹³ normal overlapping,¹⁴ and Hessian matrix¹⁵). Lung nodules can thereby be visualized better on the transformed “contrast enhanced” images. Template matching-based approaches^{16, 17, 18, 19, 20, 21} characterize geometric or intensity based features of lung nodules by using statistical models to search for matched object templates in the image space. For example, Lee et al.¹⁷ used one template matching based algorithm to detect nodules within the interior lung area and a different template matching algorithm near the lung wall areas to detect juxtapleural nodules. This method is highly scalable by simply adding specific features, as needed. However, the variability in nodule properties makes it difficult to define a global set of templates often resulting in low sensitivity levels and∕or high false positive rates. In addition, the matching process is frequently computationally extensive. Last, machine learning classifiers^{22, 23, 24, 25} characterize nodules using features extracted directly from a reference database of known (verified) nodules and these features are inputted into a learning machine for training. This approach generally requires a large data set for training and testing. For example, Suzuki et al.²⁴ described a massive training artificial neural network for this purpose.

Despite significant progress in this area, there are no optimal, widely accepted (and used) CAD schemes for lung nodule detection, to date. The difficulties in achieving this objective arise from the diversity in appearances of lung nodules (e.g., shape, size, intensity) and as important perhaps the varying appearances of normal tissue structures (e.g., vessels). Differences in CT image noise patterns can also affect CAD performance levels and robustness. We developed and tested a new geometric model based algorithm that aims to efficiently search for and detect lung nodules depicted on low dose CT images. Our hypothesis is that the use of an efficient geometric model based on the analysis of the signed distance field could minimize the impact of the large variability in lung nodule appearances and image based feature values on the performance of the scheme. This article provides a description of the approach taken and reports our preliminary test results.

MATERIALS AND METHOD

Our proposed algorithm first segments the lung regions and computes the signed distance field to identify a set of local maximas. These points are often located close to the center of the objects of interest, including nodules and vessels, and are regarded as the centers (seeds) of the suspicious regions for representing possible lung nodules. This process aims to minimize the candidate search and data analysis space while maintaining high detection sensitivity levels. The performance of the algorithm determines the maximum (upper) level of the CAD sensitivity since true-positive regions (actual nodules) missed during this stage will not be detected by the scheme. The algorithm then generates clustered volumes and analyzes their geometric shapes in order to rate the likelihood of each region being an actual lung nodule. Given a single lung CT image, our algorithm contains five basic steps (Fig. 1) including: (1) linear interpolation along the axial direction to obtain an isotropic volume data set, (2) lung segmentation aimed to minimize possible losses of juxtapleural nodules, (3) signed distance field computation of the lung regions, (4) points of interest (POI) identification, and (5) geometric shape analysis of clustered volumes of all suspicious points (POI). Each step of the algorithm plays a unique role in the detection and classification of suspicious regions. A detailed description of the implementation follows.

Figure 1.

Schematic diagram of the lung nodule detection algorithm.

Isotropic interpolation

Since our detection scheme relies on the analysis of the signed distance field of CT images, we first convert all voxels into three-dimensional (3D) Cartesian-coordinate grids with uniform spatial resolution in the 3D space to reduce possible errors due to anisotropic representation of grids. Several interpolation techniques^{26, 27, 28} have been developed for this purpose. Among them, the linear interpolation is widely used for isotropic data reconstruction because of its computational simplicity. Considering that the spatial resolution along the axial direction (slice thickness) in CT examinations is generally different from the spatial resolution within each slice, we simply perform a linear interpolation along the axial direction. Regardless of the actual resolution along the axial direction, an interpolated slice is computed in between all paired neighboring slices.

Lung segmentation

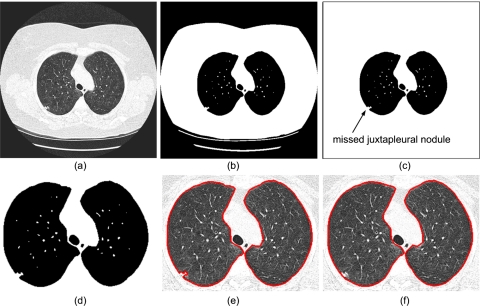
Lung segmentation is often used as a preprocessing step in CAD schemes. Although threshold-based region-filling strategies^{17, 29, 30, 31} can be used to extract the lung parenchyma quite efficiently, these strategies can also incorrectly exclude potentially important regions (i.e., juxtapleural nodules) when these regions are contiguous to the chest wall and have a similar density. Our proposed algorithm for correcting possible under-segmentation of juxtapleural nodules is illustrated in Fig. 2. This algorithm consists of two primary processes.

Figure 2.

Flowchart of the lung segmentation algorithm: (a) an original 2D CT image; (b) initial thresholded results; (c) nonlung region flooding; (d) enlargement of (c); (e) inner lung border tracing; and (f) lung border smoothing.

Threshold-based lung region extraction

This stage removes all nonlung regions from the CT images using three steps: (a) Gaussian smoothing of the 3D CT images [Fig. 2a] is used to remove isolated pockets of air between the patient and the CT bed that could lead to small contours after the lung border tracing. These small contours could be incorrectly regarded as lung borders. In our implementation, a 3D recursive Gaussian filter with a standard deviation of 1.0 mm (Ref. ³²) is used for this purpose because it requires a small number of multiplications and additions and it is independent of kernel size. (b) Gray-level thresholding [Fig. 2b] at −500 HU is used as the threshold to identify initial lung regions³³ and (c) nonlung region flood filling [Fig. 2c] is used to remove any remaining nonlung regions after the thresholding operation. A two-dimensional (2D) flooding operation is performed slice by slice using the pixels along the boundaries of the segmented lung image as flooding seeds. The reason for using a 2D rather than 3D flooding operation is that a 3D operation may result in the vascular tree extending too far into the image resulting in missing parts of the lung regions.

Lung border extraction and boundary smoothing

Two geometry based techniques are employed to extract the lung boundary and assure the inclusion of juxtapleural nodules, if any. (a) Lung boundary extraction [Fig. 2e] is performed using the inner border tracing algorithm on the first points in the left-to-right and right-to-left scan lines as seeds for lung boundary tracing. This method ignores the central regions altogether. The boundaries of the lungs in each slice are traced as a series of pixels, thus forming a collection of “directed closed anticlockwise” contours; (b) lung boundary smoothing [Fig. 2f] is performed using the Jarvis March algorithm³⁴ that computes locally rather than globally the convex hull where juxtapleural nodules may be located. First, a point with the largest x or y coordinate located on the convex region of the contour is selected as a seed. Then, the point that makes the largest right-hand turn within a local region along the contour is identified using the approach described in Ref. 34 where the “turn” rule is used to determine whether a point is located on the left side or right side of a given contour (or a line). A local region is determined by a “starting point” and a “length” representing the size of a possible juxtapleural nodule. The starting point is then replaced by the identified point with the “largest turn” and the previous step is repeated until the contour is traversed. Finally, a new contour is formed by connecting all the rightmost (or leftmost) points identified in this process and this contour is used as a representation of the smoothed lung boundary.

Signed distance field

Given a region Ω, its signed distance function determines the closest distance between a given point $\vec{p}$ and the boundary ∂Ω. This function is negative in the interior region, Ω⁻, zero on the boundary, ∂Ω, and positive in the exterior region, Ω⁺. The signed distance function d can be represented as

$$d\left(\vec{x}\right)=\text{sgn}\left(\vec{x}\right)\text{min}\mid \vec{x}-\vec{p}\mid \text{for}\text{all}\vec{p}∊\partial \Omega ,$$ (1)

where

$$\text{sgn}\left(\vec{x}\right)=\{\begin{array}{cc}1& \text{if}\vec{x}∊{\Omega }^{+}\\ 0& \text{if}\vec{x}∊\partial \Omega \\ -1& \text{if}\vec{x}∊{\Omega }^{-}\end{array}\phantom{\}}.$$ (2)

In an n-dimensional space, the signed distance field has a dimension of n+1. There are a number of choices for the distance metric, such as chessboard,³⁵ depending on the specific application of interest. We chose the Euclidean distance because it is intuitive and has a meaningful physical representation. A number of methods have been proposed³⁶ for an efficient computation of the signed distance. We chose the fast marching method³⁷ (FMM) which is based on the fact that the signed distance field can be described by the Eikonal equation

$$\mid \nabla u\mid =\sqrt{{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial u}{\partial z}\right)}^2+{\left(\frac{\partial u}{\partial z}\right)}^2}=1\text{subject}\text{to}{\phantom{\mid }u\mid }_{\partial \Omega }=0,$$ (3)

where u denotes the signed distance from a voxel to the boundary that is determined by a selected threshold as discussed below, ∇ denotes the gradient, and ∂Ω represents the boundary. To solve the nonlinear Eikonal equation numerically, Sethian developed a FMM (Ref. ³⁷) for a Cartesian grid. The use of the FMM reduces the computational complexity from O(N²) in the traditional “brute force” approach to O(N log N), where N is the total number of grid points. A detailed description of the FMM method has been described elsewhere.³⁸

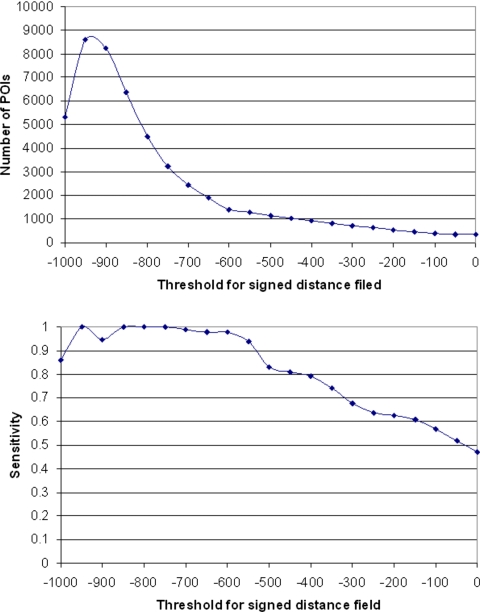
In our implementation, we first generated binary CT images by setting a specific threshold (i.e., −600 HU). The resulting images are used as an input data set to the FMM for computing the signed distance field. The region above the threshold is considered “exterior,” thereby all nodule regions have positive distance values. The performance of the algorithm may depend on the selection of this threshold because it could influence the boundary locations and the shapes quantified by the distance transform. Therefore, we randomly selected a subset of 15 CT examinations and systematically tested a series of threshold values from 0 to −1000 HU (at −50 HU increments) to examine the relationship between detection sensitivity and the average number of detected voxels representing false-positive identifications in this testing data set. The goal is to semiempirically select a threshold that covers most of the true-positive nodules while maintaining a reasonable number of false-positive identifications. We note that this is the only semiempirically selected parameter used in our scheme.

POIs

After applying the FMM to the segmented lungs, we generated a 3D image data set recording the distance field. The value at each voxel represents the shortest distance from the point to the boundary. Tissue with positive distance values in the lung region generally appears as one of three shapes: a blob (e.g., nodule), a sheet (e.g., fissure), and a tube (e.g., vessel).³⁹ The distance values along the axis of a vessel generally reach the maximum at the point where the vessel “enters” the lung because the size of a vessel decreases progressively toward the lung parenchyma. Ideally, for each vessel, there should be only one point with the maximum distance value regardless of its length. A lung nodule typically appears as a local concentration with a “blob-like” shape. The distribution of the distance values within a lung nodule decrease from the center of the nodule to its boundary with the maximum distance value typically located at the center. For a spherical nodule there should be only one point with the maximum value located at the center of the sphere. An ideal sheet-like shape (e.g., fissure), typically has multiple maximum points and these often have similar, if not equal, distance values forming a plane.

Based on these characteristics we limited our focus only on voxels with the maximum local distance values termed here the “POIs.” To reduce the total number of POIs while minimizing losses of true-positive lung nodules, we only selected for analysis voxels with the maximum distance values within specific local volumes. We are only interested in nodules larger than 3 mm in size in this study; hence, we defined the volume of interest of a local region as a 3 mm×3 mm×3 mm cube. To minimize the possible impact of image noise that may be incorrectly identified as a POI, we set a threshold of 0.5 mm on the distance value when selecting POIs.

Geometric analysis

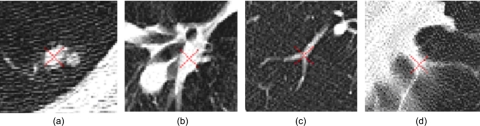
Under an ideal situation where all nodules are in the form of spheres and vessels are in the form of truncated cones, the strategy described above could yield high performance in detecting lung nodules. Unfortunately, this is not the case due to a number of reasons including but not limited to the discrete representation of an image, image noise, varying CT scanning parameters, and image reconstruction artifacts. As a result, a large number of POIs are actually located at non-nodule tissue regions leading to false-positive detections. Figure 3 shows several examples of possible locations where POIs may be located.

Figure 3.

Examples of four POI locations.

To classify POIs into two categories, namely located within nodules and located within non-nodule tissues, we tested a shape based analysis approach in which a progressive clustering is performed at each POI and a shape similarity distance to a perfect sphere is computed as the likelihood score (probability) of the region being an actual nodule. This analysis includes two stages.

Progressive clustering

A progressive clustering operation is used to estimate the shape of a region identified by the POI. Using the POI as a seed, and assessing its 26 neighboring voxels in the 3D space, the scheme clusters the voxel having the maximum distance value with the POI. Thereafter, the new search volume covers all neighboring voxels of the clustered volume from the previous step and the process is repeated. To minimize the computational cost of the clustering operation while capturing the essential shape of an object associated with the initial clustering seed (POI), we set the following “stop operation” rules: (a) the Euclidean distance from the last clustered point to the initiating POI is larger than 15 mm; or (b) the signed distance difference between the last clustered voxel and the initiating POI is larger than the resolution of the isotropic (interpolated) 3D image. When a starting POI is located within a vessel, the first stop operation rule frequently terminates the clustering process quickly. When the second stop operation condition is met, a layer around the POI is formed, namely the POI is fully enclosed by clustered voxels. This is sufficient to compute the local shape of a given POI; hence, the second rule is employed primarily to minimize computational cost. This progressive clustering method generates (grows) a 3D volume in a manner that is similar to skeletonization (i.e., medial axis extraction) of an object. Given a blob-like shape, such as a nodule, the clustered volume should be similar to a sphere. For a tube-like shape, such as a vessel, the clustered volume should be similar to a string; and for a plane-like shape, such as a fissure, the clustered volume should be similar to a plane. As a result, it is intuitive to use the similarity distance between a given clustered volume and a sphere as a summary measure associated with the probability that a clustered 3D volume actually represents a lung nodule. Using the marching cube algorithm (MCA), we transformed the clustered volume into a surface-based representation that consists of a set of triangles. Figure 4 shows the modeled result after the MCA transform is applied to the examples shown in Fig. 3.

Figure 4.

Surface-based representations of the clustered volumes representing the POIs in Fig. 3.

Shape similarity analysis

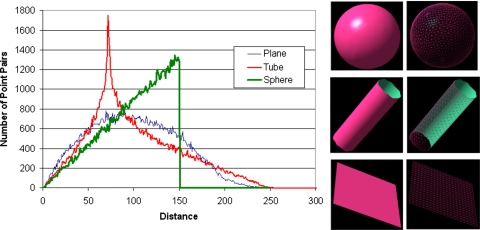
A large number of approaches have been proposed for computing similarity between shapes^{40, 41, 42, 43, 44, 45} and these are summarized in a review article.⁴⁶ We are interested here in similarity between an arbitrary shape and a sphere (e.g., an “ideal” nodule). We used the statistical based approach described by Osada et al.⁴⁵ because it is simple to implement, computationally efficient, and is invariant to fundamental geometrical transformations such as scaling, translation, and rotation. In addition, it is largely insensitive to noise, image blur, and “cracks” in a 3D model. The method includes the following steps: (a) shape function selection is simply done by measuring the Euclidean distance between two points on the surface of a 3D shape; (b) shape distribution construction is performed by sampling an adequate number of point pairs to build the associated shape distribution. Of concern during this process is that the implemented sampling strategy should result in reasonably evenly distributed sampled points on the surface of an object; (c) shape distribution normalization is performed to compensate for possible size effects on the shape distribution. We used a normalization approach that aligns the two distributions being compared by their mean values⁴⁵ because of its simplicity and applicability to our specific application. For example, Fig. 5 shows shape distributions of three typical representations after normalization and Fig. 6 shows the shape distributions of the objects presented in Fig. 4 after normalization; and (d) shape distribution comparison between paired shape distributions is computed as the sums of distance differences of the corresponding vertices used to represent these distributions

$$S\left(H_1,H_2\right)=\sqrt{\sum _{i=0}^n{\left[H_1\left(i\right)-H_2\left(i\right)\right]}^2},$$ (4)

where H₁ and H₂ are the two histograms representing the distributions, S is their similarity, and n is the number of vertices forming the histograms. In this study, H₁ represents the histogram of a sphere and H₂ is the computed histogram of a given clustered (3D) volume of interest. We used S(H₁,H₂) as a likelihood score for a clustered volume representing a true-positive nodule. To assess the performance of the scheme we computed free-response receiver operating characteristic (FROC) curves.

Figure 5.

Shape distributions of a sphere, a tube, and a plane, each in the form of a surface mesh.

Figure 6.

Shape distributions of the objects displayed in Fig. 4.

Testing a CT data set

CT images from 52 low-dose screening CT examinations were used in this preliminary study. A detailed description of the CT data acquisition (including the x-ray dose and image reconstruction) protocols has been reported elsewhere.⁸ In brief, these examinations were acquired using LightSpeed Plus 4-MDCT or LightSpeed Ultra 8-MDCT scanners (GE Healthcare). The low-dose CT acquisition protocol varied slightly depending on patient size. Exposure settings ranged from 120 to 140 kVp, 29.7±10.7 mAs, with pixel reconstruction dimensions ranging from 0.6 to 0.98 mm. Contiguous (nonoverlapping) slices (“volume scans”) encompassing the entire lung areas were acquired. Images were reconstructed with 512×512 pixel matrices using the GE Healthcare “lung” reconstruction kernel. Slice thickness was 2.5 mm in all examinations. Three board-certified chest radiologists with 3, 21, and 24 years of experience in reading chest CT images, independently read the data set. A total of 204 lung nodules were identified and classified by agreement of the independent readings and∕or a second review leading to consensus in cases of initial disagreement as noncalcified nodules. Among these nodules, 184 were determined to be of interest ranging in size from 3 to 28.9 mm and 20 were determined to be of sizes less than 3.0 mm. Forty-four of the 184 nodules that were larger than 3.0 mm were classified as “part-solid,” 16 were classified as “nonsolid”, and the remaining 124 were classified as “solid.” Fifty-eight of the nodules were located at the pleural regions. The size, location and density distributions of the 184 nodules of interest are summarized in Table 1. A reference (“truth”) file was generated to record the type (e.g., solid, nonsolid, part-solid), size (including estimated largest axis and effective size), and the center coordinate of each individual nodule.

Table 1.

The distribution by size, location, and type of the 184 nodules of interest in our data set as detected by the radiologists.

Categories of nodules	Diameter (mm)		Location		Density
	3–6	≥6	Juxtapleural	Nonjuxtapleural	Solid	Partial solid	Nonsolid
No. of nodules	56	128	58	126	124	44	16

Our computerized scheme was directly applied to all CT examinations in this data set without any operator intervention. A nodule was considered “detected” if the distance between the center of a CAD identified nodule and the recorded center of the nodule in the reference file was smaller than the recorded nodule “radius” (half of the effective size). Otherwise, the detected voxel represented a growth seed of a false-positive identification.

RESULT

Our experimental results using the 15 randomly selected examinations show that using different threshold values affects the performance curves for the signed distance field based algorithm (Fig. 7). As threshold values decreased from 0 to −600 HU, both detection sensitivity and average number of false-positive identifications per examination increased steadily. In this range sensitivity levels increased faster than false-positive identification rates. As threshold levels decreased below −600 HU the detection sensitivity reached a plateau while false-positive identification rate increased rapidly. When the threshold was set below −850 HU both sensitivity and false-positive identification rates became somewhat unstable. As a result, we set the threshold at −600 HU for the performance analysis. Using this semiempirically selected threshold, the initial four steps of the algorithm that are based on the local maximum strategy in the signed distance field identified a large number of POIs in each of 52 CT examinations, ranging from 663 to 2287 with an average of 1200 POIs per examination. Among these POIs, 175 of the 184 lung nodules of interest were detected, resulting in the maximum sensitivity level of 95.1% for the scheme. The algorithm missed nine nodules in this data set including two solid nodules with a diameter 3.1 and 3.0 mm, respectively, and seven nonsolid nodules ranging in size from 10.0 to 18.4 mm. Thus, the maximum achievable sensitivity of the algorithm in this data set was 98.8% (166 out of 168) for detecting solid and part-solid nodules and 56.3% (9 of 16) for detecting nonsolid nodules, respectively. We note that at this stage all juxtapleural nodules depicted in the data set were detected.

Figure 7.

The relationship between the selected threshold for signed distance field and the number of POIs (top) and the relationship between the selected threshold for signed distance field and the sensitivity (bottom).

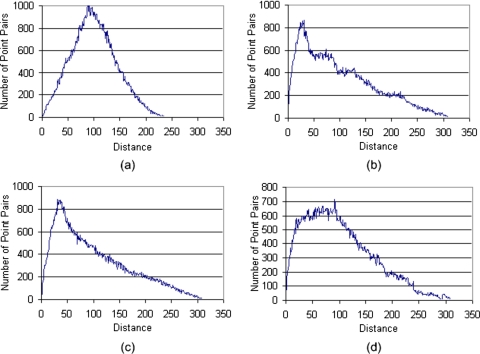
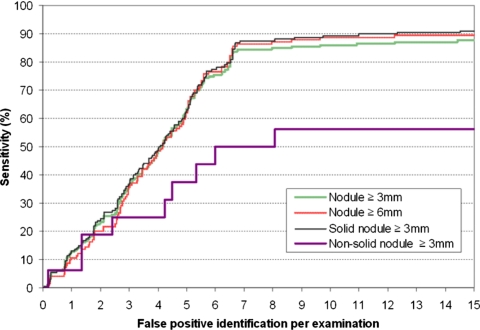
The results of the second step of our computerized scheme, namely the geometric shape analysis, are summarized by four FROC curves (Fig. 8). Two curves represent performance levels for the detection of nodules equal to or larger than 3.0 and 6.0 mm in size, respectively. The other two curves represent the performance of the scheme for the detection of either solid or part-solid nodules and for the detection of non-solid nodules, respectively. As an example, at a false-positive rate of 6.5 identifications per examination, the detection sensitivity levels of our scheme were 81.5% (150∕184) and 82.8% (106∕128) for noncalcified nodules larger than 3 mm and larger than 6 mm, respectively. At the same false-positive rate, the detection sensitivity level is 84.5% (142∕168) for the solid or part-solid nodules and 50% (8∕16) for the nonsolid nodules, which means while eliminating approximately 99.5% false-positive detections, the second step of our scheme discards 14.4% (24∕166) solid or part-solid nodules and 11.1% (1∕9) nonsolid nodules detected by the first step of the scheme. These results suggest that the detection sensitivity of our scheme was not substantially affected by nodule size.

Figure 8.

Four performance (FROC) curves for nodule detection representing different sizes of interest (≥3 and ≤6 mm) and different types (solid and nonsolid).

DISCUSSION

The computerized scheme developed and tested in this study has a number of advantages as compared with other previously developed schemes. First, it is simple and relatively easy to implement. The actual detection process is reduced to an analysis of the signed distance field of the CT images. The number of detected suspicious voxels depends on the initial threshold value that represents “the lowest” voxel value of a nodule boundary. Generally, because the low conspicuity nonsolid and small solid nodules result in lower values in their boundary contours, a lower threshold value is required to increase detection sensitivity of these subtle nodules. The threshold of −600 HU was semiempirically selected based on limited experimental data as shown in Fig. 7. As a result, the algorithm implemented with this threshold detects initially (before pruning) on average approximately 1200 voxels per examination as possible centers of suspected nodules. This number is in the same range of other previously reported schemes. For example, one study reported an initial sensitivity of 94.4% with 906 false-positive identifications per examination when applied to a set of CT scans acquired at a significantly higher dose (e.g., 120∕140 kVP and 220∕290 mAs).⁴⁸ Second, the geometric shape is the only classification criterion in determining the likelihood of a clustered 3D volume representing an actual nodule. Typically, shape analysis requires the segmentation of the suspicious regions that may often fail in particular in the case of nodules connected to the other lung tissues (e.g., vessels, airways, and arteries). Similar to a medial axis extraction process, we simply cluster the voxels with the largest signed distances within a local 3D search space. This clustering approach avoids the requirement of nodule (or region) segmentation and the resulting volume reflects a local shape. Thus, the probability of being an actual nodule is computed as the similarity distance to a sphere using a shape distribution approach. A unique characteristic of the clustering approach presented here is that our approach is relatively insensitive to nodule size (as shown in Fig. 8). Other reference shapes could be implemented as well but this work is beyond the scope of this preliminary study.

The implementation of the signed distance field and shape similarity computation is computationally efficient. For a typical CT data set used in this study, namely approximately 120 slices with a slice thickness 2.5 mm, the procedure including the isotropic interpolation, segmentation, signed distance computation, and shape analysis required approximately 5 min using a desktop PC computer (AMD Athlon™ 64×2 Dual 2.11 GHz with 2 GB of RAM) with the majority of the computation time spent on the lung area segmentation operation and the signed distance computation.

This method is also potentially applicable to other CAD schemes. This algorithm could be easily adopted as a preprocessing stage to other CAD schemes due to its simplicity, efficiency, and the limited output. Another unique characteristic is that the POI detected by this scheme is located, in the majority of instances, at (or close to) the center of the suspicious candidate region. This may be useful for other nodule segmentation methods that require knowledge of the centers of suspected regions for appropriate analyses. For example, the algorithm proposed in Ref. 47 required a manual identification of a nodule location when used for nodule segmentation. For the purpose of user interface design, it is convenient to control for the size range of nodules of interest by setting an appropriate threshold for the signed distance value, which conservatively indicates a nodule size.

Despite these advantages we note that the proposed method did miss a small fraction of nodules, namely two small solid and seven nonsolid nodules in our data set. The missed nodules are in two categories: (1) small solid nodules with sizes very close to the 3 mm cutoff and (2) nonsolid nodules with varying sizes. Missing the small solid nodules may be due to our use of a conservative threshold value for size (e.g., 0.5 mm) and possible errors generated by radiologists in measuring the actual size of these nodules. The missed nonsolid nodules were primarily the result of the initial low intensity threshold (i.e., −600 HU) we selected and the discrete nature of some of the voxels identified within the POIs thereby our inability to cluster these into an object. A lower threshold would have resulted in the detection of some of these nonsolid, low contrast nodules. However, this would have been done at the cost of substantially increasing the number of initially detected POIs (as shown in Fig. 7). We are currently investigating different approaches to optimize the threshold values for this purpose, including the possible use of other effective features specifically implemented for distinguishing nonsolid nodules. We also note that one of the possible disadvantages of this approach is the initial false-positive detection rate that is somewhat higher than those previously reported for other schemes.^{13, 49} However, the CT examinations used in this study were acquired at substantially lower doses (29.7±10.7 mAs). Hence, image noise levels in our data sets are relatively high even for “low dose scanning.” The false-positive identifications are located primarily at two types of positions namely, bifurcation of vessels and the hilum region. At these locations the clustered volumes frequently looked like spheres. Hence, other features may be required to reduce at least some of these false-positive identifications and this topic is currently under investigation. We are also exploring the use of other reference shapes including but not limited to various ellipses as well as the average size dependent of representative shapes computed or modeled from the actual ensembles of lung nodules in our databases.

Operationally, this method is memory intensive due to the requirements of the FMM algorithm. Given a data set after isotropic interpolation (400−600 slices), it is easy to exceed 2.0 GB if no prior action is taken. To alleviate this memory issue, we divided the data set into subvolumes. Last, the first two steps, namely, isotropic interpolation and lung segmentation, are used to preprocess the images sets. We recognized that the isotropic interpolation only approximated the actual tissue structure being imaged. The impact of this approach could be substantially reduced by scanning with smaller (thinner) slice thicknesses (e.g., 1.25 or 0.625 mm). However, this preliminary study suggests that even when using CT images with 2.5 mm slice thickness, the interpolation method is quite adequate for our purpose because we primarily focus on approximating the continuity of lung vessels.

CONCLUSION

We developed and tested a new and relatively simple computerized scheme for lung nodule detection based on geometric analysis of the signed distance field. This scheme was tested using 52 low-dose screening CT examinations depicting 184 nodules of interest, including 44 part-solid and 16 nonsolid nodules. The preliminary test results are encouraging in that the sensitivity of the scheme was not significantly affected by nodule size. In summary, our computerized scheme is efficient and relatively easy to implement and does not require an extensive training process that is required in other CAD schemes that include multi-image feature based machine learning classifiers. With the signed distance attached to each suspicious candidate, this scheme can support a flexible user interface allowing users to change the focus of analysis on specific nodules of interest with specific predetermined sizes. The algorithms used in this scheme can also be relatively easily adopted as the first detection stage of other CAD schemes.