Range and modulation dependencies for proton beam dose per monitor unit calculations

Abstract

Calculations of dose per monitor unit (D∕MU) are required in addition to measurements to increase patient safety in the clinical practice of proton radiotherapy. As in conventional photon and electron therapy, the D∕MU depends on several factors. This study focused on obtaining range and modulation dependence factors used in D∕MU calculations for the double scattered proton beam line at the Midwest Proton Radiotherapy Institute. Three dependencies on range and one dependency on modulation were found. A carefully selected set of measurements was performed to discern these individual dependencies. Dependencies on range were due to: (1) the stopping power of the protons passing through the monitor chamber; (2) the reduction of proton fluence due to nuclear interactions within the patient; and (3) the variation of proton fluence passing through the monitor chamber due to different source-to-axis distances (SADs) for different beam ranges. Different SADs are produced by reconfigurations of beamline elements to provide different field sizes and ranges. The SAD effect on the D∕MU varies smoothly as the beam range is varied, except at the beam range for which the first scatterers are exchanged and relocated to accommodate low and high beam ranges. A geometry factor was devised to model the SAD variation effect on the D∕MU. The measured D∕MU variation as a function of range can be predicted within 1% using the three modeled dependencies on range. Investigation of modulated beams showed that an analytical formula can predict the D∕MU dependency as a function of modulation to within 1.5%. Special attention must be applied when measuring the D∕MU dependence on modulation to avoid interplay between range and SAD effects.

INTRODUCTION

The dose per monitor unit (D∕MU) for patient-specific portals using proton beams has historically been determined by measurements with ionization chambers, diodes, film, diamonds, or other detectors.^{1, 2, 3} As a safety guard in the clinical practice of radiotherapy, the measured D∕MU is always compared with the D∕MU determined by at least one alternative method. Previously used alternative methods have included D∕MU predictions calculated by: (1) hand models,^{4, 5} (2) dose calculation modules of treatment planning systems⁶; and (3) Monte Carlo simulations.^{7, 8} In addition, as proton therapy becomes more widely utilized, treatment facilities should expect the time available for measuring D∕MU to become less and reliance on calculations as the primary determination of D∕MU to become more prevalent.

In proton radiotherapy, the beam range is usually modulated during treatment to produce a uniform dose over the region occupied by the target. The difference between the water-equivalent depths of the proximal and distal 90% doses covering this uniform dose is referred to here as the width of the spread out Bragg peak (W_SOBP). Two targets with identical ranges to their distal edges but having different thicknesses in the beam direction will require different W_SOBP. The range in the patient is defined by the depth of the distal 80% dose level (R₈₀). Although the distal 90% dose level is typically used to prescribe target coverage, R₈₀ is used in this model because it shows little dependence on the energy spread of the proton beam.⁹ When the patient is set up for treatment, the center of a target is usually placed close to the isocenter of the beamline via an imaging guidance system but the point at which the D∕MU is determined may not be at the isocenter. Any D∕MU calculation model must include dependences on R₈₀ and W_SOBP as well as the standard dependencies common in x-ray therapy such as field size and shape, fractional depth dose, and the prescription point not being located at the isocenter.

At the Midwest Proton Radiotherapy Institute (MPRI), broad therapeutic proton beams using the fixed horizontal beam line (FHBL) are formed by a double-scattering system with a rotating range modulator placed downstream of both scatterers and the beam monitoring ionization chamber, hereafter referred to as the MU chamber.^{10, 11, 12, 13} For beam ranges between 6 and 27 cm, a single physical modulator device is used for a defined modulation width. In this system, the lateral dose uniformity in the plane of the isocenter is optimized for different beam ranges by displacing the first scatterer towards or away from the isocenter. This technique results in an effective source-to-axis distance that is a function of the beam range. In this paper, the term SAD shall always refer to the effective source-to-axis distance. The D∕MU calculation model for this type of beamline must, therefore, include dependences on the SAD variation in addition to the dependencies listed above.

In this study, the range and W_SOBP dependences of D∕MU for the MPRI FHBL were investigated utilizing theoretical principles and special measurement techniques that minimized the interplay between range and W_SOBP. Special emphasis was given to the effect of the varying SAD.

MATERIALS AND METHOD

Beam delivery system

Proton beams used at MPRI are provided by the Indiana University Cyclotron Facility (IUCF) with a maximum beam range of 27.0 cm in water at the entrance to the nozzle before passing through any scatterers, modulators, or beam monitors. Each treatment room has its own energy selection system that is comprised of a pair of beryllium range shifter wedges, an analyzing magnet, and an adjustable slit. The range shifter wedges adjust the range of the primary beam in depth steps of 0.2 mm water equivalence. The spread of ranges (energies) of the degraded proton beam is precisely controlled by the slit that operates as part of a spectrometer magnet device. Before each patient treatment, the range and energy spread of the proton beam are verified by a multi-layer Faraday cup (MLFC) inserted into the beamline upstream of the nozzle. The beam range measured at the location of the MLFC, before the beam enters the nozzle, is referred to as the beam range of the beam delivery system (R_BDS). Calibration and use of the energy control and verification system are described in a companion paper.⁹

Details of the FHBL nozzle design at MPRI were reported in an earlier publication.¹⁴ Only a few aspects of the nozzle that are important to this study are given here. This nozzle is provided with two snouts for clinical use providing maximum field sizes of 10 and 20 cm diam. The snout that supports a 10 cm diam maximum field size is referred to as the “small field” snout while the snout that supports a 20 cm diam maximum field size is referred to as the “large field” snout. For a given snout, a single contoured second scatterer is used for all beam ranges (6 to 27 cm water). As the R_BDS increases, the first scatterer is moved upstream to maintain a similar beam diameter incident upon the second scatterer. Due to the limited space available in the nozzle to move the first scatterer (55 cm), two different first scatterers are used with each second scatterer to cover the entire range of beam ranges. A “low-energy” first scatterer is used for R_BDS between 6.0 and 14.0 cm while a “high-energy” first scatterer covers the regime above 14.0 cm. The high-energy first scatterer is made only of lead while the low-energy first scatterer is a composite of lead and polycarbonate. By carefully combining polycarbonate with lead in the design of the low-energy first scatterer for each snout, the water equivalent path length through the nozzle when using the low-energy scatterers is within 0.5 mm of that when using the high-energy scatterers for each snout. This scattering system design thereby provides a constant offset for each snout between the R_BDS measured with the MLFC and the R₈₀ measured in a water phantom at the treatment location. Although the isocenter-to-first scatterer distance is the same for the small and large snouts for a given R_BDS, the range loss through the nozzle is different; consequently, R₈₀ is less than R_BDS by 1.1 cm for the small snout but 2.5 cm for the large snout.

Any study of the various D∕MU dependencies requires a stable dose monitor. According to the daily quality assurance measurements performed during 2005 and 2006, the measured D∕MU at the reference condition was within ±1.0% of the standard calibration value. The beamline dose monitor system consists of a quadrant ionization chamber to monitor the beam symmetry and two sets of linear segmented ionization chambers for real-time monitoring of horizontal and vertical beam profiles. For most treatments, the lateral dose asymmetry is better than 2.5%. The MU chamber consists of a parallel plate ionization chamber with a 3.0 cm diam charge collection area, 5.0 mm air gap, and 800 volts bias. The MU chamber is located 65 cm downstream from the second scatterer and 190 cm upstream of the isocenter. The D∕MU calibration of the MU chamber was performed at a rate of 200 MU∕min. During the acceptance testing of this beamline, the D∕MU was found to vary, with respect to the D∕MU at a dose rate of 200 MU∕min, from −0.5% to +2.0% for dose rates from 50 to 600 MU∕min. A linear fit of the dose rate variation showed that, over the typical dose rates used for treatment from 100 to 250 MU∕min, only a ±0.5% variation exists; therefore, a ±1.0% variation in D∕MU is typically present in patient portal calibrations.

Data acquisition

All data were acquired using an NIST-calibrated PTW Markus parallel plate ionization chamber (PTW, Hicksville, New York) scanned in a 3D Wellhöfer water phantom (WP700). The water phantom was placed at the required location relative to the isocenter within 0.3 mm using the MPRI robotic patient positioner system.¹⁵ For each modulator, depth dose curves were measured to obtain W_SOBP for various beam ranges. A 15.5 cm diam active area parallel-plate chamber was used as a reference detector to minimize the effect of beam intensity fluctuations during the measurements. This reference detector was placed inside the nozzle upstream of the modulator position to avoid any additional fluctuation induced by the rotating modulator.

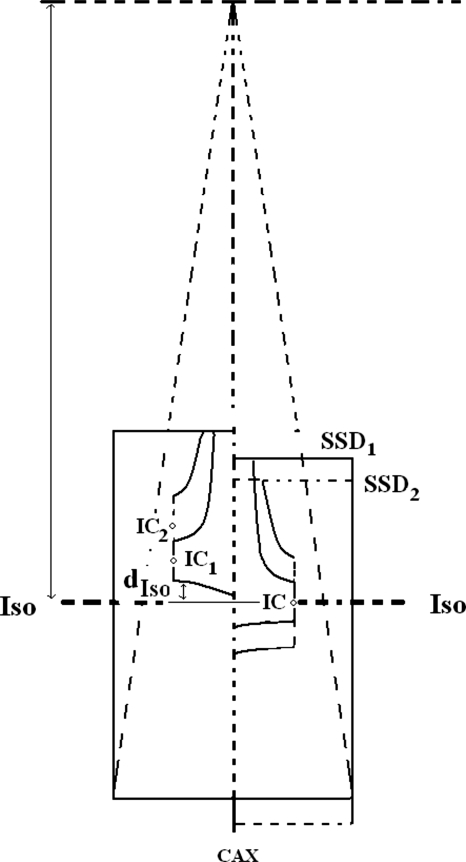
Most proton treatments are set up using an isocentric technique with the center of the range modulated region placed at the beamline isocenter. Measurements of D∕MU for those cases are usually performed by placing a water phantom according to the isocentric technique shown on the right side of Fig. 1. This technique is referred to as an isocentric measurement. When measuring D∕MU at the center of modulation for different W_SOBP and at the same beam range, the source-to-surface distance (SSD) will be different; therefore, the measured D∕MU for different modulations will include an SSD effect. Additionally, when the SAD varies significantly for different beam ranges, as is the case for the MPRI FHBL, the SSD effect on the measured D∕MU as a function of W_SOBP will vary for different beam ranges. To avoid compounding the normal W_SOBP SSD effect with the SAD dependence on range, the d_iso technique of measurement shown on the left side of Fig. 1 was devised. In this technique, measurements of D∕MU are performed by placing a water phantom such that the depth of the R₈₀ is at a defined distance from the isocenter d_iso. When R₈₀ is downstream of the isocenter, d_iso has a positive value. As in the isocentric technique, the D∕MU is measured by placing the ionization chamber (IC) at the center of the measured W_SOBP; however, to measure the D∕MU for different W_SOBP at a given beam range, the IC will be placed at different distances from the isocenter. Although the measurement point will be at different distances from the isocenter, its location is within the uniform dose distribution of the modulated region and the SSD effect seen in the isocentric technique is minimized. The d_iso technique, thus, separates the D∕MU dependencies on the W_SOBP and beam range. All measurements of D∕MU in this study were performed using the d_iso technique.

Figure 1.

Schematic drawing for measurements using isocentric and d_iso techniques. When using the isocentric technique seen on the right, measurements are preformed with different SSD for various W_SOBP having the same beam range. When using the d_iso technique seen on the left, the SSD is constant and measurement points are moved for various W_SOBP having the same beam range.

D∕MU dependence on range

The D∕MU varies with beam range due to: (1) the stopping power of the protons passing through the monitor chamber; (2) the reduction of proton fluence due to nuclear interactions within the patient; and (3) the variation of proton fluence passing through the monitor chamber due to different SADs for different beam ranges. The D∕MU range dependence can be described by those components shown in Eq. 1

$$\mathrm{D}∕\mathrm{MU}\left(R\right)=S{\left(R\right)}^{*}\psi {\left(R\right)}^{*}{B}_{\mathrm{SAD}}\left(R\right),$$ (1)

where R is the beam range used to evaluate the D∕MU dependence. Because the MU chamber is placed after the second scatterer and before the modulator, R is identical to R₈₀ of the modulated proton beam.

All three of these dependences are relative to values in a reference beam. For this study, the reference beam uses the small snout, an aperture of 10 cm diam, an air gap of 5 cm, and an R₈₀ of 15.9 cm (i.e., R_BDS, 17 cm beam range). The R₈₀ of the reference condition is labeled as R_ref.

The first term of Eq. 1 describes the range dependency on differences in stopping power (S)¹⁶ of protons traversing the MU chamber for beam ranges different than the reference beam range. This term is related to R₈₀ by Eq. 2:

$$S\left(R\right)=\frac{R_{\mathrm{ref}}^{1∕p-1}}{R^{1∕p-1}},$$ (2)

where p is the energy-range parameter (1.77 above 10 MeV). Equation 2 is based upon Geiger’s rule¹⁷ that relates proton energy to beam range and the relation between relative stopping power and beam range derived by Bortfeld.¹⁶

The second term of Eq. 1 considers the change in proton fluence due to nuclear interactions within the patient. According to the tables by Janni,¹⁸ above 20 MeV the proton fluence in tissue decreases approximately linearly with depth by nonelastic nuclear interactions. The range dependency due to the proton fluence reduction can be calculated using Eq. 3:

$$\psi \left(R\right)=\frac{1+\beta \ast R_{\mathrm{ref}}}{1+\beta \ast R},$$ (3)

where β is the proton fluence reduction parameter. A value of 0.012 cm⁻¹ for β is used to describe the trend of our measure D∕MUs.

The last term of Eq. 1 is called the geometry factor. This factor is used to describe the change in proton fluence passing through the active volume of the MU chamber due to different SADs for different beam ranges. If the SAD were constant for beam ranges different from the reference beam range, then the geometry factor would equal 1. The design of the MPRI beamline, however, as stated in the introduction, yields different SADs for different beam ranges. In addition, the MU chamber’s location midway between the effective source locations and the isocenter makes the D∕MU sensitive to small changes in the SAD. The geometry factor is represented by Eq. 4:

$$B_{\mathrm{SAD}}\left(R\right)={\left[\frac{\mathrm{SAD}\left(R\right)-Z_{\mathrm{MU}}}{\mathrm{SAD}\left(R\right)}\right]}^2\times {\left[\frac{\mathrm{SAD}\left(R_{\mathrm{ref}}\right)}{\mathrm{SAD}\left(R_{\mathrm{ref}}\right)-Z_{\mathrm{MU}}}\right]}^2,$$ (4)

where SAD(R) and SAD(R_ref) are the measured SADs for the evaluating and reference beam ranges. Z_MU is the distance of the MU chamber from the isocenter. In the case of the MPRI fixed beam line, Z_MU is 190 cm.

For calculating D∕MU for a wide patient population, SADs must be available for a variety of beam ranges and snout sizes. These SADs may be determined, for each range and snout, by measuring the D∕MU at various d_iso and fitting the D∕MU values to an inverse square function. The parameter d_iso is used as a variable to avoid interplay with the W_SOBP variable as described in the previous section. All measurements were performed with a 10 cm diam aperture, 5 cm air gap, 10 cm W_SOBP, and with the ion chamber at the center of the W_SOBP using the d_iso technique. For each R_BDS, measurements were typically performed using five d_iso values that ranged from −28 to 26 cm. The center of the SOBP (i.e., the location of measurement) was always at half the W_SOBP upstream of R₈₀. These measurement positions cover most clinical situations. To verify that the SAD is independent of field size, SADs were derived from D∕MU measurements with aperture diameters of 3.0, 5.0, and 9.0 cm with a R_BDS of 17.0 cm. To verify that the SAD is independent of W_SOBP, SADs were derived from D∕MU measurements with W_SOBP of 2.6, 5.1, 10.0, and 12.3 cm with an R_BDS of 17.0 cm.

D∕MU dependence on W_SOBP

The first step in determining the D∕MU dependence on W_SOBP was to determine the W_SOBP from measured depth dose curves. At MPRI, a single physical modulator device is used for all beam ranges to create a given W_SOBP. Depth dose curves were acquired for various modulator devices for R_BDS of 17 and 27 cm. All depth dose curves were measured using a 5 cm d_iso. During data acquisition, the wide-area parallel chamber was used as a reference and the gain was held constant on both the scanning and reference chambers. For processing the data, the depth dose curves were first normalized to the maximum value. A linear fit was then performed over a region between 0.3 cm shallower than the distal 90% and 0.8 cm deeper than the proximal 90%. The depth dose curve was then renormalized to the fit value at the midway point of the fit region. The W_SOBP was then calculated as the distance between the proximal and distal 90% as defined in the introduction.

After the W_SOBP for each device was defined, the relative D∕MU for each modulator was determined by two different methods. The first method divided the measured D∕MU of each modulator by the measured D∕MU for the modulator with a W_SOBP of 10 cm. For all modulators, the D∕MU was measured at the center of the W_SOBP with a fixed 5 cm d_iso. The second method divided the un-normalized readings at the center of each W_SOBP, relative to the reference chamber, by the un-normalized readings relative to the reference chamber at the center of the 10 cm W_SOBP. This second method was useful because much of the information required to determine D∕MU was already available from water phantom scans without needing additional measurements.

Tables of measured data can be used to describe the D∕MU dependency on W_SOBP for various ranges if there is a large interplay between the D∕MU dependences on range and W_SOBP. However, if there is minimal or no interplay between the range and W_SOBP dependences, an analytical function that describes the relationship is preferred. Such a function can be written as in Eq. 6 that makes use of the weight factor for each energy layer with a beam range R_i=R₈₀−i^*Δ where i is from 0 to n energy layer used to form modulated proton beam. The R₈₀ is the beam range of the energy layer without any modulator materials. Although the R₈₀ of a modulated beam is shorter by 0.1 cm than the R₈₀ of the highest energy layer without any modulator material, the R₈₀ of the highest energy layer is used for calculating the D∕MU dependence on W_SOBP. The weight factor for each energy layer can be theoretically predicted according to an analytical formula developed by Bortfeld and Schlegel.¹⁹ Using a theoretically calculated depth dose curve for the deepest layer and the assumption that the width of the peak of each layer was identical to the deepest layer, the weighting factors for each energy layer can be calculated using Eq. 5:

$$W_{\Delta }^i(R_i=R_{80}-i\Delta )\sim {\left(\frac{\Delta }{2}\right)}^{1-1∕p}\text{for}i=0,$$ (5)

$$\sim [{(i+\frac{\Delta }{2})}^{1-1∕p}-{(i-\frac{\Delta }{2})}^{1-1∕p}]\text{for}i\ne 0,$$

where R_i is the range of the ith layer, Δ is the constant thickness of inserted materials between layers, and P is the energy-range parameter as used in Eq. 2.

Because the width of the peak of the dose distribution from nonmodulated proton beams is almost constant for various beam ranges in the MPRI FHBL, a near constant interlayer thickness (Δ) was used to design and manufacture each modulator. The relative D∕MU for an evaluated W_SOBP with respect to reference W_SOBP can be obtained by Eq. 6:

$$\mathrm{D}∕\mathrm{MU}(m=M_{\max }∕\Delta ;n)=\raisebox{1ex}{$\sum _{i=0}^n{W}_{\Delta }^i{\left(R_i\right)}_{\mathrm{ref},W_{\mathrm{SOPB}}}$}\!\left/ \!\raisebox{-1ex}{$\sum _{j=0}^m{W}_{\Delta }^j{\left(R_j\right)}_{W_{\mathrm{SOBP}}}$}\right.,$$ (6)

where M_max is the total thickness of modulator for the evaluated W_SOBP; i.e., the sum of the m individual step thicknesses between energy layers. The number of energy layers used for the reference W_SOBP modulator is denoted by n.

RESULTS AND DISCUSSION

SAD variation as a function of beam range

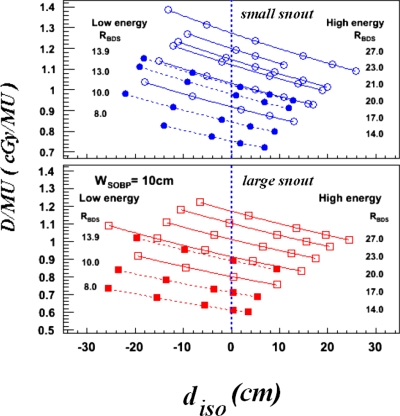
The measured data for determining the SADs for different ranges and snouts with a W_SOBP of 10 cm are shown as points in Fig. 2. These D∕MU measurements were fit by the inverse-square law to obtain the SADs. Data calculated using the fit SADs are shown as curves. The SADs extracted from the measured D∕MUs shown in Fig. 2 are plotted in the lower panel of Fig. 3 versus R_BDS.

Figure 2.

Measured D∕MU versus D_iso (distal R₈₀ to isocenter distance). Open and closed circles represent measured data from high- and low-energy beam ranges, respectively. The upper panel gives the results for the small snout while the lower panel gives the results for the large snout. Solid and dashed curves represent fits for high and low energy beam ranges, respectively.

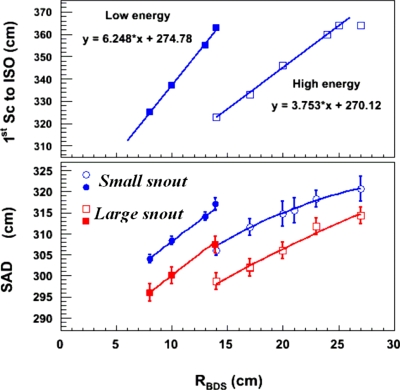
Figure 3.

The plot in the upper panel shows the first scatterer (Sc) to isocenter (ISO) distance versus R_BDS for both the low- and high-energy beam ranges. The scatterer positions are the same for both the small and large snouts. Solid lines represent fits to the measured positions. The plot in the lower panel shows the measured SADs versus R_BDS for both snouts. Open symbols represent high-energy beam ranges while closed symbols represent low-energy beam ranges. The measured SADs were fit with either lines or second order polynomials over each combination of snout size and range. Discontinuities in the SADs for a given snout were observed near an R_BDS of 14 cm where the first scatterer is changed for low- and high-energy beam ranges.

The distance of the first scatterer from the isocenter for both the low- and high-energy ranges is shown as a function of R_BDS in the upper panel of Fig. 3. For both range regions, the distances were found to vary linearly with beam range. The upper panel of Fig. 3 shows that, for an R_BDS of 14 cm, the isocenter-to-first scatterer distances for the low-energy and high-energy scatterers are 45 cm different but the bottom panel of Fig. 3 shows that the difference of SAD is only about 10 cm. Although a 10 cm difference of SAD will only generate a small inverse-square-distance effect at isocenter where the SAD is ∼320 cm, the 10 cm difference can have larger effects for the MU chamber because the distance from the source to MU chamber is only ∼130 cm. For both the small and large field snouts, the SAD varies by 20 cm when the R_BDS changes from 14 to 27 cm. A similar variation in SAD is found for R_BDS between 6 and 14 cm although the rate of change of SAD per beam range is steeper. The solid curves shown in the lower panel of Fig. 3 are either linear or second order polynomial fits to the measurements. These fits of the SAD as a function of R_BDS and snout size are used for calculating the geometry factor, B_SAD(R).

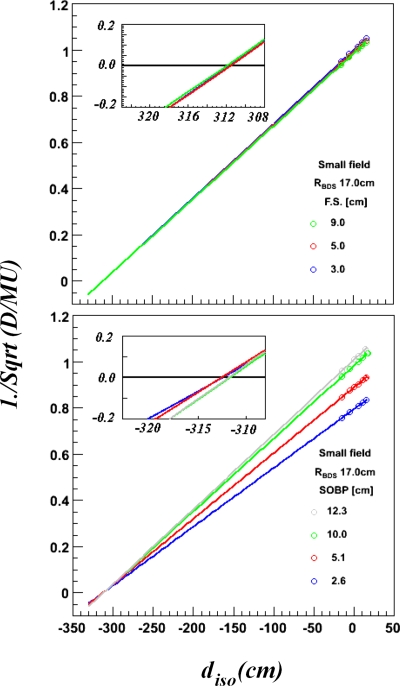
In addition to determining the change in SAD as a function of range for each snout, the change in SAD as a function of field size and W_SOBP were also investigated to estimate the uncertainty of the derived SADs. These studies were only performed using the small snout and a R_BDS of 17 cm. Figure 4 shows that the difference in derived SAD for various W_SOBP was less than 1.5 cm and for various size aperture openings was less than 1 cm. The field size and W_SOBP, thus, have little effect on the SAD.

Figure 4.

Inverse square root of D∕MU versus D_iso for R_BDS of 17 cm and small snout. The upper panel provides data for a single modulator and various field sizes. The lower panel provides data for a single field size and various W_SOBP. Open circles represent measured data while linear fits are represented by solid lines.

D∕MU dependence on range

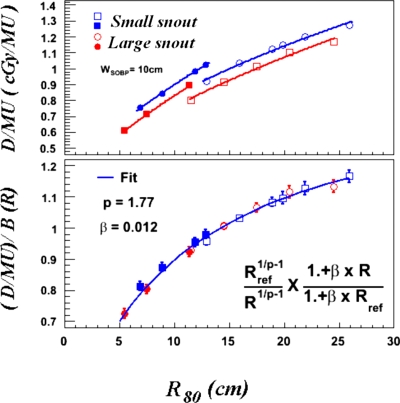
Measured D∕MUs at 0.0 cm d_iso distance are plotted as a function of R₈₀, in the upper panel of Fig. 5. In this figure, instead of plotting D∕MU against R_BDS, which is determined upstream of the scatterers and monitor chamber, R₈₀ is plotted because it is measured downstream of the monitor chambers and is, therefore, more closely related to the energy of the protons passing through the MU chamber. Discontinuities were observed at the same ranges as was observed for the derived SADs. Because the stopping powers of protons that traverse the MU chamber change smoothly as a function of range and a single modulator was used to investigate the D∕MU variation with range, the observed discontinuities must have been caused by the discontinuous SADs resulting from the change of the first scatterer between the low- and high-energy ranges. The difference in D∕MU between the small and large snouts was caused by the differences in the SADs resulting from the use of different second scatterers. The discontinuities in D∕MU can be replicated in calculations by applying the geometry factor of Eq. 2. After applying the geometry factor, a D∕MU function dependent only on range can be obtained. This function, shown in the lower panel of Fig. 5, is not dependent on any beamline devices. The range-response function without the influence of beamline devices is then described by the combination of the stopping power and nuclear interaction components of Eq. 2. Observed differences between the measured points and the fit curve are within 1.0%.

Figure 5.

The upper panel plots measured D∕MU at a d_iso of 0.0 cm as a function of R₈₀, for low- and high-energy beam ranges and small and large snouts. The same data are plotted in the lower panel after the geometry factor has been applied. The solid curve is a fit to all combinations of range and snout using the functions described in the text.

D∕MU dependence on W_SOBP

Measured depth dose curves using the same modulator for R_BDS of 17 and 27 cm produced similar uniformity and W_SOBP values. For all W_SOBP, the uniformity was within ±2%. Measured W_SOBP for the same modulator device vary only 3 mm across all beam ranges. This small difference in W_SOBP for all ranges allows one to correlate the total thickness (M_max) of each modulator to the measured W_SOBP as described in Sec. 2D.

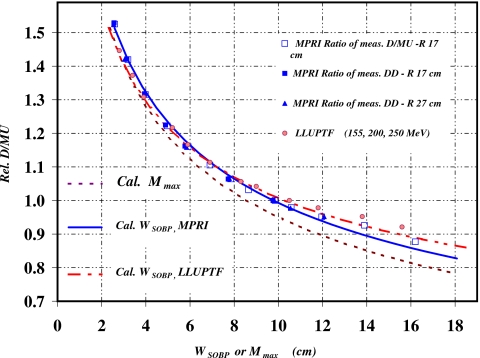
Relative D∕MU as a function of W_SOBP, obtained by either the ratio of D∕MU or the ratio of values from the measured depth doses as described in section II.E, are plotted in Fig. 6 for a R_BDS of 17 cm as open squares and closed squares, respectively, and for a R_BDS of 27 cm as closed triangles. For both measurement methods, the measured relative D∕MUs are nearly identical for both beam ranges. For comparison, the D∕MU as a function of W_SOBP obtained from Ref. 4 for the Loma Linda University Proton Treatment Facility (LLUPTF) beam lines, which likewise uses downstream physical modulator devices, are also plotted in Fig. 6. The D∕MU for each modulator at LLUPTF is the average from proton beams at three different accelerator energies: 155, 200, and 250 MeV. The corresponding R_BDS for these energies are 16.7, 25.9, and 37.8 cm, respectively. Because the LLUPTF data were obtained using an isocentric technique, an inverse square correction was applied with an assumption of a constant 250 cm SAD. With this correction, the relative D∕MUs of LLUPTF show a similar trend as measured at MPRI HFBL.

Figure 6.

Relative D∕MU as a function of W_SOBP and M_max. Measured relative D∕MU for R_BDS of 17 and 27 cm of MPRI HFBL are plotted with measured relative D∕MU of LLUPTF beam line. Measured data are plotted as symbols. The dashed curve is the result of calculations with Eq. 6 using the variable M_max while the solid and dot-dashed curves are plotted with W_SOBP by applying the corresponding nonlinear relationship between W_SOBP and M_max for MPRI and LLUPTF data.

The relative D∕MU from Eq. 6, as a function of M_max, are plotted as a dashed curve. A 0.56 cm constant thickness of Δ and a value of 1.5 for P were used. These calculated D∕MU deviate by as much as 5% from the measured values for large M_max. In clinical practice, however, measured D∕MUs are encoded according to the measured W_SOBP. Using a previously established nonlinear relationship between M_max and W_SOBP, the calculated D∕MU can be related to W_SOBP.⁹ After applying the transformation, the calculated D∕MUs matched the measured data to within 1.5% except for the 14 cm W_SOBP, which agreed within 3%. Better agreements were also observed with the corresponding W_SOBP for LLUPTF data. Using Eq. 6 with M_max values transformed from measured W_SOBP values instead of raw M_max values clearly leads to better predictions of D∕MU.

CONCLUSIONS

This study focused on range and W_SOBP dependences of D∕MU for a double scattered proton beam line; the effects of field size and shape and fractional depth dose were not addressed. By using the SAD variation to model the reconfiguration of beamline device, three D∕MU dependencies on range and one dependency on W_SOBP were found.

The first range dependency in the D∕MU response was related to the stopping power differences in the MU monitor chamber. This dependency was modeled by the function S(R). The second range dependency accounted for the loss of proton fluence in the patient due to nuclear interactions. This dependency was modeled by the function Ψ(R), which integrates the nuclear attenuation for different ranges. The third range dependency was due to the way the MPRI FHBL is reconfigured for different beam conditions. This technique results in the beam range being dependent upon SAD and snout size. Further, discontinuities of SAD were found when switching between different first scatterers for a given snout and when switching between snouts for a given range. An analytical equation was devised to predict the change in D∕MU associated with range due to the observed SAD variations. This equation, referred to as the geometry factor B(R), accounts for the MU chamber location relative to the variable SAD. Application of the geometry factor accounts for the SAD variance with range and removes the discontinuities. Application of the three functions based upon physical principles combined to predict the range dependency of D∕MU to within 1.0%.

Investigation of modulated beams showed that an analytical formula, devised from an existing theory based on the total thickness of modulator M_max, can predict the D∕MU dependency as a function of W_SOBP to within 1.5%. Special attention must be applied when measuring the D∕MU dependence on W to avoid interplays with range and SAD effects.

Future investigations will include the effect of aperture opening and compensator shape on the D∕MU using measurements in conjunction with calculations from the treatment planning system.