Abstract
Monte Carlo simulations of x-ray beams typically take parameters of the electron beam in the accelerating waveguide to be free parameters. In this paper, a methodology is proposed and implemented to determine the energy, spectral width, and beam divergence of the electron source. All treatment head components were removed from the beam path, leaving only the exit window. With the x-ray target and flattener out of the beam, uncertainties in physical characteristics and relative position of the target and flattening filter, and in spot size, did not contribute to uncertainty in the energy. Beam current was lowered to reduce recombination effects. The measured dose distributions were compared with Monte Carlo simulation of the electron beam through the treatment head to extract the electron source characteristics. For the nominal 6 and 18 MV x-ray beams, the energies were 6.51±0.15 and 13.9±0.2 MeV, respectively, with the uncertainties resulting from uncertainties in the detector position in the measurement and in the stopping power in the simulations. Gaussian spectral distributions were used, with full widths at half maximum ranging from 20±4% at 6 MV to 13±4% at 18 MV required to match the fall-off portion of the percent-depth ionization curve. Profiles at the depth of maximum dose from simulations that used the manufacturer-specified exit window geometry and no beam divergence were 2–3 cm narrower than measured profiles. Two simulation configurations yielding the measured profile width were the manufacturer-specified exit window thickness with electron source divergences of 3.3° at 6 MV and 1.8° at 18 MV and an exit window 40% thicker than the manufacturer’s specification with no beam divergence. With the x-ray target in place (and no flattener), comparison of measured to simulated profiles sets upper limits on the electron source divergences of 0.2° at 6 MV and 0.1° at 18 MV. A method of determining source characteristics without mechanical modification of the treatment head, and therefore feasible in clinics, is presented. The energies and spectral widths determined using this method agree with those determined with only the exit window in the beam path.
INTRODUCTION
Monte Carlo simulations of x-ray beams used in radiotherapy are capable of closely matching measured dose distributions.1, 2 However, because fluence is difficult to measure, it is unclear how closely the fluence determined by simulation matches the actual fluence. One difficulty is that parameters needed to simulate medical linear accelerators (linacs) are often either not known or are subject to variability from machine to machine. These unknown parameters include characteristics of the electron beam in the accelerating waveguide, including its energy, spectral distribution, and divergence. Dose distributions are also sensitive to mechanical parameters of the treatment head which are not known precisely, or even specified incorrectly by the manufacturer.3, 4 For these reasons, simulations typically take the parameters of the incident electron beam as fitting parameters,2, 5 determined by comparison to measured dose distributions in an iterative process.6 With uncertainties in both measurement and simulation, the parameter set determined by this iterative process is not necessarily unique. Given that accurate fluence calculation is dependent on accurate input parameters,1 the importance of determining incident electron beam parameters through measurement is apparent.
Typically, x-ray beams in a medical linac are produced by electrons impinging on a thick, high-Z target. Accurate determination of the photon angular and energy distributions downstream of the target by analytical means is difficult2, 7 because bremsstrahlung production and electron scattering both depend on electron energy, which is rapidly degraded in the target. Benchmark measurements of bremsstrahlung production have uncertainties of up to 5% (Refs. 7, 8) (3% in the fluence profile for field sizes of interest in radiotherapy7), adding to the uncertainty of electron source parameters determined from Monte Carlo simulations of x-ray dose distributions. Furthermore, the distribution of photons from the target is strongly peaked in the forward direction, and medical linear accelerators typically contain a metal flattening filter to flatten the beam. Dose distributions are sensitive to the material, composition, and positioning of the flattening filter both along and orthogonal to the beam axis, which adds even more to the list of parameters in the simulation.
Even aside from questions of accuracy, determination of electron source parameters by comparing measured and simulated dose distributions is limited by the precision of measurements and simulations used. Sheikh-Bagheri and Rogers3 extensively studied a generic linac, including target and flattening filter, using Monte Carlo simulation and reported the effects of altering electron source parameters. Their results, summarized in TG-105,1 showed that the sensitivity to electron source energy is such that a 0.2 MeV change in energy at 6 MeV resulted in an observable change (2%) in dose distributions, changes in the width of the energy distribution of the electron source changed the dose near the surface and at large depths by up to 2%, and beam divergences of up to 0.5° had no observable effect.
In this paper, we report on a method to determine energy, spectral width, and divergence of the beam that is independent of the simulation of bremsstrahlung in the target. The method involves the measurement of dose distributions with all treatment head components removed from the beam path, except the exit window. A Siemens Oncor linac, with nominal accelerating potentials of 6 and 18 MV in x-ray mode, was used. The simplest configuration in which the linac could be operated was with only the exit window in the beam path, since the exit window was necessary to maintain the vacuum in the accelerating waveguide. With no target or flattening filter, the beam emerging from the treatment head was predominantly comprised of electrons, and the percent-depth ionization curves resembled those of clinical electron beams. Matching simulated percent-depth ionization curves to measurements yielded the energy of the incident beam and its spectral width.
Profile widths were sensitive to both the amount of scattering in the exit window and the beam divergence. Different exit window geometries and different beam divergences resulted in different profile widths, and various combinations of the two modifications could be used to obtain a particular profile width. The amount of bremsstrahlung produced by these alternatives was investigated as a possible method of distinguishing between them. Comparisons of measurements to simulations with the target in place were used to put an upper limit on the beam divergence, which, in turn, led to a determination of the exit window thickness that was required in the simulation to match measured profile width.
This method of determining electron source parameters has several advantages over determining them by simulating photon dose distributions, whether or not the flattening filter is removed.9 Uncertainties related to positioning, geometry, and composition of components of the treatment head are minimized. Uncertainties in simulating transport through, and bremsstrahlung generation in, the removed components are eliminated. Uncertainties arising from parameters which have equal effects on dose distributions are reduced. This method is more sensitive to the spectral distribution and angular distribution of the electron source, and to properties of the exit window, than the usual method of using x-ray dose distributions.
Methodology is also presented for determining the energy and spectral width of the incident electron beam without mechanical modification of the linac. The method involves running the linac in electron mode, removing the primary scattering foil via the console, and measuring percent-depth ionization curves. Only the exit window, secondary scattering foil, and electron monitor chamber remain in the beam path. This is a practical method for linacs used clinically, where mechanical modifications may not be feasible. The same precision can be obtained in the incident beam energy and its spectral width as with the method with only the exit window in the beam path.
MATERIALS AND METHODS
Measurement
A Siemens Oncor linac installed at UCSF, and not used for clinical treatment, facilitated measurement with the treatment head in a variety of conditions. With the linac in electron mode, the monitor chamber and secondary scattering foil were removed. The primary foil was removed via the console, by selecting the empty foil slot for each energy (as for treatment with 6 MeV electrons). Beam parameters (bending magnet current, injector voltage, automatic frequency control preset, and triggers) were set to their clinical x-ray values at the console. Injector current (INJI), pulse-forming network voltage (PFN), and pulse repetition frequency preset (PRFP) were lowered from their clinical values as described below. Static and dynamic steerings were turned off for these measurements as focal spot position at the exit window does not affect the profile width or depth dose curve.
Percent depth ionization (PDI) curves and profiles were measured in a Wellhöfer water phantom. A PTW 34001 Roos parallel-plate ion chamber was used for the percent-depth ionization measurement, and a PTW CC13 thimble ion chamber was used for the profiles, because of its smaller area orthogonal to the beam. The water tank was aligned with the surface at 100 cm source-surface distance (SSD). Detector currents for the reference (CC13) and field (scanning) probes were measured with a Wellhöfer CU500E electrometer, and the field signal was divided by the reference signal. Profiles were measured both at the depth of maximum ionization (dmax) and 1 cm beyond the maximum range of the electrons (dbrem), where only dose due to bremsstrahlung was present. Depths of measurement are tabulated in Table 1. Ionization was measured for six different bending magnet currents from 12.6 to 26.3 A, spanning the range used for the 6 and 18 MV clinical beams. The Roos chamber was positioned such that zero depth corresponded to the top surface of the chamber being 1.3 mm above the water surface, based on the manufacturer’s specification of the front wall area density of 1.3 mg∕cm.
Table 1.
Depths used to measure profiles. dmax is the depth of maximum ionization and dbrem is sufficiently deep that dose only involves bremsstrahlung generated in the phantom and exit window.
| Bending magnet current (A) | dmax (cm) | dbrem (cm) |
|---|---|---|
| 12.6 | 1.3 | 4.0 |
| 15 | 1.65 | 4.8 |
| 18 | 2.05 | 5.6 |
| 21 | 2.45 | 6.5 |
| 24 | 2.8 | 7.4 |
| 26.3 | 3.0 | 8.0 |
Uncertainties in the calculated incident energy arose mainly from uncertainties in detector positioning and in stopping power ratio. The uncertainty in detector positioning depended on both its repeatability and accuracy. Percent-depth ionization curves with the full clinical beam were measured with Roos chambers in both the Wellhöfer water tank and the National Research Council of Canada (NRCC) in-house water tank with the capability of precise positioning.10 The differences in the curves were less than 0.04 cm, which was taken as the positioning accuracy. The repeatability of positioning in the Wellhöfer tank was 0.03 cm. The depth of 50% ionization I50 was determined to within 0.01 cm from each depth ionization curve by fitting a line to the fall-off region of the percent-depth ionization curve from 40% to 60% of maximum ionization. Adding these uncertainties in quadrature resulted in an uncertainty in positioning of 0.05 cm.
The 1σ uncertainty in the theoretically determined stopping power ratios is given in the ICRU 37 report as 0.5%–1%.11 Measurements of stopping power ratios, using the technique of Ref. 12, for Be, Al, Cu, and Ta agreed with the theoretical values to within 0.7%.13 The stopping power for water was not investigated in that work in as much detail, but 1% agreement with the theoretical value was obtained. A 1% uncertainty in the stopping power ratio is therefore a reasonable estimate. Adding this uncertainty in quadrature to the uncertainty in detector position resulted in total uncertainties in the calculated incident energies of 2.3% and 1.4% at 6 and 18 MV, respectively.
Recombination effects
The high beam currents in photon mode result in substantial recombination in the detector, when the linac was run with the target and flattening filter removed from the beam path. Because the recombination correction factor is proportional to dose rate, the apparent I50 is greater than the actual I50. In order to overcome this, the injector current was reduced to reduce the dose per pulse, while keeping the output (measured with an ionization chamber in water) peaked by adjusting the PFN. The recombination correction factor for a PTW 34001 Roos parallel-plate ionization chamber varies linearly with dose per pulse, and is 0.7% at 1 mGy∕pulse.14 This result was verified by measuring the detector current with detector voltages of +150 and +300 V with the detector positioned at dmax, as recommended by the TG-21 protocol.15 For the percent-depth ionization and profile measurements, dose per pulse values of 0.8 mGy at 6 MV to 0.02 mGy at 18 MV at INJI of 2100 and 1700 mV, respectively, were used. At these doses per pulse, the difference in current at high and low chamber biases was less than the noise in the measurement (1%). The resulting errors in I50 due to recombination were 3×10−3 cm at 6 MV and 2×10−4 cm at 18 MV. Both values are less than 10% of the estimated uncertainty in the positioning of the chamber. At doses per pulse sufficiently low that recombination effects were negligible, percent-depth ionization curves were measured for at least two doses per pulse. The change in apparent I50 was verified to be negligible. Measurements with the CC13 ionization chamber at low doses per pulse also showed negligible effects of recombination.
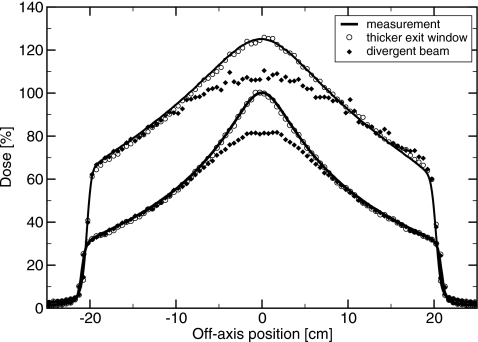
In order to verify that altering the dose per pulse did not affect the photon beam, measurements were made in the clinical geometry—that is, with the target and flattening filter in the beam path. Percent-depth ionization curves for 5×5 cm2 fields and profiles for 40×40 cm2 fields were measured with a CC13 chamber over the range of injector currents from those used in the exit-window-only measurements to those used for the clinical beams. These results are shown in Figs. 12. To within the uncertainty of the measurements, there was no difference in the dose distributions. These profiles were averaged over two sides of isocenter, and the low injector current scans were binned into 0.5 cm bins to reduce the noise. Also shown are the differences between the percent-depth ionization curves at low and high beam currents, which is zero, within uncertainty. These results suggest that reducing the injector current had minimal effect on the beam energy.
Figure 1.
Diagonal profiles measured with different injector currents with the target and flattening filter in place. Upper traces, 18 MV; lower traces, 6 MV. Data points with errors are measured with low beam current, and binned into 0.5 cm bins. Solid lines are measured with clinical beam current. The low injector currents were used for the measurements with no target or flattening filter, and the high injector currents were those used for the clinical beam. Data were averaged over two sides of isocenter.
Figure 2.
(a) Percent-depth ionization measured with different injector currents with the target and flattening filter in place and a 5×5 cm2 field. Data points with errors were measured with low beam current and binned into 0.5 cm bins. Solid lines were measured with clinical beam current. Left traces, 6 MV; right traces, 18 MV. (b) Difference between percent-depth ionization traces measured with high and low injector currents, for 6 MV. [(c) as (b)], for 18 MV.
Bremsstrahlung dose
The absorbed dose to water in the bremsstrahlung tail was determined by measurements based on the TG-51 protocol.16 Dose was measured in the bremsstrahlung tail (Dx) and at the reference point dref (De) and the ratio, Dx∕De, reported. Beam energies of 12.6 and 13.9 MeV were used. At energies above 15 MeV, the field was narrower than the 10×10 cm2 required by the TG-51 protocol, and at energies below 10 MeV the same chamber could not be used for both electrons and photons (the TG-51 protocol does not recommend cylindrical chambers for electron energies below 10 MeV and does not specify detector calibration factor kQ values for parallel plate chambers in photon beams).
Dose was measured with a Farmer-type NEL 2581 ion chamber placed in an acrylic sleeve in a Radiation Products Design (Albertville, MN) model 592-000 water tank with a Mylar window and a Keithley model MK614 electrometer. A CC13 thimble ionization chamber was attached to the front surface of the window, at the edge of the beam, and used as a reference detector. The gantry was rotated to 90°, and secondary collimators were set to 40×40 cm2. Although this value is larger than the 10×10 cm2 recommended by the TG-51 protocol, it was chosen to reduce electron scatter from the secondary collimators; the full widths at half maximum of measured profiles were close to 10 cm at 100 cm SSD. Because the size of the water tank did not allow a 40×40 cm2 field at 100 cm SSD, the tank was positioned at 59 cm SSD. The depth of measurement for electrons was dref, as determined following the TG-51 protocol: the Roos chamber was scanned along the beam axis with the water phantom at 100 cm SSD to determine I50 and hence, through TG-51, dref. Simulations showed that changing the SSD from 100 to 59 cm changes I50 by 0.02 cm, resulting in a change in dref of 0.01 cm, an amount less than the estimated uncertainty in detector positioning.
Measurement of dose in the bremsstrahlung tail followed the same method as for dose at dref, but with the Farmer chamber placed at a depth of 13 cm. Although the TG-51 protocol recommends 10 cm depth, 13 cm was chosen because it is well into the bremsstrahlung tail for the highest energy available on the linac. The protocol states that there is no significant difference in detector calibration factor kQ over the range of 5–10 cm, so the possibility of a significant difference at 13 cm was ignored. Measurement of the percent-depth ionization curve for x rays, as required for determining kQ using the protocol, was not possible because dose from the electron beam dominated the dose in shallow regions. The bulk of the bremsstrahlung was generated in the phantom, with only 10% of the dose in the bremsstrahlung tail of the 13.9 MeV beam involving x rays generated in the treatment head. Filtering the primary electrons out of the beam, as done for large field electron measurements,17 was not practical because that would have removed the source of the bremsstrahlung dose. Instead, kQ was determined by simulation. For the 13.9 MeV beam, Monte Carlo simulations (see next section for details) showed that at 8 cm depth in the water phantom, where no primary electrons remained, the average photon energy was 1 MeV. Allowing these simulated photons leaving the 8 cm of water to be incident on another water phantom resulted in a percent-depth ionization at 10 cm depth of the second phantom of 58%, which corresponds to a kQ value of 1.00. This value was used to calculate the absorbed dose. The 18 MV clinical beam, generated in the thick target and hardened by the flattening filter, has an average photon energy of 2.8 MeV and a kQ value of 0.965. The small change in kQ resulting from the large change in energy of these beams suggested that the uncertainty in the determination of kQ was negligible compared to other sources of uncertainty.
The measurements of Dx∕De were corrected for the reduced current caused by averaging the narrow profile over the 2 cm length of the detector. Because the profiles at the two depths were nearly the same width, this was a 0.5% correction.
Several factors contributed to the uncertainty in the measurement of Dx∕De. The uncertainty in the detector position was 1 mm, which led to an uncertainty in the ratio of 1% due to the slope of the depth-dose curve. Huq and Andreo18 estimated uncertainties in the dose measured according to the TG-51 protocol to be 1.3% for photon beams and 1.9% for electron beams. Adding these values in quadrature yielded an uncertainty of 3% in the ratio Dx∕De.
Simulation
Simulations were done using the EGSNRC version 4.2.2.5 (Ref. 19) and BEAMNRC version 1.78 (Ref. 20) codes for the treatment head and MCRTP (Ref. 21) for the water phantom. The treatment head was initially simulated according to parameters provided by the manufacturer. The water phantom was 60×60×16 with 0.5×0.5×0.2 cm3 voxels, with the smaller phantom and voxel size along the beam axis. Typically, a simulation used at least 2×109 particles in the incident beam, and the relative precision in dose at dmax was 0.1%. In order to obtain a good fit to measurement, electron source mean energy, spectral width, divergence, and exit window thickness were varied. A Gaussian spectral shape and Gaussian angular distribution were used.
No Russian roulette or bremsstrahlung splitting was used. The boundary crossing algorithm was Exact in the treatment head, with the boundary crossing skin depth set to 3.0 elastic mean free paths. In the phantom, where Presta-I is 35 times faster than the Exact boundary crossing algorithm22 and has an error of 0.5% for a 6 MeV beam irradiating a 10×10 cm2 field,23 Presta-I was used. Cutoff energies were 0.7 MeV for electrons and 1 keV for photons. Spin effects, bound Compton scattering, photoelectron angular sampling, Rayleigh scattering, atomic relaxations, and electron impact ionization were all on. Bremsstrahlung angular sampling was Koch–Motz, bremsstrahlung cross sections were Bethe–Heitler, and pair angular sampling was Koch–Motz. In addition to dose to water, dose to a Bragg–Gray air cavity was calculated to enable direct comparison to the measured percent-depth ionization curves.
In comparisons of simulation to measurement, uncertainties in the dose ratio Dx∕De come from several sources. The uncertainty in the measured benchmark of bremsstrahlung yield per incident electron was quoted as 5%.8 Simulation using two different Monte Carlo codes (EGSNRC and PENELOPE) (Ref. 24) resulted in bremsstrahlung yields differing by 4%. This suggests that assigning a 5% uncertainty to Dx is reasonable. Uncertainties in De can be approximated by the differences in measurements of dose with different detectors and Monte Carlo simulations, and are about 2%.17 In all, the uncertainties in Dx and De were added in quadrature to the 3% uncertainty in measurement to obtain a total uncertainty of 6%. In comparing the results of two different simulations, the statistical precision is quoted as the uncertainty. For the Dx∕De values, this was 1%.
RESULTS AND DISCUSSION
Energy and spectral width
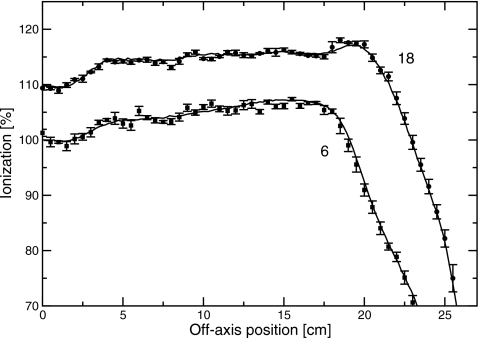
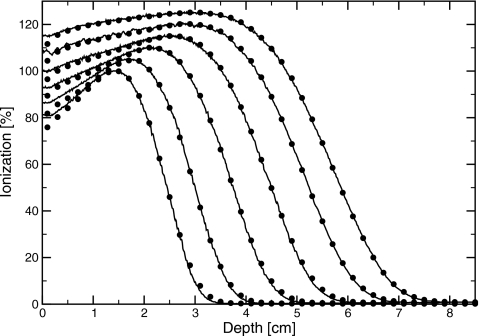
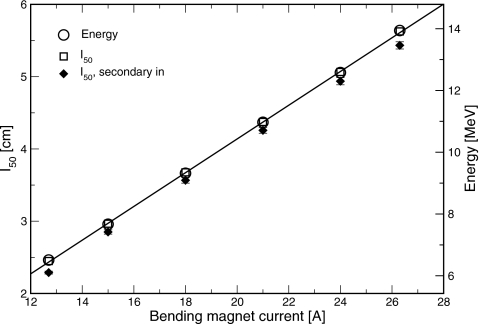
Measured percent depth-ionization curves, as a function of position in the water phantom, are shown in Fig. 3 for bending magnet currents in the range of 12.6–26.3 A. I50, determined from these data, is plotted against bending magnet current in Fig. 4. A linear relation was found, with slope of 0.234±0.001 cm∕A and intercept of −0.54±0.02 cm. Profiles measured in the plane of the waveguide (in-plane) at dmax and dbrem are shown in Figs. 56. Full widths at half maximum (FWHM) of the profiles at dmax ranged between 29.35±0.05 cm at 6 MV and 15.3±0.4 cm at 18 MV. At dbrem, FWHM were between 29.5±2.0 cm at 6 MV and 16.5±1.8 cm at 18 MV.
Figure 3.
Comparison of measured (lines) and simulated (circles) percent-depth ionization curves with only the exit window in the beam for bending magnet currents of 12.6, 15, 18, 21, 24, and 26.3 A (left to right). Simulations shown used the thicker exit window. Normalization is arbitary.
Figure 4.
Measured depth at which ionization falls to half its maximum value (left scale), and electron source energy as determined by Monte Carlo simulation (right scale) vs bending magnet current. Line is a fit of electron source energy derived from Monte Carlo vs bending magnet current. Simulated results used the thicker exit window geometry to match the measured results. Filled diamonds are the measured with the electron secondary scattering foil and monitor chamber in the beam path.
Figure 5.
Comparison of measured (lines) and simulated (circles) profiles at with only the exit window in the beam, for bending magnet currents of 12.6, 15, 18, 21, 24, and 26.3 A, from the outside in. Simulations shown used the thicker exit window geometry. Normalization is arbitary.
Figure 6.
Comparison of measured (solid) and simulated (hollow) profiles in the bremsstrahlung region, 1 cm beyond the maximum electron range, with only the exit window in the beam. For clarity, only results with bending magnet currents of 12.6 (outer trace) and 26.3 A (inner), as used for the 6 and 18 MV clinical beams, respectively, are shown. Data are binned into 2 cm bins. Simulations shown used the thicker exit window geometry. Normalization is arbitary.
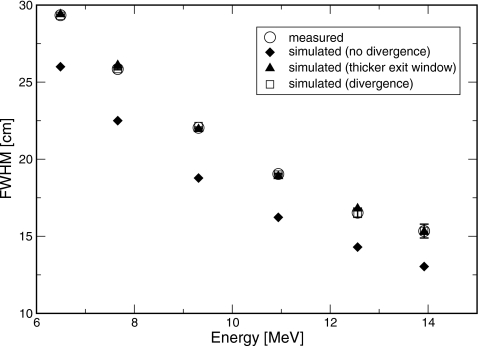
Source and geometry parameters were adjusted in the simulations to match the measured dmax profiles and depth dose curves. Simulations using the manufacturer-specified exit window thickness and no beam divergence resulted in narrower profiles than measured. The difference ranged from 3.3 to 2.3 cm at 6–18 MV, as shown in Fig. 7. There are several potential explanations for this difference. Two possibilities are that the electron source has a divergence, or that the exit window is thicker than its manufacturer-specified value. In order to match the measured data, a root-mean-square beam divergence of 3.3°–1.8° at 6–18 MV, or a 40% increase in the exit window thickness, was required. This is consistent with previous simulations17 of clinical electron beams with scattering foils and monitor chamber present, which suggested either a 25% thicker exit window or beam divergence of up to 5°. The difference in the thickness increase required in the two sets of simulations resulted from the uncertainties in the positions and thicknesses of the scattering foils in the full clinical beam simulations. The simulated percent-depth ionization and profiles with only the exit window in the beam are shown along with the measured data in Figs. 356. For clarity, only the simulations using a thicker exit window are shown.
Figure 7.
Width of profile at dmax. Measurement (solid circles), simulation with the manufacturer-specified exit window and nondivergent beam (diamonds), manufacturer-specified exit window and divergent beam (squares), and thicker exit window (triangles) are shown.
Electron source parameters determined by matching simulation to measurement using the thicker exit window model are listed in Table 2. The electron source energy was a linear function of bending magnet current, with slope of 0.546±0.005 MeV∕A and intercept of −0.49±0.09 MeV, as shown in Fig. 4. The electron source energy was also a linear function of I50, with slope of 2.34±0.01 MeV∕cm and intercept of 0.75±0.04 MeV. For beams corresponding to the clinical beams of 6 and 18 MV, the electron energies were found to be 6.51±0.15 and 13.9±0.2 MeV, respectively.
Table 2.
Measured I50 and Monte Carlo parameters of the incident electron beam used to match measured data. Energy and spectral width are the values for the simulation with the thicker exit window. Divergence values are those used with the manufacturer-specified exit window thickness. Spectral width is full width of half maximum: absolute uncertainty is 4%.
| Bending magnet current (A) | I50 (cm) | Energy (MeV) | Spectral width (%) | Divergence (°) |
|---|---|---|---|---|
| 12.6 | 2.45 | 6.51 | 20.0 | 3.3 |
| 15 | 2.96 | 7.67 | 18.8 | 2.9 |
| 18 | 3.68 | 9.32 | 17.2 | 2.4 |
| 21 | 4.37 | 10.97 | 15.8 | 2.2 |
| 24 | 5.06 | 12.58 | 14.4 | 1.8 |
| 26.3 | 5.63 | 13.94 | 13.2 | 1.8 |
The FWHM of the Gaussian spectrum used to obtain dose distributions in agreement with measurement varied from 20±4% at 6 MV to 13±4% at 18 MV. These values are greater than those reported by Sheikh-Bagheri and Rogers,3 who found that the x-ray dose distributions could be simulated using a spectrum with an effective FWHM of 9%. Differences in the present work between simulated and measured PDI curves remained, especially at low electron energies. At the low-dose portion of the percent-depth ionization curve, where the ionization is 5%–10% of the maximum, measured ionizations were up to 2% less than simulated ionizations, with the curves normalized to their maxima. At shallow depths, measured ionizations were up to 3% more than simulated. This difference has been known for more than 20 years25 and has also been observed with the large field clinical electron beam.17 The latter measurement included both the primary electron scattering foil, and collimation of the beam by the secondary collimators. This suggests that the differences between measured and simulated PDI curves did not result from scattering in the primary scattering foil from the secondary collimators. The discrepancy could be resolved with an asymmetric peak in the energy spectrum, plus a separate peak at low energy, but this low energy peak is purely hypothetical. Alternatively, there may be a systematic error in the measurement, such as a change in detector response with depth.
Bremsstrahlung production
The two simulation geometries used to match the measured dmax profile widths differed in the amount of bremsstrahlung produced. The thicker exit window simulation produced 20%–30% more photons at all angles per incident electron than the divergent beam simulation, from 6 to 18 MV. The effect on dose in the bremsstrahlung tail on the central axis was less, because 80%–90% of the dose (at 6–18 MV) involved photons generated in the phantom. A competing effect was that the photons from the exit window reaching 100 cm SSD along the central axis was largely created in the first layer of the exit window, before the electrons scattered. Adding a beam divergence thus decreased the dose in the bremsstrahlung tail along the central axis. In all, the thicker exit window model resulted in Dx∕De 13%–8% larger than the divergent beam model, from 6.5 to 13.9 MeV. At 13.9 MeV, Dx∕De determined by simulation was 0.360±0.004% (the quoted uncertainty is the statistical precision) for the thicker exit window model and 0.334±0.003% for the divergent beam model (results at 12.6 MeV are similar; see Table 3). The measured value was 0.39±0.01%. This measured value is 8% more than the value determined by simulation with the thicker exit window, and 17% more than the value determined with the divergent beam simulation. The latter value is nearly three times the uncertainty in the comparison of measurement to simulation, which is 6%. This difference in the amount of bremsstrahlung generated suggests that the discrepancy in the profile widths is more likely related to the exit window thickness, rather than beam divergence.
Table 3.
Amount of dose in the bremsstrahlung tail relative to dose at dref. Dx∕De, expressed in percent. Uncertainties in the simulations represent the statistical errors of 1%. Ratios: Thick∕Div is the ratio of simulations with the thicker exit window and beam divergence; meas∕thick is the ratio of the measured value to the value from the simulation with thicker exit window. The uncertainty in the ratio of simulated doses only includes the statistical uncertainty.
| Energy (MeV) | Simulation (%) | Measurement (%) | Ratio | ||
|---|---|---|---|---|---|
| Divergence | Thickness | Thick∕Dev | Meas∕Thick | ||
| 12.6 | 0.266±0.003 | 0.289±0.003 | 0.32±0.01 | 1.09±0.02 | 1.11±0.07 |
| 13.9 | 0.334±0.003 | 0.360±0.004 | 0.39±0.01 | 1.08±0.02 | 1.08±0.06 |
Target in place
With the target in place, but no flattening filter, the two sets of simulations produced different results. The thicker exit window model produced dose distributions in agreement with measurement, while the divergent beam model did not (see Fig. 8). With a divergent beam, the off-axis ratio was 20% higher than measured, at 20 cm off axis for a diagonal scan. This was because a portion of the bremsstrahlung is generated before the electrons scatter. In particular, the bremsstrahlung along the axis is predominantly generated by electrons directed along the beam axis. Reducing the number of these, by adding a beam divergence, reduces the bremsstrahlung dose on the central axis. Electron source divergences of 0.2° at 6 MV and 0.1° at 18 MV were sufficient to reduce dose on axis by 0.5%, giving upper limits to the beam divergence. With the target in place, altering the exit window thickness (without changing the beam divergence) had no effect on the simulated dose distributions to within 0.5%. This confirms that a beam divergence of 2°–3° is not a feasible explanation for the large profile widths, and that altering the exit window geometry is a more realistic alternative.
Figure 8.
Profiles with target in, but not the flattening filters. Top, 6 MV at 1.5 cm depth. Bottom, 18 MV at 3.2 cm depth. Solid lines are measured, filled diamonds are simulated with divergent beams, and circles simulated with the thicker exit window. Relative normalization of simulations for each energy is by dose per pulse.
Measurement in clinical settings
On many clinical machines, removing the secondary scattering foil and monitor chamber is not practical, because of the necessity of replacing them precisely in the same position. To facilitate determination of the electron source energy on linacs used clinically, percent-depth ionization curves were measured with the secondary scattering foil and monitor chamber, but not the primary scattering foil, target, or flattening filter, in the beam path. These adjustments were made via the console, without manually removing components from the treatment head. The linac was put into electron mode, the empty foil slot was selected, and softpots appropriate for the clinical x-ray beams (except with reduced dose per pulse) were chosen. Beam current was reduced, both to avoid recombination effects in the detector and to prevent damage to the monitor chamber. The depth at which ionization fell to half its maximum value, I50, is plotted in Fig. 4. The difference in I50 between measurements with and without the secondary foil and monitor chamber was 0.14±0.03 cm, averaged over six different beam energies. There was no systematic variation with beam energy in the difference.
Using the energy and spectral width of the incident beam as determined with only the exit window in the beam, as input to simulations with the secondary foil in place, gave agreement within measurement uncertainty to the measured percent-depth ionization curves. In this situation, the position and thickness of the secondary scattering foil affected the profile widths, making it more difficult to extract the exit window thickness and beam divergence. Nevertheless, the percent-depth ionization curve measured with the secondary foil in the beam path yielded the incident beam energy and spectral width.
BEAM DIVERGENCE
Comparison of measured and calculated dmax profiles with only the exit window in the beam path shows that the angular distribution is increased more than just by scatter in the exit window. The precise source of increased angular distribution is not known. As discussed above, measurements with the target in place rule out a beam divergence causing the full increase. Several possibilities, including the beam divergence, are considered here.
A beam divergence of 2°–3°, as used in the simulations with the manufacturer-specified exit window thickness, is too large to be credible. Over the length of a 1 m waveguide, an initially small beam with this divergence would increase in size to more than 7 cm diameter. Such a large diameter is clearly unrealistic. An alternative possibility is that the divergence originates in the bending magnet, only a few centimeters from the exit window. Any such divergence, however, would likely be greater in the in-plane direction (the plane in which the bending takes place) than the cross-plane direction. Measured profile widths were only 0.14±0.15 cm wider in the in-plane than cross-plane directions, averaged over six energies, with no systematic trend with energy. These differences are a small fraction of the 2.3–3.3 cm differences between measured and simulated profile widths and correspond to differences in angular divergence of 0.2°–0.3°, 10% of the total divergence required to match the measured data. Also, Parmela (Los Alamos Accelerator Code Group) simulations of the accelerating waveguide show a maximum beam divergence of 0.3°.17 Furthermore, Karzmark et al.26 wrote “typical beam transport acceptance values for medical linacs are in the ranges …±1 to 5 mrad (0.05°–0.25°) angular divergence from axis,” although this refers to a Varian linac. With the manufacturer-specified exit window thickness, divergences ten times greater than this were required to match the measured data.
Various changes to the exit window geometry could account for the observed profile width. Results of simulations with all three layers of the exit window increased in thickness by 40% are shown here to match measured dose distributions. Approximately half the increase in profile width comes from the metal sheets of the window, and half from the cooling water. Increasing either the thickness of the metal sheets by 70% or the thickness of the water by 100%, and leaving the other unchanged, resulted in a match to the measured profile width and percent-depth ionization. These different alterations produced the same amount of dose in the bremsstrahlung tail relative to dose at dref, within 2%, and therefore, given uncertainties in the comparison of simulation to measurement, the bremsstrahlung production could not be used to distinguish between these possibilities.
A plausible scenario is the presence of a bulge in one or both of the metal sheets, resulting in a thicker water channel. In this case, the linac on which the measurements were made would has changed with time. Direct measurement of the exit window thickness is impractical, but measurement of profile widths on different linacs of the same type would help to determine whether linac exit window thickness changes over time. With linacs used clinically, however, the removal of scattering foils cannot be undertaken lightly. These measurements could be done during commissioning, decommissioning, at the factory, or when the electron monitor chamber needs replacing.
Another possibility is that contaminants in the cooling water increase the amount of scatter. Simulations showed that a concentration of copper in water of 5% is required to produce the measured profile width. At a pH of 7, the solubility of copper in water is only 1 ppm,27 more than four orders of magnitude lower than required. Experimentally, on replacing the cooling water with fresh distilled water, the profile widths were unchanged within 0.5 mm. Furthermore, the resistivity of the cooling water is measured within the linac, with an acceptability criteria of 1 MΩ cm. These facts all indicate that any impurities in the cooling water had negligibly small impact on scattering.
Consider the possibility of additional material present in the treatment head. According to the manufacturer, the wave guide is fully evacuated with no material in the beam path upstream of the exit window. The beam that hits the sides of the envelope (the evacuated opening through the bending magnet) may scatter out through the exit window, but this would be diffuse and depend on beam energy, so this is an unlikely source of the increased angular distribution.
There exists the possibility that the Monte Carlo simulations did not determine the profile widths accurately. While comparison28 of simulated to measured29, 30 scattering from thin foils showed simulated profiles up to 8.7% narrower than measurement, more recent experiments31 showed differences between measurement and simulation of 2%. The measured profile widths presented here are 11%–17% greater than simulated profile widths, from 6 to 18 MV. Thus scatter in the exit window is accurately simulated.
One source parameter that was not adjusted in this paper is the spot size of the incident electron beam. Simulations of the full treatment head show that the spot size affects dose3 because features of the flattening filter are comparable in size to the spot. With the full treatment head, reducing the spot size and lowering the energy have similar effects on profiles, which complicates the determination of either parameter. Both in the present work and with the target in place but flattening filter removed,9 there is no dependence of dose on spot size.
CONCLUSIONS
The methods described in this paper allow determination of the mean energy, spectral width, and angular distribution of electrons incident on the exit window. These source parameters may be determined with experimental methodology that the clinical physicist is familiar with, without mechanical modification of the treatment head. Percent-depth ionization and profiles were measured with only the exit window in the beam path, and compared to simulation. The beam energy may be determined to high precision directly from the percent-depth ionization curve, with the accuracy limited by uncertainties in the stopping power of water and the accuracy of the positioning of the detector. The uncertainty in the energy is sufficiently low to adequately constrain the energy for simulations of the full treatment head.
Electron source energy was found to be a linear function of both bending magnet current, with slope of 0.546±0.005 MeV∕A and intercept of −0.49±0.09 MeV, and the depth at which ionization is 50% of its maximum value (I50), with slope of 2.34±0.01 MeV∕cm and intercept of 0.75±0.04 MeV. The FWHM of the Gaussian spectrum used to model the electron source ranged from 20±4% at 6 MV to 13±4% at 18 MV. The upper limit on the beam divergence was found to be 0.2° at 6 MV and 0.1° at 18 MV. With only the exit window in the beam path, the simulations differed in the amount of bremsstrahlung produced. Measured profiles were narrower than simulated profiles. Simulations with either an exit window 40% thicker than the manufacturer-specified thickness, or a beam divergence of 3.3°–1.8° from 6 to 18 MV, resulted in profile widths in agreement with measurement. Comparison of measured and simulated profiles with the x-ray target in place ruled out the possibility of a beam divergence as large as 2°–3°, suggesting that the exit window is thicker than specified.
Bremsstrahlung yield (fluence per electron) from thick targets at radiotherapy beam energies has been shown to be accurate to 5% by comparison to experimental benchmarks.8 A more accurate benchmark would improve confidence in the simulated result. Benchmark measurements of the dose in the bremsstrahlung tail, relative to dose in the electron part of the depth dose curve, would be helpful in using Monte Carlo simulation to determine the source of the added angular distribution in the clinical beams.
Determination of the electron source energy and limits on the angular distribution of the source removes a large source of uncertainty from simulations of x-ray beams. Previously these parameters had been taken to be free, determined by simulation of the beam with the target in place for unflattened or flattened beams. Knowledge of these parameters will constrain other parameters, such as the density of the flattening filter and the distance of the target to the flattener. Together, these constraints on electron source parameters presented here are an important step toward accurately and precisely determining fluence maps of photon beams. In addition, experimental determination of electron beam energy through the techniques described here has proven useful in design and commissioning of a beam line used for megavoltage cone beam computed tomography.32
ACKNOWLEDGMENTS
We thank Andrew MacDonald and Malcolm McEwen for making precise measurements of ionization and dose versus depth on our linac using their precision water phantom. Research funded by NIH through Grant No. R01 CA104777-01A2.
References
- Chetty I. J., Curran B., Cygler J. E., DeMarco J. J., Ezzell G., Faddegon B. A., Kawrakow I., Keall P. J., Liu H., Ma C.-M., Rogers D. W. O., Seuntjens J., Sheikh-Bagheri D., and Siebers J. V., AAPM Task Group Report No. 105; [DOI] [PubMed]; “Issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning,” Med. Phys. 10.1118/1.2795842 34, 4818–4852 (2007). [DOI] [PubMed] [Google Scholar]
- Verhaegen F. and Seuntjens J., “Monte Carlo modelling of external radiotherapy photon beams,” Phys. Med. Biol. 10.1088/0031-9155/48/21/R01 48, R107–R164 (2003). [DOI] [PubMed] [Google Scholar]
- Sheikh-Bagheri D. and Rogers D. W. O., “Sensitivity of megavoltage photon beam Monte Carlo simulations to electron beam and other parameters,” Med. Phys. 10.1118/1.1446109 29, 379–390 (2002). [DOI] [PubMed] [Google Scholar]
- Chibani O. and Ma C.-M., “On the discrepancies between Monte Carlo dose calculations and measurements for the 18 MV Varian photon beam,” Med. Phys. 10.1118/1.2712414 34, 1206–1216 (2007). [DOI] [PubMed] [Google Scholar]
- Ma C.-M. and Jiang S. B., “Monte Carlo modelling of electron beams from medical accelerators,” Phys. Med. Biol. 10.1088/0031-9155/44/12/201 44, R157–R189 (1999). [DOI] [PubMed] [Google Scholar]
- Aljarrah K., Sharp G. C., Neicu T., and Jiang S. B., “Determination of the initial beam parameters in Monte Carlo linac simulation,” Med. Phys. 10.1118/1.2168433 33, 850–858 (2006). [DOI] [PubMed] [Google Scholar]
- Faddegon B. A., Ross C. K., and Rogers D. W. O., “Angular distribution of bremsstrahlung from 15‐MeV electrons incident on thick targets of Be, Al and Pb,” Med. Phys. 10.1118/1.596667 18, 727–739 (1991). [DOI] [PubMed] [Google Scholar]
- Faddegon B. A., Ross C. K., and Rogers D. W. O., “Forward-directed bremsstrahlung of 10‐ to 30‐MeV electrons incident on thick targets of Al and Pb,” Med. Phys. 10.1118/1.596560 17, 773–785 (1990). [DOI] [PubMed] [Google Scholar]
- De Smedt B., Reynaert N., Flachet F., Coghe M., Thompson M. G., Paelinck L., Pittomvils G., De Wagter C., De Neve W., and Thierens H., “Decoupling initial electron beam parameters for Monte Carlo photon beam modelling by removing beam-modifying filters from the beam path,” Phys. Med. Biol. 10.1088/0031-9155/50/24/012 50, 5935–5951 (2005). [DOI] [PubMed] [Google Scholar]
- McEwen M. R., Kawrakow I., and Ross C. K., “The effective point of measurement of ionization chambers and the build-up anomaly in MV x-ray beams,” Med. Phys. 10.1118/1.2839329 35, 950–958 (2008). [DOI] [PubMed] [Google Scholar]
- ICRU, Stopping powers for electrons and positrons, ICRU, 1984.
- Faddegon B. A., Ross C. K., and Rogers D. W. O., “Measurement of collision stopping powers of graphite, aluminium and copper for 10 and 20 MeV electrons,” Phys. Med. Biol. 37, 1561–1571 (1992). [Google Scholar]
- MacPherson M. S., “Accurate Measurements of the Collision Stopping Powers for 5 to 30 MeV Electrons,” Ph.D. thesis, National Research Centre of Canada, 1984. Available online at http://inms-ienm.nrc-cnrc.gc.ca/pubs/documents/NRCC-PIRS-0626.pdf. [Google Scholar]
- Bruggmoser G., Saum R., Schmachtenberg A., Schmid F., and Schüle E., “Determination of the recombination correction factor for some specific plane-parallel and cylindrical ionization chambers in pulsed photon and electron beams,” Phys. Med. Biol. 10.1088/0031-9155/52/2/N01 52, N35–N50 (2007). [DOI] [PubMed] [Google Scholar]
- Schuls R. J., Almond P. R., Cunningham J. R., Holt J. G., Loevinger R., Suntharalingam N., Wright K. A., Nath R., and Lempert G. D., “A protocol for the determination of absorbed dose from high-energy photon and electron beams,” Med. Phys. 10.1118/1.595446 10, 741–771 (1983). [DOI] [PubMed] [Google Scholar]
- Almond P. R., Biggs P. J., Coursey B. M., Hanson W. F., Huq M. S., Nath R., and Rogers D. W. O., “AAPM’s TG-51 protocol for clinical reference dosimetry of high-energy photon and electron beams,” Med. Phys. 10.1118/1.598691 26, 1847–1870 (1999). [DOI] [PubMed] [Google Scholar]
- Faddegon B., Schreiber E., and Ding X., “Monte Carlo simulation of large electron fields,” Phys. Med. Biol. 10.1088/0031-9155/50/5/001 50, 741–753 (2005). [DOI] [PubMed] [Google Scholar]
- Huq M. S. and Andreo P., “Advances in the determination of absorbed dose to water in clinical high-energy photon and electron beams using ionization chambers,” Phys. Med. Biol. 49, R49–R104 (2004). [DOI] [PubMed] [Google Scholar]
- Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 10.1118/1.598917 27, 485–498 (2000). [DOI] [PubMed] [Google Scholar]
- Rogers D. W. O., Faddegon B. A., Ding G. X., Ma C.-M., We J., and Mackie T. R., “Beam: A Monte Carlo code to simulate radiotherapy treatment units,” Med. Phys. 10.1118/1.597552 22, 503–524 (1995). [DOI] [PubMed] [Google Scholar]
- Faddegon B., Balogh J., Mackenzie R., and Scora D., “Clinical considerations of Monte Carlo for electron radiotherapy treatment planning,” Radiat. Phys. Chem. 10.1016/S0969-806X(98)00103-0 53, 217–227 (1998). [DOI] [Google Scholar]
- Faddegon B. A., Perl J., and Asai M., “Monte Carlo simulation of large electron fields,” Phys. Med. Biol. 10.1088/0031-9155/53/5/021 53, 1497–1510 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walters B. R. B. and Kawrakow I., “Technical note: Overprediction of dose with default PRESTA-I boundary crossing in DOSXYZnrc and BEAMnrc,” Med. Phys. 10.1118/1.2402342 34, 647–650 (2007). [DOI] [PubMed] [Google Scholar]
- Faddegon B. A., Asai M., Perl J., Ross C., Sempau J., Tinslay J., and Salvat F., “Benchmarking of Monte Carlo simulation of bremsstrahlung from thick targets at radiotherapy energies,” Med. Phys. 10.1118/1.2975150 35, 4308–4317 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shortt K. R., Ross C. K., Bielajew A. F., and Rogers D. W. O., “Electron beam dose distributions near standard inhomogeneities,” Phys. Med. Biol. 10.1088/0031-9155/31/3/003 1, 235–249 (1985). [DOI] [Google Scholar]
- Karzmark C. J., Nunan C. S., and Tanabe E., Medical Electron Accelerators (McGraw-Hill, New York, 1993). [Google Scholar]
- Dyer J. A., Scrivner N. C., and Dentel S. K., “A practical guide for determining the solubility of metal hydroxides and oxides in water,” Environ. Prog. 10.1002/ep.670170112 17, 1–8 (1998). [DOI] [Google Scholar]
- Vilches M., García-Pareja S., Guerrero R., Anguiano M., and Lallena A. M., “Monte Carlo simulation of the electron transport through thin slabs: A comparative study of PENELOPE, GEANT3, GEANT4, EGSnrc and MCNPX,” Nucl. Instrum. Methods Phys. Res. B 10.1016/j.nimb.2006.11.061 254, 219–230 (2007). [DOI] [Google Scholar]
- Hanson A. O., Lanzl L. H., Lyman E. M., and Scott M. B., “Measurement of multiple scattering of 15.7 MeV electrons,” Phys. Rev. 10.1103/PhysRev.84.634 84, 634–637 (1951). [DOI] [Google Scholar]
- Kulchitsky L. A. and Latyshev G. D., “The multiple scattering of fast electrons,” Phys. Rev. 10.1103/PhysRev.61.254 61, 254–265 (1942). [DOI] [Google Scholar]
- Ross C. K., McEwen M. R., McDonald A. F., Cojocaru C. D., and Faddegon B. A., “Measurement of multiple scattering of 13 and 20 MeV electrons by thin foils,” Med. Phys. 10.1118/1.2968095 35, 4121–4131 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faddegon B. A., Wu V., Pouliot J., Gangadharan B., and Bani-Hashemi A., “Low dose megavoltage cone beam CT with an unflattened 4 MV beam from a carbon target,” Med. Phys. 10.1118/1.3013571 35, 5777–5786 (2008). [DOI] [PubMed] [Google Scholar]