Two-Component Models of Reaching: Evidence from Deafferentation in a Fitts’ Law Task

Abstract

Both feedforward and feedback mechanisms are used to ensure accurate movements. Feedback information comes primarily from vision and proprioception; the relative contributions of these modalities to on-line control of action and internal model maintenance remain unclear. We report data from an experiment in which a chronically deafferented subject (JDY) and nine controls were asked to reach to targets of different sizes both with and without vision. Movement times of controls were consistent with Fitts’ Law on trials with and without vision. JDY’s movement times were consistent with Fitts’ Law only with vision. She was inaccurate relative to controls with vision but exhibited a significantly greater decrement in performance than controls without vision. Finally, JDY’s performance on trials with vision deteriorated as a function of the number of preceding trials on which vision was not available. These data provide support for classical models of motor control that divide reaching into an initial ballistic movement guided by efference copy, and a terminal stage where sensory feedback is crucial. Furthermore, these data also demonstrate that proprioception is needed to calibrate and maintain internal models of action.

Introduction

Movement production is a multi-step process that transforms a movement goal into a set of coordinated muscle activations to achieve that goal. Although this process is still poorly understood, one of the dominant paradigms in motor control proposes that predictive elements within the motor system are responsible for this transformation [19]. These internal models store experience-based information about the input and output characteristics of the motor apparatus to provide feedforward signals to muscles and, in turn, use these feedforward signals to estimate the current and future location of an effector [16]. Feedforward derived limb state estimates are compared to sensory feedback from vision and proprioception to update the internal models for later movement production. Thus, internal models are not static but are constantly being updated to ensure accurate functioning.

The relative contributions of feedforward and feedback mechanisms to motor control remain unclear. Most research in normal subjects on the role of perceptual feedback has focused on vision; the role of proprioceptive feedback in motor controls is less clear as it is difficult to experimentally manipulate. Subjects with profound loss of proprioception offer unique opportunities to examine the isolated contribution of feedforward mechanisms to motor control because reaching for these participants without vision requires almost total reliance on feedforward control. In this study we tested JDY, a subject who developed a peripheral deafferentation more than 20 years prior to testing, as well as age-matched controls on a simple three-dimensional reaching task requiring movements both with and without vision. The design of the study manipulated the size of and distance to the to-be-reached target, two factors that are known to affect a speed-accuracy tradeoff [Fitts’ Law; 8]. Although Fitts’ crucial finding that movement times are directly related to amplitude (distance from starting point to target) and target size has been replicated many times, disagreement persists regarding the optimal Fitts’ Law formulation. In the original expression and many subsequent modifications [15], movement times are correlated with a single index of difficulty that is a function of both movement amplitude and target width. Welford and colleagues [17] developed a variant of Fitts’ Law that distinguished between these two components. On this account, reaching movements may be considered to include both an initial ballistic component as well a terminal component in which sensory feedback modulates performance; the effect of the former is modeled as movement amplitude whereas the effect of the second is modeled as target width. In Welford’s formulation, both components are independent predictors of movement times. Mackenzie and colleagues have suggested that two-part models more accurately characterize movement time data than one component formulations, especially for three-dimensional movements [11].

The first objective of this manuscript is to utilize JDY’s lack of proprioception to assess the adequacy of one- and two-part formulations of Fitts’ Law, specifically with regards to understanding the role of feedback in characterizing reaching data in three-dimensional movements. On trials with vision, one would predict JDY and controls would demonstrate a relationship between movement times that is consistent with Fitts’ Law. As both JDY and controls would be able to visually compare hand and target position during the terminal stage of the movement; movement times would be expected to be longer for smaller targets because reaching to smaller targets places greater demands on time-consuming feedback-driven correction of reach trajectory. Even without vision, the performance of control subjects would not reliably distinguish between one- and two-part Fitts’ law models, as controls would have proprioceptive feedback during the terminal stage of movement. In contrast, JDY does not have access to sensory feedback when reaching to a target without vision. If the lack of sensory feedback only has an effect on the terminal stage of movement in which closed-loop processes are particularly relevant, then we would expect that one-part models would not be able to account for JDY’s performance without vision. In contrast, two-part models, which would predict that target amplitude, but not width, should be predictive of JDY’s movement times without vision, would be able to account for JDY’s performance. Our work is distinct from previous research with deafferented subjects, in that we examine the role of feedback on the initial and terminal stages of movement.

The second issue addressed in the manuscript is the effect that long-term proprioceptive loss has on the roles that visual and proprioceptive feedback play in movement production and the integrity of internal models when proprioception is not available. These analyses focused on the trials in which vision was not present because JDY’s performance in this condition would be largely dependent on feedforward commands from internal models. As described above, internal models are maintained and modified through the use of visual and proprioceptive feedback. It is unknown whether there are any long-term effects of preventing proprioception-based maintenance of these internal models. Given that her motor system could still make vision-based modifications to her internal models, it is possible that visual input would be sufficient to maintain these models. This account predicts that JDY would show a decrement in accuracy without vision that is similar to controls. A second possibility is that JDY’s motor system may compensate for the lack of proprioception by developing more elaborated or precise internal models to afford greater feedforward control, thereby diminishing the need for sensory feedback. This would be analogous to blind subjects who develop enhanced processing in auditory or tactile domains. On this account, JDY would show a smaller decrement in accuracy without vision relative to controls. A third possible effect of proprioceptive loss on internal model accuracy is that internal models become less accurate without proprioceptive modification. One might expect this to be particularly evident when JDY lacks vision for a series of trials. Under these conditions, the lack of visual feedback would lead to a progressively worse performance as the unstable internal model degrades.

Methods

Subjects

JDY is a 45-year-old female with acquired peripheral sensory loss from the sensory form of chronic inflammatory demyelinating polyneuropathy. She was in excellent health until a flu-like illness in her mid-twenties following which she noted profound problems controlling her arms and legs; although she could feel objects, she didn’t know where her arms or legs were unless she looked at them. Neurological exam revealed relatively preserved cutaneous sensation. Using the Rivermead Test of Somatosensory Function [18], she discriminated sharp from dull perfectly on her right and left cheeks. Sharp/dull discrimination was also at least relatively preserved in her extremities; she made one error on 6 trials on the right palm but performed perfectly (n=6) on the left palm. In discriminating light touch from no touch, she was accurate for stimuli presented on her left and right cheeks (16/16), and only made one error on stimuli presented to her left and right index finger (15/16), failing to detect a touch on her right index finger. JDY was perfect in discriminating hot from cold at the right and left cheeks and hands (n=5 at each site). Finally, she performed at chance on a two-point discrimination task in which either one or two stimuli (5 mm separation) were presented to the palmar surface of the tip of the right or left index finger.

Proprioception was assessed by the examiner generating movements across single joints while the subject sat with her eyes closed. She failed to detect large amplitude movements of the fingers, wrists, or ankles. She detected movements at the elbows but was unable to determine if movements of approximately 25 degrees were flexion or extension (6/10 correct at both elbows). Finally, vibratory sensation was assessed with a 512 Hz tuning fork. Vibration detection threshold was judged to be normal at several locations on the skull. Even with maximal amplitude vibration there was no vibratory sensation in the hands or feet. She noted a faint sensation of vibration with maximal amplitude stimulation at the right and left olecranon and the right and left lateral clavicle. She was areflexic but muscle power and bulk were normal.

Nine right handed control subjects (one male, eight females) between the ages of 22 and 63 (mean age 46) also participated in the experiment. All research was approved by the Institutional Review Board of the University of Pennsylvania.

Apparatus

Subjects were seated approximately 50 cm from a 48 cm diagonal touch screen monitor (ViewSonic Graphics Series G220fb) connected to a Dell PC running E-Prime (Psychology Software Tools, Inc., Pittsburgh, PA). At this distance the face of the monitor was located near the extent of the subject’s reach. The subject’s midline was aligned with the center of the monitor. The PC was connected to a PST Deluxe Serial Response Box (Psychology Software Tools, Inc., Pittsburgh, PA) positioned such that the button row was 26.5 cm in front of the monitor. Subjects wore PLATO Visual Occlusion Spectacles (Translucent Technologies, Toronto, CA) that were opened and closed using E-Prime. JDY and controls wore a small plastic thimble (with padding inside) on their right index finger to protect them from forcefully striking their finger against the monitor.

Procedure

Before each trial, the subject was instructed to place his/her right index finger on a response button located at their body midline. After holding the response button down for one second, a fixation point was presented at the center of the screen. Next, a black circle of one of three sizes (10mm, 20mm, and 30mm in diameter) was presented at one of three positions on the screen (48 mm directly below fixation, at fixation, and 48 mm directly above fixation). Distances from the start position to the 3 targets was 39.77 cm, 43.49 cm and 47.43 cm. The subject was instructed to quickly and accurately touch the circle presented on the screen. On half of the trials, the PLATO glasses remained transparent during the entire trial. On the other half of trials, the PLATO glasses turned opaque when the subject lifted his/her hand from the response button, and remained opaque until the subject touched the touch screen monitor. Movement time was recorded as the time from lifting the subjects’ finger from the response button to when the subject touched the screen. Accuracy was recorded as the distance of the subject’s touch from the center of the circle.

Each block consisted of 36 trials, balanced for vision, target size, and movement distance. Each control subject was tested on one session, consisting of one practice block, followed by four experimental blocks. JDY performed eight blocks of trials during which her performance was stable. All trials that were 3 standard deviations outside the mean for movement time for each subject in each condition (vision, no vision) were eliminated (1.00% of trials for controls, 0.97% for JDY).

Results

Movement Time

First, we addressed how well the movement times for controls and JDY were predicted by the Shannon formulation¹ of Fitts’ Law [12] expressed as MT = a + blog₂((A/W) + 1), where a and b are empirical constants, A is movement amplitude, and W is target width. Trials with vision and without vision were analyzed separately to examine the relative contribution of feedback in each condition (see Figure 1). For controls, the Shannon formulation of Fitts’ law accounted for a significant amount of variance both with (F(1,7) = 33.05, R² = .825, p < .001; MT = 36.52(log₂ of difficulty index) + 387.94) and without vision (F(1,7) = 42.89, R² = .860, p < .001; MT = 32.27(log₂ of difficulty index) + 401.0). For JDY, Fitts’ law accounted for a significant amount of variance with vision (F(1,7) = 10.94, R² = .610; MT = 40.44(log₂ of difficulty index) + 483.36). However, Fitts’ law did not account for a significant amount of JDY’s variance without vision (F(1,7) = 1.00, R² = .125, p < .350; MT = 21.53(log₂ of difficulty index) + 533.40). For JDY with vision, the Shannon formulation of Fitts’ law accounted for less variance than any controls (R² range: .239 - .777, R² average: .473).

Figure 1.

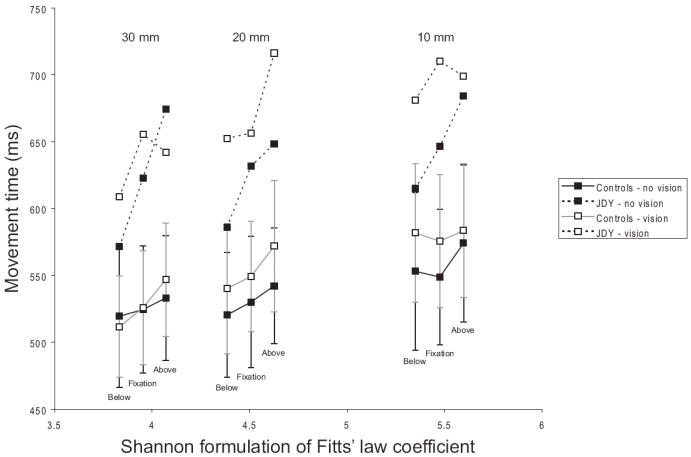
Mean movement time for JDY and controls on each condition (by target size and target distance), labeled by the Shannon formulation of Fitts’ Law coefficient for each condition. Error bars represent one standard deviation. Target width is listed at the top of the figure, with target position (relative to fixation) also labeled.

We then examined whether the Welford formulation of Fitts’ law (Welford, 1969), which has separate predictors for target amplitude and width, predicts movement times for JDY and controls. This formulation is as follows: MT = a + b_Alog₂(A) + c_Wlog₂(1/W). For controls, the Welford formulation of Fitts’ law accounted for a significant amount of variance both with vision (F(2,6) = 27.92, R² = .903, p < .001; MT = 101.99(log₂ of amplitude) + 33.47(log₂ of reciprocal of width) + 31.52) and without (F(2,6) = 33.04, R² = .917, p < .001; MT = 82.04(log₂ of amplitude) + 29.70(log₂ of reciprocal of width) + 130.08). For JDY, the Welford formulation of Fitts’ law accounted for a significant amount of variance with vision (F(2,6) = 8.66, R² = .743, p = .017; MT = 151.99(log₂ of amplitude) + 36.14(log₂ of reciprocal of width) − 124.67). In contrast to the Shannon formulation of Fitts’ law, the Welford formulation did account for a significant amount of variance for JDY on trials without vision (F(2,6) = 33.2, R² = .917, p < .001; MT = 349.66(log₂ of amplitude) + 12.49(log₂ of reciprocal of width) − 1258.31). In this analysis movement amplitude (β = .934, p > .001) but not target width (β = .211, p = .123) significantly predicted JDY’s movement times without vision. This result contrasted with similar analyses showing that both factors were significant predictors of movement time for controls participants with and without vision, as well as for JDY with vision. We also found that regressions using effective target width [13], for both Shannon and Welford formulations, were always less predictive than the same regression using physical target width.

Accuracy

To assess the role of vision in accuracy, the performance of JDY was compared to controls with a mixed design ANOVA using modified F criterion for single subject research [14], with group as the between subjects factor, and target size, target distance, and vision as within subject factors. In this analysis there was a main effect of group (F(1,8) = 42.8, p > .001), with JDY being less accurate (mean error: 22.4 mm) than controls (10.4 mm). There was also a main effect of vision (F(1,8) = 138.1, p > .001), as both controls and JDY were more accurate with vision than without vision. There was also a main effect of target distance (F(2,16) = 4.75, p = .024), as subjects were more accurate for targets that were closer compared to farther away. Most importantly, there was a vision by group interaction (F(1,8) = 34.5, p < .001); JDY exhibited a greater decrement in performance than controls without vision (mean error: JDY with vision, 12.7mm, without vision, 32.1mm; controls with vision, 7.1mm, without vision, 13.7mm). Using a t-test for comparing the performance of a single patient to controls [4], we found that JDY was less accurate than controls both with (t = 2.32, p = .024) and without (t = 8.04, p < .001) vision.

Finally, we examined how stability of internal models was affected by repeated reaches with or without visual feedback. To do so, we analyzed how average accuracy could be predicted by the number of preceding trials (either 0, 1, 2 or 3 or more) with or without vision. This was done separately for trials with and without visual feedback. The mean regression slopes for the controls and JDY are shown in Figure 2. In almost all conditions the mean slope was near 0, indicating a stable internal model because performance did not change with repeated reaching with or without vision. The one consistent exception was JDY’s performance on trials without vision that were preceded by other no-vision trials. On these trials JDY’s errors increased with repeated reaches without vision (a positive slope), a finding that was not observed in controls. A test comparing JDY’s slope to the slopes of the controls (using methods designed to compare the slopes of a single subject to a group of controls [5]) approached conventional levels of significance (Satterthwaite’s t(2) = 2.63, p = .06). No other comparisons were significant.

Figure 2.

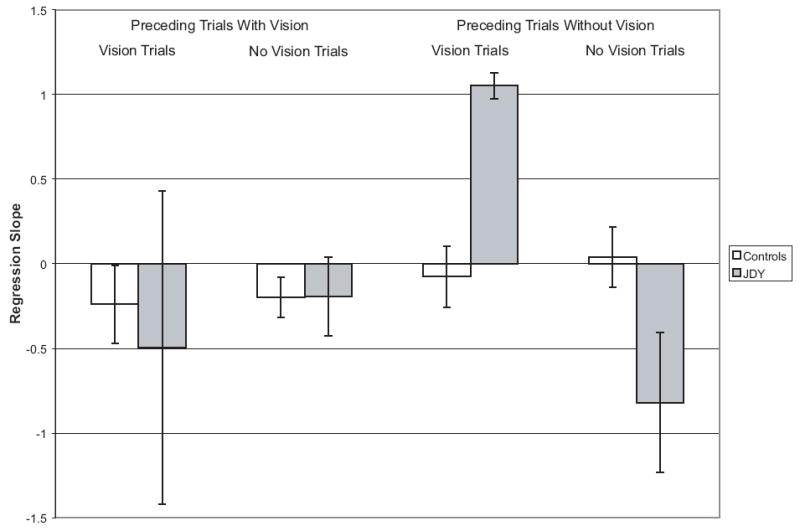
Mean regression slope for controls and regression slope for JDY (with standard error bars). Regression slopes generated from line analyzing the effect of the number of preceding trials with or without vision on accuracy on a vision or no vision trial.

General Discussion

Consistent with either one- or two-part Fitts’ Law formulations, control subjects exhibit longer movement times as target size decreases or movement distance increases both with and without vision. Additionally, their significantly less accurate performance without vision demonstrates that, at least for this task, visual information augments proprioceptive feedback. JDY differed from controls in a number of respects. First, with visual feedback her performance is in accord with both the one- and two-part models of Fitts’ Law. However, this was not the case for trials without vision. The one-part model of Fitts’ law did not account for JDY’s movement time variance, whereas the two-part model of Fitts’ law did. Furthermore, movement amplitude, but not target width, was found to be a predictor of JDY’s movement times without vision. This performance supports classical two-stage models of movement control [7, 20] according to which the terminal correction phase involves increased reliance on sensory feedback from vision and proprioception. On no-vision trials, target size was a significant predictor of movement time for controls, but not JDY, presumably because JDY did not have sensory feedback during the terminal stage of movement.

An important question is the extent to which sensory feedback as compared to information derived from a copy of the motor plan (efference copy) contributes to this terminal stage of movement. As JDY has no access to sensory information on no vision trials, the only possible source of information to guide her movement would be efference copy. Since target size is not predictive of movement time for her, we suggest that efference copy information has only a minimal contribution to the terminal stage of the movement. Instead, the terminal stage of movement is likely to critically depend on sensory feedback [1]. However, movement amplitude is a significant predictor of movement time for JDY without vision. It is likely that JDY utilizes efference copy information to a much greater degree during the initial ballistic phase of movement.

Although JDY has access to information from the motor plan during the initial ballistic phase of the movement, efference copy alone, at least in JDY, does not support normal performance. JDY was significantly less accurate than controls both with and without vision and exhibited a greater decrement in accuracy than controls when deprived of vision. These results are consistent with a previous study where accuracy in a two-dimensional reach task was examined [9]. They found that limb position feedback (whether it be a cursor or the actual limb in peripheral vision) during or before the task improved accuracy. Furthermore, they found that deafferented subjects’ accuracy decreased the longer they were without feedback regarding limb position. These data are consistent with the hypothesis that JDY’s internal models have become less precise over time due to the lack of input from proprioception. When making a movement, sensory information is compared to a predicted state estimate of limb position, resulting in the generation of an error term that feeds back to correct movements. Importantly, this process must also be used to develop future motor commands; information from the comparison of predicted and sensory information is used to refine internal models for future movements [6]. Evidence from JDY suggests that proprioception may be important to the ongoing calibration of internal models. In the absence of proprioception the specificity of predictive internal models may degrade, as manifested by JDY’s inaccurate reaching even with vision and a striking deterioration in reaching accuracy in the absence of vision. We do not suggest, however, that vision is irrelevant to the process by which internal models are generated and maintained. On the contrary, we found that JDY was less accurate on trials with vision as the number of preceding trials without vision increased, suggesting that visual information can refine internal models over a short time frame. This is also consistent with experiments with healthy subjects, finding that aiming accuracy is highly dependent on visual information from recent reaches [2]. We suggest, however, that visual information alone is not sufficient to generate a fully specified internal model.

Previous studies have shown that when vision and no-vision trials are randomized, movement strategies differ compared to when subjects have knowledge regarding the existence of visual feedback on the upcoming trial. Specifically, on randomized vision/no-vision trials, subjects plan their movements assuming no visual feedback, spending less time adjusting their movement after peak deceleration with movements characterized more by feed-forward properties [10]. Although our design puts more emphasis on feed-forward reliant strategies, there is still a clear distinction between feed-forward and feedback processes, as evidenced by the dissociable relationship between amplitude and target width in JDY’s performance.

We have argued that the difference in accuracy between JDY and controls when reaching without vision reflects differences in the precision of their internal models. An alternative possibility that must be considered is that controls have proprioceptive feedback in the absence of vision whereas JDY does not. Although proprioceptive feedback may increase accuracy somewhat in the absence of vision, we suggest that it is unlikely to account for the significant difference exhibited by JDY and controls in reaching accuracy without vision. If one assumes that visual and proprioceptive feedback contribute similarly to reaching accuracy, loss of proprioception would be expected to lead to a decrement in performance of approximately 6 mm (that is, the same decrement observed with as opposed to without vision). The decrement in performance exhibited by JDY is far greater than 6 mm. Thus, the magnitude of this difference, combined with the significant increase in error following repeated reaching without vision, supports our proposal that JDY’s internal models are functioning abnormally.

Finally, the data suggest that, in contrast to sensory systems in which neural plasticity permits enhanced processing in unaffected domains as a compensation for the loss of normal faculties, feedforward elements of the motor system exhibit no such capacity for enhancement. Whether this reflects inherent limitations in the precision of feedforward systems or the fact that visual information alone is not sufficient to refine feedforward mechanisms is unclear. It is relevant in this context that at least some subjects with central lesions may benefit to a striking degree from feedforward information. We reported a subject with a left parietal stroke who was profoundly impaired on all tests of proprioception yet reached relatively accurately when her hand position was informed by active as compared to passive movements [3]. These data suggest that JD relied on feedforward information to update her sensory state estimate.