Chunk Limits and Length Limits in Immediate Recall: A Reconciliation

Abstract

Whereas some research on immediate recall of verbal lists has suggested that it is limited by the number of chunks that can be recalled (e.g., Tulving & Patkau, 1962; Cowan, Chen, & Rouder, 2004), other research has suggested that it is limited by the length of the material to be recalled (e.g., Baddeley, Thomson, & Buchanan, 1975). We investigated this question by teaching new paired associations between words to create two-word chunks. The results suggest that both chunk capacity limits and length limits come into play. For the free recall of 12-word lists, 6 pre-learned pairs could be recalled about as well as 6 pre-exposed singletons, suggesting a chunk limit. However, for the serially-ordered recall of 8-word lists, 4 pre-learned pairs could be recalled about as well as 8 pre-exposed singletons, suggesting a length limit. Other conditions yielded intermediate results suggesting that sometimes both limits may operate together.

One of the most fundamental questions about working memory has been the nature of the rather severe limit in immediate recall of verbal lists. Miller (1956) famously proposed that recall is limited to about 7 chunks or meaningful units of information. Although he emphasized the importance of recoding information to form larger chunks when possible (e.g., recoding long binary numbers into shorter octal numbers), he nevertheless appears to have assumed that thies does not take place for lists of unrelated items without coaching, and therefore that 7 or so words are recalled as separate chunks. Cowan (2001) pointed out that people actually may be able to form multi-word chunks rapidly when a list is presented. They may do this in several ways, such as noticing corresponding elements in long-term memory (e.g., recoding the digit sequence "1995" as designating a particular year) or perhaps by using the rapid phonological learning mechanism described by Baddeley, Gathercole, and Papagno (1998) to transform the sequence into a multisyllabic chunk (e.g., "one-nine-nine-five”). It is probably for related reasons that there is a grouped presentation of digits in telephone numbers. When steps are taken to prevent chunking and rehearsal of the presented items, the limit appears to be closer to about 4 words (cf. Broadbent, 1975; Mandler, 1985).

Although Miller (1956) inaugurated the modern field of immediate-memory research with an assertion that memory was limited in the number of chunks to be recalled, that premise was investigated in relatively few studies (e.g., Johnson, 1969; Slak, 1970; Tulving & Patkau, 1962) and the field quickly moved on to many investigations of length limits in immediate recall (e.g., Baddeley et al., 1975; Brown, 1958; Conrad & Hille, 1958). In contrast to a chunk-limit hypothesis, Baddeley et al. (1975) proposed a length limit in immediate serial recall. They found that the memory limit depends on the length of the words; for example, memory was found to be superior for lists of monosyllabic, as compared to multisyllabic, words. They concluded that this effect resulted from a time-based limit caused by decay of phonological information in working memory (cf. Cowan et al., 1992; Hulme & Tordoff, 1989; Mueller, Seymour, Kieras, & Meyer (2003); Schwieckert & Boruff, 1986; Schweickert, Guentert, & Hersberger, 1990; for precursors see Brown, 1958, 1959; Conrad, 1967; Peterson & Peterson, 1959), though subsequent research has debated whether it is in fact time-based or, instead, based on the amount of phonological material in the list, a slightly different type of length limit (Caplan & Waters, 1994; Cowan, Wood, Nugent, & Treisman, 1997; Lewandowsky, Duncan, & Brown, 2004; Lovatt & Avons, 2002; Neath & Nairne, 1995; Service, 1998; for replies see Baddeley & Andrade, 1994; Cowan, Nugent, Elliott, & Geer, 2000; Mueller et al., 2003).

The purpose of the present research is to try to understand how chunk and length constraints may operate together in immediate recall. There are reasons to believe that they do operate together, each with its own boundary conditions. For example, when short and long words are mixed together in the same list, it is no longer the total length of the list that governs recall. Instead, the main factor appears to be the use of word length as a cue to break the list into two different subgroups, the short and long words (Cowan, Baddeley, & Norris, 2003; Hulme, Surprenant, Bireta, Stuart, & Neath, 2004). Recall is superior for words of whatever length is less frequent and therefore more distinct in the list: 1- or 2-syllable words (Cowan et al., 2003).

One reason why length limits have dominated the research on immediate recall is that there are some difficult issues to be addressed in the research on chunk limits. Consider, for example, what is perhaps the first study to demonstrate the operation of a chunk limit in immediate recall (Tulving & Patkau, 1962). Free recall was examined for lists of 24 words forming various levels of approximation to English syntax. Runs of items recalled in the presented order were counted as chunks. It was found that about 4 to 6 chunks could be recalled in all conditions, with the size of chunks increasing as a function of the level of approximation to English. However, the chunks were semantically related to one another so it is possible that a recalled chunk could serve as a mnemonic cue for other chunks.

Cowan (2001) examined a wide variety of situations in which it seemed reasonable that the items presented for immediate recall could not be combined into larger chunks: for example, situations in which the items to be recalled were unattended at the time of their presentation, were presented too quickly and unpredictably to allow useful rehearsal, or were presented in a complex, concurrent array. Under such circumstances, each item presented would constitute a separate chunk. Those situations appeared to converge on the estimate that adults can remember 3 or 4 items, and hence 3 or 4 chunks.

Cowan et al. (2004) extended the evidence for a chunk limit beyond Cowan (2001), not by preventing chunking of words into multi-word units, but by manipulating it. Prior research already showed that associations between words could assist in immediate recall (Cumming, Page, & Norris, 2003; Hulme, Stuart, Brown, & Morin, 2003; Stuart & Hulme, 2000). In order to create chunks that varied in size between conditions, Cowan et al.(2004) employed a training phase to manipulate the association strength within word pairs (for related research see Anderson & Matessa, 1997; Bowles & Healy, 2003; Johnson, 1978; Marmurek & Johnson, 1978; Ryan, 1969; Slak, 1970; Wickelgren, 1964, 1967). Cowan et al. presented printed words in 5 training conditions: no-study and 0-, 1-, 2-, or 4-pairing conditions. During the training phase, words in the 0- through 4-pairing conditions were presented 4 times each, but the number of presentations of singletons vs. consistent pairs depended on the condition. For example, words in the 1-pairing condition were presented once as a pair and three times as singletons; as another example, words in the 4-pairing condition always were presented in pairs during this training phase. Lists of 8 words were then presented for serial recall, with all words in a trial drawn from the same training condition. The pairing of words in the lists in the 1- through 4-pairing conditions matched the pairing that had been presented in training. There was also a cued-recall phase to assess pair learning, administered either before or after the serial-recall phase.

Cowan et al. (2004) distinguished between two ways in which performance theoretically could differ between conditions: in the number of chunks recalled, or in the size of chunks recalled (or, theoretically, both). Several methods were used to identify chunks. As a convenient simplification, it was assumed that either an individual recalled item was a single-word chunk, or a pair of items was recalled as a two-word chunk (with no possibility of even larger chunks according to this simplification). For this analysis, a pair of words was counted as a single, two-word chunk whenever the two words were both presented together within the list (which was always the case for Items 1–2, Items 3–4, and so on, in the list) and were recalled in that same order in immediate succession. A mathematical model allowed Cowan et al. to rule out the possibility that a pair recalled in that manner sometimes actually comprised two separate chunks. It considered how often just one or just the other item in a pair was recalled correctly and how often two items from a pair were recalled in the wrong serial positions, as well as using the cued-recall information, and calculated that if a pair of items was recalled in adjacent positions and in the correct order, it was almost always because the pair was recalled as a single chunk.

The results indicated that the difference between training conditions was in the mean size of the chunk (which theoretically could range from 1.0 to 2.0 monosyllables); this mean chunk size increased as a function of the number of chunks recalled (i.e., two-word chunks plus singletons) remained remarkably constant across training conditions at about three and a half chunks.

This finding of Cowan et al. (2004) seems to rule out a simple account of serial recall based only on the amount of phonological material in the list. Given that all lists were 8 words long, the simple prediction of such a model is that performance levels should be about the same for all conditions. This reinforces previous findings that the amount of phonological material alone cannot account for recall; information in long-term memory, including the familiarity of words and associations between words, also plays an important role (Hulme, Maughan, & Brown, 1991; Hulme et al., 2003; St. Aubin & Poirier, 1999; Stuart & Hulme, 2000; Thorn, Gathercole, & Frankish, 2002).

One problem with the previous research demonstrating chunk limits in immediate recall (Cowan et al., 2004; Tulving & Patkau, 1962) is that it was highly dependent on theoretical assumptions about the nature of chunks formed. Although Cowan et al. (2004) alleviated that situation by experimentally teaching paired associations to appear in the list, the teaching was incomplete and it is never totally clear whether a particular association was recalled at the time of the immediate-recall test. In the present research, we addressed this problem by teaching word pairs to 100% correct performance so that it would be reasonable to assume that all word pairs were known and retrievable during the immediate-recall tests.

Another problem is that Cowan et al. (2004) did not present materials in such a way that chunk and length constraints could be directly compared. To do so, the list length must be manipulated. Some simple, contrasting predictions can be made. If a list consists of × known pairs of words then, according to a simple version of a chunk limit, the level of recall of this list should be equivalent to the recall of a list of × unrelated singletons because both lists include × separate chunk units. According to a length limit, in contrast, a list of × known pairs of words should be recalled as well as a list of 2× unrelated singletons because both lists would include the same number of syllables and, over subjects, a comparable number of phonemes, namely the number contained in 2× words. Although it would be naive to expect that other factors do not come into play, we found, remarkably, that the chunk-based prediction held precisely in some circumstances whereas the length-based prediction held precisely in other circumstances. In still other circumstances, the results were intermediate between the two predictions, suggesting that both chunk and length constraints may operate together.

It is noteworthy that different constraints may come into play in free recall vs. serial recall. In free recall, the participant is able to report any retrievable item and receive credit for it. It makes sense that the number of retrievable items would be limited. However, an additional constraint may well apply to serial recall. The requirement that items must be reproduced in order might seem to require that links between items (or between each item and its serial position in the list) be retained, and that these links would add to the burden on a chunk-limited mechanism. However, it is well-documented (e.g., Baddeley, 1986) that there is another mental mechanism that is well-suited to the retention of serial order information, namely a phonologically-based rehearsal system. The evidence suggests that retention of a list of words of a uniform length depends on the duration of the list in terms of the number of phonemes that it contains if not, as originally assumed by Baddeley et al. (1975) and many following studies, in terms of the actual time it takes to repeat each item (Lovatt, Avons, & Masterson, 2002; Mueller, Seymour, Kieras, & Meyer, 2003). However this phonological system operates, it is length-limited as opposed to chunk-limited; thus lists of short and long words are equivalent not in how many words can be recalled, but in the spoken duration of span-length lists. To examine the implications of the serial-ordering mechanisms in recall, we carried out experiments using both free and serial recall.

Finally, in addition to training and immediate-recall phases of the experiments, we included a final free recall phase in order to provide more verification that the word pairs that were taught were accessible in long-term memory. Experiment 1 involves immediate free recall and Experiments 2 and 3 involve immediate serial recall, but all experiments include a final free recall phase at the end of the session.

At least one previous investigation tried to reconcile chunk and length constraints in recall. Specifically, Zhang and Simon (1985) developed a formula to account for their results in experiments of memory for sets of Chinese characters, in which the useful lifetime of a short-term memory trace (T) was said to be constant and the amount that could be recalled in that limited time was said to depend on both the number of chunks (C) and the number of syllables in each chunk (S), as follows:

$$\mathrm{T}=\mathrm{C}\left[\mathrm{a}+\mathrm{b}(\mathrm{S}-1)\right]$$ (1)

where a and b are constants. By rearranging that formula, it can be shown that the number of chunks recalled should be C = T/a for lists of 1-syllable chunks and C = T/(a+b) for lists of 2-syllable chunks, and that prediction can be examined with the present data.

The present state of the field should not be cast as a clean schism between investigators. Baddeley (2000) introduced a new, episodic buffer component to his model that is involved in retaining new associative links between items and might well be thought of as chunk-limited (Baddeley, 2001), similar to the focus of attention of Cowan (2001). However, it is unclear from either of those theoretical frameworks just how chunk and time limits operate in specific immediate-memory tasks.

Experiments 1 & 2

Experiments 1 and 2 both had three phases: training, immediate recall and final free recall. They differed only in that the second phase entailed immediate free recall in Experiment 1 and immediate serial recall in Experiment 2. These two similar experiments will be described together to facilitate comparisons between them.

Method of Experiment 1: free recall

Participants

In Experiment 1, 33 undergraduates participated, receiving course credit. They were native speakers of English with no known hearing deficits and normal or corrected-to-normal vision.

Apparatus and Stimuli

All verbal stimuli were presented in 0.64-cm black lettering on white on a 15-inch computer screen and were viewed at a distance of about 50cm. A set of 99 nouns was selected from the MRC Psycholinguistic Database (Wilson, 1987). Each word had 3 – 4 letters, 3 – 5 phonemes, 1 syllable, a Kucera-Francis written word frequency above 12, and a concreteness rating above 500. For each participant, 80 words randomly selected from the set were randomly assigned to 10 conditions, denoted as 12s, 12n, 6p, 8n, 8s, 4p, 6n, 6s, 4n and 4s (see Table 1). The digit indicates the number of chunks present in the list-recall phase according to the assumption that learned pairs and unassociated singletons represent two types of individual chunks, and the letter indicates whether the words were presented in training as singletons (s) or pairs (p), or were not presented at all in training (n). So, for example, in the 6p condition the list for free recall included 12 words that had been studied as 6 pairs during the training phase, and the 12s condition included 12 words that had been studied as singletons. The conditions allow a comparison of lists of the same number of assumed chunks (6p vs. 6s and 6n conditions), and lists of the same number of words (6p vs. 12s and 12n conditions). In a similar manner, the 4p condition can be compared to lists with the same number of chunks (4p vs. 4s and 4n) and the same number of words (4p vs. 8s and 8n).

Table 1.

Training Conditions Included in Each Experiment

Condition	Training Exposures	Words in List	Chunks in Lista
4n	none	4	4
4s	singleton	4	4
4p	paired	8	4
8n	none	8	8
8s	singleton	8	8
6n	none	6	6
6s	singleton	6	6
6p	paired	12	6
12n	none	12	12
12s	singleton	12	12

^aUnder the assumption that each singleton or each learned pair is one chunk.

Procedure

Participants were tested individually in a sound-attenuated room. First they carried out a familiarization and training phase, then a list-recall phase, and then a final free-recall phase.

Training Phase

The training phase included two parts: an initial presentation and cued recall. In the initial presentation, each singleton from the singleton (s) conditions and each word pair from the paired (p) conditions had one initial presentation in the center of the computer screen for 2 s. The participants were required to pronounce the words aloud as they appeared to ensure their attention to the stimuli. After a round of 40 initial presentations (6 paired presentations for the 6p condition, 12 singleton presentations for the 12 s condition, and so on), the cued recall procedure began. Either a singleton or the first word of a word pair was randomly selected from the 40 presentations, without replacement, and was presented as a cue. If the cue was a singleton, the participant was accordingly supposed to type "s" on the keyboard. If the cue was the first word of a word pair, the participant was supposed to type in the second word of the pair. If the participant's response was wrong, the correct answer, either "s" or the entire word pair, would be shown on the screen for 1s, facilitating learning. All 40 presentations recurred in a new random order until the participant was 100% correct on all of them. This rather elaborate training procedure ensured that the overall exposure to singletons in the "s" conditions and pairs in the "p" conditions was equated.

Immediate Free Recall Phase

In this phase, participants carried out 10 immediate free recall trials in a row, including one for each of the 10 conditions (12s, 12n, 6p, 8n, 8s, 4p, 6n, 6s, 4n, and 4s). Both the order of pairs within the lists and the order of lists were randomized. For each trial, a list was presented with the words in pairs; this was done to encourage memory for the pairings in the p conditions, yet give comparable presentations in the other conditions too. For the 4p and 6p conditions, the pairs that were presented in the list were the same as the pairs that had already been learned. For the 12s, 8s, 6s, and 4s conditions the pairs were based on a random arrangement of the words that had been shown in training and, for the 12n, 8n, 6n, and 4n conditions, words not yet seen in the experiment.

The participant was to recall as many words from the list as possible, by typing them into the computer in any order. Participants were given as much time as needed for the response. They initiated each list presentation by pressing the ENTER key when ready. A 1-s waiting period preceded the appearance of the first word pair. Each word pair was presented for 2 s in the center of the screen, with a successive pair replacing the previous one. After the presentation of the last pair ended, the screen showed the instruction "recall a word" and a column of response lines, one for each word. The space bar was used to advance between lines after the participant was satisfied with the spelling of the response word on the current line. All words in the response remained on the screen until the last response word was finished, showing what and how many words had been recalled. If the participant found mistakes in his or her earlier input, he or she still had three more slots at the bottom of the column to add the correct words in his response and only the correct input would be scored.

Final Free Recall Phase

In an unexpected, final free recall phase, participants were required to recall as many words as they could that they had seen in the previous immediate free recall phase, in any order. The spelling of each input of one word could be corrected as in the immediate free recall phase but the words in the response were arranged one after another in lines, rather than in a column. Exact spelling was necessary for the word to be counted correct but misspellings rarely occurred, given the high-frequency words used. All words in the response also remained on the screen until a final termination response (in this case, pressing the "0" key) was made. Participants were encouraged to recall and had more than enough spaces on the screen to type all words they had ever seen in previous phases, although they were also allowed to terminate the task at any time.

Method of Experiment 2: serial recall

The participants in this experiment were 32 undergraduates, who were native speakers of English with no known hearing deficits and normal or corrected-to-normal vision, who received course credit for their participation. None of them had participated in Experiment 1. The stimuli and procedure of Experiment 2 were identical to those of Experiment 1 except that, in place of immediate free recall, participants were instructed to carry out immediate serial recall in the second phase of the experiment. That is, they were to recall the words in their presented order. Participants were allowed to skip a space if they failed to recall the word for a particular serial position, by pressing only the space bar to leave the corresponding slot in the answer display blank.

The results from serial recall were scored in two ways. In lenient scoring, serial-recall responses were scored as if the requirement had only been for free recall. In strict scoring, credit was given only for words recalled in the correct serial position within the response, counting from the beginning of the list.

Results of Experiments 1 and 2

In both Experiments 1 and 2, we carried out several analyses, on the following: (1) the training session, (2) proportion correct immediate recall across the list as a function of training conditions, (3) proportion correct immediate recall plotted by serial positions, and (4 final free recall. These categories of evidence will be presented in turn, for Experiments 1 and 2 together.

Training Session

In Experiment 1, participants required an average of 9.45 training cycles (SD = 4.68; range = 3 to 22) to reach the 100% correct criterion level. Similarly, in Experiment 2, participants required an average of 7.91 training cycles (SD = 4.08; range = 2 to 20).

An important question about training is whether participants who required more training cycles were "over-trained" and therefore able to do better in immediate recall. That was not the case. The possibility was assessed by examining correlations between the number of training cycles and immediate recall performance (proportion correct), separately for each training condition in each experiment. Most of these correlations were non-significant. The two cases that were significant were in Experiment 1, where the correlation for the 4p condition was r = −.37 and, for the 6s condition, r = − .47. Notice that the correlations were negative, meaning that immediate-recall performance levels were higher for participants who had fewer training cycles. Thus, pervasive individual differences in mnemonic abilities seem to account for some differences in both cued-recall performance in the training phase and immediate-recall performance. There was no evidence that over-training resulted in higher performance.

Mean Proportion Correct

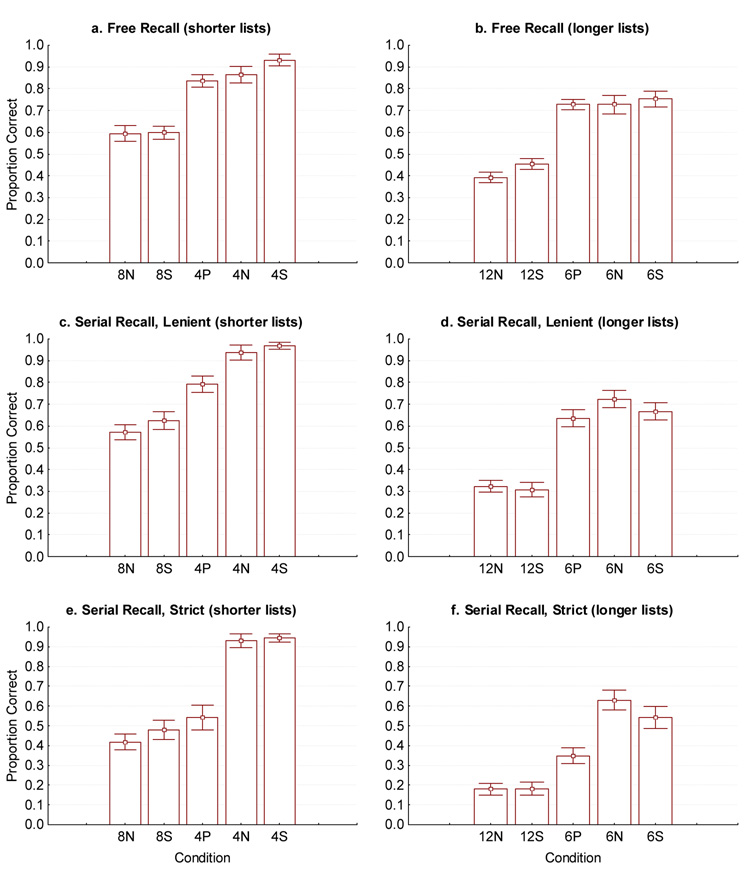
Mean proportion correct recall was calculated by averaging the proportion of words recalled in a condition across all participants. The mean proportion correct recall and the standard error of each condition are presented for both experiments (and both scoring methods for Experiment 2) in the six panels of Figure 1. Each panel represents a theoretically important set of comparisons.

Figure 1.

Proportion correct in various conditions of two experiments. Top two panels (a–b) reflect Experiment (free recall). 1a (top left), 4p and comparison conditions. 1b (top right), 6p and comparison conditions. Remaining panels (c–f) reflect Experiment 2 (serial recall). 1c (middle left), 4p and comparison conditions, lenient scoring. 1d (middle right), 6p and comparison conditions, lenient scoring. 1e (bottom left), 4p and comparison conditions, strict serial order scoring. 1f (bottom right), 6p and comparison conditions, strict serial order scoring. The number of presented chunks of each condition is assumed to equal the number of words for singleton (s) and non-studied (n) training conditions and equal to the number of word pairs for the paired (p) training conditions. Error bars are standard errors.

A one-way, repeated-measure ANOVA for each experiment and each scoring method, using all 10 conditions, showed significant main effects in each case. Duncan's post-hoc test was used to detect differences between theoretically meaningful pairs of conditions.

Experiment 1

In immediate free recall, F (9, 288) = 42.37, MSe = 0.02, p = 0.00. Performance levels in the 6p and 4p conditions were significantly better than in conditions with the same number of words learned as singletons (the 12s and 8s conditions, respectively). This demonstrates an advantage of paired-associate learning.

The 4p condition result was significantly below the 4s condition according to Duncan's test, suggesting that the analogue to the word length effect is apt in this case. Nevertheless, this length effect was small and the 4p condition was much closer to the 4s condition than it was to the 8s condition. (See Figure 1, top left.) Interestingly, there was no significant difference between the 6p and the 6s conditions. Six pairs were recalled about as well as six singletons of equal familiarity (as shown in Figure 1, top right ), so that there was no analogue to the word length effect for these longer lists. A power analysis indicated that for these 6-chunk lists, there was a statistical power of .8 to detect a difference of .12 by a t-test, and such a test produced non-significant results here, t < 1. These results are in line with a chunk-limited mechanism.

Experiment 2, lenient scoring

With lenient scoring of serial recall, the 1-way ANOVA result was F (9, 279) = 46.14, MSe = 0.03, p=0.000. Highly similar to Experiment 1, among conditions with equal list lengths, post hoc Duncan’s tests revealed a significant advantage of the 6p and the 4p conditions over the 12s and the 8s conditions, respectively, demonstrating the value of associative learning. Once more, as in free recall, the analogue to the word length effect was significant for the 4-chunk lists (4p vs. 4s; see Figure 1, middle left) but not for the 6-chunk lists (6p vs. 6s; see Figure 1, middle right). A power analysis indicated that for the 6-chunk lists, there was a statistical power of .8 to detect a difference of .16 by a t-test, and such a test produced non-significant results here, t < 1. Again, this result seems consistent with a chunk-limited mechanism.

Experiment 2, strict scoring

With strict scoring of serial recall, F (9,279) = 44.15, MSe = 0.05, p = 0.00. Post hoc Duncan’s tests showed that the significant advantage of the 4p over the 8s condition found with lenient scoring disappeared with strict scoring (as shown in Figure 1, bottom left), although the advantage of the 6p over the 12s condition remained (as shown in Figure 1, bottom right). Perhaps the most important difference from lenient scoring is that, with strict scoring, the analogue to the word length effect was now significant not only for the shorter lists (4p < 4s), but also for the longer lists (6p < 6s).

Notice that differences in the finding of a word length effect for the same lists, depending on which scoring method is used (i.e., 6-chunk lists with lenient vs. strict scoring) cannot be understood through the possibility of different response strategies. Instead, these differences suggest that word-length-sensitive and word-length-insensitive mnemonic processes may co-occur. That is a point to which we will return later.

None of the singleton (s) vs. non-studied (n) conditions with the same number of words differed in either experiment or with either scoring method, suggesting that item familiarization during training was not an important factor in these experiments.

Assessment of Zhang & Simon's (1985) theoretical formulation

As mentioned in the introduction, Zhang and Simon's theory combining chunks and time limits leads to the expectation that the number of recalled chunks, C, equals the constant duration of the phonological memory trace, T, divided by another constant. In particular, for lists of 1-syllable chunks, C = T/a and, for 2-syllable chunks, C = T/(a+b), where a and b are constants. This leads to the implication that the number of chunks recalled correctly should depend only on the number of syllables per chunk, and that this number recalled should be lower for 2-syllable chunks. If we assume that all chunks were monosyllabic in the single-presentation training conditions and disyllabic in the paired-presentation training conditions, analogous to long words, these predictions can be assessed. The proportion recalled should depend on the number of chunks in the list. Table 2 presents the mean number of chunks recalled according to this assumption in every condition of both experiments.

Table 2.

One Estimate of the Mean (and SD) of the Number of Chunks Recalled in List Recall For Every Training Condition of Experiments 1 and 2

	Experiment 1		Experiment 2
Training Condition			Lenient Scoring		Strict Scoring
	Mean	SD	Mean	SD	Mean	SD
4n	3.45	0.87	3.75	0.76	3.72	0.77
4s	3.73	0.63	3.88	0.34	3.78	0.49
4p	3.35	0.64	3.17	0.86	2.17	1.41
8n	4.76	1.64	4.56	1.58	3.34	1.75
8s	4.79	1.39	5.00	1.85	3.84	2.19
6n	4.36	1.43	4.34	1.31	3.78	1.70
6s	4.52	1.20	4.00	1.37	3.25	1.83
6p	4.36	0.84	3.81	1.34	2.09	1.40
12n	4.70	1.63	3.88	1.88	2.16	1.97
12s	5.45	1.68	3.69	2.28	2.19	2.24

Note. These means are calculated as the proportion correct times the list length for the single-presentation (s) and non-studied (n) training conditions, and as that quantity divided by 2 for the paired-presentation (p) training conditions.

The hypotheses were assessed with a 1-way ANOVA on immediate recall in all training conditions, using strict scoring of serial recall in Experiment 2 (the situation most appropriate for the model). The ANOVA was followed with Duncan’s post-hoc tests. For those data, F(9, 279) = 8.14, MSe = 2.40, p < .001. The single-syllable lists were not all equivalent; the 12s and 12n conditions were below all others in number of chunks recalled. However, all other specifications of the model were met. No other single-syllable conditions differed significantly from one another, the 4p and 6p conditions were not statistically different, and the two-syllable conditions were both significantly inferior to all of the single-syllable conditions except for the 12s and 12n conditions. The fit was much worse for free recall or lenient scoring of serial recall.

What these comparisons suggest is that the Zhang and Simon (1985) model is in fact suitable for a limited set of circumstances. It provides a good description of the strict serial order scoring of serial recall for lists up to 8 chunks long, but not for lists of 12 single-syllable chunks. Thus, it provides a good description for performance within the capacity of a phonological loop mechanism (e.g., Baddeley, 1986), but not performance for lists outside of that capacity or for free recall.

Serial Position Function for Immediate Recall

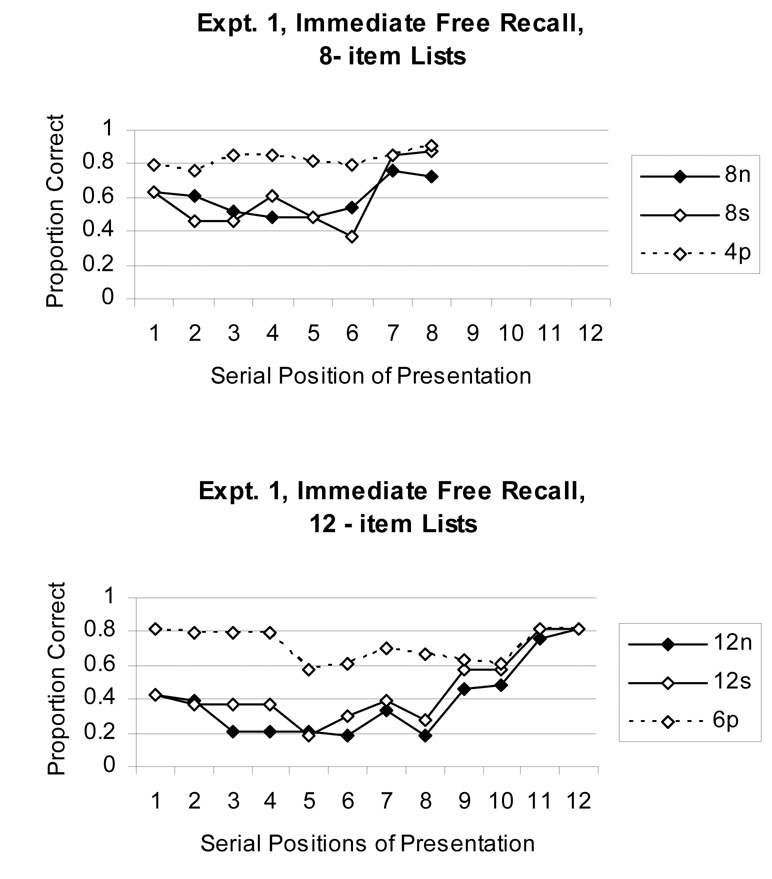
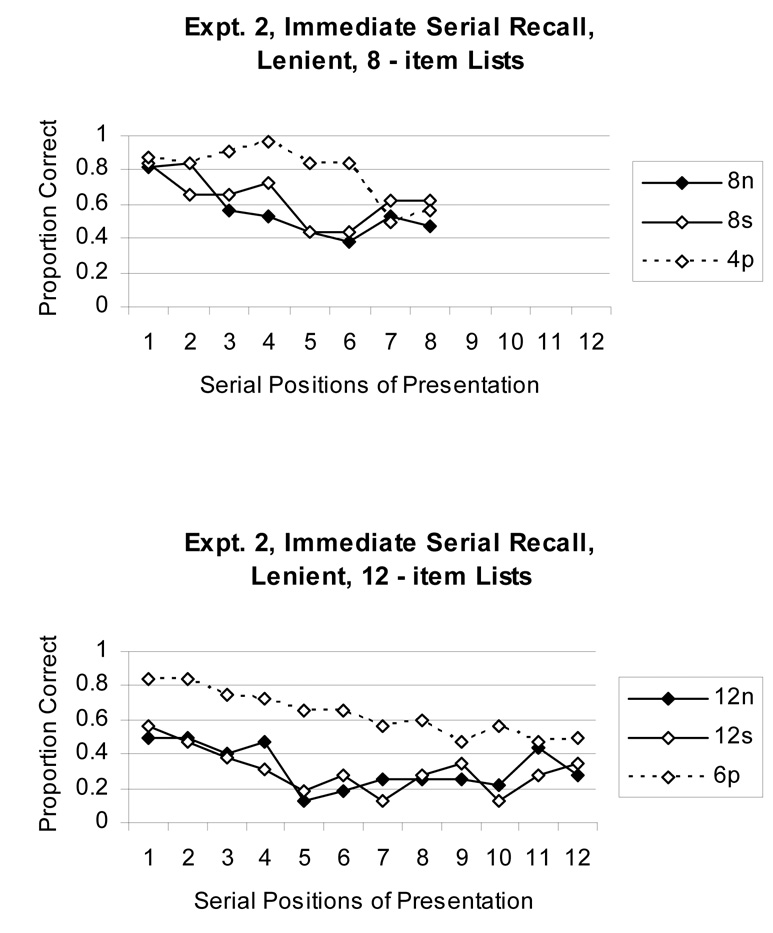
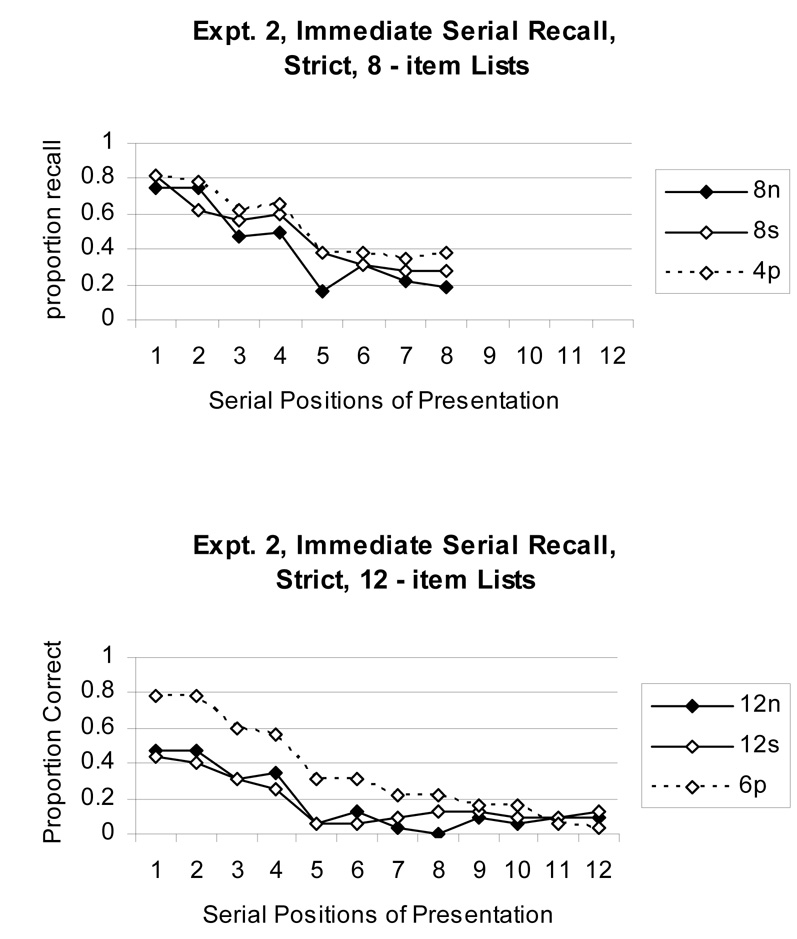
The proportion of correct list recall was computed across participants at each serial position in the to-be-recalled list, separately for each training condition. For Experiment 1 (free recall), Figure 2 shows the serial position functions for 8- and 12-word lists (top and bottom panels, respectively), the two list lengths at which learned pairs were presented. For Experiment 2 (serial recall), Figure 3 shows the same thing for the lenient scoring and Figure 4 shows it for strict scoring.

Figure 2.

Serial position functions in Experiment 1. Top panel, 8-word lists; bottom panel, 12-word lists.

Figure 3.

Serial position functions in Experiment 2 using lenient scoring. Top panel, 8-word lists; bottom panel, 12-word lists.

Figure 4.

Serial position functions in Experiment 2 using strict serial position scoring. Top panel, 8-word lists; bottom panel, 12-word lists.

For each of these panels of Figure 2 – Figure 4, a separate ANOVA was carried out with training condition (paired, single, and non-studied) and serial position as factors. However, it is only the effects involving serial position that are of interest given that training effects were covered above. The main effect of serial position was significant in each case: In Experiment 1, for 8-word lists, F(7, 224) = 5.01, MSe = 0.21; for 12-word lists, F(11,352) = 9.72, MSe = 0.25. In Experiment 2 with lenient scoring, for 8-word lists, F(7, 217) = 7.08, MSe = 0.19; for 12-word lists, F(11, 341) = 4.85, MSe = 0.23. Finally, in Experiment 2 with strict scoring, for 8-word lists, F(7, 217) = 25.07, MSe = 0.17; for 12-word lists, F(11, 341) = 25.06, MSe = 0.13.

The interaction of training effect and serial position was not as ubiquitous. It was significant only for 12-word lists in Experiment 1, F(22, 704) = 2.26, MSe = 0.18; for 8-word lists in Experiment 2 with lenient scoring, F(14, 434) = 2.98, MSe = 0.17; and for 12-word lists in Experiment 2 with strict scoring, F(22, 682) = 2.22, MSe = 0.11. In each case, p < .01 or better. These effects and the accompanying figures show the typical bow-shaped recall function for free recall and declining pattern for serial recall (though with observable chunking effects in the paired conditions when strict scoring is used), and show that the effects of training were often larger at the non-final positions of the list than they were at the end of the list. ¹

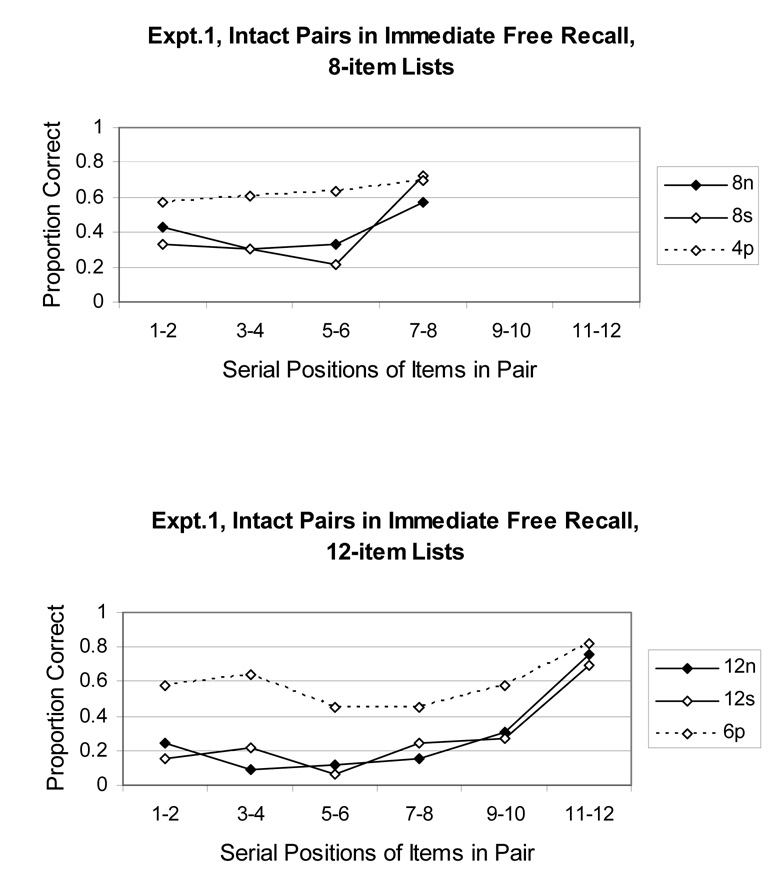
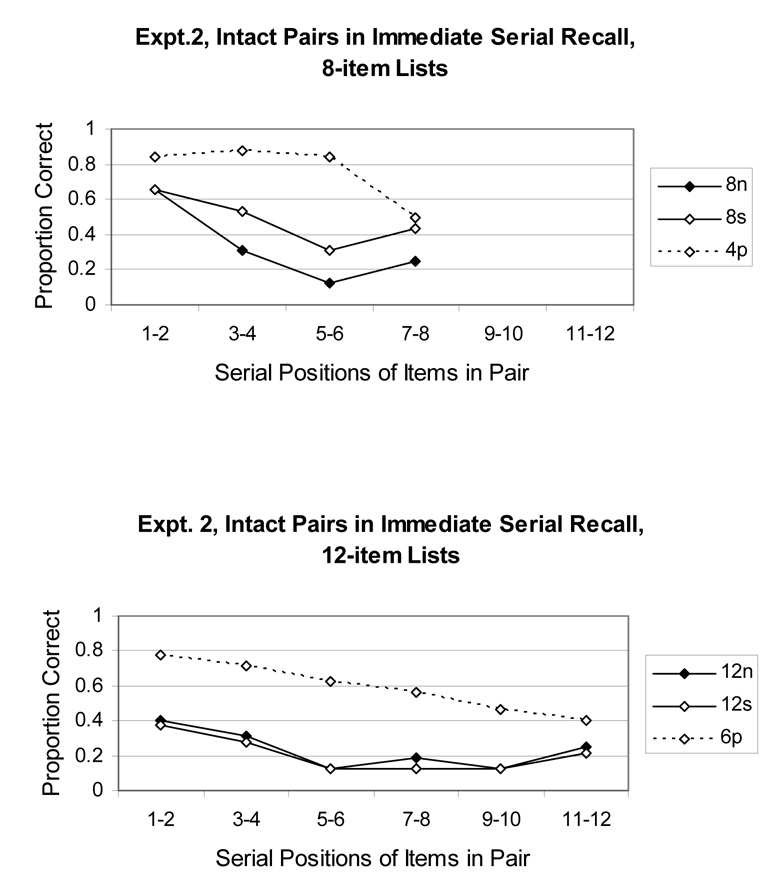
Another way to examine the serial position functions is in terms of whether the pair presented at a particular pair of serial positions was recalled intact, either in the correct two serial positions or shifted to other serial positions. This is shown for Experiment 1 in Figure 5 and for Experiment 2 in Figure 6. The figures show that, consistently across experiments and list lengths, there was little benefit for paired-associate learning for the list-final pair. In contrast, this learning contributed a great deal to performance in non-final positions. (In each condition, the benefit of the paired condition over the singleton condition for lists of the same length was generally .2 to .4 elsewhere in the list.) This result suggests a strategy shift in which a phonological form of memory was predominant in recall of the last pair whereas an association-based memory was predominant for other pairs. Nevertheless, in separate ANOVAs for each list length in each experiment, the Pair Position × Training Condition (paired, singleton, unstudied) interaction reached significance only for 8-word lists in Experiment 2, F(6, 186) = 3.55, MSe = 0.17, p < .01. That interaction modified large effects of training condition, F(2, 62) = 23.66, MSe = 0.26, p < .001, and pair position, F(3, 93) = 12.23, MSe = 0.17, p < .001.

Figure 5.

Intact pairs recalled in Experiment 1 by pairs of serial positions. Top panel, 8-word lists; bottom panel, 12-word lists.

Figure 6.

Intact pairs recalled in Experiment 2 by pairs of serial positions. Top panel, 8-word lists; bottom panel, 12-word lists.

For 8-word lists in serial recall (Experiment 2), it seems striking that there was no difference between paired and singleton conditions in a strict serial scoring (Figure 4, top panel) but a large difference between paired and singleton conditions in the proportion of pairs recalled intact (Figure 6, top panel). This discrepancy occurred because of many learned pairs being recalled intact but in the wrong serial positions in the list. The discrepancy emphasizes that there exists a mechanism that retains the items in a list and benefits from paired-associate learning, separate from the mechanism that is used to ensure that items are recalled in the correct serial positions. These may be the chunk-limited and length-limited mechanisms, respectively.

Many functions of serial recall, scored strictly, include a slight upturn at the end or recency effect. The absence of such an effect here in 8- and 12-item lists (Figure 4) may yield clues about the mechanisms of recall. However, it should not be taken to indicate that the phonological loop mechanism of Baddeley (1986) could not have come into play. For one thing, the absence of recency may have to do in part with the super-span list length. For 6-item lists (not shown), there was a slight upturn at the end. Across serial positions for this list length, the proportions correct were, in the 6s condition, .69, .66, .59, .53, .38, and .41; in the 6n condition, .84, .72, .66, .59, .47, and .50.

The equivalence of proportions correct in the 4p and 8s conditions across serial positions (Figure 4), and their inferiority to the 4s condition, strongly suggest the use of a phonological-length-based system. It is important to note that recency effects are not assumed by Baddeley to be caused by the phonological loop, but rather by other mechanisms (e.g., Baddeley & Hitch, 1993). By presenting items in pairs even in the singleton and nonstudied-item conditions, we may have enhanced the distinctiveness of items throughout the list and therefore may have eliminated a special temporal distinctiveness advantage that ordinarily characterizes both ends of the list (e.g., Brown et al., 2000; Nairne, 2002).

One can also consider the recency effect in serial recall in light of the model by Page and Norris (1998). In that model (e.g., p. 764), the recency effect is caused by the diminished likelihood that the item at the end of the list, as compared to penultimate items, will be transposed with an adjacent item. That is the case because the final item has no following item with which it can be confused. In the present study, because we presented list items grouped in pairs (in lists for all training conditions) the likelihood of recalling the penultimate item one serial position too soon has been diminished, so that the penultimate list item can be put in the correct serial position almost as often as the final item. Indeed, for 8-word lists, the proportions of serial position errors (the correct word recalled at a different serial position) were equivalent for the penultimate and final items (8s condition: .34 & .34, respectively; 8n condition: .31 & .28; 4p condition: .16 & .19). Notice also that, for lists of items that were not learned in pairs, there was an upturn for the last pair compared to previous pairs (Figure 6).

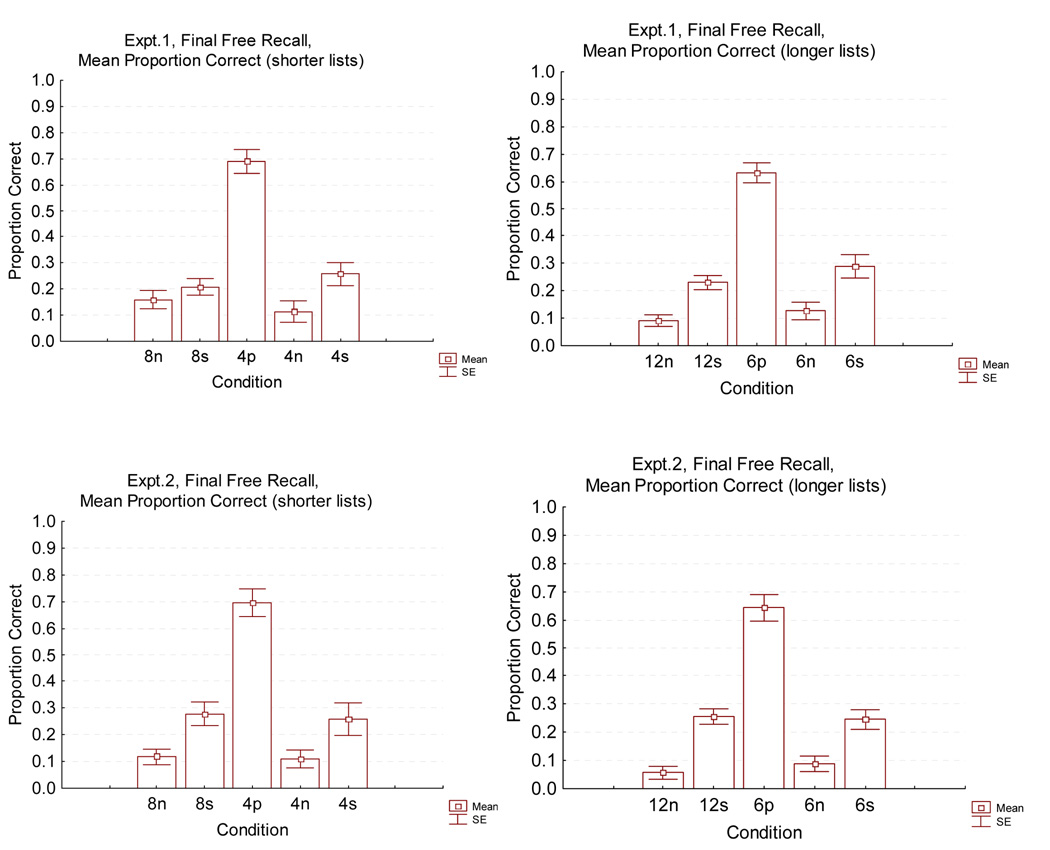
Words Recalled in Final Free Recall

The words recalled in the final free-recall phase were examined as further evidence about the long-term learning effects of paired-associate training. The proportions of words recalled in each condition of each experiment are shown in the four panels of Figure 7. The most important finding was that the proportion of words recalled in the paired conditions was always over twice as high as the proportion of words recalled in the singleton lists of the same lengths. A 1-way ANOVA by training condition produced highly significant results in both experiments (Experiment 1, F(9, 288) = 37.90, MSe = 0.04; Experiment 2, F(9, 279) = 39.45, MSe = 0.04) and the paired and corresponding singleton conditions were always significantly different by Duncan tests.

Figure 7.

Proportion correct in final free recall, in two experiments. a. Free recall, shorter lists. b. Free recall, longer lists. c. Serial recall, shorter lists. d. Serial recall, longer lists.

One way to explain the final free recall results is that paired training provided both forward and backward cues. If so, then remembering either member of a learned pair could reliably elicit memory of the other member of the learned pair. In fact, this assumption provides an excellent prediction of the final free recall of pairs in the paired-training condition intact (i.e., with its members adjacent and in the order presented in training), based solely on final free recall in the singleton-training condition. To make this prediction, we must assume that final free recall may be influenced not only by training but also by recollection of the presentation of items in immediate recall. Suppose that, for the singleton-training condition, the probability of final free recall of the first word of a pair presented in immediate recall is A and, of the second word in a pair, B. Then, if the probabilities A and B are independent, the probability of final free recall of only the first word in such a pair is A*(1−B), the probability of final free recall of only the second word is (1−A)*B, and the probability of final free recall of both words in a pair is A*B. Now, suppose that the same probabilities apply to the paired-training condition except that recollection of one item in a pair automatically cues recollection of the entire pair, which has become a single chunk in memory; and that an intact pair is consequently produced in final free recall. Then the recall of intact pairs in final free recall for the paired condition is predicted to be A*(1−B) + (1−A)*B + A*B, with A and B taken from the singleton-training condition. In the singleton condition in final free recall for Experiment 1, A = .23 and B=.22. The predicted proportion of intact pairs in final free recall in the paired condition, .40, exactly matched the obtained proportion. In Experiment 2, A = .20 and B=.25. The predicted proportion of intact pairs in final free recall in the paired condition, .46, was close to the obtained proportion, .44. Thus, the simple assumption that paired training produced permanent chunks in long-term memory allows the prediction of recall of these chunks from recall of items in the singleton condition, though there are too few data to examine the predictions in great detail.

Discussion of Experiments 1 and 2

Lists of well-learned pairs of monosyllabic words were compared to lists of equally-familiar but unpaired words from the same word pool. The most important results were as follows.

Training Session

An analysis of the training session showed that participants who required more repetitions of the words in order to learn the pairings (and to identify the singletons as such) did not have an advantage in recall. In correlational analyses, they showed slightly poorer performance than participants who only required shorter training sessions.

Words Recalled in Immediate-recall Tasks

The proportion correct recall across the list as a function of training conditions showed that the relative importance of chunk-based vs. length-based limits in recall depends upon a combination of the scoring method, the nature of recall (free vs. serial recall), and the list length. In free recall, the lists of 6 learned pairs yielded results best described as chunk-limited: the same proportion correct as lists of 6 unpaired singletons, despite the drastic difference between these lists in word length (Figure 1b). The same was true of serial recall when a lenient scoring was used (Figure 1d). In stark contrast, using a strict serial order scoring of serial recall, lists of 4 pairs yielded results best described as length-limited: the same proportion correct as lists of 8 unpaired singletons, with no effect of learning (Figure 1e). Other conditions yielded intermediate results (Figure 1a, 1c, & 1f). It seems clear from these results that the characterization of recall as based on chunks, length, or both depends on the conditions. The serial-order-retention mechanism appears to be constrained to something closer to 8 words, and is not strictly relevant for the last part of 12-word lists. However, for lists of any length, some additional chunks (singletons or learned pairs) not included in the serial-order-retention mechanism can be retained, albeit without full information regarding their places within the list.

A simple measure assuming uniform chunking conforming to the information participants acquired in the training session was calculated from the proportion correct, and this simple measure (Table 2) was used to test the model of serial recall offered by Zhang and Simon (1985). Their model subsumes the notion of chunks under a general time-based model, as explained above. Consistent with our other results, the outcome showed that the Zhang and Simon model is suitable only for the serial recall of relatively short lists using a strict serial scoring, the conditions for which the model was originally designed.

Proportion Correct by Serial Positions

The serial position functions show that the training procedure did not result in unusual recall. The bowed serial position function for free recall and the declining pattern for serial recall are typical of these types of recall. The interaction of serial position with training condition, significant in only some conditions but to some extent apparent in the graphs for each condition (Figure 2 – Figure 6), are not a matter of ceiling or floor effects; they are found at various levels of recall. They may indicate that, for the portion of the recall function that is freshest in working memory at the time of recall, namely the recency portion, participants are least likely to use associative information.

Final Free Recall

The final free recall results provided evidence that the chunks that were formed in the training session indeed could be assumed to have survived for use in immediate recall; they still played a major role in final free recall. Indeed, it is striking that the rate of recall of singletons could be used to provide an excellent prediction of the rate of recall of intact pairs for the words that had been trained as paired associates.

In sum, then, the results provide support for multiple limits in immediate recall. There are limits to free recall caused by restrictions in how many already-known chunks can be recalled. There are separate limits to serial recall caused by how much phonological material is present in the list. For serial recall, as well, if the role of phonological rehearsal in forming new chunks is taken into account, limits in how many chunks can be held may still apply (Cowan et al., 2004 and the present replication).

Experiment 3

One limitation of the first two experiments is that they cannot fully address the question of just how well a length-based account (such as that of Baddeley et al., 1975) can fit the serial recall data. Baddeley et al. showed that the number correct in serial recall was predicted by the amount that could be verbally recited in about 2 s. In the present procedure in which pairs of words were learned, it is possible that this paired-associate learning speeds up the rate of recitation to an amount commensurate with the increase in serial recall. This question was examined in the third and last experiment by repeating the procedure of Experiment 2 with a new subject sample, but with a rapid-speech procedure inserted after paired-associate training and before serial recall.

Method

Participants

The participants included 18 college students who received course credit for their participation. They were native speakers of English with corrected-to-normal vision and no known hearing deficits. Of these, two produced speech recordings that were not sufficiently audible to allow timing. These participants were excluded from the analyses, leaving a final sample of 16 (8 men and 8 women).

Apparatus, stimuli, and procedure

These were identical to Experiment 2 except for the rapid-speaking test phase that was inserted into the procedure immediately after the paired-associate training phase. There were 10 blocks of trials of rapid speaking, each with 5 trials. For each trial block, the participant read silently a sequence of words from one of the conditions, presented in the same way as for immediate recall (i.e., 2 words aligned side by side on one screen for 2 s). Then all of the words in the list were shown at the same time in a column, in an order consistent with the just-seen sequence. When the column of words appeared, the task was to read it aloud as quickly as possible. After this, the participant pressed the space bar to progress to the next trial. However, the same column of words appeared for all five trials within a trial block. The response to each trial was digitally recorded and later timed on the basis of a program that allowed accurate measurement of the oscillographic representation of the response, assisted by its sound. Note that, in order to maintain the novelty of words in the non-studied condition, different words were selected from the word pool for the rapid-speaking phase and the serial-recall phase of the experiment. To obtain recitation rates, the number of words in the list was divided by the mean response duration to yield a rate in words per second.

Results and Discussion

In Experiment 3, participants required an average of 7.28 training cycles (SD = 1.81; range = 5 to 11) to reach the 100% correct criterion level. The main results of the experiment are summarized in Table 3. One-way ANOVAs of the proportion correct across 10 conditions indicated that the results were, for the most part, similar to those of Experiment 2. In the analysis of proportion correct according to a strict serial position scoring, F(9, 135) = 24.18, MSE = 0.05, p < .001. Duncan's tests yielded same significant differences between conditions mentioned above in the results of Experiment 2. In the analysis of proportion correct according to lenient scoring, 29.03, MSE = 0.03, p < .001. Comparisons yield same results mentioned for Experiment 2 except that now 6p < 6s. That is, in this experiment the analogy to the word length effect using lenient scoring was significant even with longer lists. Perhaps the inclusion of the rapid-speech test functioned as practice, inducing somewhat more efficient rehearsal than in Experiment 2.

Table 3.

Mean (and SD) of the Proportion of Correct Recall and Pronunciation Rate By Condition in Experiment 3

	Proportion of Correct Recall				Pronunciation
Training Condition	Lenient Scoring		Strict Scoring		Rate (Words/s)
	Mean	SD	Mean	SD	Mean	SD
Condition 4p and Comparison Conditions
8n	0.41	0.20	0.37	0.18	2.79	0.40
8s	0.66	0.21	0.44	0.25	2.85	0.67
4p	0.80	0.21	0.60	0.35	3.07	0.67
4n	0.91	0.15	0.91	0.15	3.27	0.09
4s	0.97	0.09	0.97	0.09	3.45	1.01
Condition 6p and Comparison Conditions
12n	0.29	0.10	0.19	0.12	2.66	0.42
12s	0.38	0.21	0.23	0.13	2.61	0.47
6p	0.56	0.22	0.29	0.22	2.86	0.45
6n	0.70	0.32	0.60	0.40	2.77	0.59
6s	0.81	0.21	0.72	0.30	3.18	0.73

A comparable ANOVA for recitation rates (expressed in words/s) yielded F(9, 135) = 5.43, MSE = 0.23, p < .001. In Duncans' tests, the recitation speeds did not differ significantly among the 12-word lists (6p, 12n, 12s), nor among the 8-word lists (4p, 8n, 8s). Thus, there were no noticeable effects of paired-associate learning on response rates. However, there were differences due to list length and word exposure (12s, 12n < 4p, 6s, 4n, 4s; 6n < 6s, 4n, 4s; 8n, 8s < 4n, 4s; 6p, 4p < 4s).

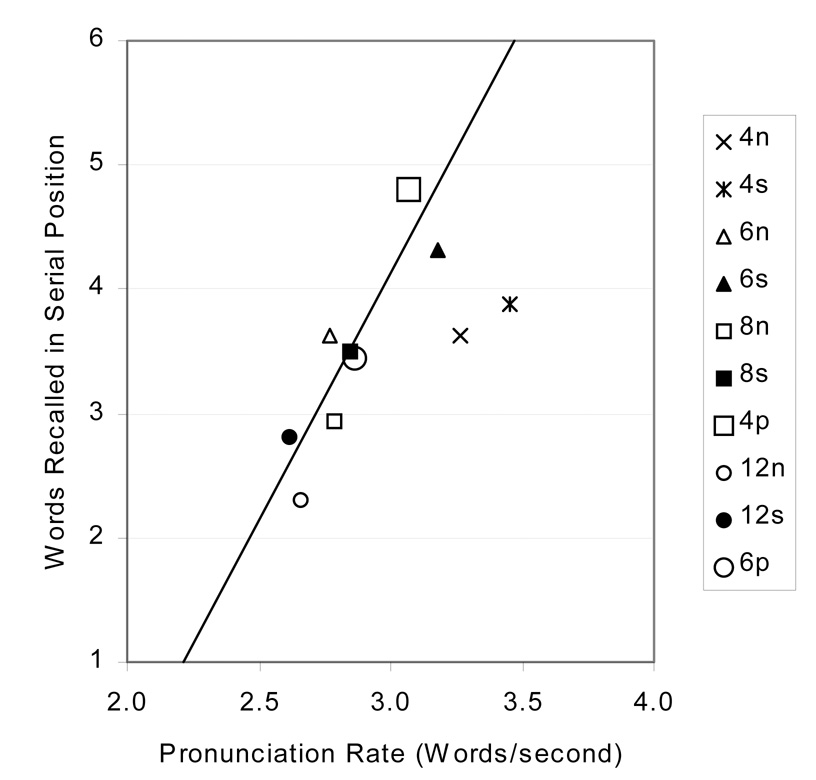
The most important result of the experiment is the relation between speech rate and the number of words recalled in their correct serial positions in the serial recall task, according to strict scoring. This relation is illustrated in Figure 8 using the speech-rate and number-correct means for each condition. (Number correct was calculated for each participant in each condition as the number of words recalled, averaged across participants.) The relation is surprisingly linear, with the exception of data from the 4n and 4s conditions. In those conditions, though, the mean number of words correct is near ceiling level, providing an inadequate test of how many words could be recalled. With those two conditions removed, the correlation between the speech-rate and number-correct means was .89. Using free scoring of the recall data, though, that relation was reduced to .52. These results show that the paired-associate technique produces serial recall data favorable to the speech rate hypothesis of Baddeley et al. (1975), provided that a strict serial scoring method is used.

Figure 8.

Scatter plot of speech rate a nd number of words recalled in the correct serial positions, for condition means in Experiment 3.

It is important to consider that Hulme et al. (1991) found that lists of words and list of nonwords, when plotted in a manner similar to Figure 8, did not produce a single linear relation, but rather separate linear relations for words and nonwords. The present findings, in which paired and singleton conditions fit on the same regression line, suggest that paired associations do not affect recall in a manner similar to lexical knowledge. (For indications that long-term memory affects working memory performance in more than one manner, see Lewandowsky & Farrell, 2000; Thorn, Gathercole, & Frankish, 2005.)

General Discussion

Like Zhang and Simon (1985), the present study provides support for the notion that chunk limits and length limits operate together in recall. However, the theoretical approach of Zhang and Simon was one in which chunk and length limits always operate together in the same way, influencing performance together. That theoretical view proved successful only in the situation in which length limits dominated: for relatively short (8-word) lists using a strict serial scoring method. This is a length that is fairly close to the 2-s limit for the length-limited mechanism discussed by Baddeley et al. (1975), whereas a 12-word list is way beyond that limit.

The present results with free and serial recall of lists of different lengths indicated instead that chunk and length constraints may operate under different circumstances. In free recall, and in serial recall using a free scoring method, performance on list of 6 learned pairs was very similar to performance on lists of 6 pre-exposed singletons, as a chunk limit would suggest. In serial recall, though, performance on lists of 4 learned pairs was very similar to lists of 8 pre-exposed singletons, as a length limit would suggest (not 4 singletons as a chunk limit would suggest). Other circumstances resulted in intermediate results, as shown in Figure 1. This dual nature of immediate recall provides important clues to the mechanisms of recall, perhaps like the finding in physics that light behaves like a wave under some circumstances and like a particle under other circumstances.

It is too soon to settle on a detailed model of results such as these. However, they do point clearly to the need for two mechanisms of recall. For 12-word lists, learned pairs relieved the burden on working memory to such an extent that the number of words recalled actually doubled. This finding only makes sense if the working-memory mechanism involved was chunk-limited. For example, if an individual's capacity were four chunks (cf. Cowan, 2001), he or she would be able to retain only four singletons. However, in the paired condition, by relying on learned associations, working memory could be dedicated to the retention of only one word from a pair and the other word in that pair could be retrieved from long-term memory, resulting in a total of 8 words recalled. The results were similar to that. In Experiment 1, the 6s, 12s, and 6p condition means were 4.52, 5.45, and 8.72 words recalled, respectively; in Experiment 2 with lenient scoring, they were 4.00, 3.69, and 7.62 words recalled, respectively. The paired means were nearly double those for the comparable singleton conditions.

For the strictly-scored serial recall of shorter lists, in striking contrast, the training hardly seemed to help at all. The 4s, 8s, and 4p condition means were 3.78, 3.84, and 4.34 words recalled. Clearly, the memory mechanism that is used to retain serial order information here is not able to benefit much, if at all, from associative information, even though that associative information is retained, as shown by the much larger number of words recalled in the 4p condition given a lenient scoring of the results (6.34 words, or 2.0 words more than were credited in strict scoring).

This result has important implications for how associative knowledge is used in immediate recall. One theoretical possibility is that phonological memory is used to preserve serial order information and that associative information works by allowing a restoration or redintegration of phonological traces that have become degraded (Hulme et al., 1997; Schweickert, 1993). However, that cannot be the case because it would be expected to result in a benefit in recall even using serial scoring. The absence of such a benefit for 8-word lists suggests that, for these lists at least, associative knowledge in long-term memory cannot be used appreciably to enhance the knowledge that is already present in the phonological memory trace. This is consistent with the proposition that there are other ways, besides redintegration, in which long-term knowledge can play a role in immediate memory tasks (Lewandowsky & Farrell, 2000; Thorn et al., 2005). The chunk representation and the phonological representation may be used separately rather than interactively; the chunk representation holds more words but the phonological representation holds clearer information about the serial order of units.

These suggestions do not answer the question of why intermediate results emerged in some circumstances: results in which the number of words recalled was mid-way between what would be expected according to a simple chunk limit and a length limit. This occurred in both free recall and serial recall, leniently scored, for lists of 4 learned pairs; and in serial recall, strictly scored, for lists of 6 learned pairs. One possibility is that a mixture of strategies is used in such situations. Participants might retain information in a chunk-limited form (Baddeley, 2001; Cowan, 2001; Tulving & Patkau, 1962) while also rehearsing a length-limited phonological trace (Baddeley, 1986), and performance could be based on some combination of these sources. For lists of 8 words, if phonological rehearsal manages to retain much of the singleton information along with its serial order information, the use of the chunk-limited mechanism may be partly redundant with the phonological system, so that the gain from learned word pairs in words recalled is moderate. (For lists of 12 words, in contrast, the ability of the phonological memory system is substantially exceeded so that the gain from learned pairs is greater.) The chunk-limited system presumably includes within-pair order information and that may allow a moderate gain in serial order information as well. It remains for future research to determine exactly how length-limited and chunk-limited storage mechanisms are combined. Although there are numerous detailed models of serial recall (for a recent review see Farrell & Lewandowsky, 2004), most of them are not designed specifically to address chunk limits (though see Davelaar, Goshen-Gottstein, Ashkenazi, Haarman, & Usher, 2005). We suspect that no model has yet been adapted to explain the combination of chunk limits and length limits that we have observed.

Under the assumption that each learned pair is a chunk, an assumption well-supported by the final free recall results (Table 3), the capacity limit in free recall and in serial recall was about 4 chunks (Table 2), consistent with evidence from a wide range of tasks (e.g., Cowan, 2001; Basak & Verhaeghen, 2003), including recent studies with lists of words (Cowan, Johnson, & Saults, 2005; Verhaeghen, Cerella, & Basak, 2004). Yet, the nature of the chunk-limited mechanism is not yet clear. It could be the focus of attention (Cowan, 2001) or it could be an episodic buffer that requires attention but then holds information temporarily (Baddeley, 2000, 2001). A primacy gradient of activation in recall (cf. Farrell & Lewandowsky, 2004; Page & Norris, 1998) theoretically could be the basis of the chunk-limited mechanism, which would explain why the advantage of paired associate learning in immediate recall was diminished at the end of lists (Figure 5–Figure 6).

Given that we have produced new associations in long-term memory, the question arises as to whether the chunk limits we have observed are based on this long-term memory information rather than a transient working-memory representation. Indeed, a comparable chunk limit has been obtained with a delayed recall of a single list (Nairne & Neath, 2001). However, as Cowan (2001) pointed out (see also Broadbent, 1971, pp. 342–343), a long retention interval would not be decisive because of the assumption that, even in long-term recall, items presumably have to be retrieved back into working memory before they can be overtly repeated.

We assume that the benefit of paired association comes from long-term memory. It is remarkable that the benefit of long-term memory was completely dependent on the testing and scoring conditions. Thus, memory of learned two-word chunks proved to be similar to memory of unassociated one-word units in the free recall of relatively long lists, as shown by the great disadvantage of the 12s condition compared to the 6p and 6s conditions, which were nearly equivalent to one another, in Figure 1b; yet, phonological length rather than the number of chunks was the decisive factor for the serial recall of shorter lists, as shown by the near-equivalence of 8s and 4p condition means, and the great advantage of the 4s condition over those two conditions, in Figure 1e.

It is worth emphasizing, however, that in neither case can the information be entirely from long-term memory. In particular, even in the paired condition, the participant still has to keep in mind which learned pair was included in the current list and which learned pair was not included. That information cannot be present in long-term memory before the immediate-recall trial begins.

In sum, the present article addresses the nature of limits in immediate-recall tasks. On one hand, it has been suggested that recall is limited by capacity expressed in chunks (Broadbent, 1975; Cowan, 2001; Cowan et al., 2004; Johnson, 1978; Miller, 1956; Tulving & Patkau, 1962; Mandler, 1985). On the other hand, it has been suggested that recall is fundamentally limited by length: the amount of time it takes to rehearse or recite the list, which differs among individuals, or at least the amount of phonological material to be recalled, which can differ among conditions (Baddeley et al., 1975; Cowan et al., 1992, 1994, 1997; Hulme & Tordoff, 1989; Mueller et al., 2003; Schweickert & Boruff, 1986). We have shown that neither formulation alone is suitable for all test circumstances but that the two are complementary.

One reason why this research finding is important is that it has a bearing on the concept of short-term memory as separate from long-term memory (Atkinson & Shiffrin, 1968; Broadbent, 1958; Cowan et al., 1994). Some researchers have argued that short- and long-term memory are not truly distinct and that a single ensemble of mnemonic principles can explain performance in both situations (e.g., Brown, Preece, & Hulme, 2000; Crowder, 1993; Nairne, 2002). This point of view was reasonable given that there were many similarities between the findings of short-term and long-term memory experiments (e.g., Bjork & Whitten, 1974; Greene, 1986; Keppel & Underwood, 1962) and given that the nature of immediate-memory limits was unclear. However, recent studies have pointed out important differences between seemingly similar phenomena in immediate recall vs. long-term recall (Cowan et al., 1994, 1997; Cowan, 1995; Davelaar et al., 2005; Mueller et al., 2003) and the present study helps to clarify the nature of short-term memory limits. Even if time, per se, does not matter for memory (Lewandowsky et al., 2004), time in the presence of rehearsal or pronunciation appears to matter, most likely because it can cause interference; and the number of chunks that can be retained at once matters.