Abstract
Working memory (WM) is the set of mental processes holding limited information in a temporarily accessible state in service of cognition. We provide a theoretical framework to understand the relation between WM and aptitude measures. The WM measures that have yielded high correlations with aptitudes include separate storage and processing task components, on the assumption that WM involves both storage and processing. We argue that the critical aspect of successful WM measures is that rehearsal and grouping processes are prevented, allowing a clearer estimate of how many separate chunks of information the focus of attention circumscribes at once. Storage-and-processing tasks correlate with aptitudes, according to this view, largely because the processing task prevents rehearsal and grouping of items to be recalled. In a developmental study, we document that several scope-of-attention measures that do not include a separate processing component, but nevertheless prevent efficient rehearsal or grouping, also correlate well with aptitudes and with storage-and-processing measures. So does digit span in children too young to rehearse.
Keywords: working memory, short-term memory, individual differences, variation in working memory, cholastic abilities, intellectual abilities, attention, capacity, storage capacity
Baddeley and Hitch (1974) highlighted a key theoretical construct, working memory (WM), which can be described generally as the set of mechanisms capable of retaining a small amount of information in an active state for use in ongoing cognitive tasks (though it now means different things to different investigators; see Miyake & Shah, 1999). If sufficient information cannot be retained in WM and integrated, it is assumed that various problems cannot be solved, and that reading or language comprehension cannot be completed. An important approach to WM has blossomed, in which experimental and psychometric methods are synthesized (e.g., Conway, Cowan, Bunting, Therriault, & Minkoff, 2002; Cowan et al., 1998; Engle, Tuholski, Laughlin, & Conway, 1999; Miyake, Friedman, Rettinger, Shah, & Hegarty, 2001).
Research on WM suggests that the measures used most often to examine individual differences have both strengths and weaknesses. A main type of strength is their strong correlation with intellectual aptitude tests, and a main type of weakness is the difficulty encountered in analyzing and interpreting WM test results. This difficulty stems largely from the reliance on dual tasks in the measurement of WM capacity (which include separate storage and processing task components). We will argue that the research literature provides hints that the strengths can be retained without using storage-and-processing measures. We will offer a theoretical framework for doing so, and for measuring WM in a more meaningful way than is found with current measurement practices. The theoretical framework is based on the notion of an adjustable attentional focus and on measures of the storage capacity of attention or its scope. The predictions tested in the present article pertain to the scope of attention, whereas the adjustable nature of the focus allows consistency with other highly relevant research (e.g., Kane, Bleckley, Conway, & Engle, 2001).
We do not judge the success of this endeavor by whether storage-and-processing measures or the proposed alternative, scope-of-attention measures, pick up more variance in aptitude tasks. Rather, success will be judged by whether the variance that is picked up contributes to our understanding of the processes underlying the generally-observed relation between WM and intelligence. By detailing some conditions in which tasks that do not include separate storage and processing components are successful in correlating with intelligence, we provide information about what mechanisms could or could not be indispensable parts of that relation. The storage-and-processing tasks could be the best WM predictors of aptitudes but still could be relatively undesirable tasks if much of their predictive value comes from mechanisms that are not central to the concept of WM (e.g., domain-specific skill in reading or arithmetic). We examine the relations between traditional WM measurement methods and the ones we favor.
Background of the Research Problem
A few papers following Baddeley and Hitch (1974) were crucial in drawing the field's attention to the strong relation between individual differences in WM performance, on one hand, and individual differences in performance on psychometric indices of scholastic and intellectual aptitudes, on the other (e.g., Case, Kurland, & Goldberg, 1982; Daneman & Carpenter, 1980; Kyllonen & Christal, 1990). Search of a popular electronic data base (PsycInfo) carried out on January 30, 2004 showed that the number of articles or dissertations that included both the phrase "working memory" and the phrase "individual differences" in the title or abstract have increased steadily since 1980. In successive 5-year periods between 1980 and 2000, the numbers of entrees were 16, 21, 60, and 113. Based on subsequent entries (97), our projection for 2001–2005 is 160, a tenfold increase from 20 years previous.
The observation of a strong relation between WM and aptitude tasks has been gained at a theoretical cost, though. It is not at all clear why the working-memory tasks work. Daneman and Carpenter (1980) suggested that, given an assumed structure of WM in which storage and processing shared resources, an adequate test of WM must tax both storage and processing. They therefore designed reading- and listening-span methods in which a processing task (comprehending sentences) was to be carried out interleaved between items in a storage task (retaining the last word of each sentence for later recall). Case et al. (1982) similarly combined counting of displays of objects and recall of the sums (counting span), and Turner and Engle (1989) combined arithmetic with word recall (operation span). Performance levels on these “storage-and-processing” types of tasks are highly interrelated. They correlate well with various mental aptitudes in adults, at a considerably higher level than do simple memory-span tasks, in which a list of items is simply presented for recall on each trial (for a meta-analysis see Daneman & Merikle, 1996). However, as we will discuss, it is far from clear how the storage-and-processing tasks are carried out, what aspects of the tasks account for the high correlations with aptitudes, and whether all such WM tasks operate similarly.
Childhood Developmental Changes in WM Performance
There have been a number of studies applying the logic of storage-and-processing types of tasks and other complex WM tasks in childhood development (e.g., Ashcraft & Kirk, 2001; Bayliss, Jarrold, Gunn, & Baddeley, 2003; Case et al., 1982; Daneman & Hannon, 2001; Gathercole & Pickering, 2000; Hitch, Towse, & Hutton, 2001; Kail & Hall, 2001; Swanson, 1996; Towse Hitch, & Hutton, 1998). The importance of such study is partly that it can help in predicting and clarifying childhood aptitudes and disabilities (e.g., Swanson, in press), and partly that it can help in clarifying the processes of WM per se. It can do the latter in several ways. First, cross-age variance provides a wider range of variability in task performance than one finds among adults (a research priority advocated, for example, by Pascual-Leone, in press). Second, cross-age differences in processing can shed light on the mechanisms of WM. For example, one possible basis of the higher predictive value of storage-and-processing tasks as opposed to single tasks such as digit span is not the inclusion of processing per se, but rather the fact that the processing component interrupts covert verbal rehearsal (cf. Baddeley, 1986) and thereby allows other processes to play a dominant role. Given that young children do not engage in much covert verbal rehearsal, or do so only inefficiently (e.g., Cowan et al., 1994; Cowan & Kail, 1996; Flavell, Beach, & Chinsky, 1966; Gathercole, Adams, & Hitch, 1994; Guttentag, 1984; Henry, 1991; Hulme & Muir, 1985; Ornstein & Naus, 1978), the superiority of storage-and-processing tasks for young children could be called into question.
Difficulties in the Interpretation of Storage-and-Processing WM Tasks
It can be argued that the storage-and-processing measures are theoretically ambiguous. They have been based on the premise that processing and storage both tap a common resource (see Daneman & Carpenter, 1980). However, within that framework, it has long been thought that some individuals require more of that common resource than others to accomplish a given task because expertise leads to efficient use of the resource (e.g., Case et al., 1982). For example, the interpretation offered by Daneman and Carpenter was that the reading-or listening-span memory score measures how much capacity is available when combined with linguistic comprehension, and therefore provides an index of the efficiency of that comprehension. However, it is possible that there are individual differences in storage itself, even with linguistic processing equated. This might take the form of individual differences in the passive storage of information, as in the phonological loop (Gathercole & Baddeley, 1993), or individual differences in how many unassociated units or chunks can be held in the focus of attention (Cowan, 2001). One person might excel in storage and another in processing, yet both might obtain the same score on a storage-and-processing type of WM task. A WM span score would not indicate which type of person had been tested.
Moreover, there is a fundamental difficulty in interpreting the results of dual tasks (of which, storage-and-processing tasks are one type). Performance on a task can be impaired by a concurrent task if there is a need for the tasks to share a general, cross-domain resource such as attention, specific resources such as verbal or spatial processing, or both of these (for discussion see Cowan, 2001). One way to tell if a general resource exists is to determine whether dual-task interference can be obtained using two tasks that share nothing in the way of more specific processes but, of course, that criterion is difficult to meet with assurance. Some studies have shown little or no dual-task interference (e.g., Cocchini, Logie, Della Sala, MacPherson, and Baddeley, 2002; Duff & Logie, 2001; Farmer, Berman, & Fletcher, 1986) but that proves only that not all tasks require a substantial amount of a general resource such as attention. Other studies have shown dual-task interference even between two tasks differing in modality (Jolicoeur, 1999) and differing in the use of verbal versus nonverbal materials (e.g., Jefferies, Lambon Ralph, & Baddeley, 2004; Morey & Cowan, 2004; Sirevaag, Kramer, Coles, & Donchin, 1989; Stevanovski & Jolicoeur, 2003). Like Cowan (2001) and Kane et al. (2004), we find it most parsimonious to assume that there is a general, amodal attentional resource, which has been assumed by other investigators for very different reasons as well (e.g., Tombu & Jolicoeur, 2003). However, in the literature on dual-task measures of WM, including the storage-and-processing tasks, there has been very little effort to use task combinations in which the storage and processing tasks share neither their sensory modality nor the types of coding that they most naturally elicit, so the basis of interference between storage and processing is usually unclear and probably complex.
Making matters worse, the types of domain-specific coding that traditionally have been associated with WM (Baddeley, 1986) may be differentially related to a general resource. Miyake et al. (2001) showed that spatial storage, with or without concurrent processing, tends to be closely related to executive function, in contrast to the separation between phonological storage and executive function. The present paper offers a rationale for measures that are simpler because they concentrate on storage, with intrinsic means to limit rehearsal and grouping.
A wide variety of possibilities for the theoretical interpretation of storage-and-processing WM tasks have been discussed in the literature. There is some evidence that participants do not always engage in attention-sharing between processing and memory maintenance, as one might assume; in some tasks, they appear to switch attention between storage and processing, provided that the processing task included rich semantic cues for retrieval of the memoranda (Copeland & Radvansky, 2001; Cowan et al., 2003; Hitch et al., 2001). There has been some concern that the feature of the processing task that impairs memory performance is the imposition of a time delay during which rehearsal is impossible (Towse, Hitch, & Hutton, 1998) or the imposition of high-frequency retrievals or processing during which rehearsal is impossible or storage is somehow interfered with (Barrouillet, Bernardin, & Camos, 2004; Saito & Miyake, 2004). Other studies have suggested that what is critical is the amount of proactive interference that is already present by the time that long list lengths are used, and individual or age differences in the ability to overcome that interference by inhibiting it (Conway & Engle, 1994; Lustig, May, & Hasher, 2001; May, Hasher, & Kane, 1999). Bayliss et al. (2003) suggest that domain-specific storage and cross-domain processing work separately, not from a common resource. Given these possibilities, it is important to investigate what we might learn from potentially simpler tasks.
Single-Task Measures of WM Capacity
There is already some evidence that some WM tasks that do not include separate storage and processing components are nevertheless capable of yielding relatively high correlations with aptitude tests. However, that evidence is still sparse and not well-integrated theoretically. Mukunda and Hall (1992) carried out a meta-analysis of the within-age correlations in adults and children between various WM tasks and various intellectual aptitude tasks, and found that one measure, running memory span (11 tests, R = .40) performed about as well as reading span (11 tests, R = .43) and better than operation span (6 tests, R = .23), counting span (3 tests, R = .28), or digit span (53 tests, R = .22). Running memory span (Pollack, Johnson, & Knaff, 1959) is a procedure in which a list of an unpredictable, long length is presented, the task being to recall as many items from the end of the list as possible after the list terminates. Unfortunately, as in most meta-analyses, different measures had to be drawn from different studies, making the comparability of the measures questionable.
Haarman, Davelaar, and Usher (2003) developed a "conceptual span" task in which list recall was to be organized according to semantic elements (e.g., in an example they offer: "lamp, pear, tiger, apple, grape, elephant, horse, fax, phone," FRUIT? Correct answer: apple, pear, grape"). Conceptual span yielded higher correlations than reading span in the prediction of aspects of reading comprehension that required unconnected semantic elements to be retained (e.g., verbal problem-solving; anomaly detection). The premise behind this task appears to be that it is a way to measure attentional capacity; attending to information may be tantamount to selecting objects by categorizing them (see Logan, 2002). Work is ongoing in our laboratory and in other laboratories to determine whether this sort of task correlates well with a wider array of aptitude tasks. Other laboratories, as well, have begun to experiment with a variety of new WM procedures, some of which do not involve a dual task (e.g., Oberauer, Süß, Wilhelm, & Wittmann, 2002).
In the literature, there appears to be no theoretical framework allowing performance on all of these WM tasks to be understood. Toward that end, an adjustable-attention framework will be described. It leads to the advocacy of certain relatively simple WM tasks that might be more easily interpretable than storage-and-processing tasks.
A Theoretical Framework for WM-Capacity Measurement Based on Adjustable Attention Exposition of the theoretical framework depends on an understanding of (1) the work that has been done to link attention to WM, (2) the reasons why that work has not yet produced a meaningful scale of WM capacity for use in examining individual differences in aptitude, and (3) theoretical underpinnings for constructing such a meaningful scale. We discuss these.
Attention is a controversial concept but large-scale treatments of it can be found in the literature (e.g., Cowan, 1995; Luck & Vecera, 2002; Näätänen, 1992; Pashler, Johnston, & Ruthruff, 2000; Shiffrin, 1988). It is beyond the scope of this article to re-review it. We use the term attention to refer to selective attention, in which some information is selected for processing at the expense of less-than-optimal processing of other information. What is important for the present approach is that at least two dimensions of attention can be discerned: the control of attention and its scope. The recent research literature on the link between attention and WM has focused primarily on the control of attention whereas, we suggest, a meaningful scale of WM capacity depends on an emphasis on the scope of attention.
Control of Attention
The control of attention was an important element of early theories of information processing (e.g., Atkinson & Shiffrin, 1968) and is embodied in the central executive component of theoretical conceptions of WM (e.g., Baddeley, 1986; Cowan, 1988, 1995). A great deal of recent research has converged on the importance of the control of attention in carrying out the standard type of WM task involving separate storage and processing components. Six strands of research on this topic can be enumerated. (1) These WM tasks correlate highly with aptitudes even when the domain of the processing task (e.g., arithmetic or spatial manipulation) does not match the domain of the aptitude test (e.g., reading) (Daneman & Merikle, 1996; Kane et al., 2004). That is to be expected if the correlations are due to the involvement of processes of attention that cut across content domains. (2) An alternative account of the correlations based entirely on knowledge can be ruled out. Although acquired knowledge is extremely important for both WM tasks and aptitude tasks (e.g., Ericsson & Kintsch, 1995), correlations between WM tasks and aptitude tasks remain even when the role of knowledge is measured and controlled for (Hambrick & Engle, 2001). (3) On tasks involving memory retrieval, dividing attention impairs performance in individuals with high WM spans but has little effect on individuals with low WM spans (Rosen & Engle, 1997). This suggests that low-span individuals do not make use of attention in the same way that high-span individuals do within these tasks. (4) Latent variable analyses (Conway et al., 2002; Engle et al., 1999) show that the portion of the variance in storage-and-processing WM tasks that is most responsible for its correlation with aptitude tests is not the portion that is in common with simple list-recall span tasks, but the portion unique to the storage-and-processing tasks. This has been taken to indicate that what is most critical is the ability to retain information in memory even while carrying out processing, an ability that would seem to require the control of attention. (5) Differences between high-and low-span individuals (measured by storage-and-processing WM tasks) have been obtained even in tasks in which the only apparent storage requirement is to hold onto the goal of the task. These differences have been obtained in situations in which there was some type of interference with goal maintenance to be overcome with the help of attentional control (Conway, Cowan, & Bunting, 2001; Kane et al., 2001; Kane & Engle, 2003). (6) Recent research has suggested that the functioning of frontal-lobe areas related to executive control of attention differ between high-and low-span individuals (as measured by storage-and-processing WM tasks). Kane and Engle (2002) reviewed evidence converging on this point. A more recent neuroimaging study by Gray, Chabris, and Braver (2003) explicitly found WM span differences in neural functioning localized in particular frontal areas, which emerged only in situations in which there was a high level of proactive interference to be overcome.
Although the emphasis on the control of attention is supported by the evidence, it does not lead naturally to a meaningful measure of the capacity of WM, if that capacity is defined as a number of items in WM. Indeed, the dependent measure of the ability to maintain a goal differs widely from one test situation to the next (cf. Conway et al., 2001; Kane et al., 2001; Kane & Engle, 2003). We argue that, in order to measure WM capacity on a common scale, it is necessary to consider the scope of attention instead of its control.
Scope of Attention
Theoretical work on information processing has long been divided on the role of attention in short-term storage. James (1890) discussed primary memory as the trailing edge of consciousness, thoroughly related to the concept of attention. This was not necessarily true of Hebb's (1949) concept of short-term storage as a reverberating neural circuit. Miller's (1956) discussion of the finding that people could retain only about 7 items also seems neutral to the involvement of attention in short-term retention. However, Broadbent's (1958) conception of a limited-capacity storage faculty seemed to view it as being the direct consequence of attention, given that an attention filter stood between a large-capacity store of information coming directly from the senses and a small-capacity store of information coming after that information was filtered. In contrast, in the conception of WM as a multi-component system (e.g., Baddeley, 1986; Baddeley & Logie, 1999), attention tended to be associated with executive control but not with storage per se; that storage was assumed to be automatic once the information was entered into it, and it was assumed to be time-limited instead of capacity-limited. Cowan (1988, 1995, 1999) advocated both attention-free and attention-dependent forms of storage, with only the attention-dependent forms limited in capacity per se.
Broadbent (1975) suggested that there is a form of storage that is limited to 3 items. Cowan (2001) reviewed a great deal of literature in support of the notion that there is a form of storage that typically can include 3 to 5 separate units, or chunks, of information in normal adults, and proposed that the special form of storage limit may be the capacity of the focus of attention, i.e., the scope of attention. Such a capacity would not replace the attention-free stores of Baddeley (1986) as the two presumably could co-exist (i.e., phonological and visuospatial buffers might exist apart from attention).
At least four related assumptions about this concept of the scope of attention are subsumed under the attention-adjustment hypothesis under investigation here: (1) that there is a limit in the capacity of the focus of attention, (2) that this limit varies between individuals, (3) that measures of this capacity are theoretically and empirically related to storage-and-processing measures of WM, and (4) that the common variance between these measures is related to intellectual aptitude measures. The first of these was the topic of previous work (especially Cowan, 2001; Cowan, Chen, & Rouder, 2004) whereas the other three are topics of the present investigation. There may be other portions of variance related to specific skills required by a particular measure, especially in the storage-and-processing measures, given that they each include a separate processing component; but our research goal is to determine if there is nevertheless considerable common variance among tasks that can be attributed to the scope of attention.
The control-of-attention and scope-of-attention hypotheses are not necessarily in conflict. Individuals who excel at controlling attention could be the same ones who have the largest scope of attention. This could be the case, for example, if attention can be adjusted. When necessary, it might zoom in to hold on to a goal in the face of interference, and perhaps a minimum of related data that is required. However, when there is no interference with the goal and the task has been well-practiced, the focus of attention could afford to zoom out to apprehend multiple items at once, up to its limit. (For a mathematical model of WM based on this concept, see Usher, Haarmann, Cohen, & Horn, 2001; for relevant experimental work see Chen, 2003.) This concept is related to the zoom lens model of attention of Eriksen and St. James (1986). We both propose that a zoomed-out setting has more breadth or covers more objects, but has less intensity or precision of processing of each object, than a zoomed-in setting. The main difference is that we propose that the focus of attention is not specific to visual processing or to its spatial aspects, but covers all modalities and codes. Our concept might also be related to the model of LaBerge and Brown (1989), who propose that there is a gradient of processing that becomes less intense as one gets further from the focus of attention. The gradient can be set narrowly or widely, and it does not matter to us whether a zoom description or a gradient-setting description is used.
As will be discussed, attention cannot be spread infinitely thinly but is limited to about 3 to 5 chunks of information (Cowan, 2001). It may be that the people who are good at locking attention onto a goal during adversity are the same ones who are good at zooming attention out to apprehend the maximal number of items, or who have the widest attentional focus. If either of these possibilities is true, there should be a strong relation between attentional control and the measured scope of attention. If one assumes that storage-and-processing measures are useful because they tap into attentional control, these measures therefore still should correlate with measures of the scope of attention.
Cowan (1995) reviewed literature suggesting that the scope of attention does not rely primarily upon frontal lobe mechanisms as the control of attention does but, rather, upon parietal lobe mechanisms. Although this distinction is not clean and absolute, frontal lobe damage often results in dysfunctions of the central executive control of attention, whereas parietal lobe damage more often results in dysfunctions of consciousness, such as unilateral neglect and anosognosia (in which an individual shows no sign of awareness of an ostensibly obvious disability, such as paralysis of a limb). Ruchkin, Grafman, Cameron, and Berndt (2003) summarized physiological evidence leading to the idea that the frontal region does not contain the information in WM directly but contains pointers to that information in more posterior regions of the cortex, potentially reinforcing the notion of a difference between a frontal control mechanism and a posterior seat of attention.
It is an open question whether the integrity of the frontal and parietal portions of the attentional system are distinct or whether they function as an integrated system, such that their levels of functioning are strongly correlated among normal individuals. It is also an open question whether individual differences in the measured scope of attention are due primarily to differences in the parietal mechanisms and to an intrinsic limit in the scope of attention, or due primarily to differences in frontal mechanisms and executive control needed to adjust (zoom in or out, and aim) the scope of attention. An unnecessarily zoomed-in focus when there is relatively little interference to be handled would decrease the apparent scope of an individual's attention in the task. The present correlational investigation does not attempt to resolve these ultimate questions, but it provides an empirical background to investigate them by documenting the relation between WM tasks with very different formats, including scope-of-attention measures that do not include a dual task but, nevertheless, correlate well with aptitude measures.
Measuring the Scope of Attention
A critical question is how to measure the scope of attention. Cowan (2001) conceived of this measure as the result of a limited-capacity attentional focus extracting chunks of information from a field of activated features in memory in order to allow an explicit memory response. The form of the activated features could include sensory, phonological, orthographic, visuospatial, semantic, or lexical features held outside of the focus of attention. (Note that common terminology often refers to “automatically activated” memory as synonymous with “passively held” memory.) The act of attending to representations within this activated memory presumably results in the construction of object representations in the focus of attention (cf. Kahneman, Treisman, & Gibbs, 1992). It is the number of objects or chunks that can be extracted and held at one time in the focus of attention that we hope to measure.
There are assumptions that must be met before it can be assumed that this use of attention during retrieval will provide a meaningful measure of the scope of attention. It must be assumed (1) that the objects or chunks of information recalled are identifiable, (2) that the activation of features persists long enough for the maximal extraction of information into the focus of attention, and (3) that the focus of attention does not engage in multiple cycles of retrieval-and-recall from the field of activated features on one trial. We will discuss each of these assumptions in turn, and then show how they apply to tasks that will be used in the present study.
Assumption 1: Identifiability of Chunks
Multiple uses of attention in memory tasks
Attention is potentially involved in the reception, maintenance, and retrieval of information. During reception and maintenance, it might be used to recode the items so as to convert them to a smaller number of separate chunks of information. If one receives the digit list 1 3 8 2 4 6, for example, it might be rapidly recoded into the three two-digit numbers 13, 82, and 46 (cf. Miller, 1956). For that reason, Miller’s magical number seven cannot be taken as evidence that seven separate chunks of information are saved. Indeed, Miller does not appear to have intended to make that claim (Miller, 1989), despite the way his 1956 article has often been portrayed. Attention also is needed to initiate a rehearsal loop that preserves the information in a passive store, even if the rehearsal loop then proceeds automatically (cf. Baddeley, 1986).
Limiting the functioning of attention during encoding and maintenance
If we wish to examine how many chunks of information can be formed from the features in activated memory after they are retrieved into the focus of attention at the time of recall, it is necessary to know the nature of information in the activated memory record. Although it is possible to carry out a learning study to estimate how the items are grouped into chunks in serial recall (Cowan, Chen, & Rouder, 2004), a simpler method is to limit grouping and rehearsal processes during presentation and maintenance of the stimuli. Critically, if familiar items are presented and conditions at encoding and maintenance prevent grouping and rehearsal, then each item constitutes a separate chunk that can be retrieved into the focus of attention. (If the items were not sufficiently familiar, some items might be represented as multiple chunks; and if grouping and rehearsal were not prevented, multiple items might be grouped together to form a smaller number of chunks.) Grouping and at least the initiation of rehearsal presumably require attention (e.g., Guttentag, 1984; Naveh-Benjamin & Jonides, 1984) so, to limit grouping and rehearsal, attention must be diverted or thwarted.
Various procedures appearing to meet that requirement led to convergent estimates of about 4 items (i.e., chunks) recalled in adults, and fewer in children (Cowan, 2001; Cowan, Elliott, & Saults, 2002). It is beyond the scope of this article to review the many convergent procedures examined in these reviews but, later, the principles will be illustrated with three such tasks used in the present study. There are several ways in which the effects of attention during stimulus encoding and maintenance can be minimized (cf. Cowan, 2001), including diverting attention, making sequences rapid and unpredictable, and presenting a brief array of items.
Diverting attention
Attention can be diverted from the stimuli to be remembered during their presentation. The classic example of this is in tests of memory for the unattended channel in selective listening with dichotic presentation (e.g., Glucksberg & Cowen, 1970; Norman, 1969). The assumption is that a stream of sensory memory for the most recent events forms even for unattended stimuli, and that attention can be switched to the past few seconds of that sensory memory stream to allow the conversion of that information to a categorized form for recall (Broadbent, 1958).
Rapid and unpredictable presentation
A sequence of items can be presented too quickly for the items to be rehearsed or grouped. This is especially effective if the number of items to be presented is unpredictable, so that each item cannot be classified as occupying a certain slot within a known list structure. Although attention has not been diverted from the stimuli, it is ineffective at producing grouping or rehearsal. The classic example of this sort of technique is running memory span (Pollack et al., 1959), which will be analyzed at greater length shortly.
Spatial array
Last, a spatial array of information containing too many items to be apprehended at once can be presented. Perhaps the first such procedure was carried out by Jevons (1871), who picked up a small handful of beans and threw them on the table to be enumerated as quickly as possible. Using himself as the subject, he found that only a small number could be counted. A better-controlled example is the classic study by Sperling (1960), who presented an array of characters to be recalled. The main point of the study was to use partial-report cues to determine how much information persisted in sensory memory but, without a partial-report cue to enable attention at encoding, only about 4 items could be recalled.
Assumption 2: Persistence of Activation of Features
Although the scope of attention presumably limits how many chunks of information can be extracted from the activated memory field, or apprehended, at once, there is another important limit that must be considered. The activated memory record could fade before more information is drawn into the focus of attention. However, at least two types of findings argue against a limitation in the persistence of activated features as the source of the memory limit in procedures reviewed by Cowan (2001): constant capacity across different decay conditions, and insensitivity to stimulus-array duration. These will be described in turn.
Constant capacity across different decay conditions
In conditions in which the activated features are short-lived, it appears that the similarity in capacity limits has held up despite very different decay parameters. For example, whereas Sperling (1960) found that the benefit of a partial-report cue (which allows sensory memory to be used efficiently) was effective only up to a fraction of a second, Darwin, Turvey, and Crowder (1972) carried out a similar procedure with a spatio-temporal array of spoken digits and found that a partial report cue was effective up to about 4 s. Thus, decay of the relevant sensory memory trace was much slower in audition. Nevertheless, in both modalities, the whole-report limit was about 4 items. It might be possible to account for these results with a theory in which the auditory modality has both slower sensory decay than vision and, for some reason, commensurately slower retrieval of information from sensory memory. However, a simpler hypothesis is that retrieval into the focus of attention is fixed across modalities, at about 4 separate items in the typical, normal adult.
Insensitivity to stimulus array duration
Second, in several array procedures (e.g., Luck & Vogel, 1997; Sperling, 1960) the duration of the array has been varied from less than 100 ms to about a half second, with little or no change in the resulting memory limit. This seems inconsistent with the view that the cause of a limited capacity is insufficiency in the duration of the temporary memory record upon which attention is focused.
Assumption 3: Single Iteration of Retrieval
The third assumption has to do with retrieval from activated memory into the focus of attention. There is the theoretical possibility that the contents of attention are recalled, after which the participant's focus of attention returns to the activated memory field again for a second cycle of retrieval, or for multiple cycles. If this happened, then the memory response would have to be taken as an overestimate of the scope of attention. There are several arguments against this, and in favor of the suggestion that the focus of attention can consult activated memory only once. Theoretically, the act of recall may interfere with the activated-memory record (Cowan, Saults, Elliott, & Moreno, 2002), or there may be a phenomenon analogous to inhibition of return (Posner, Rafal, Choate, & Vaughan, 1985), which can occur not only for spatial locations but also for previously-attended objects (Tipper, Driver, & Weaver, 1991).
For unattended auditory sequences, the acoustic memory record persists for a number of seconds (Cowan et al., 1990, 2000; Darwin et al, 1972; Glucksberg & Cowen, 1970; Norman, 1969). If the focus of attention could repeatedly access that record, it would be difficult to explain the limit to about 4 items recalled from unattended lists (Cowan, 2001; Cowan et al., 1999). Also, some procedures include a cue to examine only one object within the memory record of an array (e.g., Luck & Vogel, 1997) or list (Cowan, Johnson, & Saults, in press), yet a similar capacity limit of about 4 items is obtained.
Finally, in procedures in which recall is from the long-term memory record, so that the memory representation does not decay, we see that the pattern of recall looks different than when recall is from a short-term record. Recall from a long-term memory record includes much more than the 4-chunk limit, though they appear in bursts of about 4. This is the case in recall from a semantic category (Broadbrent, 1975; Graesser & Mander, 1978), from a sequence of digits memorized by a mnemonic expert (Wilding, 2001), and from chess boards that remain present while they are copied (Gobet & Simon, 2000). The present theoretical suggestion is that a single retrieval process occurs when retrieval is from an activated memory field, whereas multiple retrievals can occur when retrieval is from long-term memory, though both share the same capacity limit for each retrieval.
Analyses of Specific Scope-of-Attention Tasks
We argue that three tasks that will be used in Experiment 1 appear to conform to the requirements of good measures of the scope of attention. The first operates by diverting attention at the time of the presentation of items to be recalled; the second, by presenting these items at a rapid rate with an unpredictable endpoint; and the third, by presenting these items in a simultaneous array.
Memory for ignored speech
In a series of experiments (Cowan, Lichty, & Grove, 1990; Cowan, Nugent, Elliott, Ponomarev, & Saults, 1999; Cowan, Nugent, Elliott, & Saults, 2000) we have examined memory for spoken lists that were ignored while a silent, visual task requiring phonological processing was carried out. This sort of task serves the same purpose as memory for the ignored channel in selective listening (Glucksberg & Cowen, 1970; Norman, 1969) except that it avoids the problem of acoustic masking between channels. The finding in all of these studies was that there is a memory record of the ignored speech channel but that, in comparison to memory for attended speech, successful memory for ignored speech requires a shorter retention interval between presentation and test (≤2 s for maximum performance). Cowan et al. (1999) judged the capacity of memory with short test delays and found that it was about 3.5 items in adults, regardless of the list length, and smaller in children.
In the main procedure of Cowan et al. (1999), participants carried out a task in which the learned name of a picture in the center of the computer screen rhymed with the learned name of one of four peripheral pictures (to be selected with a mouse click, followed by a new central picture to be judged). Meanwhile, lists of spoken digits were to be ignored. No response was required for most such lists but, once a minute or so, the rhyming game was replaced by a digit-recall response screen shortly after the onset of the most recent list. By attracting attention to the sensory memory of the list only after it ended, rehearsal and grouping of the list during its presentation could be minimized and memory performance (recall of digits by keypress) presumably was based on the post-hoc conversion of items from an auditory sensory memory record into a categorical form in the focus of attention. Each digits was scored as correct only if it was recalled in the correct serial position, so memory of the binding between digits and serial positions in the list was required for correct responding.
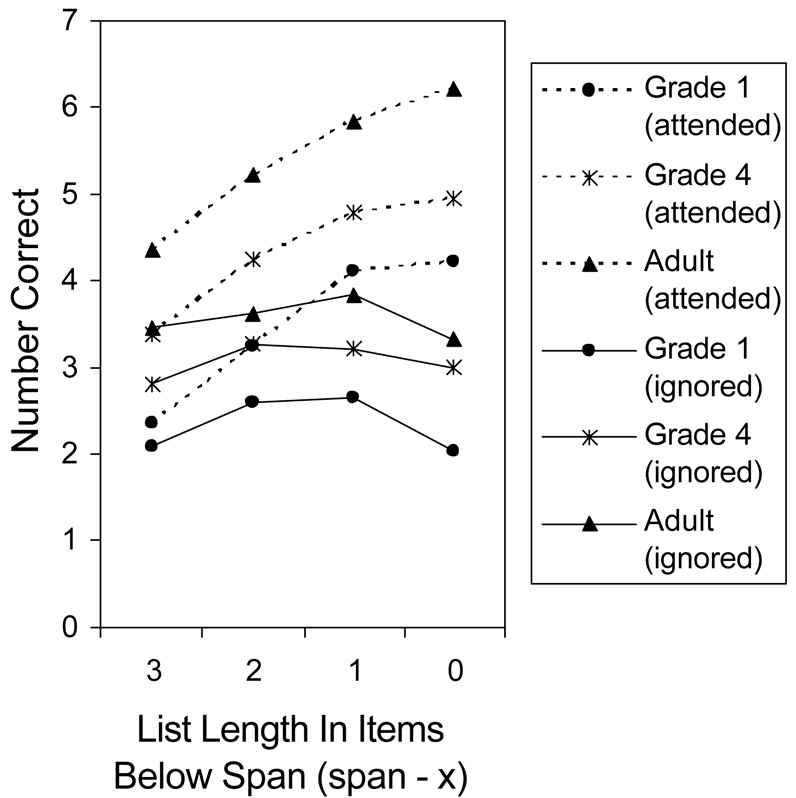
The digit list length was individually adjusted and four list lengths per individual were used: a length equal to the participant's predetermined digit span (using attended lists), and lists 1, 2, or 3 digits shorter than that. The main results of that study, reproduced in Figure 1, shows that the capacity limit for ignored lists (solid lines) was fairly constant across list lengths and increased with age. A similar finding was obtained when individuals were compared at absolute list lengths, as opposed to lengths determined relative to span (not shown).
Figure 1.
Memory for ignored speech (solid lines) and attended speech (dashed lines) in three age groups (graph parameter) as a function of set size relative to a predetermined span (x axis). Redrawn from Cowan, Nugent, Elliott, Ponomarev, & Saults (1999).
At least two points must be established before it can be inferred that these solid lines reflect the scope of attention at the time that the recall cue is presented: first, that the limit in the recall of ignored information is not a result of residual attention to the list during its presentation and, second, that the limit is not a result of a sensory memory deficit. Control conditions and experiments establish both of these points. Regarding residual attention, there was a control condition in which there was no rhyming task and the digit lists were attended (Figure 1, dashed lines). In contrast to the ignored-speech condition, it can be seen that the number correct did not remain constant across list lengths, but grew with list length. The stark difference from the results of the ignored-speech condition indicate a clear signature of attention during stimulus presentation in this task. In control conditions in which the visual task was to be carried out alone, just before and just after the ignored-speech task, performance closely matched the level on the same task in the presence of speech to be ignored. There were no tradeoffs between the visual and auditory tasks; no indication that individuals scoring better on memory for ignored speech did worse on the rhyming task, nor any indication within participants of better speech memory on trials with poorer rhyming-task performance (see Cowan et al., 2002). It would be difficult to attend to the boring and repetitive spoken lists, most of which require no response, during the more interesting rhyming game, because of habituation of orienting to the sounds (e.g., Sokolov, 1963; Cowan, 1988).
Second, the suggestion that sensory memory decay might have been the limiting factor does not agree with the findings from the short test delays that Cowan et al. (1999) used. Cowan et al. (1999, 2000) found pronounced bow-shaped serial position functions in memory for ignored speech, so sensory memory for even the early serial positions seemed to remain available at the time of list-recall testing. Cowan et al. (2000) examined the serial position effects across test delays and found severe forgetting of information from both the primacy and the recency portions of the list, in contrast to the stability of primacy effects across test delays that is found for attended lists (Jahnke, 1968). This finding reinforces the conclusion that sufficient sensory memory was available at short test delays so that performance limits were not due to sensory memory decay. Also, Cowan et al. (2000) found that, with the list length equal to a predetermined span for each individual, there was no overall age difference in the loss of information across test delays. (There was a difference at the final serial position but it was not enough to result in a significant age difference in list-wide decay.) In sum, there appears to be a constant capacity for digits within ignored lists; the capacity appears to be related to the scope of attention when it is focused on the sensory memory record of the list, as opposed to sensory memory decay; and this capacity changes with development during childhood.
Running memory span
In running memory span (Pollack et al., 1959), participants receive many verbal items in a list that ends at an unpredictable point, whereupon the items at the end of the list are to be recalled. One might think that running memory span possibly could be carried out through a very active process in which the participant retains the most recent k items and continually updates the retained set by dropping the least-recent item to make room for the newest item. Given that serial order recall is required, the relative serial positions of the items in the retained set would have to be continually updated, also. According to an alternative proposal, though, participants wait passively until the list ends and then retrieve items from the automatically activated memory stream (e.g., from sensory memory).
Two studies greatly strengthen the latter interpretation when the items are presented quickly. First, Mayes (1988) provided evidence that it is reasonable to believe that sensory information can persist for a sufficient duration in this task. He presented lists of spoken or printed digits at a rate of 900 ms/digit in a running span procedure. An advantage for spoken digits over printed digits was obtained at each of the last 7 serial positions, which suggests the presence of an auditory-modality-specific memory code at these positions (for discussion of modality effects see Nairne, 1990; Penney, 1989).
Second, Hockey (1973) gave participants instructions to process the running-span stimuli either in a passive manner (a request that was further elaborated), or in an active manner, with instructions to "Concentrate on the items as they arrive, trying to form them into groups of three" using a rhythmic type of rehearsal. The digits were recorded and presented at rates of 1, 2, and 3 digits per second. The outcome was a very clear crossover interaction of presentation rate and strategy. At slower rates, an active strategy was advantageous whereas, at faster rates, a passive strategy became advantageous. At the fastest rate across 10 serial positions, there was about a 0.3-to 0.4-item advantage for a passive strategy over an active strategy. In our experiments we have used digitally compressed speech to achieve a rate of 4 digits per second so that an active strategy cannot be used to advantage. Although attention is directed to the list during its presentation, it is rendered ineffective in producing rehearsal or grouping, so that the results are functionally equivalent to memory for ignored speech.
Visual-array comparisons
The visual array comparison task of Luck and Vogel (1997), like the task of Sperling (1960), presents a simultaneous array of objects to be remembered on every trial, typically too many to be combined into a smaller number of groups in the time available. Unlike the other tasks we have examined, and unlike Sperling's task, it is designed in such a way that there is only one response to be made on every trial, avoiding the possibility of output interference. On every trial in the condition that we use, an array of colored squares was presented briefly, followed after an inter-stimulus interval by a second array similar to the first. One square in the second array was encircled (from the onset of that array) and, if the arrays differed at all, it was in the color of the encircled square. The task was to indicate whether the arrays were the same or different. A color could be used more than once in an array so that the location of colors, and not merely their inclusion or omission from the array, had to be remembered for successful performance. Performance fell off as a function of the number of squares in the array above 3 or 4.
A simple model of performance (Cowan, 2001) can be used to estimate how many of the squares from the first array were held in WM. The model is explained in detail in Appendix A. The basic idea is that, if the participant recalls the color of the square in the first array that was at the location corresponding to the encircled square in the second array, then he or she answers correctly; otherwise, he or she guesses. This measure provides capacity estimates in the same range as a wide variety of other tasks reviewed by Cowan (2001) and is fairly constant across array set sizes above the capacity limit of 3 to 4 items.
Presumably, the arrays are presented too briefly for participants to encode items verbally and recall them as a list (e.g., top-left-blue, middle-green, and so on). We believe that participants must extract information from a visuospatial record into the focus of attention before the presentation of the second array (see Cowan, 2001). There are several relevant findings. Luck and Vogel (1997) found no effect of a 2-digit memory load on visual-array comparison performance. Morey and Cowan (2004) replicated that effect using 2-digit loads repeatedly spoken aloud, and also found no effect of overt, repeated recitation of the participant's own 7-digit telephone number during the visual-arrays task. Presumably, then, memory of the squares is not assisted by a verbal rehearsal process. Morey and Cowan found that recitation of a random 7-digit memory load did impair performance, presumably because that task taxes attention.
Cocchini et al. (2002) carried out another experiment in which, in some conditions, a visual task was combined with an auditory memory load. Unlike Morey and Cowan (2004), Cocchini et al. suggested that their data could be explained without reference to a cross-domain resource. As in Morey and Cowan, there were conditions in which verbal stimuli were presented before nonverbal stimuli and tested after the nonverbal stimuli, so that the verbal stimuli served as a memory load. It was emphasized that only a small effect of load was obtained. However, performance on the verbal memory load was 80% to 90% correct in these conditions. In contrast, in Morey and Cowan (2004), the verbal memory load was repeated correctly on only 45% of the trials, a much more difficult load. This may account for the difference in effects of the load in the two studies.
It might still be theoretically possible that the verbal and nonverbal tasks of Morey and Cowan (2004) share some mechanism other than attention. It presumably could not be verbal rehearsal because a great deal of research on articulatory suppression (see Baddeley, 1986) indicates that recitation of the verbal digit load should prevent the application of verbal rehearsal to the visual arrays. It theoretically could be a visuospatial form of rehearsal. Logie, Della Sala, and Wynn (2000) found that visual codes play a role in verbal recall. However, they used visual stimuli whereas Morey and Cowan used spoken stimuli for the digit load. Moreover, Stevanovski and Jolicoeur (2003) found considerable interference in a similar procedure with a simple tone-discrimination task between arrays. It is difficult to explain this effect on the basis of a shared visuospatial rehearsal component (presumably absent from tone discrimination), so it does appear likely that the visual array comparisons depend to some extent on retention of visual items in the focus of attention during the inter-array interval.
Recent neurophysiological studies with similar visual array comparison tasks strengthen the assumption that they rely on a capacity-limited, categorized memory for objects in the array. Vogel and Machizawa (2004) provided a cue to attend to colored squares on one side of the screen while ignoring those on the other side and used the extra event-related electrical activity on the side of the scalp contralateral to the attended field as an index of WM maintenance. This activity was found during the time between the first and second arrays and its magnitude matched the behavioral capacity limit. Like behavioral capacity, it increased up to a maximum of 3 to 4 items and then increased no more. The individual differences in electrical activity (measured as the change in activity between trials with 2 vs. 4 items in the array) correlated with the behaviorally-measured capacity at r = .78. Todd and Marois (2004) measured fMRI and found that the visual array comparison task caused capacity-limited activity in two small brain areas, the intra-occipital and intra-parietal sulci, during the inter-array period. The activity increased as a function of array size only up to a limit of 3 to 4 items, which again matched the behavioral limit. (Other areas responded in a load-dependent manner but the relation to the behavioral limit was not as clear as for these areas.) The results suggest that the scope of attention in this task is limited not because of a failure of attentional control, but because of an inherent limitation in how many objects can be included in WM at once.
Simple spans and storage-and-processing spans as potential scope-of-attention measures
It is important to note that a theory of WM capacity limits based primarily on the scope of attention might be able to explain results from more traditional measures of WM, too. For simple spans, there is the expectation of developmental changes in this regard. For adults, individual differences in rehearsal and the concomitant grouping of items play a role that may mask the influence of individual differences in the scope of attention. However, for young children, who cannot engage in sophisticated rehearsal strategies (Flavell et al., 1966), simple span tasks may well serve as adequate measures of the scope of attention.
The success of storage-and-processing spans may not be for exactly the presumed reason (e.g., Daneman & Carpenter, 1980). Instead, the critical point may be that the processing task prevents continual rehearsal and grouping of the information to be stored during the stimulus presentation. In this case, the items to be recalled must be retrieved as separate chunks (one per item) from the activated memory representation, into the focus of attention at the time of recall.
Overview of Studies
We completed two developmental experiments with a range of WM tasks and scholastic and intellectual aptitude tasks. The first experiment concentrated on WM tasks that have been tested before (although never in the same study) and a set of applied measures of scholastic ability. The second experiment provided further refinement; it concentrated on WM tasks modified to be more comparable to one another, and a set of verbal and nonverbal aptitude measures drawn from intelligence tests. The main issue is whether measures of WM designed to examine the scope of attention perform in a manner comparable to measures that involve storage and processing together, even though the scope-of-attention measures do not impose a simultaneous dual task. The scope-of-attention measures will be viewed as important even if they do not provide higher correlations with aptitudes than storage-and-processing measures, provided that they pick up much of the common variance of aptitude tasks without as much variance from specific skills that play a role in storage-and-processing spans, but are theoretically distinct from WM (e.g., language comprehension, arithmetic, and counting abilities).
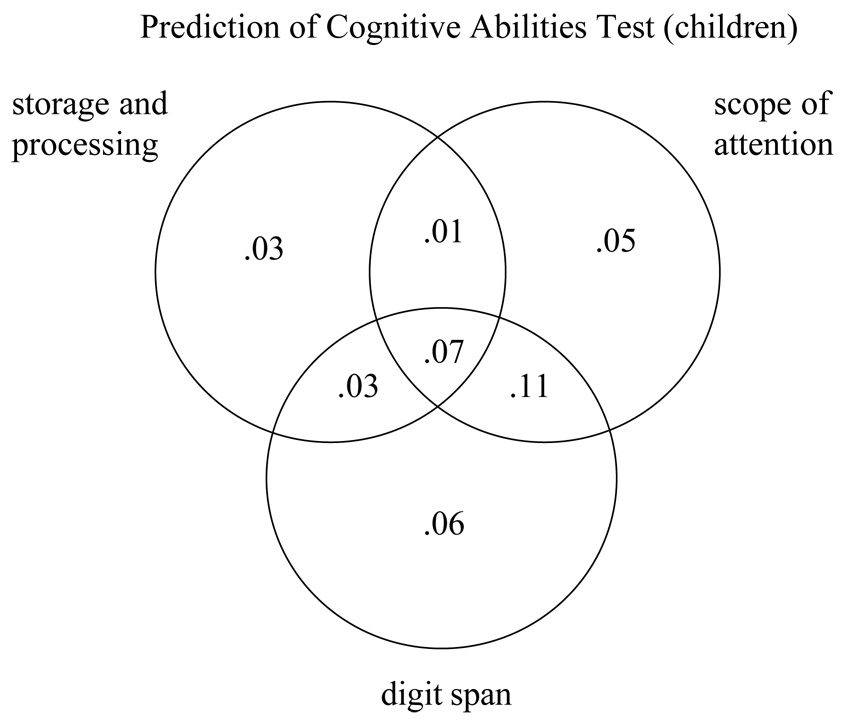
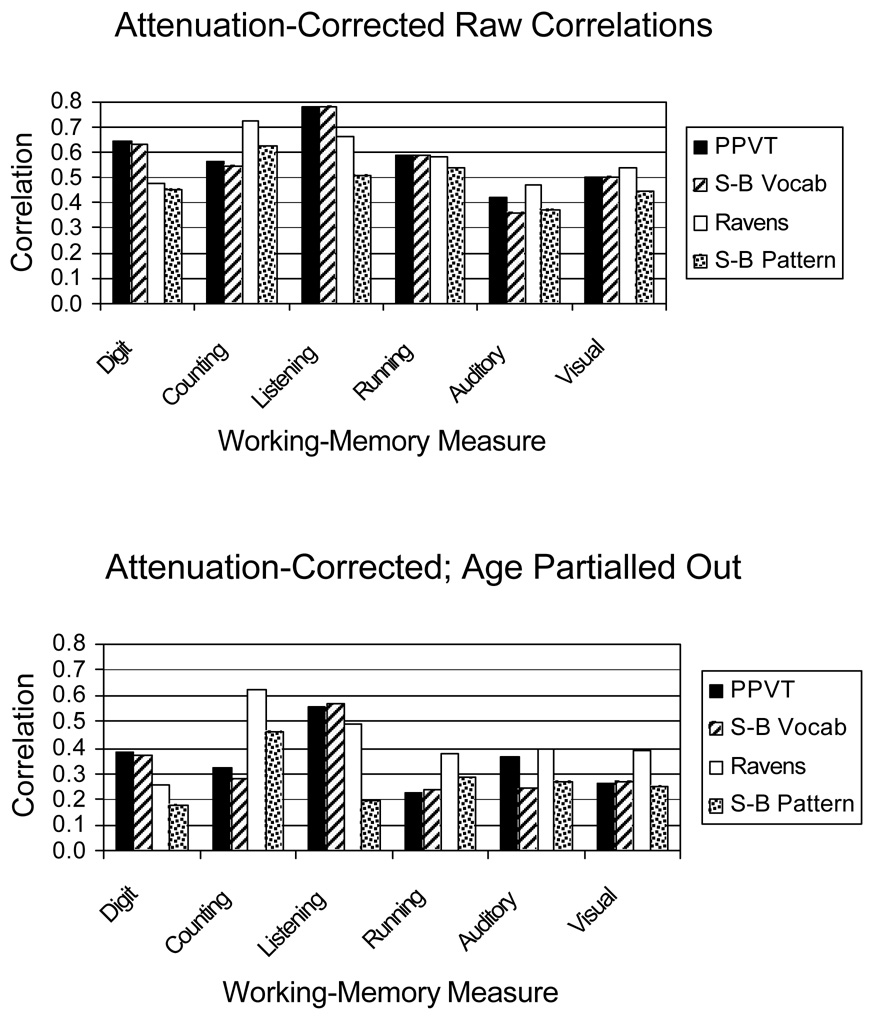
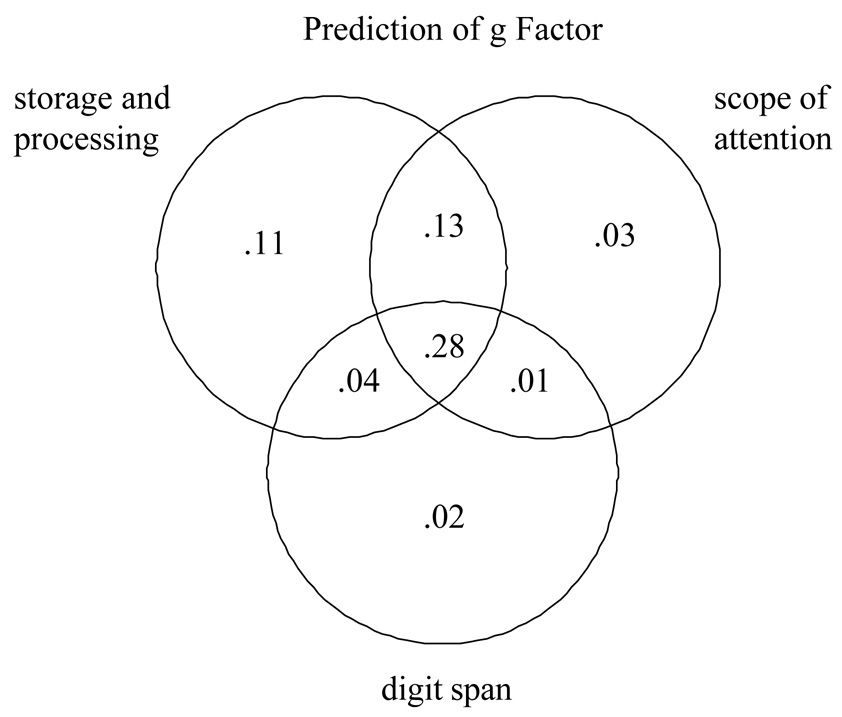
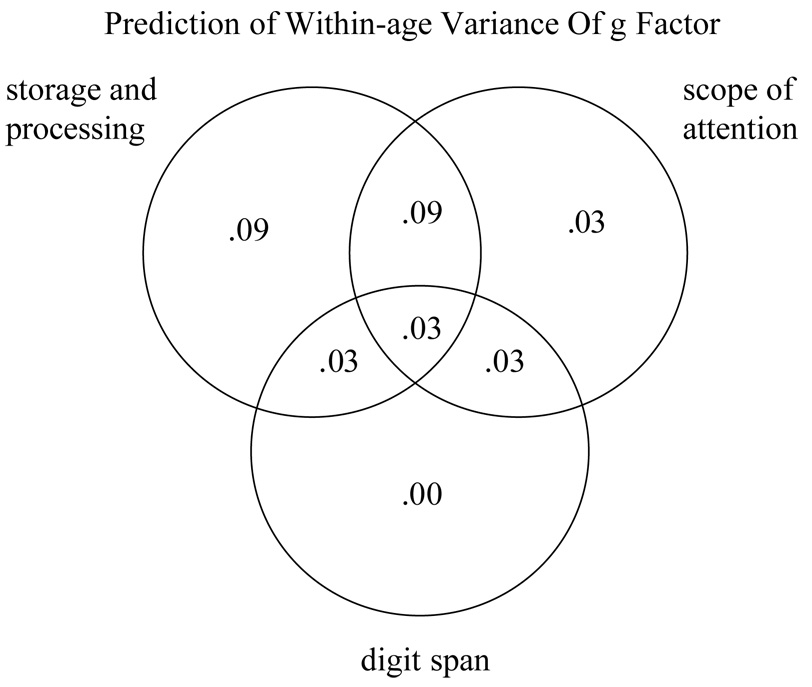
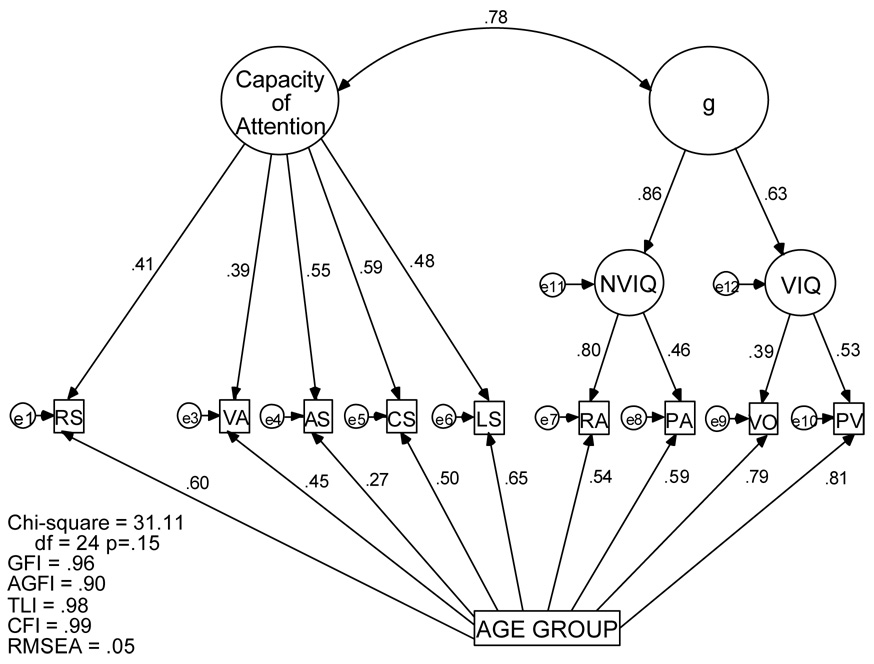
We used not only digit span, but also two storage-and-processing measures of WM (listening span and counting span) and four measures of the scope of attention (memory for ignored speech, in Experiment 1; running memory span, in both experiments; visual array comparisons, in both experiments; and a tone-sequence analogue to visual array comparisons, in Experiment 2). In Experiment 1, we used separate measures of aptitude in adults (high school grade percentiles and the American College Test, or ACT) and children (the Cognitive Abilities Test, or CAT). In Experiment 2, we used two verbal and two nonverbal intelligence measures: the vocabulary and pattern-analysis subtests of the Stanford-Binet intelligence scale (Thorndike, Hagen, & Sattler, 1986), the Peabody Picture Vocabulary Test (Dunn & Dunn, 1997), and Ravens' Progressive Matrices (Raven, Raven, & Court, 1998).
EXPERIMENT 1: APPLIED MEASURES OF APTITUDE AND WM CAPACITY
Our main expectations for the study are of three types.
Expectation 1: Predictive Value of Scope-of-Attention Tasks
Our basic expectation is that the storage-and-processing tasks and the scope-of-attention tasks should have much in common. Specifically, we expected (a) that these two types of tasks should correlate well, and (b) that the scope-of-attention procedures should capture general variance in aptitudes just about as well as storage-and-processing procedures. The expectation was that these outcomes would be obtained not only in raw correlations across age groups, but also in correlations with age-group variance removed.
Expectation 2: Task-Specific Additional Variance
We expected that additional variance on specific aptitude tests will be picked up by particular WM tasks based on what skills the two have in common. For example, listening span should correlate well with verbal aptitude measures, as both require linguistic skill. However, this skill variance should not be general across WM tasks. Thus, counting span does not require the same degree of linguistic skill as listening span, though it does require some arithmetic skill and, perhaps, spatial skill. To the extent that linguistic skill is needed in the aptitude test, there should be a unique relation between listening span and that aptitude. To the extent that certain other skills are needed in the aptitude test, there should be a unique relation between counting span and that aptitude. However, the basic expectation is that most of the variance that is shared between listening span and counting span will be shared with scope-of-attention tasks, as well.
Expectation 3: Measures of Aptitude and the Development of Rehearsal
We expected that, in participants of all ages, tasks that make it difficult to apply attention to improve encoding and maintenance processes (i.e., both storage-and-processing tasks and scope-of-attention tasks) would yield lower estimates of capacity than a task that readily permits attentive encoding, rehearsal, and grouping (digit span). However, we already know that children too young to rehearse still receive a considerable advantage from attending to a digit list as opposed to ignoring it (see Figure 1). There must be more elementary benefits of attention other than grouping and rehearsal, such as superior encoding of each item. Therefore, to determine the use of rehearsal and grouping strategies, one must look beyond the levels of performance, to the correlations between measures.
Although some rehearsal may begin at the age of 7 years (e.g., Flavell et al., 1966), rehearsal becomes markedly more cumulative and effective over the next few years, or about through fourth grade (cf. Ornstein & Naus, 1978). Without rehearsal, the digit span task should provide an estimate of the scope of attention in young children. Consequently, we expected that it should correlate with aptitudes just about as well as other WM spans in young children (in second through fourth grades), but not in older, sixth-grade children or in adults.
It may seem counter to this last prediction that Kail and Hall (2001) found that simple spans (for digits, letters, and words) did not provide as good a prediction of a criterion task as did more complex spans, including listening and reading span and a "least-number span" task in which multiple lists were presented and the lowest number in each list had to be identified and retained for subsequent recall. However, their criterion task was reading recognition and the children spanned the ages of 7 through 13 years, so the older children may differ from the younger ones in both reading and rehearsal skills. Also, much of the advantage for the storage-and-processing measures was found in the age effects. Table 1 of Kail and Hall can be used to calculate the correlations between span measures and reading recognition with age partialled out. These correlations demonstrate that the storage-and-processing tasks were not consistently more successful than the simple spans in accounting for within-age variance in reading recognition. (By our calculations, in Study 1 of Kail and Hall these correlations were, for letter and word spans, .17 and .27; for reading and listening spans, .30 and .25. In Study 2 they were, for digit and word spans, .34 and .20; for reading, listening, and least-number spans, .32, .29, and .31, respectively.) One would expect even less advantage for storage-and-processing WM tasks in the younger children examined separately. The issue clearly warrants re-examination with other aptitude tasks.
Table 1.
Experiment 1: Means and Standard Errors for Key Variables and Age Effects from ANOVAs
| Maximum | Grade 3 | Grade 5 | Adults | Age Effect | |||||
|---|---|---|---|---|---|---|---|---|---|
| Measure | Possible | Mean | SEM | Mean | SEM | Mean | SEM | F | ώ2 |
| WM Measures | |||||||||
| Digit Span | 9 | 4.61 | 0.13 | 4.98 | 0.14 | 6.79 | 0.14 | 75.35 | 0.52 |
| Counting Span | 5 | 2.81 | 0.13 | 3.40 | 0.12 | 3.62 | 0.08 | 14.86 | 0.17 |
| 6 | -- | -- | -- | -- | 3.86 | 0.10 | |||
| Listening Span | 5 | 2.00 | 0.12 | 2.70 | 0.15 | 3.50 | 0.12 | 36.29 | 0.34 |
| 6 | -- | -- | -- | -- | 3.70 | 0.14 | |||
| Running Span | 7 | 2.44 | 0.15 | 2.80 | 0.13 | 3.87 | 0.09 | 43.25 | 0.38 |
| Ignored Speech | 7 | 2.01 | 0.18 | 1.98 | 0.15 | 2.67 | 0.14 | 7.11 | 0.08 |
| Visual Arrays | 10 | 3.69 | 0.28 | 4.14 | 0.23 | 5.67 | 0.18 | 24.37 | 0.25 |
| Scholastic Ability Measures | |||||||||
| Cognitive Abilities Test (CAT) | |||||||||
| Composite | -- | 115.24 | 2.33 | 113.40 | 2.37 | -- | -- | -- | -- |
| Verbal | -- | 110.06 | 2.34 | 111.15 | 2.38 | -- | -- | -- | -- |
| Quantitative | -- | 112.27 | 2.39 | 112.31 | 2.15 | -- | -- | -- | -- |
| Nonverbal | -- | 116.09 | 2.38 | 113.28 | 2.42 | -- | -- | -- | -- |
| High School | |||||||||
| Grades Percentile | 100 | -- | -- | -- | -- | 77.11 | 2.50 | -- | -- |
| American College Test (ACT) | |||||||||
| Composite | -- | -- | -- | -- | -- | 25.11 | 0.54 | -- | -- |
| English | -- | -- | -- | -- | -- | 24.95 | 0.61 | -- | -- |
| Math | -- | -- | -- | -- | -- | 23.91 | 0.67 | -- | -- |
| Reading | -- | -- | -- | -- | -- | 26.74 | 0.65 | -- | -- |
| Science | -- | -- | -- | -- | -- | 24.12 | 0.59 | -- | -- |
Note. WM measures refer to maximum number correct (the number correct for the set size at which it was maximum). The total N (137) includes 37 third- graders, 37 sixth-graders, and 63 adults. For the CAT, N=33 third- graders and N=34 fifth-graders; and among adults, N=55 for grades percentile and N=57 for the ACT. F values were all significant at p < .001, and df = (2, 134) for measures with the full sample. ώ2 refers to partial omega squared, an estimate of the proportion of variance accounted for by the effect (Keppel, 1991).
Method
Participants
Only participants who attended two sessions and, in those sessions, completed all WM tests were included in the final sample. Those who did (N = 137) included 37 third-grade children (17 male, 20 female; mean age = 105.46 months, ranging from 97 to 121 months, SD = 5.36), 37 fifth-grade children (15 male, 22 female; mean age = 128.65 months, ranging from 119 to 143 months, SD = 5.85), and 63 adults (24 male, 39 female; mean age = 238.65 months, ranging from 217 to 512 months, SD = 41.06). An additional 7 third-graders, 7 fifth-graders, and 4 adults provided only partial data and were eliminated from the sample. All participants reported normal or corrected-to-normal vision (including color vision) and normal hearing. Children were recruited from the Columbia Public Schools system and received either $5 and a book for their participation, or $10. The adults were psychology students who received course credit.
Apparatus, Stimuli, and Procedure
The experimental sessions took place in sound-attenuated booths. A total of 7 tasks were administered over the two experimental sessions. Session 1 was about 1.5 hours in duration, and Session 2 lasted about 1 hour. Participants were given multiple opportunities for breaks throughout both sessions. Children were also rewarded with stickers at several points. Session 1 included (1) running memory span, (2) counting span, (3) listening span, and (4) visual array memory. Session 2 included (5, 6) two runs of a digit-span task (followed by a rapid-speaking task that will not be reported here) and, finally (7) a task involving memory for ignored speech. The tasks were programmed in the SuperCard language (Solutions Etcetera, Pollock Pines, CA) with the exception of the counting- and listening-span tasks, which were run on a personal computer using MEL version 2.0 (Schneider, 1988). Listening span was presented in a female voice, whereas all spoken digits were presented in a male voice.
Digit Span
This was a computerized version of the usual psychometric digit-span test, but with more trials per list length to increase the reliability. On each trial, a list of digits (selected from the set 1 – 9 randomly without replacement) was presented by computer through headphones at 68–70 dB(A), at a rate of one digit per second. The digits were recorded and presented at a normal rate, with each digit under 400 ms long. Each list was preceded by a yellow-bordered box with the word “READY” for 1 s. The list was accompanied by an empty, red-bordered box during presentation, and was followed by recall cues comprising a green-bordered box and a tone, occurring simultaneously and in pace with the list items. Each list was to be recalled aloud in the presented order. In Span Run 1 there were four 2-digit lists as practice and then test trials beginning at that same list length. There were four test trials presented at each list length and then the length increased by one item, a process that was repeated until the participant made an error on each of the four lists at a particular length, or until the maximum length of 9 items was reached. Run 2 followed the same procedure, but without practice trials.
Storage-an d-processing tasks
The version of the counting span task was adapted from Conway, Bottoms, Nysse, Haegerich, and Davis (unpublished), which was in turn modeled upon Case et al. (1982). The targets to be counted were dark blue circles, which were mixed with some dissimilar distractors (red squares and circles). Each screen included 3 to 9 targets, 1 to 5 circular distractors, and 1 to 9 square distractors, which varied independently. After several screens were presented and counted aloud by the participant, there was a signal to recall aloud the separate sums associated with all of the screens that had been presented, in the presented order. The signal was the printed word "RECALL" along with a 1000-Hz, 73-dB(A) tone. No specific sum was repeated more than once within a trial.
Participants progressed through the program by pressing the space bar when ready for the next phase of a trial. There were three practice trials with two screens each (i.e., List Length 2) and then three blocks of test trials. For children, each test trial block included one trial each at List Lengths 2, 3, 4, and 5, in that order. However, in pilot data, we learned that a higher list length was helpful in discriminating among adults, though it was discouraging to many children. Therefore, adults received blocks of trials including List Lengths 2, 3, 4, 5, and 6, and the List Length 6 trials were omitted whenever children and adults were to be compared statistically.
The version of the listening span task was adapted from a task by Kail and Hall (1999), which was in turn modeled after Daneman and Carpenter (1980). Spoken sentences were presented through speakers at 66 – 68 dB(A). The task was to listen to each sentence and determine if it was true or not. After responding "yes" (true) or "no" (false), the participant was to repeat the final word of the sentence and remember it for later. For example, one practice sentence was "A fox can drive a truck, " requiring the response "no, truck. " That sentence is typical in difficulty level (e.g., "a chicken lays eggs"; "you wear pants on your arms") and no sentence was used more than once. The recall cue was the same as in counting span and, when it was presented, the sentence-final words were to be recalled aloud in the order in which the sentences had been presented. Three two-sentence practice trials were followed by three blocks of test trials using the same list lengths and same number of trials as in counting span.
Scope-of-attention tasks
The running memory span task was a modification of one developed by Cohen and Heath (1990). The digits 1–9 were digitally recorded in a male voice and compressed to fit within a quarter-second time window, without a change in fundamental frequency, using the SoundEdit 16 program (Macromedia, Inc., San Francisco, CA). The resulting stimuli sounded clear and natural but a bit rapid, as in certain advertisements in which compressed speech is used. These digits were delivered by computer and played over headphones at 66–68 dB (A). Each trial was initiated by the participant’s keypress. One second later the word "READY" appeared for 2 s, after which a spoken list began. The list included 12 to 20 random, spoken digits (from the set 1 – 9) presented via computer at a rapid pace of four digits per second. The only restriction on randomization was that, throughout each list, a digit was never repeated within a moving window of consecutive digits whose size equaled the number of response boxes. When the digit list ended, it was replaced (270 – 280 ms after the last digit's onset) with a series of five, six, or seven response boxes to be filled in from left to right with digits, using the computer's number key pad.
There were two variants of the running-memory task for the older children and adults. However, pilot data indicated that Variant 1 was too difficult for the younger children, who therefore only completed Variant 2. In Variant 1, the instructions were to wait until the list ended and then try to recall (or guess) the last five, six, or seven digits from the end of the list (but in forward order), depending on the number of response boxes presented. This procedure began with five boxes, at which there were two practice trials followed by nine test trials. The same procedure was then repeated with six boxes, and then seven, for a total of 27 test trials. All of the boxes were to be filled on each trial. A response was scored correct only for a digit placed in the box indicating its correct serial position relative to the end of the list. The results were very similar to Variant 2 and will not be reported.
In Variant 2, which all participants received, the instructions were to wait until the list ended and then recall as many digits as possible from the end of the list (again in forward order). These digits could be typed into the boxes starting with the first box and ending with the last digit remembered or guessed. (The participant then typed zeros in the remaining boxes, given that zero never appeared in the stimulus list, as a way to advance the program to the next trial.) In the scoring procedure, the last non-zero item in the response was taken as the response for the final serial position, and credit was given only for digits recalled in the correct positions relative to that last one, whether or not any intervening digits in the response were the correct ones. This worked well, given that the most recent item was the one most often correct. For symmetry with Variant 1, the test began with seven response boxes, then six, and then five, with nine test trials per list length. Third-grade children began with two practice trials at each list length. As in Variant 1, in Variant 2 there were 27 test trials.
The visual array comparison task was adapted from Luck and Vogel (1997). On each trial, an array of solid-colored squares on a gray screen was followed by a second array that was identical to the first or differed in the color of one square. One square in the second array was encircled (from the onset of that array) and participants had been informed that, if any square's color had changed, it was that of the encircled square. They were to make a single key press indicating whether that square had changed or whether there had been no change.
On each trial, which was initiated by the participant when ready, a fixation cross was presented for 1 s and was followed by a presentation of the first array of squares for 250 ms. At an estimated viewing distance of 50 cm, the array fell within 9.8 degrees horizontal×7.3 degrees vertical visual angle of view. Squares were placed in this area at spatial locations that were determined randomly except that the minimum separation between squares (center to center) was 2.0 degrees and no square was located within 2.0 degrees of the center of the viewing area. Each square was 0.75×0.75 degrees in visual angle. The square colors were red, blue, violet, green, yellow, black, and white, and each square was assigned a color randomly with replacement (i.e., there was no restriction against the same color appearing more than once in the same array, a method that requires memory of the location of each color). The cue circle specifying the target square was black and 1 pixel thick, with a diameter of 1.5 degrees of visual angle. There was a 1-s gray screen (like the background of the arrays) between the offset of the first array and the onset of the second array. The participant answered by pressing one computer key to indicate that the color changed between arrays (the “/” key) and another key to indicate that it did not change (the “z” key). The second array remained on the screen until the response was made. Eight practice trials were followed by 128 test trials, including an equal number of trials with 4, 6, 8, or 10 squares per array, with set sizes randomly ordered across trials. Each trial ended with response feedback and participants were encouraged to take breaks between trials as needed.
The memory for ignored speech task examines memory for spoken digits when attention is presumably directed away from the digits until after their presentation ends, so that attention must then be used to retrieve unprocessed information from sensory memory. The procedure was very similar to that of Cowan et al. (1999). It included a sequence of task phases designed to train the participant, provide familiarization with the necessary stimuli, and assess the deployment of attention in the main phase of the task. Training included learning the labels of pictures of common items, to be used in several other phases.
In the main phase, participants carried out a silent game in which they had to indicate (with a mouse click) which of four peripheral pictures rhymed with a central picture, as quickly as possible, with the next rhyming-task trial beginning immediately after an answer was given to the previous one. The central picture kept changing whereas the peripheral pictures remained the same throughout each sequence leading to an auditory memory trial, and then changed as the rhyming game resumed. (At the onset of each such series, the four peripheral pictures were named aloud as they appeared on the screen one at a time, as a reminder of the correct labels.) Meanwhile, lists of digits were presented through headphones at a rate of 2 digits per second, at 55 dB(A). Most lists were to be ignored but occasionally the rhyming game was replaced by a recall probe, at which time the participant was to use the key pad to recall the last list of digits. Between 5 and 10 lists were presented, separated by 1- or 5-s silent intervals that were randomly ordered, before the recall probe was presented. This recall probe comprised a series of boxes, one for each digit in the last spoken list, that were to be filled in with digits. The task was to recall the digits from the last spoken list in the order in which they were presented. The instructions indicated that the digits should be ignored until the recall probe because they might prove to be distracting otherwise, and that the participant should then just make his or her "best guess" as to the identity of the digits. The last spoken list ended 1 or 5 s before the recall probe appeared. The 1-s retention interval provided the preferred index of how much ignored information can be pulled from the sensory memory stream into WM when attention is redirected to the digit stream, whereas the 5-s retention interval provided data on the rate of sensory memory loss over time. Replicating Cowan et al. (2000), there were no age differences in the list-wide rate of loss over time, and 5-s results will not be reported further. This main phase of the experiment included 6 trials with 5-digit lists and then 6 trials with 7-digit lists (for each list length, beginning with a 1-s retention interval and with the length of the retention intervals alternating between 1 and 5 s).
The number of digits in a list and the inter-list intervals and retention intervals differed from those of Cowan et al. (1999) but other aspects of the procedure were the same. The phases of the experiment and their purposes were as follows. (1) The participant was to type each digit upon hearing it so as to become familiar with the keypad. (2) The participant practiced recalling one 5-digit list and one 7-digit list immediately upon hearing it; there were no distracting stimuli. This was to provide familiarity with the spoken lists and their lengths. (3) The participant saw 14 sets of 5 pictures and simultaneously heard their names; with the members of each set all rhymed with one another (e.g., box, rocks, clocks, socks, fox). They then had to repeat the name of each picture successfully before the experiment could continue. (4) The silent rhyming game was practiced with no auditory stimuli until 6 correct matches were made. (5) The silent rhyming game was carried out with no auditory stimuli for 1 min. Reaction times were recorded. This serves as a pretest baseline against which one can compare performance on the rhyming game during spoken-digit presentations. (6) The main phase of the task, described above, was conducted, comprising 12 trials of memory for ignored spoken lists. (7) The silent rhyming game was carried out with no auditory stimuli for 1 min as a post-test baseline.
Task Scoring
The two versions of the running-span task in adults yielded roughly comparable results but the correlations with criterion measures were slightly higher for Version 2, the version that the children also received. Therefore, only that measure will be reported. Performance in that task was virtually identical across trials with 5, 6, or 7 response slots and the results were therefore collapsed across this variable.
In order to score all procedures in a manner that was as conceptually equivalent as possible and estimated capacity, two methods of span scoring were used. In one method (traditional span), for tasks that involved list recall with increasing list lengths, the participant's span was defined in the traditional manner, as the lowest list length at which at least 50% of the lists were recalled correctly. However, this was impossible for two of the measures of the scope of attention (ignored speech and running span) because no stimulus length produced 50% correct performance. For visual-array comparisons, which involved recognition, the span was defined as the smallest set size at which at least 75% of the responses were correct (i.e., half-way between chance and perfect performance).
A second method of scoring, maximal number correct, was available for all measures. We relied on the mean number of items correct within a list or set (for lists, the number of items recalled in the correct serial positions). Span was defined as the mean number correct at whatever list length or set size this mean number correct was maximal. For example, if a participant's mean number correct was 2.6 for 3-word lists, 3.2 for 4-word lists, and 3.0 for 5-word lists, span would be defined as 3.2. For the visual-array task, the number-correct calculation at each set size was based on a simple model of performance that corrects for guessing, as explained in Appendix A.
Results
Means and age effects, correlations, and regressions are discussed in turn with respect to the hypotheses under investigation.
Means and Age Effects
The means for WM measures yielded quite similar results for the two methods of scoring described above. The first method is reported in Appendix B. The second method of scoring involved the numerical estimate of the number correct or number of items in WM taken from whatever list length or set size produced the highest such estimate. These means are shown in Table 1, along with means for the aptitude measures. These means produced correlations that were generally slightly higher than those obtained for the first scoring method. Given the similarity in results with the two scoring methods and the greater methodological consistency between measures with the second method, it will be used in all subsequent descriptions. Table 1 also shows significant age effects for all WM measures.
Although most means matched expectations and were similar with the two scoring methods, a few discrepancies should be discussed. Although performance on visual-array comparisons was at the expected level using the 75% correct span measure, it was an item or so higher with the maximal measure. Further investigation indicated that this difference occurred because performance was quite variable from one set size to another within an individual. For example, in adults, the estimated mean capacity for 10- item arrays was 0.32 items fewer than for 8-item arrays, but the SD of that difference was 2.43 items, more than for the other measures. In future psychometric research with this procedure, it would be helpful to increase the number of trials per participant.
The ignored-speech average was about one item lower than in past research (cf. Table 1 and Figure 1). A possibly relevant difference in procedure is that the list length in the present procedure stayed fixed across trials in a block. Given that the process of retrieving items from an unattended auditory or phonological stream into a categorized form is quite difficult, there is room for proactive interference between trials (cf. Tehan & Humphreys, 1995), and that type of intrusion conceivably could be larger when there is a one-to-one correspondence between serial positions in the various lists because it could increase the structural similarity of the lists.
Figure 2 shows the means separately for each set size, for the third-grade children (top panel), fifth-grade children (middle panel), and adults (bottom panel). It includes data only for those set sizes and list lengths at which all participants in an age group were tested. It is clear from this figure that digit span increased beyond the range of the other measures. This is the first of several ways in which digit span can be distinguished from the measures in which it is not as easy to use attention to advantage during encoding.
Figure 2.
Experiment 1, mean number of items correct at each set size in each task (graph parameter) for third-grade children (top panel), fifth-grade children (middle panel), and adults (bottom panel). Values are included only for set sizes in which all participants produced data.
Separate 1-way ANOVAs were conducted within each age group on the six measures of WM. The effect was highly significant in each age group and planned comparisons indicated that, within each age group, the digit-span mean was significantly higher than the mean for each of the other five WM measures, p < .01 in each case.
Last, we considered that, in the visual-array comparison task, it might be easier to detect changes in color when the new color did not also appear elsewhere in the array. That required only the detection of a new color (similar to an extra-list feature; see Mewhort & Johns, 2000), not a new color/location combination. Research by Wheeler and Treisman (2002) confirms that the need to retain the binding between two different features increases difficulty in this sort of task. If this binding process develops with age in childhood, the difference between changes to a color that was versus was not unique in the array might be larger for younger participants. Capacity estimates were calculated separately using only trials in which the new color was or was not unique in the array, and using the same no-change control trials for the two sets of calculations. In an ANOVA of capacity estimates with age group as a between-participant factor and condition (change to a unique vs. non-unique color) as a within-participant factor, it was easier to detect a change to a unique color (M = 5.49, SEM = 0.15) than to a non-unique one (M = 4.03, SEM = 0.12), F(1, 134) = 159.27, MSE = 0.85, p < .01. However, the interaction of Age×Condition did not reach significance and was in the unexpected direction, with slightly larger differences in older participants.
Correlations
Table 2 shows the raw correlations between measures (below the diagonal), reliabilities of the measures calculated as Chronbach's Alpha across trial subsets (in bold, on the diagonal), and correlations with age group variance partialled out (above the diagonal). Age group based on year in school was used as a developmental variable in the correlations rather than age in months because of evidence that it is a stronger predictor of scholastic skills (Bentin, Hammer, & Cahan, 1991; Cahan & Cohen, 1989). It can be seen that the measures were fairly reliable and all of the correlations were significant. Clearly, as well, a large portion of the variance was age-group variance, given the lower levels of many of the correlations with age group partialled out.
Table 2.
Experiment 1, Correlations Between Measures of Working Memory
| DS | CS | LS | RS | IS | VA | |
|---|---|---|---|---|---|---|
| Digit Span (DS) | .94 | .21* | .48* | .63* | .61* | .29* |
| Counting Span (CS) | .43* | .63 | .37* | .27* | .26* | .19* |
| Listening Span (LS) | .69* | .52* | .83 | .32* | .37* | .29* |
| Running Span (RS) | .78* | .44* | .56* | .92 | .53* | .26* |
| Ignored Speech (IS) | .62* | .34* | .45* | .57* | .70 | .24* |
| Visual Arrays (VA) | .53* | .36* | .50* | .48* | .34* | .66 |
Note. N = 137. Correlations below the diagonal are raw; those above the diagonal are partial correlations with age group partialled out. For the visual arrays task, which the capacity estimate is according to Appendix A. Counting span and listening span are for List Lengths 2 through 5, and the other measures are based on all list lengths or set sizes, which all participants received. Ignored speech refers to the 1-s retention interval condition and running span refers to the “open” instructions. On the diagonals, in bold: reliability = Chronbach's Alpha.
p < .05
Table 3 shows the raw correlations among measures in adults, along with reliabilities of the measures (diagonal) and correlations corrected for attenuation, for which significance tests are unavailable. All of the WM measures correlated with the ACT composite scores except visualarray comparisons.
Table 3.
Experiment 1, Correlations Among Working-Memory and Scholastic Measures In Adults, and Reliability Estimates
| DS | CS | LS | RS | IS | VA | HG | AC | AE | AM | AR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Digit Span (DS) | .88 | .47 | .71 | .74 | .89 | .38 | .16 | .42 | |||
| Counting Span (CS) | .32* | .51 | .61 | .58 | .83 | .37 | .45 | .45 | |||
| Listening Span (LS) | .58* | .38* | .77 | .57 | .70 | .48 | .30 | .61 | |||
| Running Span (RS) | .65* | .39* | .47* | .86 | .67 | .32 | .38 | .40 | |||
| Ignored Speech (IS) | .68* | .48* | .50* | .51* | .66 | .45 | .38 | .48 | |||
| Visual Arrays (VA) | .27* | .19 | .31* | .22 | .27* | .55 | -.10 | .21 | |||
| High School Grades (HG) | .15 | .32* | .26 | .36* | .31* | -.08 | -- | .60 | |||
| ACT | |||||||||||
| Composite (AC) | .37* | .30* | .50* | .35* | .37* | .14 | .56* | .87 | |||
| English (AE) | .32* | .30* | .37* | .41* | .29* | .11 | .47* | .86* | |||
| Math (AM) | .41* | .35* | .51* | .32* | .40* | .21 | .48* | .86* | .72* | ||
| Reading (AR) | .32* | .03 | .33* | .24* | .24* | .04 | .50* | .89* | .56* | .54* | |
| Science (AS) | .15 | .26 | .44* | .13* | .27* | .13 | .50* | .89* | .64* | .72* | 67* |
Note. N=67 for spans, fewer for correlations with scholastic tests (see Table 1). Numbers along the diagonal (in bold, through AC only) are Chronbach’s Alpha measures of reliability. For the ACT, this was calculated by using the different subtests as repeated measures. Numbers below the diagonals are raw correlations. Numbers above the diagonal are correlations corrected for attenuation (no significance test available). The calculations using high school grades incorporate the assumption that these are perfectly reliable. Counting and listening span measures included List Length 6.
p < .05
Table 3 also shows that, for high school grades, the only significant correlations were with counting span (r = .32), running span (r = .36), and memory for ignored speech (r = .31). The different pattern of correlations with these two main scholastic criteria is intriguing. Two of the measures yielding relatively high correlations with the ACT (digit span, r = .37; listening span, r = .50) were not significantly correlated with high school grades (digit span, r = .15, n.s.; listening span, r = .26, n.s.). The only measures that correlated significantly with both of these practical scholastic criteria were counting span, running span, and memory for ignored speech, and perusal of the table shows that this was not the result of uniformly high reliabilities for these particular variables.
Table 4 shows correlations within children. Raw correlations are under the diagonal, which shows the reliabilities of the measures. The numbers shown above the diagonal were calculated by starting with attenuation-corrected correlations and partialling out the age effect to yield the best estimate of within-age relations. This table yields quite a different pattern than was obtained in the adults. The counting span, which had performed quite respectably in adults, was the only WM variable that was not significantly correlated with the CAT composite score (or any of the subscores). In contrast, the visual-array comparison task, which was not predictive in adults, was a good predictor in children. The highest correlations were obtained with digit span, which was only a mediocre predictor of aptitude in adults.
Table 4.
Experiment 1, Correlations Between Working-Memory and Scholastic Measures in Children, and Reliability Estimates
| DS | CS | LS | RS | IS | VA | CC | CV | CQ | |
|---|---|---|---|---|---|---|---|---|---|
| Digit Span (DS) | .88 | .41 | .51 | .68 | .67 | .36 | .64 | ||
| Counting Span (CS) | .35* | .66 | .64 | .35 | .23 | .37 | .24 | ||
| Listening Span (LS) | .44* | .48* | .75 | .32 | .31 | .42 | .53 | ||
| Running Span (RS) | .61* | .30* | .30* | .88 | .68 | .35 | .47 | ||
| Ignored Speech (IS) | .50* | .14 | .20 | .51* | .68 | .28 | .41 | ||
| Visual Arrays (VA) | .28* | .25* | .30* | .27* | .18 | .61 | .54 | ||
| CAT | |||||||||
| Composite | .52* | .15 | .37* | .38* | .31* | .38* | .84 | ||
| Verbal | .55* | .18 | .47* | .38* | .32* | .29* | .82* | ||
| Quantitative | .48* | .20 | .31* | .41* | .26* | .44* | .90* | .72* | |
| Nonverbal | .36* | .05 | .25* | .25* | .25* | .24* | .86* | .52* | .66* |
Note. N = 74 for capacity tests, fewer for the CAT (see Table 1). Numbers along the diagonal (in bold, through CC only) are Chronbach’s Alpha measures of reliability. For the CAT, this was calculated by using the different subtests as repeated measures. Numbers below the diagonals are raw correlations; numbers above the diagonal are correlations with age partialled out, based on raw correlations that have been corrected for attenuation (no significance test available).
p < .05
The visual-array capacity correlated with the CAT at about the same level when capacity was based on trials with changes to a unique color (r = .31) or a non-unique color (r = .38). In adults, neither measure correlated with high school grades or ACT composite scores.
Regression Analyses
One of the main hypotheses of the study was that storage-and-processing measures and scope-of-attention measures share substantial common variance in the prediction of scholastic abilities. Another was that predictive variance unique to the storage-and-processing measures will tend to reflect specific skills rather than WM capacity per se. Third, digit span should pick up more unique variance for children than for adults. This sort of question can be investigated by creating Venn diagrams of the portions of variance shared between three types of predictors (digit span, storage-and-processing measures, and scope-of-attention measures), shared between pairs of them, and unique to each type. This can be accomplished using a method of analysis described by Chuah and Maybery (1999), based on sets of six stepwise regressions. For a criterion variable and any three predictors A, B, and C, one needs stepwise regressions with the three variables entered in all six possible orders (ABC, ACB, BAC, BCA, CAB, CBA). One can find the unique contribution of A by finding the R2 value for a regression that includes A, B, and C and subtracting from it the R2 value for a regression that includes just B and C; the contribution shared between A and B can be determined by adding the R2 values for A and B when entered singly and subtracting from that sum the R2 value for A and B entered together; and so on, until all combinations are determined.
Table 5 shows sets of regressions carried out in the prediction of three criterion variables: ACT composite scores, high school grades, and (for children) CAT composite scores. The WM variables were entered into the regression individually, but with all variables of the same type in a single step. In the table, ΔR2 values for each step are shown along with statistical significance of these values. We also carried out regressions using factor scores for the storage-and-processing measures and the scope-of-attention measures, based on factor analyses yielding single-factor solutions. The outcome of those regressions (not shown) was very similar to those presented here, which have the advantage that they can be further decomposed, as will be seen.
Table 5.
Experiment 1, Increases in R2 for WM Measures in Stepwise Regressions Predicting Different Scholastic Indices
| Regression | College Students | Children | |||
|---|---|---|---|---|---|
| Step | Predictors | ACT | H.S. Grades | CAT | |
| 1 | Storage & Processing | .26** | .13* | .14** | |
| 2 | Digit Span | .00 | .00 | .17** | |
| 3 | Scope of Attention | .02* | .14* | .06 | |
| 2 | Scope of Attention | .02 | .09 | .16** | |
| 3 | Digit Span | .00 | .05 | .06* | |
| 1 | Scope of Attention | .18* | .18* | .24** | |
| 2 | Storage & Processing | .10* | .04 | .06 | |
| 3 | Digit Span | .00 | .05 | .06* | |
| 2 | Digit Span | .00 | .04 | .09** | |
| 3 | Storage & Processing | .10* | .04 | .04 | |
| 1 | Digit Span | .11* | .02 | .27** | |
| 2 | Storage & Processing | .15** | .11 | .04 | |
| 3 | Scope of Attention | .02* | .14* | .06 | |
| 2 | Scope of Attention | .07 | .20** | .06 | |
| 3 | Storage & Processing | .10* | .04 | .04 | |
Note. ACT = American College Test; CAT = Cognitive Abilities Test for children. CAT scores were calculated after variance from age group was partialled out but age group accounted for no variance because CAT scores were age-adjusted. WM measures of a particular type with multiple measures (storage-and-processing measures; scope-of-attention measures) were entered into the regression individually, in the same step.
p < .05
p < .01
Figure 3 shows the resulting diagram of variance in the prediction of ACT scores (adults). Overall, summing the portions of each circle, the proportion of ACT variance accounted for was .26 for storage-and-processing measures, .18 for scope-of-attention measures, and .11 for digit span; the lower value for digit span was to be expected given that rehearsal may obscure the use of attention in this task. The two largest portions of variance were those shared between all measures (.11) and those unique to the storage-and-processing measures (.10), with a somewhat smaller amount shared between storage-and-processing and scope-of-attention measures (.05).
Figure 3.
Experiment 1, prediction of ACT composite score in adults, conjointly by subsets of three types of WM variable. The diagram is based on regressions shown in Table 5. Numbers within the overlapping sections of the circles do not represent collinarity between the variables, but portions of ACT variance that are predicted in common by the WM variables shown as overlapping.
In keeping with one of our hypotheses, we asked whether the portion of ACT variance uniquely predicted by the storage-and-processing measures (.10) was general or reflected a specific skill. To investigate this question, we entered all WM measures into the regression in a single step except for one storage-and-processing measure, and then examined the ΔR2 value for the addition of the final measure. Examined in that way, listening span's unique contribution was critical, ΔR2 = .09, p < .05, whereas counting span contributed nothing and the shared variance between them accounted for only .01. The unique variance thus reflected some specific skill (e.g., language comprehension) and can be considered an impurity of this storage-and-processing measure, not a theoretical strength.
In the prediction of high school grades, the total variance predicted by the storage-and-processing measures was .13; by the scope-of-attention measures, .18; and by digit span, .02. We were unable to use the Venn diagram method because two negative areas were obtained. We therefore omitted the digit-span measure, which contributed nothing uniquely, and the resulting diagram is shown in Figure 4. The largest portions of variance were the one shared between measures (.09) and the one unique to the scope-of-attention measures (.09).
Figure 4.
Experiment 1, prediction of high school grades percentile in adults, conjointly by subsets of three types of WM variable. The diagram is based on regressions shown in Table 5. Numbers within the overlapping sections of the circles do not represent collinarity between the variables, but portions of high school grades variance that are predicted in common by the WM variables shown as overlapping.
A further analysis of the portion of high school grades variance uniquely predicted by scope-of-attention measures (.09) indicated that .06 of this variance was attributable uniquely to the two verbal measures (running span and ignored speech), .04 was unique to visual-array comparisons, and none was shared among all three. (The sum of .10 exceeded the obtained .09 due to rounding error.) However, the sum of these skill-specific variance components in this case did not reach statistical significance.
Figure 5 shows the distribution of variance for CAT composite scores in children. Overall, storage-and-processing tasks accounted for .14 of the variance, scope-of-attention tasks accounted for .24, and digit span accounted for .27. Thus, as predicted, digit span is much more predictive in children than it is in adults. A further examination shows that the largest portion was that shared between scope-of-attention tasks and digit span, though a substantial portion was shared between all of the tasks (.07).
Figure 5.
Experiment 1, prediction of within-age variance in CAT composite score in children, conjointly by subsets of three types of WM variable. The diagram is based on regressions shown in Table 5. Numbers within the overlapping sections of the circles do not represent collinarity between the variables, but portions of CAT variance that are predicted in common by the overlapping WM variables.
The relatively poor predictive quality of the storage-and-processing measures in children would not be expected based on past literature, though that literature is sparse in children. It is possible that the difficulty of the storage-and-processing tasks reduces their predictive quality relative to the other measures, which do not involve a simultaneous dual task. Yet, for that interpretation, it is puzzling that the storage-and-processing tasks and digit span are roughly comparable in variability, as Table 1 shows. Perhaps the ability to carry out a dual task is unrelated to either the theoretical scope of attention or to CAT scores, producing an irrelevant source of variance for storage-and-processing tasks in children.
Discussion
Means and Age Effects
The pattern of means and age effects in this study showed that all of the measures of WM increase with development but that digit span is higher than any other measure at every age group, as shown in Table 1 and Figure 2. The theoretical suggestion was that digit span is higher because there is no secondary task (as in the storage-and-processing spans) or built-in processing difficulty (as in scope-of-attention tasks) to interfere with the functioning of attention during reception of the list, including (but not limited to) rehearsal and grouping of items.
There is reason to believe that even the youngest children carry out some function of attention during presentation of the lists in digit span, though not rehearsal. They showed a superiority of digit span over other measures, as the older groups did. Recall that memory for attended speech surpasses memory for ignored speech in young children (Figure 1).
Our interpretation of the developmental pattern is that it has at least two components. One component is a developmental increase in the scope of attention, contributing to all of the WM measures. A second component is a developmental increase in the ability to use covert verbal rehearsal and grouping, improving the way in which digit span is carried out. This second component is not clear in the means, given some residual benefits of attention on digit span in young children. However, correlations and regressions (below) strongly support its existence.
Regressions and Correlations
Experiment 1 showed that, in predicting scholastic abilities in adults, there was considerable variance shared between storage-and-processing tasks, on one hand, and scope-of-attention tasks, on the other hand. Some of that shared variance was also shared with digit span (in the prediction of ACT scores), but some of it was not shared with digit span (in the prediction of high school grades, for which digit span was not predictive). It seems likely that the portion shared with digit span reflects a specific linguistic WM ability such as facility with phonological materials (Gathercole & Baddeley, 1993).
We propose that the portion of predictive variance shared between storage-and-processing measures and scope-of-attention measures reflects the scope of attention. Theoretically, it could contribute a great deal in both kinds of measures because both kinds prevent rehearsal and grouping during presentation of the list, in various ways explained in the introduction.
For children, digit span did strikingly well in predicting CAT scores; better than the other variables did and much better than digit span did in adults. This finding theoretically could be interpreted in at least two ways. First, rehearsal might be present in some children and not others, producing more variability in digit spans in children than in adults. However, that is not the case. In all children taken together, for maximal digit span SD = 0.83, whereas in adults, SD = 1.11. Second, as proposed above, the absence of effective rehearsal in children may make digit span a purer measure of the scope of attention than it is in adults.
EXPERIMENT 2: INTELLIGENCE MEASURES AND WM CAPACITY
A second experiment was conducted to overcome limitations in the first one. In Experiment 1, the scholastic measures could only be examined in children and adults separately and they were applied measures. In the second experiment, we included two measures of verbal ability, the Peabody Picture Vocabulary Test (PPVT: Dunn & Dunn, 1997) and the vocabulary subtest of the Stanford-Binet Intelligence Scales (Thorndike et al., 1986), and two measures of nonverbal ability, Raven's Progressive Matrices (Raven et al., 1998) and the pattern analysis subtest of the Stanford-Binet scales. These measures could be examined across all age groups.
We also changed the WM measures somewhat to address questions emerging from Experiment 1. One anomalous finding of Experiment 1 was that, among the measures of the capacity of attention, the visual-array task did not significantly correlate with scholastic measures in adults. We considered that it differs from the ignored-speech and running-span measures in two ways: (1) its memoranda are nonverbal rather than verbal in nature, and (2) they are presented visually and spatially rather than aurally and sequentially. To distinguish between these two factors, we included an auditory-sequential analogue to the visual-arrays task, using tone sequences. To make time for it and for the psychometric tests, we dropped the very time-consuming, ignored-speech task from the test battery. Also to make time, given the high reliability of the digit-span test, we carried out only a single run of digit span rather than the two runs carried out in Experiment 1. In the running-span task, the method was restricted to the one that had been used across ages in Experiment 1, i.e., Variant 2.
We also considered that, in Experiment 1, the digit-span and storage-and-processing span measures were collected with gradually increasing list lengths, whereas the capacity-of-attention measures were collected with set sizes either fixed within a block or mixed together. That could be important inasmuch as it has been shown that proactive interference grows as the span test continues (Lustig, May, & Hasher, 2001; May, Hasher, & Kane, 1999). The creation, rather than elimination, of proactive interference is theoretically desirable because the attention-related, capacity-limited WM mechanism appears to provide some immunity to proactive interference for a few items (Cowan et al., in press; Halford, Maybery, & Bain, 1988) so that, under high-interference conditions, the contributions of capacity-limited WM are presumably maximized. In Experiment 2, therefore, we altered the method of the visual array and auditory sequence tasks to be more like the other tasks. We started with small arrays and kept increasing the set size until the participant fell below 75% correct performance for a set size. In running memory span, no set-size manipulation was possible, give n that the hallmark of the procedure is unpredictable list length. However, this procedure is likely to produce a very high level of proactive interference from the large number of stimuli within each trial.
Last, we examined four age groups (not only three), yielding a widened age range, clear age trends, good estimates of within-age-group variance, and older children who could use rehearsal.
Method
Participants
Only participants who attended two sessions and, in those sessions, completed all WM tests were included in the final sample. Those who did (N = 127) included 29 second-grade children (12 male, 17 female; mean age = 99.52 months, ranging from 85 to 108 months, SD=4.97), 36 fourth-grade children (17 male, 19 female; mean age = 121.22 months, ranging from 103 to 133 months, SD=7.54), 33 sixth-grade children (20 male, 13 female; mean age = 143.00 months, ranging from 133 to 152 months, SD=5.81), and 29 adults (14 male, 15 female; mean age = 227.38 months, ranging from 217 to 255 months, SD=9.93). An additional 9 second-graders, 8 fourth-graders, 7 sixth-graders, and 3 adults provided only partial data and were omitted from the final sample.
Apparatus, Stimuli, and Procedure
All programming was accomplished using the Supercard program. The stimuli were the same as in Experiment 1 except for the addition of the auditory-sequence comparison procedure. Testing was conducted in two sessions, each lasting about 1.5 hours. In Session 1, tasks were carried out in the order: Stanford-Binet vocabulary and pattern analysis, visual arrays, auditory sequences, counting span, and listening span. In Session 2, on a different day, tasks were carried out in the order: PPVT, Raven's Standard Progressive Matrices, a rapid-speaking task that will not be described here, and running memory span. Incentives for participation included course credit for adults and a book plus $10 for children.
The digit-span task was as before except that only one span run was conducted, and with only three trials per list length instead of four. This change was made to save running time, given the extremely high reliability of digit span obtained in Experiment 2. The listening and counting span tasks involved the same materials as in Experiment 2 but the order of trials was changed to be more like the digit span. In particular, in each of these tasks, 2-item practice trials (two of them in counting span, three in listening span) were followed by three trials in a row at each list length, starting with 2-item lists and increasing until the participant failed to recall any of the three lists of a particular length correctly. In running span, the answer display always showed 6 slots and the Version 2 instructions of Experiment 1 were used. Three practice trials were followed by 27 test trials.
In the visual-arrays task, the procedure was the same as in Experiment 1 except for the selection of set sizes. Testing began with 4 practice trials with 2-item arrays. It then proceeded to 12 trials at that set size (6 with a change in color and 6 with no change). If the participant was correct on at least 9 of 12, testing proceeded to a set size one larger. When the 75% criterion was not met, a final set of 12 trials was conducted at the largest set size at which it had been met.
The auditory-sequences task was analogous to the visual-arrays task. However, the stimuli were series of sine wave tones, each 200-ms-long tones (constructed with 11-ms, linear onset and offset ramps). The tones were played one at a time with a stimulus onset-to-onset period of 400 ms. After the final tone in the first series presented on a trial, there was a 1-s silent period (with a fixation cross) and then a second tone series that was identical to the first or differed in the frequency of one tone. The tones used on a trial were drawn randomly from a set of 7, with frequencies of 500, 552.50, 610.51, 674.61, 745.44, 823.71, and 910.20 Hz (i.e., in 10.5% increments), played at 74 – 76 dB(A) over audiological headphones as measured by a sound level meter with an earphone coupler. No cue was presented to mark the tone that might have changed; although at most one tone changed between the two series on a trial, the task was to compare the entire first and second series and determine whether they were the same or different.
The psychometric tests were conducted in the age-appropriate manner stated in each of the test manuals. Two scorers independently added the test section scores and any discrepancies or problems in either administering the test or scoring it were discussed and resolved.
Despite minor differences from Experiment 1 in the way in which the data were collected, scoring of each WM measure in the present experiment was done in exactly the same manner as in Experiment 1. Auditory sequences, which were introduced only in Experiment 2, were scored in the same way as the visual arrays, using the capacity formula explained in Appendix A.
Results
Means and Age Effects
Table 6 shows the means and age effects in this experiment. The means for all measures are strikingly similar to those of Experiment 1. The added auditory-sequence-comparison procedure produced capacity estimates in keeping with the expectations of Cowan (2001), averaging between 3 and 4 items in adults and fewer in children. All age effects were significant; given that raw scores were used for the aptitude tests, the age effects for these were significant along with those for the WM tests. In this experiment, it is untenable to plot the capacities separately for each set size, given that testing for each participant stopped when performance fell under 75% correct and some participants ended at quite short set sizes.
Table 6.
Experiment 2, Means and Standard Errors of Key Variables in each Age Group and Age Effects from ANOVAs
| Grade 2 | Grade 4 | Grade 6 | Adult | Age | Effect | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Measure | Mean | SEM | Mean | SEM | Mean | SEM | Mean | SEM | F value | ώ2 |
| Working-Memory Measures | ||||||||||
| Digit Span | 4.70 | 0.16 | 4.94 | 0.11 | 5.37 | 0.14 | 6.43 | 0.22 | 22.09 | 0.33 |
| Counting Span | 2.75 | 0.19 | 3.81 | 0.15 | 4.05 | 0.19 | 4.46 | 0.16 | 16.11 | 0.26 |
| Listening Span | 1.74 | 0.10 | 2.29 | 0.09 | 2.68 | 0.12 | 3.33 | 0.15 | 31.04 | 0.42 |
| Running Span | 1.70 | 0.14 | 2.42 | 0.10 | 2.74 | 0.15 | 3.23 | 0.10 | 23.66 | 0.35 |
| Auditory Sequences | 2.83 | 0.24 | 3.33 | 0.20 | 3.99 | 0.26 | 3.74 | 0.22 | 4.53 | 0.08 |
| Visual Arrays | 3.40 | 0.25 | 4.65 | 0.25 | 4.84 | 0.26 | 5.77 | 0.33 | 11.54 | 0.20 |
| Scholastic Aptitude Measures | ||||||||||
| PPVT | 124.76 | 3.50 | 145.94 | 2.95 | 162.36 | 2.20 | 181.17 | 1.15 | 77.01 | 0.64 |
| S-B Vocabulary | 23.10 | 0.59 | 26.86 | 0.57 | 29.30 | 0.58 | 36.24 | 0.65 | 79.40 | 0.65 |
| Ravens Progressive Matrices | 31.03 | 1.83 | 38.39 | 1.26 | 41.79 | 1.38 | 46.03 | 1.41 | 17.30 | 0.28 |
| S-B Pattern Analysis | 27.03 | 1.21 | 34.75 | 1.04 | 36.42 | 0.93 | 39.72 | 0.72 | 26.54 | 0.38 |
Note. The total N (127) for all measures includes 29 in Grade 2, 36 in Grade 4, 33 in Grade 6, and 29 adults. F values all were significant at p<.05 or better with df = 3, 123. PPVT = Peabody Picture Vocabulary Test. Vocabulary and Pattern Analysis are subtests of the Stanford-Binet Intelligence Scales. ώ2 refers to partial omega squared, an estimate of the proportion of variance accounted for by the effect (Keppel, 1991).
As in Experiment 1, separate 1-way ANOVAs were conducted within each age group on the six measures of WM. The effect was highly significant in each age group and planned comparisons indicated that, within each age group, the digit-span mean was significantly higher than the mean for each of the other five WM measures, p < .01, with one exception. In fourth-grade children, the digit span and visual-array comparison means did not differ significantly.
As in Experiment 1, we examined capacity estimates from the visual-array comparison procedure based on just those trials in which the changes were to a color that was or was not already present in the array. The capacity was only marginally higher using changes to a unique color (M = 5.11, SEM = 0.17) than using changes to a non-unique color (M = 4.95, SEM = 0.14), F (3, 123) = 3.81, MSE = 0.39, p < .06. The interaction of age×condition did not approach significance, p > .1. A different result obtained for auditory arrays, for which the capacity was actually lower using changes to a unique tone (M = 4.03, SEM = 0.15) than to a non-unique tone (M = 4.32, SEM = 0.16), F(3, 123) = 9.10, MSE = 0.58, p < .01. The interaction with age group did not approach significance. The difference between patterns of performance for visual arrays versus auditory sequences was unanticipated, but it could be explained on the grounds that new repetitions in tones could be used to detect a change in pattern.
Correlations
Table 7 presents raw correlations, reliabilities of the measures and, above the diagonal, correlations corrected for attenuation. Notice that all measures were intercorrelated. Table 8 shows correlations after age-group variance was partialled out, reliabilities of the measures and, above the diagonal, age-partialled correlations based on attenuation-corrected raw correlations. Even with age partialled out, most WM measures correlated with most aptitudes (though there were exceptions). All WM measures were correlated with the most generally accepted measure of fluid intelligence, Ravens Progressive Matrices. Unlike any other WM measures, two of the three scope-of-attention measures (auditory-sequence and visual-array comparisons) were correlated with all four aptitude tests. Thus, there was no consistent advantage for storage-and-processing measures above those measures that do not include a dual task.
Table 7.
Experiment 2, Correlations Among Measures
| Measure | DS | CS | LS | RS | AS | VA | PP | VO | RM | PA |
|---|---|---|---|---|---|---|---|---|---|---|
| Digit Span (DS) | 0.89 | 0.54 | 0.68 | 0.70 | 0.50 | 0.31 | 0.64 | 0.63 | 0.48 | 0.45 |
| Counting Span (CS) | 0.47* | 0.87 | 0.70 | 0.65 | 0.50 | 0.43 | 0.57 | 0.54 | 0.72 | 0.62 |
| Listening Span (LS) | 0.60* | 0.60* | 0.86 | 0.67 | 0.51 | 0.57 | 0.78 | 0.78 | 0.66 | 0.50 |
| Running Span (RS) | 0.63* | 0.57* | 0.58* | 0.89 | 0.44 | 0.50 | 0.59 | 0.59 | 0.58 | 0.54 |
| Auditory Sequences (AS) | 0.45* | 0.44* | 0.45* | 0.40* | 0.91 | 0.40 | 0.42 | 0.35 | 0.47 | 0.37 |
| Visual Arrays (VA) | 0.28* | 0.38* | 0.51* | 0.45* | 0.36* | 0.91 | 0.50 | 0.50 | 0.53 | 0.44 |
| PPVT (PP) | 0.59* | 0.51* | 0.70* | 0.54* | 0.39* | 0.47* | 0.95 | 0.92 | 0.73 | 0.65 |
| S-B Vocabulary (VO) | 0.56* | 0.48* | 0.68* | 0.52* | 0.32* | 0.46* | 0.85* | 0.90 | 0.66 | 0.61 |
| Ravens (RM) | 0.42* | 0.63* | 0.58* | 0.51* | 0.42* | 0.48* | 0.67* | 0.59* | 0.88 | 0.75 |
| S-B Pattern Analysis (PA) | 0.41* | 0.56* | 0.45* | 0.49* | 0.34* | 0.41* | 0.61* | 0.56* | 0.68* | 0.93 |
Note. N = 127. Below the diagonal, raw correlations; above the diagonal, correlations corrected for attenuation (for which significance tests are unavailable). Scores on the diagonal (bold) are Chronbach's Alpha measures of reliability. PPVT = Peabody Picture Vocabulary Test, Ravens = Ravens Progressive Matrices. Pattern Analysis and Vocabulary are subtests of the Stanford-Binet Intelligence Scales.
p < .05
Table 8.
Experiment 2, Correlations Among Measures With Age Group Partialled Out
| Measure | DS | CS | LS | RS | AS | VA | PP | VO | RM | PA |
|---|---|---|---|---|---|---|---|---|---|---|
| Digit Span (DS) | 0.89 | 0.36 | 0.51 | 0.56 | 0.43 | 0.08 | 0.38 | 0.37 | 0.26 | 0.17 |
| Counting Span (CS) | 0.27* | 0.87 | 0.57 | 0.51 | 0.43 | 0.27 | 0.32 | 0.28 | 0.62 | 0.46 |
| Listening Span (LS) | 0.37* | 0.42* | 0.86 | 0.46 | 0.45 | 0.41 | 0.56 | 0.56 | 0.49 | 0.19 |
| Running Span (RS) | 0.44* | 0.40* | 0.32* | 0.89 | 0.37 | 0.32 | 0.23 | 0.23 | 0.38 | 0.29 |
| Auditory Sequences (AS) | 0.37* | 0.37* | 0.37* | 0.31* | 0.91 | 0.32 | 0.36 | 0.24 | 0.40 | 0.27 |
| Visual Arrays (VA) | 0.04 | 0.21* | 0.32* | 0.25* | 0.28* | 0.91 | 0.26 | 0.27 | 0.39 | 0.25 |
| PPVT (PP) | 0.28* | 0.22* | 0.39* | 0.13 | 0.31* | 0.20* | 0.95 | 0.78 | 0.60 | 0.36 |
| S-B Vocabulary (VO) | 0.24* | 0.16 | 0.36* | 0.10 | 0.18* | 0.18* | 0.57* | 0.90 | 0.46 | 0.29 |
| Ravens (RM) | 0.18* | 0.50* | 0.36* | 0.28* | 0.34* | 0.31* | 0.47* | 0.31* | 0.88 | 0.64 |
| S-B Pattern Analysis (PA) | 0.11 | 0.37* | 0.10 | 0.21* | 0.23* | 0.20* | 0.27* | 0.19* | 0.54* | 0.93 |
Note. N = 127. Below the diagonal, partial correlations with age partialled out; above the diagonal, partial correlations based upon attenuation-corrected scores (for which significance tests are unavailable). Scores on the diagonal (bold) are Chronbach's Alpha measures of reliability. PPVT = Peabody Picture Vocabulary Test. Pattern Analysis and Vocabulary are subtests of the Stanford-Binet Intelligence Scales.
p < .05
Another way to judge the validity of WM measures is to examine the profile of its correlations. Tests based on vocabulary necessarily examine crystallized intelligence (i.e., learning), whereas tests based on nonverbal patterns allow an examination of fluid intelligence that is to some degree less influenced by specific learning opportunities. For the theoretical construct of WM, it therefore could be considered problematic if the high success of a WM measure owes more to its correlations with vocabulary measures than it does to correlation with nonverbal measures.
Figure 6 shows the most theoretically meaningful profiles of correlations, which are those corrected for attenuation, including both the raw correlations (top panel) and those with age group variance partialled out (bottom panel). From these panels, the two measures that might be considered problematic are digit span and listening span. These measures appear to correlate more highly with vocabulary measures than with at least one of the nonverbal measures. For digit span, this may occur because of a reliance on phonological memory, which is instrumental in vocabulary acquisition (Baddeley, Gathercole, & Papagno, 1998). For listening span, it may occur not only for the same reason but also because of a more general linguistic influence; the sentences may be used as cues to recall of the sentence-final words (Cowan, Towse et al., 2003).
Figure 6.
Experiment 2, correlations between each WM variable and four aptitude tasks (Peabody Picture Vocabulary Test, Stanford-Binet Vocabulary subtest, Ravens Progressive Matrices, and Stanford-Binet Pattern Analysis subtest), based on attenuation-corrected raw correlations (top panel) and partial correlations, with age partialled out, based on attenuation-corrected scores (bottom panel).
Counting span is the measure with the highest correlation with nonverbal aptitude measures, although the three scope-of-attention tasks have the most even profiles across measures. Although it could be argued that there is no clear "winner, " this sort of examination provides a picture of some benefits and drawbacks of various WM measures, and it illustrates strengths of some measures that do not include separate storage and processing components.
Last, as in Experiment 1, there were no significant differences between the correlations resulting from visual-array capacities based on trials with changes to a unique versus a non-unique stimulus. The same was true of auditory sequences.
Regressions
Regression analyses were carried out in a manner comparable to Experiment 1. The main analyses are shown in Table 9. For simplicity, the criterion measure that was used was a g factor based on a factor analysis of the four aptitude scores (principal axis factoring), which yielded only a single factor that accounted for 66% of the total variance in these scores (Eigenvalue = 2.66). The factor loadings were, for the PPVT, .90; for the Stanford-Binet Vocabulary test, .84; for the Ravens, .77; and for Stanford-Binet Pattern Analysis, .73. The left-hand column of regressions is the prediction of g by WM measures, whereas the right-hand column is the prediction of g by WM measures age group variance is removed.
Table 9.
Experiment 2, Stepwise Regressions Predicting g From Three Types of WM Measure
| Targeted Variance | |||
|---|---|---|---|
| Step | Predictors | g | within-age portion of g |
| 0 | age group | -- | .66** |
| 1 | storage and processing | .56** | .08** |
| 2 | scope of attention | .04** | .02 |
| 3 | digit span | .02* | .00 |
| 2 | digit span | .03** | .00 |
| 3 | scope of attention | .03* | .01 |
| 1 | scope of attention | .45** | .06** |
| 2 | digit span | .06** | .01 |
| 3 | storage and processing | .10** | .03** |
| 2 | storage and processing | .15** | .03** |
| 3 | digit span | .02* | .00 |
| 1 | digit span | .35** | .03** |
| 2 | storage and processing | .24** | .06** |
| 3 | scope of attention | .03* | .01 |
| 2 | scope of attention | .17** | .04** |
| 3 | storage and processing | .10** | .03** |
Note. The g factor was based on all four intelligence measures. Factor analysis with principal axis factoring produced a one- factor solution and factor scores were used in the regressions. Among WM measures, storage-and-processing measures include counting and listening spans; scope-of-attention measures include running span, auditory sequences, and visual arrays. All measures of a type were entered into the analysis in a single step; very similar results were obtained in regressions using factor scores for storage-and-processing and scope-of-attention measures.
p < .05.
p < .01
The results of the analyses have been synthesized into Figure 7 and Figure 8. Figure 7 shows that the largest portion of variance in g (.28) was shared between all three types of WM measures. However, there also was a fairly large portion shared only between the storage-and-processing and scope-of-attention measures (.13), providing support for the present theoretical approach in which these two types of measures generally provide good estimates of the scope of attention, relatively free of verbal rehearsal processes that play such a large role in digit span. There also was a fairly large portion of variance in g unique to the storage-and-processing measures (.11).
Figure 7.
Experiment 2, prediction of g score based on four aptitude tests (Peabody Picture Vocabulary Test, Stanford-Binet Vocabulary subtest, Ravens Progressive Matrices, and Stanford-Binet Pattern Analysis subtest), conjointly by subsets of three types of WM variable. The diagram is based on regressions shown in Table 9. Numbers within the overlapping sections of the circles do not represent collinarity between the variables, but portions of g variance that are predicted in common by the WM variables shown as overlapping.
Figure 8.
Experiment 2, prediction of within-age-group variance in g score (with age-group variance removed) based on four aptitude tests (Peabody Picture Vocabulary Test, Stanford-Binet Vocabulary subtest, Ravens Progressive Matrices, and Stanford-Binet Pattern Analysis subtest), conjointly by subsets of three types of WM variable. The diagram is based on regressions shown in Table 9. Numbers within the overlapping sections of the circles do not represent collinarity between the variables, but portions of within-age-group g variance that are predicted in common by the WM variables shown as overlapping.
The distribution of within-age variance, shown in Figure 8, removes age-related changes in skills. From this figure, one can see that the role of digit span was greatly diminished when age-related variance was not included. The two largest proportions of within-age variance in g were those shared between storage-and-processing tasks and scope-of-attention tasks (.09) and unique to storage-and-processing tasks (.09). Only a third of the shared variance was common to both the listening and counting span tasks, suggesting that two thirds of it could reflect individual differences in specific skills, such as auditory processing for listening span and visual processing for counting span.
Structural Equation Model
Last, in order to verify that the concept of a single attentional construct is a reasonable one, a structural equation model is presented in Figure 9. This model groups together all of the measures of the scope of attention and the storage-and-processing tasks, as both types are said to provide an index to an attentional resource labeled the capacity of attention. There is a strong relation between this capacity and the g factor derived from verbal and nonverbal intelligence measures. The non-significant chi-square and fit statistics indicate a good fit. There was no significant gain from including separate scope-of-attention and storage-and-processing latent variables (chi-square = 30.38 with df = 22). As expected, adding digit spans to the model made it no longer fit (chi-square = 55.75 with df = 32, p < .01). This was expected because digit span is not a good measure of capacity in participants old enough to rehearse. The model shown above is consistent with the idea that storage-and-processing and scope-of-attention measures essentially measure the same construct, presumably the capacity or scope of attention.
Figure 9.
Structural equation model of performance in Experiment 2. Measures: RS = running span, VA = visual arrays, AS = auditory sequences, CS = counting span, LS = listening span, RA = Ravens Progressive Matrices, PA = Stanford-Binet pattern analysis, VO = Stanford-Binet vocabulary, PV = Peabody Picture Vocabulary Test, NVIQ = nonverbal IQ, VIQ = verbal IQ. Fit indices: GFI = goodness-of-fit index, AGFI = adjusted goodness-of-fit index, TLI = Tucker-Lewis index, CFI = comparative fit index, RMSEA = root mean square error of approximation.
Last, Table 10 illustrates the success of the theoretical expectation that digit span would be much more predictive of the within-age portion of g in children too young to rehearse efficiently than in older participants. To construct this table, one set of regressions was carried out on the two age groups considered too young to rehearse efficiently, the children in second and fourth grades. Another set of regressions was carried out on the sixth-grade children and adults, who presumably could rehearse more efficiently (e.g., Ornstein & Naus, 1978). In each case, age was first partialled out. The table shows that, although digit span was about as predictive as other types of WM measures of within-age-group variance in the younger subsample, it was of no predictive value for within-age-group variance in the older subsample. As in Experiment 1, this difference cannot be attributed to wider variation in scores (or in relevant abilities such as rehearsal) among the younger children. In the younger two groups combined, the digit span SD = 0.77 whereas, in the older two groups combined, SD = 1.12.
Table 10.
Experiment 2, Proportions of Within-Age Variance in g, By Types of WM Measure in Younger and Older Participants
| Measures | Grades 2 & 4 | Grade 6 & Adult |
|---|---|---|
| (n = 65) | (n = 62) | |
| Storage and Processing | 0.15* | 0.15* |
| Scope of Attention | 0.14* | 0.11* |
| Digit Span | 0.14* | 0.01 |
| All WM Measures | 0.24* | 0.17* |
Note. Storage-and-processing measures include counting and listening spans; scope-of-attention measures include running span, auditory sequences, and visual arrays. Within-age variance in g refers to a partial R2 after age group variance is removed.
Discussion
This experiment provides a comparison of three different types of WM measures in the prediction of verbal and nonverbal aptitudes. As in Experiment 1, it can be seen that scope-of-attention measures provide a reasonable alternative or supplement to storage-and-processing measures. Scope-of-attention measures do not provide the highest correlations with the aptitude measures; overall, storage-and-processing measures do. However, scope-of-attention measures were found to have certain advantages. First, it was only the nonverbal scope-of-attention measures that were found to correlate significantly with all four of the aptitude tests even when age- group variance was removed (Table 8). Second, the scope-of-attention measures tended to have an even profile across verbal and nonverbal aptitude measures (Figure 6). Third, they picked up considerable variance in common with the storage-and-processing measures (Figure 7 & Figure 8) without including as much unique predictive variance; and, given that two-thirds of the unique within-age variance in g provided by the storage-and-processing measures appeared to be due to specific skills rather than abilities shared between listening and counting spans, the scope-of-attention measures generally seem to provide purer measures of WM capacity than the storage-and-processing measures.
Digit span was shown to be predictive of aptitude in younger participants, but not in older ones. As in Experiment 1, this supports the notion that digit span provides an impure measure of WM capacity not specifically because it fails to include a dual task (as the scope-of-attention tasks do not include one, either), but because it allows covert verbal rehearsal and grouping of items. This rehearsal and grouping is presumably prevented in the other WM tasks by various imposed processing difficulties, as discussed in the introduction.
GENERAL DISCUSSION
There is now a considerable variety of studies in which relationships between different types of WM procedures and intellectual aptitudes, and their development, have been assessed (e.g., Ashcraft & Kirk, 2001; Booth, MacWhinney, & Harasaki, 2000; Caplan & Waters, 1999; Conway et al., 2002; Cowan et al., 2003; Daneman & Hannon, 2001; Daneman & Merikle, 1996; Engle et al., 1999; Fry & Hale, 1996; Gathercole & Pickering, 2000; Haarman, Davelaar, & Usher, 2003; Hedden & Park, 2003; Hitch et al., 2001; Hutton & Towse, 2001; Kyllonen & Christal, 1990; Lustig et al., 2001; Miyake, Friedman, Rettinger, Shah, & Hegarty, 2001; Oberauer et al., 2002; Salthouse, 1996; Swanson, 1996). Yet, there is not much agreement in the field as to the definition of WM, the best measures to examine it, or why these measures work (e.g., see the differences of opinion within the chapters of Miyake & Shah, 1999). The present study addresses these unknowns. What is unique about this study is the incorporation of measures designed or selected according to the theoretical view that it is possible to measure how many chunks of information can be held in the focus of attention at one time (Cowan, 2001). As discussed above, this is done essentially by overwhelming or distracting attention at the time that stimuli are presented, which means that items cannot be grouped together. Items then must be extracted from a passively maintained (i.e., “activated”) memory trace at the time of recall. If the items are familiar to begin with then the hope is that, at the time of recall, each item that is recalled was retrieved from the passive trace into the focus of attention as a single, separate chunk formed in the focus of attention. Cowan (2001) summarized many phenomena that appeared to meet these criteria and produced convergent capacity estimates. The proposal is that the relevant portion of the variance in the popular storage-and-processing measures (e.g., Daneman & Carpenter, 1980; Turner & Engle, 1989) also reflects this scope of attention.
Based on this proposal, three basic expectations were generated and will be evaluated in turn. They are (1) that scope-of-attention tasks will be predictive, i.e., will both correlate with storage-and-processing tasks and prove useful in predicting scholastic and intellectual aptitudes; (2) that additional predictive ability of the conventional, storage-and-processing tasks can be traced to specific skills, not general WM; and (3) that, in children too young to rehearse, even simple digit span will yield high correlations with aptitudes. We then discuss theoretical implications, including remaining issues that the present study cannot resolve. The possibility of coherence with other research comes from an adjustable-attention hypothesis in which the focus of attention can zoom in to hold on to a goal and the minimally-required additional data, as in recent studies by Engle and colleagues (e.g., Kane et al., 2001), or zoom out to apprehend (retrieve into the focus of attention) a field of items.
Expectation 1: The Predictive Value of Scope-of-Attention Tasks
The primary expectation of the present study was that scope-of-attention tasks would be predictive; more specifically, (a) that a substantial amount of variance would be shared between storage-and-processing tasks, on one hand, and scope-of-attention tasks, on the other, and (b) that this shared variance would predict intellectual aptitudes. Both of these expectations were fairly well-met and will be considered in turn.
Correlations Between Storage-and-Processing Tasks and Scope-of-Attention Tasks
In Experiment 1, all six correlations between the two storage-and-processing tasks and the three scope-of-attention tasks were significant, even with age group partialled out (Table 2). The highest of these correlations (e.g., between listening span and running span: r = .56; rp = .37) compare favorably with the correlations between listening span and counting span (r = .52; rp = .37). In Experiment 2, in which both types of measures were obtained more uniformly, with incremental set sizes in a span-type procedure (except running span), the results were similar. Raw correlations between the two types of measures (Table 7) were all significant and remained so with age partialled out (Table 8). The highest of these (listening and running spans, r = .58; with age partialled out, counting and running spans correlated higher, rp = .40) again were comparable to the correlations between counting span and listening span (r = .60; rp = .42). There is no evidence in these correlations of a property that consistently distinguishes storage-and-processing measures from scope-of-attention measures of WM.
The belief that both types of measures capture substantial variance that cuts across content domains is reinforced by correlations between visual-array comparisons and measures based on acoustically-presented materials. Of particular interest, the raw correlations between visual arrays and listening span were hefty (in Experiments 1 & 2, r = .50 and r = .51, respectively). These correlations remained significant with age group variance partialled out. The domain-generality of WM has also been emphasized by Kane et al. (2004). However, the present results indicate that this generality extends to at least some comparisons between dual-task and single-task measures of WM.
To capture considerable variance in aptitudes in more mature participants, it appears necessary that the WM task include processing impediments to rehearsal and grouping, presumably because performance is then based on the scope of attention (Cowan, 2001). This interpretation can help to account for a wide range of findings. It can account for the finding that the difficulty of the processing task within storage-and-processing tasks is not particularly critical (Duff & Logie, 2001), given that even a relatively easy task might interfere with rehearsal and grouping processes almost as much as a more difficult task, by tying up articulatory processes and central executive processes needed to initiate rehearsal and grouping (cf. Baddeley, 1986; Naveh-Benjamin & Jonides, 1984). It also can account for the finding that the proportion of the retention interval that is filled with a retrieval task, even an easy one such as reading off numerals on the screen, is critical (Barrouillet et al., 2004). The time spent on retrieval is time unavailable to initiate and execute rehearsal and grouping.
Prediction of Scholastic and Intellectual Aptitudes
Figure 3 – Figure 5 (in Experiment 1) and Figure 7 – Figure 8 (in Experiment 2) summarize well the relation between storage-and-processing tasks and scope-of-attention tasks in terms of their joint and unique prediction of aptitudes. From these figures it is possible to calculate how much of the predictive abilities of the storage-and-processing measures were shared by the scope-of-attention measures. The answer is 62% (for the ACT), 69% (for high school grades), 57% (for the CAT), 73% (for the g factor), and 50% (for the within-age-group portion of g). Looking at the total variance in aptitude predicted by each kind of measure, in Experiment 1, the advantage in prediction of the ACT was for the storage-and-processing measures (.26 of the variance) as opposed to the scope-of-attention measures (.18). However, the advantage in prediction of high school grades, and of the CAT in children, favored the scope-of-attention measures (.18 and .24, respectively) over storage-and-processing measures (.13 and .14, respectively). In Experiment 2, in prediction of g and of the within-age portion of g, there was just a slight advantage for the storage-and-processing measures (.56 and .24, respectively) over scope-of-attention measures (.45 and .18). Clearly, the two types of measures shared considerable variance in the prediction of aptitudes, and were relatively similar in their predictive abilities. That is to be expected if the shared predictive variance reflects the scope of attention.
An exception to the success of the scope-of-attention measures is that visual-array comparisons did not correlate with practical measures of aptitude in adults (ACT scores or high school grades Experiment 1). Given that this was the only measure of WM for visual arrays as opposed to verbal or auditory sequences, it suggests that the practical measures of aptitude were heavily influenced by auditory and verbal skills. For evidence that there is considerable generality of WM and its importance for aptitudes across domains despite the additional influence of domain-specific skills, see Kane et al. (2004).
Expectation 2: Task-Specific Additional Variance
Further analyses served to investigate the nature of the variance, in prediction of aptitudes, that was not shared between the storage-and-processing and the scope-of-attention measures, but was unique to one of them. These analyses were not intended to be complete but to investigate relatively large portions of the variance. It turned out that these portions of the predictive variance primarily reflected skills specific to one task. In Experiment 1, the .10 of the variance in the prediction of ACT scores unique to the storage-and-processing measures was entirely the result of listening-span variance. The .09 of the variance in high school grades percentile unique to the scope-of-attention measures could be attributed to specific skills unique to the two verbal measures (.06) and to visual arrays (.04; the three measures summing to .10 due to rounding error), with none due to variance shared between all three. In Experiment 2, the within-age variance in g scores that was uniquely predicted by storage-and-processing tasks (.09) was largely the result of skills specific to listening span and counting span, though there was a residual component shared between them (.03). It is possible that there is a small contribution of the difficulty of combining two tasks, reflected in that shared component. On balance, though, the results are consistent with the view that variance unique to either storage-and-processing measures or scope-of-attention measures primarily reflects specific skills, whereas the variance shared between them is more indicative of the processes rightly conceived as WM. These shared processes, we contend, could reflect the scope of attention even in the storage-and-processing tasks.
Expectation 3: Measures of Aptitude and the Development of Rehearsal
In children too young to rehearse efficiently (e.g., Naus & Ornstein, 1978; see introduction for other references), even digit span should serve as a good correlate of aptitude. This expectation was met resoundingly. In Experiment 1, digit span was more successful than any other measure in the prediction of within-age variance in CAT scores in third- and fifth-grade children (Figure 5), whereas it was substantially poorer than the other WM measures in the prediction of the ACT and high school grades in adults (Figure 3 & Figure 4). In Experiment 2, digit span was at least as good as the other measures in predicting within-age variance in g for the younger two age groups, whereas it was not predictive at all in the older two age groups. In the older groups, we propose, rehearsal allows items to be grouped and memorized and the ability to use strategic processing in this way is separate from the scope of attention. Therefore, digit spans do not reliably indicate the scope of attention in these older participants.
Summary of Findings and Conclusions
In sum, we have documented that several measures without a separate processing component, but with impediments to rehearsal and grouping, correlate well with storage-and-processing tasks and with measures of aptitudes in children and adults. We also have shown that digit span correlates well with aptitudes in younger children, but not in older children or adults. This we attribute to the absence of efficient rehearsal and grouping in the younger children. A great deal of research described in the introduction reinforces the notion that an important concept underlying these findings is that individual differences in the measured scope of attention are important for individual differences in aptitudes. The scope of attention is a simple, traditional concept related to the notion of WM and we believe that its value as a construct has been reinforced by these findings.
Unresolved Theoretical Issues
Although these findings point toward an agenda for research, there are important points that they leave unresolved. First, Table 1 and Table 6 show considerable variation in the means of different scope-of-attention measures. According to the theoretical assumption that each scope-of-attention task measures the number of chunks held and the assumption that the capacity limit is general across modalities and domains, no difference in means would be expected. Clearly, the differences that exist suggest either that the measures are not completely pure or that individuals can hold a different number of chunks in different processing domains. This is an important issue for future research but we find it more parsimonious to assume for now that the tasks are impure.
In relation to the notion that the essential quality of a successful WM task is that it measures individual differences in the ability to control attention (e.g., Engle et al., 1999; Kane et al., 2001), it is not yet clear what role the scope of attention plays in a unified theory of the deployment of attention in WM tasks. One possibility is that the scope of attention does not meaningfully vary between normal individuals within an age group but that the process of zooming in to hold onto a goal and zooming out to apprehend a maximal field of objects (cf. Chen, 2003; Usher et al., 2001) is a function of the ability to control attention. An alternative possibility is that the basic scope of attention itself, and not only the control of attention, varies among individuals. There is not yet direct support for either theory.
Indirect support for the second theory comes from evidence that the brain representation of attentional control and attentional capacity may differ (see Cowan, 1995). For example, consider the finding of non-frontal loci for capacity limits in a visual-array comparison task (Todd et al., 2004) along with documented individual differences in event-related signals related to capacity in that task (Vogel & Machizawa, 2004), in contrast to pronounced prefrontal loci for the control of attention (e.g., Kane & Engle, 2002). If both attentional control and the scope of attention vary among individuals, then additional questions include (1) how interrelated or independent these faculties are, and (2) to what extent each of them is fundamentally responsible for individual differences in aptitudes.
An examination of task differences seems relevant to these questions. In particular, all but one of our storage-and-processing and scope-of-attention WM measures involved auditory or phonological sequences to be remembered, and resulted in correlations with at least some aptitude measures in both younger and older participants in both experiments. Visual-array comparisons were an exception in that they involved visual arrays to be remembered, and did not correlate with either high school grades or ACT scores in Experiment 1. One might speculate from this finding that a general scope of attention (as one presumably examines in visual-array comparisons) is not an important source of individual differences in WM, which therefore might be attributed instead to the control of attention in the retention of auditory and phonological sequences. However, there are reasons to question this speculation. Table 3 shows that digit span correlated with ACT scores about as well as did counting span, suggesting that ACT scores are highly weighted toward verbal skill as opposed to general WM ability. The table also shows that, corrected for attenuation, all of the correlations between visual arrays and other WM measures in adults fell within the range of .32 to .48. What is more revealing is the success of visual-array comparisons as a correlate of the within-age variance in all of the intelligence measures in Experiment 2, as shown in Table 8. It might be hypothesized, then, that visual-array comparisons do not include many verbal or auditory processing skills but do pick up variance that could be attributed to the general scope of attention.
This suggestion also must be viewed in light of two other recent studies that involve visual arrays and fail to provide support for the importance of the scope of attention. First, Tuholski, Engle, and Baylis (2001) found that individual differences in enumeration of a small number of objects in a simultaneous display (i.e., subitizing) were not related to operation span. However, there is evidence that pattern matching plays an important role in subitizing (e.g., Logan & Zbrodoff, 2003), so that it may not be a direct measure of the scope of attention as Cowan (2001) had supposed (although see Basak & Verhaeghen, 2003). Second, Bleckley, Durso, Crutchfield, Engle, & Khanna (2003) found that high-operation-span individuals were able to allocate attention to a ring in which a target was expected to appear, excluding the area inside of the ring, whereas low-span individuals allocated attention as a solid disk that included the irrelevant area inside of the relevant ring. This study clearly shows that high- and low-span individuals differ in something other than the scope of attention, but it does not indicate that they do not also differ on the scope of attention. The results that were obtained are fully compatible with the possibility that individuals with a large scope of attention are the same ones who have good control of attention; it does not provide evidence for or against that hypothesis because it does not provide a measure of the scope of attention. This remains a key question for further research.
It also will be important to determine how the concept of the scope of attention influences cognitive capabilities. A priori, a key consideration is that the ability to carry out computations and mental manipulations of various sorts could be dependent on the ability to hold in mind the data while it is processed (for relevant work see Logie & Gilhooly, 1998). Although passive storage sometimes may suffice, it also may be necessary to use attention as a holding device (e.g., Anderson & Lebière, 1998; Lovett, Reder, & Lebière, 1999). That concept has played a central role in neoPiagetian theories of cognitive development, in which developmental maturation of thought is attributed to an increase in the available WM space, either because the space increases with maturation (Pascual-Leone, 1970) or because of increased efficiency in the use of the available space (Case et al., 1982). Current developmental work along these lines suggests that there are limitations in the complexity of concepts that can be represented and understood by children of different developmental levels; specifically, in the number of dimensions of a stimulus display that can be taken into consideration at once (e.g., Andrews & Halford, 2002; Halford, Wilson, & Phillips, 1998). Closely-related work also emphasizes that stimulus complexity limits the capabilities of executive control at a particular level of cognitive maturation (cf. Zelazo & Frye, 1998). However, this concept of complexity has not yet been directly related to the scope of attention. For example, it makes sense to speculate that an individual who can attend to four objects at once would be better prepared to understand a two-way interaction of factors than an individual who can attend to only two objects at once, but there appears to be no relevant evidence.
The work on the scope of attention also may be related to the episodic buffer, a component of WM that recently has been proposed to serve the function of storage for combinations of elements that cannot be included in the phonological or visuospatial storage mechanisms (Baddeley, 2000, 2001). It would be helpful in future work to determine what the definitive measurements of the episodic buffer are; whether these measurements can be made relatively free of contamination from domain-specific skills; whether these measurements change with childhood development and, if so, why and how they change; and whether they capture the same common variance in aptitudes that the storage-and-processing measures and the scope-of-attention measures capture. Related to this is the question of whether the observed capacity limit of about 4 chunks on average in adults (Cowan, 2001) is truly the focus of attention, or is a closely-linked, temporary store that is formed with the help of attention but is then independent of attention for its short-term maintenance (cf. Oberauer, 2002). The latter could describe the episodic buffer of Baddeley (2000, 2001).
Finally, in addition to providing options for the cleaner measure of what is important within WM, the present study allows a fresh look at the demands of various WM tasks, including capacity demands that are intentionally tapped and specific skills that are unintentionally tapped by WM measures. Storage-and-processing tasks are complex but dominate the WM literature, we believe, largely because each new study can rely on past findings with those tasks. The disadvantage of that approach is similar to the disadvantage of a snowball that has grown beyond control and continues to plunge downhill. We have, metaphorically, provided a barrier intended to break up that snowball and allow a more carefully-considered reshaping of some of the snow.
Acknowledgments
Some of the data from the conventional WM measures (counting-, listening-, and digit-span tasks) and the scholastic tests in Experiment 1 were reported by Cowan et al. (2003), which focused on response timing. These measures are included here in order to examine their relation to less conventional tasks in the same study that have not been reported previously: the running-span, ignored-speech, and visual-array tasks that we used to assess the capacity of the focus of attention.
This study was conducted with funding from NIH Grant HD-21338 awarded to the first author. We thank Jebby Arnold, Ryan Brunner, Troy Johnson, Matt Moreno, and Jennifer Norris for excellent assistance and we thank Moshe Naveh-Benjamin and Jeff Rouder for helpful comments.
Appendix A
Calculation of Capacity in the Visual Array Task
Performance levels in the visual array task were used to estimate capacity in two ways: in a way described by Pashler (1988) and in another way described briefly by Cowan (2001). Pashler (1988) developed a formula to estimate the number of items in WM based on the hit and false alarm rates. Pashler's formula assumed that, upon examining a briefly presented array of N items, the subject is able to apprehend a certain fixed number of items, k. The apprehension of these items would allow a change to be detected if one of these k items should happen to be the changed item. Thus, with probability k/N, the change is detected. If the change is not detected, the subject guesses “yes, there was a change” with a probability g. Thus, the formula for the hit rate H is
| (1) |
(This formula was misreported by Pashler due to a moved bracket, but the intent was clear from the text.) The false alarm rate FA (incorrectly guessing “yes” when there was no change) was taken as an estimate of g:
| (2) |
Substituting FA for g in Equation 1 and rearranging terms, it can be calculated that
| (3) |
Although this equation gives a rough estimate of memory capacity, it makes the assumption that WM is not used to improve performance in the no-change situation. A more realistic assumption for our task is that there would be no guesswork for k items in the unchanged array. The false alarm rate FA may be influenced by the number of items for which no memory trace is available, N-k. In this case, FA would not be a fair estimate of g.
One consequence of the assumption that FA = g is that FA does not always have the intended effect on the estimate of k. In particular, if H = 1.0 then, according to Equation 3, k = N no matter what the value of FA. A hit rate of 1.0 or nearly so could occur primarily because of a strong bias toward guessing, “yes, there has been a change.” One further suspects that a hit rate of nearly, but not quite, 1.0 would be almost as problematic within this approach.
In the revised formula described by Cowan (2001) it is assumed, as by Pashler, that k items can be apprehended. Equation 1 remains valid. However, it is assumed that if there is no change between the two arrays, and if the cued item happens to be an item that is included within the set k that the subject apprehended, then that knowledge will allow the subject to answer correctly that no change has occurred. If there is no such knowledge (for N-k items), then the subject still will answer correctly with a probability 1-g, where g is again the probability of guessing “yes.” For this revised theory, given that memory is used to respond in the no-change situation, it is useful to define performance in terms of the rate of correct rejections, CR. The assumptions just stated then lead to the following expression:
| (4) |
The memory capacity can be estimated by adding Equations 1 and 4:
| (5) |
Rearranging terms from Equation 5,
| (6) |
In these same terms it can also be shown that, by substituting FA = 1-CR, Equation 3 based on Pashler (1988) can be restated as
| (7) |
Thus, the present estimate of capacity (Equation 6) is equal to Pashler’s estimate (Equation 7) multiplied by the correct rejection rate, CR. The revised method yields capacity estimates that are more constant across set sizes and less variable than those produced by Pashler's estimate. For the present Experiment 1 data set (including all age groups), using the revised method, the mean (and SD) capacity estimates for displays of 4, 6, 8, and 10 items, respectively, were 2.78 (0.95), 2.97 (1.62), 3.30 (2.02), and 3.21 (2.09) items. In contrast, according to Pashler's estimate, the means (and SDs) were 3.23 (0.86), 3.64 (2.19), 4.18 (2.90), and 4.18 (2.71) items. The revised estimation method will be used in data analyses.
Appendix B
Alternative Method of Scoring in Experiment 1
This method of scoring involved the longest list length of at least 50% correct for the digit, counting, and listening span; average number correct for running span and ignored speech; and the largest set size of at least 75% correct for visual-array comparisons. For these variables, respectively, the third-grade means (with SEMs) were 5.08 (0.16), 2.84 (0.18), 1.95 (0.15), 2.03 (0.14), 1.65 (0.16), and 5.51 (0.41). For fifth-grade children, the corresponding means were 5.49 (0.17), 3.54 (0.17), 2.65 (0.18), 2.42 (0.12), 1.60 (0.12), and 6.03 (0.41) and, for adults, they were 7.35 (0.14), 3.97 (0.11), 3.86 (0.12), 3.39 (0.09), 2.31 (0.12), and 8.22 (0.26). These results are in keeping with the expectation that digit span produces higher performance than the other measures. In visual-array comparisons, note that the value of 8.22 in adults is not out of line with expectations; according to the capacity formula explained in Appendix A, 75% correct on a set size of 8 items corresponds to a capacity of 4.0 items.
Contributor Information
Nelson Cowan, University of Missouri – Columbia.
Emily M. Elliott, Louisiana State University
J. Scott Saults, University of Missouri - Columbia.
Candice C. Morey, University of Missouri - Columbia
Sam Mattox, University of Missouri - Columbia.
Anna Hismjatullina, University of Missouri - Columbia.
Andrew R.A. Conway, University of Illinois - Chicago
References
- Anderson JR, Lebière C. Atomic components of thought. Hillsdale, NJ: Erlbaum; 1998. [Google Scholar]
- Andrews G, Halford GS. A cognitive complexity metric applied to cognitive development. Cognitive Psychology. 2002;45:153–219. doi: 10.1016/s0010-0285(02)00002-6. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH, Kirk EP. The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General. 2001;130:224–237. doi: 10.1037//0096-3445.130.2.224. [DOI] [PubMed] [Google Scholar]
- Atkinson RC, Shiffrin RM. Human memory: A proposed system and its control processes. In: Spence KW, Spence JT, editors. The psychology of learning and motivation: Advances in research and theory. Vol. 2. New York: Academic Press; 1968. pp. 89–195. [Google Scholar]
- Baddeley AD. Oxford Psychology Series #11. Oxford: Clarendon Press; 1986. Working memory. [Google Scholar]
- Baddeley A. The episodic buffer: a new component of working memory? Trends in cognitive sciences. 2000;4:417–423. doi: 10.1016/s1364-6613(00)01538-2. [DOI] [PubMed] [Google Scholar]
- Baddeley A. The magic number and the episodic buffer. Behavioral and Brain Sciences. 2001;24:117–118. [Google Scholar]
- Baddeley A, Gathercole S, Papagno C. The phonological loop as a language learning device. Psychological Review. 1998;105:158–173. doi: 10.1037/0033-295x.105.1.158. [DOI] [PubMed] [Google Scholar]
- Baddeley A, Hitch GJ. Working memory. In: Bower G, editor. Recent advances in learning and motivation. Vol. VIII. New York: Academic Press; 1974. [Google Scholar]
- Baddeley AD, Logie RH. Working memory: The multiple-component model. In: Miyake A, Shah P, editors. Models of Working Memory: Mechanisms of active maintenance and executive control. Cambridge, U.K: Cambridge University Press; 1999. pp. 28–61. [Google Scholar]
- Barrouillet P, Bernardin S, Camos V. Time constraints and resource sharing in adults’ working memory spans. Journal of Experimental Psychology: General. 2004;133:83–100. doi: 10.1037/0096-3445.133.1.83. [DOI] [PubMed] [Google Scholar]
- Basak C, Verhaeghen P. Subitizing speed, subitizing range, counting speed, the Stroop effect, and aging: Capacity differences and speed equivalence. Psychology & Aging. 2003;18:240–249. doi: 10.1037/0882-7974.18.2.240. [DOI] [PubMed] [Google Scholar]
- Bayliss DM, Jarrold C, Gunn DM, Baddeley AD. The complexities of complex span: Explaining individual differences in working memory in children and adults. Journal of Experimental Psychology: General. 2003;132:71–92. doi: 10.1037/0096-3445.132.1.71. [DOI] [PubMed] [Google Scholar]
- Bentin S, Hammer R, Cahan S. The effects of aging and first-grade schooling on the development of phonological awareness. Psychological Science. 1991;2:271–274. [Google Scholar]
- Bleckley MK, Durso FT, Crutchfield JM, Engle RW, Khanna MM. Individual differences in working memory capacity predict visual attention allocation. Psychonomic Bulletin & Review. 2003:884–889. doi: 10.3758/bf03196548. [DOI] [PubMed] [Google Scholar]
- Booth JR, MacWhinney B, Harasaki Y. Developmental differences in visual and auditory processing of complex sentences. Child Development. 2000;71:981–1003. doi: 10.1111/1467-8624.00203. [DOI] [PubMed] [Google Scholar]
- Broadbent DE. Perception and communication. New York: Pergamon Press; 1958. [Google Scholar]
- Broadbent DE. The magic number seven after fifteen years. In: Kennedy A, Wilkes A, editors. Studies in long-term memory. Wiley; 1975. pp. 3–18. [Google Scholar]
- Cahan S, Cohen N. Age versus schooling effects on intelligence development. Child Development. 1989;60:1239–1249. [PubMed] [Google Scholar]
- Caplan D, Waters GS. Verbal working memory and sentence comprehension. Behavioral & Brain Sciences. 1999;22:77–126. doi: 10.1017/s0140525x99001788. [DOI] [PubMed] [Google Scholar]
- Case R, Kurland DM, Goldberg J. Operational efficiency and the growth of short-term memory span. Journal of Experimental Child Psychology. 1982;33:386–404. [Google Scholar]
- Chen Z. Attentional focus, processing load, and Stroop interference. Perception & Psychophysics. 2003;65:888–900. doi: 10.3758/bf03194822. [DOI] [PubMed] [Google Scholar]
- Chuah YML, Maybery MT. Verbal and spatial short-term memory: Common sources of developmental change? Journal of Experimental Child Psychology. 1999;73:7–44. doi: 10.1006/jecp.1999.2493. [DOI] [PubMed] [Google Scholar]
- Cocchini G, Logie RH, Della Sala S, MacPherson SE, Baddeley AD. Concurrent performance of two memory tasks: Evidence for domain-specific working memory systems. Memory & Cognition. 2002;30:1086–1095. doi: 10.3758/bf03194326. [DOI] [PubMed] [Google Scholar]
- Cohen RL, Heath M. The development of serial short-term memory and the articulatory loop hypothesis. Intelligence. 1990;14:151–171. [Google Scholar]
- Conway RA, Cowan N, Bunting MF. The cocktail party phenomenon revisited: The importance of working memory capacity. Psychonomic Bulletin & Review. 2001;8:331–335. doi: 10.3758/bf03196169. [DOI] [PubMed] [Google Scholar]
- Conway ARA, Cowan N, Bunting MF, Therriault DJ, Minkoff SRB. A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence. 2002;30:163–183. [Google Scholar]
- Conway ARA, Engle RW. Working memory and retrieval: A resource-dependent inhibition model. Journal of Experimental Psychology: General. 1994;123:354–373. doi: 10.1037//0096-3445.123.4.354. [DOI] [PubMed] [Google Scholar]
- Conway ARA, Bottoms BL, Nysse KL, Haegerich TM, Davis SL. Working memory capacity and distractibility in children. (unpublished) [Google Scholar]
- Copeland DE, Radvansky GA. Phonological similarity in working memory. Memory & Cognition. 2001;29:774–776. doi: 10.3758/bf03200480. [DOI] [PubMed] [Google Scholar]
- Cowan N. Evolving conceptions of memory storage, selective attention, and their mutual constraints within the human information processing system. Psychological Bulletin. 1988;104:163–191. doi: 10.1037/0033-2909.104.2.163. [DOI] [PubMed] [Google Scholar]
- Cowan N. Oxford Psychology Series, No. 26. New York: Oxford University Press; 1995. Attention and memory: An integrated framework. [Google Scholar]
- Cowan N. An embedded-processes model of working memory. In: Miyake A, Shah P, editors. Models of Working Memory: Mechanisms of active maintenance and executive control. Cambridge, U.K: Cambridge University Press; 1999. pp. 62–101. [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24:87–185. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Cowan N, Chen Z, Rouder JN. Constant capacity in an immediate serial-recall task: A logical sequel to Miller (1956) Psychological Science. 2004;15:634–640. doi: 10.1111/j.0956-7976.2004.00732.x. [DOI] [PubMed] [Google Scholar]
- Cowan N, Elliott EM, Saults JS. The search for what is fundamental in the development of working memory. In: Kail R, Reese H, editors. Advances in Child Development and Behavior. Vol. 29. 2002. pp. 1–49. [DOI] [PubMed] [Google Scholar]
- Cowan N, Johnson TD, Saults JS. Capacity limits in list item recognition: Evidence from proactive interference. Memory. doi: 10.1080/09658210344000206. (in press) [DOI] [PubMed] [Google Scholar]
- Cowan N, Kail R. Covert processes and their development in short-term memory. In: Gathercole S, editor. Models of short-term memory. Hove, U.K: Erlbaum Associates, Ltd.; 1996. pp. 29–50. [Google Scholar]
- Cowan N, Keller T, Hulme C, Roodenrys S, McDougall S, Rack J. Verbal memory span in children: Speech timing clues to the mechanisms underlying age and word length effects. Journal of Memory and Language. 1994;33:234–250. [Google Scholar]
- Cowan N, Lichty W, Grove TR. Properties of memory for unattended spoken syllables. Journal of Experimental Psychology: Learning, Memory, & Cognition. 1990;16:258–269. doi: 10.1037//0278-7393.16.2.258. [DOI] [PubMed] [Google Scholar]
- Cowan N, Nugent LD, Elliott EM, Ponomarev I, Saults JS. The role of attention in the development of short-term memory: Age differences in the verbal span of apprehension. Child Development. 1999;70:1082–1097. doi: 10.1111/1467-8624.00080. [DOI] [PubMed] [Google Scholar]
- Cowan N, Nugent LD, Elliott EM, Saults JS. Persistence of memory for ignored lists of digits: Areas of developmental constancy and change. Journal of Experimental Child Psychology. 2000;76:151–172. doi: 10.1006/jecp.1999.2546. [DOI] [PubMed] [Google Scholar]
- Cowan N, Saults JS, Elliott EM, Moreno M. Deconfounding serial recall. Journal of Memory and Language. 2002;46:153–177. [Google Scholar]
- Cowan N, Towse JN, Hamilton Z, Saults JS, Elliott EM, Lacey JF, Moreno MV, Hitch GJ. Children’s working-memory processes: A response-timing analysis. Journal of Experimental Psychology: General. 2003;132:113–132. doi: 10.1037/0096-3445.132.1.113. [DOI] [PubMed] [Google Scholar]
- Cowan N, Wood NL, Wood PK, Keller TA, Nugent LD, Keller CV. Two separate verbal processing rates contributing to short-term memory span. Journal of Experimental Psychology: General. 1998;127:141–160. doi: 10.1037//0096-3445.127.2.141. [DOI] [PubMed] [Google Scholar]
- Daneman M, Carpenter PA. Individual differences in working memory and reading. Journal of Verbal Learning & Verbal Behavior. 1980;19:450–466. [Google Scholar]
- Daneman M, Hannon B. Using working memory theory to investigate the construct validity of multiple-choice reading comprehension tests such as the SAT. Journal of Experimental Psychology: General. 2001;130:208–223. doi: 10.1037//0096-3445.130.2.208. [DOI] [PubMed] [Google Scholar]
- Daneman M, Merikle PM. Working memory and language comprehension: A Meta-Analysis. Psychonomic Bulletin & Review. 1996;3:422–433. doi: 10.3758/BF03214546. [DOI] [PubMed] [Google Scholar]
- Darwin CJ, Turvey MT, Crowder RG. An auditory analogue of the Sperling partial report procedure: Evidence for brief auditory storage. Cognitive Psychology. 1972;3:255–267. [Google Scholar]
- Duff SC, Logie RH. Processing and storage in working memory span. Quarterly Journal of Experimental Psychology. 2001;54(A):31–48. doi: 10.1080/02724980042000011. [DOI] [PubMed] [Google Scholar]
- Dunn Lloyd M, Dunn Leota M. Examiner's manual for the PPVT-III Peabody Picture Vocabulary Test. Third Edition. American Guidance Service; 1997. [Google Scholar]
- Engle RW, Tuholski SW, Laughlin JE, Conway ARA. Working memory, short-term memory, and general fluid intelligence: A latent-variable approach. Journal of Experimental Psychology: General. 1999;128:309–331. doi: 10.1037//0096-3445.128.3.309. [DOI] [PubMed] [Google Scholar]
- Ericsson KA, Kintsch W. Long-term working memory. Psychological Review. 1995;102:211–245. doi: 10.1037/0033-295x.102.2.211. [DOI] [PubMed] [Google Scholar]
- Eriksen CW, St. James JD. Visual attention within and around the field of focal attention: A zoom lens model. Perception & Psychophysics. 1986;40:225–240. doi: 10.3758/bf03211502. [DOI] [PubMed] [Google Scholar]
- Farmer EW, Berman JVF, Fletcher YL. Evidence for a visuo-spatial scratch-pad in working memory. Quarterly Journal of Experimental Psychology. 1986;38A:675–688. [Google Scholar]
- Flavell JH, Beach DH, Chinsky JM. Spontaneous verbal rehearsal in a memory task as a function of age. Child Development. 1966;37:283–299. [PubMed] [Google Scholar]
- Fry AF, Hale S. Processing speed, working memory, and fluid intelligence: Evidence for a developmental cascade. Psychological Science. 1996;7:237–241. [Google Scholar]
- Gathercole SE, Adams A-M, Hitch GJ. Do young children rehearse? An individual-differences analysis. Memory & Cognition. 1994;22:201–207. doi: 10.3758/bf03208891. [DOI] [PubMed] [Google Scholar]
- Gathercole SE, Baddeley AD. Working memory and language. Hove, U.K: Erlbaum; 1993. [Google Scholar]
- Gathercole SE, Pickering SJ. Working memory deficits in children with low achievements in the national curriculum at 7 years of age. British Journal of Educational Psychology. 2000;70:177–194. doi: 10.1348/000709900158047. [DOI] [PubMed] [Google Scholar]
- Glucksberg S, Cowen GN., Jr Memory for nonattended auditory material. Cognitive Psychology. 1970;1:149–156. [Google Scholar]
- Gobet F, Simon HA. Five seconds or sixty? Presentation time in expert memory. Cognitive Science. 2000;24:651–682. [Google Scholar]
- Graesser A, II, Mandler G. Limited processing capacity constrains the storage of unrelated sets of words and retrieval from natural categories. Journal of Experimental Psychology: Human Learning and Memory. 1978;4:86–100. [Google Scholar]
- Gray JR, Chabris CF, Braver TS. Neural mechanisms of general fluid intelligence. Nature Neuroscience. 2003;6:316–322. doi: 10.1038/nn1014. [DOI] [PubMed] [Google Scholar]
- Guttentag RE. The mental effort requirement of cumulative rehearsal: A developmental study. Journal of Experimental Child Psychology. 1984;37:92–106. [Google Scholar]
- Haarman HJ, Davelaar EJ, Usher M. Individual differences in semantic short-term memory capacity and reading comprehension. Journal of Memory and Language. 2003;48:320–345. [Google Scholar]
- Halford GS, Maybery MT, Bain JD. Set-size effects in primary memory: An age-related capacity limitation? Memory & Cognition. 1988;16:480–487. doi: 10.3758/bf03214229. [DOI] [PubMed] [Google Scholar]
- Halford GS, Wilson WH, Phillips S. Processing capacity defined by relational complexity: Implications for comparative, developmental, and cognitive psychology. Behavioral and Brain Sciences. 1998;21:723–802. doi: 10.1017/s0140525x98001769. [DOI] [PubMed] [Google Scholar]
- Hambrick DZ, Engle RW. Effects of domain knowledge, working memory capacity, and age on cognitive performance: An investigation of the knowledge- is-power hypothesis. Cognitive Psychology. 2001;44:339–387. doi: 10.1006/cogp.2001.0769. [DOI] [PubMed] [Google Scholar]
- Hebb DO. Organization of behavior. New York: Wiley; 1949. [Google Scholar]
- Hedden T, Park DC. Contributions of source and inhibitory mechanisms to age-related retroactive interference in verbal working memory. Journal of Experimental Psychology: General. 2003;132:93–112. doi: 10.1037/0096-3445.132.1.93. [DOI] [PubMed] [Google Scholar]
- Henry LA. The effects of word length and phone mic similarity in young children's short-term memory. Quarterly Journal of Experimental Psychology. 1991;43A:35–52. [Google Scholar]
- Hitch GJ, Towse JN, Hutton U. What limits children's working memory span? Theoretical accounts and applications for scholastic development. Journal of Experimental Psychology: General. 2001;130:184–198. doi: 10.1037//0096-3445.130.2.184. [DOI] [PubMed] [Google Scholar]
- Hockey R. Rate of presentation in running memory and direct manipulation of input-processing strategies. Quarterly Journal of Experimental Psychology (A) 1973;25:104–111. [Google Scholar]
- Hulme C, Muir C. Developmental changes in speech rate and memory span: A causal relationship? British Journal of Developmental Psychology. 1985;3:175–181. [Google Scholar]
- Jahnke JC. Delayed recall and the serial-position effect of short-term memory. Journal of Experimental Psychology. 1968;76:618–622. doi: 10.1037/h0025692. [DOI] [PubMed] [Google Scholar]
- James W. The principles of psychology. NY: Henry Holt; 1890. [Google Scholar]
- Jefferies E, Lambon Ralph MA, Baddeley AD. Automatic and controlled processing in sentence recall: The role of long-term and working memory. Journal of Memory and Language. 2004;51:623–643. [Google Scholar]
- Jevons WS. The power of numerical discrimination. Nature. 1871;3:281–282. [Google Scholar]
- Jolicoeur P. Restricted attentional capacity between sensory modalities. Psychonomic Bulletin & Review. 1999;6:87–92. doi: 10.3758/bf03210813. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Treisman A, Gibbs BJ. The reviewing of object files: Object-specific integration of information. Cognitive Psychology. 1992;24:175–219. doi: 10.1016/0010-0285(92)90007-o. [DOI] [PubMed] [Google Scholar]
- Kail R, Hall LK. Sources of developmental change in children's word-problem performance. Journal of Educational Psychology. 1999;91:660–668. [Google Scholar]
- Kail R, Hall LK. Distinguishing short-term memory from working memory. Memory & Cognition. 2001;29:1–9. doi: 10.3758/bf03195735. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Bleckley MK, Conway ARA, Engle RW. A controlled-attention view of working-memory capacity. Journal of Experimental Psychology: General. 2001;130:169–183. doi: 10.1037//0096-3445.130.2.169. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Engle RW. The role of prefrontal cortex in working-memory capacity, executive attention, and general fluid intelligence: An individual-differences perspective. Psychonomic Bulletin & Review. 2002;9:637–671. doi: 10.3758/bf03196323. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Engle RW. Working- memory capacity and the control of attention: The contributions of goal neglect, response competition, and task set to Stroop interference. Journal of Experimental Psychology: General. 2003;132:47–70. doi: 10.1037/0096-3445.132.1.47. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Hambrick DZ, Tuholski SW, Wilhelm O, Payne TW, Engle RW. The generality of working- memory capacity: A latent-variable approach to verbal and visuo-spatial memory span and reasoning. Journal of Experimental Psychology: General. 2004;133:189–217. doi: 10.1037/0096-3445.133.2.189. [DOI] [PubMed] [Google Scholar]
- Keppel G. Design and analysis: A researcher’s handbook. Third edition. Upper Saddle River, NJ: Prentice Hall; 1991. [Google Scholar]
- Kyllonen PC, Christal RE. Reasoning ability is (little more than) working-memory capacity?! Intelligence. 1990;14:389–433. [Google Scholar]
- LaBerge D, Brown V. Theory of attentional operations in shape identifications. Psychological Review. 1989;96:101–124. [Google Scholar]
- Logan GD. An instance theory of attention and memory. Psychological Review. 2002;109:376–400. doi: 10.1037/0033-295x.109.2.376. [DOI] [PubMed] [Google Scholar]
- Logan GD, Zbrodoff NJ. Subitizing and similarity: Toward a pattern-matching theory of enumeration. Psychonomic Bulletin & Review. 2003;10:676–682. doi: 10.3758/bf03196531. [DOI] [PubMed] [Google Scholar]
- Logie RH, Della Sala S, Wynn V. Visual similarity effects in immediate verbal serial recall. Quarterly Journal of Experimental Psychology. 2000;53A:626–646. doi: 10.1080/713755916. [DOI] [PubMed] [Google Scholar]
- Logie RH, Gilhooly KJ. Working memory and thinking. Hove, UK: Psychology Press, Ltd; 1998. [Google Scholar]
- Lovett MC, Reder LM, Lebière C. Modeling working memory in a unified architecture: An ACT-R perspective. In: Miyake A, Shah P, editors. Models of working memory: Mechanisms of active maintenance and executive control. Cambridge: Cambridge University Press; 1999. pp. 135–182. [Google Scholar]
- Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997;390:279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vecera SP. Attention. In: Pashler H, Yantis S, editors. Steven's handbook of experimental psychology. third edition. New York: Wiley; 2002. pp. 235–286. [Google Scholar]
- Lustig C, May CP, Hasher L. Working memory span and the role of proactive interference. Journa l of Experimental Psychology: General. 2001;130:199–207. doi: 10.1037//0096-3445.130.2.199. [DOI] [PubMed] [Google Scholar]
- May CP, Hasher L, Kane MJ. The role of interference in memory span. Memory & Cognition. 1999;27:759–767. doi: 10.3758/bf03198529. [DOI] [PubMed] [Google Scholar]
- Mayes JT. On the nature of echoic persistence: Experiments with running memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1988;14:278–288. [Google Scholar]
- Mewhort DJK, Johns EE. The extralist-feature effect: Evidence against item matching in short-term recognition memory. Journal of Experimental Psychology: General. 2000;129:262–284. doi: 10.1037//0096-3445.129.2.262. [DOI] [PubMed] [Google Scholar]
- Miller GA. The magical number seven, and or minus two: Some limits on our capacity for processing information. Psychological Review. 1956;63:81–97. [PubMed] [Google Scholar]
- Miller GA. George A. Miller. In: Lindzey Gardner, editor. A history of psychology in autobiography. Vol. VIII. Stanford, CA: Stanford University Press; 1989. pp. 391–418. [Google Scholar]
- Miyake A, Friedman NP, Rettinger DA, Shah P, Hegarty M. How are visuospatial working memory, executive functioning, and spatial abilities related? A latent variable analysis. Journal of Experimental Psychology: General. 2001;130:621–640. doi: 10.1037//0096-3445.130.4.621. [DOI] [PubMed] [Google Scholar]
- Miyake A, Shah P, editors. Models of Working Memory: Mechanisms of active maintenance and executive control. Cambridge, U.K: Cambridge University Press; 1999. [Google Scholar]
- Morey CC, Cowan N. When visual and verbal memories compete: Evidence of cross-domain limits in working memory. Psychonomic Bulletin & Review. 2004;11:296–301. doi: 10.3758/bf03196573. [DOI] [PubMed] [Google Scholar]
- Mukunda KV, Hall VC. Does performance on memory for order correlate with performance on standardized measures of ability? A meta-analysis. Intelligence. 1992;16:81–97. [Google Scholar]
- Näätänen R. Attention and brain function. Hillsdale, N.J: Erlbaum; 1992. [Google Scholar]
- Nairne JS. A feature model of immediate memory. Memory & Cognition. 1990;18:251–269. doi: 10.3758/bf03213879. [DOI] [PubMed] [Google Scholar]
- Naveh-Benjamin M, Jonides J. Maintenance rehearsal: A two-component analysis. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10:369–385. [Google Scholar]
- Norman DA. Memory while shadowing. Quarterly Journal of Experimental Psychology. 1969;21:85–93. doi: 10.1080/14640746908400200. [DOI] [PubMed] [Google Scholar]
- Oberauer K. Access to information in working memory: exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:411–421. [PubMed] [Google Scholar]
- Oberauer K, Süβ H-M, Wilhelm O, Wittmann WW. The multiple faces of working memory: Storage, processing, supervision, and coordination. Intelligence. 2002;31:167–193. [Google Scholar]
- Ornstein PA, Naus MJ. Rehearsal processes in children's memory. In: Ornstein PA, editor. Memory development in children. Hillsdale, NJ: Erlbaum; 1978. pp. 69–99. [Google Scholar]
- Pascual- Leone JA. Mathematical model for the transition rule in Piaget's developmental stages. Acta Psychologica. 1970;32:301–345. [Google Scholar]
- Pascual- Leone J. A neoPiagetian view of developmental intelligence. In: Wilhelm O, Engle RW, editors. Understanding and measuring intelligence. London: Sage; (in press) [Google Scholar]
- Pashler H. Familiarity and visual change detection. Perception & Psychophysics. 1988;44:369–378. doi: 10.3758/bf03210419. [DOI] [PubMed] [Google Scholar]
- Pashler H, Johnston JC, Ruthruff E. Attention and performance. Annual Review of Psychology. 2000;52:629–651. doi: 10.1146/annurev.psych.52.1.629. [DOI] [PubMed] [Google Scholar]
- Penney CG. Modality effects and the structure of short-term verbal memory. Memory & Cognition. 1989;17:398–422. doi: 10.3758/bf03202613. [DOI] [PubMed] [Google Scholar]
- Pollack I, Johnson IB, Knaff PR. Running memory span. Journal of Experimental Psychology. 1959;57:137–146. doi: 10.1037/h0046137. [DOI] [PubMed] [Google Scholar]
- Posner MI, Rafal RD, Choate LS, Vaughan J. Inhibition of return: Neural basis and function. Cognitive Neuropsychology. 1985;2:211–228. [Google Scholar]
- Raven J, Raven JC, Court JH. Raven Manual: Section 3. Standard Progressive Matrices Including the Parallel and Plus versions. 2000 Edition. Oxford, U.K: Oxford Psychologists Press Ltd.; 1998. (p. SPM29) [Google Scholar]
- Rosen VM, Engle RW. The role of working memory capacity in retrieval. Journal of Experimental Psychology: General. 1997;126:211–227. doi: 10.1037//0096-3445.126.3.211. [DOI] [PubMed] [Google Scholar]
- Ruchkin DS, Grafman J, Cameron K, Berndt RS. Working memory retention systems: A state of activated long-term memory. Behavioral and Brain Sciences. 2003;26:709–777. doi: 10.1017/s0140525x03000165. [DOI] [PubMed] [Google Scholar]
- Saito S, Miyake A. On the nature of forgetting and the processing-storage relationship in reading span performance. Journal of Memory and Language. 2004;50:425–443. [Google Scholar]
- Salthouse TA. The processing-speed theory of adult age differences in cognition. Psychological Review. 1996;103:403–428. doi: 10.1037/0033-295x.103.3.403. [DOI] [PubMed] [Google Scholar]
- Shiffrin RM. Attention. In: Atkinson RC, Herrnstein RJ, Lindzey G, Luce RD, editors. Stevens' handbook of experimental psychology. Vol. 2. New York: Wiley; 1988. pp. 739–811. [Google Scholar]
- Shiffrin RM. Short-term memory: A brief commentary. Memory & Cognition. 1993;21:193–197. doi: 10.3758/bf03202732. [DOI] [PubMed] [Google Scholar]
- Sirevaag EJ, Kramer AF, Coles MGH, Donchin E. Resource reciprocity: An event-related brain potentials analysis. Acta Psychologica. 1989;70:77–97. doi: 10.1016/0001-6918(89)90061-9. [DOI] [PubMed] [Google Scholar]
- Sokolov EN. Perception and the conditioned reflex. NY: Pergamon Press; 1963. [Google Scholar]
- Sperling G. The information available in brief visual presentations. Psychological Monographs. 1960;74 (Whole No. 498) [Google Scholar]
- Stevanovski B, Jolicoeur P. Poster presented at the annual convention of the Psychonomic Society. British Columbia, Canada: Vancouver; 2003. Nov, Attentional limitations in visual short-term memory. [Google Scholar]
- Swanson HL. Individual and age-related differences in children’s working memory. Memory and Cognition. 1996;24:70–82. doi: 10.3758/bf03197273. [DOI] [PubMed] [Google Scholar]
- Swanson HL. Working memory, intelligence and learning disabilities. In: Wilhelm O, Engle RW, editors. Understanding and measuring intelligence. London: Sage; (in press) [Google Scholar]
- Tehan G, Humphreys MS. Transient phonemic codes and immunity to proactive interference. Memory & Cognition. 1995;23:181–191. doi: 10.3758/bf03197220. [DOI] [PubMed] [Google Scholar]
- Thorndike RL, Hagen EP, Sattler JM. Stanford-Binet Intelligence Scale: Fourth Edition. Itasca, IL: Riverside Publishing Co. 1986:39. [Google Scholar]
- Tipper SP, Driver J, Weaver B. Object-centered inhibition of return of visual attention. Quarterly Journal of Experimental Psychology. 1991;43(A):289–298. doi: 10.1080/14640749108400971. [DOI] [PubMed] [Google Scholar]
- Todd JJ, Marois R. Capacity limit of visual short-term memory in human posterior parietal cortex. Nature. 2004;428:751–754. doi: 10.1038/nature02466. [DOI] [PubMed] [Google Scholar]
- Tombu M, Jolicoeur P. A central capacity sharing model of dual-task performance. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:3–18. doi: 10.1037//0096-1523.29.1.3. [DOI] [PubMed] [Google Scholar]
- Towse JN, Hitch GJ, Hutton U. A reevaluation of working memory capacity in children. Journal of Memory and Language. 1998;39:195–217. [Google Scholar]
- Tuholski SW, Engle RW, Baylis GC. Individual differences in working memory capacity and enumeration. Memory & Cognition. 2001;29:484–492. doi: 10.3758/bf03196399. [DOI] [PubMed] [Google Scholar]
- Turner ML, Engle RW. Is working memory capacity task dependent? Journal of Memory and Language. 1989;28:127–154. [Google Scholar]
- Usher M, Haarmann H, Cohen JD, Horn D. Neural mechanism for the magical number 4: competitive interactions and non- linear oscillations. Behavioral and Brain Sciences. 2001;24:151–152. [Google Scholar]
- Vogel EK, Machizawa MG. Neural activity predicts individual differences in visual working memory capacity. Nature. 2004;428:749–751. doi: 10.1038/nature02447. [DOI] [PubMed] [Google Scholar]
- Wheeler ME, Treisman AM. Binding in short-term visual memory. Journal of Experimental Psychology: General. 2002;131:48–64. doi: 10.1037//0096-3445.131.1.48. [DOI] [PubMed] [Google Scholar]
- Wilding J. Over the top: Are there exceptions to the basic capacity limit? Behavioral and Brain Sciences. 2001;24:152–153. [Google Scholar]
- Zelazo PD, Frye D. Cognitive complexity and control: II. The development of executive function in childhood. Current Directions in Psychological Science. 1998;7:121–126. [Google Scholar]