Abstract
Camouflage is frequently used in the animal kingdom in order to conceal oneself from visual detection or surveillance. Many camouflage techniques are based on masking the familiar contours and texture of the subject by superposition of multiple edges on top of it. This work presents an operator, Darg, for the detection of three-dimensional smooth convex (or, equivalently, concave) objects. It can be used to detect curved objects on a relatively flat background, regardless of image edges, contours and texture. We show that a typical camouflage found in some animal species seems to be a ‘countermeasure’ taken against detection that might be based on our method. Detection by Darg is shown to be very robust, from both theoretical considerations and practical examples of real-life images.
Keywords: camouflage breaking, countershading, Thayer's principle, apatetic coloration, computer vision, convexity
1. Introduction
Visual camouflage is used by animals as well as humans in order to conceal or obscure their visual signature. In the field of computer vision, work related to camouflage can be roughly divided into two: camouflage assessment and design (e.g. Copeland & Trivedi 1997; Gretzmacher et al. 1998), and camouflage breaking. Despite the ongoing research, only little has been said in the computer vision literature on visual camouflage breaking (Marouani et al. 1995; Guilan & Shunqing 1997; McKee et al. 1997; Ternovskiy & Jannson 1997; Huimin et al. 1999).
This paper addresses the issue of camouflage breaking from a computer vision point of view. For this task, we present a mathematical operator which is based on the assumption that the concealed subject is a smooth three-dimensional convex object. Thus, the goal of the operator, called Darg, is to detect three-dimensional convex or concave objects in two-dimensional representations (Tankus et al. 1997; Tankus & Yeshurun 1998). Darg is applied directly to the grey-level function of the image. It responds to smooth three-dimensional convex or concave patches in objects and is not limited by any particular light source or reflectance function. It does not attempt to restore the three-dimensional scene and is a very robust operator that can detect subjects in highly cluttered scenes even under camouflages classified by human viewers as very hard to break. In contrast to the existing attempts to break camouflage (Marouani et al. 1995; Guilan & Shunqing 1997; McKee et al. 1997; Ternovskiy & Jannson 1997; Huimin et al. 1999), our operator is context free; its only a priori assumption about the target is its being three-dimensional and convex (or concave). In order to evaluate the performance of the operator in breaking camouflage, we juxtaposed Darg with a representative edge-based operator. Only a small portion of the comparison can be provided in this paper (but see also Tankus et al. 1999 and Tankus & Yeshurun 2001).
We present biological evidence that detection of the convexity of the grey-level function may be employed by visual systems of predators to break the camouflage. This is based on Thayer's principle of countershading (Thayer 1896a,b, 1909; Poulton & Thayer 1902), which observes that some animals, whose body is three-dimensional convex, use apatetic coloration to prevent their image (under sunlight) from appearing as convex grey level to a viewer (see also Boynton 1952; Portmann 1959; Behrens 1978, 1988). This implies that other animals may break the camouflage based on the convexity of the grey levels they see (or else there was no need in such an apatetic coloration). For flat animals (e.g. moths), countershading is inappropriate, and other camouflage strategies (general resemblance and disruptive patterns) may be used. Hence, other breaking methods should be considered for these cases, but these are outside the scope of this paper.
The biological literature investigates the role of countershading in specific species (as individuals or colonies) and explains their usage for the camouflage (Stauffer et al. 1999; Braude et al. 2001). Several studies quantified the effectiveness of countershading as a camouflage showing that countershaded prey had significantly lower levels of predation than non-countershaded controls, and that countershading was effective against some species of prey birds but not others (Edmunds & Dewhirst 1994; Ruxton et al. 2004; Speed et al. 2005; Rowland et al. 2007). Luminescent countershading is used by fish, squid and shrimp in order to remain cryptic to silhouette scanning predators. The current research deals with the effects of lighting and gravity on countershading reflexes in these species (Ferguson et al. 1994; Latz 1996; Lindsay et al. 1999; Blake & Chan 2007). Recently, a new species of disc-winged bat (Thyroptera devivoi) has been described, and found to have a distinct countershading with dark brown dorsal fur, which is in contrast to pale brown ventral fur with frosted tips (Gregorin et al. 2006).
Section 2 defines the operator Darg for convexity-based detection. Section 2a gives intuition for Darg and is of particular importance for understanding its behaviour. Section 3 uses Darg for camouflage breaking. Section 3a brings the biological evidence for camouflage breaking by the detection of grey-level convexity. Section 3b establishes the connection between the biological evidence and the specific convexity detector Darg. Section 4 delineates a camouflage breaking comparison of an edge-based method with our convexity detector. Concluding remarks are given in §5.
2. Yarg, Darg: operators for the detection of convex domains
We next define an operator for the detection of three-dimensional objects with smooth convex and concave domains.
Let I(x,y) be an input image, and the Cartesian representation of the gradient map of I(x,y). Let us convert ▽I(x,y) into its polar representation (i.e. to the magnitude and direction of the gradient). The gradient argument is defined by
where the two dimensional arctangent is
and the one-dimensional arctan(t) denotes the inverse function of tan(t) so that .
The proposed convexity detection mechanism, which we denote Yarg, is simply the y-derivative of the argument map
To obtain an isotropic operator based on Yarg, we rotate the original image by 0°, 90°, 180° and 270°, operate Yarg and rotate the results back to their original positions. The sum of the four responses is the response of an operator, which we name Darg (the name was chosen to represent Differentiation of the ARGument (i.e. direction) of the gradient).
(a) Intuitive description of the operator
(i) What does Yarg detect?
Yarg detects the zero crossings of the gradient argument. This stems from the last step of the gradient argument calculation: the two-dimensional arctangent function. The arctangent function is discontinuous at the negative part of the x-axis; therefore, its y-derivative approaches infinity there. In other words, Yarg approaches infinity at the negative part of the x-axis of the arctan, when this axis is being crossed. This limit reveals the zero crossings of the gradient argument (see Tankus et al. 1997 for more details).
(ii) Why detect zero crossings of the gradient argument?
Yarg detects zero crossings of the gradient argument of the intensity function I(x,y). The existence of zero crossings of the gradient argument enforces a certain range of values on the gradient argument (trivially, values near zero). Considering the intensity function I(x,y) as a surface in three-dimensional space, the gradient argument ‘represents’ the direction of the normal to the surface. Therefore, a range of values of the gradient argument means a certain range of directions of the normal to the intensity surface. This enforces a certain structure on the intensity surface itself.
In Tankus et al. (1997), we have characterized the structure of the intensity surface as either a paraboloidal structure or any differentiable strongly monotonically increasing transformation of a paraboloidal structure (figure 1). Since paraboloids are arbitrarily curved surfaces, they can be used as a local approximation of three-dimensional convex or concave surfaces (recall that our input is discrete, and the continuous functions are only an approximation!). The detected intensity surface patches are therefore those exhibiting three-dimensional convex or concave structure. The convexity is three-dimensional, because it refers to the convexity of the intensity surface I(x,y), which is a two-dimensional surface in three-dimensional space (figure 1b), not convexity of contours (which is one-dimensional curve in the two-dimensional plane). The three-dimensional convexity of the intensity surface is characteristic of intensity surfaces emanating from smooth three-dimensional convex bodies.
Figure 1.
(a) Paraboloidal grey levels: I(x,y)=x2+5y2. (b) The paraboloidal grey levels of (a), presented as a two-dimensional surface in three-dimensional space. (c) Gradient argument of (a). Discontinuity ray at the negative x-axis. (d) Yarg of (a) (=(∂/∂y) of (c)). (e) Rotation of (a) (90° c.c.w.), calculation of gradient argument and inverse rotation. (f) Rotation of (a) (90° c.c.w.), calculation of Yarg and inverse rotation. (g) Response of Darg, the isotropic operator. (h) Darg2 (the square of (g)).
(iii) How to detect zero crossings of the gradient argument?
Zero crossings of the gradient argument can be detected in various methods. The trivial method would be to compute the gradient argument, and search for a change of sign in it. A more sophisticated method would be to smooth the gradient argument map beforehand (e.g. by a convolution with a Gaussian), in order to make the detection more robust. The suggested operator is even more robust to noise, due to the approach to infinity described above. In practice, this approach to infinity appears as a very strong response whenever zero crossing takes place. The approach is robust to scale changes in the detected subject, various lighting conditions and orientation (pose) of the subject (see Tankus & Yeshurun 2001).
(iv) Summary
We detect the zero crossings of the gradient argument by detecting the infinite response of Yarg at the negative x-axis (of the arctan). These zero crossings occur where the intensity surface is three-dimensional convex or concave. Convex smooth three-dimensional objects usually produce three-dimensional convex intensity surfaces. Thus, detection of the infinite responses of Yarg results in the detection of the domains of the intensity surface, which characterize three-dimensional smooth convex or concave subjects.
3. Camouflage breaking
The robustness of the operator under various conditions (illumination, scale, orientation, texture) has been thoroughly studied in Tankus et al. (1997). As a result, the smoothness condition of the detected three-dimensional convex objects can be relaxed (i.e. the surface may not be smooth and contain edges). In this paper, we further increase the robustness demands from the operator by introducing very strong camouflage.
(a) Biological evidence for camouflage breaking by convexity detection
Next, we exhibit evidence of biological camouflage breaking based on the detection of the convexity of the intensity function. This matches our idea of camouflage breaking by direct convexity estimation (using Darg). We bring further evidence that not only can intensity convexity be used to break the camouflage, but also there are animals whose colouring is suited to prevent this specific kind of camouflage breaking.
It is well known that under directional light, a smooth three-dimensional convex object produces a convex intensity function. The biological meaning is that when the trunk of an animal (the convex subject) is exposed to top lighting (sunlight), a viewer sees shades (convex intensity function). As we shall see, these shades may reveal the animal, especially in the surroundings that break up shadows (e.g. woods) (see Portmann 1959). This supports the Darg approach of camouflage breaking by detecting the convexity of the intensity function.
It has been suggested that the ability to trace an animal based on these shadow effects has led in many animals, during thousands of years of evolution, to coloration of animals that dissolves the shadow effects. This countershading coloration was first observed at the end of the nineteenth century (Thayer 1896a,b, 1909; Poulton & Thayer 1902), and is known as Thayer's principle. Portmann describes Thayer's principle: ‘If we paint a cylinder or sphere in graded tints of gray, the darkest part facing toward the source light, and the lightest away from it, the body's own shade so balances this color scheme that the outlines becomes dissolved. Such graded tints are typical of vertebrates and of many other animals.’ (Portmann 1959). When the animal is under top lighting (usually sunlight), the gradual change in albedo neutralizes the convexity of the intensity function. Had no countershading been used, the intensity function would have been convex, exposing the animal to convexity-based detectors (such as Darg). Figure 2a (upper row) uses ray tracing to demonstrate Thayer's principle of countershading when applied to cylinders. It presents three cylinders: A, a cylinder of constant albedo under top lighting; B, a countershaded cylinder under ambient lighting (produced by mapping a convex texture); and C, a cylinder with the combined effect of countershading albedo and top lighting. While the first two cylinders produce convex grey levels (i.e. a gradual change in intensity), the countershaded one breaks up the shadow effect (equal to convex intensity function); its intensity map is flat.
Figure 2.
(a) Operation of Darg2 on a countershaded cylinder. Column A: a smooth cylinder under top lighting. Column B: the countershaded cylinder under ambient lighting. Column C: the countershaded cylinder under top lighting. The countershaded cylinder can barely be noted under top lighting, due to the camouflage. Under top lighting, the response of Darg is much stronger when the cylinder is smooth than when it is countershaded, showing that this type of camouflage is effective against Darg. (b) Cross sections (parallel to the y-axis, at the centre of the image) of (i) the intensity functions. Thayer's countershading yields a flat intensity function for a cylinder. (ii) Darg2. Dashed curve, column A; dotted curve, column B; solid curve, column A. Under top lighting, the flattened intensity function of the countershaded cylinder has a lower Darg response than that of the convex intensity function of the smooth cylinder.
The existence of countermeasures to convexity-based detectors implies that there might exist predators that can use convexity-based detectors similar to Darg.
(b) Thayer's countershading against Darg-based detection
Let us demonstrate how Thayer's principle of countershading can be used to camouflage against Darg-based detectors. In figure 2a (lower row), we operate Darg on each of the images of the cylinders (of the upper row). As can be seen, the countershaded cylinder under top lighting (figure 2a, column C) attains much lower Darg values than the smooth cylinder under the same lighting (figure 2a, column A). This is because countershading turns the intensity function from convex to (approximately) planar.
To see the transition from a convex intensity function to a planar one due to camouflage, we draw (figure 2b(i)) the vertical cross sections of the intensity functions of the cylinder images. The smooth cylinder under top lighting (column A) produces a convex cross section. The albedo, or the countershaded cylinder under ambient lighting (column B), consists of graded tints of grey (i.e. convex countershading). Finally, the countershaded cylinder under top lighting (column C) produces a flat intensity function, which means a lower probability of detection by Darg.
We verify that the flat intensity function is indeed harder to detect using Darg than the convex intensity function: we show that Darg has a lower response to the countershaded cylinder under top lighting than it has to the smooth cylinder under the same lighting. This is obvious from figure 2b(ii), which shows the vertical cross sections of the responses of Darg to the various images of the cylinder.
This demonstrates that Thayer's principle of countershading is an effective camouflage technique against convexity-based camouflage breakers and, more specifically, against Darg. One can thus speculate that convexity-based camouflage breaking might also exist in nature (or else, the camouflage against it would be unnecessary).
(c) Neuronal implementation of Darg
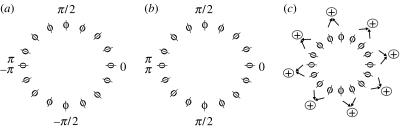
In order for an operator to be employed by a visual system of a predator, its neuronal implementation should be feasible. We next suggest a possible implementation for Darg based on the hypercolumns of the primary visual cortex (V1) (Hubel & Wiesel 1974). A hypercolumn is a set of cortical columns, each of which is responsive to a certain orientation of lines in its visual field. The hypercolumn contains the full range of orientation preferences (0° to 180°) and is organized around pinwheels, with one set of preferences for each ocular dominance column (Levine 1985; Bressloff & Cowan 2003). If, while watching an input image, the output of cells in this hypercolumn is weighted according to the direction they represent (figure 3a), local differentiation of the outputs will implement Yarg, yielding a high response at the negative x-axis as required. While differentiation can be implemented as a difference between neural outputs, summation of outputs is far more common in the cortex. Changing the negative weights in our model to positive only (figure 3b), and employing summation near the negative x-axis instead of difference, will preserve the qualitative results (i.e. high response at the negative x-axis) and provide a more implementable model. Finally, to implement the Darg operator, one has to rotate the Yarg operator to all orientations. The neuronal implementation of this process will result in a local summation of the outputs of the orientation-dependent cells (figure 3c). This simple neuronal implementation lends support to the idea that Darg may serve in a biological vision system.
Figure 3.
Neuronal implementation of Darg. (a) A cortical hypercolumn. Each circle represents a column, with the bar indicating the preferred direction of cells in this column (i.e. the direction of an input line to which they fire most). Local differentiation of the angle function near angles π and −π would yield a high response, similar to Yarg. (b) The same hypercolumn, with only positive weights (i.e. angles). (c) Neural implementation of Darg. Local summation of orientation-dependent cells may detect convexity.
4. Experimental results
In this section, we juxtapose the Darg operator with a typical edge-based operator—the radial symmetry transform (Reisfeld et al. 1995)—as camouflage breakers. This operator seeks generalized symmetry in the edge map of an image around multiple central locations. It evaluates the contribution of edges around the point to symmetry from all sides of the point. The transform has been shown to generalize several edge-based attentional operators (e.g. detectors of high curvature, centre of gravity, corners) (Reisfeld et al. 1995). We compare Darg with edge-based methods, because they have been suggested to be important in biological camouflage breaking, for example, through prey patterning that causes superexcitation of a predator's edge detectors (Osorio & Srinivasan 1991).
(a) Implementation
The first step in the computation of both Darg and radial symmetry is the computation of the image gradient. This has been done by convolution with a Gaussian in one direction and with the derivative of a Gaussian on the other. The radii of the Gaussian were two pixels in each direction.
The radial symmetry operator is scale dependent, while the peaks of Darg are not. Therefore, we have compared Darg with radial symmetry of radii: 10 and 30 pixels (i.e. two radial symmetry transformations performed for each original image). In this paper, only one radius is introduced per original, but similar results were obtained for the other radius as well.
The gradient argument was computed in a neighbourhood of radius 30 pixels. A threshold of 65 per cent of the maximal value was applied to both Darg2 and radial symmetry maps to isolate regions of interest (marked by ‘plus’ signs in figures 4 and 5).
Figure 4.
Persian fallow deer (Dama dama mesopotamica) lying in a stony environment. (a) Detection by radial symmetry. The tones of the deer blend with the background, making the stones more prominent for edge-based methods. (b) Radial symmetry. (c) Detection by Darg. Darg detects the deer, breaking the camouflage. (d) Darg2.
Figure 5.
Nubian ibex (Capra ibex nubiana) in a rocky habitat. (a) Detection by radial symmetry. Edge-based methods fail to detect the ibex due to its apatetic coloration. (b) Radial symmetry. (c) Detection by Darg. By contrast, Darg responds to the convexity of the intensity function of the ibex, thus isolating it from the background. (d) Darg2.
(b) Apatetic coloration in animal
Animals use various types of camouflage to hide themselves, one of which is apatetic coloration (also known as background matching). In this type of camouflage, the colour, brightness or pattern of the animal matches one or several background types. Unlike countershading (also known as ‘self-shadow concealment’ when used for concealment), this type of camouflage does not account for the light falling on the animal. Figure 4 exhibits a natural camouflage of a Persian fallow deer (Dama dama mesopotamica) on stony ground. The camouflaged deer has few edges marked on its back, to prevent detection due to an abrupt disappearance of environmental edges. While these edges activate edge-based detectors to a small degree, they are not strong enough to be isolated from the environment. Indeed, the vast majority of the locations detected by radial symmetry concentrate outside the boundaries of the image of the deer. Thus, the deer would probably not be spotted by an edge-based detector. Darg, however, produces three strong peaks, which match the trunk of the animal, being the most smooth three-dimensional convex region in the image (from a photographic viewpoint).
Figure 5 shows a Nubian ibex (Capra ibex nubiana) on a rocky hillside, under the shades of a tree (not seen in the picture). Owing to the apatetic colouring, the rocky background produces much stronger edges than the ibex, thus attracting edge-based methods. Radial symmetry specifies no single target, and the vast majority of detected locations are away from the subject. This is due to the subject being smooth and surrounded by edges formed by the rocks, which distract the radial symmetry transform from the ibex. Darg detects the ibex as it appears smooth (from the photographic distance), and is three-dimensional and convex. Of note is that the ibex appears much smaller in figure 5 than the Persian fallow deer in figure 4. Darg is able to detect both animals despite the difference in their scale using exactly the same settings (i.e. the same radii and thresholds were employed).
(c) Countershading: an effective camouflage against Darg
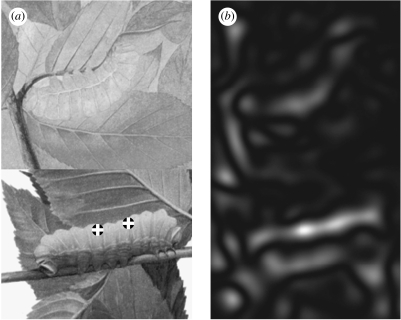
Figure 6 demonstrates the effectiveness of countershading as a camouflage against convexity-based detectors such as Darg. Two images of a caterpillar are juxtaposed: countershaded and non-countershaded. The response of Darg to the countershaded caterpillar image is far lower than that to the non-countershaded one, as shown in figure 6b. This lends further support to the conclusion that detection of the convexity of the grey-level function may be employed by visual systems of predators to break the camouflage.
Figure 6.
Darg fails to detect a countershaded caterpillar. Countershaded and non-countershaded caterpillars are present in the upper and lower parts of the image, respectively. (a) Detection by Darg. Countershading flattens the grey-level function, so Darg misses the countershaded caterpillar. (b) Darg2. Pay attention to the strong stripe for the non-countershaded caterpillar, and the weaker response to the countershaded caterpillar.
5. Conclusions
Thayer's principle states that various animals use countershading as a major basis for camouflage. The observation of such a countermeasure in animals implies that other animals might use convexity detection to break the camouflage (or otherwise, there was no need for the countermeasure). We therefore suggested an operator for convexity detection, Darg, that might be employed in the visual system of predators. Darg is basically intended for the detection of image domains emanating from smooth convex or concave three-dimensional objects, but the smoothness assumption can be relaxed. We speculate that the operator might be employed in biological vision systems because (i) it is highly effective in camouflage breaking, as was demonstrated in a comparison with an edge-based method (radial symmetry), (ii) there appears to be camouflages (i.e. countershading) developed especially against it (e.g. in caterpillars), and (iii) its implementation by a neural network is very simple.
Acknowledgments
A.T. and Y.Y. were supported by the Minerva Minkowski Center for Geometry, and by a grant from the Israel Academy of Science for Geometric Computing.
Footnotes
One contribution of 15 to a Theme Issue ‘Animal camouflage: current issues and new perspectives’.
References
- Behrens R.R. On visual art and camouflage. Leonardo. 1978;11:203–204. doi:10.2307/1574143 [Google Scholar]
- Behrens R.R. The theories of Abbott H. Thayer: father of camouflage. Leonardo. 1988;21:291–296. doi:10.2307/1578658 [Google Scholar]
- Blake R.W., Chan K.H.S. Swimming in the upside down catfish Synodontis nigriventris: it matters which way is up. J. Exp. Biol. 2007;210:2979–2989. doi: 10.1242/jeb.006437. doi:10.1242/jeb.006437 [DOI] [PubMed] [Google Scholar]
- Boynton M.F. Abbott Thayer and natural history. Osiris. 1952;10:542–555. doi:10.1086/368563 [Google Scholar]
- Braude S., Ciszek D., Berg N.E., Shefferly N. The ontogeny and distribution of countershading in colonies of the naked mole-rat (Heterocephalus glaber) J. Zool. 2001;253:351–357. doi:10.1017/S0952836901000322 [Google Scholar]
- Bressloff P.C., Cowan J.D. A spherical model for orientation and spatial-frequency tuning in a cortical hypercolumn. Phil. Trans. R. Soc. Lond. B. 2003;358:1643–1667. doi: 10.1098/rstb.2002.1109. doi:10.1098/rstb.2002.1109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copeland A.C., Trivedi M.M. Models and metrics for signature strength evaluation of camouflaged targets. SPIE. 1997;3070:194–199. doi:10.1117/12.281557 [Google Scholar]
- Edmunds M., Dewhirst R.A. The survival value of countershading with wild birds as predators. Biol. J. Linn. Soc. 1994;51:447–452. doi:10.1111/j.1095-8312.1994.tb00973.x [Google Scholar]
- Ferguson G.P., Messenger J.B., Budelmann B.U. Gravity and light influence the countershading reflexes of the cuttlefish Sepia officinalis. J. Exp. Biol. 1994;191:247–256. doi: 10.1242/jeb.191.1.247. [DOI] [PubMed] [Google Scholar]
- Gregorin R., Goncalves E., Lim B.K., Engstrom M.D. New species of disk-winged bat Thyroptera and range extension for T. discifera. J. Mammal. 2006;87:238–246. doi:10.1644/05-MAMM-A-125R1R1.1 [Google Scholar]
- Gretzmacher F.M., Ruppert G.S., Nyberg S. Camouflage assessment considering human perception data. SPIE. 1998;3375:58–67. doi:10.1117/12.327177 [Google Scholar]
- Guilan S., Shunqing T. Method for spectral pattern recognition of color camouflage. Opt. Eng. 1997;36:1779–1781. doi:10.1117/1.601322 [Google Scholar]
- Hubel D.H., Wiesel T.N. Uniformity of monkey striate cortex: a parallel relationship between field size, scatter, and magnification factor. J. Comp. Neurol. 1974;158:295–306. doi: 10.1002/cne.901580305. doi:10.1002/cne.901580305 [DOI] [PubMed] [Google Scholar]
- Huimin L., Xiuchun W., Shouzhong L., Meide S., Aike G. The possible mechanisms underlying visual anti-camouflage: a model and its real-time simulation. IEEE Trans. Syst. Man Cybern. Part A. 1999;29:314–318. doi:10.1109/3468.759290 [Google Scholar]
- Latz M. I. 1996 Physiological mechanisms in the control of bioluminescent countershading in a midwater shrimp. In Zooplankton: sensory ecology and physiology (eds P. H. Lenz, D. K. Hartline, J. E. MacMillan & D. L. MacMillan), pp. 163–174. Amsterdam, The Netherlands: Gordon & Bread.
- Levine M.D. McGraw-Hill; New York, NY: 1985. Vision in man and machine. [Google Scholar]
- Lindsay S.M., Frank T.M., Kent J., Partridge J.C., Latz M.I. Spectral sensitivity of vision and bioluminescence the midwater shrimp Sergestes similis. Biol. Bull. 1999;197:348–360. doi: 10.2307/1542789. doi:10.2307/1542789 [DOI] [PubMed] [Google Scholar]
- Marouani, S., Huertas, A. & Medioni, G. 1995 Model-based aircraft recognition in perspective aerial imagery. In Proc. Int. Symp. Comp. Vis., USA, pp. 371–376. (doi:10.1109/ISCV.1995.477030)
- McKee S.P., Watamaniuk S.N.J., Harris J.M., Smallman H.S., Taylor D.G. Is stereopsis effective in breaking camouflage? Vis. Res. 1997;37:2047–2055. doi: 10.1016/s0042-6989(96)00330-6. doi:10.1016/S0042-6989(96)00330-6 [DOI] [PubMed] [Google Scholar]
- Osorio D., Srinivasan M.V. Camouflage by edge enhancement in animal coloraion patterns and its implications for visual mechanisms. Proc. R. Soc. B. 1991;244:81–85. doi: 10.1098/rspb.1991.0054. doi:10.1098/rspb.1991.0054 [DOI] [PubMed] [Google Scholar]
- Portmann, A. 1959 Animal camouflage pp. 30–35. Ann Arbor, MI: The University of Michigan Press.
- Poulton E.B., Thayer A.H. The meaning of the white under sides of animals. Nature. 1902;65:596–597. doi:10.1038/065596a0 [Google Scholar]
- Reisfeld D., Wolfson H., Yeshurun Y. Context free attentional operators: the generalized symmetry transform. Int. J. Comp. Vis. 1995;14:119–130. doi:10.1007/BF01418978 [Google Scholar]
- Rowland H.M., Speed M.P., Ruxton G.D., Edmunds M., Stevens M., Harvey I.F. Countershading enhances cryptic protection: an experiment with wild birds and artificial prey. Anim. Behav. 2007;74:1249–1258. doi:10.1016/j.anbehav.2007.01.030 [Google Scholar]
- Ruxton G.D., Speed M.P., Kelly D.J. What, if anything, is the adaptive function of countershading? Anim. Behav. 2004;68:445–451. doi:10.1016/j.anbehav.2003.12.009 [Google Scholar]
- Speed M.P., Kelly D.J., Davidson A.M., Ruxton G.D. Countershading enhances crypsis with some bird species but not others. Behav. Ecol. 2005;16:327–334. doi:10.1093/beheco/arh166 [Google Scholar]
- Stauffer J.R.J., Hale E.A., Seltzer R. Hunting strategies of a lake Malawi cichlid with reverse countershading. Copeia. 1999;4:1108–1111. doi:10.2307/1447987 [Google Scholar]
- Tankus, A. & Yeshurun, Y. 1998 Detection of regions of interest and camouflage breaking by direct convexity estimation. In IEEE Workshop on Visual Surveillance, Bombay, India, pp. 42–48. (doi:10.1109/WVS.1998.646019)
- Tankus A., Yeshurun Y. Convexity-based visual camouflage breaking. Comp. Vis. Im. Underst. 2001;82:208–237. doi:10.1006/cviu.2001.0912 [Google Scholar]
- Tankus A., Yeshurun Y., Intrator N. Face detection by direct convexity estimation. Patt. Recog. Lett. 1997;18:913–922. doi:10.1016/S0167-8655(97)00067-6 [Google Scholar]
- Tankus A., Yeshurun Y., Intrator N. Face detection and camouflage breaking by direct convexity estimation. In: Cantoni V., Gesu V.D., Setti A., Tegolo D., editors. Human and machine perception 2: emergence, attention and creativity. Kluwer; Dordrecht, The Netherlands: 1999. pp. 59–70. [Google Scholar]
- Ternovskiy I.V., Jannson T. Mapping-singularities-based motion estimation. SPIE. 1997;3173:317–321. doi:10.1117/12.294525 [Google Scholar]
- Thayer A.H. Further remarks on the law which underlies protective coloration. Auk. 1896a;13:318–320. [Google Scholar]
- Thayer A.H. The law which underlies protective coloration. Auk. 1896b;13:124–129. [Google Scholar]
- Thayer A.H. An arraignment of the theories of mimicry and warning colours. Popul. Sci. Month. NY. 1909;75:550–570. [Google Scholar]